Introduction

Mountain aquifers represent one of the largest and most valuable sources of water in northern Italy and are necessary to meet the water needs of the population. In recent decades, different hydrological issues, such as the gradual drying up of many springs, low discharge rates during dry months, and formerly perennial springs becoming seasonal, have been reported in studies from throughout the Italian Alps and Apennines (Gattinoni and Francani 2010; Forestieri et al. 2018; Padulano et al. 2019;). In addition, because mountain springs are fed by shallow groundwater resources, they are often highly vulnerable to contamination (Christie et al. 2013; Amanzio et al. 2015a, b).

Optimising the current and future management of mountain groundwater resources and understanding their recharging systems from a hydrogeological perspective is necessary for developing adequate resource management strategies. In addition, groundwater resources must be correctly quantified to provide information for the assessment of the effects of climate change on water resources (Leone et al. 2020). In this context, new automated techniques and tools need to be applied to the estimation of aquifer hydrogeological parameters to fully understand the dynamics of exhausting available groundwater resources.

Over decades, a large number of methodologies have been developed to derive hydrogeological information about mountain spring-recharging systems. Known methods for analysing hydrograph recession periods are based on the Boussinesq and Maillet equations (Boussinesq 1904; Maillet 1905). The Boussinesq equation is used to determine hydrogeological parameters, while the Maillet exponential formula generates good fits for hydrograph recession curves and accurately describes recession phenomena over long periods (Kovács et al. 2005); any deviation from the exponential trend may indicate the presence of hydraulic anisotropies (Amit et al. 2002; Fiorillo 2014). However, in some cases, the exponential method was found to overestimate the period of the influenced regime and underestimate the dynamic volume of the aquifer (Dewandel et al. 2003).

Various recent studies have expanded autocorrelation and cross-correlation methods and applied them to mountain spring-monitoring datasets. In particular, the univariate (autocorrelation) method has been used to analyse the characteristics and structure of individual time series; the bivariate (cross-correlation) method has been used to investigate the connection between input and output time series (Amanzio et al. 2015a, b; Lo Russo et al. 2015). Several applications of auto- and cross-correlation methods examining the relation between rainfall and daily spring discharge are available in the literature on karst spring environments (Angelini 1997; Larocque et al. 1998; Panagopoulos and Lambrakis 2006).

Fiorillo and Doglioni (2010), Lo Russo et al. (2015) and Banzato et al. (2017) have recently demonstrated how aquifer drainage models and mountain spring vulnerability can be evaluated by analysing continuous measurements of discharge (Q), precipitation (P), temperature (T) and electrical conductivity (EC). Different methods have been proposed to assess the vulnerability level of an aquifer (Gogu and Dassargues 2000). As springs are usually located in mountainous zones, the use of parametric methods such as SINTACS (Civita and De Maio 1997), DRASTIC (Aller et al. 1987) or GOD (Foster 1987) is often impossible; these methods are primarily based on hydrostratigraphic information usually unavailable in mountainous areas since core drillings are somewhat rare in such locations. However, spring-monitoring datasets continuously recorded by multiparametric probes are usually available; these data can be used to properly analyse groundwater vulnerability in mountain areas. Utilising monitored parameters, Galleani et al. (2011) proposed a new analytical approach called the Vulnerability Estimator for Spring Protection Areas (VESPA) index, which is a useful methodological tool to assess the behaviour of mountain spring drainage systems through analysing spring responses to different recharge impulses.

Since the analytical examination of individual recession periods can generate inconsistencies related to the complexity of groundwater circulation, analysing the recorded values for mountain springs by comparing different recession periods and applying different methodologies is essential for properly characterising recharge systems (Gizzi et al. 2020; Cerino Abdin et al. 2021). To do this, data processing times must be shortened; researchers and applied hydrogeologists must develop new automated techniques and tools to apply in mountain aquifer analysis.

Different types of automated calculation codes have been developed to properly analyse spring hydrographs. The RC software developed by the Hydro Office of the Department of Hydrogeology of Comenius University in Bratislava (in collaboration with the Department of Hydrogeology and Geothermal Energy of the Geological Survey of Slovak Republic) and the USGS GW Toolbox (Barlow et al. 2017) are two well-known examples. However, RC software and USGS GW Toolbox do not allow the estimation of the vulnerability index using methods such as VESPA, and they do not apply autocorrelation and cross-correlation functions to analyse recorded signals.

This paper introduces SOURCE (a semi-automatic tool for Spring mOnitoring data analysis and aqUifeR CharactErization), a simplified tool that allows automating the hydrogeological characterisation of spring aquifers. Input data (flow rate, temperature, hydraulic conductivity and rainfall) for particular time intervals can be selected and uploaded in a formatted Excel file. The data can be processed, providing graphical outputs and values for the main hydrodynamic parameters of the analysed aquifer.

The main functionalities of this tool are presented through a case study of the Mascognaz mountain springs (Aosta Valley, north-western Italy). The beta version of this software has been developed within the framework of the INTERREG ITALY-SWITZERLAND RESERVAQUA project, which aims to quantify and identify water reserves to protect cross-border mountain water springs like the Mascognaz springs.

In the proposed paper, after an introduction of the geological and hydrogeological features of the selected case study (the Mascognaz springs) and the methodologies available for the spring analysis, a description of the SOURCE Code, the application procedure and the potential resulting from its use are proposed.

Methods

Case study: the Mascognaz springs

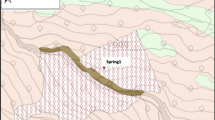
The Mascognaz springs are one of the most important test sites in the Aosta Valley mountain sector. Over the last decade, several projects by researchers from Politecnico di Torino have installed sophisticated instruments, such as multiparametric water probes, different types of sensors and a meteorological station, to continuously monitor the two Mascognaz springs and collect information on their recharging systems. This equipment and the data it has continuously gathered are readily available to researchers, allowing them to accurately study how climate change influences aquifer recharge in a mountain basin not fed by a glacier. In addition, trend data for the Mascognaz springs can be compared to meteorological trend data for the valley.

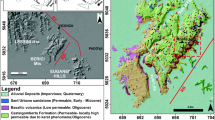
Both Mascognaz springs (Mascognaz 1 and Mascognaz 2) are located inside the Mascognaz Valley (Ayas Municipality, Aosta Valley), at an elevation of 1870 m above sea level (Fig. 1). The Mascognaz Valley has a typical alpine climate, with cold winters and cool summers. Autumn has the highest monthly rainfall, with approximately 110 mm per month. Summer has the lowest monthly rainfall, with a mean of about 30 mm per month.

Fig. 1
figure 1

Mascognaz springs location

Full size image

The Mascognaz springs are located within the Combin geological complex, which belongs to the Piedmont Zone geological sequence and consists of metabasalts and subordinate Mesozoic metasediments representative of the local impermeable bedrock (Dal Piaz 1992). Overlaying Quaternary cover sheets consist mostly of glacial and landslide deposits of variable thickness. A highly permeable shallow aquifer supplies the Mascognaz springs. The Quaternary deposits over the Mascognaz springs catchment area (10 km2) have a maximum estimated depth of 20 m.

Due to the suitable monitoring datasets provided by the multiparameter probes and meteorological station, the Mascognaz springs were selected as an ideal case study for this study (Fig. 2). Extensive information on the local hydrogeological setting and the catchment area, which indicated that the groundwater divide and watershed boundaries coincide, is useful for properly understanding and characterising the results obtained from the water spring analysis.

Fig. 2
figure 2

Overview of the instruments installed in the Mascognaz 1 spring

Full size image

Spring recession curve analysis

Analysing spring discharge hydrographs is one of the most useful tools when studying mountain springs and defining aquifer characteristics, such as the type and quantity of its groundwater reserves.

There have been several studies on recession curve modelling, each establishing different mathematical relationships between the water spring discharge parameter (Q) and recording time (t). Boussinesq (1904) and Maillet (1905) proposed two different analytical formulas that describe the dependence of the flow rate at a specified time (Qt) on the flow rate at the beginning of the recession (Q0). These formulas allow for the calculation of the available water volume at different moments in time. Boussinesq developed an exact analytical solution of the diffusion equation that describes flow through a porous medium by assuming a porous, free, homogeneous and isotropic aquifer limited by an impermeable horizontal layer at the level of the outlet:

$${Q}_{t}= \frac{{Q}_{0}}{{\left(1+\alpha (t-{t}_{0}\right)}^{2}},$$
(1)

where Qt (m3/s) is the flow rate value at t ≠ t0, Q0 is the flow rate at t = t0 and α is the recession coefficient, a constant that depends only on the aquifer hydraulic systems, as shown as follows:

$$\alpha =\frac{\sqrt{{Q}_{0}}-\sqrt{{Q}_{t}} }{ \sqrt{{Q}_{t}}t}.$$
(2)

Maillet showed that the recession of a spring can be represented by an exponential formula, implying a linear relationship between the hydraulic head and flow rate:

$${Q}_{t}= {Q}_{0}{e}^{-\alpha (t-{t}_{0})},$$
(3)

where the recession coefficient α can be determined using the following equation:

$$\alpha = \frac{\mathrm{log}{Q}_{0}-\mathrm{log}{Q}_{t} }{{e}^{(t-{t}_{0})}}.$$
(4)

In both methods, the recession coefficient equations are used to determine important hydrogeological parameters: W0, the groundwater volume stored above spring level at the end of the recharging season (beginning of the recession; Eqs. 5 and 7), and Wd, the groundwater volume stored at the end recession period (Eqs. 6 and 8):

Boussinesq (1904)

$$Wo=\frac{ {Q}_{0}}{\alpha {(1+\alpha t)}^{2}}\times 86400,$$
(5)
$${W}_{d}=\left[\frac{{Q}_{0}}{\alpha }-\frac{{Q}_{0}}{\alpha \left(1+\alpha t\right)}\right]\times 86400.$$
(6)

Maillet (1905)

$${W}_{0}= \frac{{Q}_{0}}{\alpha } \times 86400,$$
(7)
$${W}_{d}= \frac{\left({Q}_{0}-{Q}_{t}\right)}{\alpha } \times 86400.$$
(8)

Autocorrelation and cross-correlation functions

The autocorrelation function (ACF) can evaluate the linear dependency of successive values of a single parameter for a defined time series. The method is univariate and quantifies the memory effect that corresponds to the temporal reciprocal influence on subsequent data of a single dataset.

Statistically, the autocorrelation of a random process describes the correlation between values of the process at different points in time as a function of the two times or the time difference. The autocorrelation for a distance τ corresponds to the covariance of all measurements xt and measurements with a time distance xτ+τ, according to the following equation:

$$\mathrm{cov}\tau = \frac{1}{n - \tau }{\sum }_{t=1+\tau }^{n}{x}_{t}{x}_{t-\tau }-{ X}_{t}{X}_{t-\tau },$$
(9)

where x is a time series, n is the number of measurements in the time series, τ is the time distance between two measurements, and X is the average value of the sample. The autocorrelation coefficient (ACC) ranges from − 1 to 1. An ACC of 1 means that the compared time series are identical.

When using the ACF on hydrological data, a slow decline indicates an aquifer characterised by low draining properties, low permeability or major groundwater storage. Conversely, a fast decline indicates a more rapid flow of water through the aquifer and/or limited storage capacity (Imagawa et al. 2013; Reberski et al. 2013).

Traditionally, the ACC accounts for Q data, and the main hydrogeological assessment is obtained through such an analysis. However, the ACC values can also be applied to T and EC, and these analyses can be used to validate the hydrogeological view of the spring memory effect, which is based on Q data. The time-level stabilities of T, EC and Q can be good markers of a high residence time in an aquifer (Lo Russo et al. 2015).

To identify any instances of pronounced similarity or linear correlation between individual data, two different time series can be compared using the cross-correlation function (CCF; e.g. rainfall versus discharge parameters). Cross-correlation analysis is based on an equation similar to the ACF. If two-time series are marked as variables X and Y, and n is the number of pairs that are compared in one step (k) of the CCF, the cross-correlation coefficient can be obtained by the following (Box and Jenkins 1974):

$${R}_{xy}\left(K\right)=\frac{n\sum XY-\sum \mathrm{X}\sum \mathrm{Y}}{\sqrt{\left[n\sum {X}^{2}-{\left(\sum X\right)}^{2}\right] \times \left[n\sum {Y}^{2}-{\left(\sum Y\right)}^{2}\right]}}.$$
(10)

Values of Rxy(K) can range between − 1 (perfect negative correlation) and + 1 (perfect positive correlation); a value of 0 indicates no correlation.

As with the ACC, the CCF is an established technique that is usually applied on Q and P datasets. However, the CCF can also assess T and EC datasets, and such analyses could be used to validate hydrogeological considerations of the time-lag response and maximum Rxy(K) values.

Furthermore, the pollution vulnerability index of different springs can be estimated using the lag time derived from cross-correlation analysis. This statistical method can be applied to explore the relationship between discharge and rainfall, as well as the relation between electrical conductivity and rainfall.

VESPA index

Properly identifying the vulnerability level of a mountain aquifer and its associated springs is necessary to protect aquifers from potential pollution sources and preserve water quality over time.

Aquifers are fed by rainfall, snowmelt and surface runoff, collectively known as neo-infiltration water. Water from these sources infiltrates the ground and becomes part of the underground flow. Since neo-infiltration water can transport pollutants into groundwater systems, the rate at which neo-infiltration water enters groundwater systems and its velocity towards a spring must be accurately evaluated.

Galleani et al. (2011) combined monitored hydrogeological parameters and proposed a new analytical approach called the Vulnerability Estimator for Spring Protection Areas (VESPA) index, which assesses the behaviour of spring drainage systems through an analysis of their responses to different recharge impulses.

The VESPA index V is defined using the following relationship (Banzato et al. 2017):

$$V= c\left(\rho \right)\beta \gamma ,$$
(11)

where c(ρ) is the correlation factor. This factor is defined by the following equation:

$$c\left(\rho \right)= \left[\mu \left(-\rho \right)+ \alpha \mu \left(\rho \right)\right]\left|\rho \right|.$$
(12)

The ρ value represents the correlation coefficient between Q and EC, calculated using over 1 year of continuous hourly data (Eq. 13):

$$\rho = \frac{{\int }_{0}^{{t}_{0}}\left(Q- {Q}_{m}\right)\left(t\right)\left(\sigma -{\sigma }_{m}\right)\left(t\right)dt}{\sqrt{{\int }_{0}^{{t}_{0}}{\left(Q-{Q}_{m}\right)}^{2}}\left(t\right)dt\sqrt{{\int }_{0}^{{t}_{0}}{\left(\sigma -{\sigma }_{m}\right)}^{2}}\left(t\right)dt},$$
(13)

where σ and σ(m) are the EC value at the time t and EC average calculated over the year, respectively.

The function μ(ρ) is the Heaviside step function (Eq. 14):

$$u\left(\rho \right)=\left\{1 \rho \ge 0 ; 0 \rho <0 \right\},$$
(14)

where α is the scaling coefficient, which can range from 0 and 1 but is generally assumed to be 0.5. The variables β and γ are the temperature and discharge factors, respectively, and are defined by the following equations:

$$\beta ={\left\{\frac{ {T}_{\mathrm{max}}-{T}_{\mathrm{min}}}{1^\circ \mathrm{C}}\right\}}^{2},$$
(15)
$$\gamma = \frac{ {Q}_{\mathrm{max}}-{Q}_{\mathrm{min}}}{{Q}_{\mathrm{med}}},$$
(16)

where Tmax and Tmin are the maximum and minimum temperatures, and Qmax, Qmin and Qmed are the maximum, minimum and average discharge values for the monitoring period.

According to Eq. (11), spring vulnerability is strictly related to a change in one of the parameters (Q, T or EC).

The ρ correlation coefficient defines the aquifer behavioural category and identifies the type of response to the infiltrative input. From the value of the correlation coefficient ρ, drainage systems can be classified into one of three categories: highly effective (replacement effects prevail and − 1 ≤ ρ ≤ − 0.2); moderately effective (piston flow prevails and 0.2 ≤ ρ ≤ 1); and weakly effective (the homogenisation phenomenon prevails and − 0.2 ≤ ρ ≤ 0.2).

Based on the computed values of the VESPA index, a spring’s vulnerability level can be defined according to the classification in Table 1 (Galleani et al. 2011).

Table 1 VESPA index values and their vulnerability levels (Galleani et al. 2011)
Full size table

Code

The dynamics of mountain groundwater resource depletion are heavily influenced by climate conditions. Annual variations in snow and rain precipitation impact the hydrodynamic characteristics and exhaustion modalities of springs. As such, it is necessary to develop new automated techniques that will allow researchers to estimate the main parameters of mountain aquifers quickly and accurately. To propose a new, advanced, semi-automatic tool for spring characterisation that uses available parameter datasets, the above-described methodologies were implemented in Python code.

Python is a high-level programming language with an object-oriented approach created by Guido van Rossum in 1991. The first version of this study’s Python code was developed in 2014 at Politecnico di Torino within the framework of the Interreg Project between Italy and Switzerland. Over time, the tool was updated with the latest libraries of Python. To improve software performance, the number of libraries used has been limited, with preference given to common libraries over more experimental ones. In addition to the standard Python libraries, code for the proposed tool utilised the following:

  • Numpy (https://numpy.org/), the fundamental package for scientific computing;

  • Matplotlib (https://matplotlib.org/), a comprehensive library for creating static, animated and interactive visualisations; and

  • Scipy (https://www.scipy.org/), a Python-based ecosystem of open-source software for mathematics, science and engineering.

The script of the final version of the code was connected to a Postgres Database, where all input information is stored. The final program can accept tabulated data in an Excel spreadsheet and is usable in virtual environments on Linux, Mac and Windows OS.

To be correctly input into SOURCE, Excel files must have a first sheet named “Spring_data” that contains the water spring data and a second sheet named “Meteo_data” that contains the meteorological data. With this format, it is possible to run the script and set parameters using the proposed GUI interface (Fig. 3). The following information is also required (Fig. 4):

  • Filename: the file path of the Excel document, type string;

  • Date start: the start date for the data, type string;

  • Date stop: the stop date for the data, type string;

  • Water spring name: name of the spring to be analysed, type string;

  • Select type of analysis: a choice of ‘All’, ‘Recession curves’, ‘VESPA vulnerability index’, ‘Plot data’ or ‘Auto & Cross-correlation’; and

  • Select method for recession curves: a choice of ‘All’, ‘Maillet’, ‘Boussinesq’ or ‘none’.

Fig. 3
figure 3

GUI of the proposed python tool

Full size image
Fig. 4
figure 4

SOURCE tool flow chart for mountain spring data analysis

Full size image

Results

Input data were recorded by the multiparametric probes installed in the Mascognaz 1 spring. Specific time intervals were selected, and the data for this period were processed using the final version of the described Python code. Graphical outputs and hydrodynamic parameter values for the analysed aquifer were obtained. The monitoring datasets for the years 2012–2013, 2014–2015, 2015–2016 and 2016–2017 were selected for analysis, and the outputs below were obtained and presented:

  • Spring hydrographs

  • Recession curves

  • VESPA index

  • Autocorrelation and cross-correlation coefficients

Spring hydrograph

The first graphical output that can be obtained is hydrographs for the spring under analysis. As reported in Fig. 5, the Mascognaz 1 spring hydrographs were obtained by analysing data from the selected time range and show variation in quick flow at the end of the winter period. Pronounced discharge fluctuations in the fast-flow regime of the Mascognaz spring were due to contributions from snowmelt and the rapid infiltration of precipitation during the autumn season. Abundant rainfall occurred during the autumn period of the selected hydrographic years, causing the formation of a new peak and a decrease in the recorded values of T and EC. Since the depletion curve was in approximately ideal conditions for each year analysed and was only weakly influenced by infiltration events, the recession coefficients calculated using the Boussinesq (1904) and Maillet (1905) methods can be considered reliable.

Fig. 5
figure 5

Mascognaz 1 spring hydrographs (NW Start 2011–04–06, Stop 2012–02–12; NE Start 2014–03–05 Stop 2015–02–24; SW Start 2015–02–25 Stop 2016–03–11; SE Start 2016–03–12 Stop 2017–01–25) for rainfall (violet lines), flow rate (blue lines), electrical conductivity (green lines) temperature (red lines)

Full size image

Recession curve

The second possible graphical output is recession curves (Fig. 6). The aquifer parameters, calculated using the Boussinesq (1904) and Maillet (1905) methods, are reported in Table 3. The flow rate estimates from the Boussinesq method closely matched the actual values reported for the years 2012–2013, 2015–2016 and 2017–2018, but not for the year 2014–2015 (Fig. 6).

Fig. 6
figure 6

Mascognaz 1 recession curves based on the Boussinesq (1904) and Maillet (1905) methods

Full size image

The duration of the exhaustion period, the time between snowmelt peaks and the annual minimum point before the new recharge influence the α value. The minimum estimated value for α was 0.0094 (2011–2012, Boussinesq) and the maximum value was 0.0206 (2014–2015, Boussinesq). The fluctuation depended mainly on the amount of snowfall in winter (Table 2).

Table 2 Aquifer parameters calculated using the Boussinesq (1904) and Maillet (1905) methods
Full size table

The VESPA index

The third type of information that can be obtained from SOURCE is the value of the VESPA index. The vulnerability index of the spring had a medium value for all the years analysed (Table 3). The obtained ρ correlation coefficients for each year in the selected timeframe identify the spring as a weakly effective drainage system where the homogenisation phenomenon prevails.

Table 3 VESPA index values obtained for the Mascognaz 1 spring
Full size table

Autocorrelation and cross-correlation coefficient

The correlogram is a commonly used tool for checking the randomness of a dataset. If they are random, autocorrelations should be near zero for any time-lag separations considered. The correlation analysis was first performed on flow rate (Q) data. The distribution trend of the correlation coefficient reported in Fig. 7 can be identified as a Gaussian curve; the correlation coefficient values are concentrated in a narrow range of values, and so the maximum autocorrelation is obtained with a very short lag time (Fig. 8).

Fig. 7
figure 7

PDF of the estimated correlation coefficients (2011 dataset)

Full size image
Fig. 8
figure 8

Estimated correlation coefficients, considering different time lags (2011 dataset)

Full size image

As reported in Table 4, the correlation values tended to change over time. The Mascognaz spring autocorrelation lag varied within a narrow band across years, implying the series is not significantly correlated with the delayed series; the variations from one instant or period to another are random phenomena (i.e. there is an accidental component, or the stochastic part prevails; Fig. 9).

Table 4 Correlation coefficient values obtained for the Mascognaz spring 1, considering different analysed datasets
Full size table
Fig. 9
figure 9

Autocorrelation diagrams

Full size image

Understanding the correlation period between precipitation and spring response requires eliminating the influence of the winter recharge period until the peak due to melting. Springs do not respond to winter and spring precipitation; the water that arrives at springs depends on the melting process, which is correlated with temperature fluctuations rather than precipitation.

Precipitation values were recorded by the Mascognaz meteorological station. The type of precipitation (solid or liquid) was determined using the Parsivel 2 of the OTT, a modern laser disdrometer. The beginning of the period selected for cross-correlation analysis was considered coincident with the beginning of the exhaustion period; this was also true for the recession analysis using the Maillet and Boussinesq methods.

Comparing data from different years within the selected period revealed that the lag time between rainfall and discharge tended to be short. As shown in Fig. 10, the considered lag time was 3 days; analysing all years within the considered period resulted in a maximum value of 4 days and a minimum value of 1 (Table 5).

Fig. 10
figure 10

Cross-correlation between rainfall and flow rate

Full size image
Table 5 Cross-correlation coefficient values obtained for the Mascognaz 1 spring
Full size table

To verify the validity of the tool proposed and presented in this work, all the results derived from the application were checked with manual calculations carried out using Excel spreadsheets. By comparing the values obtained for the hydrodynamic parameters of the aquifer (α, W0 and Wd) and the estimated indexes of vulnerability (V index) for all studied seasons, the proposed tool was found to be completely reliable.

Conclusions

New automated tools can potentially be applied to estimate aquifer hydrogeological parameters and monitor water spring behaviour. The effects of climate change on mountain springs can be intense, and tools are needed to guarantee a correct understanding of the dynamics of available resource exhaustion.

In this paper, SOURCE is an advanced semi-automatic Python tool that automates the hydrogeological characterisation of spring aquifers. This tool was tested through an analysis of the Mascognaz 1 mountain springs. Graphical outputs, as well as hydrodynamic parameter values (e.g. VESPA index and auto- and cross-correlation coefficients) for an aquifer, can be obtained from SOURCE. These graphs and values are crucial for understanding the hydrogeological processes that characterise spring aquifers and for developing a proper groundwater resource management strategy.

Unlike the software currently available through various university (e.g. RC software and the USGS GW Toolbox), the proposed tool provides an accurate estimation of the vulnerability index and also provides a recorded signal analysis using autocorrelation and cross-correlation statistical functions. A single software package that contains all the main methods of water spring analysis has the potential to significantly reduce analysis times.

The SOURCE intuitive interface allowed not only researchers and hydrogeologists, but also non-expert users to test the software and correctly use its functionalities for mountain spring analysis.

SOURCE is an open-source software tool, and the code is available for free download at https://www.diati.polito.it/ricerca/aree/geologia_applicata_geografia_fisica_e_geomorfologia.

The authors are open to all comments and advice from users that could help to further implement the code and improve the performances.