Introduction

Land degradation (LD) is now a critical environmental issue worldwide, posing a threat to food security and socio-economic development, and the problem will worsen without rapid remedial action (Jiang et al. 2019; Shao et al. 2020). Land degradation, defined as declining capability of the biological or economic productivity of land to provide ecosystem services, is closely connected to food security, human well-being, and development (Wieland et al. 2019; Crossland et al. 2018; Gichenje et al. 2019). It is caused by a combination of direct factors (land use/land cover changes (LULCC), climate change) and indirect factors (population pressure, socioeconomic, and social–ecological conditions, interactions between humans and nature, land management policy), and can vary in severity over time and with location (Riva et al. 2017; Okpara et al. 2018; Gichenje et al. 2019). As a result of human activities, such as land use change, LD can alter hydrological conditions that are crucial for water resources and sustainable river basin management (Aladejana et al. 2018; Jiang et al. 2019; Haghighi et al. 2020). Therefore, efforts to prevent land degradation must be taken by agencies and governments worldwide (Keesstra et al. 2016; Solomun et al. 2018). To assess LD, it is necessary to consider both natural and human-induced factors, e.g., climate change, urbanization, and rising demand for food and fuel (AbdelRahman et al. 2018; Wunder and Bodle 2019; Liniger et al. 2019). Owing to major concerns about conserving land for ecosystem services and the impact of LD on societies and the environment, soil, and water protection has become an important issue for international organizations working with sustainable development (Solomun et al. 2018; Djanibekov et al. 2018). Identifying the causes of LD is essential for its prevention. Globally, LULCC (decline in rangeland area and conversion to farmland with low productivity) is recognized as a major driver of LD (Krkoška Lorencová et al. 2016). An increasing proportion of land with low productivity and a lack of financial resources for land managers in developing countries are exacerbating the risk of LD and lowering resilience within rangeland landscapes (Darabi et al. 2018; Pirnia et al. 2018; Cowie et al. 2019; Pirnia et al. 2019).

To our knowledge, most previous studies assessing LD conditions have used geographic information system (GIS) and remote sensing techniques in spatial assessments of LD risk based on the environmental conditioning variables (Prăvălie et al. 2017; Mariano et al. 2018; Cerretelli et al. 2018). Spatiotemporal patterns of land use change (anthropogenic factors) are the main factor in land degradation (Bewket and Sterk 2005; Gebremicael et al. 2018). Other researchers have reported that direct anthropogenic disturbances in environments and ecosystems can increase land degradation (Ahiablame and Shakya 2016; Davudirad et al. 2016; Aladejana et al. 2018; Schwieger and Mbidzo 2020; Shao et al. 2020). Jaquet et al. (2015) found that outmigration has led to land degradation in a western Nepal watershed. Wei et al. (2020) examined the impacts of land degradation on lake and reservoir water quality and showed a clear trend for degradation, with significant adverse impacts on lake/reservoir water quality. Yatheendradas et al. (2008) concluded that land degradation is the result of dynamic and complex interactions between LULCC, climate variables, and hydrological processes in a watershed.

The environmental problems associated with LD are particularly severe in dryland regions, which poses a threat to many people, especially in developing countries, such as Iran (Khosravi et al. 2015; Darabi et al. 2018). During the recent decades, land degradation in Iran (e.g., soil erosion, such as gully development) has accelerated in Iran due to many factors, such as increasing population, socio-economic development, LULCC (demand for agricultural products has resulted in large-scale conversion of rangeland and forest to cropland), over-exploitation of water resources, geology and topography, and climate change (Pour et al. 2009; Seraji et al. 2009; Davudirad et al. 2016; Bakhshandeh et al. 2019).

Owing to the many interacting factors causing LD, machine learning techniques could be useful in LD risk mapping. In this study, we applied four novel machine learning algorithms, namely Support Vector Machine (SVM), Multivariate Adaptive Regression Splines (MARS), Generalized Linear Model (GLM), and Dragonfly Algorithm (DA). These have already been successfully applied in other fields, e.g., in flood risk and hazard mapping, fog-water harvesting, agricultural drought assessment, and groundwater risk assessment (Zhao et al. 2019; Darabi et al. 2020; Karimidastenaei et al. 2020; Rahmati et al. 2020; Choubin et al. 2020).

Many studies have pointed out that knowledge about LD conditions, especially in arid and semi-arid regions with rapid industrialization and urbanization, is important for achieving the global aim of sustainable development in the long term (Gu et al. 2016; Tripathi et al. 2017; Cao et al. 2018; Van Haren et al. 2019; Giuliani et al. 2020). Hence, the aim of the present study was to develop a new quantitative LD mapping approach using machine learning techniques, benchmark models, and selected socio-environmental conditioning variables. Different types of data and information were used with the four different machine learning algorithms to develop distributed maps of LD risk for the case of a watershed in Iran. The novelty of the study lies in (1) comparing conventional algorithms (support vector machine (SVM), multivariate adaptive regression spline (MARS), and generalized linear model (GLM)) with new algorithms, including DA, for LD mapping applications; (2) developing a spatial framework for LD mapping by applying new conditioning factors; (3) considering and introducing important socio-environmental variables in land degradation; and (4) evaluating socio-environmental conditioning variables for creating useful LD maps based on the model results.

Materials and methods

Study area

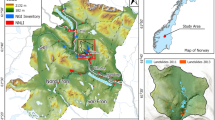
The Pole-Doab watershed (49° 04′ 15′′–49° 52′ 12′′ E, 33° 44′ 42′′–34° 12′ 13′′ N) covers an area of 1740 km2 in central Iran (Fig. 1). It lies within a semi-arid-moderate to semi-arid-cold region based on the Domartan climate index, with maximum temperature in July (42 °C) and minimum temperature in January (− 25.7 °C). The precipitation regime is rainfall–snow, with a mean annual total (1988–2017) of 430 mm, which mainly falls during November, December, and May. The topography of the Pole-Doab watershed consists of rugged and mountainous terrain surrounding plains, with elevation varying from around 1809 m above sea level (asl) on the plains to 3342 m asl in the mountains. This complex topography and steep gradients create a high risk of LD, particularly when combined with human-induced activities such LULCC, urbanization, and industrialization in the watershed (Davudirad et al. 2016). The Pole-Doab watershed is one of the main sub-basins in headwaters of the Qareh–Chai river basin, which has been regulated by the Saveh reservoir since 1995. The Shazand plain, located in the center of the watershed, is used intensively for agriculture (Davudirad et al. 2016). In addition, considerable recent development of infrastructure, industries, and urban areas has altered lifestyles significantly. These rapid LULCC (increasing agriculture, urban expansion, industrial development) have led to extensive land degradation (Davudirad et al. 2016; Sadeghi et al. 2019; Hazbavi et al. 2020).

Fig. 1
figure 1

Location of the study area, the Pole-Doab watershed in central Iran

Full size image

Methods

Field measurements of land degradation

Several processes associated with LD, including water and wind erosion and soil fertility decline, were considered in LD risk mapping. Information on these processes in the Pole-Doab watershed was extracted from an inventory of LD sites in the region, based on field surveys and some documents from the Forest, Range, and Watershed Management Organization of Markazi Province, Iran. The LD sites, which represented different types of degradation (e.g., gully erosion, riverside erosion, surface erosion, and mining), were plotted in an LD inventory map (Fig. 2). In order to prepare an urban LD risk map, degraded areas and non-degraded areas were allocated a value of 1 and 0, respectively. Hence, the historical occurrence of LD was a source of essential information. In field surveys in the Pole-Doab watershed, 200 degraded sites (value = 1) and 200 non-degraded sites (value = 0) were chosen randomly for the analysis. For the purposes of the present study, the LD inventory map was randomly divided into two groups, training/learning and testing/validation datasets. The training dataset, which comprised 70% of the LD (140 points), was used for training/leaning of the machine learning algorithms. The validation dataset, which comprises 30% the LD inventory (60 points), was used for validation of the models. Non-land degraded locations were selected randomly at a distance from the land degraded areas, as suggested in the literature (Hong et al. 2018; Rahmati et al. 2020; Darabi et al. 2020). Therefore, 200 non-land degraded locations were selected, with 70% of the non-land degraded inventory (140 points) used for model training and 30% (60 points) to validate the machine learning algorithms.

Fig. 2
figure 2

Examples of land degradation in the Pole-Doab watershed: Riverside erosion (a, d, n), stream erosion (b, c, k, l), gully erosion (e, m, g), mining (f, i), badlands (j), and pollution and industrial causes (k)

Full size image

Dragonfly algorithm (DA)

A number of intelligence algorithms have been developed in the recent years and these have enormous potential to solve non-linear problems. Intelligence algorithms perform intelligent behavior by collecting conditioning factors to solve problems. The Dragonfly Algorithm (DA), one of the pioneer intelligence algorithms, has been extensively studied in the recent years (Mirjalili 2016; KS and Murugan 2017; Jafari and Chaleshtari 2017; Díaz-Cortés et al. 2018; Shilaja and Arunprasath 2019; Li et al. 2020). It is a meta-heuristic optimization algorithm that was developed using the particle swarm optimization technique with distinctive and extraordinary swarming behavior, which is intended to represent a tiny predator in nature, because of its simple and easy implementation. The main inspiration and purpose of the DA is to hunt and migrate through static and dynamic swarming, based on the unique and superior swarming behavior of dragonflies (KS and Murugan 2017; Shilaja and Arunprasath 2019). The DA starts the optimization procedure by generating a set of random solutions for a specific problem. The situation and stage vectors of dragonflies are booted by random values defined within the minimum and maximum values of the variables (Mirjalili 2016). In this study, the DA was used as an artificial intelligence algorithm to prepare a LD risk map based on socio-environmental conditioning variables. DA can be described by the expression:

$$ X_i = \left( {X_i^1 ,X_i^d \ldots ,X_i^N } \right) $$
(1)

where N is size of the population of dragonflies, i = 1, 2, 3, … N, and \( X_i^d \) refers to the position of the ith dragonfly in dth dimension of the search space.

Based on the initial position values (randomly produced between the lower and upper limits of the variables), the fitness function is evaluated. For updating the velocity and position of the separation, alignment, cohesion, food, and enemy coefficients are calculated as follows:

$$ S_i = - \mathop \sum \limits_{j = 1}^N X - X_i $$
(2)
$$ A_i = \frac{{\sum_{i = 1}^N V_i }}{N} $$
(3)
$$ C_i = \frac{{\sum_{i = 1}^N X_i }}{N} - X $$
(4)
$$ \begin{aligned} F_i = X^+ - X \hfill \\ E_i = X^- - X \hfill \\ \end{aligned} $$
(5)

where Si, Ai, Ci, Fi, and Ei are the weights for separation, alignment, cohesion, food, and enemy factors for each dragonfly; Vi and Xi refer to the velocity and position of the ith individual; X refers to the position of the current individual; and N indicates the number of individuals (KS and Murugan 2017; Rahman and Rashid 2019; Debnath et al. 2020).

Support vector machine (SVM)

Support vector machine (SVM) model is a classification/regression method with a set of linear indicator functions based on non-parametric statistical learning theory (Mountrakis et al. 2011). It specifies the boundary of classes by an optimization algorithm (Sajedi-Hosseini et al. 2018). The particular attributes of decision level in SVM enable high extension capability of the learning machine, which makes it effective in handling non-separable training datasets (Drucker et al. 1996). The main difficulty in SVM modeling lies in selecting important modeling variables. Transformation of data in SVM is carried out using kernel mathematical functions, and there are numerous standard transformations which can be applied for specific purposes. The SVM kernel functions were used here to transform data into two classes, consisting of land-degraded and non-land-degraded locations (0, 1). The ability of SVM is reliant on choosing suitable kernel functions (e.g., sigmoid kernel, radial basis function (RBF), linear kernel, polynomial kernel). According to the previous studies (Tien Bui et al. 2012; Hong et al. 2018; Choubin et al. 2019), RBF provides the most accurate results. It was therefore used in the present study in R software (‘e1071’ package) (Meyer et al. 2019). The RBF kernel is commonly used in SVM classification in various kernelized learning algorithms, and is defined as (Vert et al. 2004; Cura 2020):

$$ K\left( {x_i ,x_j } \right) = { \exp }\left( { - \frac{{\left\| {x_i , - x_j } \right\|^2 }}{2 \times \sigma^2 }} \right) $$
(6)

where \( x_i {\text{and}} x_j \) are two features for the RBF kernel (\( K\left( {x_i ,x_j } \right) \)); \( x_i - x_j \) is Euclidean distance between two features; and \( \sigma \) is a free parameter. The RBF kernel value decreases with distance and ranges between 0 and 1 (x = x’).

Multivariate adaptive regression splines (MARS)

The Multivariate Adaptive Regression Splines (MARS) approach is an adaptive modeling process of machine learning techniques that can be used for identifying relationships between a set of independent variables and response variables with high-dimensional data (Friedman 1991). In MARS, relationship modeling between a response variable and independent conditioning factors is performed with simple functions (Darabi et al. 2020). In essence, it is a local regression procedure that utilizes a collection of foundation functions to model non-linear complex communications. The prognosticator space is splined into multiple overlapping places, called spline functions, which are appropriate. The MARS model uses the following equation (Xu et al. 2010; Zhang and Goh 2016; Serrano et al. 2020):

$$ \hat{f}\left( x \right) = \mathop \sum \limits_{i = 1}^k c_i \times B_i \left( x \right) , $$
(7)

where \( B_i \left( x \right) \) shows the base function of the MARS model (which may be a sole spline function or a yield (interaction) of more than two spline functions); \( c_i \) is a constant coefficient; and i is the size of the base function contained in the model. The base function is defined as:

$$ B_i \left( x \right) = \left\{ {\begin{array}{*{20}c} x & { {\text{if}} \quad x \ge 0} \\ 0 & {\text{otherwise}} \\ \end{array} } \right.. $$
(8)

For each dataset in MARS, m explanatory and n individual variables are defined (n × m basic functions). To obtain and prune the definitive model in MARS, a progressive selection of basic functions is used, which leads to a much overfitted model. In the present study, the method was built in R software, using the “earth” package.

Generalized linear model (GLM)

Generalized linear model (GLM), an extension of the predictable linear regression model, was formulated by Nelder and Wedderburn (1972) to produce answers based on the Maximum Likelihood (ML) of the training variables. The GLM allows the dataset to be overfitted by exponential distribution (normal, binomial, or gamma distribution) (Nordin et al. 2020). Regression methods, including linear, logistic, and log-linear regression, have been widely used to obtain the best model to illustrate the communication between a dependent parameter and multiple independent parameters (Ozdemir and Altural 2013; Karimidastenaei et al. 2020). The GLM approach can be used to process data of different types, such as normal data, Bernoulli success/failure data, Poisson count data, and others (McCullagh and Nelder 1989). A detailed description of the GLM model is presented by Breslow (1996). In a GLM, each dependent variable (here Y) is assumed to be created from a distribution in an exponential family. The mean of the distribution (μ) depends on the independent variables (X). In the GLM, the linear predictor is given as (Nordin et al. 2020):

$$ E\left( Y \right) = \mu \times g^{ - 1} \left( {X\beta } \right), $$
(9)

where E(Y), Xβ, and g are the value of Y, linear predictor, and the link function, respectively. In this context, the variance (V) is typically a function of \( \mu \):

$$ {\text{Var}}\left( Y \right) = V\left( \mu \right) = V\left( {g^{ - 1} \left( {X\beta } \right)} \right). $$
(10)

It is suitable if V tracks from an exponential distribution, but it may simplify matters if V is a function of the predicted value. The β parameter is naturally estimated with the maximum likelihood (ML) and maximum quasi-likelihood (MA-L), or Bayesian models. In this study, the GLM model was run in the R software environment.

Land degradation conditioning factors

There are many different types of LD worldwide and many different conditioning variables can be distinguished depending on the region and causes of LD. Thus in general, there is no universal definition of LD or of conditioning factors (Sklenicka 2016). In the present study, based on land degradation conditions in the Pole-Doab watershed, 18 biophysical conditioning variables were identified and categorized into three groups: topographic variables (elevation, slope, curvature, topographic wetness index, terrain ruggedness index, sky view factor, aspect); human-induced variables (land use, population density, population growth rate, residential and industrial expansion, distance to road); and geo-environmental variables (geology, soil type, precipitation, wind effect, distance to river, C-factor). The scale and resolution of these land degradation conditioning factors, classified into three groups, are presented in Table 1.

Table 1 Land degradation conditioning factors
Full size table

Topographic variables

Digital elevation model (DEM) We used a 30-m resolution digital elevation model (obtained from the Forest, Range, and Watershed Management Organization of Markazi province) which shows the 1809–3342 m asl altitude variation in the watershed (Fig. 3a).

Fig. 3
figure 3

Topographic variables used in land degradation risk mapping: a elevation, b slope aspect, c curvature, d topographic wetness index, e terrain ruggedness index, f sky view factor, and g aspect

Full size image

Slope (%) We derived slope values from the 30-m DEM in ArcGIS 10.5 using the slope tool Spatial Analyst. The slope values in the watershed varied from 0% to more than 67.60% (Fig. 3b).

Curvature Curvature was derived from the DEM and categorized into three classes (Fig. 3c): concave (< − 0.05, upwardly concave surface), flat (− 0.05 to 0.05), and convex (> 0.05, upwardly convex surface) (Karimidastenaei et al. 2020; Tehrany et al. 2019).

Topographic wetness index (TWI) TWI, which indicates soil moisture content and spatial variability in surface saturation, was used to quantify local topographical impacts on LD conditions (Fig. 3d). It was calculated using ArcGIS 10.5 as (Zhu et al. 2018; Karimidastenaei et al. 2020):

$$ {\text{TWI}} = Ln\left( {\frac{{A_{\text{S}} }}{\tan \beta }} \right), $$
(11)

where AS is the local upslope drainage area for a certain grid cell and β is the local slope.

Terrain ruggedness index (TRI) TRI, which was developed by Riley et al. (1999), was calculated using SAGA GIS to explain the elevation difference between a given point (cell) and the mean of surrounding points (eight-cell matrix cells). TRI quantifies surface roughness by including maximum elevation values in the surroundings of a given point or cell in a DEM (Riley et al. 1999; Karimidastenaei et al. 2020). In the Pole-Doab watershed, TRI values varied from highly rugged (46.00) to completely level surface (0 m) (Fig. 3e).

Sky view factor (SVF) SVF is the visible sky in a hemisphere centered visible from the ground at a given point (cell in the raster map). It varies significantly with the topography of different regions and is used to account for obstruction of the overlying sky hemisphere by surrounding land surface as an adjustment factor, with regions with lower visibility related to lower LD risk (Zakšek et al. 2011; Bernard et al. 2018). It is defined as:

$$ {\text{SVF}} = \frac{1}{N} \times \mathop \sum \limits_{i = 1}^N \left[ {\cos \beta \times \cos^2 \beta \varphi_i + \sin \beta \times \cos \left( {\emptyset_i - \alpha } \right) \times \left( {90 - \varphi_i - \sin \varphi_i \times \cos \varphi_i } \right)} \right],$$
(12)

where N is the number of directions, \( \varphi_i \) and \( \emptyset \) are horizon angle and azimuth in the ith direction, respectively, around each cell in an elevation map, and α and β are the slope aspect and angle, respectively. In the present study, SVF was calculated using SAGA GIS, and the value for the study watershed varied from absolutely horizontal surface (= 1) to absolutely obstructed land surface (= 0) (Fig. 3f).

Aspect Aspect affects solar radiation received in a mountainous watershed and plays an important role in environmental changes. As the Pole-Doab watershed is located in the northern hemisphere, its north-facing slopes are less exposed to sunlight than south-facing slopes and thus have a higher moisture content, which influences the temperature gradient and surface warming and leads to differences in erosion pattern (Darabi et al. 2014, 2016) (Fig. 3g).

Human-induced variables

A number of human-induced conditioning factors of LD have been identified in previous studies (Huber-Sannwald et al. 2006; Lu et al. 2007; Prăvălie et al. 2017; Mekonnen et al. 2018; Speranza et al. 2019). We selected five of these for use in LD risk mapping in the study watershed.

Land use Land use information was prepared using Operational Land Imager (OLI) images from the Landsat 8 satellite, with path 165 and row 036-037. The images were acquired from the USGS dataset for 04 June 2019. In a pre-processing step, atmospheric correction of Landsat-OLI data was carried out using QUick Atmospheric Correction (QUAC) in ENVI 5.3 software. Using the maximum likelihood method (supervised classification), a land use map was then prepared in the ENVI 5.3 software (El-Khoury et al. 2015; Pullanikkatil et al. 2016; Torabi Haghighi et al. 2018). In the Pole-Doab watershed, there are seven land use types: Bare land, dry farming, irrigation farming, orchard, rangeland, residential, and rock zones, occupying an area of 59.86 km2 (3.44%), 441.78 km2 (25.39%), 205.49 km2 (11.81%), 666.739 km2 (38.32%), 89.85 km2 (5.16%), and 140.80 km2 (8.09%), respectively (Fig. 4a).

Fig. 4
figure 4

Human-induced variables used in land degradation risk mapping: a land use, b population density in the 10 counties in the Pole-Doab watershed, c population growth rate in the different counties, d residential and industrial area expansion, and e distance to road

Full size image

Population density The impact of population density on LD is unclear, but it is obvious that higher population density (population per unit area) would lead to more land degradation, with more serious degradation in areas with higher population density (Li et al. 2015). In this study, the impact of population density on LD risk in the Pole-Doab watershed was estimated based on human-induced changes in 10 counties within the watershed (Amiriyeh, Astaneh, Pole-Doab, Khorram dasht, Sadeh, Shamsabad, Gharehkahriz, Kazzaz, Koohsar, and Nahremian) (Fig. 4b).

Population growth rate Population growth rate is mainly responsible for population pressure on natural ecosystems (rangeland) and also conversion of rangeland to farmland and residential areas, which can affect flooding, sediment yield, and soil erosion, and consequently land degradation conditions. Population growth leads to increasing demand for housing and other facilities, which in turn leads to increased area of impervious surface as a result of urban development, infrastructure construction, and deforestation (Li et al. 2015). According to census data for Iran, the population growth rate in counties in the Pole-Doab watershed has increased rapidly in the recent decades (1976–2016) (Davudirad et al. 2016). We therefore assessed the impact of population pressure on LD risk in the Pole-Doab watershed by considering the population growth rate in the 10 counties in the watershed (Fig. 4c).

Residential and industrial area expansion Rapid urbanization and industrialization and conversion of neutral land to impervious land can affect LD conditions by increasing surface runoff and flooding conditions (Li et al. 2015). In this study, we used residential and industrial area expansion in the Pole-Doab watershed 1973–2016 (produced using TerrSet software) as a human-induced variable in LD risk mapping (Fig. 4d).

Distance to road Distance to road as impervious surface, and also as an indicator of development and infrastructure construction, is an important factor in LD risk mapping (Li et al. 2015). Here it was derived using the distance module in GIS 10.5 for each raster cell (Fig. 4e).

Geo-environmental variables

Geology The geology of a watershed can affect soil erosion and land degradation in two ways: (1) As an intrinsic effect related to the geological formation; and (2) as an effect of external and indirect factors such as climate (e.g., weathering). In this study, the geology of the watershed was divided into four formations: Quaternary, limestone, granite-granodiorite, and sandstone-shale (Fig. 5a).

Fig. 5
figure 5

Geo-environmental variables used in land degradation risk mapping: a geology, b soil type, c annual precipitation, d wind effect, e distance to river, and f C-factor

Full size image

Soil type Land type is typically defined by soil type and land form, which can affect soil erosion and land degradation (Nunes et al. 2011; Qiang et al. 2016). In this study, watershed soil types were divided into seven categories: alluvial fans, colluvium fans, hills, lowland, mountains, piedmont plains, and plateau and upper terraces (Fig. 5b).

Precipitation Annual precipitation data for 13 stations run by the Iranian Meteorological Organization (IRIMO) were used to produce a precipitation map for the Pole-Doab watershed. Analysis of the interpolation accuracy was carried out based on root mean square error (RMSE) in ArcGIS GIS 10.5, so the simple Kriging interpolation method was selected as it has the lowest RMSE (0.96) (Darabi et al. 2016). Mean annual precipitation varied from 461 mm in the west and southwest to 298 mm in the east and northeast of the study area (Fig. 5c).

Wind effect Land degradation by wind is one of the most serious environmental problems related to soil erosion, threatening environmental quality, ecosystem services, and land productivity (Chi et al. 2019). Wind effect assessments are relatively rare in the literature, due to poor data availability. Because the amount of evapotranspiration is greatly affected by high winds and high temperatures in summer (Fenta et al. 2020), wind effect was included as a biophysical variable for LD risk mapping in the present study (Fig. 5d). Information on wind effect in the study watershed was obtained based on the DEM in the SAGA GIS software.

Distance to river According to data on riverside and riverbed erosion obtained from local authorities and in field surveys, distance to river plays an important role in LD in the Pole-Doab watershed. The Euclidean distance to the river was calculated using the distance module in GIS 10.5 (Fig. 5e).

C-factor C-factor, a surface cover and roughness factor considered to show the effect of cropping and management practices on erosion conditions, is a critical indicator characterizing LD. C-factor mapping can provide suitable information for improving spatial and temporal modeling of land degradation and soil erosion. It is one of the most sensitive spatiotemporal factors, as it follows plant growth dynamics (Berendse et al. 2015; Vaverková et al. 2019). In this study, C-factor used to consider the impact of soil and vegetation in LD risk mapping. It was derived using Landsat OLI (165-036 and 165-037) images for 04 June 2019 (Fig. 5f), which were obtained from the USGS website (Almagro et al. 2019). In a first step, Normalized Difference Vegetation Index (NDVI), which has a direct linear correlation to C-factor, was computed using Landsat data:

$$ {\text{NDVI}}_{\text{OLI}} = \frac{{\rho {\text{band}}5_{OLI} - \rho {\text{band}}4_{\text{OLI}} }}{{\rho {\text{band}}5_{OLI} + \rho {\text{band}}4_{\text{OLI}} }} . $$
(13)

C-factor was then calculated as:

$$ C = \left( {\left( {1 - {\text{NDVI}}} \right)/2} \right), $$
(14)

where ρ is the reflectance value of spectral bands for Landsat-OLI image: band 4OLI: Red, band 5OLI: NIR. C-factor varies in value from 0 to +1, representing good to bad conditions for soil erosion.

Calculation of land degradation index

Machine learning methods automate analytical model building, based on the idea that the model can learn from data, identify patterns, and make decisions (here prediction of LD index) with minimal human intervention. In this study, calculations of LD index were carried out using GIS layers (with ascii format), which were categorized into three groups (topographic, human-induced, and geo-environmental variables), prepared in the same way in Arc map (with the same resolution, scale, and coordinate system), and considered as independent variables. Information related to LD (as point data) was considered as other input for the machine learning algorithms. Hence, after learning based on the above inputs, the models used in this study proceeded to predict the LD index as a final map with ascii format. All 18 conditioning variables, together with the 200 points selected as LD locations, were used in the R program to produce LD risk maps by the machine learning models. Using the natural break method (Tehrany et al. 2015; Choubin et al. 2019; Darabi et al. 2020) in ArcGIS 10.5, the LD risk was then classified into five classes: very low, low, moderate, high, and very high.

Model assessment

All machine learning models used in this study were assessed using the receiver-operator characteristic-area under the curve (ROC–AUC), which has been widely used for evaluating model performance (Frattini et al. 2010; Choubin et al. 2018; Darabi et al. 2020). The ROC–AUC value ranges from 0 to 1, with a value of 0.5–0.6, 0.6–0.7, 0.7–0.8, 0.8–0.9, and 0.9–1 indicating weak, average, good, very good, and excellent model performance, respectively (Choubin et al. 2018). The Kappa index, which employs model classification probabilities based on the null hypothesis to calculate the agreement by chance, was also used in model assessment. According to Monserud and Leemans (1992), the Kappa index is divided into five classes, with values of k < 0.4, 0.4 < k < 0.55, 0.55 < k < 0.85, 0.85 < k < 0.99, and 0.99 < k < 1.00 indicating poor, moderate, good, excellent, and perfect model performance, respectively. All model assessments were carried out in R software.

The importance of the 18 selected conditioning variables was evaluated for models showing high accuracy and precision. Visual assessment of model performance was carried out using a Taylor diagram (Taylor 2001) and three statistics: correlation coefficient, normalized standard deviation, and root mean square error (RMSE). In the Taylor diagram, models with high accuracy are close to the observations (Choubin et al. 2018).

Importance of variables

The importance of the conditioning variables was calculated from the results obtained through applying the selected model based on the ROC–AUC and Kappa index. The importance of independent variables (here topographic, human-induced, and geo-environmental variables) was calculated based on the frequency of dependent variables (here degraded locations) and spatial variation in the independent variables, using the instructions of the selected model. In the selected model, importance of variables was considered as the reduction in node impurity weighted by the probability of reaching that node. The probability of the node was considered as the number of points influencing the node divided by the sum for the points (the more important the variable, the higher the value).

Results

Spatial distribution of land degradation

The spatial distribution maps of land degradation, obtained using the SVM, GLM, MARS, and DA algorithms, indicated that most parts of the Pole-Doab watershed were affected by LD, with high and low degradation conditions (Fig. 6a–d). All models showed the same overall spatial pattern, with high degradation in the south and southwest of the watershed. However, the spatial resolution at local scale derived from the different models varied. Regions with the highest (1.00) and lowest (0.00) risk of land degradation were successfully recognized by the DA, SVM, GLM, and MARS algorithms. In the spatial distribution of LD, the risk value ranged from 0.00 to 1.00. Using the natural break method in ArcGIS 10.5, the LD risk was divided into five classes: very low, low, moderate, high, and very high, the spatial distribution zones for which are presented in Fig. 6e–h. The LD risk maps obtained with all four algorithms indicated that the south of the Pole-Doab watershed is most exposed to degradation conditions. Based on degraded area obtained from SVM, GLM, MARS, and DA (Fig. 6e–h), the land area with a very high degradation risk represented 19.16%, 19.29%, 21.76%, and 22.40%, respectively, of the total area of the Pole-Doab watershed (Table 2). The LD risk maps also showed that most of the watershed was affected by some type of degradation, with more than 40% of the area falling into high and very high zones according to all algorithms. It is worth mentioning that some of the predictive variables used in the analysis may vary over time, leading to uncertainty in the results. Precipitation is one such variable, but since long-term precipitation data from 13 meteorological stations were used in the present analysis, the associated uncertainty was considered to be minimized.

Fig. 6
figure 6

Land degradation maps based on the benchmark algorithms: a SVM, b GLM, c MARS, and d DA, and e–h the respective risk zone classification

Full size image
Table 2 Area of the study watershed falling within different land degradation zones according to the SVM, GLM, MARS, and DA models
Full size table

Model performance

Validation is an important phase in evaluation of model accuracy. For quantitative comparison of the models, ROC–AUC and Kappa index were used. The maps obtained for LD risk were compared with the validation data, to assess the performance of each model. ROC–AUC determines the probability of correctly and incorrectly labeled pixels, with values close to 1 indicating a perfect model with maximum precision and values ≤ 0.5 indicating that the model is not suitable for the analysis. The accuracy and efficiency of the SVM, GLM, MARS, and DA models, based on ROC–AUC and Kappa index, are shown in Table 3. The highest ROC–AUC values were obtained for DA (0.880), followed by SVM (0.864), GLM (0.829), and MARS (0.825) (Table 3). The ROC–AUC curves of the SVM, GLM, MARS, and DA models for the validation dataset are presented in Fig. 7. In terms of Kappa index, SVM, GLM, MARS, and DA achieved a value of 0.886, 0.823, 0.812, and 0.892 rates, respectively, indicating excellent performance in all cases (Fig. 7). The results obtained in this study cannot be directly compared with those reported in previous studies, because the models we used have not been employed previously in LD risk mapping. An advantage of the machine learning algorithms used in this study was that interactions between natural hazards and biophysical factors causing LD were uncovered.

Table 3 Performance of the SVM, GLM, MARS, and DA models, based on ROC–AUC and Kappa index (higher values indicate greater model accuracy)
Full size table
Fig. 7
figure 7

Receiver-operator characteristic-area under the curve (ROC–AUC) for the SVM, GLM, MARS, and DA models, and the validation dataset

Full size image

The Taylor diagram of model performance in producing land degradation risk maps indicated that the DA algorithm had a lower RMSE and higher correlation than the other algorithms (Fig. 8), which were approximately equal in this regard. Comparing the standard deviation of the models revealed that the DA and SVM algorithms were closer to observed values and more in agreement than the others. The standard deviation of the algorithms ranked the models in the order: DA, SVM, GLM, and then MARS. This indicates that DA had the highest accuracy and the other models (SVM, GLM, MARS) could not satisfactorily predict the LD risk map.

Fig. 8
figure 8

Taylor diagram comparing the performance of the SVM, GLM, MARS, and DA models in land degradation risk mapping

Full size image

Rank variables

According to the aims of the study, the variables were classified into two types, (1) independent variables and (2) dependent variables. The importance of the different variables in LD risk mapping was assessed based on the results obtained with the DA model (selected model), due to its high efficiency and precision. Among the topographic variables, slope (first rank) had the highest importance value (5.842), followed by elevation (3.960), aspect (1.363), terrain ruggedness index (1.294), topographic wetness index (1.215), sky view factor (1.095), and curvature (0.963) (Table 4). Among the human-induced variables, land use (second rank) was the most important (2.974), followed by residential and industrial area expansion (1.539), population density (1.287), population growth rate (1.254), and distance to road (1.222) (Table 3). Among the geo-environmental variables, geology (third rank) had the highest importance value (2.168), followed by C-factor (2.020), precipitation (1.998), land type (1.723), distance to river (1.341), and wind effect (1.086) (Table 4).

Table 4 Relative importance of different topographic, human-induced, and geo-environmental variables as land degradation conditioning factors
Full size table

Discussion

Assessment of land degradation status is important for watershed planning and management to protect water quality in lakes and reservoirs. Since LD has accelerated during recent years, precise spatial LD risk mapping is needed to assist authorities in making reliable and reasonable decisions on rehabilitation or restoration of ecosystems and in prioritizing investments. Land degradation problems can arise at three levels: (1) local (field) level, which leads to decreased land productivity and impacts on local businesses, (2) regional level, which causes many problems for downstream infrastructure regarding decreasing water quality, changes in the hydrological process and flood damage, and also reduced dam capacity by sedimentation, and (3) global level, increasing emissions of greenhouse gases and global warming in the long term (Kust et al. 2018; Chasek et al. 2019; Smetanova et al. 2019). The importance and causes of LD problems vary at each level and differ from case to case. Each individual case at each level involves different types of land use and land cover (e.g., riversides, hills, agricultural areas, steep slopes, deforested areas). Therefore, planners and managers must know the capability and potential of different land uses in interacting with different conditioning factors (such as social and environmental variables) in order to prevent or reduce LD. In previous studies, LD assessments have been performed using different methodologies and scales of analysis. However, machine learning algorithms have not been used previously for this purpose, although they are widely used in assessments of other environmental issues, e.g., flood risk, groundwater pollution, and landslide risk (Tehrany et al. 2015; Termeh et al. 2018; Choubin et al. 2018; Moghaddam et al. 2020; Pourghasemi et al. 2020; Bozdağ et al. 2020). In the present study, we employed four different machine learning algorithms (SVM, MARS, GLM, and DA, advantages and disadvantages of models has been provided in appendix) to generate high quality and accurate LD risk maps for the Pole-Doab watershed in central Iran. Assessments of model performance indicated that DA had the highest accuracy and efficiency, with the greatest learning and prediction power in LD risk mapping. The analysis also clearly revealed the role of different conditioning factors in the LD process. Overall, the models and selected biophysical variables applied in this study provided excellent results and can be recommended for studies in other regions with different conditions and types of land degradation. Land degradation is caused by multiple forces (Cowie et al. 2019), but in this study the main conditioning variables in different categories were found to be slope (topographic variable), land use (human-induced variable), and geology (geo-environmental variable).

Conclusions

Land degradation is an important environmental issue that threatens the sustainability of economic growth and the welfare of the many people, especially rural societies depending on agriculture for their livelihoods. It can also have significant harmful effects globally, e.g., on biodiversity, climate change, and water resources. Good knowledge about the rate of LD would thus be helpful at local, national, and global scale. To this end, we applied machine learning algorithms in LD risk mapping for the Pole-Doab watershed, Iran. We charted the existing conditions for LD and assessed the future trajectory of LD status, as decision support for soil and water resources conservation. Using a novel framework employing socio-environmental conditioning variables in LD risk mapping, based on field measurements and documents describing LD conditions, we showed that serious LD is occurring in the study area. We also showed that this increase in LD is the result of unplanned urbanization with population explosion, development of multiple industries, and agricultural expansion involving conversion of natural rangeland to agricultural land, leading to more frequent flood events. These results demonstrate the significant role of unsustainable development in LD in the study area. Additional long-term monitoring, considering climatic change and anthropogenic disturbances, is recommended to provide accurate decision support for future LD prevention efforts.