Advertisement

Modelling the Mont Terri HE-D experiment for the Thermal–Hydraulic–Mechanical response of a bedded argillaceous formation to heating

  • B. Garitte
  • T. S. NguyenEmail author
  • J. D. Barnichon
  • B. J. Graupner
  • C. Lee
  • K. Maekawa
  • C. Manepally
  • G. Ofoegbu
  • B. Dasgupta
  • R. Fedors
  • P. Z. PanEmail author
  • X. T. Feng
  • J. Rutqvist
  • F. Chen
  • Jens Birkholzer
  • Q. Wang
  • O. Kolditz
  • H. Shao
Open Access
Thematic Issue
First Online:
Part of the following topical collections:
  1. DECOVALEX 2015

Abstract

Coupled thermal–hydrological–mechanical (THM) processes in the near field of deep geological repositories can influence several safety features of the engineered and geological barriers. Among those features are: the possibility of damage in the host rock, the time for re-saturation of the bentonite, and the perturbations in the hydraulic regime in both the rock and engineered seals. Within the international cooperative code-validation project DECOVALEX-2015, eight research teams developed models to simulate an in situ heater experiment, called HE-D, in Opalinus Clay at the Mont Terri Underground Research Laboratory in Switzerland. The models were developed from the theory of poroelasticity in order to simulate the coupled THM processes that prevailed during the experiment and thereby to characterize the in situ THM properties of Opalinus Clay. The modelling results for the evolution of temperature, pore water pressure, and deformation at different points are consistent among the research teams and compare favourably with the experimental data in terms of trends and absolute values. The models were able to reproduce the main physical processes of the experiment. In particular, most teams simulated temperature and thermally induced pore water pressure well, including spatial variations caused by inherent anisotropy due to bedding.

keywords

Geological disposal Argillacceous sedimentary rock Coupled THM processes Anisotropy 

Introduction

Geological disposal is currently considered as the most viable method for the long-term management of heat-emitting radioactive waste. The method consists of emplacing the waste in geological formations with the provision of engineered barriers. The geological formations together with the engineered barriers provide a multi-barrier system for the long-term containment and isolation of the waste. Many multi-disciplinary, international collaborative research projects are being conducted to improve the understanding of the long-term evolution and performance of this multi-barrier system. The DECOVALEX project (www.decovalex.org) that started in the early 1990s is such an initiative, focusing on the development and validation of mathematical models in order to simulate that evolution. The models being developed make extensive use of experimental data from either laboratory experiments or large scale in situ experiments for their verification, calibration and validation. The understanding of the coupling between THM processes, and the ability to quantify their interaction are crucial for the assessment of the evolution of the geological and engineered barriers and how this evolution would affect long-term safety. Under DECOVALEX, the strategy to further the above understanding is through a joint effort between many different research teams to develop models, compare the approaches and results, and validate the models with experimental data.

The HE-D experiment at Mont Terri was modelled as one part of Task B1 of the present phase of DECOVALEX (DECOVALEX-2015). Task B1 was proposed in order to investigate and further the understanding of the THM response of argillaceous host rocks and of the bentonite buffer induced by heating. The HE-D test is an in situ thermal test in the Opalinus Clay host rock at the Mont Terri Underground Rock Laboratory. The Opalinus Clay is an argillaceous rock formation being considered as a candidate host rock for geological disposal in Switzerland. The rock formation is inherently anisotropic, due to the presence of bedding planes. This inherent anisotropy is one of the main challenges faced by the research teams in the development of mathematical models to simulate the THM processes that prevailed during the HE-D experiment.

The configuration and measurements of the HE-D test are described in Wileveau and Rothfuchs (2007). Wileveau and Rothfuchs (2007) also reported modelling exercises in support of the ongoing test that helped to identify features important to include in conceptual models and parameterization, including heat loss and thermal properties. Hoxha et al. (2006) found that the major factors affecting hydromechanical response were the plastic dilatancy of the rock near the heater and the change in water viscosity and expansivity as temperatures evolved. They also suggested that discrepancies of estimated and simulated pore water pressure could be explained by increases in hydraulic conductivity associated with damage due to strain. In modelling the HE-D experiment, Gens et al. (2007) identified the relative importance of different coupling combinations for THM processes. Comparing results from an isotropic axisymmetric model and full 3D model with anisotropy, Gens et al. (2007) also concluded that the difference in temperature calculated between the two models was noticeable, especially at further distances from the heaters.

The focus of this paper, the HE-D test, is the first of the three steps that make up Task B1 of DECOVALEX-2015. The first two steps are used to build knowledge needed for modelling of the third step:

  • Step 1a Modelling the HE-D experiment, to study THM processes in Opalinus Clay.

  • Step 1b Modelling the CIEMAT column cells to study THM processes in the buffer materials.

  • Step 2 Modelling the HE-E experiment to study THM processes in both the Opalinus Clay and the buffer materials.

The second and the third steps are described in companion papers (Graupner et al. 2017; Garitte et al. 2017).

This paper, on HE-D heating test, describes the approaches and mathematical models used by the research teams, compares the modelling results between the research teams and with the experimental data and discusses lessons learned with respect to our understanding of coupled THM processes in sedimentary rocks such as the Opalinus Clay and our ability to model them. Eight (8) modelling teams were involved in Task B1. Table 1 shows the colour code associated with each team, which will be used later in this paper for the comparison of modelling results. Table 1 also shows the computer code(s) and associated numerical method(s) used by each team.
Table 1

Colour codes, computer codes and numerical methods used by the teams in Task B1

UFZ, Helmholtz Centre for Environmental Research; BGR, Federal Institute for Geosciences and Natural Resources; CAS, State Key Laboratory of Geomechanics and Geotechnical Engineering, Institute of Rock and Soil Mechanics, Chinese Academy of Sciences; LBNL, Lawrence Berkeley National Laboratory; DOE, U.S. Department of Energy; ENSI, Swiss Federal Nuclear Safety Inspectorate; CNSC, Canadian Nuclear Safety Commission; IRSN, French Institute for Radiological Protection and Nuclear Safety; JAEA, Japan Atomic Energy Agency; KAERI, Korea Atomic Energy Research Institute; CNWRA, SwRI Center for Nuclear Waste Regulatory Analyses; NRC, Nuclear Regulatory Commission; FEM, Finite Element Method; IFD, Integrated Finite Difference Method; FDM, Finite Difference Method; EPCA, Elasto-Plastic Cellular Automaton Method

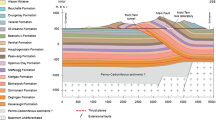
The two in situ experiments providing the data used in this task were performed at the Mont Terri Underground Research Laboratory (URL) located in the Opalinus Clay (www.mont-terri.ch). Figure 1 shows the geological profile of the URL. Figure 2 shows the URL layout and the location of the two in situ experiments. The Opalinus Clay is stiff layered Mesozoic clay of marine origin. Its layered structure results in cross-anisotropic properties, oriented according to the sedimentation plane (bedding plane). In the Mont Terri URL, the bedding plane strike is perpendicular to the axis of the motorway tunnel. At the location of the two in situ experiments (HE-D and HE-E), the bedding dips at approximately 45°.
Fig. 1

Geological profile of the Mont Terri URL site

Fig. 2

Location of the two in situ experiments analysed in this work in the Mont Terri URL (green circle HE-D, red circle HE-E)

Description of the HE-D experiment

The HE-D experiment was run in 2004–2005 and included 340 days of heating. The modelling teams were provided with a detailed description of the experimental set-up as summarized here in order to develop their conceptual and mathematical models. The set-up consists of a horizontal 30 cm diameter heating borehole and instrumentation boreholes (Fig. 3). Two heating devices, each of 2 m length, were installed in the boreholes. The temperature field was measured in the heating borehole (around 16 temperature sensors) and in the rock mass (around 23 temperature sensors in the instrumentation boreholes). The pore water pressure and strain response of the rock mass were monitored in the instrumentation boreholes, using 11 piezometers and 3 extensometers (containing around ten strain measurement intervals each).
Fig. 3

Plan view of the HE-D experiment, including the heating borehole and the main instrumentation boreholes

The layout of the heating borehole, including the associated temperature sensors, is presented in Fig. 4. The origin of the reference system is the mouth of the heating borehole. In the HE-D experiment (Wileveau and Rothfuchs 2007), the x-axis is defined in a horizontal direction perpendicular to the borehole and pointing away from the MI niche. Therefore, the right-hand rule was not respected. In this paper, we consider the x-axis to point towards the MI niche (as indicated with the red arrows in Fig. 3), in order to have a right-hand ruled reference system. Heater 1 was installed in the interval y = [8–10 m] and heater 2 in the interval y = [10.8–12.8 m].
Fig. 4

Layout of the heating borehole

Approximately one month after installation and pressurization, the heaters were switched on with a total power of 650 W (325 W per heater). The heaters were then left under this constant power for 90 days. The power was then increased to 1950 W (975 W per heater) and maintained at that level for 248 days. At the end of this second heating stage, the heaters were switched off (Fig. 5). Heater 2 became depressurized due to a leak of internal oil 109 days after the start of heating (24-07-2004). This event did not noticeably affect the development of the test. Wileveau and Rothfuchs (2007) mentions that some power loss might affect the applied power input given in Fig. 5 (right) because of (1) electrical power loss through the different system components, (2) heat dissipation through the main borehole (especially through the metallic tubing), and (3) the oil leakage event. Non-uniformity of the heat flux applied to the rock was also considered a possibility.
Fig. 5

Timeline of the HE-D experiment: excavation of the main borehole, pressurization and heating

All the instrumentation had been installed before the heating started. The temperature was measured along two boreholes (D1 and D2) drilled from the HE-D niche (Figs. 6, 7).
Fig. 6

Location of temperature measurement sensors (borehole BHE-D1)

Fig. 7

Location of temperature measurement sensors (borehole BHE-D2)

Figure 8 shows a cross-section of the heating borehole and its surroundings, looking from the heater borehole mouth towards the heaters, where the position of the pore pressure sensors and associated temperature sensors has been indicated, together with their longitudinal position. The trace of the bedding plane has also been indicated on this figure (bedding plane containing the heater axis makes an angle of approximately 45° with the horizontal and passes above the MI niche). Pore pressure measurements by the sensors located below the main borehole were quite successful. However, the probes located above the main borehole showed a rather slow response attributed to difficulties encountered in deaeration of the sensor area.
Fig. 8

Location of temperature and pore water pressure sensors

Finally, sliding micrometer extensometers were installed in two boreholes (D4 and D5, Fig. 9) to measure incremental deformations at 1 m intervals. Special care was taken to ensure accuracy in the direction and length of the instrumentation boreholes.
Fig. 9

Location of sliding micrometer extensometers (BHE-D5)

All instruments were in place before the drilling of the main borehole containing the heaters. This allowed the initial state and hydromechanical effects during excavation to be recorded.

Model development

The modelling teams used the above geometric information to build a conceptual model of the HE-D experiment. The test history shown below was shared by the teams for consistency purposes (considering 6/04/2004 as day 0):

  • Day −29: Excavation: borehole diameter = 0.30 m.

  • Day −28: Heaters emplaced and pressurized (1 MPa).

  • Day 0: First heating phase: 325 W/heater.

  • Day 91: Second heating phase: 975 W/heater.

  • Day 339: Cooling phase begins.

  • Day 518: End of test.

Conceptualization of THM processes in the HE-D experiment

THM processes in the context of geological disposal were discussed by Tsang (1987) who used an interaction diagram similar to the one shown in Fig. 10 in order to discuss the coupling of THM processes. Following that discussion, the international DECOVALEX project was started in 1991 and has been continuing for many phases up to the present one. Coupled THM models were developed, calibrated, validated and improved throughout the different phases of DECOVALEX.
Fig. 10

Interaction diagram for coupled THM processes in a porous medium

The conceptualization of the HE-D experiment follows many similar coupled processes shown in Fig. 10. The fundamental assumption is the idealization of Opalinus Clay as a porous medium. Opalinus Clay at the Mont Terri URL is essentially saturated with water in the pores although de-saturation due to ventilation effects can occur around galleries that have been left open for prolonged periods of time. In the case of the HE-D experiment, the excavation of the heating tunnel was performed in a period of approximately 7 days. Lining, tubing and pressurization followed immediately after excavation (Fig. 5, left diagram). The borehole was drilled with compressed air and the borehole diameter is relatively small (30 cm), in order to minimize the formation of microcracks along the walls. The heaters were also installed in a rock mass sufficiently far from the existing niche (Fig. 1), and the rock mass around the heaters is saturated as evidenced by positive pore water pressure measurements (Zhang et al. 2007). Due to the above considerations, it could be assumed that during the HE-D experiment the Opalinus Clay mass affected by heating would be saturated. When heat is supplied to the Opalinus Clay, the THM processes that take place can be conceptualized as illustrated in Fig. 11. Focusing on a Representative Elementary Volume (REV) that contains both the water and solid phases, the following processes are assumed to occur:
Fig. 11

Conceptualization of physical processes in the HE-D experiment—REV is the representative elementary volume and T is temperature

  • Near the heat source the temperature increases. The heat dissipates away from the heat source by conduction in the solid matrix, and by both conduction and convection in the pore water. However, due to the very low permeability of the Opalinus Clay (in the range of 10−19–10−20 m2, see Table 3), heat convection is negligible.

  • The temperature increase causes thermal expansion of both the solid matrix and the pore water. This expansion is constrained by the existing in situ stress in the Opalinus Clay formation; therefore, thermal stresses will develop in the solid matrix. The thermal expansion coefficient of the pore water is much higher than the one of the solid matrix. Therefore, the solid matrix inhibits the expansion of the water, resulting in an increase in the pore water pressure. Zones closer to the heat source would experience higher pressure increases.

  • The increase in pressure in the vicinity of the heat source results in a hydraulic gradient that triggers pore water flow away from the heat source. That flow will gradually dissipate the increase in pore pressure in the vicinity of the heat source.

Mathematical models of THM processes for saturated isotropic porous media have been developed in the past (e.g. Nguyen and Selvadurai 1995). Opalinus Clay would exhibit the same coupled THM processes; however, the bedded nature of the clay suggested that anisotropic effects could be significant. Gens et al. (2007) analysed the HE-D experiment as follows. The Opalinus Clay is a stiff layered Mesozoic clay of marine origin. When saturated stiff clays are subjected to thermal loading, they develop a strong pore pressure response. In turn, the generated pore pressures will impact on subsequent THM behaviour. The performance of the HE-D experiment provided the opportunity to observe in situ the development of coupled THM behaviour in this type of material. The intensity of cross-coupling between the different aspects of the problem turned out to be very variable and could be organized in a hierarchical manner:

  • The strongest coupling is found from thermal to hydraulic and mechanical behaviour. The pore pressure generation is primarily controlled by temperature increase and the largest contributor to deformation and displacements is thermal expansion.

  • Significant but more moderate effects are identified from the coupling of hydraulic to mechanical behaviour. The dissipation of pore pressures induces additional displacements and strains, but because of the high clay stiffness, are smaller than thermally induced deformations.

  • In principle, mechanical damage could impact the hydraulic results because of the development of a higher permeability due to material damage. The damaged zone, however, appears to be very limited in this case and the effects appear to be insignificant.

  • There is no noticeable coupling from hydraulic to thermal behaviour. Practically, all heat transport is by conduction and the thermal conductivity of the material does not change, as the material remains saturated throughout.

Governing equations

From the conceptual understanding of the physical phenomena described above, the governing equations of the models are developed by considering a Representative Elementary Volume (REV) as illustrated in Fig. 11, and invoking the basic principles of conservation of mass, heat and momentum. Additionally, constitutive relationships that are specific to the material thermal, hydraulic and mechanical behaviour must also be assumed. The governing equations are very similar for all teams, since they were based on the same basic principles as discussed in the previous section. For example, the governing equations formulated by the CNSC consist of five coupled partial differential equations with temperature (T), pore pressure (p) and displacement vector (u i ) as primary unknowns:
$$\frac{\partial }{{\partial x_{i} }}\left( {\kappa_{ij} \frac{\partial T}{{\partial x_{j} }}} \right) + q = \rho C\frac{\partial T}{\partial t}$$
(1)
$$\begin{aligned} & \frac{\partial }{{\partial x_{i} }}\left( {\frac{{\rho_{\text{w}} k_{ij} }}{\mu }\left( {\frac{\partial p}{{\partial x_{j} }} + \rho_{\text{w}} g \, j} \right)} \right) + \rho_{\text{w}} \left[ {\frac{ - n}{{K_{\text{w}} }} + \frac{n - \alpha }{{K_{\text{s}} }}} \right]\frac{\partial p}{\partial t} \\ & \quad + \rho_{\text{w}} \alpha \frac{\partial }{\partial t}\left( {\frac{{\partial u_{\text{k}} }}{{\partial x_{\text{k}} }}} \right) + \rho_{\text{w}} \left( {\left( {1 - \alpha } \right)\beta - n\beta_{\text{w}} - \left( {1 - n} \right)\beta_{\text{s}} } \right)\frac{\partial T}{\partial t} = 0 \\ \end{aligned}$$
(2)
$$\frac{1}{2}C_{ijkl} \left( {\frac{{\partial^{2} u_{k} }}{{\partial x_{j} \partial x_{k} }} + \frac{{\partial^{2} u_{l} }}{{\partial x_{i} \partial x_{l} }}} \right) + \alpha \frac{{\partial p_{f} }}{{\partial x_{i} }} = 0$$
(3)
A summary of the meaning and hypotheses used for each equation is given as follows:
  1. (a)

    Equation of heat conservation:

     
Equation (1) is derived from the consideration of conservation of heat. In addition, it is assumed that:

  • Local thermodynamic equilibrium exists between the liquid and solid; therefore, the temperature is the same in the two phases at a point around a REV.

  • Heat conduction is the dominant mechanism of heat transport, and convection due to pore water flow could be neglected due to low permeability of OPA, resulting in low pore water velocity.

In Eq. (1), κ ij is the thermal conductivity tensor (W/m/°C), ρ is the density of the bulk medium (kg/m3), C is the bulk specific heat of the medium (J/kg/°C) and q accounts for distributed heat generation in the poroelastic medium (W/m3).
  1. (b)

    Equation of conservation of mass for the pore water:

     
Equation (2) is derived from considerations of mass conservation of pore water. Equation (2) has four terms, and the assumptions underlying each one are as follows:

  • The first term of the equation results from a generalization of Darcy’s law of non-isothermal pore water flow in a saturated porous media. In this term, k ij is the saturated permeability tensor (m2), μ (kg/m/s) is the viscosity of water, and ρ w is the density of water, which are both functions of temperature.

  • The second term is a storage term coming from considerations of compressibility of the water and the solid phase, where n is porosity, 1/K w is the coefficient of compressibility of water (Pa−1) and 1/K s is the coefficient of compressibility of the solid phase (Pa−1).

  • The third term is a storage term originating from the consideration of compressibility of the porous skeleton.

  • The fourth term represents water flow due to the difference in thermal expansion between the water and the solid material, where β w, β s and β (1/°C) are the coefficient of volumetric thermal expansion of the water, the solid material and the solid skeleton, respectively.

  1. (c)

    Equation of momentum conservation:

     
Equation (3) is derived from the consideration of momentum conservation of the porous medium. Since inertial effects are neglected, Eq. (3) reduces to the equation of equilibrium of the porous medium. The major assumption in Eq. (3) is that Biot’s effective stress principle is valid. Therefore, external loads will result in a total stress σ in the porous medium, which would result in an effective stress σ′ in the solid skeleton and a pressure in the pore water according to the equation:
$$\sigma = \sigma^{\prime} + \alpha p$$
(4)
where α is Biot’s coefficient of poroelasticity.

The other parameters of Eq. (3) are C ijkl , the stiffness tensor that relates stress to strain and β, the coefficient of volumetric thermal expansion of the solid matrix. All teams involved with this work assumed the rock to be elastic; therefore, the stiffness tensor was derived from Hooke’s law. However, to take into account the anisotropy induced by bedding, most teams used Hooke’s law for a transversely isotropic material, with five independent elastic constants as detailed in the next section.

Numerical models

The governing equations, with their corresponding boundary and initial conditions, were numerically solved with different computer codes that use various numerical methods. BGR/UFZ, ENSI used the finite element method, with the OpenGeosys computer code (Kolditz et al. 2014). CNSC and JAEA also used the finite element method, with the COMSOL (COMSOL AB 2013) and THAMES codes, respectively. CAS used a self-developed numerical code EPCA3D, which is a combination of multiple techniques and theories, such as finite element method, cellular automaton, elasto-plastic theory and principle of statistics (Pan et al. 2009a, b; Pan and Feng 2013). CNWRA used the Finite Difference code FLAC and set up their model for Step 1a with the following conditions: a 2D-axisymmetric model centred on the heater borehole axis of a 8 m radius and a 28 m length; assumed water-saturated conditions; ambient conditions on exterior boundaries; symmetry conditions on the borehole axis; applied heat load and pressure on the heated borehole section; and material parameter values based on previous reports on HE-D modelling. KAERI used the Finite Difference code FLAC3D. LBNL used TOUGH-FLAC, based on linking the TOUGH2 multiphase flow simulator (Integral Finite Difference) with the FLAC3D geomechanical code (Finite Difference Method) (Rutqvist et al. 2002, 2014). The combined TOUGH2 and FLAC3D codes (TOUGH-FLAC) were applied for simulating sequentially coupled multiphase fluid flow and heat transport coupled with geomechanical issues (stress and deformation) (Rutqvist et al. 2002; Rutqvist 2011). Except for CNWRA, who used an axisymmetric model, all teams used a 3D representation of the geometry. The main features and assumptions of the numerical models are summarized in Table 2. It is worth noting that all teams assumed a poroelastic behaviour for the rock mass, except for LBNL who used a Mohr–Coulomb criterion to determine the onset of potential plastic deformations. Typical geometries and meshes are shown in Fig. 12. The main input parameters used by the teams are summarized in Table 3. As shown in Tables 2 and 3, most teams considered the anisotropy of the THM properties of the Opalinus Clay.
Table 2

Main features and assumptions of numerical models

Fig. 12

Mesh illustration: LBNL left and JAEA right

Table 3

Main Opalinus Clay parameters considered by the teams

  

BGR

CAS

CNSC

CNWRA

ENSI

JAEA

KAERI

LBNL

Young’s modulus in the bedding plane (MPa)

E h

9300

10,000

8000

7000

10,000

6000

10,000

5000

Anisotropy ratio

E h/E v

1.6

2.5

2.7

1.0

2.5

1.0

2.5

1.0

Poisson’s ratio (−)

ν hh

0.33

0.24

0.24

0.3

0.24

0.27

0.24

0.3

νvh

0.38482

0.33

0.33

–

0.33

–

0.33

–

Shear modulus (MPa)

G vh

2338.71

1200

1000

2756.0

1613.0

–

1200.0

1920.0

Cohesion (MPa)

c′

       

2.2–5

Friction angle (°)

φ

       

23–25

Biot (−)

α

0.6

0.6

0.6

–

0.0

0.6

 

0.6

Porosity

n

0.137

0.137

0.157

0.137

0.2

0.157

0.157

0.15

Bulk density (kg/m3)

 

2500

2340

2450

2450.0

2740.0

2450.0

2450.0

2700.0

Intrinsic permeability (m2) (α k is the anis. ratio)

k //

2.E−19

1.E−19

4.E−20

5.E−20

2.E−20

1.E−20

1.E−19

5.E−20

k per

2.E−20

5.E−20

1.E−20

5.E−20

4.E−21

–

5.E−20

5.E−20

k 0 *

1E−19

8.E−20

3.E−20

5.E−20

1.E−20

–

8.E−20

5.E−20

α k *

10

2

4

1

5

–

2

1

Thermal conductivity [W/(mK)]

λ //

2.15

2.15

2.15

1.77

2.15

–

2.15

2.15

λ per

1.2

1.19

1.19

1.77

1.19

–

1.19

1.19

λ 0 *

1.77

1.77

1.77

1.77

1.77

2.15

1.77

1.77

α λ *

1.79

1.79

1.79

1.00

1.79

–

1.79

1.79

Heat capacity of the porous medium (J kg−1 K−1)

C s

995

995

800

1000

800

800

1000

900

Linear solid thermal expansion coefficient (K−1)

b s

1.40E−05

1.00E−05

1.50E−05

1.60E−05

2.60E−05

2.60E−05

2.60E−05

1.40E−05

* Dependent parameters

The initial conditions for the boundary value problems are presented in Table 4. The initial pore water pressure at Mont Terri is approximately 2 MPa. The lower value used by most of the teams reflects the fact that the HE-D area was subjected to drainage well before the start of the test through the nearby galleries (Gallery 98 and MI niche).
Table 4

Initial conditions considered by the teams

Computation type

BGR

CAS

CNSC

CNWRA

ENSI

JAEA

KAERI

LBNL

3D

3D

3D

2D axisymmetric

3D

3D

3D

3D

THM

THM

THM

THM

THM

THM

THM

THM

Total stresses (MPa)

 σ xx

5

4.5

4.5

4.28

–

0

4.5

5

 σ yy

3

2.5

2

4.28

–

0

2.5

2

 σ zz

7

6

6.5

–

–

0

6

7

Water pressure (MPa)

 p w

0.9

0.9

1

0.1–0.9

0.1–0.978

2

1.2

0.9

Temperature (°C)

 T

15

15

15

15

15

15

15

15

The main boundary conditions are:

  • on the heaters

  • on the external boundaries

Most teams applied heat fluxes to the heaters, but some of them applied temperature directly. Those applying heat fluxes considered the heat loss mentioned in the previous section (by including all elements in borehole BHE D0 or by estimation). Hydraulic boundary conditions at the heater surface were either drained or undrained.

External boundary conditions (surrounding galleries) were taken into account in different ways. In general, the teams were required to consider atmospheric pressure, stress relaxation and varying temperature at those boundaries.

Verification with analytical solutions

Verification of numerical results with analytical solutions provides confidence in the adequacy of the numerical model (in terms of mesh size, time step and assumed boundary conditions) and its implementation into the computer code. The CAS, CNSC and BGR/UFZ teams compared their numerical results with analytical solutions proposed by Booker and Savvidou (1985) for a point heat source in an infinite isotropic porous medium (Wang et al. 2016). Analytical solutions for transversely isotropic media (such as could be assumed for Opalinus Clay) do not presently exist. However, the temperature solution from Booker and Savvidou (1985) could be transformed in order to take this transverse anisotropy into account (Garitte et al. 2012; Nguyen et al. 2016).

A comparison of the modelling results with the analytical solution, using the input parameters in Table 5, is presented in Fig. 13. The modelling results compare satisfactorily with the analytical solution providing confidence in the model implementation. Some slight discrepancy is, however, noticed. This is attributable to mesh discretization, but mainly to boundary effects, since the analytical solution is based on an infinite medium, while the numerical models were developed for finite domains surrounding the point heat source. The research teams have tested those two factors by refining the mesh and extending the boundaries of the numerical models farther from the heat source. The results presented in Fig. 13 are the final ones where a visually satisfactory agreement is found between the numerical and analytical solutions.
Table 5

Input parameters for the verification with analytical solution

Point heat source

300

W

Bulk density

2445

kg/m3

Bulk heat capacity

1000

J/kg/K

Vertical thermal conductivity

1

W/m/K

Horizontal thermal conductivity

2.1

W/m/K

Fig. 13

Verification of the models developed by CAS (a) CNSC and BGR/UFZ (b, Nguyen et al. 2016) with an analytical solution

Modelling results and comparison with measurements from the HE-D experiment

Modelling results are compared with the measurements of different sensors in this section. The positions of the sensors are illustrated in Fig. 8.

Temperature

In this section, modelled temperature is compared to the measurements from the HE-D experiment. The modelling results are represented by solid (“in the bedding plane”) or dashed (direction perpendicular to the bedding plane) lines, with the exception of the results of JAEA that are represented with solid symbols. The colour code used for the teams is defined in Table 1.

The modelled temperature profiles obtained by the different teams at the end of the second heating stage are presented in Fig. 14. Five measured data points are also shown. Their orientation relative to the bedding plane is indicated. All teams (except CNWRA and JAEA) used the same cross-anisotropic thermal conductivity values. Nevertheless, the comparison of the modelling results of the different teams shows significant differences between them (in the order of ~20 °C), especially close to the heaters. As will be discussed later, the main reasons for these differences are attributable to different mesh discretization, representation of the heat source and consideration of anisotropy. Consistent with the in situ measurements, for each team the modelled temperature in the bedding plane is higher than that in the perpendicular direction since the thermal conductivity parallel to bedding is higher.
Fig. 14

Measured (symbols) and modelled (lines) radial temperature profiles around Heater 1 on 23-02-2005, i.e. just before the heaters were switched off (full lines modelling results parallel to bedding plane and dashed lines modelling results perpendicular to bedding plane)

The modelled and measured temperature evolution at the heater surface is presented in Fig. 15. Most teams applied a power loss coefficient; however, the modelled temperature is generally higher than the measured temperature. Temperature sensors installed in the heater borehole are in a very high gradient zone and are thus very sensitive to errors in their positions. They were thus not allocated a high weight in calibrating the models. Teams applying a heat flux at the heater/rock surface as a boundary condition obtained different temperatures in the bedding and in the perpendicular directions (LBNL and CAS). Measurements in the two directions do not show this difference (probably because of the high thermal conductivity of the heater casing). KAERI represented the heater and all elements inside the heating borehole very carefully, resulting in a good reproduction of the heater temperature.
Fig. 15

Measured (symbols) and modelled (lines) temperature evolution at the heater surface (Heater 1) over a 1-year period. Measurements are represented by open circles and diamonds. Orange circles and diamonds are modelling results of JAEA

The measured and modelled temperature evolution in the rock mass is illustrated in Figs. 16 and 17. Temperature is plotted for sensors HED B03 and HED B14 (2 sensors at different distances from the heater but with very similar measured temperatures because of their different orientation relative to the bedding plane) and for sensors HED B15 and HED B16 (two sensors in the bedding plane but at different distances from the heater). The teams considering anisotropic thermal conduction reached a satisfactory agreement with the measurements, although a discrepancy of several degrees between the different teams is observed.
Fig. 16

Measured (symbols) and modelled (lines) temperature evolution in HEDB03 and HEDB14 (at the end of boreholes BHE-D-3 and BHE-D14 shown in Fig. 3) over a 1-year period. Measurements are represented by open circles and diamonds. Modelling results are represented by lines (solid lines for HEDB03 and dashed lines for HEDB14). Orange circles and diamonds are modelling results of JAEA

Fig. 17

Measured (symbols) and modelled (lines) temperature evolution in HEDB15 and HEDB16 (at the end of borehole BHE-D15 and BHE-D16 shown in Fig. 3) over a 1-year period. Measurements are represented by open circles and diamonds. Modelling results are represented by lines (solid lines for HEDB15 and dashed lines for HEDB16). Orange circles and diamonds are modelling results of JAEA

Temperature profiles along the two boreholes containing only temperature sensors (HED B1 and B2) are shown in Figs. 18 and 19. These figures allow the capability of the models to reproduce the measured temperature field over a relatively large rock volume to be checked. Reproduction of the measurements by the models is satisfactory, although significant differences between the models are observed (even between those using the same thermal parameters).
Fig. 18

Measured (symbols) and modelled (lines) temperature profiles in borehole BHE-D1

Fig. 19

Measured (symbols) and modelled (lines) temperature profile in borehole BHE-D2

Pore water pressure

In this section, modelled pore water pressure is compared to the measurements from the HE-D experiment. A pore pressure rise generally results from an increase in temperature due to the differential rate of expansion of the clay skeleton, solid phase and water. Sensitivity analyses showed that pore water pressure increases with decreases in thermal conductivity or intrinsic permeability (Ofoegbu et al. 2015). The mechanism underlying the hydraulic behaviour in the clay is a competition between the generation of pore pressures by the differential thermal expansion of liquid and solid and the dissipation of pore pressures, the rate of which is controlled mainly by the water permeability. Hence, although temperature is increasing continuously, the pore water pressure may stop increasing and even start decreasing during the test. The variation of intrinsic water permeability and the drainage boundary conditions are therefore bound to have a profound effect on the excess pore water pressure response.

The modelled radial pore water pressure profiles are shown in Figs. 20 and 21. These profiles are snapshots at the time when the maximum pore pressure is observed at sensors HED B03 and B14 and just before the heating was switched off, respectively. Excess pore water pressure and its drainage during the heating phase were clearly observed by all modelling teams.
Fig. 20

Modelled radial pore water pressure profiles around Heater 11 on 31-07-2004, i.e. around the time maximum pore water pressure is reached in the sensors studied below (full lines modelling results parallel to bedding plane and dashed lines modelling results perpendicular to bedding plane)

Fig. 21

Modelled radial pore water pressure profiles around Heater 1 on 23-02-2005, i.e. just before the heaters were switched off (full lines modelling results parallel to bedding plane and dashed lines modelling results perpendicular to bedding plane)

JAEA used a higher initial pore water pressure value than the other teams. This does not seem to cause a large difference in the calculated excess pore water pressure induced by heating. The pore water pressure rise is influenced instead by the hydraulic boundary condition applied by the teams at the heater surface. LBNL and BGR applied an undrained condition. This approach results in a higher excess pore water pressure increase than for the other teams as, in this case, drainage is only allowed towards the rock mass. In addition to the drainage conditions, the magnitude of the excess pore water pressure rise is probably also affected by the values selected by the teams for permeability and thermal expansion of the solid skeleton.

Excess pore water pressure since the start of heating is shown in Figs. 22 and 23 at four sensor locations (comparison between modelled results and measurements). The models satisfactorily reproduce: (1) the measured increase in pore water pressure and (2) the subsequent drainage of the excess pore water pressure. The small differences in the permeability and thermal expansion values selected by the teams do not seem to lead to significant differences in the pore water pressure response. Teams applying an undrained hydraulic boundary condition at the heater (such as BGR and LBNL) predict a slower drainage rate.
Fig. 22

Measured (symbols) and modelled (lines) excess pore water pressure evolution in HEDB03 and HEDB14 since the start of heating. Measurements are represented by open circles and diamonds. Modelling results are represented by lines (solid lines for HEDB03 and dashed lines for HEDB14). Orange circles and diamonds are modelling results of JAEA

Fig. 23

Measured (symbols) and modelled (lines) excess pore water pressure evolution in HEDB15 and HEDB16. Measurements are represented by open circles and diamonds. Modelling results are represented by lines (solid lines for HEDB15 and dashed lines for HEDB16). Orange circles and diamonds are modelling results of JAEA

For completeness, the absolute pore water pressure evolution is shown in Figs. 24 and 25.
Fig. 24

Measured (symbols) and modelled (lines) pore water pressure evolution in HEDB03 and HEDB14. Measurements are represented by open circles and diamonds. Modelling results are represented by lines (solid lines for HEDB03 and dashed lines for HEDB14). Orange circles and diamonds are modelling results of JAEA

Fig. 25

Measured (symbols) and modelled (lines) pore water pressure evolution in HEDB15 and HEDB16. Measurements are represented by open circles and diamonds. Modelling results are represented by lines (solid lines for HEDB15 and dashed lines for HEDB16). Orange circles and diamonds are modelling results of JAEA

Strain

In this section, modelled strain is compared to the measurements from the HE-D experiment. Based on the conceptual understanding discussed in “Conceptualization of THM processes in the HE-D experiment” section, upon heating the rock mass can be roughly divided in two zones. In the first zone, the rock undergoes a significant temperature increase. This triggers expansion of the rock in all directions, and the magnitude of this expansion is mainly dependent on the thermal expansion coefficient of the rock. The second zone is not reached by the heat wave, and its temperature is close to initial conditions. Nevertheless, this zone is subject to a compression in the direction radial to the heater and an expansion in the circumferential direction as a reaction to the thermal expansion of the heated zone close to the heater. Hence, deformation in the second zone is a mechanical process, mainly governed by the stiffness of the rock.

Results are shown for a circumferential (pt 7–8) and radial (pt 4–5) interval relative to the heaters in Figs. 26 and 27, respectively. In the circumferential interval, most of the teams satisfactorily represent the measurement trend (direct extension of the interval upon heating) as well as the measurement magnitude. The modelled extension amplitude varies by a factor of four between the smallest extension (KAERI) and the largest one (ENSI), although those two teams used exactly the same value for the thermal expansion of the solid skeleton.
Fig. 26

Measured (symbols) and modelled (lines) strain evolution in interval 7–8 of HEDB05 (labelled as BHE-D5 in Figs. 3, 9). Measurements are represented by open circles and diamonds. Orange circles and diamonds are modelling results of JAEA

Fig. 27

Measured (symbols) and modelled (lines) strain evolution in interval 4–5 of HEDB05 (labelled as BHE-D5 in Figs. 3, 9). Measurements are represented by open circles and diamonds. Orange circles and diamonds are modelling results of JAEA

In the radial interval, most of the teams also represented the measurement trend well (direct compression after start of heating and extension later on), as well as the measurement magnitude.

Influence of bedding

As discussed in the previous sections, bedding in the Opalinus Clay results in an anisotropic response of its THM response to heating. Both the thermal and hydraulic conductivities are higher in the direction of the bedding planes, resulting in a faster propagation of the heat and hydraulic fronts along the direction parallel to bedding as compared to the perpendicular direction. As a result, points located at the same radial distance from the heat source but at different angles show significant differences in the recorded evolution of temperature and pore pressure. This feature has been well simulated by most teams. As an illustration, Fig. 28 shows the temperature and pore pressure fields simulated by the CAS. The fields have characteristic elliptical shapes, with the major axis oriented along the direction of bedding.
Fig. 28

Temperature and pore pressure fields from CAS model, at section y = 8985 m after 280 days of heating. a Temperature (°C), b pore pressure (MPa)

Conclusion

The HE-D experiment at Mont Terri is a valuable study for the understanding of coupled THM processes in Opalinus Clay. Very extensive experimental data on the evolution of temperature, pore water pressure and deformation have been gathered before, during and after the heating of the rock mass from two heaters. In this collaborative research effort, eight research teams developed conceptual and mathematical models to interpret the data and to improve their understanding of the THM response of the rock mass. Although there are variations in input parameters and conceptualizations, the models were all based on the theory of thermal poroelasticity. Considering the nature of the experiment with a significant number of sensors, each of which is associated with some experimental uncertainty (location, measurement itself, power input), the agreement between experimental and simulated values of temperature, pore pressure and strain is considered to be very good. Although some quantitative discrepancies might be found between modelling results and experimental data, most modelling results were successful in capturing the main physics that prevailed in the experiment: the strong coupling between THM processes that is responsible for the pore pressure increase, and the important effect of inherent anisotropy due to stratification of the Opalinus Clay.

The temperature field generated by the heaters is influenced by the inherent anisotropy of the Opalinus Clay due to bedding. The heat pulse propagates faster in the direction parallel to bedding as compared to the perpendicular direction. Therefore, at the same radial distance from the heaters, the temperature is higher in the direction perpendicular to bedding as compared to the parallel direction. Models that took that anisotropy into account can adequately simulate the above feature. In terms of absolute values, the temperature predicted by the teams agrees reasonably well with each other’s and with the measurements. Although some teams included thermal convection in their models, due to the low permeability of the rock, it was found that conduction is the primary heat transport process. Some differences in the values of temperature predicted by modelling teams, especially at points close to the heaters can be attributed to the following factors:

  • Different treatments of the heat loss and to mesh discretization near the heater, which may also influence the heat flow. It is recommended that in future comparative modelling exercises similar to this one, a preliminary benchmark step, using existing analytical solutions, be performed. In the present study, only three teams performed such a benchmark exercise.

  • Better representation of the heat source and refinement of the numerical grid near the heater appear to improve the prediction of temperature distributions. Because hydrological and mechanical conditions both depend strongly on temperature, better prediction of temperature magnitude and distribution are important for reasonable predictions of water pore pressure and mechanical strain.

  • Incorporation of anisotropic properties generally improved overall comparisons with measured temperature data. Results from isotropic models matched some locations well and other locations poorly, depending on the geometric relationship between the heater location, the measurement location, and the bedding plane.

All teams were successful in predicting the process of thermally induced pressure generation in the rock. The increase in temperature causes thermal expansion in both the solid skeleton and the pore fluid. Since the rock mass has a low permeability, and the thermal expansion coefficient of the fluid is higher than the one of the solid skeleton, the temperature transient triggers an increase in the pore fluid pressure. The pore fluid pressure gradually dissipates when drainage takes place away from the heat source. In order to satisfactorily match the measured pore pressure, the models must first satisfactorily simulate the temperature. It is also shown by some teams that the consideration of temperature-dependent viscosity, thermal expansivity and density of water can play a noticeable influence on the predicted values of pore pressure. Hoxha et al. (2006) also reported the same finding. The thermally induced pore pressure is significantly influenced by the rock permeability and its stiffness (represented by the Young’s modulus for elastic models). Parametric studies (Selvadurai and Nguyen 1996; Gens et al. 2007; Ofoegbu et al. 2015) showed that the pore pressure is higher for lower permeability and higher stiffness. A high pore pressure can induce hydrofracturing, when it exceeds the minimum principal stress. In the HE-D experiment, hydrofracturing might have occurred at some points. For example at HE-DB03, the measured pore pressure reached a maximum value of 4 MPa and is higher than the subhorizontal minimum principal stress estimated to be in the range of 2–3 MPa. However, at the dismantling of the HE-D experiment, cores recovered at radial distances of 20 cm from the heaters (Wileveau and Rothfuchs 2007) showed that there is limited observable fracturing resulting from heating. On the other hand, Gens et al. (2007) indicated that the measured unconfined Young’s moduli showed a decrease in value by a factor of six within 2 m of the heating boreholes, suggesting that the damage zone might extend to the same distance into the rock. In this study, only one team included a Mohr–Coulomb yield criterion in their model, while all other teams assumed linear elasticity for the rock. Although the assumption of linear elasticity results in adequate simulations of the pore pressure and the thermal strain in the rock, damage and plastic behaviour should be further investigated in the future. Hoxha et al. (2006) showed the noticeable influence of the constitutive model adopted for the mechanical behaviour of the rock on the predicted values of the pore pressure. When plasticity and damage is induced in the rock, there is a reduction in its stiffness accompanied by an increase in its permeability. As previously mentioned, those two factors have a significant impact on the magnitude of the generated pore pressure and its subsequent dissipation rate.

Post-closure safety assessments of a high-level waste repository are typically performed for a suite of evolution scenarios spanning very long time periods after closure. The early near-field evolution of the repository would have a significant influence on the overall long-term evolution scenarios. Coupled THM processes that prevail in the engineered barriers, including the bentonite-based seals, and the surrounding host rock will govern the early near-field evolution of the repository. Task B1 of DECOVALEX was an excellent opportunity for researchers to confirm their understanding of those processes in order to assess the validity of evolution scenarios assumed in long-term safety assessment. By developing mathematical models, in a stepwise manner, to predict and interpret heating experiments in the rock (HE-D in situ experiment), in the bentonite seals (laboratory column tests) and in the combined bentonite seals/rock system (the in situ HE-E experiment), the authors have achieved a better understanding of near-field THM processes and acquired a higher confidence in the mathematical models used to quantify those processes. The present paper covers the first step of Task B1, modelling of the HE-D experiment. Companion papers (Graupner et al. 2017; Garitte et al. 2017) will report on the authors’ efforts on the last two steps of Task B1.

Notes

Acknowledgements

The members of the Task B1 like to express their thanks for the financial supports provided by the Funding Organizations of the DECOVALEX-2015 project, and measured data of experiments supplied by National Cooperative for the Disposal of Radioactive Waste (NAGRA), Switzerland. ANDRA led the HE-D experiment and is gratefully acknowledged for the quality of the measurements provided during this experiment. CAS team’s work was financially supported by international cooperation project of Chinese Academy of Sciences (No. 115242KYSB20160024). National Natural Science Foundation of China (Nos. 51322906, 41272349).

References

  1. Booker JR, Savvidou C (1985) Consolidation around a point heat source. Int J Numer Anal Methods Geomech 9:173–184CrossRefGoogle Scholar
  2. COMSOL AB (2013) COMSOL Multiphysics release notes, version 4.3bGoogle Scholar
  3. Garitte B, Bond A, Millard A, Zhang C, English M, Mcdermott C, Nakama S, Gens A (2012) Analysis of hydro-mechanical processes in a ventilated tunnel in an argillaceous rock on the basis of different modelling approaches. DECOVALEX-2011 project, final report of Task A (KTH)Google Scholar
  4. Garitte B, Shao H, Wang XR, Nguyen TS, Li Z, Rutqvist J, Birkholzer J, Wang WQ, Kolditz O, Pan PZ, Feng XT, Lee C, Graupner BJ, Maekawa K, Manepally C, Dasgupta B, Stothoff S, Ofoegbu G, Fedors R, Barnichon JD (2017) Evaluation of the predictive capability of coupled thermo-hydro-mechanical models for a heated bentonite/clay system (HE-E) in the Mont Terri Rock Laboratory. Environ Earth Sci 76:64. doi: 10.1007/s12665-016-6367-x CrossRefGoogle Scholar
  5. Gens A, Vaunat J, Garitte B, Wileveau Y (2007) In-situ behaviour of a stiff layered clay subject to thermal loading. Observations and interpretation. Géotechnique 57(2):207–228CrossRefGoogle Scholar
  6. Graupner B et al (2017) Comparative modelling of the coupled thermal-hydrological-mechanical (THM) processes in a heated bentonite pellet column with hydration. Environ Earth Sci (Submitted)Google Scholar
  7. Hoxha D, Jiang Z, Homand F, Giraud A, Su K, Wileveau Y (2006) Impact of THM constitutive behaviour on the rock-mass response: case of HE-D experiment in Mont Terri Underground Rock Laboratory. In: Van Cotthem A, Charlier R, Thimus JF, Tshibangu JP (eds) EUROCK 2006—multiphysics coupling and long term behaviour in rock mechanics. Taylor & Francis Group, London, pp 199–204CrossRefGoogle Scholar
  8. Kolditz O, Shao H, Wang W-Q, Bauer B (2014) Thermo-hydro-mechanical-chemical processes in fractured porous media—modelling and benchmarking. Springer, HeidelbergGoogle Scholar
  9. Nguyen TS, Selvadurai APS (1995) Coupled thermal-mechanical-hydrological behaviour of sparsely fractured rock: implications for nuclear fuel waste disposal. Int J Rock Mech Min Sci Geomech Abstr 32:465–479CrossRefGoogle Scholar
  10. Nguyen S, Shao H and Garitte B (2016) Transient heat conduction in a transversal isotropic porous medium. In: Thermo-hydro-mechanical chemical processes in fractured porous media: benchmarking initiatives, Springer. ISBN 978-3-319-29224-3. doi: 10.1007/978-3-319-29224.3
  11. Ofoegbu G, Dasgupta B, Manepally C, Fedors R (2015) Thermal-hydrological-mechanical modeling of a saturated clay shale, report on the HE-D test modeling. Center for Nuclear Waste Regulatory Analyses, San Antonio, TX. NRC ADAMS Accession No. ML15161A530. http://www.nrc.gov/docs/ML1516/ML15161A530.pdf
  12. Pan PZ, Feng XT (2013) Numerical study on coupled thermo-mechanical processes in Äspö pillar stability experiment. J Rock Mech Geotech Eng 5(2):136–144CrossRefGoogle Scholar
  13. Pan PZ, Feng XT, Hudson JA (2009a) Study of failure and scale effects in rocks under uniaxial compression using 3D cellular automata. Int J Rock Mech Min Sci 46(4):674–685CrossRefGoogle Scholar
  14. Pan PZ, Feng XT, Huang X, Cui HQ, Zhou H (2009b) Coupled THM processes in EDZ of crystalline rocks using an elasto-plastic cellular automaton. Environ Geol 57(6):1299–1311CrossRefGoogle Scholar
  15. Rutqvist J (2011) Status of the TOUGH-FLAC simulator and recent applications related to coupled fluid flow and crustal deformations. Comput Geosci 37:739–750CrossRefGoogle Scholar
  16. Rutqvist J, Wu Y-S, Tsang C-F, Bodvarsson G (2002) A modeling approach for analysis of coupled multiphase fluid flow, heat transfer, and deformation in fractured porous rock. Int J Rock Mech Min Sci 39:429–442CrossRefGoogle Scholar
  17. Rutqvist J, Zheng L, Chen F, Liu H-H, Birkholzer J (2014) Modeling of coupled thermo-hydro-mechanical processes with links to geochemistry associated with bentonite-backfilled repository tunnels in clay formations. Rock Mech Rock Eng 47:167–186CrossRefGoogle Scholar
  18. Selvadurai APS, Nguyen TS (1996) Scoping analyses of the coupled thermalhydrological-mechanical behaviour of the rock mass around a nuclear fuel waste repository. Eng Geol 47:379–400CrossRefGoogle Scholar
  19. Teodori SP, Gaus I, Köhler S, Weber HP, Rösli U, Steiner P, Trick T, Garcià Siñeriz JL, Nussbaum C, Wieczorek K, Schuster K, Mayor JC (2011) Mont Terri HE-E experiment: as-built report. Arbeitsbericht NAB 11-25 (NAGRA)Google Scholar
  20. Tsang CF (1987) Introduction to coupled processes. In: Tsang CF (ed) Coupled processes associated with nuclear waste repositories. Academic Press, San Diego, pp 1–8CrossRefGoogle Scholar
  21. Wang X, Nguyen S, Shao H, Wang W (2016) Consolidation around a point heat source. In: Thermo-hydro-mechanical chemical processes in fractured porous media: benchmarking initiatives. Springer, Berlin. ISBN 978-3-319-29224-3, doi: 10.1007/978-3-319-29224.3
  22. Wileveau Y, Rothfuchs D (2007) THM behaviour of host rock (HE-D) experiment: study of thermal effects on opalinus clay—synthesis. Mont Terri technical report TR2006-01Google Scholar
  23. Zhang CL, Rothfuchs T, Jockwer N, Wieczorek KL, Tittrich J, Müller J, Hartwig L, Komischke M (2007) Thermal effects on the opalinus clay: a joint heating experiment of ANDRA and GRS at the mont terri URL (HE-D Project). TR 2007–02, Gesellschaft für Anlagenund Reaktorsicherheit (GRS) mbH, Berlin, GermanyGoogle Scholar

Copyright information

© The Author(s) 2017

Open AccessThis article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.

Authors and Affiliations

  • B. Garitte
    • 1
  • T. S. Nguyen
    • 2
    Email author
  • J. D. Barnichon
    • 3
  • B. J. Graupner
    • 4
  • C. Lee
    • 5
  • K. Maekawa
    • 6
  • C. Manepally
    • 7
  • G. Ofoegbu
    • 7
  • B. Dasgupta
    • 7
  • R. Fedors
    • 8
  • P. Z. Pan
    • 9
    Email author
  • X. T. Feng
    • 9
  • J. Rutqvist
    • 10
  • F. Chen
    • 10
  • Jens Birkholzer
    • 10
  • Q. Wang
    • 11
  • O. Kolditz
    • 11
  • H. Shao
    • 12
  1. 1.NAGRAWettingenSwitzerland
  2. 2.Canadian Nuclear Safety CommissionOttawaCanada
  3. 3.Institut de Radioprotection et de Sûreté NucléaireFontenay-aux-RosesFrance
  4. 4.Swiss Federal Nuclear Safety InspectorateBruggSwitzerland
  5. 5.Korea Atomic Energy Research InstituteTaejonKorea
  6. 6.Japan Atomic Energy AgencyHokkaidoJapan
  7. 7.Center for Nuclear Waste Regulatory AnalysesSan AntonioUSA
  8. 8.U.S. Nuclear Regulatory CommissionWashingtonUSA
  9. 9.State Key Laboratory of Geomechanics and Geotechnical Engineering, Institute of Rock and Soil MechanicsChinese Academy of SciencesWuhanChina
  10. 10.Lawrence Berkeley National LaboratoryBerkeleyUSA
  11. 11.Helmholtz Centre for Environmental ResearchLeipzigGermany
  12. 12.Federal Institute for Geosciences and Natural ResourcesHanoverGermany

Personalised recommendations