Abstract
Agricultural intensification in semiarid regions comes at a cost of relatively high water losses through evapotranspiration and can contribute to releases of nutrients and pesticides that affect downstream water quality. In addition, highly managed river basins may be particularly sensitive to future climate change. However, effects on retention–attenuation of nutrients are difficult to quantify due to the complexity and variability of relevant processes. We here use the example case of the large (covering 1.3% of the earth’s land surface) and extensively irrigated Aral Sea Drainage Basin (ASDB) in Central Asia, together with 73 general circulation model (GCM) projection results and field-data driven nitrogen retention–attenuation modeling, to investigate to which extent projected future climate change (for years 2025, 2050 and 2100) can influence nitrogen loads and concentrations in the water systems of the basin. Results for the principal Amu Darya River of the ASDB suggest that riverine concentrations of nitrogen will decrease considerably throughout the coming century. This is due to projected climate-related decreases in runoff and river discharge, which increases internal nitrogen recirculation ratios, average transport distances and nitrogen retention–attenuation. However, in groundwater near the agricultural fields, there is in contrast a risk of considerable nitrogen accumulation. More generally, the sensitivity of nitrogen concentrations in the ADRB to climate-driven changes in runoff and discharge is likely to be shared with many highly managed basins in arid and semiarid regions of Central Asia, and the world.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
A main part of renewable water resources in agriculturally well-developed, semiarid and arid regions of Central Asia, as well as South-Eastern Australia, the Middle-East, Northern Africa and the Western USA, is currently diverted and used for irrigation (Kotb et al. 2000; Hauer and Lorang 2004; Venot and Molle 2008; Walker et al. 2009). Meeting irrigation needs of water-demanding crops (e.g., rice and cotton) in such regions generally comes at the cost of high water loss through evapotranspiration (ET). This implies decreased runoff, which modifies hydrological conditions at local to global scales, potentially impacting water availability (Shibuo et al. 2007; Jarsjö et al. 2012; Jaramillo and Destouni 2015).
Agricultural intensification is frequently also associated with heavy use of nitrogen (N) (Gordon et al. 2008; Johansson et al. 2009; Törnqvist et al. 2011), which accelerates the cycling of N, contributing globally to observed increases in N-loads in world rivers (Seitzinger et al. 2010). This has led to several negative effects on ecosystems and human health. They differ between regions and include failure to reach health-based water quality criteria, eutrophication, blooms of toxic algae, sea bottom death and loss of biodiversity (Foley et al. 2005; Conley et al. 2009; Törnqvist et al. 2011).
However, in principle, the modified hydrological conditions of irrigated basins can also fundamentally impact the waterborne transport pathways and travel times, in such a way that retention–attenuation of nutrients increases. Hence, even if accumulation of excess N occur at and near agricultural fields, a sufficiently increased retention–attenuation would imply decreased net substance loading to downstream recipients. Notably, laboratory experiments as well as experiments at agricultural plots have shown that the degree of water recirculation, which is a measure of water-reuse, is a critical parameter that is positively correlated with nitrogen retention–attenuation and negatively correlated with the nitrogen concentrations of the outflowing water (Takeda et al. 1997; Feng et al. 2004; Hitomi et al. 2006).
In all cases, projections of future hydrological conditions and nutrient loads need to account for ongoing climate change, since it profoundly changes runoff patterns and thereby also creates quite modified conditions regarding the cycling and attenuation of substances (Palmer et al. 2008; Törnqvist et al. 2015). For instance, projected future temperature increases will generally enhance ET and may reinforce already existing effects of irrigation-induced ET increases (e.g., Jarsjö et al. 2012). Consequently, climate can influence attenuation and transformation of nutrients and pesticides, for instance through its control on transport pathways and residence times (Bloomfield et al. 2006; Howarth et al. 2006). However, effects may differ considerably between regions and can be difficult to detect, not least due to the complexity and variability of relevant processes (Destouni and Darracq 2009). Furthermore, in predictions of future development, it is in particular precipitation and freshwater flux trends that are subject to relatively large uncertainty (e.g., Asokan et al. 2016). Uncertainties have, however, been shown to decrease considerably if multi-model ensemble average outputs are used from global circulation models (GCMs), instead of individual GCM output (e.g., Jarsjö et al. 2012; Bring et al. 2015).
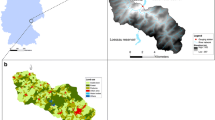
Rivers in Asia are expected to experience large future changes in the loading and export of N, compared to global average conditions, for instance due to population dynamics and heavy fertilizer use (Seitzinger et al. 2010). Targeting here specifically processes in areas that already are hydrologically modified by water diversions and irrigation, we use the example case of Central Asia and its Aral Sea Drainage Basin (ASDB; covering 1.3% of the earth’s land surface; Fig. 1a), which is large and extensive enough to be well resolved by general circulation models (GCMs). The region has been subject to large-scale irrigation development (e.g., Rakhmatullaev et al. 2010; Törnqvist and Jarsjö 2012), with the irrigation area increasing from 2.5 million ha in 1910 to 7.4 million ha in 1990. This has resulted in hydrological changes at scales that thus far are unprecedented in the world, with drastic discharge decreases in the principal Amu Darya and Syr Darya Rivers, drying of the Aral Sea and water quality deterioration including salinization of the region’s water sources (Jarsjö and Destouni 2004; Shibuo et al. 2006; Micklin 2007; Johansson et al. 2009).
a Location map of the Aral Sea Drainage Basin (ASDB, delimited by the thick red solid line, based on the basin delineation by Shibuo et al. 2007) in Central Asia, and its two principal rivers Amu Darya and Syr Darya. Irrigated areas are shown in green. b Principal sketch of water rerouting and recirculation in the ASDB, for which the recirculation ratio r is defined as r = ΣQdiv/Qout
The focus on Central Asia and ASDB is further motivated by ASDB being the first case where historic increases in basin-scale water recirculation have been quantitatively related to observed decreases in riverine N-loads (Törnqvist et al. 2015). There are two main mechanisms that can cause this relation. First, nitrogen may be increasingly exposed to the atmosphere as irrigation expansion brings more water to the soil surface, which for instance can favor nitrogen removal through denitrification. Second, as return flows from upstream regions increasingly are being reused for irrigation of downstream fields, total flow path lengths through the groundwater systems can increase (Törnqvist et al. 2015). This may cause increased filtering of N through the groundwater system and enhanced N retention–attenuation. In particular, defining the recirculation ratio r as the ratio between the sum of all water diversions along the river (Qdiv) and the river outflow from the basin (Qout; see schematic illustration of Fig. 1b), Törnqvist et al. (2015) developed quantitative expressions for how the considerable increases in r during the period 1960–2000 were related to distinct decreases in dissolved inorganic nitrogen concentrations [DIN] in Amu Darya River, despite increasing N fertilizer use within the basin. Recognizing that such quantitative, cause and effect understanding of past development is key for developing dependable future predictions, we here aim at investigating to which extent projected future climate change can further influence fundamental characteristics of the system, such as the recirculation ratio of irrigation and river water. We use above-mentioned quantitative expressions to investigate if this, in turn, can affect future basin-scale nitrogen cycling and attenuation, even in the limiting case that current water diversions and nitrogen application practices are maintained also in the future, which may have important implications for the status and management of water resources in ASDB and Central Asia.
Study site
With an area of 1,874,000 km2, ASDB covers the main part of Central Asia and is shared among Kazakhstan, Turkmenistan, Uzbekistan, Afghanistan, Kyrgyzstan and Tajikistan (Fig. 1a; water divide shown with red solid line). The two principal rivers Amu Darya and Syr Darya originate in the mountains of Tajikistan and Kyrgyzstan, where most (67%) of ASDB’s renewable water resources are formed. The Amu Darya River Basin (ADRB) has an extent of 465,000 km2 (Asarin et al. 2010). The main part of this basin is a low lying arid plain with low precipitation (below 100 mm year−1 in the Amu Darya delta) and high ET. The mountainous areas in the south–east part of the basin are much wetter with on average 500 mm precipitation per year. The temperature is on average 15 °C in the lower areas and below 0 °C in the highest regions (CRU dataset; Mitchell and Jones 2005).
The discharge of Amu Darya River at Kziljar (near its former outlet to the Aral Sea; Fig. 1a) has reduced drastically due to the large irrigation expansion starting in the 1950s. During the period 1960–2000, the irrigated areas expanded by 40,000 ha year−1 in the Amu Darya River basin. As a result, 3,650,000 ha was irrigated by 47 km3 diverted river water in the year of 2000 (Aus Der Beek et al. 2011). Cotton and wheat are the dominant crops in the irrigated fields, which in turn are dominated by relatively water-inefficient furrow irrigation practices where significant water losses occur as water is led to the fields in open channels and is distributed over the fields in trenches between rows of crops (e.g., Törnqvist and Jarsjö 2012). Before the irrigation expansion, the average river discharge at the outlet of the basin was 70 km3 year−1 (Crosa et al. 2006; Törnqvist et al. 2015). Due to the river water diversions and ET losses over the irrigated fields, the Amu Darya discharge at the outlet has decreased (Fig. 2a, light blue symbols) down to around 6 km3 year−1 after 1980 (Fig. 2a, dark blue symbols; Benduhn and Renard 2004; Jarsjö et al. 2012; Oberhänsli et al. 2009). Since the total water diversions Qdiv to the expanding irrigated areas increased rapidly between 1960 and 1980 at the same time as the discharge Qout decreased, the recirculation ratio r, defined as the ratio between these two parameters (Fig. 1b) also increased rapidly from a value around 1.4 in 1960 to an average value of 5.7 during the period 1980–2000 (dashed blue line in Fig. 2b; Törnqvist et al. 2015).
Whereas the content of N in the soils of the region varies approximately between 0.01 and 0.07% (Kienzler 2010), magnitudes of up to 250 kg ha−1 year−1 of N have been applied on irrigated fields as a result of agricultural intensification. Consequently, total amounts of N applied in the basin were around 160,000 ton year−1 in 1960, and increasing to an average of between 400,000 and 420,000 ton year−1 during the period 1980–2000 (Fig. 2b; Törnqvist et al. 2015). Estimates of the annual mean concentration of dissolved inorganic nitrogen (DIN) in the Amu Darya River exist for the Kziljar station, located near the Aral Sea outlet. They were computed from monthly monitoring data, as the sum of NO3-N, NO2-N and NH4-N concentrations, as further specified in Törnqvist et al. (2015). Counter intuitively, these DIN concentrations (which approximately equal total N concentrations) have been decreasing significantly since the 1960s (Fig. 2c; light red symbols), reaching values of around 0.5 mg L−1 after 1980 (Fig. 2c; dark red symbols), arguably being a result of increased DIN retention–attenuation (Törnqvist et al. 2015) at the above-mentioned high degrees of basin-scale water recirculation.
Methods
Multi-GCM projections of future climate changes
Acknowledging that the ensemble mean output of multiple GCMs yields considerably more dependable results than the output of a single GCM (Jarsjö et al. 2012; Bring et al. 2015), we extracted projected changes in temperature and precipitation between different future periods and the reference period 1961–1990 (∆T and ∆P) from 73 GCM projections reported in three previous studies (Asokan et al. 2016; Jarsjö et al. 2012; Lioubimtseva and Henebry 2009). The results were used as input in the hydrological modeling (see “Hydrological modeling” section). Three sets of projections of ∆T and ∆P for the former Soviet Central Asia between the years of 2025, 2050 and 2100, respectively, and reference period 1961–1990 were obtained from Lioubimtseva and Henebry (2009). They are based on 17 different GCM projections from the fourth assessment report (AR4) of the Intergovernmental Panel on Climate Change (IPCC 2007), i.e., UIUC-EQ, CSIRO2-EQ, NCAR-DOE, CSIRO1-EQ, GFDK-TR, BMRC-EQ, HadCM2, CSIRO-TR, ECHAM1, CCSR-NIES, ECHAM3, CCC-EQ, ECHAM4, UKHI-EQ, CGCM1-TR, UKTR and ECHAM5. Another set of projections of ∆T and ∆P in the ASDB between the period 2010–2039 (i.e., around 2025) and the reference period 1961-1990 was obtained from Jarsjö et al. (2012). These projections are based on 14 different GCMs from AR4, i.e., CSIRO-CSMK3, ECHAM5-MPEH5, GFDL-GFCM_20_21, HADCM3, NIES-MIMR, CNCM3, ECHOG, GIER, HADGEM, INCM3, IPCM4, MRCGCM, NCCCSM, NCPCM, CSIRO-MK2, ECHAM4, GFDL99-R30, HADCM3, CCSR-NIES and CCCma-CGCM2. Finally, four sets of projected △T and △P in the ASDB between the reference period and the periods 2010–2039 (i.e., around 2025) and 2070–2099 (i.e., around 2085) were taken from Asokan et al. (2016). Specifically, we here consider the two models (GFDL-ESM2G and MPI-ESM-MR) that came out as best performing regarding historical water flux changes in ASDB, out of the 22 Coupled Model Intercomparison Project, Phase 5 (CMIP5) models that were evaluated by Asokan et al. (2016). The two models were run for the Representative Concentration Pathway (RCP) 2.6 scenario, as well as for the RCP 8.5 scenario.
Hydrological modeling
Present results are based on off-line hydrological modeling, which implies that GCM output is used as input for the hydrological model. For instance, if one would directly use the paired ∆T and ∆P output from the here considered 73 GCM models, the hydrological model would be run 73 times. However, since several GCM models in the present case gave similar ∆T and ∆P outputs, some hydrological model runs would not give much new information using such a procedure. In order to increase the information content of each hydrological model run, we here instead discretized the total prediction envelopes of ∆T and ∆P using even spacing, choosing a resolution that gives a matrix of i × j evenly spaced nodes where i = j = 11. The ∆T i and ∆P j values of each node were added to a baseline map (from the CRU TS 2.1 database; Mitchell and Jones 2005) of reference period temperature (T0) and reference period precipitation (P0), i.e., T future,i = T 0 + ∆T i and P future,i = P 0 + ∆P j . This resulted in 121 pairs of Tfuture,i and Pfuture,i maps of ASDB that were used as input to a total of 121 hydrological model runs. In turn, these runs gave 121 ASDB maps with distributed annual runoff values, from which the cumulative Amu Darya River discharge Qfuture at the basin outlet was extracted (more hydrological model details are given in a separate paragraph below). The 121 values of Qfuture hence corresponded to the 121 different combinations of T 0 + ∆T and P 0 + ∆P according to the nodes of the matrix. The change in river discharge ∆Q was obtained by subtracting the Q 0 value from Q future, where Q 0 was obtained for ∆T = 0 and ∆Q = 0. The values of those nodes were finally interpolated to produce a continuous hydrological response map that visualizes the responses of the Amu Darya River discharge to climate change within the total envelopes of ∆T and ∆P given by the 73 GCM models.
The water flow routines of the PCRaster-based Polflow model (De Wit 2001) were used to quantify the changes in river discharge from projected future climate change. The distributed hydrological PCRaster model has previously been used to model hydro-climatic responses in the ASDB and other catchments (Shibuo et al. 2007; Destouni et al. 2010; Jarsjö et al. 2012; Törnqvist and Jarsjö 2012; Asokan et al. 2010). The model is based on a water balance approach of Q = P − ET − ∆S, where ∆S is the storage change which is assumed to be negligible on the considered long-term basis. The modeling in this study follows similar procedures as in Shibuo et al. (2007) and Jarsjö et al. (2012) to examine climate change impacts under current irrigation practices. P and T data from CRU TS 2.1 database (Mitchell and Jones 2005) were used to calculate potential ET (ETp) using Langbein method (1949) and actual ET (ETa) using Turc method (Turc 1954). Irrigation water was rerouted from the river to irrigated areas according to Global map of irrigated areas (Siebert et al. 2005) and applied as extra precipitation. Digital elevation data from Shuttle Radar Topography Mission (SRTM 2004) were used to generate flow pathways and flow accumulation of runoff R expressed as R = P − ETa. The river discharge (Q) in a specific point was generated as the sum of flow accumulation in all contributing upstream grid cells.
Water recirculation, nitrogen retention–attenuation model and data
Analogous to the work of Törnqvist et al. (2015) we assume that nitrogen undergoes first-order degradation along hydrological flow pathways, expressed as exp[-λT], where λ is the attenuation rate and T is the mean travel time. The magnitude of internal flow redistribution within the basin is characterized by a water recirculation ratio r, as defined previously in Fig. 1b. A certain fraction (f) of Qdiv is assumed to be lost through ET over the irrigated fields. This dimensionless fraction is expressed as f = ETirr/Qdiv where ETirr is the additional ET (expressed in units of flow) from the irrigation of the basin. ETirr was calculated from the Polflow modeling (see “Hydrological modeling” section) as the total ET under conditions of irrigation and water rerouting (ETirr+nat) minus natural ETnat, i.e., ET without rerouting of river water. The nitrogen attenuation rate λ was further assumed to change as function of r due to increased flow path lengths, where λ(r) = λ(1 + αr) and α is a constant that allows for different significance of r on the attenuation effect for different conditions. The outflow–inflow concentration ratio (Cout/Cin) can then be expressed analytically as (Törnqvist et al. 2015):
where β = (1 + αr)·((f 1)r/(1 + fr) 1)−1, C out(r) is the concentration at the basin outlet, and C in is the concentration of upstream runoff.
An effective value of the basin-scale attenuation product λT for nitrogen was estimated by matching Eq. (1) to observation data from the 20-year period 1960–1980 with a low r-value (1.4). The basin characteristic λT-value was then tested to fit observation data from 1981 to 2000 that were characterized by a much larger r (5.7) due to irrigation intensification. For these periods, monthly observations of dissolved inorganic nitrogen concentrations [DIN] were available from at Kziljar gauging station close to the Aral Sea outlet (Nasrulin and Zahidova 2002). Dissolved inorganic nitrogen concentrations were computed as the sum of NO3-N, NO2-N and NH4-N concentrations. As also explained in Törnqvist et al. (2015), a main reason for focusing on DIN is that it comprises highly soluble and dominant (in particular NO3 −) forms of nitrogen in agriculturally impacted river systems, and since monitoring data existed for these fractions. The data were used to estimate C out (r = 1.4) and C out (r = 5.7). Corresponding C in values were calculated as basin-scale N input not taken up by crops divided by upstream modeled R (R = P − ETnat). The derived basin-scale value of λT for nitrogen was used in combination with GCM-based projections of future river flow to estimate possible climate-driven changes in riverine nitrogen concentrations at the outlet.
Results and discussion
Changing regional climate
In the considered near-future period (around 2025), the mean annual temperatures of Central Asia (Fig. 3a, blue circles) including the ASDB (Fig. 3a, purple and black circles) are projected to become considerably higher than in the reference period 1961–1990, with values of ∆T (i.e., future temperature minus historic temperature) between 1.0 and 2.0 °C. The GCM projection results converge on showing positive and further increasing ∆T after 2025, with ∆T-values from 1.7 to 2.8 °C around 2050 (Fig. 3a, squares), and from 1.4 to 5.0 °C around 2100 (Fig. 3a, triangles).
a Projections of future change in temperature ΔT and precipitation ΔP in the ASDB according to 14 GCM projections from AR4 for 2025 (Jarsjö et al. 2012), 51 GCM projections from AR4 for Central Asia around 2025, 2050 and 2100 (Lioubimtseva and Henebry 2009) and 4 GCM projections from CMIP5 for ASDB around 2025 and 2085. The large dashed rectangle shows the prediction envelope considered in current hydrological modeling. b Modeled flow change ∆Q in the Amu Darya River near its outlet, in response to a relatively wide window of ∆T and ∆P combinations that covers all ∆T and ∆P combinations of the considered 73 GCM projections. The ensemble mean values and standard deviation of the multi-model output from AR4 are indicated with colored symbols and error bars, respectively, and the output of the best-performing CMIP5 models according to the ASDB evaluation of Asokan et al. (2016) is shown with black (open and closed) symbols
Individual GCM results for precipitation differences (∆P) are inconclusive, because some GCMs project negative ∆P (i.e., future precipitation < historic precipitation), whereas others project positive ∆P (future precipitation > historic precipitation). The range of ∆P-values is higher for projections of the more distant future. Specifically, it increases from between −16 and 26 mm year−1 (–6 and +10%, respectively, of the historical P) for 2025 to between −53 and 76 mm year−1 (−21 and +30%, respectively, of the historical P) for 2100. This demonstrates that individual GCMs projections of Central Asian precipitation are particularly uncertain for the distant future. However, calculation of the ensemble average ∆P for the different time periods considered here shows that ∆P is positive in all cases (+4.9 mm year−1 for 2025, +4.0 mm year−1 for 2050 and +13 mm year−1 for 2100), which indicates increased future precipitation.
Considerably overlapping prediction envelopes for Central Asia (from Lioubimtseva and Henebry 2009) and ASDB (from Jarsjö et al. 2012; Asokan et al. 2016) show that the range of projected future changes for ASDB is similar to that of Central Asia (Fig. 3a). Furthermore, ∆T and ∆P projections are similar for the ASDB and the ADRB, with differences in the ensemble mean values between the basins (e.g., in 2025 ∆T = 1.53 °C for ASDB and ∆T = 1.48 °C for ADRB) being much smaller than the difference in output between individual models within each basin. Particularly, since a relatively large prediction envelope was considered in the hydrological modeling of “River flow response to projected climate changes” section (0 ≤ ∆T ≤ 5 °C; −20% ≤ ∆P ≤ +30%) it may be seen as representative for Central Asia, ASDB as well as ADRB.
River flow response to projected climate changes
Figure 3b shows modeled river flow changes ∆Q (i.e., Q of the considered future periods minus Q of the reference period 1961–1990) within the envelope of future ∆T and ∆P given by the 73 considered GCM projections. There is a wide range of ∆Q (between −25 and +20 km3 year−1; see scale bar of Fig. 3b) within this envelope. In other words, the different projections of ∆T and ∆P from single GCMs (Fig. 3a) yield relatively different ∆Q-results, which are inconclusive regarding even the direction of ∆Q (i.e., positive or negative). However, considering the ensemble average output (Fig. 3b; colored symbols) for the different considered time periods, the results converge on showing negative ∆Q, with values ranging from −3 km3 year−1 around 2025 (Fig. 3b; blue circle) to—7 km3 year−1 around 2100 (Fig. 3b; green triangle). In addition, standard deviations around the ensemble averages (Fig. 3b; error bars) mainly encompass negative values of ∆Q. Similarly, the best-performing CMIP5 models show negative ∆Q-results for the high radiative forcing scenarios around 2085 (Fig. 3b; filled, black triangles). Results diverge for lower radiative forcing and shorter time horizons (Fig. 3b; circles and open triangles).
Notably, due to water losses related to the extensive irrigation in the ADRB, a relevant reference flow reflecting current conditions of Amu Darya River is around 6 km3 year−1 only (see “Study site” section). Illustrating how much projected future climate change alone can further modify this reference flow, we add the ∆Q-values from the ensemble projections to the reference value. The results demonstrate that the projected ensemble average temperature and precipitation changes are associated with considerably decreased discharges of Amu Darya River, by around 50% (6−3 = 3 km3 year−1) in 2025 and to compete dry-out at the outlet (6−7 < 0 km3 year−1) in 2100.
Implications for irrigation water recirculation and nitrogen attenuation
Figure 4a shows how potential future climate-driven changes in Amu Darya River discharge (∆Q) influences the water recirculation ratio r = Q div/Q out of its basin, considering the case that current water diversion practices are maintained also in the future (i.e., keeping Q div constant). In this case, changes in r will be inversely proportional to future changes in Q out, future, which can be expressed in terms of the current outflow Q out,current and a climate-driven change in future discharge ∆Q (e.g., from Fig. 3b) as Q out, future = Q out,current + ∆Q. For instance, Fig. 4a shows that a climate-driven ∆Q of +4 km3 year−1 in the Amu Darya River discharge would yield an r decrease from today’s value of 5.7 (orange circle) to 3.7. However, whereas projections of some individual GCMs suggested such river discharge increases, ensemble average results showed that Amu Darya River discharge is likely to decrease in the future. Considering instead a negative ∆Q of −4 km3 year−1, Fig. 4a shows that r would increase considerably from today’s value of 5.7 to approximately 17.
a Relation between climate-driven change in river discharge ∆Q at the ADRB outlet and the water recirculation ratio r, and projected future b r-values of Amu Darya Drainage Basin and c N concentrations in its downstream river water in years 2025, 2050 and around 2085–2100, based on output from CMIP5 and AR4 climate models
Historically, the main driver of change in r has been irrigation expansion (Törnqvist et al. 2015), which has increased Qdiv and consequently ADRB’s r-value from 1.4 in 1960 to today’s value of 5.7. The present result illustrates that, even without further direct modifications of Q div, the r-value is now also sensitive to climate-driven ∆Q, and in particular to negative ∆Q. The reason for the increased sensitivity is that the current outflow Q out,current is approximately equally large as plausible values of climate-driven ∆Q, which has large impact on r = Q div/(Q out,current + ∆Q). This did not use to be the case, since Q out historically was much higher than today, such that any given ∆Q to larger extent was dwarfed by this high outflow value.
We note that the use of water in the upstream, Tajik part of the Amu Darya River Basin, is likely to increase in the future, since there is an ongoing expansion of hydropower, in addition to demands from the agricultural sector (e.g., Jalilov et al. 2016). The hydropower expansion is expected to decrease water availability, particularly during the growing season when the need is high in the downstream, agriculturally dominated Uzbek part of the basin. Our basic assumption, that current basin-scale net water diversions Qdiv (and associated net water use) will be maintained rather than continuing to increase in the future, is, however, consistent with prevailing conditions of severe water shortage. The reason is that any further increases in upstream water use will almost certainly be largely compensated by forced decreases in downstream water use, due to lack of water.
There is at the same time high potential to considerably decrease the water use in the agricultural sector. Water savings may also become necessary in the long run, if water shortage will increase in a future climate. Water losses in inefficient irrigation and distribution systems, characterized by furrow irrigation and open distribution channels, then need to be reduced by improving irrigation techniques and infrastructure (Bekchanov et al. 2016). For instance, it has been estimated that a basin-wide improvement of irrigation methods could lead to water savings of 1 km3 year−1 or more in the Aral Sea Drainage Basin (Törnqvist and Jarsjö 2012). Water can additionally be saved by reducing the water-demanding cultivation of cotton and rice to the benefit of, e.g., tree plantations and cultivation of maize, melon, mung bean, potato and vegetables (Bobojonov et al. 2013; Djanibekov et al. 2013).
The possible reduction in irrigation water use by 1 km3 year−1 from improving current practices corresponds to changing the recirculation ratio r in the Amu Darya River Basin from today’s value of 5.7–4.9 (i.e., about 15% decrease). This scenario may be optimistic, at least when considering the near future, since such large-scale improvements are associated with high initial costs, which may delay implementation. Basin-wide changes in today’s cropping practices that may save large quantities of water are furthermore not anticipated in the near future, since changes in governmental policies then are required, which have not yet been seen (Abdullaev and Rakhmatullaev 2015). For these reasons, and for comparative purposes, we will in the following continue to explore impacts of ongoing climate change alone, allowing us to identify the (specific) system sensitivity to climate variables under the assumption that current net water diversions will be maintained at a constant level in the future.
Figure 4b shows more specifically how the current r-value of the Amu Darya River Basin (equal to 5.7) is expected respond to projected changes in hydro-climatic conditions in the coming century, based on ∆Q estimated from average ∆T and ∆P of the best-performing CMIP5 climate models (red bars) and the multi-model ensemble average ∆T and ∆P from the AR4 model runs (blue bars). In 2025, Fig. 4b shows that r is expected to be anywhere between essentially unchanged (according to the CMIP5-results) to being twice as high as today (according to the AR4-results). However, despite this discrepancy on near-future r-values, both the CMIP5-results and the AR4-results show robustly that r-values will be orders of magnitudes higher toward the end of the century (2085–2100). For the AR4-models, results are available also for the year 2050, suggesting that r-values will be yet higher than in 2025, but not as high as in 2100.
The average [DIN] near the outlet of the Amu Darya River around 1960 (r = 1.4) was 3–4 times higher than in the 1981–2000 period (Fig. 2c; r = 5.7); previous results demonstrated that this observed decrease in [DIN] could be reproduced by Eq. (1) based on the corresponding historical changes in r (Fig. 2b; Törnqvist et al. 2015). Correspondingly, the bars of Fig. 4c show the expected future [DIN], normalized by the 1981–2000 [DIN] of Amu Darya River, assuming that the water recirculation will change in according to Fig. 4b, and that the attenuation of N can be described with the attenuation product λT = 1 (Eq. 1), which is a value that is consistent with historical observations of N attenuation in Amu Darya River Basin (Törnqvist et al. 2015). Independent assessments additionally show that this attenuation product value agrees with observed attenuation of nitrogen at the field scale (Darracq et al. 2010a, b; Persson et al. 2011).
Specifically, Fig. 4c then shows that in 2025, N concentrations (and in particular [DIN]) may be expected to range essentially between values similar to, or slightly above current [DIN] (red bar; CMIP5-results), down to distinct [DIN] reductions by approximately a factor 4 (blue bar; AR4-results). The error bars show the sensitivity of this result with respect to assumed λT, within the possible range of 0.8 < λT < 1.4. This uncertainty appears to be smaller than the effect of the uncertain output from the climate models (i.e., the differences in results based on the AR4 models and the CMIP5 models).
Despite these uncertainties, all model results converge on showing that in year 2050 and after, climate-driven enhancement of the recirculation ratios in ASDB will be sufficient to increase retention–attenuation of DIN by several orders of magnitude, which would decrease riverine [DIN] at the basin outlet. This is a considerable effect that apparently has played a role also in the past, as reflected by the coinciding historical increases in r and decreases in [DIN] observed in the lower parts of the Amy Darya River (Törnqvist et al. 2015). Without further investigation, one cannot exclude the possibility that similar effects of enhanced retention–attenuation can have contributed to decreasing [DIN] trends observed in several rivers of irrigated basins across the world, despite unchanged or increased fertilizer use (e.g., Bouraoui and Grizzetti 2011; Lohrenz et al. 2008), in contrast to the global average trends of increasing [DIN] (Seitzinger et al. 2010). Regarding future conditions in Central Asia, climate projections (Lioubimtseva and Henebry 2009; Koirala et al. 2014) suggest that temperatures will increase and runoff decrease in a similar way as in the ASDB, which implies that also other Central Asian rivers may be subject to similar changes in retention–attenuation of DIN as the here investigated principal Amu Darya River. Notably, even though this implies that downstream river waters would contain less DIN in the future, this does not exclude the risk of considerable DIN accumulation in soil water and groundwater closer to the agricultural fields. This is because of the prolonged flow path lengths related to increased recirculation of water (see also Hitomi et al. 2006; Wilcock et al. 2012), which can potentially lead to more efficient filtering and hence retention of DIN in these water systems.
Observations made at the plot scale have furthermore shown that the concentration of substances other than nitrogen, for example phosphorous and organic matter, can also decrease in downstream recipients when the water recirculation increases. This is due to increased retention and comes at the cost of elevated upstream concentrations in the agricultural plots (Feng et al. 2004; Hama 2012). It is hence plausible that other substances than the here studied nitrogen are impacted by large-scale, climate-driven changes in recirculation ratios. The ongoing and severe salinization of the soils at and near agricultural fields in the downstream part of the Amu Darya River Basin (e.g., Johansson et al. 2009) may then also be impacted by climate-driven changes in recirculation ratios. More specifically, whereas the current salinization could be attributed mainly to agricultural intensification, there is now an apparent risk that ongoing climate change can further aggravate the salinization of agricultural soils, since the re-recirculation of already saline return flows may increase in the future as a result of climate-related water shortage.
Conclusions
Results based on ensemble average GCM output from 73 multi-model projections converge on showing trends of considerably increasing temperature and slightly increasing precipitation in Central Asia and the Aral Sea Drainage Basin (ASDB), and decreasing discharge (Q) in its principal Amu Darya River, throughout the coming century (∆T = +5 °C, ∆P = +13 mm year−1 and ∆Q = −7 km3 year−1 in 2100). In contrast, results based on single GCMs were not consistent, showing large spread and including contradictory results on the direction of precipitation and Q change.
There is today a high degree of river water diversion and irrigation water reuse (recirculation ratio r = 5.7) in the Amu Darya River Basin (ADRB) that covers a large part of ASDB. Whereas this is a result of expansion of irrigated agriculture, present results show that even without further agricultural expansion, the r-value of ADRB is likely to continue to increase during the coming decades. This is because r has now (due to the expansion) become highly sensitive to climate-driven changes in runoff and river discharge (e.g., a ∆Q of −4 km3 year−1 would drive r from 5.7 to 17).
Parallel results across different scales have shown a strong dependence between r and the retention–attenuation of DIN. Using a basin-scale analytical recirculation model adopted for the nitrogen loading conditions of ADRB, we show that DIN concentrations may decrease considerably in downstream river waters in the future, due to projected climate-related increases in r. A plausible reason is that total flow path lengths through the groundwater systems will increase as r increases, leading to more efficient filtering of DIN, and enhanced DIN retention. This is associated with a risk of considerable DIN accumulation in soil water and groundwater near the agricultural fields, even though the previously mentioned enhanced retention implies that downstream river waters would contain less DIN in the future. More generally, the sensitivity of r and [DIN] in ADRB to climate-driven changes in runoff and discharge is likely to be shared with many highly managed basins in arid and semiarid regions of Central Asia, and the world.
References
Abdullaev I, Rakhmatullaev S (2015) Transformation of water management in Central Asia: from State-centric, hydraulic mission to socio-political control. Environ Earth Sci 73(2):849–861
Asarin AE, Kravtsova VI, Mikhailov VN (2010) Amudarya and Syrdarya Rivers and their deltas. In: Kostinaoy A (ed) The Aral Sea environment. Springer, Berlin, pp 101–121
Asokan SM, Jarsjö J, Destouni G (2010) Vapor flux by evapotranspiration: effects of changes in climate, land use, and water use. J Geophys Res. doi:10.1029/2010JD014417
Asokan SM, Rogberg P, Bring A, Jarsjö J, Destouni G (2016) Climate model performance and change projection for freshwater fluxes: comparison for irrigated areas in Central and South Asia. J Hydrol Regional Studies 5:48–65
Aus Der Beek T, Voß F, Flörke M (2011) Modelling the impact of global change on the hydrological system of the Aral Sea basin. Phys Chem Earth 36(13):684–695
Bekchanov M, Ringler C, Bhaduri A, Jeuland M (2016) Optimizing irrigation efficiency improvements in the Aral Sea Basin. Water Resour Econ 13:30–45
Benduhn F, Renard P (2004) A dynamic model of the Aral Sea water and salt balance. J Mar Syst 47(1):35–50
Bloomfield JP, Williams RJ, Gooddy DC, Cape JN, Guha P (2006) Impacts of climate change on the fate and behaviour of pesticides in surface and groundwater—a UK perspective. Sci Total Environ 369(1–3):163–177
Bobojonov I, Lamers JP, Bekchanov M, Djanibekov N, Franz-Vasdeki J, Ruzimov J, Martius C (2013) Options and constraints for crop diversification: a case study in sustainable agriculture in Uzbekistan. Agroecol sustain food 37(7):788–811
Bouraoui F, Grizzetti B (2011) Long term change of nutrient concentrations of rivers discharging in European seas. Sci Total Environ 409(23):4899–4916
Bring A, Asokan SM, Jaramillo F, Jarsjö J, Levi L, Pietroń J, Prieto C, Rogberg P, Destouni G (2015) Implications of freshwater flux data from the CMIP5 multimodel output across a set of Northern Hemisphere drainage basins. Earth’s Future 3(6):206–217
Conley DJ, Björck S, Bonsdorff E, Carstensen J, Destouni G, Gustafsson BG, Hietanen S, Kortekaas M, Kuosa H, Markus Meier HE, Müller-Karulis B (2009) Hypoxia-related processes in the Baltic Sea. Environ Sci Technol 43(10):3412–3420
Crosa G, Froebrich J, Nikolayenko V, Stefani F, Galli P, Calamari D (2006) Spatial and seasonal variations in the water quality of the Amu Darya River (Central Asia). Water Res 40(11):2237–2245
Darracq A, Destouni G, Persson K, Prieto C, Jarsjö J (2010a) Quantification of advective solute travel times and mass transport through hydrological catchments. Environ Fluid Mech 10(1–2):103–120
Darracq A, Destouni G, Persson K, Prieto C, Jarsjö J (2010b) Scale and model resolution effects on the distributions of advective solute travel times in catchments. Hydrol Process 24(12):1697–1710
De Wit MJM (2001) Nutrient fluxes at the river basin scale. I: the PolFlow model. Hydrol Process 15(5):743–759
Destouni G, Darracq A (2009) Nutrient cycling and N2O emissions in a changing climate: the subsurface water system role. Environ Res Lett 4(3):035008
Destouni G, Asokan SM, Jarsjö J (2010) Inland hydro-climatic interaction: effects of human water use on regional climate. Geophys Res Lett 37(18):L18402. doi:10.1029/2010GL044153
Djanibekov N, Sommer R, Djanibekov U (2013) Evaluation of effects of cotton policy changes on land and water use in Uzbekistan: application of a bio-economic farm model at the level of a water users association. Agric Syst 118:1–13
Feng YW, Yoshinaga I, Shiratani E, Hitomi T, Hasebe H (2004) Characteristics and behavior of nutrients in a paddy field area equipped with recycling irrigation system. Agric Water Manag 68(1):47–60
Foley JA, DeFries R, Asner GP, Barford C, Bonan G, Carpenter SR, Chapin FS, Coe MT, Daily GC, Gibbs HK, Helkowski JH, Holloway T, Howard EA, Kucharik CJ, Monfreda C, Patz JA, Prentice IC, Ramankutty N, Snyder NK (2005) Global consequences of land use. Science 309(5734):570–574
Gordon LJ, Peterson GD, Bennett EM (2008) Agricultural modifications of hydrological flows create ecological surprises. Trends Ecol Evol 23(4):211–219
Hama T (2012) Cyclic irrigation for reducing nutrients and suspended solids loadings from paddy fields in Japan. In: Garcia-Garizabal I (ed) Irrigation—water management, pollution and alternative strategies. In Tech, Rijeka, Croatia. ISBN: 978–953–51–0421–6
Hauer FR, Lorang MS (2004) River regulation, decline of ecological resources, and potential for restoration in a semi-arid lands river in the western USA. Aquat Sci 66(4):388–401
Hitomi T, Yoshinaga I, Feng YW, Shiratani E (2006) N removal function of recycling irrigation system. Water Sci Technol 53(2):101–109
Howarth RW, Swaney DP, Boyer EW, Marino R, Jaworski N, Goodale C (2006) The influence of climate on average nitrogen export from large watersheds in the Northeastern USA. Biogeochemistry 79(1–2):163–186
IPCC (2007) Climate change 2007: synthesis report. In: Pachauri RK, Allen MR, Barros VR, Broome J, Cramer W, Christ R, Church JA, Clarke L, Dahe Q, Dasgupta P, Dubash NK (eds) Contribution of working groups I, II and III to the fourth assessment report of the intergovernmental panel on climate change. Switzerland, Geneva
Jalilov SM, Keskinen M, Varis O, Amer S, Ward FA (2016) Managing the water-energy-food nexus: gains and losses from new water development in Amu Darya River basin. J Hydrol 539:648–661
Jaramillo F, Destouni G (2015) Local flow regulation and irrigation raise global human water consumption and footprint. Science 350(6265):1248–1251
Jarsjö J, Destouni G (2004) Groundwater discharge into the Aral Sea after 1960. J Mar Syst 47(1–3):109–120
Jarsjö J, Asokan SM, Prieto C, Bring A, Destouni G (2012) Hydrological responses to climate change conditioned by historic alterations of land-use and water-use. Hydrol Earth Syst Sci 16(5):1335–1347
Johansson O, Aimbetov I, Jarsjö J (2009) Variation of groundwater salinity in the partially irrigated Amudarya River delta, Uzbekistan. J Mar Syst 76(3):287–295
Kienzler KM (2010) Improving the N use efficiency and crop quality in the Khorezm region, Uzbekistan. Ph.D. Dissertation. Der Hohen Landwirtschaftlichen Fakultät der Rheinischen Friedrich-Wilhelms-Universität, Bonn, Germany. Available at: http://hss.ulb.uni-bonn.de/2010/1983/1983-print.pdf
Koirala S, Hirabayashi Y, Mahendran R, Kanae S (2014) Global assessment of agreement among streamflow projections using CMIP5 model outputs. Environ Res Lett 9(6):064017
Kotb THS, Watanabe T, Ogino Y, Tanji KK (2000) Soil salinization in the Nile Delta and related policy issues in Egypt. Agric Water Manage 43(2):239–261
Langbein WB (1949) Annual runoff in the USA. US Geological Survey Circular 52:14 US Department of the Interior, Washington
Lioubimtseva E, Henebry GM (2009) Climate and environmental change in arid Central Asia: impacts, vulnerability, and adaptations. J Arid Environ 73(11):963–977
Lohrenz SE, Redalje DG, Cai WJ, Acker J, Dagg M (2008) A retrospective analysis of nutrients and phytoplankton productivity in the Mississippi River plume. Cont Shelf Res 28(12):1466–1475
Micklin P (2007) The Aral Sea disaster. Annu Rev Earth Planet Sci 35:47–72
Mitchell TD, Jones PD (2005) An improved method of constructing a database of monthly climate observations and associated high-resolution grids. Int J Climatol 25(6):693–712
Nasrulin A, Zahidova M (2002) The experience of creation of the GIS System of ecological monitoring in Aral Sea Basin. J Prob Mech 4:38–43
Oberhänsli H, Weise SM, Stanichny S (2009) Oxygen and hydrogen isotopic water characteristics of the Aral Sea, Central Asia. J Marine Syst 76(3):310–321
Palmer MA, Reidy Liermann CA, Nilsson C, Flörke M, Alcamo J, Lake PS, Bond N (2008) Climate change and the world’s river basins: anticipating management options. Front Ecol Environ 6(2):81–89
Persson K, Jarsjö J, Destouni G (2011) Diffuse hydrological mass transport through catchments: scenario analysis of coupled physical and biogeochemical uncertainty effects. Hydrol Earth Syst Sci 15(10):3195–3206
Rakhmatullaev S, Huneau F, Kazbekov J, Le Coustumer P, Jumanov J, El Oifi B, Motelica-Heino M, Hrkal Z (2010) Groundwater resources use and management in the Amu Darya River Basin (Central Asia). Environ Earth Sci 59(6):1183–1193
Seitzinger SP, Mayorga E, Bouwman AF, Kroeze C, Beusen AHW, Billen G, Van Drecht G, Dumont E, Fekete BM, Garnier J, Harrison JA (2010) Global river nutrient export: a scenario analysis of past and future trends. Global Biogeochem Cy 24(4):GB0A08. doi:10.1029/2009GB003587
Shibuo Y, Jarsjö J, Destouni G (2006) Bathymetry-topography effects on saltwater-fresh groundwater interactions around the shrinking Aral Sea. Water Resour Res 42:W11410. doi:10.1029/2005WR004207
Shibuo Y, Jarsjö J, Destouni G (2007) Hydrological responses to climate change and irrigation in the Aral Sea drainage basin. Geophys Res Lett 34(21):L21406. doi:10.1029/2007GL031465
Siebert S, Döll P, Hoogeveen J, Faures JM, Frenken K, Feick S (2005) Development and validation of the global map of irrigation areas. Hydrol Earth Syst Sci 9(5):535–547
SRTM (2004) Hole-filled seamless SRTM (Shuttle Radar Topography Mission) data V1, International Centre for Tropical Agriculture, CIAT. http://gisweb.ciat.cgiar.org/sig/90m_data_tropics.htm. Accessed 02 Nov 2010
Takeda I, Fukushima A, Tanaka R (1997) Non-point pollutant reduction in a paddy-field watershed using a circular irrigation system. Water Res 31(11):2685–2692
Törnqvist R, Jarsjö J (2012) Water savings through improved irrigation techniques: basin-scale quantification in semi-arid environments. Water Resour Manag 26(4):949–962
Törnqvist R, Jarsjö J, Karimov B (2011) Health risks from large-scale water pollution: trends in Central Asia. Environ Int 37(2):435–442
Törnqvist R, Jarsjö J, Thorslund J, Rao PSC, Basu NB, Destouni G (2015) Mechanisms of basin-scale nitrogen load reductions under intensified irrigated agriculture. PLoS ONE 10(3):e0120015. doi:10.1371/journal.pone.0120015
Turc L (1954) Le bilan d’eau des sols: relations entre les précipitations l’évaporation et l’écoulement. Ann Agron 5:491–595
Venot JP, Molle F (2008) Groundwater depletion in the Jordan highlands: can pricing policies regulate irrigation water use? Water Resour Manag 22(12):1925–1941
Walker BH, Abel N, Anderies JM, Ryan P (2009) Resilience, adaptability, and transformability in the goulburn-broken catchment, Australia. Ecol Soc 14(1):12
Wilcock RJ, Müller K, van Assema GB, Bellingham MA, Ovendenet R (2012) Attenuation of N, phosphorus and E. coli inputs from pasture runoff to surface waters by a farm wetland: the importance of wetland shape and residence time. Water Air Soil Pollut 223(2):499–509
Acknowledgements
The work was funded by the Swedish International Development Cooperation Agency (Sida).
Author information
Authors and Affiliations
Corresponding author
Additional information
This article is part of a Topical Collection in Environmental Earth Sciences on “Water in Central Asia”, guest edited by Daniel Karthe, Iskandar Abdullaev, Bazartseren Boldgiv, Dietrich Borchardt, Sergey Chalov, Jerker Jarsjö, Lanhai Li and Jeff Nittrouer.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Jarsjö, J., Törnqvist, R. & Su, Y. Climate-driven change of nitrogen retention–attenuation near irrigated fields: multi-model projections for Central Asia. Environ Earth Sci 76, 117 (2017). https://doi.org/10.1007/s12665-017-6418-y
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s12665-017-6418-y