Abstract
The storage of hydrogen in underground reservoirs comprises a potential solution for balancing the fluctuating energy production from wind and solar power plants. In this concept, electrolysers are used to transform excessively produced electrical energy into chemical energy in the form of hydrogen. The resulting large volumes of hydrogen are temporarily stored in subsurface formations purely or in mixture with other gases. In times of high energy demand, the chemical energy is transformed back into electricity by fuel cells or engine generators. Key aspects in the development period and the subsequent cyclic operations of such a storage are the hydrodynamic behavior of hydrogen and its interaction with residual fluids in the reservoir. Mathematically, the behavior can be described by a compositional two-phase flow model with water and gas as phases and all relevant chemical species as components (H2, H2O, CH4, CO2, N2, H2S, etc.). The spatial variation of the gas phase composition between injected and initial gas leads to density and viscosity contrasts which influence the displacement process. The mixing of gases with different compositions is governed by molecular diffusion or mechanical dispersion dependent on the flow velocity. In the present paper, a numerical case study in a depleted gas reservoir was performed. The storage was charged with hydrogen for 5 years. Subsequently, 5 years of seasonal cyclic operation were simulated to predict injection and production rates, pressure response and composition of the produced gas stream .
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
While conventional energy sources are capable to produce electricity continuously, the power generation of renewable energy is strongly fluctuating as a result of environmental influences. In the context of the energy transition, it is therefore required to expand the storage capabilities for electrical energy (BMBF 2011). An intermediate storage is required to handle the imbalance between energy production and demand. One promising answer is the conversion of electricity into hydrogen as an energy carrier, which is then stored in underground formations, referred to as underground hydrogen storage (UHS) (Crotogino et al. 2010). Potential targets are aquifers, depleted gas reservoirs or solution mined caverns. Hydrogen is thereby generated by electrolysis, which is considered as a clean procedure, because it is produced from renewable energy sources. Once hydrogen has been generated and stored intermediately, different applications are conceivable. The “POWER-to-GAS” concept includes adding hydrogen into the consisting gas supply system and production of synthesized methane by using hydrogen and carbon dioxide (Müller-Syring et al. 2011). Additionally, a reconversion of hydrogen into electricity can be implemented by power stations or fuel cells (Ganser and Eng 2013). A special emphasis could be placed on the utilization of fuel cells in vehicles.
The storage of pure hydrogen and hydrogen gas mixtures in porous geological formations was rarely done in the past. The different characteristics of hydrogen, e.g., density, viscosity and reactivity, compared to natural gas or methane can lead to unexpected behavior. These aspects were theoretically considered in the papers of Paterson (1983) and Carden and Paterson (1979). In the present paper the possible effects are investigated by numerical modeling. Particular attention is thereby given to the mixing effects between hydrogen and other gases in the reservoir. An equivalent numerical model could be used in practice for the planning of an UHS including the determination of optimal well locations and the optimal injection and withdrawal rates during development and operation of the storage.
Hydrodynamic aspects during development and operation of UHS
As mentioned before, both aquifers and depleted gas reservoirs can be used to develop underground hydrogen storages. However, the governing processes during the development period will be different for aquifers which are initially saturated only by water or brine and depleted gas reservoirs which can have a high residual gas saturation, but exhibit depleted reservoir pressures.
Development period in aquifers
In aquifers a gas bubble is created during the development period; hence, the aquifer water is displaced. This displacement process could be inefficient because hydrogen has a low viscosity and very low density in contrast to water. The mobility ratio between hydrogen gas and water is estimated to be in the order of 2–5 which is unfavorable (Ho and Webb 2006). Consequences could be the occurrence of strongly pronounced viscous fingering and gravity override of the water phase, which was investigated in Tek (1989) and Paterson (1983). Paterson (1983) concluded from theoretical considerations that the viscous fingers could spread very far laterally below the cap rock and hydrogen could get lost beyond the spill point of the structure. In Tek (1989) the conditions for stable and instable displacement were derived mathematically. Both works conclude that the injection rate can be used as a control parameter for viscous fingering or gravity override. If the injection rate is low, the gravitational and capillary forces will be stronger than the viscous forces and hence, the displacement becomes more stable. In Hagemann et al. (2015) these findings were confirmed by numerical simulations. However, the simulation results show that the development period, using a low injection rate, could take several years. The required time depends on the aquifer geometry, the hydraulic properties of the reservoir rock and the hydrodynamic properties of the fluids. All these phenomena are well known from natural gas storages in aquifers, but with hydrogen they will be more prominent.
Development period in depleted gas reservoirs
In depleted gas reservoirs, some residual gas remains in the reservoir. If the influx of aquifer water into the reservoir was weak, the residual gas saturation almost corresponds to the initial gas saturation and only the pressure was depleted. A problem could be the displacement of the residual gas by hydrogen. Different schemes are suggested in the literature for the transformation of gas storages from one gas to another, which can also be applied for the development of an UHS (Tek 1989). A simple transformation by cyclic injection and production using the same wells could result in a highly contaminated gas production, especially in the first years of operation. In other transformation schemes, hydrogen is injected on one edge of the reservoir. Therefore, the residual gas is pushed to the other side of the reservoir or could be simultaneously produced on the opposite side. This sweeping strategy potentially results in a more pure hydrogen production; however, a mixing between the different gases is inevitable.
Alternative cushion gases
In Tek (1989) and Pfeiffer and Bauer (2015) it was suggested to inject nitrogen during the development period of an aquifer storage site. Despite the lower investment costs for nitrogen as cushion gas, it has a higher viscosity and density than hydrogen and even than methane. Hence, the displacement of water is more efficient. The disadvantage is the intensive mixing of hydrogen and nitrogen when the cyclic operation is started. The simulation study in Pfeiffer and Bauer (2015) has shown that the hydrogen concentration in the produced gas stream is only around 50–80 % during the first years. In the same way as mentioned before, a different cushion gas can also be used in depleted gas reservoirs. It seems reasonable to use the already available natural gas as part of the cushion gas, while further required cushion gas will be delivered by the injected gas. The density difference could be utilized to separate the gases by injecting hydrogen into the top of the structure (Tek 1989). In Oldenburg (2003), carbon dioxide was suggested to be used as cushion gas. In this case, the density segregation would be relatively strong, because at typical reservoir conditions, carbon dioxide is very dense in comparison with hydrogen.
Operation period
UHS will be operated in a cyclic way with alternating periods of injection, withdrawal and idle. Depending on the energy production and demands, the periods can be longer or shorter. Similar to underground gas storages a seasonal operation, where the storage is charged during the summer months and discharged during the winter months, is conceivable. If the UHS is used to balance electrical energy, more frequent changes in the operation are possible dependent on the weather conditions. The storage process has to provide high production rates, usually one or two orders of magnitude higher than the depletion process of a reservoir. Hence, the main driving force during the operation will be compression and expansion of the gas bubble. A certain amount of gas always remains in the reservoir as cushion gas. The displacement of gas by water from an aquifer potentially plays only a minor role as drive mechanism during production. It must be ensured that the produced gas stream fulfills the requirements of pureness and additionally a low water cut is favorable.
Selective technology
A completely different operation strategy, called the “selective technology” was suggested in Hagemann et al. (2015) and Panfilov (2010). The idea is to use an aquifer where horizontal impermeable or almost impermeable barriers exist. The storage is operated by two different well systems. The first system of wells is used to inject hydrogen into the bottom of the reservoir. The hydrogen starts to rise, because of buoyancy forces in the water phase. The rising gas is retarded at several barriers until it flows around or through these barriers. When the hydrogen reaches the cap rock of the reservoir, it is produced by the second system of wells, before it has the chance to spread laterally. The complexity of this operation strategy is the planning of storage time which corresponds to the characteristic time of hydrogen rising from the bottom to the top.
Mixing of gaseous components
The mixing of different gaseous components plays a major role when a depleted gas reservoir is transformed to an UHS or when an alternative cushion gas is used. The mixing is influenced by mobility ratios, density differences, molecular diffusion and mechanical dispersion (Tek 1989).
Mobility ratio
Mobility differences in a gas–gas displacement arise mainly due to different dynamic viscosities. Hydrogen has a very low viscosity which results in a mobility ratio around 1.5 for the system H2–CH4 and 4 for the system H2–CO2. This could result in an instable displacement when hydrogen is injected to displace another gas. However, this effect is much less than in a case of a gas–water displacement because the miscibility leads to a high dispersion of the front which acts as stabilizing force (Ho and Webb 2006).
Density difference
Hydrogen has a very small molecular mass which results in large density differences compared to other gases. The effect can have negative influence when the injection aims to displace another gas but gravity override occurs. However, as mentioned before, the effect can be also used to keep different gases segregated, e.g., when CO2 is used as cushion gas (Tek 1989).
Molecular diffusion
Molecular diffusion is generally considered as a slow process when compared to advective/convective transport (Tek 1989). The molecular diffusion coefficient \(\tilde{D}_{\text {diff}}\) for hydrogen in the gaseous state is relatively high, in the order of \(1\times 10^{-6}\) m\(^{2}/\)s. The effective molecular diffusion coefficient depends on porosity, saturation state and tortuosity of the porous medium. As molecular diffusion is proportional to the concentration gradient, it will be fast at the beginning, but when the concentration gradients decrease its influence will also decrease. It is independent of advective/convective transport, thus, it could become the governing process during idle periods.
Mechanical dispersion
Mechanical dispersion, in contrast, is a mixing process which takes place due to the movement of fluids in the porous medium. It arises from variations in the velocity which can occur on different scales, ranging from microscopic to reservoir scale (Tek 1989). The mechanical dispersion coefficient \(\tilde{D}_{\text {disp}}\) depends on the velocity and direction of flow and can be formulated as follows (Scheidegger 1958):
where a is the dispersivity in (m), \(\Vert v\Vert\) is the flow velocity in the principle direction, the subscript L refers the longitudinal direction and the subscript T refers the transverse direction. The dispersivity of the porous medium depends on its tortuosity and heterogeneity. However, the experimental measured values vary by several orders of magnitude. As the process is strongly depending on the considered scale, laboratory measurements cannot be directly transferred to reservoir scale (Tek 1989). Tracer tests, which have been performed on reservoir scale, have shown that the longitudinal dispersivity is between 1 and 100 m (Tek 1989; Carriere et al. 1985; Laille et al. 1986). The transverse dispersivity is usually one or two orders smaller. Assuming flow velocities of several meters per day, which are common in gas storages, the longitudinal mechanical dispersion coefficient will be around \(5\times 10^{-4}\) m\(^{2}/\)s. Hence, the mixing by mechanical dispersion is expected to be much more pronounced than only by molecular diffusion.
Conceptual simulation of displacement processes
As indicated in Sect. 2, the hydrodynamic and substance specific behavior of hydrogen represents still a large uncertainty in porous underground storage applications. In this context, especially the very small density and viscosity of hydrogen are suspected to complicate an effective displacement of a native reservoir fluid. The first operation period of porous underground storage schedules the sufficient concentration incline of the target storage gas in the drainage area of the production wells. The efficiency of this displacement process depends on the physical properties of the displacing gas and the native reservoir fluid. The two classical porous underground gas storage types are depleted gas reservoirs and water saturated anticline structures. Depending on the native reservoir fluid, these storage candidates are characterized by deviating displacement processes and demand special requirements during the storage operation. A short introduction into the hydrodynamic behavior of both storage types is given below.
Displacement efficiency
In a porous medium, it is possible to quantitatively estimate the efficiency of a displacement process by considering the microscopic and macroscopic displacement efficiency. The dimensionless measure E is therefore the volume fraction of the displacing fluid to the total pore volume.
The microscopic displacement efficiency \(E_{\text {D}}\) describes the displacement of the initial reservoir fluid at pore scale. According to Terry (2001), this factor is mainly influenced by the interfacial and surface tensions between the displacing and displaced fluid, the reservoir wettability as well as the shape of the relative permeabilities curves.
The simulation cases implemented in this paper are focusing on the macroscopic displacement efficiency, \(E_{\text {V}}\), which expresses the capability of the displacing fluid to mobilize the initial fluid in a volumetric sense. In this context, the allocation of the wells, the reservoir permeability distribution, gravity forces and the mobility of the initial and injected fluid are significant. The injection of a less viscous and dense fluid into a reservoir can provoke the appearance of at least two physical effects which interfere with the macroscopic displacement efficiency.
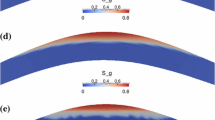
Comparison of a gas–gas (a) and gas–water (b) displacement in a 2D vertical cross section. The black dashes indicate the well perforation locations. As a result of the hydrogen injection, gravity override occurs. a Hydrogen conc. in an initially gas saturated reservoir. b Gas saturation in an initially water saturated reservoir
Gravity override
As a result of buoyancy, two immiscible fluids inside a closed system tend to dispose according to their density. In comparison with cavern storage operations, gravity segregation in a porous subsurface medium is normally attenuated. The sequence of geological deposition typically leads to a much higher horizontal than vertical permeability, which restricts fluid migration across the layering. However, the very small molecular mass of hydrogen causes a large density contrast of the occurring fluids so that an amplified hydrogen accumulation below the highest sealing layer has to be assumed. In order to obtain a qualitative impression of gravity override, two examples of hydrogen injection into a gas saturated (Fig. 1a) and water saturated (Fig. 1b) reservoir were simulated. Thereby, a two-dimensional cross section of the later introduced reservoir model was adapted by standardizing the grid dimensions and increasing the amount of grid cells in z-direction. The horizontal permeability is defined as 100 mD, while the vertical permeability is 10 times smaller. Hydrogen is constantly injected into the source placed at the left part of the reservoir, while the native fluid is produced from the sink placed at the right part of the structure. The simultaneous operation of an injection and a production well allows the pressure balancing. In the first case, the reservoir is initially saturated with 98 % gas, composed of approximately 80 mol% nitrogen and 20 mol% methane.
The injection of hydrogen leads to a relatively uniform displacement although the effect of gravity segregation is already indicated. In the second case, hydrogen is injected into a fully water saturated reservoir, which causes a very poor and unilateral displacement of the native reservoir fluid. The effect of gravity override is a function of the occurring density contrast. At the initial reservoir conditions of 170 bar and 125 \(^\circ\)C, hydrogen is roughly 75 kg/m\(^3\) less dense than methane and approximately 125 kg/m\(^3\) lighter than nitrogen. This relation becomes even more unfavorable in case hydrogen is injected into an aquifer, where a density difference between hydrogen and water of 937 kg/m\(^3\) has to be expected (NIST 2016). Besides the density contrast, gravity override is furthermore promoted by small injection rates and large vertical permeabilities (Terry 2001).
Viscous fingering
Besides gravity override, viscous fingering is another undesired physical phenomenon which is commonly linked to gas injection processes. The adverse relation between a displacing highly mobile fluid and a displaced sluggish native fluid promotes a unilateral displacement. The arising finger-shaped front can be provoked by several factors and can additionally occur on different stages. Besides viscous fingering at pore and volumetric scale, it is possible to further distinguish between viscous fingering in miscible and immiscible displacement processes.
The multiphysics simulator COMSOL was used to numerically simulate the displacement front in a hydrogen–gas (Fig. 2a) and a hydrogen–water (Fig. 2b) system. In both cases, hydrogen is constantly injected from the left side of the model, while the native fluid is produced from the opposite side. The distance between the injection and production side amounts 10 m, while the pressure difference results into 0.05 bar. The arising displacement process is disturbed by a small reservoir heterogeneity which can be obtained by the four small squares next to the injection boundary. This model heterogeneity is numerically required in order to initiate viscous fingering, but simultaneously it is small enough to not restrict the flow potential. The permeability disturbance initially interferes with the hydrogen–methane displacement, but the displacement front is then stabilized by diffusion and dispersion forces. Consequently Fig. 2a shows a stable displacement front between the two gases. In case of the hydrogen–water displacement (Fig. 2b), the permeability heterogeneity generates viscous fingers which dominate the subsequent displacement process. While the gas–gas displacement is characterized by a front velocity of 5 m/day, the hydrogen–water front migrates with 0.4 m/day through the model.
Comparison of a gas–gas and gas–water displacement in a 2D horizontal cross section where the four squares represent a permeability anomaly (250 mD) within the homogeneous (500 mD) model. The gas–gas displacement (a) is characterized by a uniform hydrogen spreading, while the gas–water displacement (b) shows viscous fingering. a Hydrogen conc. in a hydrogen–gas displacement. b Gas saturation in a hydrogen–water displacement
Numerical implementation
The numerical case study performed in the next section was implemented in the open-source software DuMu\(^{x}\) (Flemisch et al. 2011). Generally DuMu\(^{x}\) allows the simulation of flow and transport processes in porous media and is itself based on the Distributed and Unified Numerics Environment (DUNE) toolbox which provides an open-source foundation for the solution of partial differential equations with grid-based methods (Bastian et al. 2008). As a fundamental benefit, DuMu\(^{x}\) permits the user to independently advance the simulations by developing new instructions. In the previous paper (Hagemann et al. 2015), the simulation studies were focused on structured 2D grids with isotropic and homogenous properties of the porous medium. Such grids have been imported in the format of “dune-alugrid” (Dedner et al. 2014). In this publication, the numerical investigations are extended to 3D applications by importing and computing on realistic unstructured grids with heterogeneous reservoir properties. The “opm-parser” (Flornes et al. 2016) and “dune-corner point” (Bastian et al. 2016) modules were used to import and adapt these grids for the usage within DuMu\(^{x}\). Some fundamental adjustments of the DuMu\(^{x}\) code were necessary to ensure the 3D simulations.
Program adjustments
DuMu\(^{x}\) offers two different spatial discretization schemes. In the previous publications, the default box method was used which is appropriate for conforming grids. For the processing of geological more complex reservoir structures in corner-point format, the more conventional cell-centered finite volume method is recommended.
Since DuMu\(^{x}\) was initially developed to compute near surface ground water processes, the expected default permeability range does not cover the very small permeability values of deeper hydrocarbon reservoirs. In this case, an automatic request of a DuMu\(^{x}\) control function aborts the simulation since a physically incorrect result is misleadingly assumed. By adapting the equivalent permeability threshold value, larger value ranges can be computed.
During the adjustments from structured 2D grids to unstructured 3D reservoir applications, further numerical challenges occurred. Comprehensive geological reservoir models that are created in Petrel (Schlumberger 2016), typically consist of very irregular grid geometries and structures. Individual cells can for example deviate from the cuboid cell shape by instead assuming a rectangular prismatic shape which are also known as “degenerate cells”. These cells especially occur in those regions, where grid horizons are merging into each other. At geological faults, where an offset between the layers exits, it is additionally possible that the grid model becomes non-conforming. To meet the complexity of these irregular grid structures, some fundamental computation settings were modified. The flux between two neighboring cells depends on the difference in pressure potential and the transmissibility between the cells. The standard method in DuMu\(^{x}\) of calculating the transmissibility is accomplished by taking the face area, the harmonic mean of the two cell permeabilities and the distance between the cell centers. However, the deviating sizes and shapes of neighboring cells lead to a certain inaccuracy which is resulting in numerical instability. A better solution includes the initial calculation of the two transmissibilities from each cell center to their common face center, referred to as “half-block transmissibility” (cf. “Appendix 2”). Subsequently, the total transmissibility between the cells is calculated by taking half of the harmonic mean of these half-block transmissibilities. This option was implemented by the DuMu\(^{x}\) developers and is available since the DuMu\(^{x}\) release 2.8. Additionally, an adjustment for the cell and face center determination within the dune-corner point methods was required. While Petrel (Schlumberger 2016) exports the grid geometry by specifying the eight corner-point coordinates of a single cell, simulation programs initially determine the cell and face center points to ensure the mass balance calculation between neighboring cells. The standard setting to determine the cell and face centers is the calculation of its centroids. In contrast, our experience in DuMu\(^{x}\) indicates that the numerical accuracy and stability can be improved by determining the face center coordinates by calculating the arithmetic mean of its four corner points. The cell centers are subsequently calculated by taking the arithmetic mean of the center points of the upper and lower faces (cf. “Appendix 3”). This method is also suggested in Nilsen et al. (2012) and is believed to be common in commercial reservoir simulators. This adjustment especially helped to improve the mass transfer between degenerate cells and its neighboring cells.
Case initialization
The initialization of the reservoir was done in hydrostatic equilibrium where the gas–water contact (GWC) was defined at 3452 m with a pressure of 170 bar. The phase pressures and saturations were calculated by using the pressure gradients and capillary pressure relation. All performed simulations use the Neumann conditions to specify the spatial derivative of the partial differential flux equation at the boundary of the reservoir. Defining this value as zero, the boundary of the grid is set to a no-flow boundary.
Wells are represented by source or sink terms. From a mathematical point of view, they represent specific points or lines in the reservoir, where mass is either added or extracted from the closed system. Since the geographic well coordinates naturally deviate from the calculated cell center positions, it is necessary to find a reasonable approach to identify the cells which contain a well. We developed therefore a Matlab code, which automatically assigns the geographic well coordinate to the closest occurring cell center coordinate. By invoking these positions and defining a mathematical well model, the activity of wells can be numerically executed.
Peaceman’s well model
The injection and production of fluids is realized by implementing Peaceman’s well model. In contrast of using a constant injection or production rate, Peaceman’s well model automatically adjusts the amount of injected or extracted mass to the reservoir response. This can for example avoid an unrealistic high pressure in the near wellbore area and takes furthermore the mobility of the occurring fluids into account (Chen 2007). Certainly the size of an invoked grid cell significantly exceeds the real well diameter which sophisticates the well impact on the reservoir. Grid refinement around the well position allows a better representation of the reality but indeed requires considerable numerical expanse. In contrast, the implementation of Peaceman’s well model ensures a more simple comprise between representing the reality and defining a mathematical representation. By introducing an equivalent radius, Peaceman was able to find a connection between the occurring grid cell pressure and the bottom-hole flowing pressure. It is possible to approach the quantity of the equivalent radius, by either solving the analytical well flow model, numerically solving the pressure equation or directly calculating the yielding pressure between the well and its neighboring grid cells. The quantity of the equivalent radius amounts to approximately one-fifth of the average grid cell length. The simplest expression of Peaceman’s well model is listed below and is valid for a homogeneous reservoir and single-phase fluid flow:
where Q is the injection or production rate in (kg/s), \(\rho\) is the fluid density in (kg/m\(^3\)), \(K_{xy}\) is the horizontal permeability of the grid cell containing the well in (m\(^2\)), \(h_{z}\) is the grid cell height in (m), \({\mu }\) is the fluid viscosity in (Pa s), \(r_{\text {e}}\) is the equivalent radius in (m), \(r_{\text {w}}\) is the geometrical well radius in (m) and s is the wellbore skin factor. Besides the physical behavior of the fluid density and viscosity, the difference of a defined bottom-hole flowing pressure \({P_{\text {wf}}}\) and the actual reservoir pressure P in the well grid cell adjusts the amount of the injected or extracted mass to the arising reservoir response. The multi-compositional two-phase flow formulation of our model for UHS requires the additional consideration of phase mobilities and concentrations of the components. Since our model is based on the balance of moles, a modification of the units is necessary. For injection, it is sufficient to consider the gas phase:
where \(\hat{Q}\) is the injection or production rate in (mol/s) and \(c_{\text {g}}^{k,\text {inj}}\) is the composition of the injected gas. Molar density, dynamic viscosity and relative permeability are the actual values in the well grid cell. For production, both phases need to be considered:
where \(c_{\text {g}}^{{k}}\) and \(c_{\text {w}}^{{k}}\) in this case are also the actual values in the grid cell containing the well. A scaling of the Dirac delta function is required to transform the point or line source to a volume source, where \(V_{\text {c}}\) is the volume of the well grid cell (cf. Eq. 18).
Hydrogen storage scenario
The hydrodynamic properties and challenges of hydrogen displacement processes have been theoretically and numerically introduced in the previous chapters. The results provide a solid foundation for the conduction of a comprehensive long-term underground hydrogen storage feasibility study.
Geology
In order to numerically assess the technical feasibility of underground hydrogen storages, an appropriate reservoir grid was chosen whose properties resembles the typical reservoir shape of conventional gas storages. The used geological model is part of one of the largest on-shore gas fields in Europe. Due to the enormous dimension of the entire sandstone reservoir, a large amount of hydrogen is required to achieve a sufficient storage deliverability.
Cross section through the reservoir: The storage horizons can be identified by their porosity values, the four independent sandstone layers (red) are separated by tight interlayers (blue), the perforation of the operation well is illustrated by the yellow dashes. Overall \(26 \times 37\times 13\) grid cells build the skeleton of the reservoir
Results of the hydrogen storage scenario: The reservoir pressure is more than duplicated, the alternating mass injection and withdrawal leads to the cyclic pressure increase and reduction (a), the storage operation period is characterized by much larger hydrogen injection rates (b), the gas inventory versus the average reservoir pressure indicates a loss-free operation (c), the evaluation of the hydrogen fraction of the extracted gas shows an seasonal increase of the gas purity (d). a AVG. reservoir pressure response during storage operation. b Hydrogen injection and production rates. c Hysteresis plot. d Hydrogen concentration produced gas
By cutting a much smaller prismatic fragment, whose cross sectional shape resembles a geological anticline structure, a more suitable grid model was created. With the help of Petrel (Schlumberger 2016), the initial slightly coarse grid structure was improved by reducing the grid volume by the factor 9. The arising fragment model has an approximate ground plan of 800 m times 1200 m and a gross reservoir thickness of 50 m which yields to an average grid cell size of 32 m in x, 31 m in y and 3.8 m in z-direction. Four independent, highly porous and permeable sandstone layers represent the potential storage horizons which are separated by tight clay layers. The sandstone layers are defined according to their original porosity (in average 13.08 %) and permeability (in average 22.40 mD) values. Above the gas–water contact at 3452 m, the reservoir is up to 90 % gas saturated. The major gas components are represented by roughly 80 mol% nitrogen and 20 mol% methane. A cross section through the reservoir is displayed in Fig. 3 where the figure is vertically stretched by the factor 7.
Reservoir cross section for the illustration of the hydrogen (a, c, e) nitrogen (b, d, f) concentration development. With advancing amount of injection cycles, the hydrogen concentration within the formation is increasing. a Hydrogen conc. before 1st production cycle. b Nitrogen conc. before 1st production cycle. c Hydrogen conc. after 1st production cycle. d Nitrogen conc. after 1st production cycle. e Hydrogen conc. before last production cycle. f Nitrogen conc. before last production cycle
Schedule
The implemented hydrogen underground storage scenario includes a total period of 10 years. During the development period, the reservoir is step-wise charged with hydrogen, while the subsequent 5 years simulate the annual cyclic operation period.
Using a depleted gas reservoir as storage structure, initially an appropriate storage charging period is necessary in order to obtain a sufficient storage deliverability. The deliverability is a function of the total gas inventory and is increasing with increasing reservoir pressure. In view of porous underground storage applications, Tek (1989) subdivides the total gas inventory into two types. First a substantial fraction of the gas inventory has to remain within the storage structure in order to guarantee a required minimum reservoir pressure. This so-called cushion gas is either intentionally not produced or is physically non-recoverable since it is trapped within the geological structure. The actual gas of interest is referred to as working gas. This gas can be withdrawn without damaging the long-term deliverability of the gas storage. After the establishment of a high and homogeneous hydrogen concentrated region in the well drainage area, the gas production during the operation period ensures the recovery of hydrogen.
Development period
Qualitative observation parameters for the evaluation of the hydrogen storage scenario are plotted in Fig. 4. The first 5 years schedule an alternating shape of 6 months of injection and 6 months of idle. As a result of the step-wise hydrogen injection, the initial reservoir pressure is increased from 170 to 370 bar. Thereby the injection rate is controlled by Peaceman’s well model (constant injection pressure value) which explains the curved reservoir pressure increase (Fig. 4a). Initially, a large amount of hydrogen is injected but since the well grid pressure progressively approaches the set injection pressure, the amount of mass injection declines (Fig. 4b). The average daily injection rate is targeted at roughly 250.000 Sm\(^{3}\)/day which corresponds to an cumulative annual hydrogen addition of roughly 47 million Sm\(^{3}\). After 5 years, the storage inventory consists of 194.5 million Sm\(^{3}\) of the native nitrogen–methane mixture and 236.6 million Sm\(^{3}\) of hydrogen.
Operation period
The storage operation period starts again with an injection period in which further hydrogen is added into the storage structure. The average reservoir pressure is thereby increased to a final pressure of 400 bar, which should guarantee the storage deliverability. As this value is still 20 bar below the initial reservoir pressure, a safe storage operation is achievable. At this point of the maximum gas storage level, the reservoir contains more than 271 million Sm\(^{3}\) hydrogen. The cross section through the reservoir (Fig. 5a) shows a high and homogeneous hydrogen concentration in the vicinity of the injection well. This allows the completion of the storage charging period and the first commencement of a 4-month long production period. This extraction process is controlled by a production pressure of 300 bar which yields to a total cyclic average gas extraction of 107.7 million Sm\(^{3}\). As a result of the gas withdrawal, Fig. 5c shows the hydrogen concentration reduction within the formation. Accordingly, the nitrogen concentration within the top region of the structure increases (Fig. 5d). The hydrogen fraction of the extracted gas is plotted in Fig. 4d and shows a seasonal hydrogen fraction increase from an initial value of 82 mol% to a final value of 85.2 mol%. This indicates a closed reservoir system, where gas losses, due to migration or gas dissolution, are insignificant. Furthermore nitrogen and methane are seasonally extracted from the reservoir as impurities of the produced gas, while the injection gas purely consists of hydrogen. Consequently, the hydrogen concentration inside the storage formation is increasing. A common method to monitor gas losses in porous underground storage is given by plotting the reservoir pressure versus the total gas inventory (Fig. 4c). In a physical ideal and technical gas loss-free case, the resulting hysteresis slope of a closed reservoir will be identical during the gas injection and withdrawal. In contrast, gas losses can be identified by a scattered pressure response and a cyclic shifting of the hysteresis course. A parabolic shape of the injection and withdrawal line characterizes water driven reservoirs (Tek 1989). The resulting hysteresis of the last four operation cycles are plotted in Fig. 4c and indicate a gas loss-free operation. In this context, it is important to remind the mathematical no-flow boundaries of the reservoir system. The simulation focuses on the numerical investigation of gas mixing processes in underground hydrogen storages and does not contain scientific significance about possible hydrogen diffusion into sealing layers. Before implementing a numerical approach, the investigation of hydrogen diffusivity into caprocks initially requires essential experimental research. Furthermore Fig. 6a illustrates that the initial reservoir pressure is in hydrostatic equilibrium. The comprehensive hydrogen injection predominantly leads to the pressure increase within the storage horizons, while the pressure is slightly increasing in the interlayers (Fig. 6b). Since water is hardly compressible and the gas is injected into a closed system, the pressure duplication leads only to a slight shifting of the GWC in vicinity of the operation well (Fig. 7).
Technical aspects
The conversion of excessive energy into hydrogen as chemical long-term energy carrier is a promising approach to advance and progress the energy transition. Although the process of converting electricity into hydrogen as a chemical energy carrier is continuously improving, hydrogen generation will always be associated with energy losses. However, promising hydrogen generation concepts can already reach efficiency factors above 70 % (Toepler and Lehmann 2014).
The concept of storing large gas amounts in a porous subsurface medium has been successfully applied for decades. Consequently, the research and planning of hydrogen storages can benefit from the widespread experience of conventional natural gas storages. The technical feasibility of long-term storages is demonstrated by the 21 German porous underground gas storage (UGS) facilities which stored overall 10.6 billion Sm\(^3\) working gas in 2013 (LBEG 2014).
As a disadvantage of hydrogen storage technology, the relatively small calorific value of hydrogen confines the UHS efficiency. Compared to methane, hydrogen has roughly an one-third smaller energy content per standard cubic meter. However, the numerical simulation calculates a peak hydrogen inventory of 271 million Sm\(^3\) which corresponds to a calorific value of 813 GWh. Neglecting conversion losses, this amount equals the annual electricity consumption of roughly 259,600 German average households. The simulation includes an annual withdrawal period of 4 months, which allows to balance the seasonable fluctuating gas demand. Using the hydrogen storage in this conventional sense, the extracted hydrogen amount of 107.7 million Sm\(^3\) is sufficient to exclusively ensure the gas consumption of roughly 43,500 households during the consumption intensive period between January and April (Schlomann et al. 2004).
Conclusions
In the framework of the H2STORE joint research project, a first comprehensive porous underground hydrogen storage scenario was numerically implemented. Besides the simulation of a development and storage operation period of a UHS, hydrodynamic characteristics of hydrogen injection into porous media were presented. The qualitative analysis of the simulated storage scenario indicates the large energy storage potential of UHS-facilities.
-
The computation of hydrogen distribution within the reservoir was extended by numerically implementing mechanical dispersion. Together with diffusion, mechanical dispersion leads to amplified mixing of the gas components.
-
The DuMu\(^{x}\) simulation considerations were successfully extended from homogeneous 2D to heterogeneous 3D applications. The use of a conventional cell-centered finite volume method ensures the irregular grid geometries processing. Irregular cell shapes, merging layers and non-confirming grids require modifications of the fundamental computation methods.
-
The numerical implementation of Peaceman’s well model adapts the mass injection and extraction to the reservoir response.
-
Numerical case studies of hydrogen injection indicate that gravity override and viscous fingering in aquifer structures complicate an efficient displacement of the native fluid. In contrast, both physical phenomena play a minor role in gas saturated reservoirs.
-
A comprehensive hydrogen storage scenario was implemented inside a depleted gas reservoir. During the development period, the reservoir pressure was re-pressurized to initial conditions by injecting 271 million Sm\(^{3}\) hydrogen. The stable displacement of the gaseous native reservoir fluid ensures the establishment of a homogeneous and highly hydrogen concentrated area in the vicinity of the operation well. The storage operation is characterized by the alternate injection and withdrawal of hydrogen which ensures an annual gas withdrawal of 107.7 million Sm\(^{3}\). The average hydrogen concentration of the extracted gas amounts 82 mol% in the first production cycle is increasing to 85.2 mol% during the last production period.
References
Bastian P, Blatt M, Dedner A, Engwer C, Klöfkorn R, Ohlberger M, Sander O (2008) A generic grid interface for parallel and adaptive scientific computing. Part I: abstract framework. Computing 82(2–3):103–119
Bastian P et al (2016) Distributed and unified numerics environment. http://dune-project.org. Accessed 19 Feb 2016
BMBF (2011) Förderinitiative Energiespeicher. https://www.bmbf.de/foerderungen/bekanntmachung.php?B=639. Accessed 20 Jan 2016
Brooks R, Corey T (1964) Hydraulic properties of porous media
Carden P, Paterson L (1979) Physical, chemical and energy aspects of underground hydrogen storage. Int J Hydrogen Energy 4(6):559–569
Carriere J, Fasanino G, Tek M, et al (1985) Mixing in underground storage reservoirs. In: SPE annual technical conference and exhibition. Society of Petroleum Engineers
Chen Z (2007) Reservoir simulation: mathematical techniques in oil recovery, vol 77. SIAM, Philadelphia
Colonna J, Brissaud F, Millet J et al (1972) Evolution of capillarity and relative permeability hysteresis. Soc Pet Eng J 12(01):28–38
Cordazzo J, Maliska CR, Silva A (2002) Interblock transmissibility calculation analysis for petroleum reservoir simulation. In: 2nd meeting on reservoir simulation, Universidad Argentina de la Empresa, Buenos Aires, Argentina, November, pp 5–6
Crotogino F, Donadei S, Bünger U, Landinger H (2010) Large-scale hydrogen underground storage for securing future energy supplies. In: 18th World hydrogen energy conference, pp 16–21
Dedner A, Klöfkorn R, Nolte M (2014) The DUNE-ALUGrid module. arXiv preprint arXiv:1407.6954
Flemisch B, Darcis M, Erbertseder K, Faigle B, Lauser A, Mosthaf K, Müthing S, Nuske P, Tatomir A, Wolff M et al (2011) DuMu\(^{x}\): DUNE for multi-phase, component, scale, physics,. flow and transport in porous media. Adv Water Resour 34(9):1102–1112
Flornes K, Lie K, Rustad A, Rasmusssen A, Sandve T, Hove J (2016) Open Porous Media. http://opm-project.org. Accessed 19 Feb 2016
Ganser C, Eng B (2013) New energy storage concept for renewable energies in the form of potential energy storage. Techniken zur Energiewende p 70
Hagemann B, Panfilov M, Ganzer L (2016) Multicomponent gas rising through water with dissolution in stratified porous reservoirs—application to underground storage of H\(_2\) and CO\(_2\). J Nat Gas Sci Eng 31:198–213
Hagemann B, Rasoulzadeh M, Panfilov M, Ganzer L, Reitenbach V (2015) Hydrogenization of underground storage of natural gas. Comput Geosci 20:595–606
Heinemann ZE (2005) Introduction to reservoir simulation. Montanunivertät Leoben, Leoben
Ho CK, Webb SW (2006) Gas transport in porous media. Springer, Berlin
Juanes R, Spiteri E, Orr F, Blunt M (2006) Impact of relative permeability hysteresis on geological CO\(_2\) storage. Water Resour Res 42:12
LBEG (2014) Erdoel Erdgas Kohle 130:402–414
Laille J, Coulomb C, Tek M, et al (1986) Underground storage in cerville-velaine, france: a case history in conversion and inert gas injection as cushion substitute. In: SPE annual technical conference and exhibition. Society of Petroleum Engineers
Müller-Syring G, Henel M, Krause H, Rasmusson H, Mlaker H, Köppel W, Höcher T, Sterner M, Trost T (2011) Power-to-gas: Entwicklung von Anlagenkonzepten im Rahmen der DVGW-Innovationsoffensive. In: Artikel aus GWF-Gas/Erdgas November, pp 770–777
NIST (2016) Thermophysical properties of fluid systems. http://webbook.nist.gov/chemistry/fluid. Accessed 2 Mar 2016
Nilsen HM, Natvig JR, Lie KA et al (2012) Accurate modeling of faults by multipoint, mimetic, and mixed methods. SPE J 17(02):568–579
Oldenburg CM (2003) Carbon dioxide as cushion gas for natural gas storage. Energy Fuels 17(1):240–246
Panfilov M (2010) Underground storage of hydrogen: In situ self-organisation and methane generation. Transp porous med 85(3):841–865
Paterson L (1983) The implications of fingering in underground hydrogen storage. Int J Hydrogen Energy 8(1):53–59
Pfeiffer WT, Bauer S (2015) Subsurface porous media hydrogen storage-scenario development and simulation. Energy Proc 76:565–572
Poling BE, Prausnitz JM, John Paul O, Reid RC (2001) The properties of gases and liquids, vol 5. McGraw-Hill, New York
Scheidegger AE (1958) The physics of flow through porous media. Soil Sci 86(6):355
Schlomann B, Gruber E, Eichhammer W, Kling N, Diekmann J, Ziesing HJ, Rieke H, Wittke F, Herzog T, Barbosa M, et al (2004) Energieverbrauch der privaten Haushalte und des Sektors Gewerbe, Handel, Dienst-leistungen (GHD). Zusammenarbeit mit dem DIW Berlin, TU München, GfK Nürnberg, IE Leipzig, im Auftrag des Bundesministeriums für Wirtschaft und Arbeit, Karlsruhe, Berlin, Nürnberg, Leipzig, München
Schlumberger (2016) https://www.software.slb.com/products/petrel. Accessed 22 June 2016
Tek MR (1989) Underground storage of natural gas: theory and practice, vol 171. Springer, Berlin
Terry RE (2001) Enhanced oil recovery. Encycl Phys Sci Technol 18:503–518
Toepler J, Lehmann J (2014) Wasserstoff und Brennstoffzelle. Technologien und Marktperspektiven. Springer, Berlin. Online verfügbar unter http://www.worldcat.org/oclc/864451428
Toleukhanov A, Panfilov M, Panfilova I, Kaltayev A (2012) Bio-reactive two-phase transport and population dynamics in underground storage of hydrogen: natural self-organisation. In: ECMOR XIII-13th European conference on the mathematics of oil recovery
Acknowledgments
This study is part of the H2STORE project sponsored by the German Federal Ministry of Education and Research (BMBF). The authors would like to thank the DuMu\(^{x}\) development group and especially Bernd Flemisch from the University of Stuttgart for providing us an interface between Schlumberger Petrel (2016) and DuMu\(^{x}\) and his support for optimizing the DuMu\(^{x}\) code for corner-point grids.
Author information
Authors and Affiliations
Corresponding author
Additional information
This article is part of a Topical Collection in Environmental Earth Sciences on “Subsurface Energy Storage”, guest edited by Sebastian Bauer, Andreas Dahmke, and Olaf Kolditz.
Appendices
Appendix 1: Mathematical model of two-phase transport for UHS
The mathematical model for two-phase flow and compositional transport in UHS was already developed in previous papers (Panfilov 2010; Toleukhanov et al. 2012; Hagemann et al. 2015), while in this study a purely hydrodynamic model was used. Panfilov (2010), Toleukhanov et al. (2012) and Hagemann et al. (2015) focus on the coupled bio-reactive effects. The mathematical model, which was used for the simulations in this paper, is summarized in this section for completeness.
The molar balance for each chemical component is formulated as follows:
where \(\phi\) is the porosity, \(\rho\) is the molar density in (mol/m\(^{3}\)), c is the molar concentration, S is the saturation, v is the advective volumetric velocity in (m/s) and J is the diffusive/dispersive flux in (mol/(s m\(^{2}\))) , \(q^{k}\) the source of the sink term (mol/(s m\(^{3}\))) and the subscripts g and w denote the gas and water phase, respectively, and the superscript k refers to the chemical component.
The momentum balance at macroscale is formulated by Darcy’s law:
where K is the absolute permeability in (m\(^{2}\)), \(k_{r}\) is the relative permeability, P is the phase pressure in (Pa), \(\hat{\rho }\) is the phase density in (kg/m\(^{3}\)), and g is the gravity acceleration in (m/s\(^{2}\)).
The diffusive/dispersive flux is the sum of molecular diffusion and mechanical dispersion:
where \(D^{k}_{\text {diff},i}\) is the effective molecular diffusion coefficient of component k in phase i in (m\(^{2}\)/s) and \(D^{k}_{\text {disp},i}\) is the effective mechanical dispersion coefficient of component k in phase i in (m\(^{2}\)/s).
The molecular diffusion in the gas phase is formulated by Stefan–Maxwell equation, which was simplified by Blanc’s law (Poling et al. 2001), while the molecular diffusion in the water phase is formulated by Fick’s law:
where \(\tau\) is the tortuosity of the porous medium, \(\tilde{D}^{ij}_{\text {diff},g}\) is the binary diffusion coefficient between component i and component j in the gas phase (m\(^{2}\)/s) and \(\tilde{D}^{k}_{\text {diff},w}\) is the diffusion coefficient of component k in water in (m\(^{2}\)/s).
The mechanical dispersion coefficient is calculated by accepting its relationship to the Darcy velocity (Scheidegger 1958):
where \(a_\mathrm{L}\) is the longitudinal dispersivity in (m) and \(a_{T}\) is the transverse dispersivity in (m).
The hydraulic properties of the porous medium (capillary pressure and relative permeability) are correlated by Brooks–Corey laws (Brooks and Corey 1964):
where \(P_\mathrm{e}\) is the entry capillary pressure in (Pa) and \(S_{we}\) is the normalized water saturation:
where \(S_\mathrm{wirr}\) is the irreducible (or connate) water saturation and \(S_\mathrm{gr}\) is the residual gas saturation. At this point, the history dependence of relative permeability and capillary pressure on previous alternating displacement processes (drainage and imbibition) should be mentioned. In several papers, it was shown that this effect can have a recognizable influence in underground gas storages (Colonna et al. 1972; Juanes et al. 2006). However, for simplicity, this is not considered here.
The hydrodynamic properties of the fluid phases (density and dynamic viscosity) are correlated with respect to pressure, temperature and phase composition. The phase composition is determined at the equilibrium between gas and water by the equality of the fugacity:
where f is the fugacity coefficient in (Pa). The calculation of fugacity coefficients of gaseous components within the water phase is based on Henry’s law.
The system of equations is closed by the sum of saturations and concentrations:
The injection and production of fluids through storage wells is implemented as source or sink term. The wells are represented as point or line source which can be inserted in the molar balance as follows (Chen 2007):
where \(\hat{Q}^{k,w}\) is the injection (positive) or withdrawal (negative) rate of component k in well w in (mol/s), \(\delta\) is the Dirac delta function and \(x^{w}\) is the coordinate of well w.
Appendix 2: Half-block transmissibility
As mentioned in Sect. 5, the transmissibility determination was revised from a “permeability averaging” to a “half-block transmissibility”-based method. This modification supports the numerical stability of DuMu\(^{x}\) by adapting the mass transfer calculation to a heterogeneous grid environment. The implemented method now includes the initial determination of the half-block transmissibilities. In one of the six possible directions, the half-block transmissibility T is defined as following (Cordazzo et al. 2002; Heinemann 2005):
where K is the permeability of the grid cell in (m\(^{2}\)), A is the area of the face in (m\(^{2}\)), L is the distance between the cell center and the face center in (m). The total transmissibility \(T_{12}\) between two cells is then calculated by taking the half of the harmonic mean (a full contact between the cells is assumed) (Cordazzo et al. 2002; Heinemann 2005):
The difference between the “half-block transmissibility” and the standard “permeability averaging” method becomes distinct, whenever unstructured grid structures with heterogeneous rock properties are processed (Fig. 8).
In this case, the two half-block transmissibilities result in:
Consequently the total transmissibility yields in:
While the “half-block transmissibility” method averages the permeability and the distances between face and cell centers, the other method averages only the permeability:
The total transmissibility then amounts:
Appendix 3: Cell and face centers
Petrel exportfiles (Schlumberger 2016) or comparable corner-point grids provide each coordinate of the eight vertices of a grid cell. As the fundamental basis of all grid-based reservoirs simulators, initially the coordinates of the face and cell centers have to be determined. This can be done in different ways:
-
The centroids (balance points) of the cells and faces can be used.
-
As an alternative, initially the face centers of the (up to) six cell faces are determined by calculating the arithmetic mean of its four vertex coordinates:
$$\begin{aligned} x_\mathrm{fc}& = \frac{1}{4}\sum _{i=1}^{4}x_{i}, \quad y_\mathrm{fc}=\frac{1}{4}\sum _{i=1}^{4}y_{i},\nonumber \\ z_\mathrm{fc}& = \frac{1}{4}\sum _{i=1}^{4}z_{i} \end{aligned}$$(25)then cell center is the arithmetic mean of the top and bottom face centers:
$$\begin{aligned} x_\mathrm{cc}& = \frac{1}{2}\sum _{i=1}^{2}x_{\mathrm{fc}i}, \quad y_\mathrm{cc}=\frac{1}{2}\sum _{i=1}^{2}y_{\mathrm{fc}i},\nonumber \\ z_\mathrm{cc}& = \frac{1}{2}\sum _{i=1}^{2}z_{\mathrm{fc}i} \end{aligned}$$(26)
Depending on the shape of the grid cell, the above introduced cell center determination methods result into considerable deviating results. In Fig. 9, a simplified grid with a “degenerate cell” in the center is shown.
The length L is significantly longer when the centroid method is used. This results in a drastic underestimation of the transmissibility (cf. Eq. 19) in direction to grid cell 2 and 7, while the transmissibility in direction to grid cell 5 is overestimated. Due to the frequent occurrences of degenerate cells inside the processed grid, we consequently used the arithmetic mean method (Eqs. 25, 26) for the face and cell center coordinate determination.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Feldmann, F., Hagemann, B., Ganzer, L. et al. Numerical simulation of hydrodynamic and gas mixing processes in underground hydrogen storages. Environ Earth Sci 75, 1165 (2016). https://doi.org/10.1007/s12665-016-5948-z
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s12665-016-5948-z