Abstract
Prediction of hydrogeochemical effects of geological CO2 sequestration is crucial for planning an industrial or even experimental scale injection of carbon dioxide gas into geological formations. This paper presents a preliminary study of the suitability of saline aquifer associated with a depleted oil field in Czech Part of Vienna Basin, as potential greenhouse gas repository. Two steps of modeling enabled prediction of immediate changes in the aquifer and caprocks impacted by the first stage of CO2 injection and the assessment of long-term effects of sequestration. Hydrochemical modeling and experimental tests of rock–water–gas interactions allowed for evaluation of trapping mechanisms and assessment of CO2 storage capacity of the formations. In the analyzed aquifer, CO2 gas may be locked in mineral form in dolomite and dawsonite, and the calculated trapping capacity reaches 13.22 kgCO2/m3. For the caprock, the only mineral able to trap CO2 is dolomite, and trapping capacity equals to 5.07 kgCO2/m3.
Similar content being viewed by others
Explore related subjects
Discover the latest articles, news and stories from top researchers in related subjects.Avoid common mistakes on your manuscript.
Introduction
Prediction of hydrogeochemical effects of geological CO2 sequestration is crucial for planning an industrial or even experimental scale injection of carbon dioxide gas into geological formations (e.g., Bachu et al. 1994, 2007). Experimental examinations of the CO2–brine–water system behavior serve precise results of short-term reactions and their products (e.g., Kaszuba et al. 2005; Lin et al. 2008; Rosenbauer et al. 2005). On the other hand, they give only an approximation of the long-term phenomena that occur within the geologic space. Coupled numerical models, incorporating kinetic transport through porous media and thermodynamic issues of the multiphase system are the most helpful in prognosing the injection impact on the hosting and insulating rock environment (e.g., Gunter et al. 1993; Perkins and Gunter 1995; White et al. 2005).
Batch experiments and geochemical modeling allow for the assessment of geochemical evolution without taking into account the fluid flow and chemical transport. Such approach is a simplification as the real geochemical evolution in gas–rock–brine systems occurs through a complex interplay of fluid and heat flow, and chemical transport processes. The geologic storage of CO2 is possible due to several physicochemical mechanisms, and one of them is the mineral trapping. These processes evolve over time, since CO2 injection, and at an early stage of the project, they are dominated by structural, stratigraphic or hydrodynamic trapping. They are ruled mainly by the following physical processes: fluid flow in liquid and gas phases under pressure and gravity forces, capillary pressure effects and heat flow by conduction, convection and diffusion. Transport of aqueous and gaseous species by advection and molecular diffusion is considered in both liquid and gas phases. (Xu et al. 2003). After CO2 injection is finished, numerous trapping mechanisms become increasingly important. CO2 may be partially contained via residual trapping as the plume moves away from the well. The gas also mixes with and dissolves in the formation water at the leading and trailing edges of the plume (solubility trapping). Dissociation of the CO2 dissolved in the formation water creates acidity that reacts with minerals in the formation and may dissolve fast reacting carbonate minerals (if present) in the acidified zone surrounding the injection well, leading to an increase in dissolved bicarbonate (so-called ionic trapping). In the longer term, dissolution of silicates such as plagioclase and chlorite causes pH to increase, and carbonates may precipitate in the previously acidified zone as CO2 partial pressure declines (mineral trapping) (Golding et al. 2013).
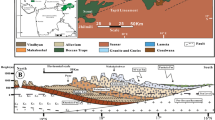
For the purpose of this work, hydrochemical modeling under no-flow conditions was carried out. It based on the information regarding the petrophysical and mineralogical characteristics of the formation, pore water composition, pressure and temperature values and kinetic reaction rate constants. The study was performed in the framework of research pilot project for geological storage of CO2 in the Czech Republic, conducted within the area of the Vienna Basin–Fig. 1.
Geological setting
The potential storage site is situated in the depleted oil field Brodské of Middle Badenian age, in the Moravian part of the Vienna Basin–Fig. 2. The basin is associated with a classical thin-skinned pull-apart basin of Miocene age, which sedimentary fill is overlying the Carpathian thrust belt (Decker 1996). The petroleum systems of the Vienna basin Miocene sedimentary carapace and entire the Carpathian region in Moravia are mostly associated with the Jurassic source rocks (Picha and Peters 1998). Hydrocarbons generated within the formation supplied several oil and gas fields in the Miocene reservoirs, mostly via several major fault and fracture zones. Lower Badenian sediments of total thickness of about 700 m, consist from the basal conglomerates, covered with clays thickness up to 350 m thick. Considering the carbon dioxide sequestration, the aquifer of Middle Badenian age represented by 50- to 80-m-thick sands (that were also collector for oil and gas) was taken into account in our study. The overlying caprock, about 100 m thick, is built of pelitic sediments, containing agglutinated foraminifera fossils. The Upper Badenian sands and pelitic sediments are about 200 m thick (Krejcí et al. 2015).
Schematic cross section of the Brodské oil field (Krejčí et al. 2015)
Modeling scheme and input data
Modeling scheme
The applied scheme was designed to represent dual scale phenomena typical for relatively short-term injection and for longer-term sequestration. Simulations of water–rock–gas interactions were performed with use of the Geochemist’s Workbench (GWB) 9.0–geochemical software (Bethke 1996, 2008). The GWB package was used for equilibrium and kinetic modeling of gas–brine–water system in two stages. The first one was aimed at simulating the immediate changes in the aquifer and caprock impacted by the beginning of CO2 injection, the second–enabled assessment of long-term effects of sequestration. The reactions quality and progress were monitored, and their effects on formation porosity and mineral sequestration capacity (CO2 trapping in form of carbonates) were calculated. The CO2–brine–rock reactions were simulated using two modeling procedures:
-
1.
Equilibrium modeling was applied to reproduce the composition of pore water, basing on the sample chemical composition equilibrated with the formation rock mineralogy. The model required the thermodynamic data for the reacting minerals, their abundance in the assemblages within the host- and the caprock, relative fraction of pore water and the information on its physicochemical parameters,
-
2.
Kinetic modeling was carried out in order to evaluate changes in the hydrogeochemical environment of the formation, due to the injection and CO2 storage. This stage considered the pore water composition calculated in the previous step (equilibrium modeling). The sliding fugacity path of CO2 gas was applied to simulate the introduction of the gas into the system and the desired pressure buildup within 100 days. This simplification assumed also the complete mixing between the gas and brine, from the beginning of the reactions in modeled system. This enabled the assessment of volumes and amounts of mineral phase precipitating or being dissolved during the simulated reactions, and their influence on porosity changes and amounts of CO2 sequestered.
Thermodynamic database “thermo.dat” (built-in the GWB package) containing activity coefficients calculated on the basis of “B-dot” equation (Helgeson and Kirkham 1974) (an extended Debye-Hückel model) was applied.
Mineralogical characteristics of the formation
Composition of mineral assemblage of the samples considered in the model was determined by means of XRD analysis–Table 1.
Petrophysical characteristics of the formation
Porosity
Values of porosity of 27.3 % for the aquifer and 8 % for the caprock the porosimetric properties of the examined rocks were determined by means of Mercury Intrusion Porosimetry (Autopore 9220 Micrometrics Injection Porosimeter). Density of the rock samples was measured with use of helium AccuPyc 1330 pycnometer. The method allowed for the determination of pore size distribution and the “effective” porosity related to pores with the radius between 0.01 and 100 μm.
Specific surface area
Reaction model required the input of the mineral specific surface areas–SSAs. They were calculated assuming spherical grains of different diameters for sandstones and fine-grained rocks. The SSA [cm2/g] is calculated using the radius, molar volume and molecular weight of each of mineral after the following formula:
where A−sphere area [cm2], v−molar volume [cm3/mol], V−sphere volume [cm3], and MW−molecular weight [g/mol] of a given mineral phase. Values of the specific surface areas used in calculations are presented in Table 2.
Pressure, temperature and CO2 fugacity
The modeling was performed assuming the formation pressure at the level of hydrostatic pressure proposed. There is no information of underpressure or overpressure conditions within the sedimentary complex under consideration. Pressure and temperature relevant to the depth of modeled environments are given in Table 3. Temperature values were accepted after the archival well-log data.
As the utilized software−GWB−requires the gas pressure input in form of fugacity–a measure of a chemical potential in the form of adjusted pressure. The appropriate values (Table 3) were calculated using online calculator of the Duan Group (http://www.geochem-model.org/models/co2/), after (Duan et al. 2006).
Pore water composition
Analyses of the formation water were carried out using standard methods, including in situ measurements, assuring the quality of interpretation. The chemical compositions of the formation water in the aquifer–host environment, and the caprock, for the purpose of the simulation were obtained by equilibration of the formation water (Table 4) with the minerals assemblage typical for the modeled environments (Table 2).
Kinetic rate parameters
The following kinetic dissolution/precipitation rate equation simplified after Lasaga (1984) was used in the calculations:
where rk−reaction rate ([mol s−1], dissolution−rk > 0, precipitation–rk < 0), AS−mineral’s surface area (cm2), kT−rate constant [mol cm−2 s−1] at the temperature T, Q−activity product (−), K−equilibrium reaction for the dissolution reaction (−).
According to the above equation, a given mineral precipitates when it is supersaturated or dissolves when it is undersaturated at a rate proportional to its rate constant and the surface area. The Arrhenius law expresses the dependence of the rate constant−kT on the temperature−T:
where k25−rate constant at 25 °C [mol m−2 s−1], EA−activation energy [J mol−1], R−gas constant (8,3143 J K−1 mol−1), T−absolute temperature (K).
The kinetic rate constants for the minerals involved in modeled reactions (Table 5) were taken from Palndri and Kharaka (2004).
Results
Reaction of carbon dioxide with water producing the carbonic acid is of the greatest importance for the mineral sequestration process, because just the aqueous form of CO2 (not the molecular form–CO2(g)) can react with the aquifer rocks. Solubility of CO2 is the function of temperature, pressure and ionic strength of the solution. CO2 solubility in 1 m NaCl solution, at the temperature of 40 °C and 100 bar pressure–similar to the possible disposal conditions in the aquifer considered–equals to ca. 1 Mol, and it is lower by 23 % than in pure water (calculated basing on Duan and Sun 2003; Duan et al. 2006).
Dissociation of H2CO3 results in pH decrease, reaching its minimum at about 50 °C (Rosenbauer et al. 2005). Therefore, high availability of H+ ions, at relatively lower temperatures, enhances hydrolysis of minerals forming the aquifer rock matrix. Carbonic acid dissociation initiates several reactions involving mineral phases and pore fluids, in consequence leading to the mineral or solubility CO2 trapping.
In this work, at each modeled stage (injection and storage), the brine of a given chemistry (Table 4) was considered. Its volume was set, assuming full-water saturation, at the value allowing to obtain the required porosity (Table 4), considering the volume of mineral assemblage (Table 1), as a complement to 10,000 cm3. The system temperature and CO2 fugacity were accepted at the levels shown in Table 3. The reactions in the aquifer and caprock systems considered are described in this chapter.
Aquifer
Stage 1: 100 days of CO2 injection
At the first stage, the CO2 injection, lasting for 100 days, causes the increase in gas fugacity to the assumed value: fCO2–68.88 bar. In effect, a significant elevation of CO2(aq) and HCO3 − concentrations (Reaction 1) as well as the drop of pore waters’ pH from 6.6 (value in formation water equilibration with the mineral assemblage) to 4.8 pH is observed–Fig. 3. Total porosity grows in the sandstone by relative 3.6 %–virtually not influencing the injected fluid penetration into the aquifer.
Increase in porosity is controlled mainly by the transformation of gypsum, to anhydrite (Reaction 2), described, e.g., in Ostroff (1964), and the dissolution calcite. Primary gypsum becomes completely depleted in this process. The amounts (mol) of the minerals precipitated or dissolved in this processes, per 10,000 cm3 of modeled rock, are shown in Fig. 4.
Calcite dissolution also increases hydrocarbonate ions concentration (Reaction 3):
Calcite (and chlorite) dissolution may enhance dawsonite formation together with chalcedony and ordered dolomite (however, the vast part of which could be transformed from dolomite, which is present in the primary mineral assemblage of the rock)–Fig. 4, Reaction 4.
Stage 2: 10,000 years since the termination of CO2 injection
At the beginning of the second stage, CO2 fugacity drops rapidly from 59.62 bar to the value of approximately 30 bar, next a slower decrease to 1 bar, reached in 3000 years of storage, is noted–Fig. 5. The CO2(aq) concentration falls in the same manner, while HCO3 − concentrations are decreasing within the 0- to2500-year period. In the next 500 years, they increase in the concentration of 0.3 molal and stabilize around this level. The pH shows an adversely proportional trend to the CO2 fugacity; after 3000 years, the reaction of pore fluid stabilizes at approximately 6.4 pH. The porosity decreases and reaches about 26.8 %, which is 0.5 percent point less than the primary value. This is caused mainly by the precipitation of ordered dolomite, chalcedony and dawsonite (volume of these phases exceeds the volume of dissolved minerals)–Fig. 6.
The mineral trapping mechanism is in general controlled by the same reactions as described for the injection stage: dissolution of calcite and dolomite, and precipitation of dolomite ord. together with dawsonite and chalcedony. This latter Reaction (5), consuming calcite and albite (constituents of the rock matrix) as well as hydrogen ions from the solution, might be responsible for the significant increase in the pH of pore waters
Transformation from dolomite (14 mol dissolved) is not the only cause for formation of ordered dolomite (17 mol precipitated)–Fig. 6. The remaining 3 mol of ordered structure CaMg(CO3)2 is produced in the Reaction (4)–dissolution of calcite and chlorite.
Caprocks
Stage 1: 100 days of CO2 injection
At the first stage, the CO2 injection, lasting for 100 days, causes the increase in gas fugacity to the assumed 59.62 bar. In effect, a significant elevation of CO2(aq) concentrations and a decline of pH to 4.7 are observed. In general, the reactions in the caprock system proceed in a similar manner as in the case of the aquifer–Fig. 7. This is connected with similar mineralogical compositions (Table 1) and pore water chemistry (Table 4), typical for the two formations considered. The porosity increase is mainly related to the transformation of gypsum (which is exhausted in this process) into anhydrite, Reaction (2). The volume of newly formed anhydrite exceeds the gypsum by over 50 %. Total porosity increases in the caprock by relative 7 %–this phenomenon may increase the penetration of injected fluid into the insulating layer.
Calcite and chlorite dissolution triggers the precipitation of dawsonite, chalcedony and ordered dolomite–Fig. 7, Reaction (4) or (6).
Significant amounts of ordered structure dolomite, however, are transformed from dolomite (as described earlier). Some part of dolomite ord. may also originate from Reaction (7), which consumes calcite, bicarbonate and magnesium ions from the pore solution and results in the decrease in pH.
Stage 2: 10,000 years since the termination of CO2 injection
At the beginning of the second stage, CO2 fugacity drops rapidly from 59.62 bar to the value below 0.001 bar, next an increase to 0.002 bar is noted–Fig. 8. The CO2(aq) and HCO3 concentrations fall in the same manner, this is accompanied by a quick rise of pH to the value of 7.5, and in the remaining period, the reaction of pore fluid stabilizes at approximately 7.4 pH. The porosity reaches the value of about 9.15 %.
In the first period of storage, the increasing porosity is controlled by the substantial decay of dolomite and aluminosilicates: clinochlore 14A, albite and K-feldspar (Fig. 9), whose volume is not substituted by the precipitating phases as ordered dolomite and saponite or muscovite. A possible Reaction (8) is hydrogen-consuming and may be responsible in part for the growth of pH.
The mineral trapping mechanism is in general ruled by: dissolution of dolomite and calcite and dolomite ord. precipitation–Fig. 9. The dolomite ord. precipitation might be controlled by the sulfide-catalyzed mechanism as reported in Zhang et al. (2012).
Experimental results
Core samples were placed in the reaction chamber of the RK1 autoclave; construction details of the experimental apparatus RK1 were described in Labus and Bujok (2011). The chamber was filled to 3/4 volume with brine (Table 4), flushed with CO2 gas in order to evacuate the air from the free space and heated. Next, the CO2 was injected to the desired pressure, the temperature was set at 43 °C (± 0.2° C), to achieve the reservoir conditions, under which the CO2 occurs in supercritical phase. Swinging movement of the autoclave facilitated mixing of the fluids and enhanced the contact between liquid and solid phases. Experiment was carried on for 75 days in order to simulate the initial period of storage. During this time temperature, pressure and pH (using a high-pressure electrode) were monitored. At the end of the experiment, the autoclave was depressurized. The reacted samples were dried in a vacuum dryer; next their outer fragments were separated, powdered and examined by means of XRD analysis. XRD analysis of reacted sample–Br45 caprock–revealed differences in mineral composition, compared to the primary assemblage (Fig. 10). The results could not be interpreted in a simple way, because the powdered fragments consisted of the very superficial parts of the reacted cores as well as their inner, less reacted or even chemically unchanged parts. Nevertheless, the observations could support the modeling results particularly with regard to the dissolution of calcite, muscovite, feldspars and the increased abundance of dolomite.
Storage capacity
The trapping capacity of analyzed formations (Table 6) was calculated under the following assumptions. The unitary volume of modeled rock–UVR–aquifer or caprock is equal to 0,01 m3, the primary porosity value (prior to storage) is equal to np, and then, the rock matrix volume measured in UVR in 1 m3 of formation is 100(1-np). Due to the modeled reactions, certain quantities of carbonate minerals dissolve or precipitate per each UVR. On this basis, the CO2 balance and eventually quantity of CO2 trapped in mineral phases are calculated. Modeled chemical constitution of pore water allows calculation of the quantity of carbon dioxide trapped in the form of solution. After simulated 10 ka of storage, the final porosity is nf. Pore space is assumed to be filled with pore water of known (modeled) concentrations of CO2-containing aqueous species, e.g., HCO3 −, CO2(aq), CO3 2−, NaHCO3 (expressed in terms of mgHCO3 −/dm3). The explanation on the example of aquifer rock is given below.
The primary porosity–np–is 0.273; thus, 1 m3 of formation contains 72.7 UVRs. For each UVR, 16.66 mol of dolomite ord. precipitates, trapping 33.329 mol of CO2 (each mole of dolomite traps two mole of CO2); additionally, 2.37 mol dawsonite precipitates as well. Per each UVR 1.29 mol of calcite, 14.14 mol dolomite and 1.103 mol ankerite are dissolved (each mole of ankerite releases two mole of CO2). The difference in quantity of CO2 trapped in the precipitating and dissolved minerals is equal to 3.917 mol per UVR; thus, 296.72 mol CO2 is trapped in 1 m3 of the formation.
After 20 ka of storage, the final mass of pore fluid per UVR is equal to 2.7733 kg; therefore, 1 m3 of formation is assumed to contain 277.33 kg of pore water. The difference in HCO3 − concentrations in the primary fluid (0.01244 molal) and the fluid after 10,000 years of storage (0.04206) equals to 0.0296 molal; difference in CO2aq concentrations is 0.01531, and in NaHCO3 concentrations is 0.004374, respectively. Therefore, approximately 0.049 mol CO2 is trapped in solution per 1 m3 formation.
In our previous work (Labus et al. 2011), regarding the CO2 storage in the Upper Silesian Coal Basin (Poland), we utilized data allowing for more complex modeling and sequestration capacity evaluation. Model calculations enabled the estimate of pore space saturation with gas, changes in the composition and pH of pore waters, and the relationships between porosity and permeability changes and crystallization or dissolution minerals in the rock matrix. On the basis of two-dimensional model, the processes of gas and pore fluid migration within the analyzed aquifers were also characterized, including the density driven flow based on the changing in time density contrasts between supercritical CO2, the initial brine and the brine with CO2 dissolved. These outcomes may give an approximation of the proportions between the different trapping mechanisms. Their magnitudes reached: 2.5–7.0 kg/m3 for the dissolved phase–CO2(aq), −1.2–9.9 kg/m3 for the mineral phase–SMCO2, but as much as 17–70 kg/m3 for the supercritical phase–SCCO2.
Conclusions
This work was aimed at preliminary determination of suitability for the purpose of CO2 sequestration, of the aquifer associated with the depleted oil field Brodské, in the Moravian part of the Vienna Basin. Identification of possible water–rock–gas interactions was performed by means of geochemical modeling in two stages simulating the immediate changes in the rocks impacted by the injection of CO2, and long-term effects of sequestration.
Hydrogeochemical simulation of the CO2 injection into aquifer rocks demonstrated that dehydration of gypsum (resulting in anhydrite formation) and dissolution of calcite are responsible for the increase in porosity. Dissolution of calcite and chlorite enables precipitation of dawsonite–NaAlCO3(OH)2, chalcedony and ordered dolomite. Significant amounts of the latter one, however, result from the transformation of primary dolomite, which was present in the original rock matrix, before the injection.
According to the hydrogeochemical model of the second stage (10,000 years of storage), the mineral trapping mechanism in aquifer is in general controlled by the same reactions as described for the injection stage. Additionally precipitation of dawsonite and chalcedony may occur, in effect of calcite and albite dissolution; this reaction contributes to a considerable increase in pH.
In general, the reactions in the caprock system proceed in a similar manner as in the case of the aquifer. Nevertheless, a considerable decay of primary dolomite together with aluminosilicates, which is not balanced with precipitation of secondary minerals, is responsible for increase in porosity in the first period of storage.
Previous studies proved that the caprock is also the environment for geochemical reactions that, in geological time frame, might be of importance with regard not only to the repository integrity but also to CO2 trapping or release. When modeling the contact zone between the aquifer and insulating layers Labus (2012) reported the process of CO2 desequestration, associated with the dissolution of carbonate minerals, operating in the lower part of caprock. On the other hand Xu et al. (2005) observed the most intense geochemical evolution in the first 4 meters of the caprock but some mineralogical changes (including siderite formation) reached the boundary of the model, i.e., 10 m from the aquifer–caprock interface. The mineral trapping capacity of the caprock leveled at approximately 10 kg/m3 while in the aquifer it was almost 80 kg/m3 (Xu et al. 2005). All this means that the caprock should be taken into account for calculating when calculating the CO2 trapping, because it may constitute at least a few percent in the whole repository.
Our laboratory experiment, reproducing water–rock–gas interactions in possible storage site during the injection stage supports the modeling results particularly with regard to the dissolution of calcite and aluminosilicates, as well as to an increase in relative share of dolomite and quartz in the rock matrix.
The phases capable of mineral CO2 trapping in the discussed aquifer are dolomite ord. and dawsonite, while dolomite, calcite and ankerite are susceptible to degradation. The trapping capacity calculated according to the results of modeling performed; for the aquifer levels at 13.22 kg CO2/m3, these values comparable to the ones obtained in simulations regarding other geologic formations considered as perspective CO2 repositories (e.g., Xu et al. 2003; Labus et al. 2010; Labus 2012). In the analyzed caprock, the only mineral able to trap CO2 is ordered structure dolomite, while dolomite or calcite tends to degrade. Dawsonite formed during the injection stage is quickly and completely dissolved during the storage stage. Trapping capacity of the caprock totals at 5.07 kgCO2/m3. Amount of carbon dioxide that could be trapped in pore water reaches 0.6 kgCO2/m3 of aquifer formation.
The work carried out constitutes the initial recognition stage of suitability of analyzed aquifer for CO2 storage. Its full characteristic in this respect requires detailed determination of the anisotropy of hydrogeological parameters and mineralogical composition of the formation. The models of transport and reaction, created on this basis and calibrated on the experimental results, shall provide information on the spatial distribution of trapping capacity values and variability of gas–rock–water interactions.
References
Bachu S, Gunter WD, Perkins EH (1994) Aquifer disposal of CO2: hydrodynamic and mineral trapping. Energy Convers Manag 35(4):269–279
Bachu S, Bonijoly D, Bradshaw J, Burruss R, Holloway S, Christensen NP, Mathiassen OM (2007) CO2 storage capacity estimation: methodology and gaps. Int J Greenhouse Gas Control 1:430–443
Bethke CM (1996) Geochemical reaction modeling. Oxford University Press, New York
Bethke CM (2008) Geochemical and biogeochemical reaction modeling. Cambridge University Press, Cambridge
CO2CRC (2008) Storage capacity estimation, site selection and characterisation for CO2 storage projects. Cooperative Research Centre for Greenhouse Gas Technologies, Canberra. CO2CRC Report No. RPT08-1001
Decker K (1996) Miocene tectonics at the Alpine-Carpathian junction and the evolution of the Vienna Basin. Mitt Ges Geol Bergbaustud Oesterreich 41:33–44
Duan ZH, Sun R (2003) An improved model calculating CO2 solubility in pure water and aqueous NaCl solutions from 273 to 533 K and from 0 to 2000 bar. Chem Geol 193:257–271
Duan ZH, Sun R, Zhu C, Chou IM (2006) An improved model for the calculation of CO2 solubility in aqueous solutions containing Na+, K+, Ca2+, Mg2+, Cl−, and SO4 2−. Mar Chem 98(2–4):131–139
Golding, SD, Dawson GKW, Boreham CJ, Mernagh T (2013) ANLEC Project 7-1011-0189: Authigenic carbonates as natural analogues of mineralisation trapping in CO2 sequestration: a desktop study Manuka, ACT, Australia: Australian National Low Emissions Coal Research and Development
Gunter WD, Perkins EH, McCann TJ (1993) Aquifer disposal of CO2-rich gases: reaction design for added capacity. Energy Convers Manag 34(9–11):941–948
Helgeson HC, Kirkham DH (1974) Theoretical prediction of the thermodynamic behavior of aqueous electrolytes at high pressures and temperatures, II. Debye- Hückel parameters for activity coefficients and relative partial molal properties. Am J Sci 274:1199–1261
Kaszuba JP, Janecky DR, Snow MG (2005) Experimental evaluation of mixed fluid reactions between supercritical carbon dioxide and NaCl brine: relevance to the integrity of a geologic carbon repository. Chem Geol 217:277–293
Krejčí O, Kociánová L, Krejčí V, Paleček M, Krejčí Z (2015) Structural maps and cross-sections (Package V1.5). REPP-CO2 Report, NF-CZ08-OV-1-006-2015
Labus K (2012) Phenomena at interface of saline aquifer and claystone caprock under conditions of CO2 storage. Ann Soc Geol Pol 82(3):255–262
Labus K, Bujok P (2011) CO2 mineral sequestration mechanisms and capacity of saline aquifers of the Upper Silesian Coal Basin (Central Europe)–Modeling and experimental verification. Energy 36:4974–4982
Labus K, Tarkowski R, Wdowin M (2010) Assessment of CO2 sequestration capacity based on hydrogeochemical model of Water-Rock-Gas interactions in the potential storage site within the Bełchatów area (Poland). Miner Resour Manag XXVI(2):69–84
Labus K, Bujok P, Leśniak G, Klempa M (2011) Study of reactions in water-rock-gas system for the purpose of CO2 aquifer sequestration (in Polish; English abstract). Wydawnictwo Politechniki Śląskiej, Gliwice
Lasaga AC (1984) Chemical kinetics of water-rock interactions. J Geophys Res 89:4009–4025
Lin H, Fujii T, Takisawa R, Takahashi T, Hashida T (2008) Experimental evaluation of interactions in supercritical CO2/water/rock minerals system under geologic CO2 sequestration conditions. J Mater Sci 43:2307–2315
Ostroff AG (1964) Conversion of gypsum to anhydrite in aqueous salt solutions. Geochim Cosmochim Acta 23:1363–1372
Palndri JL, Kharaka YK (2004) A compilation of rate parameters of water-mineral interaction kinetics for application to geochemical modeling. US Geological Survey. Open File Report 2004 1068: 1–64
Perkins EH, Gunter WD (1995) Aquifer disposal of CO2-rich greenhouse gases: modelling of water-rock reaction paths in a siliciclastic aquifer. In: Kharaka YK, Chudaev OV (eds) Proceedings of the 8th international symposium on water-rock interaction. Balkema, Rotterdam, pp 895–898
Picha FJ, Peters KE (1998) Biomarker oil-to-source rock correlation in the Western Carpathians and their foreland, Czech Republic. Petroleum Geoscience 4:289–302
Rosenbauer RJ, Koksalan T, Palandri JL (2005) Experimental investigation of CO2–brine–rock interactions at elevated temperature and pressure: implications for CO2 sequestration in deep-saline aquifers. Fuel Process Technol 86:1581–1597
White SP, Allis RG, Moore J, Chidsey T, Morgan C, Gwynn W, Adams M (2005) Simulation of reactive transport of injected CO2 on the Colorado Plateau, Utah, USA. Chem Geol 217:387–405
Xu T, Apps JA, Pruess K (2003) Reactive geochemical transport simulation to study mineral trapping for CO2 disposal in deep arenaceous formations. J Geophys Res 108(B2):2071–2084
Xu T, Apps JA, Pruess K (2005) Mineral sequestration of carbon dioxide in a sandstone–shale system. Chem Geol 217:295–318
Zhang F, Xu H, Konishi H, Kemp JM, Roden EE, Shen Z (2012) Dissolved sulfide-catalyzed precipitation of disordered dolomite: implications for the formation mechanism of sedimentary dolomite. Geochim Cosmochim Acta 97:148–165
Acknowledgments
This work was supported by Polish Ministry of Science and Higher Education (Grant N N525 363137) and the National Programme for Sustainability I (2013–2020) financed by the state budget of the Czech Republic–Institute of Clean Technologies for Mining and Utilization of Raw Materials for Energy Use, identification code: LO1406.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Labus, K., Bujok, P., Klempa, M. et al. Preliminary geochemical modeling of water–rock–gas interactions controlling CO2 storage in the Badenian Aquifer within Czech Part of Vienna Basin. Environ Earth Sci 75, 1086 (2016). https://doi.org/10.1007/s12665-016-5879-8
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s12665-016-5879-8