An extended MABAC method based on prospect theory with unknown weight information under Fermatean fuzzy environment for risk investment assessment in B&R

Abstract

The assessment of investment risk for the countries along the route in Belt and Road (B&R) can be deemed as a multiple criteria group decision making (MCGDM) issue since multiple investment options based on diverse criterions are assessment by experts. Pondering that the complexity and uncertainty of the assessment setting and the cognition fuzziness and psychological behavior of experts bring challenges to risk assessment, this paper designed an integrated MCGDM risk investment evaluation framework by synthesizing MABAC method and prospect theory under Fermatean fuzzy setting. Firstly, a Fermatean fuzzy interactive distance measure is presented to ascertain the weight of evaluation experts and criterions. Next, some Fermatean fuzzy Frank aggregation operators based upon the proposed Frank operations are developed to fuse Fermatean fuzzy information efficiently. In addition, an innovative evaluation framework for risk investment is designed based on improved prospect theory MABAC and CRITIC approaches. Conclusively, an empirical concerning risk investment issues in B&R is employed to confirm the applicability and feasibility of the constructed evaluation framework, involving the simulation experiments on sensitivity analysis and contrast studies. The assessment information provided by investors using the linguistic assessment terms based upon their cognition ability of them. These outcomes obtained by the propounded method and comparison analysis further emphasize the validity and salient merits of the propounded framework and provide several auxiliary suggestions for investors.

1 Introduction

B&R has made outstanding contributions to economic construction and cultural exchanges among countries around the world since it was first proposed in 2013. The investment projects are growing rapidly among countries under the background of B&R because different countries have different advantages in their geographical and cultural differences. As an advocate for B&R, China’s foreign investment covers 188 countries (regions) and the cumulative direct investment in countries along the belt and road has reached 117.31 billion dollars.¹ In addition, the investment decision possesses much uncertainty and fuzziness during the procedure of risk assessment because of the complicated investment setting faced by the companies and managers. As a consequence, proposing a scientific and rational risk assessment technique is not only significant for investors or companies to adjust their project schemes dynamically and avoid risk reasonably, but also provides feasible suggestions for the investment department to specify the investment plan.

As the assessment of investment risk involves multiple investment options and investors, it can be viewed as a multiple criteria group decision making issue. MCGDM is the procedure that ranks finite number of schemes according to multiple conflicting criterions on the basis of evaluations ascertained by diverse decision experts. Information representation models and decision approaches are two important research issues in the process of multiple criteria decision analysis.

$\bullet$:

For the uncertain information expression. The increasing sophistication of decision environment and the vagueness of investors’ cognition make investors hard to ascertain a pleasing investment programme based upon the diverse criteria and preferences. In order to valid portray the uncertain and vague assessment information, the indeterminacy information representation models including interval value, rough set and fuzzy set (Zadeh 1965) are introduced to fully express the assessment viewpoint and cognition of experts. As an effective extension of fuzzy, the conception of FFS (Senapati and Yager 2019b) is propounded as a novel information representation model from two aspects to efficiently portray the fuzziness and ambiguity of evaluation information. Owing to its unique advantages in expressing uncertain information representation, it has received more attention by researchers to extend basic theory and decision methods. Hence, this research focuses on the construction of decision approach under Fermatean fuzzy setting to resolve the investment risk assessment issues.

$\bullet$:

For the construction of decision approach. The Multi-Attributive Border Approximation area Comparison (MABAC) method is an innovative decision approach proposed by Pamucar and Cirovic (2015) to acquire more accurate decision outcomes. In view of its distinct merits in multiple criteria decision analysis, MABAC method has been generalized to different uncertain contexts to construct decision algorithms and assessment models but there has been no investigation building decision approach to Fermatean fuzzy environment for developing decision analysis. In addition, the psychological behavior of experts plays an important role in the process of investment risk assessment. Prospect theory has been proved to be an effective behavioral decision theory to describe the risk preference of experts in the analysis of risk decision-making problems.

In light of the literature overview and discussion, the research motivations of this paper can be outlined as below:

$\spadesuit$:

As an important branch of information measure, the distance measure is a worthwhile tool to distinguish the difference of two objectives. The existing distance measure of FFS is proposed through taking into account the membership grade (MG) and nonmembership grade (NMG), which will lead to information loss and unreasonable phenomenon in the course of comparison. Accordingly, we further propound a generalized Fermatean fuzzy interactive distance measure to pondering the cross-assessment of the decision information.

$\spadesuit$:

At present, most Fermatean fuzzy aggregation operators are based on algebraic operations which ignore the flexibility of the information fusion process. As mentioned, the Frank t-norm and t-conorm possess an adjustable parameter to make up the deficiency of algebraic operations. In addition, the Frank operations failed to investigate on FFS to fuse the Fermatean fuzzy information. Therefore, we present several Fermatean fuzzy Frank operators to aggregate the set of information.

$\spadesuit$:

The weight information is a vital part of addressing complex decision issues. Most Fermatean fuzzy decision approaches assume that the weight of attribute and expert is given in according to the subjective preference of expert, which ignores the impact of the decision information itself. Hence, we construct the similarity-based method and improved CRITIC algorithm based on the generalized interactive distance to ascertain the important degree of expert and criteria, severally

$\spadesuit$:

Unfortunately, the classical MABAC method is not expanded to deal with the MCGDM issue with Fermatean fuzzy assessment information. In addition, the extant Fermatean fuzzy decision approaches fail to take into consideration the behave characteristic of experts by prospect theory. As a consequence, we generalize the MABAC method based on prospect theory to Fermatean fuzzy setting for building the risk investment evaluation framework.

$\spadesuit$:

Because the existing approaches possess several defects in solving complex risk investment evaluation problems. In addition, the risk investment evaluation problem in the context of B&R has not been investigated through utilizing the Fermatean fuzzy assessment information. Therefore, we build an innovative risk assessment framework on the basis of the advanced FF-CRITIC-MABAC approach and further provide decision support and risk management for risk evaluation problems.

Based upon the explored motivations, this article puts forward a fused Fermatean fuzzy MCGDM approach through synthesizing the generalized interactive distance measure, Fermatean fuzzy Frank weighted averaging (geometric) operators and an enhanced CRITIC-MABAC method. Further, we verify its practicality by an illustrative example of risk investment evaluation in the setting of B&R. Accordingly, the contributions of this research can be displayed in the following:

$\checkmark$:

we propound the generalized Fermatean fuzzy interactive distance measure for considering the cross assessment of decision information;

$\checkmark$:

Based upon the Frank t-norm and t-conorm, we build the Fermatean fuzzy Frank operational rules and further present several Fermatean fuzzy Frank operators;

$\checkmark$:

An integrated FF-CRITIC-MABAC method based on the prospect theory, generalized Fermatean fuzzy interactive distance measure and Fermatean fuzzy Frank operators is constructed to support the application of risk management;

$\checkmark$:

A demonstrative example of risk investment evaluation is employed to test the applicability of the Fermatean fuzzy risk assessment framework and comparison studies are also conducted to highlight the merits of the designed framework.

To accomplish the above aims, the remainder of this essay is arranged as below: Sect. 2 discusses the related research of this study. Section 3 looks back on several fundamental background knowledge required for this research. A generalized Fermatean fuzzy interactive distance measure is propounded in Sect. 4. In Sect. 5, several Fermatean fuzzy Frank operations are developed and the related properties and cases are explored in detail. An integrated FF-CRITIC-MABAC risk assessment framework is built up through combining the proposed distance measure, aggregation operators and prospect theory Sect. 6. In Sect. 7, a risk investment case is employed to further validate the practicability of the propounded decision framework, and the comparisons are implemented to highlight the effectiveness, applicability and superiority of the decision framework. Several conclusion remarks and research prospects are listed in the end.

2 Related work

This section retrospects and discusses the related works of this research.

2.1 Fermatean fuzzy set

Fuzzy set theory has attained prevailing concerns from a multitude of scholars and investigators in the aspect of disposing of uncertainty and ambiguity information. In order to portray the assessment opinion of experts based on their cognition more comprehensive, several generalizations of fuzzy set including intuitionistic fuzzy set (Atanassov 1986) and Pythagorean fuzzy set (Yager 2014) are propounded as powerful uncertain information representation model to express vague information. Intuitionistic fuzzy set expresses experts’ advice or opinions with the aid of MG and NMG meeting the condition $0\le MG+NMG \le 1$. Afterwards, Pythagorean fuzzy set is advanced through expanding the range of the limitation condition of MG and NMG to further make up the deficiency of IFS. In actual decision issues, when an expert provides his assessment information via the $MG=0.7$ and $NMG=0.8$, it is obvious that intuitionistic fuzzy set and Pythagorean fuzzy are invalid in dealing with this special situation because of $0.7+0.8>1$ and $0.7^{2}+0.8^{2}>1$. Consequently, an innovative uncertainty information expression tool called Fermatean fuzzy set (Senapati and Yager 2019b) is put forward to model the fuzziness information via MG and NMG with the condition $0\le MG^{3}+NMG^{3} \le 1$. Evidently, the above special case can be disposed of through utilizing FFS because of $0.7^{3}+0.8^{3}=0.855<1$. In view of the significant superiority in representing uncertain information the increasing complexity of decision environment, the research based on FFS receives more and more by scholars and acquired lots of investigation achievements (Senapati and Yager 2019a, c; Yang et al. 2021). For instance, Liu et al. (2019a) advanced the Fermatean fuzzy linguistic set and the related operations to ponder the combination of FFS and linguistic variable. In order to enhance the flexibility of operations under the Fermatean fuzzy context, several Dombi operators of FFS and TOPSIS techniques are synthesized to build up MCGDM method (Aydemir and Gunduz 2020). In addition, Garg et al. (2020) developed an evaluation model for COVID-19 testing facility using Fermatean fuzzy Yager operators. Keshavarz-Ghorabaee et al. (2020) constructed a green construction assessment model with the assistance of Fermatean fuzzy WASPAS approach. Shahzadi and Akram (2021) brought forward the Fermatean fuzzy soft set and built a group decision algorithm to select antivirus masks. Hadi et al. (2021) presented several novel aggregation operators based upon the Hamacher operations to build decision algorithm. To further the uncertainty of membership and nonmembership grade, Jeevaraj (2021) built up the interval-valued FFS theory and proposed the related basic operations, score function and distance measures. Deng and Wang (2021) also study novel MCDM approaches based upon the evidential theory and entropy measure. Gul (2021) proposed three improved approaches based on SAW, ARAS and VIKOR methods to choose a desirable testing laboratory in COVID-19. In addition, most operations of FFS are constructed based on the algebraic norm, which lacks robustness and flexibility during the procedure of computation. More research on FFS can further be investigated in literature (Mishra and Rani 2021; Mishra et al. 2021; Rani and Mishra 2021). With the help of the above Fermatean fuzzy research, we can obtain that the current distance of FFS only considers the comparison of MG and NMG, which fails to resolve several special cases. In addition, some aggregation operators also lack flexibility during the course of information fusion. Accordingly, this research tries to propose novel distance measures and integration operators.

2.2 CRITIC method

As a dispensable element in the procedure of decision analysis, weight of criteria symbols the information quality of the considered criteria and has a certainty impact on the ultimate decision outcomes. The CRITIC method is proved as a powerful algorithm to objectively ascertain weight information of criterion through the correlation coefficient (Diakoulaki et al. 1995). In light of the superiority of CRITIC in the aspect of determining weight information, lots of investigators research it and synthesize it with other decision techniques to build diverse decision approaches or assessment frameworks (Ghorabaee et al. 2017; Rostamzadeh et al. 2018; Mohamadghasemi et al. 2020; Peng and Garg 2021). Peng et al. (2019) redefined the operations of PFS and presented a novel 5G assessment method based on a new score function and CRITIC method. Liu et al. (2020b) constructed an investment decision model based upon an improved distance measure and CRITIC method under probabilistic hesitant fuzzy environment. Afterwards, Wu et al. (2020) combined the cloud model theory and CRITIC approach to develop the urban rail transit operation safety assessment framework. For the hybrid assessment issue, Xu et al. (2020) built up a comprehensive assessment model based on BWM, CRITIC approach and Gray relation analysis to address evaluation issues with hybrid information. Lai and Liao (2021) propounded a MCDM decision method through synthesizing the DNMA and CRITIC methods under linguistic D number to select an optimal blockchain platform. In light of the literature on FFS, the CRITIC method is extended based on the score function of FFS to determine criterion weight. However, we find that the correlation coefficient between criterions computed by score function will cause unreasonable outcomes. Compared with the score function, the distance measure has a stronger ability to distinguish the difference through considering the cross assessment of FFS. Accordingly, this paper extended the CRITIC approach based upon the presented generalized interactive distance measure to acquire more rational weight information of criterions.

2.3 MABAC method

MCDM is a vital part of modern decision science which provides a systemic framework and algorithm to select the desirable alternatives under the considered multiple criterions. Many researchers or scholars explored different decision approaches to provide decision support for solving practical complex decision problems such as TOPSIS method, SAW method, VIKOR approach and so forth. Recently, an efficient and scientific decision technique called Multi-Attributive Border Approximation area Comparison is propounded for evaluators to develop decision analysis more accurately (Pamucar and Cirovic 2015). The core of the MABAC approach is to determine a satisfying option based upon the distance from alternatives to the border approximation area. In light of the merits of MABAC method in developing decision analysis, it has been extended to diverse fuzzy settings, such as Pythagorean fuzzy set (Peng and Yang 2016), interval-valued intuitionistic fuzzy set (Xue et al. 2016; Liu et al. 2019b), single-valued neutrosophic linguistic set (Ji et al. 2018), linguistic interval-valued Pythagorean fuzzy set (Garg 2020) and so on. In addition, (Jia et al. 2019) constructed the extended MABAC method under intuitionistic fuzzy rough context to proposed novel MCGDM method. Liu et al. (2020a) built up an assessment framework by aggregated the bipolar fuzzy MABAC method and SWARA approach to evaluate occupational health and safety risk. In order to take into consideration the risk preference and psychological factors in decision analysis, Wang et al. (2018) extended the initial MABAC method based upon the prospect theory to picture fuzzy environment to ponder the behavior preference of evaluators in decision analysis. Liu and Cheng (2020) put forward an improved MABAC method by combining the regret theory and probability multi-valued neutrosophic set. Apart from these investigations, Shen et al. (2020) constructed the entended MABAC method through taking into account the reliability of information to assess the regional circular economy development scheme. More investigations about the MABAC method can refer to the literature (Luo and Liang 2019; Dorfeshan and Mousavi 2019; Fan et al. 2020; Gong et al. 2020). The existing works on extension of MABAC method show its stronger capability in decision analysis and assessment model establishment. However, in literature reviewing, we can find that there is no research regarding the MABAC method based on CRITIC approach and prospect theory under the Fermatean fuzzy setting.

2.4 The assessment of risk investment

The assessment of risk investment is an imperative issue for social economic construction and development, which can also benefit investors or departments to make rational investment plans and evade risk. So far, researchers have achieved several investigations on the assessment of risk investment in various practical application domains. Duan et al. (2018) constructed a comprehensive assessment model on the basis of entropy weight and fuzzy integrated evaluation methods to evaluate the overseas energy investment risk of nations in B&R. Yuang et al. (2018) built up a comprehensive assessment system for the electric Power Investment Risk and utilized the fuzzy integration model to evaluate the electric power investment risk of countries in B&R. Based on the analysis of the obtained decision outcomes, several policy suggestions for investors are provided to help enterprises enhance investment efficiency. Yuan et al. (2019) proposed an integrated decision model based upon the combination weight and TODIM approach to evaluate the overseas investment risk of coal-fired power plants. Kim et al. (2018) also built a risk evaluation model by combining the analytic hierarchy process method and fuzzy inference system to assess the investment risk of overseas steel-plant project. Wu et al. (2020) assessed the investment risk of renewable energy on the basis of ANP-cloud approach for nations in B&R. Furthermore, to more accurate express experts’ assessment viewpoint, Liu et al. (2020c) propounded a hybrid decision assessment framework based on the extended VIKOR method under hesitant fuzzy linguistic setting to evaluate the wind power investment risk of diverse areas. Gou et al. (2021) pioneered a novel assessment model based on the prospect theory and linguistic preference ordering for the risk evaluation of construction project investment, which has a higher consistency because it utilizes the consensus reaching model to obtain the collective prospect theory matrix. Hashemizadeh et al. (2021) considered the uncertainty in the course of investment risk assessment and further constructed a comprehensive assessment framework based upon the analytic network process and TODIM method to assist investors evaluate the investment projects. Ilbahar et al (2022) put forward a modified failure mode and effect analysis through synthesizing the prospect theory analytic hierarchy process under interval-valued intuitionistic fuzzy environment to evaluate the risks in renewable energy investments. Thus far, no research has suggested the investment risk assessment by utilizing the Fermatean fuzzy CRITIC-MABAC method based on prospect theory.

3 Preliminaries

This section reviews several basic conceptions including FFS and Frank operations which will be utilized in the construction of our decision framework.

3.1 FFS

The conception of FFS is originally propounded to further represent uncertain information more effective than IFS and PFS. In what follows, we illustrate the definitions and operations of FFS (Senapati and Yager 2019b).

Definition 1

(Senapati and Yager 2019b) Assume Z is a domain of discourse. A Fermatean fuzzy set (FFS) F on Z is represented as

$$\begin{aligned} F=\{\langle z, \zeta _{F}(z), \eta _{F}(z)\rangle \mid z\in Z\} \end{aligned}$$

wherein $\zeta _{F}(z): Z \rightarrow [0, 1]$ and $\eta _{F}(z): Z \rightarrow [0, 1]$ severally signify the grade of membership and non-membership of the element z to F with the restriction that $0\le \left( \zeta _{F}(z)\right) ^{3}+ \left( \eta _{F}(z)\right) ^{3} \le 1$. The pair $F=\left( \zeta _{F}(z), \eta _{F}(z)\right)$ is usually utilized to signify a Fermatean fuzzy number (FFN) and simply as $F=\left( \zeta _{F}, \eta _{F}\right)$ with $0\le \zeta _{F}^{3}+ \eta _{F}^{3}\le 1$. The hesitancy grade of z belonging to F is denoted $\pi _{F}(x)=\root 3 \of {1-\left( \zeta _{F}(z)\right) ^{3}- \left( \eta _{F}(z)\right) ^{3}}$.

Definition 2

(Senapati and Yager 2019b) For two arbitrary FFNs $F_{1}=\left( \zeta _{F_{1}}, \eta _{F_{1}} \right)$ and $F_{2}=\left( \zeta _{F_{2}}, \eta _{F_{2}} \right)$, the basic operational laws of are $F_{1}$ and $F_{2}$ generated by algebraic operations are defined as below:

$$\begin{aligned} (1) \;&F_1\oplus _{A} F_2=\left( \root 3 \of {1-\left( 1-\left( \zeta _{F_{1}}\right) ^{3}\right) \left( 1-\left( \zeta _{F_{2}}\right) ^{3}\right) }, \eta _{F_{1}}\eta _{F_{2}}\right) ;\\ (2) \;&F_1 \otimes _{A} F_2=\left( \zeta _{F_{1}} \zeta _{F_{2}}, \root 3 \of {1-\left( 1-\left( \eta _{F_{1}}\right) ^{3}\right) \left( 1-\left( \eta _{F_{2}}\right) ^{3}\right) }\right) ; \\ (3) \;&\kappa \cdot _{A} F_1=\left( \root 3 \of {1-\left( 1-\left( \zeta _{F_{1}}\right) ^{3}\right) ^{\kappa }}, \left( \eta _{F_{1}}\right) ^{\kappa }\right) , \kappa>0; \\ (4) \;&F_{1}^{\kappa }=\left( \left( \zeta _{F_{1}}\right) ^{\kappa }, \root 3 \of {1-\left( 1-\left( \eta _{F_{1}}\right) ^{3}\right) ^{\kappa }}\right) , \kappa >0; \\ (5) \;&F_{1}^{c}=\left( \eta _{F_{1}}, \zeta _{F_{1}} \right) . \end{aligned}$$

In addition, the score function, accurate function and ranking method for two FFNs are defined as below.

Definition 3

(Senapati and Yager 2019b) Given a FFN $F=\left( \zeta _{F}, \eta _{F} \right)$, the score function ${\mathscr {S}}(F)$ and accuracy function ${\mathscr {A}}(F)$ of F are severally defined as

$$\begin{aligned}&{\mathscr {S}}(F)=\left( \zeta _{F}\right) ^{3}-\left( \eta _{F}\right) ^{3}, \;\text {and}\; {\mathscr {S}}(F) \in [-1, 1]; \end{aligned}$$

(1)

$$\begin{aligned}&{\mathscr {A}}(F)=\left( \zeta _{F}\right) ^{3}+\left( \eta _{F}\right) ^{3}, \;\text {and}\; {\mathscr {A}}(F) \in [0, 1]. \end{aligned}$$

(2)

Definition 4

(Senapati and Yager 2019b) For two arbitrary FFNs $F_{1}=\left( \zeta _{F_{1}}, \eta _{F_{1}} \right)$ and $F_{2}=\left( \zeta _{F_{2}}, \eta _{F_{2}} \right)$. ${\mathscr {S}}(F_1)$ and ${\mathscr {S}}(F_2)$ are the score function of $F_{1}$ and $F_{2}$, respectively. ${\mathscr {A}}(F_1)$ and ${\mathscr {A}}(F_2)$ are the score function of $F_{1}$ and $F_{2}$, severally. Then, the comparison algorithm between $F_{1}$ and $F_{2}$ is depicted as below:

• (1) If ${\mathscr {S}}(F_1) < {\mathscr {S}}(F_2)$, then $F_1$ is smaller than $F_2$, signified as $F_1 \prec F_2$;

• (2) If ${\mathscr {S}}(f_1) = {\mathscr {S}}(F_2)$, then, we need to compare their accuracy values:

  • If ${\mathscr {A}}(F_1) > {\mathscr {A}}(F_2)$, then $F_1$ is bigger than $F_2$, signified as $F_1 \succ F_2$;

  • If ${\mathscr {A}}(F_1) = {\mathscr {A}}(F_2)$, then $F_1$ is no difference with $F_2$, signified as $F_1 \sim F_2$.

Definition 5

Suppose that $F_{1}, F_{2}, F_{3}$ be three FFNs. A function ${\hat{D}}: FFN \times FFN \rightarrow R$ is a Fermatean fuzzy distance measure if it meets the following axioms:

$$\begin{aligned} (P1)\,&0 \le {\hat{D}}\left( F_{1}, F_{2}\right) \le 1;\\ (P2)\,&{\hat{D}}\left( F_{1}, F_{2} \right) ={\hat{D}}\left( F_{2}, F_{1} \right) ;\\ (P3)\,&{\hat{D}}\left( F_{1}, F_{2} \right) =0 \;\text {iff}\; F_{1}=F_{2};\\ (P4)\,&\;\text {If}\; F_{1} \subseteq F_{2} \subseteq F_{3}, \;\text {then}\; {\hat{D}}\left( F_{1}, F_{3} \right) \ge {\hat{D}}\left( F_{1}, F_{2} \right) \\&\quad \;\text {and} {\hat{D}}\left( F_{1}, F_{3} \right) \ge {\hat{D}}\left( F_{2}, F_{3} \right) . \end{aligned}$$

3.2 Frank T-norm and S-norm

Definition 6

(Frank 1979) Frank T-norm and S-norm signify the Frank product and Frank sum operation severally. Given two any real numbers $\alpha , \beta$, Frank T-norm and S-norm are defined as below:

$$\begin{aligned}&T_{{\mathscr {F}}}\left( \alpha , \beta \right) =\log _{\lambda }\left( 1+\frac{\left( \lambda ^{\alpha }-1 \right) \left( \lambda ^{\beta }-1 \right) }{\lambda -1} \right) ,\\&\quad \alpha , \beta \in [0, 1], \lambda \in [1, \infty ];\\&S_{{\mathscr {F}}}\left( \alpha , \beta \right) =1-\log _{\lambda }\left( 1+\frac{\left( \lambda ^{1-\alpha }-1 \right) \left( \lambda ^{1-\beta }-1 \right) }{\lambda -1} \right) ,\\&\quad \alpha , \beta \in [0, 1], \lambda \in [1, \infty ]. \end{aligned}$$

Remark 1

Frank T-norm and S-norm possess the following special cases:

• (1) When $\lambda \rightarrow 1$, Frank operations will degenerate into Algebraic operations: $T_{{\mathscr {F}}}\left( \alpha , \beta \right) =T_{A}\left( \alpha , \beta \right) =\alpha \otimes \beta =\alpha \beta , S_{{\mathscr {F}}}\left( \alpha , \beta \right) =S_{A}\left( \alpha , \beta \right) =\alpha \oplus \beta =\alpha + \beta -\alpha \beta .$

• (2) When $\lambda \rightarrow 1+\infty$, Frank operations will degenerate into Lukasiewict operations: $T_{{\mathscr {F}}}\left( \alpha , \beta \right) =T_{L}\left( \alpha , \beta \right) =\max \{0, \alpha + \beta -1 \}, S_{{\mathscr {F}}}\left( \alpha , \beta \right) =S_{L}\left( \alpha , \beta \right) =\min \{\alpha + \beta , 1 \}$.

4 Fermatean fuzzy interactive distance measure

Distance measure plays a significant element in the construction of decision methodologies and the procedure of decision analysis. However, the extant research of Fermatean fuzzy distance measure is relatively less. Accordingly, we put forward the generalized Fermatean fuzzy interactive distance measure.

Definition 7

Suppose that $F=(F_{1}, F_{2}, \ldots , F_{n})$ and $G=(G_{1}, G_{2}, \ldots , G_{n})$ are two vectors of FFNs, wherein $F_{j}=\left( \zeta _{j}^{F}, \eta _{j}^{F} \right)$, $G_{j}=\left( \zeta _{j}^{G}, \eta _{j}^{G} \right)$. Then the generalized Fermatean fuzzy interactive distance measure ${\mathscr {D}}^{(\rho )} (\rho \ge 1)$ between F and G is defined as:

$$\begin{aligned} {\mathscr {D}}^{(\rho )}\left( F, G\right) =\left( \frac{1}{3n} \sum _{j=1}^{n} \left( \begin{array}{ll} \left| \left( \zeta _{j}^{F}\right) ^{3}-\left( \zeta _{j}^{G}\right) ^{3} \right| ^{\rho } +\left| \left( \eta _{j}^{F}\right) ^{3}-\left( \eta _{j}^{G}\right) ^{3} \right| ^{\rho } + \\ \left| \max \left\{ \left( \zeta _{j}^{F}\right) ^{3}, \left( \eta _{j}^{G}\right) ^{3} \right\} -\max \left\{ \left( \zeta _{j}^{G}\right) ^{3}, \left( \eta _{j}^{F}\right) ^{3} \right\} \right| ^{\rho } \end{array} \right) \right) ^{\frac{1}{\rho }}, \end{aligned}$$

(3)

in which $\left| \max \left\{ \left( \zeta _{j}^{F}\right) ^{3}, \left( \eta _{j}^{G}\right) ^{3} \right\} -\max \left\{ \left( \zeta _{j}^{G}\right) ^{3}, \left( \eta _{j}^{F}\right) ^{3} \right\} \right|$ signifies an interactive assessment between F and G.

Especially, the generalized Fermatean fuzzy interactive distance measure shall yield to Fermatean fuzzy interactive Hamming distance measure when $\rho = 1$, namely,

$$\begin{aligned} {\mathscr {D}}^{(\rho )}\left( F, G\right) =\frac{1}{3n} \sum _{j=1}^{n} \left( \begin{array}{ll} \left| \left( \zeta _{j}^{F}\right) ^{3}-\left( \zeta _{j}^{G}\right) ^{3} \right| +\left| \left( \eta _{j}^{F}\right) ^{3}-\left( \eta _{j}^{G}\right) ^{3} \right| \\ + \left| \max \left\{ \left( \zeta _{j}^{F}\right) ^{3}, \left( \eta _{j}^{G}\right) ^{3} \right\} -\max \left\{ \left( \zeta _{j}^{G}\right) ^{3}, \left( \eta _{j}^{F}\right) ^{3} \right\} \right| \end{array} \right) . \end{aligned}$$

The generalized Fermatean fuzzy interactive distance measure shall yield to Fermatean fuzzy interactive Euclidean distance measure when $\rho = 2$, namely,

$$\begin{aligned} {\mathscr {D}}^{(\rho )}\left( F, G\right) =\left( \frac{1}{3n} \sum _{j=1}^{n} \left( \begin{array}{ll} \left| \left( \zeta _{j}^{F}\right) ^{3}-\left( \zeta _{j}^{G}\right) ^{3} \right| ^{2} +\left| \left( \eta _{j}^{F}\right) ^{3}-\left( \eta _{j}^{G}\right) ^{3} \right| ^{2} + \\ \left| \max \left\{ \left( \zeta _{j}^{F}\right) ^{3}, \left( \eta _{j}^{G}\right) ^{3} \right\} -\max \left\{ \left( \zeta _{j}^{G}\right) ^{3}, \left( \eta _{j}^{F}\right) ^{3} \right\} \right| ^{2} \end{array} \right) \right) ^{\frac{1}{2}}. \end{aligned}$$

Theorem 1

The ${\mathscr {D}}^{(\rho )}\left( F, G\right)$ is a Fermatean fuzzy distance measure between two FFSs F and G on Z.

Proof 1

It is obvious that ${\mathscr {D}}^{(\rho )}$ meets the axiom (P1)–(P3), we only prove the condition (P4).

(P4) Assume that F, G and H are three FFSs on Z. Since $F \subseteq G \subseteq H$, then one has

$$\begin{aligned}&\left| \left( \zeta _{j}^{F}\right) ^{3}-\left( \zeta _{j}^{G}\right) ^{3} \right| ^{\rho } \le \left| \left( \zeta _{j}^{F}\right) ^{3}-\left( \zeta _{j}^{H}\right) ^{3} \right| ^{\rho },\\&\quad \;\left| \left( \eta _{j}^{F}\right) ^{3}-\left( \eta _{j}^{G}\right) ^{3} \right| ^{\rho } \le \left| \left( \eta _{j}^{F}\right) ^{3}-\left( \eta _{j}^{H}\right) ^{3} \right| ^{\rho },\\&\left| \left( \zeta _{j}^{G}\right) ^{3}-\left( \zeta _{j}^{H}\right) ^{3} \right| ^{\rho } \le \left| \left( \zeta _{j}^{F}\right) ^{3}-\left( \zeta _{j}^{H}\right) ^{3} \right| ^{\rho },\\&\quad \;\left| \left( \eta _{j}^{G}\right) ^{3}-\left( \eta _{j}^{H}\right) ^{3} \right| ^{\rho } \le \left| \left( \eta _{j}^{F}\right) ^{3}-\left( \eta _{j}^{H}\right) ^{3} \right| ^{\rho }, \end{aligned}$$

and

$$\begin{aligned}&\left| \max \left\{ \left( \zeta _{j}^{F}\right) ^{3}, \left( \eta _{j}^{G}\right) ^{3}\right\} - \max \left\{ \left( \zeta _{j}^{G}\right) ^{3}, \left( \eta _{j}^{F}\right) ^{3}\right\} \right| \\&\quad \le \left| \max \left\{ \left( \zeta _{j}^{F}\right) ^{3}, \left( \eta _{j}^{H}\right) ^{3}\right\} - \max \left\{ \left( \zeta _{j}^{H}\right) ^{3}, \left( \eta _{j}^{F}\right) ^{3}\right\} \right| ,\\&\left| \max \left\{ \left( \zeta _{j}^{G}\right) ^{3}, \left( \eta _{j}^{H}\right) ^{3}\right\} - \max \left\{ \left( \zeta _{j}^{H}\right) ^{3}, \left( \eta _{j}^{G}\right) ^{3}\right\} \right| \\&\quad \le \left| \max \left\{ \left( \zeta _{j}^{F}\right) ^{3}, \left( \eta _{j}^{H}\right) ^{3}\right\} - \max \left\{ \left( \zeta _{j}^{H}\right) ^{3}, \left( \eta _{j}^{F}\right) ^{3}\right\} \right| . \end{aligned}$$

Hence, we have

$$\begin{aligned} {\mathscr {D}}^{(\rho )}\left( F, H\right)&=\left( \frac{1}{3n} \sum _{j=1}^{n} \left( \begin{array}{ll} \left| \left( \zeta _{j}^{F}\right) ^{3}-\left( \zeta _{j}^{H}\right) ^{3} \right| ^{\rho } +\left| \left( \eta _{j}^{F}\right) ^{3}-\left( \eta _{j}^{H}\right) ^{3} \right| ^{\rho } + \\ \left| \max \left\{ \left( \zeta _{j}^{F}\right) ^{3}, \left( \eta _{j}^{H}\right) ^{3} \right\} -\max \left\{ \left( \zeta _{j}^{H}\right) ^{3} \left( \eta _{j}^{F}\right) ^{3} \right\} \right| ^{\rho } \end{array} \right) \right) ^{\frac{1}{\rho }} \\&\ge \left( \frac{1}{3n} \sum _{j=1}^{n} \left( \begin{array}{ll} \left| \left( \zeta _{j}^{F}\right) ^{3}-\left( \zeta _{j}^{G}\right) ^{3} \right| ^{\rho } +\left| \left( \eta _{j}^{F}\right) ^{3}-\left( \eta _{j}^{G}\right) ^{3} \right| ^{\rho } + \\ \left| \max \left\{ \left( \zeta _{j}^{F}\right) ^{3}, \left( \eta _{j}^{G}\right) ^{3} \right\} -\max \left\{ \left( \zeta _{j}^{G}\right) ^{3}, \left( \eta _{j}^{F}\right) ^{3} \right\} \right| ^{\rho } \end{array} \right) \right) ^{\frac{1}{\rho }}\\&={\mathscr {D}}^{(\rho )}\left( F, G\right) \end{aligned}$$

Similarly, we have ${\mathscr {D}}^{(\rho )}\left( F, H\right) \ge {\mathscr {D}}^{(\rho )}\left( G, H\right)$.

Accordingly, the distance measure ${\mathscr {D}}^{(\rho )}\left( F, G\right)$ meets the properties (P4) in Definition 5, which means that is a distance measure between FFSs.

Theorem 2

Suppose that $F=\left\{ F_{j}|j=1, 2, \cdots , n\right\}$ and $G=\left\{ G_{j}|j=1, 2, \cdots , n\right\}$ are two vectors of FFNs, wherein $F_{j}=\left( \zeta _{j}^{F}, \eta _{j}^{F} \right)$, $G_{j}=\left( \zeta _{j}^{G}, \eta _{j}^{G} \right)$. Then

$$\begin{aligned} (\mathbf{T1} )\,&{\mathscr {D}}^{(\rho )}\left( F_{j}, G_{j} \right) ={\mathscr {D}}^{(\rho )}\left( \left( F_{j}\right) ^{c}, \left( G_{j}\right) ^{c} \right) ;\\ (\mathbf{T2} )\,&{\mathscr {D}}^{(\rho )}\left( F_{j}, \left( G_{j}\right) ^{c} \right) ={\mathscr {D}}^{(\rho )}\left( \left( F_{j}\right) ^{c}, G_{j} \right) ;\\ (\mathbf{T3} )\,&{\mathscr {D}}^{(\rho )}\left( F_{j}, \left( F_{j}\right) ^{c} \right) =1 \;\text {iff}\; F_{j} \;\text {is a crisp set};\\ (\mathbf{T4} )\,&{\mathscr {D}}^{(\rho )}\left( F_{j}, \left( F_{j}\right) ^{c} \right) =0 \;\text {iff}\; \zeta _{j}^{F}=\eta _{j}^{F} \;\text {for}\; z \in Z. \end{aligned}$$

Proof 2

We only prove T1 and T3, the remainder is similar to prove.

$\mathbf{T1}$ Since $\left( F_{j}\right) ^{c}=\left( \eta _{j}^{F}, \zeta _{j}^{F} \right)$ and $\left( G_{j}\right) ^{c}=\left( \eta _{j}^{G}\, \zeta _{j}^{G} \right)$, then

$$\begin{aligned} {\mathscr {D}}^{(\rho )}\left( F, G\right)&=\left( \frac{1}{3n} \sum _{j=1}^{n} \left( \begin{array}{ll} \left| \left( \zeta _{j}^{F}\right) ^{3}-\left( \zeta _{j}^{G}\right) ^{3} \right| ^{\rho } +\left| \left( \eta _{j}^{F}\right) ^{3}-\left( \eta _{j}^{G}\right) ^{3} \right| ^{\rho } + \\ \left| \max \left\{ \left( \zeta _{j}^{F}\right) ^{3}, \left( \eta _{j}^{G}\right) ^{3} \right\} -\max \left\{ \left( \zeta _{j}^{G}\right) ^{3}, \left( \eta _{j}^{F}\right) ^{3} \right\} \right| ^{\rho } \end{array} \right) \right) ^{\frac{1}{\rho }} \\&=\left( \frac{1}{3n} \sum _{j=1}^{n} \left( \begin{array}{ll} \left| \left( \eta _{j}^{F}\right) ^{3}-\left( \eta _{j}^{G}\right) ^{3} \right| ^{\rho } +\left| \left( \zeta _{j}^{F}\right) ^{3}-\left( \zeta _{j}^{G}\right) ^{3} \right| ^{\rho } + \\ \left| \max \left\{ \left( \eta _{j}^{F}\right) ^{3}, \left( \zeta _{j}^{G}\right) ^{3} \right\} -\max \left\{ \left( \eta _{j}^{G}\right) ^{3}, \left( \zeta _{j}^{F}\right) ^{3} \right\} \right| ^{\rho } \end{array} \right) \right) ^{\frac{1}{\rho }} \\&={\mathscr {D}}^{(\rho )}\left( \left( F_{j}\right) ^{c}, \left( G_{j}\right) ^{c} \right) . \end{aligned}$$

$\mathbf{T3}$

$$\begin{aligned} {\mathscr {D}}^{(\rho )}\left( F_{j}, \left( F_{j}\right) ^{c} \right)&=\left( \frac{1}{3n} \sum _{j=1}^{n} \left( \begin{array}{ll} \left| \left( \zeta _{j}^{F}\right) ^{3}-\left( \eta _{j}^{F}\right) ^{3} \right| ^{\rho } +\left| \left( \eta _{j}^{F}\right) ^{3}-\left( \zeta _{j}^{F}\right) ^{3} \right| ^{\rho } + \\ \left| \max \left\{ \left( \zeta _{j}^{F}\right) ^{3}, \left( \zeta _{j}^{F}\right) ^{3} \right\} -\max \left\{ \left( \eta _{j}^{F}\right) ^{3}, \left( \eta _{j}^{F}\right) ^{3} \right\} \right| ^{\rho } \end{array} \right) \right) ^{\frac{1}{\rho }} \\&=\left( \frac{1}{n} \sum _{j=1}^{n} \left| \left( \zeta _{j}^{F}\right) ^{3}-\left( \eta _{j}^{F}\right) ^{3} \right| ^{\rho } \right) ^{\frac{1}{\rho }}, \end{aligned}$$

If ${\mathscr {D}}^{(\rho )}\left( F_{j}, \left( F_{j}\right) ^{c} \right) =1$, then we can attain $\zeta _{j}^{F}=1, \eta _{j}^{F}=0$ or $\eta _{j}^{F}=0, \zeta _{j}^{F}=1$ with the aid of $0 \le \zeta _{j}^{F}, \eta _{j}^{F} \le 1$. Assume that $F_{j}$ is a crisp set, then $\zeta _{j}^{F}=1, \eta _{j}^{F}=0$ or $\eta _{j}^{F}=0, \zeta _{j}^{F}=1$. Obviously, ${\mathscr {D}}^{(\rho )}\left( F_{j}, \left( F_{j}\right) ^{c} \right) =1$.

Theorem 3

Let $P=\left( p_{ij} \right) _{m\times n}$ and $Q=\left( q_{ij} \right) _{m\times n}$ be two Fermatean fuzzy matrices, wherein $p_{ij}=\left( \zeta _{ij}^{p}, \eta _{ij}^{p}\right)$ and $q_{ij}=\left( \zeta _{ij}^{q}, \eta _{ij}^{q}\right)$ are the FFNs. Based on the presented distance measure of FFNs, the distance between the matrices P and Q is described as follows:

$$\begin{aligned} \overline{{\mathscr {D}}}\left( P, Q \right) =\sqrt{ \frac{1}{3mn} \sum \limits _{i=1}^{m} \sum \limits _{j=1}^{n} \left( \begin{array}{lll}\left| \left( \zeta _{ij}^{p}\right) ^{3}-\left( \zeta _{ij}^{q}\right) ^{3} \right| ^{2}+\left| \left( \eta _{ij}^{p}\right) ^{3}-\left( \eta _{ij}^{q}\right) ^{3} \right| ^{2} \\ +\left| \max \left\{ \left( \zeta _{ij}^{p}\right) ^{3}, \left( \eta _{ij}^{q}\right) ^{3} \right\} -\max \left\{ \left( \zeta _{ij}^{q}\right) ^{3}, \left( \eta _{ij}^{p}\right) ^{3} \right\} \right| ^{2} \end{array}\right) }. \end{aligned}$$

(4)

5 Fermatean fuzzy Frank aggregation operators

5.1 Frank operations

Based upon the Frank operations, we shall propound several operational rules of FFNs under this part which are the foundation to build up aggregation operators. Several worthwhile properties and characteristics are also discussed.

Definition 8

For two arbitrary FFNs $F_{1}=\left( \zeta _{F_{1}}, \eta _{F_{1}} \right)$ and $F_{2}=\left( \zeta _{F_{2}}, \eta _{F_{2}} \right)$, the Frank sum signified by $F_{1} \oplus _{{\mathscr {F}}} F_{2}$ and Frank product signified by $F_{1} \otimes _{{\mathscr {F}}} F_{2}$ on the basis of Frank norm operations are respectively defined as follows:

$$\begin{aligned} (1)\;&F_{1}\oplus _{{\mathscr {F}}} F_{2} =\left( \begin{array}{ccc}\root 3 \of {1-\log _{\lambda }\left( 1+\frac{\left( \lambda ^{1-(\zeta _{F_{1}})^{3}}-1 \right) \left( \lambda ^{1-(\zeta _{F_{2}})^{3}}-1 \right) }{\lambda -1} \right) }, \root 3 \of {\log _{\lambda }\left( 1+\frac{\left( \lambda ^{(\eta _{F_{1}})^{3}}-1 \right) \left( \lambda ^{(\eta _{F_{2}})^{3}}-1 \right) }{\lambda -1} \right) } \end{array}\right) ; \end{aligned}$$

(5)

$$\begin{aligned} (2)\;&F_{1} \otimes _{{\mathscr {F}}} F_{2} =\left( \begin{array}{ccc}\root 3 \of {\log _{\lambda }\left( 1+\frac{\left( \lambda ^{(\zeta _{F_{1}})^{3}}-1 \right) \left( \lambda ^{(\zeta _{F_{2}})^{3}}-1 \right) }{\lambda -1} \right) }, \root 3 \of {1-\log _{\lambda }\left( 1+\frac{\left( \lambda ^{1-(\eta _{F_{1}})^{3}}-1 \right) \left( \lambda ^{1-(\eta _{F_{2}})^{3}}-1 \right) }{\lambda -1} \right) } \end{array}\right) . \end{aligned}$$

(6)

Theorem 4

For two arbitrary FFNs $F_{1}=\left( \zeta _{F_{1}}, \eta _{F_{1}} \right)$ and $F_{2}=\left( \zeta _{F_{2}}, \eta _{F_{2}} \right)$. Assume that $F_{3}=F_{1}\oplus _{{\mathscr {F}}} F_{2}$ and $F_{4}=F_{1}\otimes _{{\mathscr {F}}} F_{2}$ hold, then $F_{3}$ and $F_{4}$ are still FFN.

Theorem 5

Suppose that n be any real number and $F_{1}=\left( \zeta _{F_{1}}, \eta _{F_{1}} \right)$ is a FFN. We can obtain the multiplication operation of $F_{1}$ denoted as $n \cdot _{{\mathscr {F}}} F_{1}$ as below:

$$\begin{aligned} n \cdot _{{\mathscr {F}}} F_{1} =\left( \root 3 \of {1-\log _{\lambda }\left( 1+\frac{\left( \lambda ^{1-(\zeta _{F_{1}})^{3}}-1 \right) ^{n}}{\left( \lambda -1\right) ^{n-1}} \right) }, \root 3 \of {\log _{\lambda }\left( 1+\frac{\left( \lambda ^{(\eta _{F_{1}})^{3}}-1 \right) ^{n}}{\left( \lambda -1\right) ^{n-1}} \right) } \right) , \end{aligned}$$

(7)

where $n \cdot _{{\mathscr {F}}} F_{1}=\overbrace{F_{1}\oplus _{{\mathscr {F}}}F_{1}\oplus _{{\mathscr {F}}} \cdots \oplus _{{\mathscr {F}}} F_{1}}^{n}$ is a FFN for arbitrary positive real number n.

Proof 3

We utilize the mathematical induction method on n to prove that Eq. (7) holds for all n.

(a) when $n=1$, one has

$$\begin{aligned} 1 \cdot _{{\mathscr {F}}} F_{1} =\left( \root 3 \of {1-\log _{\lambda }\left( 1+\frac{\left( \lambda ^{1-(\zeta _{F_{1}})^{3}}-1 \right) ^{1}}{\left( \lambda -1\right) ^{1-1}} \right) }, \root 3 \of {\log _{\lambda }\left( 1+\frac{\left( \lambda ^{(\eta _{F_{1}})^{3}}-1 \right) ^{1}}{\left( \lambda -1\right) ^{1-1}} \right) } \right) =\left( \zeta _{F_{1}}, \eta _{F_{1}} \right) . \end{aligned}$$

Hence, Eq. (7) is valid for $n=1$.

(b) Assume that Eq. (7) is valid for $n=y$, then we can deduce that Eq. (7) is valid for $n=y+1$, namely,

$$\begin{aligned} \left( y+1\right) \cdot _{{\mathscr {F}}} F_{1}=\left( \root 3 \of {1-\log _{\lambda }\left( 1+\frac{\left( \lambda ^{1-(\zeta _{F_{1}})^{3}}-1 \right) ^{y+1}}{\left( \lambda -1\right) ^{y+1-1}} \right) }, \root 3 \of {\log _{\lambda }\left( 1+\frac{\left( \lambda ^{(\eta _{F_{1}})^{3}}-1 \right) ^{y+1}}{\left( \lambda -1\right) ^{y+1-1}} \right) } \right) . \end{aligned}$$

Furthermore

$$\begin{aligned} y \cdot _{{\mathscr {F}}} F_{1} \oplus _{{\mathscr {F}}} F_{1}&= \left( \root 3 \of {1-\log _{\lambda }\left( 1+\frac{\left( \lambda ^{1-(\zeta _{F_{1}})^{3}}-1 \right) ^{y}}{\left( \lambda -1\right) ^{y-1}} \right) }, \root 3 \of {\log _{\lambda }\left( 1+\frac{\left( \lambda ^{(\eta _{F_{1}})^{3}}-1 \right) ^{y}}{\left( \lambda -1\right) ^{y-1}} \right) } \right) \oplus _{{\mathscr {F}}} \left( \zeta _{F_{1}}, \eta _{F_{1}} \right) \\&=\left( \root 3 \of {1-\log _{\lambda }\left( 1+\frac{\left( \lambda ^{1-(\zeta _{F_{1}})^{3}}-1 \right) ^{y+1}}{\left( \lambda -1\right) ^{y}} \right) }, \root 3 \of {\log _{\lambda }\left( 1+\frac{\left( \lambda ^{(\eta _{F_{1}})^{3}}-1 \right) ^{y+1}}{\left( \lambda -1\right) ^{y}} \right) } \right) \end{aligned}$$

Hence, Eq. (7) is valid for $n=y+1$ namely, Eq. (7) holds for all n.

Next, we prove the $n \cdot _{{\mathscr {F}}} F_{1}$ is also a FFN. Since $0\le \zeta _{F_{1}}, \eta _{F_{1}}\le 1$, then one has

$$\begin{aligned}&0\le \root 3 \of {1-\log _{\lambda }\left( 1+\frac{\left( \lambda ^{1-(\zeta _{F_{1}})^{3}}-1 \right) ^{n}}{\left( \lambda -1\right) ^{n-1}} \right) } \le 1, \, 0\le \root 3 \of {\log _{\lambda }\left( 1+\frac{\left( \lambda ^{(\eta _{F_{1}})^{3}}-1 \right) ^{n}}{\left( \lambda -1\right) ^{n-1}} \right) }\le 1. \end{aligned}$$

Moreover, since $0 \le \eta _{F_{1i}}^{3} \le 1-\zeta _{F_{1}}^{3}$, then one has

$$\begin{aligned}&0\le \left( \root 3 \of {1-\log _{\lambda }\left( 1+\frac{\left( \lambda ^{1-(\zeta _{F_{1}})^{3}}-1\right) ^{n}}{\left( \lambda -1\right) ^{n-1}} \right) } \right) ^{3} +\left( \root 3 \of {\log _{\lambda }\left( 1+\frac{\left( \lambda ^{(\eta _{F_{1}})^{3}}-1 \right) ^{n}}{\left( \lambda -1\right) ^{n-1}} \right) } \right) ^{3}\\&\le 1-\log _{\lambda }\left( 1+\frac{\left( \lambda ^{1-(\zeta _{F_{1}})^{3}}-1\right) ^{n}}{\left( \lambda -1\right) ^{n-1}} \right) +\log _{\lambda }\left( 1+\frac{\left( \lambda ^{(1-\zeta _{F_{1}}^{3})^{3}}-1 \right) ^{n}}{\left( \lambda -1\right) ^{n-1}} \right) =1 \end{aligned}$$

That means $n \cdot _{{\mathscr {F}}} F_{1}$ is a FFN. Based on this proof, we achieve the proof of Theorem 5.

In the same manner, we can derive the exponentiation operation of $F_{1}$ signified as $F_{1}^{\wedge _{{\mathscr {F}}} n}$ and further acquire the Theorem 6.

Theorem 6

Suppose that n be any real number and $F_{1}=\left( \zeta _{F_{1}}, \eta _{F_{1}} \right)$ is a FFN. We can obtain the exponentiation operation of $F_{1}$ denoted as $F_{1}^{\wedge _{{\mathscr {F}}} n}$ as below:

$$\begin{aligned} F_{1}^{\wedge _{{\mathscr {F}}} n} =\left( \root 3 \of {\log _{\lambda }\left( 1+\frac{\left( \lambda ^{(\zeta _{F_{1}})^{3}}-1 \right) ^{n}}{\left( \lambda -1\right) ^{n-1}} \right) }, \root 3 \of {1-\log _{\lambda }\left( 1+\frac{\left( \lambda ^{1-(\eta _{F_{1}})^{3}}-1 \right) ^{n}}{\left( \lambda -1\right) ^{n-1}} \right) } \right) . \end{aligned}$$

(8)

where $F_{1}^{\wedge _{{\mathscr {F}}} n}=\overbrace{F_{1}\otimes _{{\mathscr {F}}}F_{1}\otimes _{{\mathscr {F}}} \cdots \otimes _{{\mathscr {F}}} F_{1}}^{n}$ is a FFN for arbitrary positive real number n.

Based upon Theorem 5 and6, we can acquire the following multiplication and exponentiation operations for arbitrary positive real number $\kappa$.

$$\begin{aligned} (1)\;&\kappa \cdot _{{\mathscr {F}}} F_{1} =\left( \root 3 \of {1-\log _{\lambda }\left( 1+\frac{ \left( \lambda ^{1-(\zeta _{F_{1}})^{3}}-1 \right) ^{\kappa }}{\left( \lambda -1\right) ^{\kappa -1}} \right) }, \root 3 \of {\log _{\lambda }\left( 1+\frac{\left( \lambda ^{(\eta _{F_{1}})^{3}}-1 \right) ^{\kappa }}{\left( \lambda -1\right) ^{\kappa -1}} \right) } \right) , \end{aligned}$$

(9)

$$\begin{aligned} (2)\;&F_{1}^{\wedge _{{\mathscr {F}}} \kappa } =\left( \root 3 \of {\log _{\lambda }\left( 1+\frac{\left( \lambda ^{(\zeta _{F_{1}})^{3}}-1 \right) ^{\kappa }}{\left( \lambda -1\right) ^{\kappa -1}} \right) }, \root 3 \of {1-\log _{\lambda }\left( 1+\frac{\left( \lambda ^{1-(\eta _{F_{1}})^{3}}-1 \right) ^{\kappa }}{\left( \lambda -1\right) ^{\kappa -1}} \right) } \right) . \end{aligned}$$

(10)

In addition, we can deduce the following worthwhile properties based upon Fermatean fuzzy Frank operations.

Theorem 7

For two arbitrary FFNs $F_{1}=\left( \zeta _{F_{1}}, \eta _{F_{1}} \right)$ and $f_{2}=\left( \zeta _{F_{2}}, \eta _{F_{2}} \right)$ and $\kappa , \kappa _{i}(i=1, 2) >0$. Then the following properties of the Fermatean fuzzy Frank operations are hold.

$$\begin{aligned} (1)\;&F_{1}\oplus _{{\mathscr {F}}} F_{2}=F_{2}\oplus _{{\mathscr {F}}} F_{1}; \\ (2)\;&F_{1}\otimes _{{\mathscr {F}}} F_{2}=F_{2}\otimes _{{\mathscr {F}}} F_{1}; \\ (3)\;&\kappa _{1} \cdot _{{\mathscr {F}}} F_{1}\oplus \kappa _{2} \cdot _{{\mathscr {F}}} F_{1}=\left( \kappa _{1}+\kappa _{2}\right) \cdot _{{\mathscr {F}}} F_{1};\\ (4)\;&\kappa \cdot _{{\mathscr {F}}} \left( F_{1}\oplus _{{\mathscr {F}}} F_{2}\right) =\kappa \cdot _{{\mathscr {F}}} F_{1}\oplus _{{\mathscr {F}}} \kappa \cdot _{{\mathscr {F}}} F_{2};\\ (5)\;&F_{1}^{\wedge _{{\mathscr {F}}} \kappa _{1}}\otimes F_{1}^{\wedge _{{\mathscr {F}}} \kappa ^{2}}=F_{1}^{\wedge _{{\mathscr {F}}} (\kappa _{2}+\kappa _{2})};\\ (6)\;&\left( F_{1}\otimes _{{\mathscr {F}}} F_{2}\right) ^{\kappa }=F_{1}^{\wedge _{{\mathscr {F}}} \kappa } \otimes \wedge _{{\mathscr {F}}} F_{2}^{\wedge _{{\mathscr {F}}} \kappa }. \end{aligned}$$

It is straightforward to derive the mentioned properties with the aid of Definition 8 and Eqs. (9)–(10), so we omit the proof of this theorem because of the space.

5.2 Two Fermatean fuzzy Frank weighted averaging operators

In this subsection, we develop the Fermatean fuzzy Frank weighted average (FFFWA) operator and Fermatean fuzzy Frank weighted geometric (FFFWG) operator based upon the defined Frank operations of FFNs. At the same time, we explore several worthwhile properties of the propounded operators.

Definition 9

Suppose that $F_{j}=\left( \zeta _{F_{j}}, \eta _{F_{j}} \right)$ be a family of FFNs, FFFWA operator is a mapping from $\Lambda ^{n}$ to $\Lambda$. If

$$\begin{aligned}&FFFWA\left( F_{1}, F_{2}, \cdots , F_{n} \right) =\left( \varpi _{1}\cdot _{{\mathscr {F}}} F_{1} \right) \oplus _{{\mathscr {F}}}\nonumber \\&\quad \left( \varpi _{2}\cdot _{{\mathscr {F}}} F_{2} \right) \oplus _{{\mathscr {F}}} \cdots \oplus _{{\mathscr {F}}} \left( \varpi _{n}\cdot _{{\mathscr {F}}} F_{n} \right) , \end{aligned}$$

(11)

then FFFWA is called Fermatean fuzzy Frank weighted average operator, where $\Lambda$ signifies the set of FFNs and $\varpi _{j}$ be the weight of $F_{j}$ with $\varpi _{j} \in [0, 1]$ with $\sum _{{j}=1}^{n}\varpi _{j}=1$. Moreover, FFFWA operator will yield to FFFA operator when $\varpi _{j}=(\frac{1}{n}, \frac{1}{n}, \cdots , \frac{1}{n})^{T}$.

The following theorem can be attained on the basis of Definition 8 and Theorem 5.

Theorem 8

Suppose that $F_{j}=\left( \zeta _{F_{j}}, \eta _{F_{j}} \right)$ be a family of FFNs. Then the fusion value attained through utilizing the FFFWA operator is still a FFN and represented as

$$\begin{aligned} FFFWA\left( F_{1}, F_{2}, \cdots , F_{n} \right) =\left( \begin{array}{ccc}\root 3 \of {1-\log _{\lambda }\left( 1+\prod \limits _{j=1}^{n}\left( \lambda ^{1-(\zeta _{F_{j}})^{3}}-1 \right) ^{\varpi _{j} }\right) }, \\ \root 3 \of {\log _{\lambda }\left( 1+\prod \limits _{j=1}^{n}\left( \lambda ^{(\eta _{F_{j}})^{3}}-1 \right) ^{\varpi _{j}} \right) } \end{array}\right) . \end{aligned}$$

(12)

Proof 4

Based upon the Frank operations in Definition 8, we shall prove the Eq. (12) with the assistance of mathematical induction: It is apparent that Eq. (12) is valid for $n=2$. Assume that Eq. (12) is valid for $n=x$, one has

$$\begin{aligned} FFFWA\left( F_{1} ,F_{2}, \cdots , F_{x} \right) =\left( \begin{array}{ccc}\root 3 \of {1-\log _{\lambda }\left( 1+\prod \limits _{j=1}^{x}\left( \lambda ^{1-(\zeta _{F_{j}})^{3}}-1 \right) ^{\varpi _{j} }\right) }, \\ \root 3 \of {\log _{\lambda }\left( 1+\prod \limits _{j=1}^{x}\left( \lambda ^{(\eta _{F_{j}})^{3}}-1 \right) ^{\varpi _{j}} \right) } \end{array}\right) . \end{aligned}$$

In the next, when $n=x+1$, one has

$$\begin{aligned}&FFFWA\left( F_{1}, F_{2}, \cdots , F_{x+1} \right) =FFFWA\left( F_{1} ,F_{2}, \cdots , F_{x} \right) \oplus _{{\mathscr {F}}} \left( \varpi _{1}\cdot _{{\mathscr {F}}} F_{1} \right) \\&=\left( \root 3 \of {1-\log _{\lambda }\left( 1+\prod \limits _{j=1}^{x}\left( \lambda ^{1-(\zeta _{F_{j}})^{3}}-1 \right) ^{\varpi _{j} }\right) }, \root 3 \of {\log _{\lambda }\left( 1+\prod \limits _{j=1}^{x}\left( \lambda ^{(\eta _{F_{j}})^{3}}-1 \right) ^{\varpi _{j}} \right) } \right) \\&\oplus _{{\mathscr {F}}} \left( \root 3 \of {1-\log _{\lambda }\left( 1+\frac{\left( \lambda ^{1-(\zeta _{F_{1}})^{3}}-1 \right) ^{\varpi _{1}}}{\left( \lambda -1\right) ^{\varpi _{1}-1}} \right) }, \root 3 \of {\log _{\lambda }\left( 1+\frac{\left( \lambda ^{(\eta _{F_{1}})^{3}}-1 \right) ^{\varpi _{1}}}{\left( \lambda -1\right) ^{\varpi _{1}-1}} \right) } \right) \\&=\left( \root 3 \of {1-\log _{\lambda }\left( 1+\prod \limits _{j=1}^{x+1}\left( \lambda ^{1-(\zeta _{F_{j}})^{3}}-1 \right) ^{\varpi _{j} }\right) }, \root 3 \of {\log _{\lambda }\left( 1+\prod \limits _{j=1}^{x+1}\left( \lambda ^{(\eta _{F_{j}})^{3}}-1 \right) ^{\varpi _{j}} \right) } \right) . \end{aligned}$$

Accordingly, Eq. (12) is valid for $n=x+1$, which achieves the proof.

The following properties of FFFWA operator can be attained on the basis of Theorem 8.

Property 1

(Idempotency) Suppose that $F_{j}=\left( \zeta _{F_{j}}, \eta _{F_{j}} \right)$ be a family of FFNs. If $F_{j}=\left( \zeta _{F}, \eta _{F} \right) =F$ for all $F_{j}$. Then

$$\begin{aligned} FFFWA\left( F_{1}, F_{2}, \cdots , F_{n} \right) =F \end{aligned}$$

(13)

Proof 5

$$\begin{aligned}&FFFWA\left( F_{1} ,F_{2}, \cdots , F_{n} \right) \\&=\left( \root 3 \of {1-\log _{\lambda }\left( 1+\prod \limits _{j=1}^{n}\left( \lambda ^{1-(\zeta _{F_{j}})^{3}}-1 \right) ^{\varpi _{j} }\right) }, \root 3 \of {\log _{\lambda }\left( 1+\prod \limits _{j=1}^{n}\left( \lambda ^{(\eta _{F_{j}})^{3}}-1 \right) ^{\varpi _{j}} \right) } \right) \\&=\left( \root 3 \of {1-\log _{\lambda }\left( 1+\prod \limits _{j=1}^{n}\left( \lambda ^{1-(\zeta _{F})^{3}}-1 \right) ^{\varpi _{j} }\right) }, \root 3 \of {\log _{\lambda }\left( 1+\prod \limits _{j=1}^{n}\left( \lambda ^{(\eta _{F})^{3}}-1 \right) ^{\varpi _{j}} \right) } \right) \\&=\left( \root 3 \of {1-\log _{\lambda }\left( 1+\left( \lambda ^{1-(\zeta _{F})^{3}}-1 \right) ^{\sum \limits _{j=1}^{n}\varpi _{j} }\right) }, \root 3 \of {\log _{\lambda }\left( 1+\left( \lambda ^{(\eta _{F})^{3}}-1 \right) ^{\sum \limits _{j=1}^{n}\varpi _{j}} \right) } \right) \\&=\left( \zeta _{F}, \eta _{F} \right) =F \end{aligned}$$

which achieves the proof of Property 1.

Property 2

(Monotonicity) Suppose that $F_{j}=\left( \zeta _{F_{j}}, \eta _{F_{j}} \right)$ and $\breve{F}_{j}=\left( \breve{\zeta }_{\breve{F}_{j}}, \breve{\eta }_{\breve{F}_{j}} \right)$ be two families of FFNs. If $\zeta _{F_{j}} \ge \breve{\zeta }_{\breve{F}_{j}}$ and $\eta _{F_{j}} \le \breve{\eta }_{\breve{F}_{j}}$ for all $F_{j}$. Then

$$\begin{aligned} FFFWA\left( F_{1}, F_{2}, \cdots , F_{n} \right) \ge FFFWA\left( \breve{F}_{1}, \breve{F}_{2}, \cdots , \breve{F}_{n} \right) . \end{aligned}$$

(14)

Proof 6

Since $\zeta _{F_{j}} \ge \breve{\zeta }_{\breve{F}_{j}}$ and $\eta _{F_{j}} \le \breve{\eta }_{\breve{F}_{j}}$, then

$$\begin{aligned}&\root 3 \of {1-\log _{\lambda }\left( 1+\prod \limits _{j=1}^{n}\left( \lambda ^{1-(\zeta _{F_{j}})^{3}}-1 \right) ^{\varpi _{j} }\right) } \ge \root 3 \of {1-\log _{\lambda }\left( 1+\prod \limits _{j=1}^{n}\left( \lambda ^{1-(\breve{\zeta }_{\breve{F}_{j}})^{3}}-1 \right) ^{\varpi _{j}}\right) }\\&\root 3 \of {\log _{\lambda }\left( 1+\prod \limits _{j=1}^{n}\left( \lambda ^{(\eta _{F_{j}})^{3}}-1 \right) ^{\varpi _{j}} \right) } \le \root 3 \of {\log _{\lambda }\left( 1+\prod \limits _{j=1}^{n}\left( \lambda ^{(\breve{\eta }_{\breve{F}_{j}})^{3}}-1 \right) ^{\varpi _{j}} \right) }. \end{aligned}$$

Furthermore, based on the score function of FFN, one has

$$\begin{aligned}&\quad {\mathscr {S}}\left( FFFWA\left( F_{1}, F_{2}, \cdots , F_{n} \right) \right) \\&=\left( \root 3 \of {1-\log _{\lambda }\left( 1+\prod \limits _{j=1}^{n}\left( \lambda ^{1-(\zeta _{F_{j}})^{3}}-1 \right) ^{\varpi _{j} }\right) } \right) ^{3}-\left( \root 3 \of {\log _{\lambda }\left( 1+\prod \limits _{j=1}^{n}\left( \lambda ^{(\eta _{F_{j}})^{3}}-1 \right) ^{\varpi _{j}} \right) } \right) ^{3} \\&\ge \left( \root 3 \of {1-\log _{\lambda }\left( 1+\prod \limits _{j=1}^{n}\left( \lambda ^{1-(\breve{\zeta }_{\breve{F}_{j}})^{3}}-1 \right) ^{\varpi _{j} }\right) } \right) ^{3}-\left( \root 3 \of {\log _{\lambda }\left( 1+\prod \limits _{j=1}^{n}\left( \lambda ^{(\breve{\eta }_{\breve{F}_{j}})^{3}}-1 \right) ^{\varpi _{j}} \right) } \right) ^{3} \\&={\mathscr {S}}\left( FFFWA\left( \breve{F}_{1}, \breve{F}_{2}, \cdots , \breve{F}_{n} \right) \right) . \end{aligned}$$

Next, we discuss the following two situations:

(a) If ${\mathscr {S}}\left( FFFWA\left( F_{1}, F_{2}, \ldots , F_{n} \right) \right) >{\mathscr {S}}\left( FFFWA\left( \breve{F}_{1}, \breve{F}_{2}, \ldots , \breve{F}_{n} \right) \right)$, through the comparison rules, we can attain $FFFWA\left( F_{1}, F_{2}, \ldots , F_{n} \right) > FFFWA\left( \breve{F}_{1}, \breve{F}_{2}, \ldots , \breve{F}_{n} \right)$.

(b) If ${\mathscr {S}}\left( FFFWA\left( F_{1}, F_{2}, \ldots , F_{n} \right) \right) ={\mathscr {S}}\left( FFFWA\left( \breve{F}_{1}, \breve{F}_{2}, \ldots , \breve{F}_{n} \right) \right)$, through the comparison rules, we shall compare the accuracy function of them. Based upon the inequation, one has

$$\begin{aligned}&\quad {\mathscr {H}}\left( FFFWA\left( F_{1}, F_{2}, \cdots , F_{n} \right) \right) \\&=\left( \root 3 \of {1-\log _{\lambda }\left( 1+\prod \limits _{j=1}^{n}\left( \lambda ^{1-(\zeta _{F_{j}})^{3}}-1 \right) ^{\varpi _{j} }\right) } \right) ^{3}+\left( \root 3 \of {\log _{\lambda }\left( 1+\prod \limits _{j=1}^{n}\left( \lambda ^{(\eta _{F_{j}})^{3}}-1 \right) ^{\varpi _{j}} \right) } \right) ^{3} \\&= \left( \root 3 \of {1-\log _{\lambda }\left( 1+\prod \limits _{j=1}^{n}\left( \lambda ^{1-(\breve{\zeta }_{\breve{F}_{j}})^{3}}-1 \right) ^{\varpi _{j} }\right) } \right) ^{3}+\left( \root 3 \of {\log _{\lambda }\left( 1+\prod \limits _{j=1}^{n}\left( \lambda ^{(\breve{\eta }_{\breve{F}_{j}})^{3}}-1 \right) ^{\varpi _{j}} \right) } \right) ^{3} \\&={\mathscr {S}}\left( FFFWA\left( \breve{F}_{1}, \breve{F}_{2}, \cdots , \breve{F}_{n} \right) \right) . \end{aligned}$$

which achieves the proof of Property 2.

Property 3

(Boundedness) Suppose that $F_{j}=\left( \zeta _{F_{j}}, \eta _{F_{j}} \right)$ be a family of FFNs. If $F^{+}=\left( \max \limits _{1 \le j \le n} \zeta _{F_{j}}, \min \limits _{1 \le j \le n} \eta _{F_{j}}\right)$ and $F^{-}=\left( \min \limits _{1 \le j \le n} \zeta _{F_{j}}, \max \limits _{1 \le j \le n} \eta _{F_{j}}\right)$. Then

$$\begin{aligned} F^{-}\le FFFWA\left( F_{1}, F_{2}, \cdots , F_{n} \right) \le F^{+}. \end{aligned}$$

(15)

Proof 7

Based upon the monotonicity of FFFWA operator, one has

$$\begin{aligned}&FFFWA\left( F_{1}, F_{2}, \cdots , F_{n} \right) \le FFFWA\left( F_{1}^{+}, F_{2}^{+}, \cdots , F_{n}^{+}\right) ;\\&FFFWA\left( F_{1}, F_{2}, \cdots , F_{n} \right) \ge FFFWA\left( F_{1}^{-}, F_{2}^{-}, \cdots , F_{n}^{-}\right) . \end{aligned}$$

Furthermore, based upon the idempotency of FFFWA operator, one has

$$\begin{aligned} FFFWA\left( F_{1}^{+}, F_{2}^{+}, \cdots , F_{n}^{+}\right) =F_{j}^{+},\; FFFWA\left( F_{1}^{-}, F_{2}^{-}, \cdots , F_{n}^{-}\right) =F_{j}^{-}. \end{aligned}$$

Accordingly, $F^{-}\le FFFWA\left( F_{1}, F_{2}, \cdots , F_{n} \right) \le F^{+}$ holds.

Theorem 9

Suppose that $F=\left( \zeta _{F}, \eta _{F} \right)$, $F_{j}=\left( \zeta _{F_{j}}, \eta _{F_{j}} \right)$ and $\breve{F}_{j}=\left( \breve{\zeta }_{\breve{F}_{j}}, \breve{\eta }_{\breve{F}_{j}} \right)$ be three families of FFNs. $\varpi _{j}(j=1(1)n)$ signifies the degree of importance of $F_{j}$ with $\varpi _{j} \in [0, 1]$ with $\sum _{{j}=1}^{n}\varpi _{j}=1$. Then the following properties hold for all j.

$$\begin{aligned}&(1)\, FFFWA\left( \xi \cdot _{{\mathscr {F}}} F_{1}, \xi \cdot _{{\mathscr {F}}} F_{2}, \cdots , \xi \cdot _{{\mathscr {F}}} F_{n} \right) \\&\quad = \xi \cdot _{{\mathscr {F}}} FFFWA\left( F_{1}, F_{2}, \cdots , F_{n} \right) , \xi >0;\\&(2)\, FFFWA\left( F_{1} \oplus _{{\mathscr {F}}} F, F_{2} \oplus _{{\mathscr {F}}} F, \cdots , F_{n}\oplus _{{\mathscr {F}}} F \right) \\&\quad =FFFWA\left( F_{1}, F_{2}, \cdots , F_{n} \right) \oplus _{{\mathscr {F}}} F; \\&(3)\, FFFWA\left( \xi \cdot _{{\mathscr {F}}}F_{1} \oplus _{{\mathscr {F}}} F, \xi \cdot _{{\mathscr {F}}}F_{2} \oplus _{{\mathscr {F}}} F, \cdots , \xi \cdot _{{\mathscr {F}}}F_{n}\oplus _{{\mathscr {F}}} F \right) \\&\quad =\xi \cdot _{{\mathscr {F}}} FFFWA\left( F_{1}, F_{2}, \cdots , F_{n} \right) \oplus _{{\mathscr {F}}} F;\\&(4)\, FFFWA\left( F_{1}\oplus _{{\mathscr {F}}}\breve{F}_{1} , F_{2}\oplus _{{\mathscr {F}}}\breve{F}_{2} , \cdots , F_{n}\oplus _{{\mathscr {F}}}\breve{F}_{n} \right) \\&\quad =FFFWA\left( F_{1}, F_{2}, \cdots , F_{n} \right) \oplus _{{\mathscr {F}}} FFFWA\left( \breve{F}_{1}, \breve{F}_{2}, \cdots , \breve{F}_{n} \right) . \end{aligned}$$

In what follows, we investigate two especial instances for the Theorem 8.

Case 1

When we assign the value of $\lambda \rightarrow 1$, then we can acquire

$$\begin{aligned}&\lim \limits _{\lambda \rightarrow 1 }FFFWA\left( F_{1}, F_{2}, \cdots , F_{n} \right) \\&\quad =FFWA\left( F_{1}, F_{2}, \cdots , F_{n} \right) \\&\quad =\left( \root 3 \of {1-\prod \limits _{j=1}^{n}\left( 1-\left( \zeta _{F_{j}}\right) ^{3}\right) ^{\varpi _{j} }}, \prod \limits _{j=1}^{n}\left( \eta _{F_{j}}\right) ^{\varpi _{j}} \right) , \end{aligned}$$

which is Fermatean fuzzy weighted average (FFWA) operator propounded by Senapati and Yager (2019b).

Case 2

When we assign the value of $\lambda \rightarrow +\infty$, then we can acquire

$$\begin{aligned}&\lim \limits _{\lambda \rightarrow 1 }FFFWA\left( F_{1}, F_{2}, \cdots , F_{n} \right) \\&\quad = FFAWA\left( F_{1}, F_{2}, \cdots , F_{n} \right) \\&\quad =\left( \root 3 \of {\sum \limits _{j=1}^{n}\varpi _{j}\left( \zeta _{F_{j}}\right) ^{3}}, \root 3 \of {\sum \limits _{j=1}^{n}\varpi _{j}\left( \eta _{F_{j}}\right) ^{3}} \right) , \end{aligned}$$

which is Fermatean fuzzy arithmetic weighted average (FFAWA) operator propounded by Senapati and Yager (2019b).

Definition 10

Suppose that $F_{j}=\left( \zeta _{F_{j}}, \eta _{F_{j}} \right)$ be a family of FFNs, $\varpi _{j}(j=1(1)n)$ be the weight of fusion-related with $\varpi _{j} \in [0, 1]$ with $\sum _{{j}=1}^{n}\varpi _{j}=1$. FFFOWA operator is a mapping from $\Lambda ^{n}$ to $\Lambda$. If

$$\begin{aligned}&FFHOWA\left( F_{1}, F_{2}, \cdots , F_{j} \right) =\left( \varpi _{1}\cdot _{{\mathscr {F}}} F_{\epsilon (1)} \right) \oplus _{{\mathscr {F}}}\nonumber \\&\quad \left( \varpi _{2}\cdot _{{\mathscr {F}}} F_{\epsilon (2)} \right) \oplus _{{\mathscr {F}}} \cdots \oplus _{{\mathscr {F}}} \left( \varpi _{n}\cdot _{{\mathscr {F}}} F_{\epsilon (n)} \right) , \end{aligned}$$

(16)

then FFFOWA is called as Fermatean fuzzy Frank ordered weighted average operator, wherein $\left( \epsilon (1), \epsilon (2), \ldots , \epsilon (n) \right)$ is a permutation of $\left( 1, 2, \ldots , n \right)$ within $F_{\epsilon (j-i)}\ge F_{\epsilon (j)}$ for $j=2,3, \ldots , n$ and $\Lambda$ signifies the set of FFNs.

Theorem 10

Suppose that $F_{j}=\left( \zeta _{F_{j}}, \eta _{F_{j}} \right)$ be a family of FFNs. Then the fusion value acquired through utilizing the FFFOWA operator is still a FFN and represented as

$$\begin{aligned}&FFFOWA\left( F_{1}, F_{2}, \ldots , F_{n} \right) = \left( \begin{array}{ccc}\root 3 \of {1-\log _{\lambda }\left( 1+\prod \limits _{j=1}^{n}\left( \lambda ^{1-(\zeta _{F_{\epsilon (j)}})^{3}}-1 \right) ^{\varpi _{j} }\right) }, \\ \root 3 \of {\log _{\lambda }\left( 1+\prod \limits _{j=1}^{n}\left( \lambda ^{(\eta _{F_{\epsilon (j)}})^{3}}-1 \right) ^{\varpi _{j}} \right) } \end{array}\right) . \end{aligned}$$

(17)

wherein wherein $\left( \epsilon (1), \epsilon (2), \ldots , \epsilon (n) \right)$ is a permutation of $\left( 1, 2, \ldots , n \right)$ within $F_{\epsilon (j-i)}\ge F_{\epsilon (j)}$ for $j=2,3, \ldots , n$, $\varpi _{j}(j=1(1)n)$ be the degree of importance of fused data with $\varpi _{j} \in [0, 1]$ with $\sum _{{j}=1}^{n}\varpi _{j}=1$.

The proof is similar to the Theorem 8.

5.3 Two Fermatean fuzzy Frank weighted geometric operators

Definition 11

Suppose that $F_{j}=\left( \zeta _{F_{j}}, \eta _{F_{j}} \right)$ be a family of FFNs, FFFWG operator is a mapping from $\Lambda ^{n}$ to $\Lambda$. If

$$\begin{aligned} FFFWG\left( F_{1}, F_{2}, \cdots , F_{j} \right) =\left( F_{1} \right) ^{\wedge _{{\mathscr {F}}} \varpi _{1}} \oplus _{{\mathscr {F}}}\left( F_{2} \right) ^{\wedge _{{\mathscr {F}}} \varpi _{2}} \oplus _{{\mathscr {F}}} \left( F_{n} \right) ^{\wedge _{{\mathscr {F}}} \varpi _{n}} , \end{aligned}$$

(18)

then FFFWG is called as Fermatean fuzzy Frank weighted geometric operator, wherein $\Lambda$ signifies the set of FFNs and $\varpi _{j}(j=1(1)n)$ be the weight of $F_{j}$ with $\varpi _{i} \in [0, 1]$ with $\sum _{{j}=1}^{n}\varpi _{j}=1$.

The following theorem can be attained on the basis of Definition 11.

Theorem 11

Suppose that $F_{j}=\left( \zeta _{F_{j}}, \eta _{F_{j}} \right)$ be a family of FFNs. Then the fusion value attained through utilizing the FFFWG operator is still a FFN and represented as

$$\begin{aligned} FFFWG\left( F_{1}, F_{2}, \cdots , F_{n} \right) =\left( \begin{array}{ccc}\root 3 \of {\log _{\lambda }\left( 1+\prod \limits _{j=1}^{n}\left( \lambda ^{(\zeta _{F_{j}})^{3}}-1 \right) ^{\varpi _{j}} \right) }, \\ \root 3 \of {1-\log _{\lambda }\left( 1+\prod \limits _{j=1}^{n}\left( \lambda ^{1-(\eta _{F_{j}})^{3}}-1 \right) ^{\varpi _{j} }\right) } \end{array}\right) . \end{aligned}$$

(19)

The proof of Theorem 11 is similar to Theorem 8.

Similar to the FFFWA operator, the FFFWG operator also possesses the following properties.

Property 4

(Idempotency) Suppose that $F_{j}=\left( \zeta _{F_{j}}, \eta _{F_{j}} \right)$ be a family of FFNs. If $F_{j}=\left( \zeta _{F}, \eta _{F} \right) =F$ for all $F_{j}$. Then

$$\begin{aligned} FFFWG\left( F_{1}, F_{2}, \cdots , F_{n} \right) =F \end{aligned}$$

(20)

Property 5

(Monotonicity) Suppose that $F_{j}=\left( \zeta _{F_{j}}, \eta _{F_{j}} \right)$ and $\breve{F}_{j}=\left( \breve{\zeta }_{\breve{F}_{j}}, \breve{\eta }_{\breve{F}_{j}} \right)$ be two families of FFNs. If $\zeta _{F_{j}} \ge \breve{\zeta }_{\breve{F}_{j}}$ and $\eta _{F_{j}} \le \breve{\eta }_{\breve{F}_{j}}$ for all $F_{j}$. Then

$$\begin{aligned} FFFWG\left( F_{1}, F_{2}, \cdots , F_{n} \right) \ge FFFWG\left( \breve{F}_{1}, \breve{F}_{2}, \cdots , \breve{F}_{n} \right) . \end{aligned}$$

(21)

Property 6

(Boundedness) Suppose that $F_{j}=\left( \zeta _{F_{j}}, \eta _{F_{j}} \right)$ be a family of FFNs. If $F^{+}=\left( \max \limits _{1 \le j \le n} \zeta _{F_{j}}, \min \limits _{1 \le j \le n} \eta _{F_{j}}\right)$ and $F^{-}=\left( \min \limits _{1 \le j \le n} \zeta _{F_{j}}, \max \limits _{1 \le j \le n} \eta _{F_{j}}\right)$. Then

$$\begin{aligned} F^{-}\le FFFWG\left( F_{1}, F_{2}, \cdots , F_{n} \right) \le F^{+}. \end{aligned}$$

(22)

Theorem 12

Suppose that $F=\left( \zeta _{F}, \eta _{F} \right)$, $F_{j}=\left( \zeta _{F_{j}}, \eta _{F_{j}} \right)$ and $\breve{F}_{j}=\left( \breve{\zeta }_{\breve{F}_{j}}, \breve{\eta }_{\breve{F}_{j}} \right)$ be three families of FFNs. $\varpi _{j}$ signifies the degree of importance of $F_{j}$ with $\varpi _{j} \in [0, 1]$ with $\sum _{{j}=1}^{n}\varpi _{i}=1$. Then the following properties hold for all j.

$$\begin{aligned}&(1)\, FFFWG\left( \xi \cdot _{{\mathscr {F}}} F_{1}, \xi \cdot _{{\mathscr {F}}} F_{2}, \cdots , \xi \cdot _{{\mathscr {F}}} F_{n} \right) = \xi \cdot _{{\mathscr {F}}} FFFWG\left( F_{1}, F_{2}, \cdots , F_{n} \right) , \xi >0;\\&(2)\, FFFWG\left( F_{1} \oplus _{{\mathscr {F}}} F, F_{2} \oplus _{{\mathscr {F}}} F, \cdots , F_{n}\oplus _{{\mathscr {F}}} F \right) =FFFWG\left( F_{1}, F_{2}, \cdots , F_{n} \right) \oplus _{{\mathscr {F}}} F; \\&(3)\, FFFWG\left( \xi \cdot _{{\mathscr {F}}}F_{1} \oplus _{{\mathscr {F}}} F, \xi \cdot _{{\mathscr {F}}}F_{2} \oplus _{{\mathscr {F}}} F, \cdots , \xi \cdot _{{\mathscr {F}}}F_{n}\oplus _{{\mathscr {F}}} F \right) =\xi \cdot _{{\mathscr {F}}} FFFWG\left( F_{1}, F_{2}, \cdots , F_{n} \right) \oplus _{{\mathscr {F}}} F;\\&(4)\, FFFWG\left( F_{1}\oplus _{{\mathscr {F}}}\breve{F}_{1} , F_{2}\oplus _{{\mathscr {F}}}\breve{F}_{2} , \cdots , F_{n}\oplus _{{\mathscr {F}}}\breve{F}_{n} \right) =FFFWG\left( F_{1}, F_{2}, \cdots , F_{n} \right) \oplus _{{\mathscr {F}}} FFFWG\left( \breve{F}_{1}, \breve{F}_{2}, \cdots , \breve{F}_{n} \right) . \end{aligned}$$

In what follows, we investigate two especial instances for Theorem 11.

Case 3

When we assign the value of $\lambda \rightarrow 1$, then we can acquire

$$\begin{aligned} \lim \limits _{\lambda \rightarrow 1 }FFFWG\left( F_{1}, F_{2}, \cdots , F_{n} \right)&=FFWG\left( F_{1}, F_{2}, \cdots , F_{n} \right) \\&=\left( \prod \limits _{j=1}^{n}\left( \eta _{F_{j}}\right) ^{\varpi _{j}}, \root 3 \of {1-\prod \limits _{j=1}^{n}\left( 1-\left( \zeta _{F_{j}}\right) ^{3}\right) ^{\varpi _{j} }} \right) , \end{aligned}$$

which is Fermatean fuzzy weighted germetric (FFWG) operator on the basis algebraic norm operations propounded by Senapati and Yager (2019b).

Case 4

When we assign the value of $\lambda \rightarrow +\infty$, then we can acquire

$$\begin{aligned} \lim \limits _{\lambda \rightarrow 1 }FFFWG\left( F_{1}, F_{2}, \cdots , F_{n} \right)&= FFAWG\left( F_{1}, F_{2}, \cdots , F_{n} \right) \\&=\left( \root 3 \of {\sum \limits _{j=1}^{n}\varpi _{j}\left( \zeta _{F_{j}}\right) ^{3}}, \root 3 \of {\sum \limits _{j=1}^{n}\varpi _{j}\left( \eta _{F_{j}}\right) ^{3}} \right) , \end{aligned}$$

which is Fermatean fuzzy arithmetic weighted geometric (FFAWG) operator propounded by Senapati and Yager (2019b).

Definition 12

Suppose that $F_{j}=\left( \zeta _{F_{j}}, \eta _{F_{j}} \right)$ be a family of FFNs, $\varpi _{j}(j=1(1)n)$ be the weight of fusion-related with $\varpi _{j} \in [0, 1]$ with $\sum _{{j}=1}^{n}\varpi _{j}=1$. FFFOWG operator is a mapping from $\Lambda ^{n}$ to $\Lambda$. If

$$\begin{aligned} FFHOWG\left( F_{1}, F_{2}, \cdots , F_{j} \right) =\left( \varpi _{1}\cdot _{{\mathscr {F}}} F_{\epsilon (1)} \right) \oplus _{{\mathscr {F}}}\left( \varpi _{2}\cdot _{{\mathscr {F}}} F_{\epsilon (2)} \right) \oplus _{{\mathscr {F}}} \cdots \oplus _{{\mathscr {F}}} \left( \varpi _{n}\cdot _{{\mathscr {F}}} F_{\epsilon (n)} \right) , \end{aligned}$$

(23)

then FFFOWG is called as Fermatean fuzzy Frank ordered weighted geometric operator, wherein $\left( \epsilon (1), \epsilon (2), \ldots , \epsilon (n) \right)$ is a permutation of $\left( 1, 2, \ldots , n \right)$ within $F_{\epsilon (j-i)}\ge F_{\epsilon (j)}$ for $j=2,3, \ldots , n$ and $\Lambda$ signifies the set of FFNs.

Theorem 13

Suppose that $F_{j}=\left( \zeta _{F_{j}}, \eta _{F_{j}} \right)$ be a family of FFNs. Then the fusion value computed through utilizing the FFFOWG operator is still a FFN and represented as

$$\begin{aligned}&FFFOWG\left( F_{1} ,F_{2}, \cdots , F_{n} \right) = \left( \begin{array}{ccc}\root 3 \of {\log _{\lambda }\left( 1+\prod \limits _{j=1}^{n}\left( \lambda ^{(\eta _{F_{\epsilon (j)}})^{3}}-1 \right) ^{\varpi _{j}} \right) }, \\ \root 3 \of {1-\log _{\lambda }\left( 1+\prod \limits _{j=1}^{n}\left( \lambda ^{1-(\zeta _{F_{\epsilon (j)}})^{3}}-1 \right) ^{\varpi _{j} }\right) }\end{array}\right) . \end{aligned}$$

(24)

wherein wherein $\left( \epsilon (1), \epsilon (2), \cdots , \epsilon (n) \right)$ is a permutation of $\left( 1, 2, \cdots , n \right)$ within $F_{\epsilon (j-i)}\ge F_{\epsilon (j)}$ for $j=2,3, \cdots , n$, $\varpi _{j}(j=1(1)n)$ be the degree of importance of fused data with $\varpi _{j} \in [0, 1]$ with $\sum _{{j}=1}^{n}\varpi _{j}=1$.

The proof is similar to the Theorem 8.

The relation between FFFWA operator and FFFWG operator will be explored as follows:

Theorem 14

Suppose that $F_{j}=\left( \zeta _{F_{j}}, \eta _{F_{j}} \right)$ be a family of FFNs and $\varpi _{j}(j=1(1)n)$ be the weight of $F_{j}$ with $\varpi _{j} \in [0, 1]$ with $\sum _{{j}=1}^{n}\varpi _{j}=1$. Then

$$\begin{aligned}&(1)\;FFFWA\left( F_{1}^{c} ,F_{2}^{c}, \cdots , F_{n}^{c} \right) =\left( FFFWG\left( F_{1} ,F_{2}, \cdots , F_{n} \right) \right) ^{c};\\&(2)\;FFFWG\left( F_{1}^{c} ,F_{2}^{c}, \cdots , F_{n}^{c} \right) =\left( FFFWA\left( F_{1} ,F_{2}, \cdots , F_{n} \right) \right) ^{c};\\&(3)\;FFFWG\left( F_{1} ,F_{2}, \cdots , F_{n} \right) \le FFFWA\left( F_{1} ,F_{2}, \cdots , F_{n} \right) . \end{aligned}$$

Proof 8

Since $F_{j}^{c}=\left( \eta _{F_{j}},\zeta _{F_{j}}\right)$, then we have

$$\begin{aligned} FFFWA\left( F_{1}^{c} ,F_{2}^{c}, \cdots , F_{n}^{c} \right) =\left( \begin{array}{ccc}\root 3 \of {1-\log _{\lambda }\left( 1+\prod \limits _{j=1}^{n}\left( \lambda ^{1-(\eta _{F_{j}})^{3}}-1 \right) ^{\varpi _{j} }\right) }, \\ \root 3 \of {\log _{\lambda }\left( 1+\prod \limits _{j=1}^{n}\left( \lambda ^{(\zeta _{F_{j}})^{3}}-1 \right) ^{\varpi _{j}} \right) } \end{array}\right) . \end{aligned}$$

Furthermore,

$$\begin{aligned}&\left( FFFWG\left( F_{1} ,F_{2}, \cdots , F_{n} \right) \right) ^{c}\\&=\left( \left( \root 3 \of {\log _{\lambda }\left( 1+\prod \limits _{j=1}^{n}\left( \lambda ^{(\zeta _{F_{j}})^{3}}-1 \right) ^{\varpi _{j}} \right) }, \root 3 \of {1-\log _{\lambda }\left( 1+\prod \limits _{j=1}^{n}\left( \lambda ^{1-(\eta _{F_{j}})^{3}}-1 \right) ^{\varpi _{j} }\right) } \right) \right) ^{c}\\&=\left( \root 3 \of {1-\log _{\lambda }\left( 1+\prod \limits _{j=1}^{n}\left( \lambda ^{1-(\eta _{F_{j}})^{3}}-1 \right) ^{\varpi _{j} }\right) }, \root 3 \of {\log _{\lambda }\left( 1+\prod \limits _{j=1}^{n}\left( \lambda ^{(\zeta _{F_{j}})^{3}}-1 \right) ^{\varpi _{j}} \right) } \right) . \end{aligned}$$

Accordingly, $FFFWA\left( F_{1}^{c} ,F_{2}^{c}, \cdots , F_{n}^{c} \right) =\left( FFFWG\left( F_{1} ,F_{2}, \cdots , F_{n} \right) \right) ^{c}$ holds. Homoplastically, the remainder can be proved by the same manner, which achieves the proof of Theorem 14.

6 An improved Fermatean fuzzy CRITIC-MABAC approach based on prospect theory

Under this section, an innovative MCGDM methodol is designed by synthesizing the CRITIC method, prospect theory and MABAC approach under Fermatean fuzzy setting. Firstly, a generalization description of the Fermatean fuzzy MCGDM decision issue is given. Then, the weight of expert is determined by the similarity method and presented generalized interactive distance measure, the weight of the criterions is also computed with the aid of improved CRITIC technique. Subsequently, a multi-stage decision framework is designed through synthesizing the CRITIC, prospect theory and improved MABAC approach to settle the complete unknown weight information. Finally, the proposed decision framework is outlined in the form of visualization.

6.1 The statement of the MCGDM issue

Aiming at a Fermatean fuzzy MCGDM decision problem, a decision expert $E^{l} (e=l, 2, \ldots , L)$ provide his(her) for alternatives under different criterions can be collected as a decision matrices ${\hat{E}^{l}}=\left( {\hat {{\mathscr{T}}}}_{ij}^{l}\right) _{m\times n}$ shown as:

$$\begin{aligned} {\hat{E}^{l}}=\left( {\hat {{\mathscr{T}}}}_{ij}^{l}\right) _{m\times n}= \begin{pmatrix} {\hat {{\mathscr{T}}}}_{11}^{l}=\left( {\hat{\zeta }}_{11}^{l}, {\hat{\eta }}_{11}^{l}\right) & {\hat {{\mathscr{T}}}}_{12}^{l}=\left( {\hat{\zeta }}_{12}^{l}, {\hat{\eta }}_{12}^{l}\right) & \cdots & {\hat {{\mathscr{T}}}}_{1n}^{l}=\left( {\hat{\zeta }}_{1n}^{l}, {\hat{\eta }}_{1n}^{l}\right) & \\ {\hat {{\mathscr{T}}}}_{21}^{l}=\left( {\hat{\zeta }}_{21}^{l}, {\hat{\eta }}_{21}^{l}\right) &{\hat {{\mathscr{T}}}}_{22}^{l}=\left( {\hat{\zeta }}_{22}^{l}, {\hat{\eta }}_{22}^{l}\right) & \cdots & {\hat {{\mathscr{T}}}}_{2n}^{l}=\left( {\hat{\zeta }}_{2n}^{l}, {\hat{\eta }}_{2n}^{l}\right) &\\ \vdots & \vdots & \ddots & \vdots \\ {\hat {{\mathscr{T}}}}_{m1}^{l}=\left( {\hat{\zeta }}_{m1}^{l}, {\hat{\eta }}_{m1}^{l}\right) & {\hat {{\mathscr{T}}}}_{m2}^{l}=\left( {\hat{\zeta }}_{m2}^{l}, {\hat{\eta }}_{m2}^{l}\right) & \cdots & {\hat {{\mathscr{T}}}}_{mn}^{l}=\left( {\hat{\zeta }}_{mn}^{l}, {\hat{\eta }}_{mn}^{l}\right) &\\ \end{pmatrix} \end{aligned}$$

(25)

in which $\Upsilon =\{\Upsilon _1, \Upsilon _2, \ldots , \Upsilon _m \}$ is a collection of alternatives. $C=\{C_1, C_2, \ldots , C_{n}\}$ is a family of criterions with the weight vector being $\omega =(\omega _1, \omega _2, \ldots , \omega _n)^{T}$ with $\omega _j \in [0, 1]$ and $\sum _{j=1}^{n}\omega _j=1$. Suppose that $E=\{E_{1}, E_{2}, \ldots , E_{l}, \ldots , E_{L}\}$ is a family of evaluators possessing the weight information $\nu =\{\nu _{1}, \nu _{2}, \ldots , \nu _{L}\}^{T}$ and $\nu \in [0, 1], \sum _{l=1}^{L}\nu _{l}=1$. The evaluators provide their assessment information for alternative $\Upsilon _{i}$ under the criterions $C_{j}$ by the form of FFN ${\hat {{\mathscr{T}}}}_{ij}=\left( {\hat{\zeta }}_{ij}^{l}, {\hat{\eta }}_{ij}^{l}\right)$, where ${\hat{\zeta }}_{ij}^{l}, {\hat{\eta }}_{ij}^{l} \in [0, 1]$ and $0 \le \left( {\hat{\zeta }}_{ij}^{l}\right) ^{3}+\left( {\hat{\eta }}_{ij}^{l}\right) ^{3}\le 1$. The aim of the issue is to discover the optimal alternative of attaining the order relation of alternatives.

6.2 An aggregated FF-CRITIC-MABAC group decision method based on prospect theory

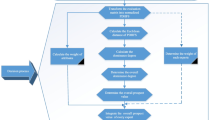
In this phase, a fused MCGDM methodology is propounded through combining CRITIC method, prospect theory and MABAC approach to ascertain the order relation of the alternatives to cope with the risk assessment problem with unknown weight information of expert and criteria. The propounded FF-CRITIC-MABAC approach can fully ponder the behavior preference, psychological factors and ambiguity of decision experts during the procedure of assessment. The detailed steps of the presented FFMEMCDM methodology are portrayed in Fig. 1.

For Fig. 1, it portrays the presented assessment framework with five stages, involving initial assessment information determination, weight determination, decision analysis and so forth. The first stages is the determination of decision criterions and alternatives and the construction of normalized assessment matrices. Then the expert weight is determined based on the proposed Fermatean fuzzy interactive distance measure and Fermatean fuzzy Frank operators. The assessment matrices of experts are aggregated into a single collective matrix through the presented FFFWA operator in stage 3. The stage 4 computes the criterion weight by improved CRITIC method using the proposed Fermatean fuzzy interactive distance measure. The decision analysis stage is finished on the basis of improved prospect theory MABAC approach utilizing the developed distance measure and Fermatean fuzzy Frank operators.

Fig. 1

The framework of FF-CRITIC-MABAC approach

Step 1: The collection of decision information.

For a classical MCGDM issue, we will first build an experts committee and invite them to provide their preference standpoint for alternatives with respect to the chosen criteria. Considering the cognitive psychology and expression habits of experts, the linguistic terms displayed in Table 1 are employed to describe the cognitive preference information.

Step 1-1: Experts give their assessment opinion in the form of linguistic expression according to the predefined linguistic terms and their cognition capability, which can be displayed in Table 1.

Table 1 Linguistic terms for experts to assess the alternatives

Step 1-2: Transform assessment opinion depicted by linguistic terms listed in Table 1 to FFNs based on the mapping from linguistic terms to FFNs and obtain the experts’ opinion.

Step 1-3: Attaining the standardized decision experts matrices $E^{l}=\left( {\mathscr {T}}_{ij}^{l}\right) _{m\times n}$ with the aid of the Eq. (26).

$$\begin{aligned} {\mathscr {T}}_{ij}^{l}=\left( \zeta _{ij}^{l}, \eta _{ij}^{l}\right) = \left\{ \begin{array}{ll} \left( {\hat{\zeta }}_{ij}, {\hat{\eta }}_{ij}^{l} \right), & {C_{j}\,\text{is\,benefit\,criterion}}; \\ \left( {\hat{\eta }}_{ij}, {\hat{\zeta }}_{ij}^{l} \right) , & {C_{j} \text{is\,cost\,criterion}}. \end{array} \right. \end{aligned}$$

(26)

Step 2: Determination of expert weight.

In light of the difference of knowledge background and cognition capability of decision expert, the importance degree of every decision expert is usually not equal in resolving a given decision making issue. In order to bring into full play the role of experts in decision-making, the ascertaining of experts’ importance degree is vital for developing decision analysis. Hence, the weight of decision expert is determined in our decision framework on the basis of the developed distance measure of FFNs. Suppose that L decision experts are invited to take part in the decision, they provide their preference information expressed as FFN ${\mathscr {T}}_{ij}^{l}=\left( \zeta _{ij}^{l}, \eta _{ij}^{l}\right)$ for alternatives $\Upsilon =\{\Upsilon _{i}| i=1, 2, \ldots , m \}$ with respect to the attributes $C=\{C_j| j=1, 2, \ldots , n\}$ according to their cognition and experience for the decision issue.

Driven by the academic idea of TOPSIS method in Boran et al. (2009), the concept of closeness degree is used to calculate the weight of experts, that is, the smaller the distance between the decision expert matrix and the ideal matrix, the greater the weight of decision experts. Here, the ideal matrix of all expert matrices is signified as $E^{*}=\left( {\mathscr {T}}_{ij}^{*}\right) _{m\times n}=\left( \zeta _{ij}^{*}, \eta _{ij}^{*}\right)$, wherein the ${\mathscr {T}}_{ij}^{*}$ is determined through the Fermatean fuzzy Frank average operator displayed in Eq. (27).

$$\begin{aligned} {\mathscr {T}}_{ij}^{*}=FFFA\left( {\mathscr {T}}_{ij}^{1}, {\mathscr {T}}_{ij}^{2} \cdots , {\mathscr {T}}_{ij}^{L} \right) = \left( \begin{array}{ccc}\root 3 \of {1-\log _{\lambda }\left( 1+\prod \limits _{l=1}^{L}\left( \lambda ^{1-\left( \zeta _{ij}^{l}\right) ^{3}}-1 \right) ^{\frac{1}{L}} \right) }, \\ \root 3 \of {\log _{\lambda }\left( 1+\prod \limits _{l=1}^{L}\left( \lambda ^{\left( \eta _{ij}^{l}\right) ^{3}}-1 \right) ^{\frac{1}{L}} \right) } \end{array}\right) . \end{aligned}$$

(27)

With the assistance of the propounded matrix distance measure stated in Eq. (3), the similarity measure $SM\left( {\mathscr {T}}_{ij}^{l}, {\mathscr {T}}^{*} \right)$ between the ideal matrix $E^{*}=\left( {\mathscr {T}}_{ij}^{*}\right) _{m\times n}$ and decision expert matrix $E^{l}=\left( {\mathscr {T}}_{ij}^{l}\right) _{m\times n}$ can be ascertained by Eq. (28):

$$\begin{aligned} SM\left( {\mathscr {T}}_{ij}^{l}, {\mathscr {T}}^{*} \right) =\frac{{\mathscr {D}}^{(\rho )} \left( {\mathscr {T}}_{ij}^{l}, {{\mathscr {T}}^{c}}^{*} \right) }{{\mathscr {D}}^{(\rho )}\left( {\mathscr {T}}_{ij}^{l}, {\mathscr {T}}^{*} \right) + {\mathscr {D}}^{(\rho )} \left( {\mathscr {T}}_{ij}^{l}, {{\mathscr {T}}^{c}}^{*} \right) }. \end{aligned}$$

(28)

Then, the weights of expert $\nu _{l} (l=1, 2, \ldots , L)$ are calculated via the Eq. (29).

$$\begin{aligned} \nu _{l}=\frac{SM\left( {\mathscr {T}}_{ij}^{l}, {\mathscr {T}}^{*} \right) }{\sum _{l=1}^{L}SM\left( {\mathscr {T}}_{ij}^{l}, {\mathscr {T}}^{*} \right) }. \end{aligned}$$

(29)

Where $\nu _{l} \in [0, 1], \sum _{l=1}^{L}\nu _{l}=1$.

According to the mentioned steps, the weight of every decision expert is attained.

Step 3: Attaining the fused assessment decision opinion.

In this step, we employ the FFFWA operator to fuse the matrices of decision experts and further obtain the comprehensive assessment opinion of alternatives under different experts. Hence, we create the aggregated Fermatean fuzzy decision matrix ${\mathscr {T}}_{ij}=\left( {\tilde{h}}_{ij}\right) _{m\times n}$ as below,

$$\begin{aligned} {\tilde{h}}_{ij}=FFFWA\left( F_{1}, F_{2}, \ldots , F_{n} \right) =\left( \begin{array}{ccc} \root 3 \of {1-\log _{\lambda }\left( 1+\prod \limits _{j=1}^{n}\left( \lambda ^{1-\left( \zeta _{F_{j}}^{l}\right) ^{3}}-1 \right) ^{\nu _{l} }\right) }, \\ \root 3 \of {\log _{\lambda }\left( 1+\prod \limits _{j=1}^{n}\left( \lambda ^{\left( \eta _{F_{j}}^{l}\right) ^{3}}-1 \right) ^{\nu _{l}} \right) } \end{array}\right) . \end{aligned}$$

(30)

Step 4: Ascertain the weight information of attributes.

Attribute (Criteria) is an important branch for decision experts to implement a reasonable decision analysis and then to acquire several more accurate management suggestions. Different attributes and their weights can reflect rich assessment information for decision experts to construct a decision framework. Accordingly, the determination of attributes’ weights is particularly significant for attaining more scientific and credible assessment results. After determining the Fermatean fuzzy comprehensive assessment matrix ${\mathscr {T}}_{ij}=\left( {\tilde{h}}_{ij}\right) _{m\times n}$, we utilize the improved Fermatean fuzzy CRITIC method on the basis of the presented Fermatean fuzzy interactive distance measure to ascertain the criteria weight. The detailed steps of improved Fermatean fuzzy CRITIC method are stated as below:

Step 4-1: Calculate the standard deviation $\ell _{j}$ of diverse criterions by Eq.(31).

$$\begin{aligned} \ell _{j}=\sqrt{\frac{1}{m} \sum _{i=1}^{m}\left( {\mathscr {D}}^{(\rho )} \left( {\tilde{h}}_{ij}, \overline{{\tilde{h}}_{j}}\right) \right) ^{2} } \end{aligned}$$

(31)

wherein

$$\begin{aligned} \overline{{\tilde{h}}_{j}} =\frac{1}{m}\sum _{i=1}^{m} {\tilde{h}}_{ij} =\left( \begin{array}{ccc}\root 3 \of {1-\log _{\lambda }\left( 1+\prod \limits _{i=1}^{m}\left( \lambda ^{1-\left( \zeta _{ij}\right) ^{3}}-1 \right) ^{\frac{1}{m}} \right) }, \\ \root 3 \of {\log _{\lambda }\left( 1+\prod \limits _{i=1}^{m}\left( \lambda ^{\left( \eta _{ij}\right) ^{3}}-1 \right) ^{\frac{1}{m}} \right) } \end{array}\right) . \end{aligned}$$

Step 4-2: Calculate the correlation coefficient $\varrho _{jk}$ between criterion $C_{j}$ and $C_{k}$ by Eq.(32).

$$\begin{aligned} \varrho _{jk}=\frac{ \sum _{i=1}^{m}\left( {\mathscr {D}}^{(\rho )} \left( {\tilde{h}}_{ij}, \overline{{\tilde{h}}_{j}}\right) \right) \left( {\mathscr {D}}^{(\rho )} \left( {\tilde{h}}_{ik}, \overline{{\tilde{h}}_{k}}\right) \right) }{ \sqrt{\sum _{i=1}^{m} \left( {\mathscr {D}}^{(\rho )} \left( {\tilde{h}}_{ij}, \overline{{\tilde{h}}_{j}}\right) \right) ^{2} \sum _{i=1}^{m} \left( {\mathscr {D}}^{(\rho )} \left( {\tilde{h}}_{ik}, \overline{{\tilde{h}}_{k}}\right) \right) ^{2}}}, \end{aligned}$$

(32)

in which $\overline{{\tilde{h}}_{k}} =\frac{1}{m}\sum _{i=1}^{m} {\tilde{h}}_{ik}$.

Step 4-3: Evaluate the objective weight of each criterion by Eq.(33).

$$\begin{aligned} \omega _j=\frac{\ell _{j}\sum \limits _{k=1}^{n}\left( 1-\varrho _{jk}\right) }{\sum \limits _{j=1}^{n} \left( \ell _{j}\sum \limits _{k=1}^{n}\left( 1-\varrho _{jk}\right) \right) }. \end{aligned}$$

(33)

Step 5: Determine the decision reference point.

Because the decision reference point is the average value of all alternatives under the criteria $C_{j}$, we determine the decision reference point based upon the Fermatean fuzzy Frank geometric average operator displayed in Eq.(34).

$$\begin{aligned} \check{{\tilde{h}}}_{j}=\left( \prod \limits _{i=1}^{m}\left( {\tilde{h}}_{ij}\right) \right) ^{\frac{1}{m}}=\left( \begin{array}{ccc}\root 3 \of {\log _{\lambda }\left( 1+\prod \limits _{i=1}^{m}\left( \lambda ^{\left( \zeta _{ij}\right) ^{3}}-1 \right) ^{\frac{1}{m}} \right) }, \\ \root 3 \of {1-\log _{\lambda }\left( 1+\prod \limits _{i=1}^{m}\left( \lambda ^{1-\left( \eta _{ij}\right) ^{3}}-1 \right) ^{\frac{1}{m}} \right) }\end{array}\right) . \end{aligned}$$

(34)

Step 6: Ascertain the Fermatean fuzzy prospect decision matrix $R=(r_{ij})_{m \times n}$ by Eq.(35)

$$\begin{aligned} r_{ij}=\pi \left( \xi _{j} \right) {\tilde{v}}\left( {\tilde{h}}_{ij} \right) \end{aligned}$$

(35)

wherein

$$\begin{aligned} \pi \left( \xi _{j} \right) = \left\{ \begin{array}{ll} \frac{\xi _{j}^{\varphi }}{\left( \xi _{j}^{\varphi }+\left( 1-\xi _{j} \right) ^{\varphi } \right) ^{\frac{1}{\varphi }}},\;&{} {\mathscr {S}}\left( {\tilde{h}}_{ij} \right) - {\mathscr {S}}\left( \check{{\tilde{h}}}_{j}\right) \ge 0 \\ \frac{\xi _{j}^{\phi }}{\left( \xi _{j}^{\phi }+\left( 1-\xi _{j} \right) ^{\phi } \right) ^{\frac{1}{\phi }}},\;&{} {\mathscr {S}}\left( {\tilde{h}}_{ij} \right) - {\mathscr {S}}\left( \check{{\tilde{h}}}_{j}\right) < 0 \\ \end{array} \right. \end{aligned}$$

$$\begin{aligned} {\tilde{v}}\left( {\tilde{h}}_{ij}\right) = \left\{ \begin{array}{ll} \ln \left( 1+\mu \cdot {\mathscr {D}}^{(\rho )}\left( {\tilde{h}}_{ij}, \check{{\tilde{h}}}_{j} \right) \right) \;&{} {\mathscr {S}}\left( {\tilde{h}}_{ij} \right) - {\mathscr {S}}\left( \check{{\tilde{h}}}_{j}\right) \ge 0 \\ -\chi \ln \left( 1-\varsigma \cdot {\mathscr {D}}^{(\rho )}\left( {\tilde{h}}_{ij}, \check{{\tilde{h}}}_{j} \right) \right) \;&{} {\mathscr {S}}\left( {\tilde{h}}_{ij} \right) - {\mathscr {S}}\left( \check{{\tilde{h}}}_{j}\right) < 0 \\ \end{array} \right. \end{aligned}$$

where $\check{{\tilde{h}}}_{j}$ signifies the reference point of criteria $C_{j}$, ${\mathscr {S}}\left( {\tilde{h}}_{ij}\right)$ and ${\mathscr {S}}\left( \check{{\tilde{h}}}_{j}\right)$ denote the score value of ${\tilde{h}}_{ij}$ and $\check{{\tilde{h}}}_{j}$, severally. ${\mathscr {D}}^{(\rho )}\left( {\tilde{h}}_{ij}, \check{{\tilde{h}}}_{j} \right)$ indicates the generalized interactive distance measure between ${\tilde{h}}_{ij}$ and $\check{{\tilde{h}}}_{j}$. Based upon the investigation outcome of Tversky and Kahneman (1992) and Hao et al. (2017), we can attain $\mu =\varsigma =0.88$, $\chi =2.25$, $\varphi =0.61$ and $\phi =0.69$.

Step 7: Attain the weighted decision matrix $U=(u_{ij})_{m \times n}$ by Eq.(36).

$$\begin{aligned} u_{ij}=\omega _{j} r_{ij} \end{aligned}$$

(36)

where $\omega _{j}$ is the weight of criterion $C_{j}$ and $r_{ij}$ is the prospect theory value determined by Eq.(35).

Step 8: Acquire the border approximation area $B=[b_{1}, b_{2}, \cdots , b_{n} ]$ for every criteria $C_{j}$ by Eq.(37):

$$\begin{aligned} b_{j}=\left( \prod \limits _{i=1}^{m}u_{ij}\right) ^{\frac{1}{m}}. \end{aligned}$$

(37)

where $u_{ij}$ signifies the element of the weighted decision matrix and m is the number of alternatives.

Step 9: Ascertain the distance matrix ${\mathscr {D}}=(\check{d}_{ij})_{m \times n}$ between the weighted decision matrix Q and border approximation area B by Eq.(38):

$$\begin{aligned} \check{d}_{j}=r_{ij}-b_{j}. \end{aligned}$$

(38)

Step 10: Determine the order relation of alternatives based upon the function value of $\varepsilon (\Upsilon _i)$ by Eq.(39):

$$\begin{aligned} \varepsilon (\Upsilon _i)=\sum \limits _{j=1}^{n}\check{d}. \end{aligned}$$

(39)

Step 11: End.

7 An illustrative example

With the great breakthroughs of B&R in economic development and society construction, the risks and challenges in the process of cooperation and investment also follow. In particular, the risk loss caused by different factors in the process of project investment is bound to bring about the impact of investment and development of the project. The unstable social environment and other factors make the process of venture capital highly uncertain. Fortunately, FFS can deal with uncertainty and fuzziness effectively. In order to enhance the high speed rail construction and provide more assistance for people from all over the world. The ABC company will select a suitable country to develop the construction of high speed rail project under the background of B&R initiative. After the joint discussions of relevant departments and experts, five vital attributes $(C_1, C_2, C_3, C_4,C_5)$ related to the investment project are chosen after discussion and analysis. The detailed depiction and introduction of the attributes are illustrated In Table 2. After that, four experts from four fields have set up an evaluation committee based on political stability, credit risk and law and regulation. Five criterions of financial risk and infrastructure risk are used to rank the above-mentioned six countries(deemed alternative in this example) $\Upsilon =\{\Upsilon _1, \Upsilon _2, \ldots , \Upsilon _6 \}$ and further provide decision-making suggestions for investment departments.

Table 2 Depictions of the criteria for risk investment assessment in B&R

7.1 Address the Risk investment of B&R via the presented FF-CRITIC-MABAC

Step 1: The collection of decision information.

Step 1-1: We obtain the decision matrix for the assessment of investment country from four experts shown in Table 3.

Table 3 Decision matrix for the assessment of risk investment provided experts using the linguistic term

Step 1-2: Transform the linguistic assessment opinion terms to FFNs, which is listed in Table 4.

Table 4 Decision matrix for the evaluation of risk investment by FFNs

Step 1-3: Attaining the standardized decision experts matrices $E^{l}=\left( {\mathscr {T}}_{ij}^{l}\right) _{m\times n}$ with the aid of the Eq. (26), which is listed in Table 5.

Table 5 Normalized decision matrix for the evaluation of risk investment by FFNs

Step 2: In light of Eqs.(27)–(29), the weight of decision expert is calculated as

$$\begin{aligned} \nu _{1}=0.2301,\; \nu _{2}=0.2451,\; \nu _{3}=0.2448,\; \nu _{4}=0.2801. \end{aligned}$$

Step 3: Based upon the FFFA operator displayed in Eq.(30), we can obtain the comprehensive assessment matrix portrayed in Table 6.

Table 6 The comprehensive decision matrix obtained by the FFFWA operator

Step 4: With the assistance of Eqs. (31)–(33), the result of criterion weight is figured out as below:

$$\begin{aligned} \omega _{1}=0.1839,\; \omega _{2}=0.2319,\; \omega _{3}=0.3359,\; \omega _{4}=0.1566,\; \omega _{5}=0.0916. \end{aligned}$$

Step 5: Based on the Eq. (34), we obtain the reference point of every criteria shown as

$$\begin{aligned} \check{{\tilde{h}}}=\left\{ \begin{aligned}&\left( 0.8364, 0.3468\right) , \left( 0.7721, 0.4665\right) , \left( 0.7904, 0.4590\right) , \\&\qquad \left( 0.7889, 0.4462\right) , \left( 0.7974, 0.4165\right) \end{aligned} \right\} . \end{aligned}$$

Step 6: Based on the reference point of each attribute, let $\mu =\varsigma =0.88$, $\chi =2.25$, $\varphi =0.61$ and $\phi =0.69$ and $\xi =\left( 0.0363, 0.5031, 0.1511, 0.1370, 0.1724\right)$, the Fermatean fuzzy prospect decision matrix $R=(r_{ij})_{m \times n}$ can be ascertained shown as:

$$\begin{aligned} R=(r_{ij})_{m \times n}= \left( \begin{array}{ccccc} 0.0111 &{} 0.0597 &{} 0.0560 &{} 0.0424 &{} 0.0857 \\ 0.0182 &{} 0.3131 &{} 0.0882 &{} 0.1457 &{} 0.1263 \\ 0.0611 &{} 0.1929 &{} 0.0408 &{} 0.1121 &{} 0.0604 \\ 0.0129 &{} 0.0681 &{} 0.0494 &{} 0.0295 &{} 0.0565 \\ 0.0244 &{} 0.1016 &{} 0.0639 &{} 0.0387 &{} 0.0317 \\ 0.0222 &{} 0.1138 &{} 0.1905 &{} 0.0395 &{} 0.0251 \\ \end{array} \right) \end{aligned}$$

Step 7: Attain the weighted decision matrix $U=(u_{ij})_{m \times n}$.

$$\begin{aligned} U=(u_{ij})_{m \times n} \left( \begin{array}{ccccc} 0.0020 &{} 0.0138 &{} 0.0188 &{} 0.0066 &{} 0.0079 \\ 0.0033 &{} 0.0726 &{} 0.0296 &{} 0.0228 &{} 0.0116 \\ 0.0112 &{} 0.0447 &{} 0.0137 &{} 0.0176 &{} 0.0055 \\ 0.0024 &{} 0.0158 &{} 0.0166 &{} 0.0046 &{} 0.0052 \\ 0.0045 &{} 0.0236 &{} 0.0215 &{} 0.0061 &{} 0.0029 \\ 0.0041 &{} 0.0264 &{} 0.0640 &{} 0.0062 &{} 0.0023 \\ \end{array} \right) \end{aligned}$$

Step 8: Acquire the border approximation area $B=[b_{1}, b_{2}, \cdots , b_{n} ]$ for every criteria $C_{j}$ through the Eq. (37).

$$\begin{aligned} b_{j}=\left\{ 0.0039, 0.0276, 0.0236, 0.0088, 0.0051\right\} . \end{aligned}$$

where $u_{ij}$ signifies the element of the weighted decision matrix and m is the number of alternatives.

Step 9: Ascertain the distance matrix ${\mathscr {D}}=(\check{d}_{ij})_{m \times n}$ between the weighted decision matrix U and border approximation area B with the help of Eq. (38):

$$\begin{aligned} {\mathscr {D}}=(\check{d}_{ij})_{m \times n} \left( \begin{array}{ccccc} -0.0018 &{} -0.0137 &{} -0.0048 &{} -0.0021 &{} 0.0028 \\ -0.0005 &{} 0.0450 &{} 0.0060 &{} 0.0140 &{} 0.0065 \\ 0.0074 &{} 0.0171 &{} 0.0099 &{} 0.0088 &{} 0.0004 \\ -0.0015 &{} 0.0118 &{} -0.0070 &{} -0.0042 &{} 0.0001 \\ 0.0006 &{} -0.0040 &{} -0.0022 &{} -0.0027 &{} -0.0022 \\ 0.0002 &{} -0.0012 &{} 0.0404 &{} -0.0026 &{} -0.0028 \\ \end{array} \right) \end{aligned}$$

Step 10: Compute the function values and rank of alternatives by Eq. (39):

$$\begin{aligned}&\varepsilon (\Upsilon _1)=-0.0198,\qquad \varepsilon (\Upsilon _2)=0.0710,\qquad \varepsilon (\Upsilon _3)=0.0238,\;\\&\varepsilon (\Upsilon _4)=-0.0244,\qquad \varepsilon (\Upsilon _5)=-0.0105,\qquad \varepsilon (\Upsilon _6)=0.0340. \end{aligned}$$

Based on the function values of alternatives, we can obtain final rank is $\Upsilon _{2} \succ \Upsilon _{6} \succ \Upsilon _{3} \succ \Upsilon _{5} \succ \Upsilon _{1}\succ \Upsilon _{4}$, so the optimal option is the secondly alternative.

7.2 Parameters analysis

The sensitivity analysis of parameters can help decision experts to efficiently analyze the fluctuation of ultimate decision outcomes. Therefore, we explore the effect of the final ranking result through adjusting the parameter $\chi$, the function values and sorting results attained under different parameters are displayed in Table 7 and Fig. 2. Here, Tversky and Kahneman (1992) and Hao et al. (2017) acquired the parameter values after experiment exploration and get $\mu =\varsigma =0.88$, $\chi =2.25$, $\varphi =0.61$ and $\phi =0.69$. We will focus on the variation trend of function value and ranking result produced by parameter $\chi$. We take the parameter $\chi$ from one to thirty and achieve the decision results and the order relation of alternatives, which are shown as Table 7. From it, we can know that the optimal selection of the decision alternative fails to change with respect to the adjustable parameter. Moreover, although the risk attitude parameter has a bit impact on the final ordering of alternative, the alternative $\Upsilon _{2}, \Upsilon _{6}$ and $\Upsilon _{3}$ are always ranked in the top three, which means the propounded decision approach is relatively stable and robust.

Table 7 The impact of $\chi$ for the ultimate decision results

Fig. 2

The score values of alternatives under diverse parameters

7.3 Validity test of the proposed approach

The ultimate decision results obtained by the presented FF-CRITIC-MABAC method shows that the rank is $\Upsilon _{2} \succ \Upsilon _{6} \succ \Upsilon _{3} \succ \Upsilon _{5} \succ \Upsilon _{1}\succ \Upsilon _{4}$, namely, the $\Upsilon _{2}$ is the optimal option. To validate the efficiency of the developed method, we utilize the test standards proposed by Wang and Triantaphyllou (2018) to verify the effectiveness of the proposed decision approach.

Standard 1: When the assessment value of non-optimal scheme is replaced by another worse assessment value, the valid decision method will not change the optimal option because of the change of assessment information.

Standard 2: An effective decision method should follow the principle of transitivity.

Standard 3: When the original decision problem is decomposed into several decision subproblems, we employ the decision method to resolve the mentioned sub-problems and synthesize their ultimate ranking results. The comprehensive ranking outcome will maintain consistency with the ranking results obtained from the original problem, which shows that this method is effective for coping with decision problems.

In what follows, we utilize the mentioned three stands to test the propounded decision method. Based on the initial decision matrices, we obtain the rank of alternative as $\Upsilon _{2} \succ \Upsilon _{6} \succ \Upsilon _{3} \succ \Upsilon _{5} \succ \Upsilon _{1}\succ \Upsilon _{4}$, the best options are $\Upsilon _{2}$. From Standard 1, the assessment information of $\Upsilon _{3}$ is replaced by its complement and displayed in Table 8. Next, we utilize the FF-CRITIC-MABAC method to recompute the new problem, the function values and rank of alternatives are obtained severally as $\varepsilon (\Upsilon _1)=0.0054, \varepsilon (\Upsilon _2)=0.0442, \varepsilon (\Upsilon _3)=0.0053, \varepsilon (\Upsilon _4)=-0.0149,\;\varepsilon (\Upsilon _5)=-0.0125,\;\varepsilon (\Upsilon _6)=0.0015.$ and $\Upsilon _{2} \succ \Upsilon _{1} \succ \Upsilon _{3} \succ \Upsilon _{6} \succ \Upsilon _{5}\succ \Upsilon _{4}$. We can find that the optimal is not altered after replacing the suboptimal alternative by another inferior option, that means the Standard 1 is valid.

Table 8 The improved comprehensive decision matrix

In view of the standard 2 and standard 3, we first decompose initial problem to four sub-problems listed as $\{\Upsilon _{2}, \Upsilon _{3}, \Upsilon _{6}\}$, $\{\Upsilon _{3}, \Upsilon _{4}, \Upsilon _{5}\}$, $\{\Upsilon _{1}, \Upsilon _{4}, \Upsilon _{5}\}$ and $\{\Upsilon _{4}, \Upsilon _{5}, \Upsilon _{6}\}$. The we utilize the proposed method to respectively compute the above sub-problems and acquire the associated outcomes are $\{\Upsilon _{2} \succ \Upsilon _{6} \succ \Upsilon _{3}\}$, $\{\Upsilon _{3} \succ \Upsilon _{5} \succ \Upsilon _{4}\}$, $\{\Upsilon _{5} \succ \Upsilon _{1} \succ \Upsilon _{4}\}$ and $\{\Upsilon _{6} \succ \Upsilon _{5} \succ \Upsilon _{4}\}$. After that, we aggregate these sub-ranks and obtain a complete rank of alternative shown as $\Upsilon _{2} \succ \Upsilon _{6} \succ \Upsilon _{3} \succ \Upsilon _{5} \succ \Upsilon _{1}\succ \Upsilon _{4}$, which is same with the initial rank. Consequently, the proposed method also meets the standard 2 and standard 3.

7.4 Comparative analysis

Recently, several Fermatean fuzzy decision approaches based on different theories are put forward by researchers to tackle diverse practical decision issues. However, these existing approaches fail to ponder the psychological behavior and interaction of decision makers in the stage of information fusion and decision analysis, especially in the face of risk decision-making issues. This paper designs an integrated FF-CRITIC-MABAC decision framework based on prospect theory to make up the mentioned defect in risk decision problems analysis. To validate the validly and reasonability of the FF-CRITIC-MABAC decision framework, we implement a contrastive analysis on the basis of the existing methods involving FF-TOPSIS method (Senapati and Yager 2019b), FF-WASPAS method (Keshavarz-Ghorabaee et al. 2020) and FF-ARAS method (Gul 2021). The comparison analysis will be divided into three parts to validate the effectiveness and analyze the significant advantages of our proposed FF-CRITIC-MABAC method, including the numerical comparisons, further characteristic contrast and the distinct merits of the proposed method.

Part I: Theoretical comparisons

In this part, the theoretical comparison between the FF-CRITIC-MABAC method and other Fermatean fuzzy decision techniques are discussed from the aspects of expert information integration, weight determination and sorting. The proposed method is proposed based on the novel Fermatean fuzzy Frank aggregation operators and generalized interactive distance to further strengthen the flexibility and robustness of the decision analysis procedure. The mentioned three methods (Senapati and Yager 2019b; Keshavarz-Ghorabaee et al. 2020; Gul 2021) utilize the weighted average operators to aggregation Fermatean fuzzy information while ignoring the flexibility of information stages. In addition, the criteria weight of the above three approaches assume that the weight is given in advance, which is unreasonable for analyzing the actual decision issues. For the two defects analyzed above, the advanced method conquers its validly based upon the innovative Fermatean fuzzy Frank operators and the improved CRITIC method using the presented interactive distance measure. These can prove that the proposed method has certain advantages in theory.

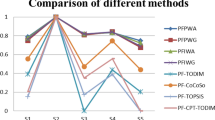
Part II: Numerical comparisons

The Numerical comparison between the presented FF-CRITIC-MABAC method and other Fermatean fuzzy decision techniques are conducted to further unfold the validity and feasibility. We utilize the previous Fermatean fuzzy decision approach including FF-TOPSIS method (Senapati and Yager 2019b), FF-WASPAS method (Keshavarz-Ghorabaee et al. 2020) and FF-ARAS method (Gul 2021) to do with the above risk investment empirical and attain the corresponding decision outcomes. The utility values and ranks obtained through the aforementioned methods are displayed in Table 9 and Fig. 3. Based upon the decision result derived by the mentioned Fermatean fuzzy decision approaches, we can find that the best selection deduced by FF-TOPSIS method and FF-ARAS method are the same as the FF-CRITIC-MABAC approach, namely, $\Upsilon _{2}$ is the optimal alternative, which further confirms the efficiency and rationally of the designed approach. Furthermore, the overall ranking of the alternatives between the above two methods and the presented method is slightly different. The main reason is that the FF-CRITIC-MABAC approach is not only simple and easy to operate, but also takes into consideration the diverse risk preference of decision experts in the course of decision.

Table 9 The comparison results obtained through different Fermatean fuzzy decision approaches

Fig. 3

Ranking orders under diverse Fermatean fuzzy method

Part III: Further comparisons

Further comparisons based on the designed approach and other Fermatean fuzzy approaches are conducted by comparing the weight of expert and criterion, expert information fusion stage and the decision analysis stage. The further comparison studies between the extant methods involving FF-TOPSIS method (Senapati and Yager 2019b), FF-WASPAS method (Keshavarz-Ghorabaee et al. 2020), FF-ARAS method (Gul 2021) FFYWA operator (Garg et al. 2020) and the designed approach are depicted as below and the features comparisons are also recapitulated in Table 10

Table 10 Characteristic comparison between the propounded methods and other Fermatean fuzzy decision algorithms

Compared with the FF-TOPSIS method proposed in Senapati and Yager (2019b). The FF-TOPSIS method is built based on the Euclidean distance measure and known criterion weight to deal with MCDM issues. However, it has the following two defects to model decision analysis. (1) The psychological behavior of decision experts are ignored in the process of decision analysis, especially to settle the risk decision issues, the bounded rationality of expert should be considered for attaining a more rationality decision outcomes. (2) The criterion weight subjectively given by experts will acquire the inaccuracy results because the objectivity of practical decision data is ignored in decision procedure. In comparison, the proposed FF-CRITIC-MABAC method overcomes the mentioned defects through integrating the prospect theory and improved CRITIC weight technique. Hence, our proposed method in this paper is more universal and rational than the FF-TOPSIS method.

Compared with the FF-ARAS method proposed in Keshavarz-Ghorabaee et al. (2020). The FF-ARAS method is proposed based on the basic Fermatean fuzzy weighted averaging operator and known weigh information. The FF-ARAS method attains the ultimate ranking of alternatives based on the utility values of alternative and assumes that the decision expert is complete rationality in dealing with decision issues. Actually, the complicated decision setting and vagueness of experts’ cognition will cause psychological changes of experts, so the results obtained by FF-ARAS will be quite different from the actual intuitive results. In contrast, the proposed approach can fuse experts’ assessment information by Fermatean fuzzy Frank operators and make the aggregation procedure more nimble. Meanwhile, it fully takes into account the risk preference of experts by the improved prospect theory MABAC approaches. Thus, the developed method is more reasonable than other Fermatean fuzzy decision algorithms in dealing with complex risk decision problems.

Compared with the FF-WASPAS method proposed in Gul (2021). The FF-WASPAS method conducts decision analysis based on utility theory and utilizes the basic fusion theory to comprehensively integrate the assessment information of alternatives. Although it is easy to implement and obtain the result rapidly, it fails to ponder the influence of personal features and the risk attitude of experts in comparing the evaluation. Hence, the FF-WASPAS method is not fit to settle the decision problem with risk preference. By comparison, the paper constructs a novel risk decision assessment based on CRITIC-MABAC method to validly resolve the uncertain complex assessment problem with unknown weight information. The outcomes acquired by the proffered method will closer the practical situation and expert cognition.

Part IV: Merits analysis

In light of the mentioned comparison investigation with the related literature, the merits and features of the extant approaches and the proposed approach are recapitulated as follows.

$\checkmark$ The propounded FF-CRITIC-MABAC method can effectively portray the uncertain and ambiguous assessment information with the aid of FFS. First, a mapping is provided for investors to assist evaluators to provide their suitable judgments with the assistance their cognition capability and experiences. Then we obtain the Fermatean fuzzy assessment matrices through transforming the linguistic term to FFNs, which provides a closer way to express the preference of evaluators.

$\checkmark$ The FF-CRITIC-MABAC approach can take into account the interactive evaluation between different assessment information based on the generalized interactive distance measure. Based on the propounded distance measure, a similarity-based method is constructed to compute the weight information of evaluators, and an improved CRITIC method is built to ascertain the weight information of assessment criterions. Accordingly, the presented approach can fully utilize the assessment information through the cross-evaluation measure and further provide a reasonable algorithm to resolve complicated decision issues with unknown weight information.

$\checkmark$ The FF-CRITIC-MABAC approach provides an uncertain and fuzzy risk investment assessment framework based on prospect theory, which can effectively address the uncertainty and cognition fuzziness of the risk management procedure by pondering the risk preference attitude of investors. Compared with other Fermatean fuzzy decision approaches, the presented method possesses more capabilities than other methods, especially in settling the complex and indeterminacy risk investment issues.

8 Conclusions

This paper builds up a FF-CRITIC-MABAC risk assessment framework to validly address the risk investment assessment problem under the background of B&R. Firstly, we first brought forward a generalized interactive distance measure through taking into account the cross-assessment of the decision information. Secondly, we advanced several Frank integration operators to fuse the Fermatean fuzzy information and prove several properties of these operators. What’s more, we present the similarity-based method and improved CRITIC algorithm based on the generalized interactive distance to compute the weight of expert and criteria, respectively. Based on the proposed Fermatean fuzzy Frank operators, interactive distance measure and prospect theory, an integrated FF-CRITIC-MABAC risk assessment framework is constructed to address the risk assessment problems with unknown weight information. The parameter analysis and contrast studies prove that the presented method is stable and valid to resolve risk investment assessment problems through taking into account the psychological behavior of investors.

However, it also has several limitations that it fails to ponder the heterogeneous information of diverse decision attributes. Because the criterion signifies different actual significance in the decision problems, the real number, interval number or linguistic term may be better suited to represent the views of experts. In the future research, we will first improve the assessment framework and build a stronger evaluation algorithm to deal with issues with multi-source mixed information (Saeed et al. 2022). Then, we can extend other decision methods such TODIM and DNMA method based on the proposed distance measure and Fermatean fuzzy Frank operators to handle decision issues. In addition, we shall enhance the application of the propounded approach in the domain of low-carbon tourism destination selection, evaluation of renewable energy sources and ecological product quality assessment and so forth (Unver et al. 2021; Ejegwa et al. 2022). Apart from these expectations, we can also develop severe novel operations (Rong et al. 2021) and operators (Rong et al. 2020) to supply decision support under the Fermatean fuzzy and other fuzzy environment setting.

Appendix

All Abbreviations and symbols used throughout the manuscript are illustrated in Tables 11 and 12 respectively.

Table 11 Full names of abbreviations related this paper

Table 12 Full names of abbreviations related this paper