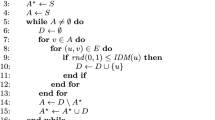1 Introduction

Nowadays, millions of users are involved in social networks (SNs), growing exponentially the number of active users. This growth is extended to the amount of behavioral data and, therefore, all classical network-related problems are becoming computationally harder. SNs can be defined as the representation of social interactions that can be used to study the propagation of ideas, social bond dynamics, disease propagation, viral marketing, or advertisement, among others (D’angelo et al. 2009; Klovdahl 1985; Barabási and Pósfai 2016; Reza et al. 2014).

SNs are used not only for spreading positive information but also malicious information. In general, research devoted to maximize the influence of positive ideas is called Influence Maximization (Nguyen Hung et al. 2016). Thus, solving successfully this problem allows the decision-maker to decide the best way to propagate information about products and/or services. On the contrary, SNs can be also used for the diffusion of malicious information like derogatory rumors, disinformation, hate speech, or fake news. These examples motivate research about how to reduce the influence of negative information. This family of problems is usually known as Influence Minimization (Khalil Elias et al. 2013; Luo et al. 2014; Xinjue et al. 2018; Qipeng et al. 2015).

A SN is usually modeled with a graph G(V, E) where the set of nodes V represents the users and each relation between two users is modeled as a pair \((u,v) \in E\), with \(u, v \in V\) indicating that user u is connected to or even can transmit information to user v. Kempe et al. (2003) originally formalized the influence model to analyze how the information is transmitted among the users of a SN. Given a SN with \(|V| = n\) nodes where the edges (relational links) represent the spreading or propagation process on that network, the task is to choose a seed node set S of size \(k<n\) with the aim of maximizing the number of nodes in the network that are influenced by the seed set S. This results in a combinatorial optimization problem known as the Social Network Influence Maximization problem (SNIMP).

The evaluation of the influence of a given seed set S requires the definition of an Influence Diffusion Model (IDM) (Kempe et al. 2015). This model is responsible for deciding which nodes are affected by the information received from their neighboring nodes in the SN. The most extended IDMs are: Independent Cascade Model (ICM), Weighted Cascade Model (WCM), and Linear Threshold Model (LTM). All of them are based on assigning an influence probability to each relational link in the SN. ICM, which is one of the most used IDMs, considers that the influence probability is the same for each link, and it is usually a small probability, being 1% a widely accepted value. On the contrary, WCM considers that the probability of a user v for being influenced by user u is proportional to the in-degree of user v, i.e., the number of users that can eventually influence user v. Therefore, the probability of influencing user v is defined as \(1/d_{ in }(v)\), where \(d_{ in }(v)\) is the in-degree of user v. The latter model, LTM, requires a specific activation weight for each link in the SN. Given those weights, a user will be influenced if and only if the sum of the weights of its neighbors if larger than or equal to a given threshold. In this paper we consider the ICM since it is one of the most popular IDMs in the literature. In particular, ICM views influence as being transmitted through the network in a tree-like fashion, where the seed nodes are the roots.

The SNIMP then involves finding a seed set S, with \(|S| = k\) (where k is an input parameter), that maximizes the number of users influenced and, as a consequence, the spread of information through the network. In mathematical terms,

$$\begin{aligned} S^{\star } \leftarrow {\mathop {{{\,\mathrm{arg\,max}\,}}}\limits _{S \in \mathcal {S}}} ICM (G, S, p, ev) \end{aligned}$$

where \(\mathcal {S}\) is the set of all possible solutions (i.e., seed set setups), p is the probability of a user to be influenced, and ev is the number of iterations of the Monte Carlo simulation used to run the ICM (see Sect. 3.1).

The SNIMP was initially formulated in Richardson et al. (2003) and it was later proven to be \(\mathcal {NP}\)-hard for most IDMs in Kempe et al. (2015). As with many other \(\mathcal {NP}\)-hard problems, heuristic and metaheuristic algorithms, such as greedy and evolutionary algorithms, have been considered to solve the problem by effectively exploring the solution space, avoiding the analysis of every possible subset of nodes (Banerjee et al. 2020).

This work presents a novel metaheuristic approach for dealing with the SNIMP, allowing us to find high quality solutions in short computing time. Our main goal is to design an efficient algorithm where the use of Monte Carlo simulation required for the IDM application is minimized, thus increasing the efficiency of the algorithm. To do so, we make use of the Greedy Randomized Adaptive Search Procedure (GRASP) framework, characterized for its efficiency when designing solutions for \(\mathcal {NP}\)-hard combinatorial optimization problems. Our procedure is based on two stages. On the one hand, a greedy constructive procedure based on the 2-step neighborhood which is randomized to diversify the search with the aim of exploring a wider portion of the solution space. On the other hand, we introduce an efficient local search method. Specifically, it relies on an intelligent neighborhood exploration strategy for finding local optima with respect to the constructed solutions. The proposed procedure is validated over a set of 35 instances widely used in the context of social influence maximization, and benchmarked against both the classical methods based on greedy hill-climbing strategies (Goyal et al. 2011; Leskovec et al. 2007) and the state-of-the-art solution procedure for SNIMP based on particle swarm optimization (Banerjee et al. 2020). The results obtained clearly demonstrate the efficacy of the proposed methodology.

The remainder of the work is structured as follows. Section 2 reviews the related literature, detailing the different approaches followed to deal with different problems derived from the social influence maximization. The proposed approach is described in Sect. 3, where Sect. 3.1 introduces the influence diffusion model selected in this research, Sect. 3.2 presents the construction method proposed for providing high quality initial solutions, and Sect. 3.3 describes the local search proposed for finding local optimum with respect to a given neighborhood structure. Section 4 presents the experimental results considering a public dataset which has been previously used for this task, divided into preliminary experiments devoted to adjust the search parameters (Sect. 4.1), and final experiments to perform a competitive testing to evaluate the quality of the proposal (Sect. 4.2). Finally, Sect. 5 draws some conclusions derived from this research.

2 Literature review

In this section, we introduce some related work about SNIMP and IDM as well as a brief survey of existing methods for solving this problem, either based on heuristics or computational intelligence algorithms.

Richardson et al. (2003) initially formulated the problem of selecting target nodes in SNs. However, Kempe et al. (2003) were the first to solve the SNIMP formulating it as a discrete optimization problem. It has been shown that the SNIMP is \(\mathcal {NP}\)-hard (Kempe et al. 2015). Kempe et al. (2003) proposed a greedy hill-climbing algorithm with an approximation of \(1-1/e -\epsilon\), being e the base of the natural logarithm and \(\epsilon\) any positive real number. This result indicates that the algorithm is able to find solutions which are always within a factor of at least 63% of the optimal value under the three IDMs described in Sect. 1.

As a consequence of the computational effort required to evaluate the ICM, Kempe et al. (2003) also proposed several greedy heuristics based on SN analysis metrics such as degree and closeness centrality (Stanley and Katherine 1994). These methods only require one run of a Monte Carlo simulation to validate the single solution obtained using heuristic functions, thus increasing the efficiency at the cost of a loss of efficacy. When the considered metric is the degree of the node, the algorithm is called high-degree heuristic.

Several extensions of those first greedy algorithms were later proposed. In particular, Leskovec et al. (2007) introduced the Cost-Effective Lazy Forward (CELF) selection which exploited the submodularity property to significantly reduce the run time of the greedy hill-climbing algorithm, becoming over 700 times faster than the original procedure. The rationale is that the expansion of each node is computed a priori and it only needs to be recomputed for a few nodes. Meanwhile, Chen et al. (2009) used the concept of degree-discount heuristics to optimize the high-degree heuristic. The greedy selection function considers the redundancy between likely influenced nodes and does not include those reached by the already selected seed nodes to provide a better estimation of the total spread.

In Goyal et al. (2011) a new algorithm called CELF++ was proposed with the aim of improving the efficiency of the original CELF. It leans on the property of submodularity of the spread function for IDM, avoiding unnecessary computations. According to the authors it is 35-55% faster than CELF.

A large number of works have been developed in the area since those first proposals (Şimşek and Kara 2018). Different kinds of heuristic and metaheuristic algorithms have been considered to solve the SNIMP. Table 1 summarizes the most recent approaches, including the algorithm type and the specific IDM considered.

Table 1 Summary of the literature published for the SNIMP in the last 20 years
Full size table

Analyzing previous studies we can conclude that more complex metaheuristic approaches usually result in better solutions than simple greedy approaches. Yang and Weng (2012) proposed an Ant Colony Optimization (ACO) algorithm based on a parameterized probabilistic model to address the SNIMP. They used the degree centrality, distance centrality, and simulated influence methods for determining the heuristic values.

Meanwhile, the method based on Simulated Annealing (SA) presented in Li et al. (2017) applied two heuristic methods to accelerate the convergence process of SA, along with a new method of computing influence spread to speed up the proposed algorithm. In Bucur et al. (2017), an Evolutionary Multi-objective Optimization (EMO) algorithm (Lamont et al. 2007) was proposed for SNIMP, where the two considered objectives were maximizing the influence of a seed set and minimizing the number of nodes in the seed set jointly.

As said before, some heuristics have been proposed as time-saving solutions for greedy decisions: random, degree, and centrality (Kempe et al. 2003). The random heuristic selects nodes randomly, without considering node influence, to form the seed set in the network. Degree and centrality heuristics derive from the definition of the node influence in SN analysis (Stanley and Katherine 1994). Degree centrality heuristic usually produces less accurate results to the SNIMP. Alternatively, the high-degree heuristic targets the SNIMP by taking into account prior knowledge of the node’s neighbors (Chen et al. 2009).

Recently, a complete survey on SNIMP has been presented in Banerjee et al. (2020). In that work, authors experimentally compare the results obtained by the most recent algorithms. The survey concludes that the particle swarm optimization approach by Gong et al. (2016) obtains the best results in the literature, so we will use that algorithm to benchmark our proposal. This survey has become one of the most relevant research in the area of influence maximization problems.

The aforementioned metaheuristic methods are able to obtain good results but usually require large computational times. Our proposal considers a method combining the use of heuristic functions and Monte Carlo simulations for limiting the number of ICM evaluations that tries to balance the quality of the obtained solutions and the required computing time. With the aim of reducing the required computing time, we consider a GRASP, combining good heuristic solutions that are quickly generated and an efficient local search method which minimizes the number of Monte Carlo evaluations to further improve the initial solution. The use of GRASP in Graph Theory and Network Science has led to several successful research in the last years (Pérez-Peló et al. 2019, 2020; Gil-Borrás et al. 2020).

3 Algorithmic approach

The method presented in this work aims at finding high quality solutions in reasonable computing time. In order to do so, we propose a metaheuristic algorithm. Metaheuristics are one of the most extended techniques for solving hard optimization problems. They are able to guide the search in order to escape from local optima, with the goal of finding high quality solutions in a reduced computing time.

GRASP is a metaheuristic framework developed in the late 1980s Feo and Resende Mauricio (1989) and formally introduced in Feo and Resende Mauricio (1994). We refer the reader to Resende Mauricio et al. (2010), Resende Mauricio and Celso (2013) for a complete survey of the last advances in this methodology. GRASP is a multi-start framework divided into two distinct stages. The first one is a greedy, randomized, and adaptive construction of a solution. The second stage applies an improvement method to obtain a local optimum with respect to a certain neighborhood, starting from the constructed solution. This methodology is able to find a trade-off between the diversification of the randomized construction phase and the intensification of the local search procedure, allowing the algorithm to escape from local optima and perform a wider exploration of the search space. These two phases are repeated until a termination criterion is met, returning the best solution found during the search.

3.1 Influence diffusion model

Before defining the algorithmic proposal, it is necessary to provide a formal definition of the IDM considered in this work, which is the ICM introduced in Sect. 1. Due to the probabilistic nature of ICM, the most extended way of evaluating the spread is by conducting a Monte Carlo simulation. However, even a single iteration of the simulation in ICM is rather time-consuming. Algorithm 1 shows the pseudocode of the Monte Carlo simulation to evaluate the spread of information through a SN named G given a seed set S. Specifically, it receives four input parameters: the graph which models the SN, a tentative solution, the probability of a user to be influenced, and the number of iterations of the corresponding Monte Carlo simulation.

figure a

The algorithm starts by initializing the set which stores the number of infected users (step  1). It then performs a number of predefined iterations ev (steps \(2-18\)), finding in each iteration which are the influenced nodes by the given seed set S. Initially, the set of nodes \(A^{\star }\) reached by the initial seed set, S, is actually the seed set (step  3). Then, the method iterates until no new nodes are influenced (steps 5–16). In each iteration of the inner for-loop, the neighbors of each node reached in the previous one are traversed (steps 8–12). For each neighbor, a random number is generated. If this number is smaller than the probability of infection p, then the neighboring node becomes infected (steps 9–11). At the end, the set of infected nodes is updated (step 14) as well as the nodes infected in the previous iteration (step 15). Finally, the algorithm returns the mean number of infected nodes among all the simulations performed, i.e., I divided by ev (step 19). Notice that this value is considered as the objective function to be optimized when solving the SNIMP. That is, the seed set maximizing the spread value over the network would compose the optimal solution to the problem. It is worth mentioning that, as infection is a stochastic process, the ICM must be run several times (ev in our case) to achieve an appropriate estimation, thus resulting in a Monte Carlo simulation.

In order to illustrate the evaluation of a solution under the ICM, Fig. 1 shows an example of a SN with 9 nodes and 13 directed edges, where each pair (u, v) denotes that the user v may be influenced by u. Information represents anything that can be passed across connected peers within a network. The influence level given by a node is determined by the adoption or propagation process. Let us consider \(k=2\) for this example graph.

Fig. 1
figure 1

SN with 9 nodes and 13 edges. Two feasible solutions \(S_1\) and \(S_2\) are represented, each of them resulting in a different set of influenced users

Full size image

Figure 1a shows solution \(S_1\) where the seed set is conformed with nodes C and G. Without loss of generality we will assume, for this example, that \(p=1\) (i.e., all the nodes are always infected by their neighbors). Simulating the diffusion model we can see how nodes D, E, and H are directly influenced by the seed set. After that, node H influences node I. Different levels of influence are represented by a gray gradient from black to white. Therefore, if we consider a single evaluation of the Monte Carlo simulation, the objective function value of \(S_1\) is \(ICM (G,S_1,p,1) = 6\). Figure 1b depicts solution \(S_2 = \{{\texttt {A,F}}\}\). Similarly to Fig. 1a, a gray gradient indicates the process of influence over the network, resulting in an objective function value of \(ICM (G,S_2,p,1) = 9\), since all nodes are influenced. Notice that, following this evaluation, \(S_2\) is better than \(S_1\). However, it is important to remark that a single iteration for the Monte Carlo simulation is not significant, so we have decided to perform \(ev=\)100 evaluations of the simulation as it is customary in the literature for the SNIMP (Bucur and Iacca 2016; Bucur et al. 2018). Additionally, we set \(p=0.01\) as stated in previous works Bucur and Iacca 2016; Kempe et al. 2003; Gong et al. 2016. Then, for the sake of simplicity, we refer to ICM(G, S, 0.01, 100) as ICM(G, S) in the remaining of the paper.

3.2 Construction phase

The construction phase of GRASP is designed to generate an initial solution and it is usually guided by a greedy selection function which helps the constructive method to select the next elements to be included in the partial solution (see Algorithm 2).

In order to favor diversification, the first node to be included in the solution S is selected at random from the set of SN nodes V (step 1). The candidate list CL is created with all the nodes but v (step 2) and the node v is included as the only node in the initial solution S (step 3). Then, the constructive method iteratively adds new elements to the solution until it becomes feasible, being composed of k nodes (steps 4–12). In each iteration, the minimum and maximum value of the greedy heuristic function is evaluated (steps 5–6). Then, a threshold \(\mu\) is calculated (step 7), which is required for creating the Restricted Candidate List (RCL) with the most promising nodes (step 8). This threshold directly depends on the value of the input parameter \(\alpha\), which is in the range [0, 1]. Notice that this parameter indicates the greediness or randomness of the constructive procedure. On the one hand, if \(\alpha = 0\), then the threshold is evaluated as \(g_{\max }\), becoming a totally greedy algorithm (i.e., the RCL only includes the best choice in each iteration). On the other hand, if \(\alpha =1\) then \(\mu = g_{\min }\), resulting in a completely random method (i.e., the RCL includes every feasible choice in each iteration). Since this parameter is tuned experimentally, we refer the reader to Sect. 4 to analyze the experiments performed to select the best value for \(\alpha\). Finally, the next node is selected at random from the RCL (step 9), including it in the solution (step 10) and updating the CL (step 11). The method ends when k elements are included in the seed set, returning the constructed solution S (step 13).

figure b

The greedy heuristic function g used in steps 5-6 is one of the key features when designing a constructive procedure in the context of GRASP. In this work we propose two different greedy functions to generate initial solutions. The first one, named \(g_{ ne }\), is a heuristic based on the first and second degree neighbors of a given node (usually known as 2-step in SN analysis Stanley and Katherine 1994). Given a node u, its out-degree is defined as \(d^+_u = |N_u^+=|\), where \(N_u^+ = \{w \in V : (u,w) \in E\}\) is the set of adjacent nodes to u.

Thus, the first greedy function calculates the sum of the out-degree of u plus the out-degree of its neighbors. This heuristic function is based on the two-hop area (Sen et al. 2014) and three-degree theory (Christakis and Fowler 2009) hypothesis, indicating that there exists an intrinsic decay when increasing the maximum neighborhood level. More formally,

$$\begin{aligned} g_{ ne }(u) = d_u^+ + \sum _{v\in N_u^+} d_v^+ \end{aligned}$$

If we analyze this metric over the graph depicted in Fig. 1, the value of \(g_{ ne }\) over vertex F, for instance, is evaluated as \(g_{ ne }(\texttt {F}) = d_{\texttt {F}}^+ + d_{\texttt {E}}^+ + d_{\texttt {G}}^+ = 2 + 2 + 2 = 6\). In order to reduce the computational effort of updating the value of this greedy function for each node, the method updates the value just for the affected nodes, which are those nodes to which the selected one is directly connected. For instance, in case of selecting node F, only nodes E and G must be updated, by subtracting the out-degree of the selected node F. This efficient update mechanism allows the algorithm to minimize the relevance of those vertices that are directly influenced by one of the selected nodes.

The second greedy function, named \(g_{cc}\), considers the nodes clustering coefficient as a heuristic value. It estimates the likelihood that nodes in a graph tend to cluster together. In mathematical terms, the clustering coefficient is defined as (in a directed network):

$$\begin{aligned} g_{ cc }(u) = \dfrac{\left| \{ (v,w) \in E : v,w \in N_u^+ \} \right| }{ d_u^+ \cdot (d_u^+ - 1) } \end{aligned}$$

It is worth mentioning that, to speed up this computation, every value is pre-calculated before the execution of the algorithm. We refer the reader to Watts and Strogatz (1998) for a detailed description of the implementation of this metric.

Let us illustrate how we can evaluate this value with an example. Considering again the SN depicted in Fig. 1, the evaluation of the clustering coefficient of node F is performed as \(g_{ cc } = \dfrac{| (\texttt {G},\texttt {E}) |}{d_{\texttt {F}}^+ \cdot (d_{\texttt {F}}^+ - 1)} = \dfrac{1}{2} = 0.5\).

Given \(g_{ ne }\) and \(g_{ cc }\) as greedy functions, we propose two different constructive procedures \(C_{ ne }\) and \(C_{ cc }\), each one based on a different greedy function. The impact and influence of each constructive procedure in the generated solutions will be deeply analyzed in Sect. 4.

3.3 Local search phase

The second phase of GRASP involves improving the solution generated by the constructive procedure in each iteration with the aim of reaching a local (ideally global) optimum. In the context of GRASP, this phase can be accomplished by using simple local search procedures or more complex heuristics like Tabu Search or even a hybrid metaheuristic (Martí et al. 2018). The high complexity of the problem under consideration has led us to propose a low time consuming local search procedure.

Before defining a local search method, it is necessary to introduce the neighborhood to be explored. The neighborhood of a solution S is defined as the set of solutions that can be reached by performing a single move over S. In the context of SNIMP, we propose a swap move \(Swap (S, u, v)\) where node u is removed from the seed set, being replaced by v, with \(u \in S\) and \(v \notin S\). This swap move is formally defined as:

$$\begin{aligned} Swap (S, u, v) = S \setminus \{u\} \cup \{v\} \end{aligned}$$

Thus, the neighborhood \(N_{ s }\) of a given solution S consist of the set of solutions that can be reached from S by performing a single swap move. More formally,

$$\begin{aligned} N_{ s }(S) = \{ Swap (S,u,v) \quad \forall \ u \in S \wedge \forall \ v \in V\setminus S \} \end{aligned}$$

The next step to define the proposed local search procedure consists in indicating the way in which the neighborhood is explored. Even considering an efficient implementation of the objective function evaluation, the vast size of the resulting neighborhood, \(k \cdot (n - k)\), makes the complete exploration of the neighborhood not suitable for the SNIMP. Therefore, an intelligent neighborhood exploration strategy is presented with the aim of reducing the number of solutions explored within each neighborhood. This reduction in the size of the search space is performed by exploring just a small fraction, \(\delta\), of the available nodes for the swap node.

Since we are limiting the number of nodes considered in the local search approach, it is recommended to select the most promising ones to be involved in the swap moves. In the context of SNIMP, a node with a large out-degree can eventually influence a larger amount of nodes. Following this idea, we sort the candidate nodes to be included in the seed set in descending order with respect to their out-degree, while the candidate nodes to be removed from the seed set are sorted in ascending order with respect to their out-degree. Sect. 4 details the impact of the number of selected nodes, determined by \(\delta\), in the results obtained with the local search procedure.

Finally, we need to indicate which moves will be accepted during the search. In particular, two strategies are usually considered: Best Improvement and First Improvement (Hansen and Mladenović 2006). On the one hand, the former explores, in each iteration, the complete neighborhood, moving to the best solution in it. On the other hand, the latter moves to the first solution that achieves an improvement in the objective function value, without requiring to explore the complete neighborhood. Due to the computational effort required to evaluate a solution for the SNIMP, we propose a First Improvement approach, which does not need to explore all the solutions in the neighborhood, thus reducing the number of objective function evaluations required and consequently the overall run time.

Notice that the objective function evaluation consists in a Monte Carlo simulation, being the most computationally demanding part of the proposed algorithm. For this reason, the proposed local search aims to limit the number of required simulations, thus leading to a more efficient procedure.

4 Computational experiments and analysis of results

The aim of this section is to describe the computational experiments designed to evaluate the performance of the proposed algorithms and to analyze the obtained results. All the experiments have been performed in an Intel Core i7 (2.6 GHz) with 8GB RAM and the algorithms were implemented using Java 9. The source code has also been made publicly available.Footnote 1

The set of SNs considered in this paper have been entirely obtained from the most relevant works found in the literature, in order to provide a fair comparison among the analyzed algorithms. All of them are publicly available in Stanford Network Analysis Project (SNAP): https://snap.stanford.edu/. Relevant information about these instances is collected in Table 2, where some papers in which each instance has been used are included.

Table 2 Nodes and edges of the instances used in this work
Full size table

First of all, it is important to indicate which values are used for the ICM algorithm with the corresponding Monte Carlo simulation. In all the experiments, as stated in Sect. 3.2, 100 simulations of the ICM are performed with a probability of influence of 0.01. These parameter values are the most extended ones in the related literature. The number of seed nodes k to conform a solution is selected in the range \(k=\{10, 20,30,40,50\}\) as stated in Bucur and Iacca (2016), Kempe et al. (2003), Salavati and Abdollahpouri (2019), thus obtaining \(7 \cdot 5 = 35\) different problem instances (resulting from the combination of 7 networks and 5 seed set sizes).

The experiments are divided into two parts: preliminary and final experimentation. The former (Sect. 4.1) refers to those experiments performed to select the best parameters to set up our algorithm, while the latter (Sect. 4.2) validates the best configuration, comparing it with the best methods found in the state of the art.

All the experiments developed report the following metrics: Avg., the average objective function value (i.e., the number of influenced nodes, in average, after 100 simulations); Time (s), the average computing time required by the algorithm in seconds; Dev(%), the average deviation with respect to the best solution overall found in the experiment; and #Best, the number of times that the algorithm matches the best solution.

4.1 Preliminary experimentation to setup the final GRASP method

The preliminary experimentation has been performed with a small set of 10 instances out of 35 to avoid overfitting. This selection comprises, approximately 30% of the global set and it provides enough variability in instances and values of k.

The first preliminary experiment is designed to find the best value for the \(\alpha\) parameter in each of the proposed constructive procedures (see Sect. 3.2). Table 3 shows the detailed results for each constructive procedure when considering \(\alpha =\{0.25, 0.50, 0.75, RND \}\), where RND indicates that the value of \(\alpha\) is selected at random in each construction (thus allowing the algorithm for a higher and balanced search space diversification). The method is executed 100 independent times per instance, returning the best constructed solution.

Table 3 Results of the constructive procedure when generating 100 solutions, considering different \(\alpha\) values for both heuristic functions
Full size table

As it can be drawn from the table, the best results are consistently provided by the greedy function based on the two-step neighbors, \(C_{ ne }\), both in quality and run time. In particular, the best results are obtained when considering \(\alpha = RND\), with 8 best solutions and 0.11% of average deviation. The small deviation value indicates that, even in the cases in which it is not able to reach the best solution, it remains really close to it. Besides, it is the second best choice in terms of run time, with a slight difference with respect to the best option. Therefore, we select \(C_{ ne }\) as the best constructive procedure with \(\alpha = RND\).

The second preliminary experiment is devoted to analyze the influence of the number of explored nodes in the neighborhood for the local search phase. In particular, we have tested \(\delta = \{ 10, 20, 30, 40 \}\), being \(\delta\) the number of nodes explored in each local search iteration. Table 4 shows the influence that the number of nodes explored \(\delta\) has in the performance of the local search procedure. Notice that an independent local search is applied to each one of the 100 constructed solutions, returning the best solution found overall.

Table 4 Influence of the number of nodes \(\delta\) explored in each iteration of the local search procedure when coupled with the constructive procedure
Full size table

The obtained results show that the best \(\delta\) value is 30, reaching the smallest deviation and the largest number of best solutions found, although in this case the results are more similar in every metric. However, it is more computationally demanding than the remaining values, being two or even three times slower than the other \(\delta\) values. Furthermore, \(\delta = 20\) is the quickest variant (almost 2.5 times faster than \(\delta = 30\)) and it presents a very good performance: a promising average objective function value and average deviation with respect to the best value (272.46 versus 274.42 and 0.56% versus 0.51%, respectively). For this reason, we select \(\delta = 20\) as our design choice for the final algorithm.

It is important to remark the relevance of the introduced intelligent neighborhood exploration strategy in the performance of the whole algorithm. Specifically, the best identified local search method (with \(\delta = 20\)) spends 26.03 seconds on solving the smallest instance (WikiVote), obtaining an objective function value of 165.32. If we do not consider the \(\delta\) parameter and execute an exhaustive local search, it needs 15793.09 seconds (i.e., more than 600 times longer) to find the local optima with a value of 165.59. We do not extend this experiment for the remaining instances since the computing time is unacceptable.

Having performed the preliminary experiments, we can conclude that the best results are obtained with the configuration greedy function=\(g_{ ne }\), \(\alpha = RND\), and \(\delta = 20\). These parameter values will be used to set up the final version of the algorithm.

4.2 Final experimentation to benchmark the final GRASP method with state-of-the-art results

In order to analyze the quality of the proposed algorithm, we perform a competitive testing with the best methods found in the state of the art by considering the complete set of 35 instances. In this experiment, three additional algorithms are considered: CELF (Leskovec et al. 2007), the well-known greedy hill-climbing algorithm; CELF++ (Goyal et al. 2011), the improved version of CELF (Leskovec et al. 2007); and PSO (Gong et al. 2016), the particle swarm optimization algorithm which is considered the state of the art for social influence analysis according to the recent experimental study developed in Banerjee et al. (2020). Table 5 collects the final results obtained in this competitive testing, where we report for each method and instance the value of the objective function (Avg.) and the associated computing time in seconds (Time(s)). Notice that Avg. is not an integer value since it is the average value of the 100 runs of the ICM in the Montecarlo simulation. We have also included a final row in this table (G.Avg.) with the average values of the objective function and Time (s), computed across the set of 35 instances.

Table 5 Competitive testing of the proposed GRASP algorithm with respect to the best algorithms found in the literature: CELF, CELF++, and PSO
Full size table

We would like to first highlight the results obtained with PSO, since it is ranking the last one even being considered the state of the art for this problem. The rationale behind this is that the original work (Gong et al. 2016) considers small size instances (from 410 to 15233 nodes) and the quality of the solutions provided by PSO deteriorates when the instance size increases, as it can be derived from Table 5. Meanwhile, CELF and its improved version CELF++ are able to reach better solutions, still being competitive with the state-of-the-art algorithms. However, only CELF++ is able to match the best-known solution in 1 instance (out of 35). Finally, the best results are obtained with the proposed GRASP algorithm, which is able to reach the best solution found in all the 35 instances. Furthermore, the computing time is smaller than the second best algorithm, CELF++ (39.04 versus 60.09 seconds on average).

As can be observed in Table 5, CELF is able to provide high quality solutions in small computing time. In order to further analyze these results, we conduct an additional experiment to compare our constructive procedure (i.e., only using the first stage of the GRASP procedure and not considering the application of the local search) with CELF. In this case, the average objective function for \(C_{ ne }\) is 227.83, which compares favorably to the result achieved with CELF, which is 208.33. In both cases, the computing time is approximately 6 seconds.

Analyzing the computing time required for each algorithm, we can clearly see that CELF and CELF++, as completely greedy approaches, are not really affected by increasing the size of the seed set. On the contrary, the computing time required for PSO and GRASP is affected by the size of the seed set since larger k-values lead the local improvement method to perform a larger number of iterations. However, if we take a closer vision of the results obtained with GRASP, we can conclude that this increase in the number of iterations and, therefore, in the computing time allows the algorithm to reach better solutions. In the case of PSO, the increase of computing time is even much more noticeable but it does not usually result in better solutions, suggesting that the PSO algorithm is particularly suitable for solving small size instances.

In order to validate these results, we have conducted a non-parametric Friedman test for ranking all the compared algorithms. The p-value obtained, smaller than 0.0005, confirms that there are statistically significant differences among the algorithms. The algorithms sorted by ranking are GRASP (1.00), CELF++ (2.44), CELF (2.79), and PSO (3.77). We finally perform the well-known non-parametric Wilcoxon statistical test for pairwise comparisons, which answers the question: do the solutions generated by both algorithms represent two different populations? The resulting p-value smaller than 0.0005 when comparing GRASP with each other algorithm confirms the superiority of the proposed GRASP algorithm. Therefore, GRASP emerges as one of the most competitive algorithms for the SNIMP, being able to reach high quality solutions in small computing time.

5 Conclusions

In this paper a quick GRASP algorithm for solving the SNIMP has been presented. Two constructive procedures are proposed, with the one based on the two-step neighborhood being more competitive one than that based on the clustering coefficient. Furthermore, the idea of using local information allows the algorithm to construct a complete solution in a small computing time. Then, a local search based on swap moves is presented. Since an exhaustive exploration of the search space is not suitable for this problem, we propose an intelligent neighborhood exploration strategy which limits the region of the search space to be explored, focusing on the most promising areas. This rationale leads us to provide high quality solutions in reasonable computing time, even for the largest instances derived from real-world SNs commonly considered in the SNIMP area. Since the intelligent neighborhood exploration strategy is parameterized, if the computing time is not a relevant factor, the region explored can be easily extended to find better solutions, thus increasing the required computational effort. This fact makes the proposed GRASP algorithm highly scalable. The results obtained are supported by Friedman test and then the pairwise Wilcoxon test, confirming the superiority of the proposal with respect to the classical and state-of-the-art solution procedures in the area.

In our future work, we plan to study the adaptation of techniques developed in this work to influence minimization problems. This adaptation can be useful for minimizing the impact of fake news and monitor those users which can eventually transmit misinformation through the network (Wei-Neng et al. 2019; Wang et al. 2017).