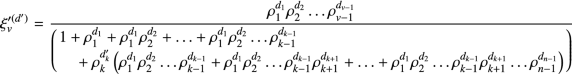Abstract
This paper aims to present some novel prioritized aggregation operators for aggregating complex intuitionistic fuzzy values (CIFVs). The aggregation operators are developed by assigning non-negative real numbers called as priority degrees among strict priority levels. The presented work is divided into three folds. The first fold is that uncertainties in the data are represented using CIFVs which have the characteristic of portraying membership and non-membership degrees over the unit disc of the complex plane. The second fold is to present prioritized averaging and geometric operators without priority degrees, prioritized averaging and geometric operators with priority degrees, prioritized ordered weighted averaging and geometric operators with priority degrees based on basic unit interval monotonic (BUM) function for aggregating dependent CIFVs. A number of propositions related to proposed operators are proved. The third fold is that a group decision-making approach based on proposed operators is developed and is applied on a decision-making problem. The results of proposed method are compared with several existing studies. The comparative study results reveal that the proposed approach is valid and gives fair results. The characteristics of the developed method are also compared with several existing approaches which highlight the superiority of the presented work over prevailing techniques. Besides this, the role of the priority degrees on aggregation result is also discussed in detail.
Similar content being viewed by others
References
Ali M, Smarandache F (2017) Complex neutrosophic set. Neural Comput Appl 28(7):1817–1834
Ali M, Dat LQ, Son LH, Smarandache F (2018) Interval complex neutrosophic set: formulation and applications in decision-making. Int J Fuzzy Syst 20:986–999
Alkouri AMJS, Salleh AR (2012) Complex intuitionistic fuzzy sets. In: AIP conference proceedings, vol 1482. American Institute of Physics, pp 464–470
Alkouri AM, Salleh AR (2013) Complex Atanassov’s intuitionistic fuzzy relation. Abstr Appl Anal 2013:287382
Atanassov KT (1986) Intuitionistic fuzzy sets. Fuzzy Sets Syst 20:87–96
Bakbak D, Ulucay V (2019) Multicriteria decision-making method using the cosine vector similarity measure under intuitionistic trapezoidal fuzzy multi-numbers in architecture. In: 6th International Multidisciplinary Studies Congress (Multicongress’ 19) Gaziantep, Türkiye
Bakbak D, Ulucay V, Sahin M (2019) Intuitionistic trapezoidal fuzzy multi-numbers and some arithmetic averaging operators with their application in architecture. In: 6th international multidisciplinary studies congress (Multicongress’ 19) Gaziantep, Türkiye
Bi L, Dai S, Hu B (2018) Complex fuzzy geometric aggregation operators. Symmetry 10(7):251
Dai S, Bi L, Hu B (2019) Distance measures between the interval-valued complex fuzzy sets. Mathematics 7(6):549
Dick S, Yager RR, Yazdanbakhsh O (2016) On pythagorean and complex fuzzy set operations. IEEE Trans Fuzzy Syst 24(5):1009–1021
Gao H (2018) Pythagorean fuzzy hamacher prioritized aggregation operators in multiple attribute decision making. J Intell Fuzzy Syst 35:2229–2245
Garg H (2016a) Generalized intuitionistic fuzzy interactive geometric interaction operators using Einstein t-norm and t-conorm and their application to decision making. Comput Ind Eng 101:53–69
Garg H (2016b) Some series of intuitionistic fuzzy interactive averaging aggregation operators. Springer Plus 5(1):1–27
Garg H (2016c) A new generalized pythagorean fuzzy information aggregation using Einstein operations and its application to decision making. Int J Intell Syst 31:886–920
Garg H (2017) Generalized Pythagorean fuzzy geometric aggregation operators using Einstein t-norm and t-conorm for multicriteria decision-making process. Int J Intell Syst 32(6):597–630
Garg H, Rani D (2019a) Some generalized complex intuitionistic fuzzy aggregation operators and their application to multicriteria decision-making process. Arab J Sci Eng 44(3):2679–2698
Garg H, Rani D (2019b) A robust correlation coefficient measure of complex intuitionistic fuzzy sets and their applications in decision-making. Appl Intell 49(2):496–512
Garg H, Rani D (2020a) Generalized geometric aggregation operators based on t-norm operations for complex intuitionistic fuzzy sets and their application to decision-making. Cogn Comput 12(3):679–698
Garg H, Rani D (2020b) Robust averaging-geometric aggregation operators for complex intuitionistic fuzzy sets and their applications to MCDM process. Arab J Sci Eng 45:2017–2033
Garg H, Rani D (2020c) Novel aggregation operators and ranking method for complex intuitionistic fuzzy sets and their applications to decision-making process. Artif Intell Rev 53:3595–3620
Garg H, Gwak J, Mahmood T, Ali Z (2020) Power aggregation operators and VIKOR methods for complex q-rung orthopair fuzzy sets and their applications. Mathematics 8(4):538
Gou X, Xu Z, Lei Q (2016) New operational laws and aggregation method of intuitionistic fuzzy information. J Intell Fuzzy Syst 30:129–141
Gulistan M, Khan S (2020) Extentions of neutrosophic cubic sets via complex fuzzy sets with application. Complex Intell Syst 6:309–320
Khalaf MM, Alharbi SO, Chammam W (2019) Similarity measures between temporal complex intuitionistic fuzzy sets and application in pattern recognition and medical diagnosis. Discrete Dyn Nat Soc 2019:1–16
Khan MSA, Abdullah S, Ali A, Amin F (2019) Pythagorean fuzzy prioritized aggregation operators and their application to multi-attribute group decision making. Granul Comput 4:249–263
Kumar T, Bajaj RK (2014) On complex intuitionistic fuzzy soft sets with distance measures and entropies. J Math 2014:972198
Li B, Xu Z (2019) Prioritized aggregation operators based on the priority degrees in multicriteria decision-making. Int J Intell Syst 34(9):1985–2018
Liu P, Mahmood T, Ali Z (2020) Complex q-rung orthopair fuzzy aggregation operators and their applications in multi-attribute group decision making. Information 11(1):5
Ngan RT, Son LH, Ali M, Tamir DE, Rishe ND, Kandel A (2020) Representing complex intuitionistic fuzzy set by quaternion numbers and applications to decision making. Appl Soft Comput 87:105961
Ramot D, Milo R, Friedman M, Kandel A (2002) Complex fuzzy sets. IEEE Trans Fuzzy Syst 10(2):171–186
Ramot D, Friedman M, Langholz G, Kandel A (2003) Complex fuzzy logic. IEEE Trans Fuzzy Syst 11(4):450–461
Rani D, Garg H (2017) Distance measures between the complex intuitionistic fuzzy sets and its applications to the decision-making process. Int J Uncertain Quantif 7(5):423–439
Rani D, Garg H (2018) Complex intuitionistic fuzzy power aggregation operators and their applications in multicriteria decision-making. Expert Syst 35(6):e12325
Thirunavukarasu P, Suresh R, Ashokkumar V (2017) Theory of complex fuzzy soft set and its applications. Int J Innov Res Sci Technol 3(10):13–18
Ulucay V, Deli I, Sahin M (2019) Intuitionistic trapezoidal fuzzy multi-numbers and its application to multi-criteria decision-making problems. Complex Intell Syst 5:65–78
Verma R, Sharma B (2015) Intuitionistic fuzzy Einstein prioritized weighted average operators and their application to multiple attribute group decision making. Appl Math Inf Sci 9(6):3095–3107
Wang W, Liu X (2011) Intuitionistic fuzzy geometric aggregation operators based on Einstein operations. Int J Intell Syst 26:1049–1075
Wang W, Liu X (2012) Intuitionistic fuzzy information aggregation using Einstein operations. IEEE Trans Fuzzy Syst 20(5):923–938
Xu Z (2007) Intuitionistic fuzzy aggregation operators. IEEE Trans Fuzzy Syst 15(6):1179–1187
Xu Z, Yager RR (2006) Some geometric aggregation operators based on intuitionistic fuzzy sets. Int J Gen Syst 35(4):417–433
Yager RR (2008) Prioritized aggregation operators. Int J Approx Reason 48:263–274
Yager RR (2009) Prioritized OWA aggregation. Fuzzy Optim Decis Mak 8:245–262
Yazdanbakhsh O, Dick S (2018) A systematic review of complex fuzzy sets and logic. Fuzzy Sets Syst 338:1–22
Yu D (2011) Intuitionistic fuzzy prioritized operators and their application in multi-criteria group decision making. Technol Econ Dev Econ 19(1):1–21
Yu D (2012) Group decision making based on generalized intuitionistic fuzzy prioritized geometric operator. Int J Intell Syst 27:635–661
Yu W, Zhang Z, Zhong Q (2019) Consensus reaching for MAGDM with multi-granular hesitant fuzzy linguistic term sets: a minimum adjustment-based approach. Ann Oper Res 1–24. https://doi.org/10.1007/s10479-019-03432-7
Zadeh LA (1965) Fuzzy sets. Inf Control 8:338–353
Zhang Z, Yu W, Martinez L, Gao Y (2019) Managing multigranular unbalanced hesitant fuzzy linguistic information in multiattribute large-scale group decision making: A linguistic distribution-based approach. IEEE Trans Fuzzy Syst 28:2875–2889
Zhang Z, Gao Y, Li Z (2020a) Consensus reaching for social network group decision making by considering leadership and bounded confidence. Knowl Based Syst 204:106240
Zhang Z, Kou X, Yu W, Gao Y (2020b) Consistency improvement for fuzzy preference relations with self-confidence: an application in two-sided matching decision making. J Oper Res Soc. https://doi.org/10.1080/01605682.2020.1748529
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare no conflict of interest.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendix
Appendix
Proof of Proposition 1
For \((d_1,d_2, \ldots , d_{n-1})\rightarrow (1,1, \ldots , 1)\) we obtain that \(T_v^{(d)}=\prod \nolimits _{k=1}^{v-1} \big (S({\mathcal {G}}_k)\big )^{d_k}\rightarrow \prod \nolimits _{k=1}^{v-1} S({\mathcal {G}}_k)=T_v\), which gives that \(\xi _v^{(d)}\rightarrow \xi _v\). Hence,
\(\square \)
Proof of Proposition 2
For \((d_1,d_2, \ldots , d_{n-1})\rightarrow (0,0, \ldots , 0)\), we have \(T_v^{(d)}=\prod \nolimits _{k=1}^{v-1} \big (S({\mathcal {G}}_k)\big )^{d_k}=1\). It gives that \(\xi _v^{(d)}=\frac{T_v^{(d)}}{\sum \nolimits _{v=1}^n T_v^{(d)}}=\frac{1}{n}\). Hence, \(\lim _{(d_1,d_2, \ldots , d_{n-1})\rightarrow (0,0, \ldots , 0)} \text {CIFPA}_{d}\big ({\mathcal {G}}_1,{\mathcal {G}}_2, \ldots , {\mathcal {G}}_n\big )=\frac{1}{n} \big ({\mathcal {G}}_1 \oplus {\mathcal {G}}_2 \oplus \cdots \oplus {\mathcal {G}}_n\big ).\) \(\square \)
Proof of Proposition 3
Since, \(d_1 \rightarrow +\infty \). Now, for each \(v=2,3, \ldots , n\), we have \(T_v^{(d)}=\prod \nolimits _{k=1}^{v-1} \big (S({\mathcal {G}}_k)\big )^{d_k}=\big (S({\mathcal {G}}_1)\big )^{+\infty }\big (S({\mathcal {G}}_2)\big )^{d_2} \ldots \) \(\big (S({\mathcal {G}}_{v-1})\big )^{d_{v-1}}=0\) because \(0< S({\mathcal {G}}_1) < 1\). It gives that \(\sum \nolimits _{v=1}^n T_v^{(d)}=T_1^{(d)}=1\) which implies that \(\xi _1^{(d)}=\frac{T_1^{(d)}}{\sum \nolimits _{v=1}^n T_1^{(d)}}=1\) and \(\xi _v^{(d)}=\frac{T_v^{(d)}}{\sum \nolimits _{v=1}^n T_v^{(d)}}=0\) for each \(v=2,3, \ldots , n\). Hence, \( \lim _{d_1\rightarrow +\infty } \text {CIFPA}_{d}\big ({\mathcal {G}}_1,{\mathcal {G}}_2, \ldots , {\mathcal {G}}_n\big )={\mathcal {G}}_1\). \(\square \)
Proof of Proposition 4
Since \((d_1,d_2, \ldots , d_k, d_{k+1}) \rightarrow (0,0 \ldots , 0, +\infty )\) therefore,
Thus, \(\sum \nolimits _{v=1}^n T_v^{(d)}=k+1 \) and \(\xi _v^{(d)}=\frac{T_v^{(d)}}{\sum \nolimits _{v=1}^n T_v^{(d)}} \rightarrow \frac{1}{k+1}\) for each \(v=1,2, \ldots , k+1\) and \(\xi _v^{(d)}=\frac{T_v^{(d)}}{\sum \nolimits _{v=1}^n T_v^{(d)}} \rightarrow \frac{0}{k+1}=0\) \(\forall \) \(v=k+2,k+3, \ldots , n\). Hence, \(\lim _{(d_1,d_2, \ldots , d_k, d_{k+1}) \rightarrow (0,0 \ldots , 0, +\infty )} \text {CIFPA}_{d}\big ({\mathcal {G}}_1,{\mathcal {G}}_2, \ldots , {\mathcal {G}}_n\big )=\frac{1}{k+1}\big ({\mathcal {G}}_1 \oplus {\mathcal {G}}_2 \oplus \cdots \oplus {\mathcal {G}}_{k+1}\big ).\) \(\square \)
Proof of Proposition 5
Since \((d_1,d_2, \ldots , d_k, d_{k+1}) \rightarrow (1,1 \ldots , 1, +\infty )\) therefore,
Thus, \(\sum \nolimits _{v=1}^n T_v^{(d)}\rightarrow \sum \nolimits _{v=1}^{k+1} T_v \) and \(\xi _v^{(d)}=\frac{T_v^{(d)}}{\sum \nolimits _{v=1}^n T_v^{(d)}} \rightarrow \frac{T_v}{\sum \nolimits _{v=1}^{k+1} T_v}\) for each \(v=1,2, \ldots , k+1\) and \(\xi _v^{(d)}=\frac{T_v^{(d)}}{\sum \nolimits _{v=1}^n T_v^{(d)}} \rightarrow \frac{0}{\sum \nolimits _{v=1}^{k+1} T_v}=0\) for each \(v=k+2,k+3, \ldots , n\). Hence, \(\lim _{(d_1,d_2, \ldots , d_k, d_{k+1}) \rightarrow (0,0 \ldots , 0, +\infty )} \text {CIFPA}_{d}\big ({\mathcal {G}}_1,{\mathcal {G}}_2, \ldots , {\mathcal {G}}_n\big )=\text {CIFPA}\big ({\mathcal {G}}_1,{\mathcal {G}}_2, \ldots , {\mathcal {G}}_{k+1}\big ).\) \(\square \)
Proof of the Proposition 6
Since \(d_k < d^{\prime }_k\)
-
(a)
When \(v \le k\). For convenience, let \(S({\mathcal {G}}_v)=\rho _v \). Now,

Similarly, we can obtain that
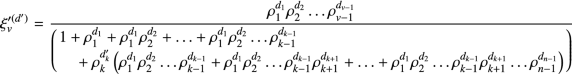
For simplicity, let \(\mathcal {A}=1+\rho ^{d_1}_1+\rho ^{d_1}_1\rho ^{d_2}_2 + \cdots +\rho ^{d_1}_1 \rho ^{d_2}_2 \ldots \rho ^{d_{k-1}}_{k-1}\) and \(\mathcal {B}=\rho ^{d_1}_1 \rho ^{d_2}_2 \ldots \rho ^{d_{k-1}}_{k-1}+\rho ^{d_1}_1 \rho ^{d_2}_2 \ldots \rho ^{d_{k-1}}_{k-1}\rho ^{d_{k+1}}_{k+1}+ \cdots + \rho ^{d_1}_1 \rho ^{d_2}_2 \ldots \rho ^{d_{k-1}}_{k-1}\rho ^{d_{k+1}}_{k+1} \ldots \rho ^{d_{n-1}}_{n-1}\). Then, we obtain that
$$\begin{aligned} \xi ^{(d)}_v = \frac{\rho ^{d_1}_1 \rho ^{d_2}_2 \ldots \rho ^{d_{v-1}}_{v-1}}{\mathcal {A}+\rho ^{d_{k}}_{k}\mathcal {B}} ~~~~ \text {and} ~~~~ \xi ^{(d^\prime )}_v = \frac{\rho ^{d_1}_1 \rho ^{d_2}_2 \ldots \rho ^{d_{v-1}}_{v-1}}{\mathcal {A}+\rho ^{d^\prime _{k}}_{k}\mathcal {B}} \end{aligned}$$Now, since \(d_k < d^{\prime }_k\). It implies that \(\rho ^{d_{k}}_{k} \ge \rho ^{d^\prime _{k}}_{k}\) which leads to \(\mathcal {A}+\rho ^{d_{k}}_{k}\mathcal {B}\ge \mathcal {A}+\rho ^{d^\prime _{k}}_{k}\mathcal {B}\). It gives that \(\frac{1}{\mathcal {A}+\rho ^{d_{k}}_{k}\mathcal {B}}\le \frac{1}{ \mathcal {A}+\rho ^{d^\prime _{k}}_{k}\mathcal {B}}\) which implies that, \(\frac{\rho ^{d_1}_1 \rho ^{d_2}_2 \ldots \rho ^{d_{v-1}}_{v-1}}{\mathcal {A}+\rho ^{d_{k}}_{k}\mathcal {B}} \le \frac{\rho ^{d_1}_1 \rho ^{d_2}_2 \ldots \rho ^{d_{v-1}}_{v-1}}{\mathcal {A}+\rho ^{d^\prime _{k}}_{k}\mathcal {B}}\). Hence, \(\xi ^{(d)}_v \le \xi ^{\prime (d^\prime )}_v\) for \(v \le k\).
-
(b)
When \(v > k\), we have
$$\begin{aligned} \xi ^{(d)}_v= & {} \frac{\rho ^{d_1}_1 \rho ^{d_2}_2 \ldots \rho ^{d_{k-1}}_{k-1}\rho ^{d_{k}}_{k}\rho ^{d_{k+1}}_{k+1} \ldots \rho ^{d_{v-1}}_{v-1}}{\mathcal {A}+\rho ^{d_{k}}_{k}\mathcal {B}} ~~~~ \text {and} \\ \xi ^{(d^\prime )}_v= & {} \frac{\rho ^{d_1}_1 \rho ^{d_2}_2 \ldots \rho ^{d_{k-1}}_{k-1}\rho ^{d^\prime _{k}}_{k}\rho ^{d_{k+1}}_{k+1} \ldots \rho ^{d_{v-1}}_{v-1}}{\mathcal {A}+\rho ^{d^\prime _{k}}_{k}\mathcal {B}} \end{aligned}$$Since \(d_k < d^{\prime }_k\). It implies that \(\rho ^{d_{k}}_{k} \ge \rho ^{d^\prime _{k}}_{k}\) which leads to \(\frac{\rho ^{d^\prime _{k}}_{k}}{\rho ^{d_{k}}_{k}}\le 1\). Now,
$$\begin{aligned} \xi ^{(d)}_v= & {} \frac{\rho ^{d_1}_1 \rho ^{d_2}_2 \ldots \rho ^{d_{k-1}}_{k-1}\rho ^{d_{k}}_{k}\rho ^{d_{k+1}}_{k+1} \ldots \rho ^{d_{v-1}}_{v-1}}{\mathcal {A}+\rho ^{d_{k}}_{k}\mathcal {B}} \\= & {} \frac{\left( \rho ^{d_1}_1 \rho ^{d_2}_2 \ldots \rho ^{d_{k-1}}_{k-1}\rho ^{d_{k}}_{k}\rho ^{d_{k+1}}_{k+1} \ldots \rho ^{d_{v-1}}_{v-1}\right) \left( \frac{\rho ^{d^\prime _{k}}_{k}}{\rho ^{d_{k}}_{k}}\right) }{\left( \mathcal {A}+\rho ^{d_{k}}_{k}\mathcal {B}\right) \left( \frac{\rho ^{d^\prime _{k}}_{k}}{\rho ^{d_{k}}_{k}}\right) } \\= & {} \frac{\rho ^{d_1}_1 \rho ^{d_2}_2 \ldots \rho ^{d_{k-1}}_{k-1}\rho ^{d^\prime _{k}}_{k}\rho ^{d_{k+1}}_{k+1} \ldots \rho ^{d_{v-1}}_{v-1}}{\mathcal {A}\left( \frac{\rho ^{d^\prime _{k}}_{k}}{\rho ^{d_{k}}_{k}}\right) +\rho ^{d^\prime _{k}}_{k}\mathcal {B} } \\ \end{aligned}$$Further, since \(\frac{\rho ^{d^\prime _{k}}_{k}}{\rho ^{d_{k}}_{k}}\le 1\). It gives that \(\mathcal {A} \left( \frac{\rho ^{d^\prime _{k}}_{k}}{\rho ^{d_{k}}_{k}}\right) \le \mathcal {A}\) which leads to \(\mathcal {A} \left( \frac{\rho ^{d^\prime _{k}}_{k}}{\rho ^{d_{k}}_{k}}\right) + \rho ^{d^\prime _{k}}_{k}\mathcal {B}\le \mathcal {A} +\rho ^{d^\prime _{k}}_{k}\mathcal {B}\). It implies that
$$\begin{aligned} \frac{1}{\mathcal {A} \left( \frac{\rho ^{d^\prime _{k}}_{k}}{\rho ^{d_{k}}_{k}}\right) + \rho ^{d^\prime _{k}}_{k}\mathcal {B}} \ge \frac{1}{\mathcal {A} +\rho ^{d^\prime _{k}}_{k}\mathcal {B}} \end{aligned}$$and therefore,
$$\begin{aligned}&\frac{\rho ^{d_1}_1 \rho ^{d_2}_2 \ldots \rho ^{d_{k-1}}_{k-1}\rho ^{d^\prime _{k}}_{k}\rho ^{d_{k+1}}_{k+1} \ldots \rho ^{d_{v-1}}_{v-1}}{\mathcal {A} \left( \frac{\rho ^{d^\prime _{k}}_{k}}{\rho ^{d_{k}}_{k}}\right) + \rho ^{d^\prime _{k}}_{k}\mathcal {B}} \\&\quad \ge \frac{\rho ^{d_1}_1 \rho ^{d_2}_2 \ldots \rho ^{d_{k-1}}_{k-1}\rho ^{d^\prime _{k}}_{k}\rho ^{d_{k+1}}_{k+1} \ldots \rho ^{d_{v-1}}_{v-1}}{\mathcal {A} +\rho ^{d^\prime _{k}}_{k}\mathcal {B}} \end{aligned}$$Hence, \(\xi ^{(d)}_v \ge \xi ^{\prime (d^\prime )}_v\) for \(v > k\).
\(\square \)
Proof of the Proposition 8
Since, \((d_1,d_2, \ldots , d_{n-1})\rightarrow (0,0, \ldots , 0)\). Therefore, for \(v=2,3, \ldots , n\), \(T_v^{(d)}=\prod \nolimits _{k=1}^{v-1} \rho _k^{d_k}=\rho _1^{d_1} \rho _2^{d_2} \ldots \rho _{v-1}^{d_{v-1}} \) \(\rightarrow \rho _1^0 \rho _2^0 \ldots \rho _{v-1}^0=1\) and \(T^{(d)}_1=1\). So, \(T^{(d)}= \sum \nolimits _{v=1}^n T^{(d)}_v \rightarrow n\). It gives that
Hence,
\(\square \)
Proof of the Proposition 9
Since, \(d_1\rightarrow +\infty \). Therefore, for each \(v=2,3, \ldots , n\) we have, \(T^{(d)}_v=\prod \nolimits _{k=1}^{v-1} \rho ^{d_k}_k=\rho ^{d_1}_1\rho ^{d_2}_2 \ldots \rho ^{d_{v-1}}_{v-1} \rightarrow \rho ^{\infty }_1 \rho ^{d_2}_2 \ldots \rho ^{d_{v-1}}_{v-1}=0\) and \(T^{(d)}_1=1\). It implies that \(T^{(d)}=\sum \nolimits _{v=1}^n T^{(d)}_v=1\). It leads to that
Let \({\mathcal {G}}_1={\mathcal {G}}_{\sigma (k)}\) for some \(k=1,2, \ldots , n\). Then, using the Eq. (18), we obtain that \(\xi ^{(d)}_1 , \xi ^{(d)}_2 , \ldots , \xi ^{(d)}_{k-1} \rightarrow 0\), \(\xi ^{(d)}_{k} \rightarrow 1\), \(\xi ^{(d)}_{k+1} , \xi ^{(d)}_{k+2}, \ldots , \xi ^{(d)}_{n} \rightarrow 0\). Hence,
\(\square \)
Proof of the Proposition 10
Since, \((d_1,d_2, \ldots , d_k, d_{k+1})\rightarrow (0,0, \ldots , 0, +\infty )\). Therefore, for each \(v=2,3, \ldots , k+1\), \(T^{(d)}_v=\prod \nolimits _{k=1}^{v-1} \rho ^{d_k}_k\) \(=\rho ^{d_1}_1\rho ^{d_2}_2 \ldots \rho ^{d_{v-1}}_{v-1} \rightarrow \rho ^{0}_1 \rho ^{0}_2 \ldots \rho ^{0}_{v-1}=1\) and when \(v=k+2, k+3, \ldots , n\), \(T^{(d)}_v=\prod \nolimits _{k=1}^{v-1} \rho ^{d_k}_k=\rho ^{d_1}_1\rho ^{d_2}_2 \ldots \rho ^{d_k}_k \rho ^{d_{k+1}}_{k+1} \ldots \rho ^{d_{v-1}}_{v-1} \rightarrow \rho ^{0}_1 \rho ^{0}_2 \ldots \rho ^{0}_{k} \rho ^{+\infty }_{k+1}\rho ^{d_{k+2}}_{k+2} \ldots \rho ^{d_{v-1}}_{v-1}=0\). It gives that \(T^{(d)}=\sum \limits _{v=1}^n T_v^{(d)} \rightarrow k+1\).
Since, \(\big (\tau (1),\tau (2), \ldots , \tau (k+1)\big )\) is an arrangement of \((1,2, \ldots , k+1)\) such that \(S({\mathcal {G}}_{\tau (v-1)}) \ge S({\mathcal {G}}_{\tau (v)})\) for each \(v=2,3, \ldots , k+1\). Also, we have assumed that \(\big (\sigma (1), \sigma (2), \ldots , \sigma (n) \big )\) is an arrangement of \((1,2, \ldots , n)\) such that \(S({\mathcal {G}}_{\sigma (v-1)}) \ge S({\mathcal {G}}_{\sigma (v)})\) for each \(v=2,3, \ldots , n\). As, \(\big \{{\mathcal {G}}_1,{\mathcal {G}}_2, \ldots , {\mathcal {G}}_{k+1}\big \} \subseteq \big \{{\mathcal {G}}_1,{\mathcal {G}}_2, \ldots , {\mathcal {G}}_n\big \}\) therefore, there must exist natural numbers \(1 \le m_1, m_2, \ldots , m_{k+1} \le n\) satisfying \({\mathcal {G}}_{\tau (1)}={\mathcal {G}}_{\sigma (m_1)}\), \({\mathcal {G}}_{\tau (2)}={\mathcal {G}}_{\sigma (m_2)}\), \(\ldots \), \({\mathcal {G}}_{\tau (k+1)}={\mathcal {G}}_{\sigma (m_{k+1})}\). Using the Eq. (18), we have
and all other weights tend to 0. Hence,
\(\square \)
Proof of the Proposition 11
Since, \((d_1,d_2, \ldots , d_k, d_{k+1})\rightarrow (1,1, \ldots , 1, +\infty )\). Let \(\rho _1 \rho _2 \ldots \rho _{v-1}={\mathbb {T}}_v\) for \(v=2,3, \ldots , k+1\); \({\mathbb {T}}_1=1\) and \({\mathbb {T}}=\sum \nolimits _{v=1}^{k+1} {\mathbb {T}}_v\). Therefore, for each \(v=2,3, \ldots , k+1\), \(T^{(d)}_v=\prod \nolimits _{k=1}^{v-1} \rho ^{d_k}_k=\rho ^{d_1}_1\rho ^{d_2}_2 \ldots \rho ^{d_{v-1}}_{v-1} \rightarrow \rho ^{1}_1 \rho ^{1}_2 \ldots \rho ^{1}_{v-1}={\mathbb {T}}_v\). Further, for \(v=k+2, k+3, \ldots , n\), \(T^{(d)}_v=\prod \nolimits _{k=1}^{v-1} \rho ^{d_k}_k=\rho ^{d_1}_1\rho ^{d_2}_2 \ldots \rho ^{d_k}_k \rho ^{d_{k+1}}_{k+1} \ldots \rho ^{d_{v-1}}_{v-1} \rightarrow \rho ^{1}_1 \rho ^{1}_2 \ldots \rho ^{1}_{k} \rho ^{+\infty }_{k+1}\rho ^{d_{k+2}}_{k+2} \ldots \rho ^{d_{v-1}}_{v-1}=0\). It implies that \(T^{(d)}=\sum \nolimits _{v=1}^n T^{(d)}_v=T^{(d)}_1+T^{(d)}_2+ \cdots + T^{(d)}_{k+1}={\mathbb {T}}_1+{\mathbb {T}}_2+{\mathbb {T}}_3+ \cdots +{\mathbb {T}}_{k+1}=\sum \nolimits _{v=1}^{k+1} {\mathbb {T}}_v={\mathbb {T}}\).
Now, assume that \(\big (\tau (1),\tau (2), \ldots , \tau (k+1)\big )\) is an arrangement of \((1,2, \ldots , k+1)\) such that \(S({\mathcal {G}}_{\tau (v-1)}) \ge S({\mathcal {G}}_{\tau (v)})\) for each \(v=2,3, \ldots , k+1\). Further, let \(\mathbb {H}_0=\phi \) and \(\mathbb {H}_v=\big \{{\mathcal {G}}_{\tau (z)}|z=1,2, \ldots , v\big \}\) for \(v=1,2, \ldots , k+1\). Also, we have assumed that \(\big (\sigma (1), \sigma (2), \ldots , \sigma (n) \big )\) is an arrangement of \((1,2, \ldots , n)\) such that \(S({\mathcal {G}}_{\sigma (v-1)}) \ge S({\mathcal {G}}_{\sigma (v)})\) for each \(v=2,3, \ldots , n\). As, \(\big \{{\mathcal {G}}_1,{\mathcal {G}}_2, \ldots , {\mathcal {G}}_{k+1}\big \} \subseteq \big \{{\mathcal {G}}_1,{\mathcal {G}}_2, \ldots , {\mathcal {G}}_n\big \}\) therefore, there must exist natural numbers \(1 \le m_1, m_2, \ldots , m_{k+1} \le n\) satisfying \({\mathcal {G}}_{\tau (1)}={\mathcal {G}}_{\sigma (m_1)}\), \({\mathcal {G}}_{\tau (2)}={\mathcal {G}}_{\sigma (m_2)}\), \(\ldots \), \({\mathcal {G}}_{\tau (k+1)}={\mathcal {G}}_{\sigma (m_{k+1})}\). Further, we have
Now, using the Eq. (18), we have
and all other weights tend to 0. Finally, using the Definition 13, we obtain that
Hence, \(\lim _{(d_1,d_2, \ldots , d_k, d_{k+1})\rightarrow (1,1, \ldots , 1, +\infty )} \text {CIFPOWA}_{d}\big ({\mathcal {G}}_1,{\mathcal {G}}_2, \ldots , {\mathcal {G}}_n\big ) =\text {CIFPOWA}\big ({\mathcal {G}}_1,{\mathcal {G}}_2, \ldots , {\mathcal {G}}_{k+1}\big )\). \(\square \)
Rights and permissions
About this article
Cite this article
Garg, H., Rani, D. New prioritized aggregation operators with priority degrees among priority orders for complex intuitionistic fuzzy information. J Ambient Intell Human Comput 14, 1373–1399 (2023). https://doi.org/10.1007/s12652-021-03164-2
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s12652-021-03164-2