A budget feasible peer graded mechanism for iot-based crowdsourcing

Abstract

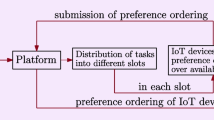
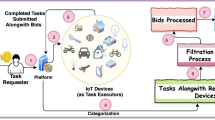
We develop and extend a line of recent works on the design of mechanisms for heterogeneous tasks assignment problem in ’crowdsourcing’. The budgeted market we consider consists of multiple task requesters and multiple IoT devices as task executers. In this, each task requester is endowed with a single distinct task along with the publicly known budget. Also, each IoT device has valuations as the cost for executing the tasks and quality, which are private. Given such scenario, the objective is to select a subset of IoT devices for each task, such that the total payment made is within the allotted quota of the budget while attaining a threshold quality. For the purpose of determining the unknown quality of the IoT devices we have utilized the concept of peer grading. In this paper, we have carefully crafted a truthful budget feasible mechanism for the problem under investigation that also allows us to have the true information about the quality of the IoT devices. Further, we have extended the set-up considering the case where the tasks are divisible in nature and the IoT devices are working collaboratively, instead of, a single entity for executing each task. We have designed the budget feasible mechanisms for the extended versions. The simulations are performed in order to measure the efficacy of our proposed mechanism.

Appendices

Appendix

A omitted proofs from Sect. 5

1.1 A1. Proof of Lemma 2

Fix a task requester $\mathbb {R}_j$ and a task $\mathbb {T}_j$. From the construction of TUBE-TAP, it is clear that, the maximum payment that any winning IoT device will be paid is $\frac{\mathbb {B}_j}{k}$; where k is the largest index obtained in the ordering of IoT devices that satisfies $b_{k}^{j} \le \frac{\mathbb {B}_j}{k}$. Now, the total payment $\mathbb {\varvec{P}}_j$ is given as:

$$\begin{aligned} \mathbb {\varvec{P}}_j = \sum \limits _{\mathbb {E}_i \in \mathbb {A}_j} \mathbb {\varvec{P}}_i^j \le \sum _{\mathbb {E}_i \in \mathbb {A}_j} \frac{\mathbb {B}_j}{k} = \frac{\mathbb {B}_j}{k} \times k = \mathbb {B}_j \end{aligned}$$

From here we can say that, $\mathbb {\varvec{P}}_j \le \mathbb {B}_j$. As this is true for any task $\mathbb {T}_j$, so the budget feasibility will hold for all the available tasks i.e. $\sum \limits _{\mathbb {A}_j \in \mathbb {A}} \sum \limits _{\mathbb {E}_i \in \mathbb {A}_j} \mathbb {\varvec{P}}_i^j \le \sum \limits _{\mathbb {T}_j \in \mathbb {T}}\mathbb {B}_j$. This completes the proof.

1.2 A2. Proof of Lemma 4

By the definition of indicator random variable, we can write $X_j^i$ is 1 when $\mathbb {U}$ occurs and 0 when $\mathbb {U}$ does not occurs. So, as $X_j^i$ = I{$\mathbb {U}$}. Taking expectation both side, we get from definition of expectation

$$\begin{aligned} E[X_j^i] = E[I\{\mathbb {U}\}] = Pr\{\mathbb {U}\} \end{aligned}$$

The detailing of this lemma is provided in draft version Singh et al. (2018a).

1.3 A3. Proof of Lemma 6

Fix an IoT device $\mathbb {E}_i$. In similar line the proof is illustrated in Cormen et al. (2009). Our proof is divided into two cases. From Lemma 5 it can be seen that the probability that $\mathbb {E}_i$ will be considered for any task $\mathbb {T}_j$ is p. Let $X^{i}_{kl} = I\{A_{kl}^{i}\}$ be the indicator random variable associated with an event that the IoT device $\mathbb {E}_i$ is rejected for at least l tasks starting form $k^{th}$ task. It is to be noted that, the participation in one time slot by the IoT device is independent of the participation in other time slots. So, for any given event $X^{i}_{kl}$, the probability that for all l tasks the IoT device is rejected is given as

$$\begin{aligned} Pr\{A_{kl}^{i}\} = p\cdot p~\cdot \cdot \cdot l~times = p^l \end{aligned}$$

(9)

As in our case, k varies from 1 to $k_i - l +1$ (i.e. $1 \le k \le k_i - l +1$), so the total number of such rejections could be formulated as:

$$\begin{aligned} Y = \sum \limits _{k=1}^{k_i-l+1} X^{i}_{kl} \end{aligned}$$

Taking expectation both side, we get

$$\begin{aligned} E[Y] = E\bigg [\sum \limits _{k=1}^{k_i-l+1} X^{i}_{kl}\bigg ] \end{aligned}$$

By linearity of expectation, we get

$$\begin{aligned} = \sum \limits _{k=1}^{k_i-l+1} E[X^{i}_{kl}] \end{aligned}$$

From the definition of expectation in Lemma 4, we have

$$\begin{aligned} E[Y]= \sum \limits _{k=1}^{k_i-l+1} Pr\{A_{kl}^{i}\} \end{aligned}$$

Using equation 9, we get

$$\begin{aligned} = \sum \limits _{k=1}^{k_i-l+1} p^l \end{aligned}$$

$$\begin{aligned} E[Y] = (k_i-l+1) \cdot p^l \end{aligned}$$

Now, for $l = c \log _p k_i$ and for some positive constant c, we obtain

$$\begin{aligned} E[Y] & = (k_i-c \log _p k_i+1)\cdot p^{c \log _p k_i} \\ & = (k_i-c \log _p k_i+1) \cdot k_i^c\\ & = k_i^{c+1} - ck_i^c \log _p k_i + k_i^c\\ & = \Theta (k_i^c) \end{aligned}$$

From here we can conclude that, for some constant $c \ge 1$ the longest continuous rejection boils down to $\Theta (\log _p k_i)$. Hence, the claim survived.

1.4 A4. Proof of Lemma 7

Fix an IoT device $\mathbb {E}_i$. As $\mathbb {E}_i$ has shown interest on $k_i$ tasks that are present in different time slots. The probability that $\mathbb {E}_i$ will be considered for task $\mathbb {T}_j$ is p (Pr{$\mathbb {E}_i$ is not considered for task $\mathbb {T}_j$} = $1-p$). Also, it can be seen that, the consideration of $\mathbb {E}_i$ in any time slot is independent of other time slots. So, the probability that $\mathbb {E}_i$ will not be considered at all for any of the $k_i$ tasks is given as:

$$\begin{aligned} Pr[X^i < 1] & = (1-p) \cdot (1-p) \ldots k_i~times \\ & = (1-p)^{k_i} \end{aligned}$$

Following the inequality $1+x \le e^x$, we get

$$\begin{aligned} Pr[X^i < 1] \le e^{-p\cdot k_i} = \frac{1}{e^{p\cdot k_i}} \end{aligned}$$

Now, the probability that any $\mathbb {E}_i$ will be considered at least once is given as

$$\begin{aligned} Pr[X^i \ge 1] \ge \bigg (1-\frac{1}{e^{p\cdot k_i}}\bigg ) \end{aligned}$$

Hence, the claim survives. Also, for $p=\ln 2$, we can see that

$$\begin{aligned}&Pr[X^i \ge 1] \ge \bigg (1-\frac{1}{e^{\ln 2\cdot k_i}}\bigg ) \\&\quad = \bigg (1-\frac{1}{2k_i}\bigg ) \end{aligned}$$

It can be concluded that, the term $\frac{1}{2k_i}$ represents that any arbitrary $\mathbb {E}_i$ will not be considered at all is very small, and can say that it is very unlikely to occur. So, the term $(1-\frac{1}{2k_i})$ will be quite large and hence can say that any IoT device could be considered for at least once with larger probability.

B. Omitted proofs from Sect. 6.6

1.1 B1. Proof of Lemma 9

At any $i^{th}$ iteration of the Algorithm 5, say a sub-task $\mathbb {T}_j^i$ of task $\mathbb {T}_j$ is having the highest estimated time among the other sub-tasks. From the construction of NoTUBE, the sub-task $\mathbb {T}_j^i$ is a potential candidate for getting the IoT device(s). It is quite clear from Algorithm 5 that, with each assignment of IoT device to the sub-task $\mathbb {T}_j^i$, an estimated time of the sub-task under consideration goes down monotonically. Once the substantial number of IoT devices is allocated to sub-task $\mathbb {T}_i^j$, a new sub-task comes up as a potential candidate for getting the IoT devices, we call this as switch. So, in this lemma we are trying to answer the query: what is the substantial number of IoT devices in expectation that is to be assigned to any sub-task with highest estimated time before the switch happens?

Let us suppose the assignment of substantial number of IoT devices to a sub-task as a Bernoulli trials. So, we have a sequence of Bernoulli trials, each with probability of assigning IoT device to the sub-task $\mathbb {T}_j^i$ be p and the probability of not assigning the IoT device to the sub-task $\mathbb {T}_j^i$ is $q = 1-p$. It can be observed that, the switch can occur after $1^{st}$ assignment, or $2^{nd}$ assignment, or $3^{rd}$ assignment and so on. Making this argument more explicit, we let $X_i$ be the random variable associated with an event in which the switch occurs after ith assignment: $X_i$ = I{switch occurs after ith assignment}. Let X be the random variable denoting the total number of assignment before the switch happens. So, X has values in the range $\{1,2,3,\ldots \}$ and for $x \ge 1$,

$$\begin{aligned} Pr\{X = x\} = \underbrace{(1-p) \cdot (1-p) \cdot \ldots \cdot (1-p)}_{\begin{array}{c} \text {{ x}-1 times} \end{array}} \cdot ~ p \end{aligned}$$

(10)

since we have $x-1$ number of IoT device(s) assigned to any sub-task before the switch occurs. It can be seen that, the probability distribution in Eq. 10 is said to be geometric distribution. Now, the expected value of random variable in which we are interested in is given as:

$$\begin{aligned} E[X] & = \sum \limits _{x=1}^{\infty } x \cdot (1-p)^{x-1} \cdot p\\ & = \frac{p}{p-1} \cdot \sum \limits _{x=0}^{\infty } x \cdot (1-p)^{x} \\ & = \frac{p}{p-1} \cdot \frac{1-p}{p^2}\\ & = \frac{p}{p-1} \cdot \frac{1-p}{p} \cdot \frac{1}{p}\\ E[X] & = \frac{1}{p} \end{aligned}$$

Now, if we have value of p as $\frac{1}{2}$ then we get $E[X] = 2$, which is a small constant. Similarly, for $p=\frac{1}{3}$ we have $E[X]=3$. Hence the claim survives.

1.2 B2. Proof of Theorem 1

Fix a task $\mathbb {T}_j$. For any arbitrary sub-task, it may happen that the subset of the IoT devices that are the member of the grand coalition can form the sub-coalition (coalition other than the grand coalition) and could achieve the estimated completion time of the sub-task. The result of which, two things could be observed: (1) the IoT devices in the sub-coalition will have to utilize more of their battery power as they will be getting larger part of the sub-task this time as compared to the part they were getting in the grand coalition but within their battery power drainage time; (2) the IoT devices in the sub-coalition is guaranteed to be paid more than they were in the grand coalition.

The benefit raised in point (2) from IoT device point of view will motivate the IoT devices to form the sub-coalition and gain. Hence, the IoT devices are gaining by manipulating the system. So, NoTUBE is not truthful.