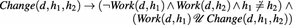Abstract
In order to evaluate the effectiveness of the security measures undertaken to protect a distributed system (e.g., protecting privacy of data in a network or in an information system) one should, among other things, perform a risk assessment. In this paper, we introduce a logical framework that allows one to reason about risk by means of operators that formalize causes, effects, preconditions, prevention and mitigation of events that may occur in the system. We give tableau rules and discuss a number of interesting variants that could be considered, prove soundness and completeness for some of the resulting tableau systems, and give an algorithm for satisfiability.











Similar content being viewed by others
Notes
We have here a kind of positive modal logic, in which \(\square \) and \(\diamondsuit \) are not duals (since we have no negation in front of formulas of the second layer). This is not a problem as positive modal logics have been well studied (see, e.g., (Dunn 1995; Viganò 2000), where different accessibility relations are considered for \(\square \) and \(\diamondsuit \)), but of course a full modal logic (in which \(\diamondsuit A = \lnot \square A\)) could be considered as well.
This operator is often called prevention in the literature, but here we use the name block to avoid confusion with the symbol for precondition.
Hence, for \(\vartheta =w_1 w_2 \cdots \), we have \(\fancyscript{I}(\vartheta ) = \fancyscript{I}(\vartheta , w_1) \fancyscript{I}(\vartheta , w_2) \cdots = w_1 w_2 \cdots \). Strictly speaking, we should use different symbols for labels in the syntax and traces/worlds in the semantics, but for simplicity we abuse notation and use the same symbols, and use labels and worlds/traces as synonyms.
Note that the rule \((\lhd = \cong )\) is an extension of the second layer rule \((\lhd =)\). With rule \((\lhd =)\) we can find two equal worlds when we deal with just one trace, instead rule \((\lhd = \cong )\) allows us to do the same but when we deal with different traces.
We could, if needed, introduce also another set to consider specific hospital wards.
In this case study, we assume that \( Work \) is monotonic, but we could also formalize the case when members of the staff change the hospital at which they work:
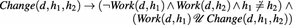
The members of the staff can use and propagate the patient’s data for purposes other than curing the patient. The goal is to permit the members of the staff to access at the patient’s data, but only when those data are really needed.
We haven’t given the procedure and the algorithm for the systematic tableau construction of the formulas of the third layer, thus we build the tableau interactively step by step.
The usual procedure in standard tableau systems is to show that the tableau for \(\lnot X\) is closed, so that \(\lnot X\) is unsatisfiable and thus \(X\) is satisfiable. We cannot apply this procedure as the formulas in the second layer of our system do not admit an outermost negation.
In the first and second layer we do not deal with different traces. Thus, if two labels are in relation with each other, then they represent worlds that are on the same trace.
References
AVANTSSAR (2008) Deliverable 5.1: problem cases and their trust and security requirements. http://www.avantssar.eu
Aven T (2004) Risk analysis and science. Int J Reliab Qual Safety Eng 11(1):1–15
Bartsch S (2010) A calculus for the qualitative risk assessment of policy override authorization. In: Makarevich OB, Elçi A, Orgun MA, Huss S A, Babenko LK, Chefranov AG, Varadharajan V (eds) Proceedings of the 3rd international conference on security of information and networks, SIN 2010, ACM, pp 62–70
Basin D, D’Agostino M, Gabbay DM, Matthews S, Viganò L (eds) (2000) Labelled deduction. Kluwer, Dordrecht
Basin DA, Caleiro C, Ramos J, Viganò L (2009) Labelled tableaux for distributed temporal logic. J Logic Comput 19(6):1245–1279
Bell J (2003) A common sense theory of causation. In: Blackburn P, Ghidini C, Turner RM, Giunchiglia F (eds) Modeling and using context, LNCS, vol 2680. Springer, pp 40–53
Chapin PC, Skalka C, Wang XS (2005) Risk assessment in distributed authorization. In: Atluri V, Samarati P, Küsters R, Mitchell JC (eds) Proceedings of the 2005 ACM workshop on formal methods in security engineering, FMSE 2005, ACM, pp 33–42
Cristani M, Karafili E, Viganò L (2012) Towards a logical framework for reasoning about risk. In: Quirchmayr G, Basl J, You I, Xu L, Weippl E (eds) CD-ARES 2012, Proceedings of the 2nd IFIP international workshop on security and cognitive informatics for Homeland Defense (SeCIHD’12), in conjunction with ARES 2012, LNCS, vol 7465. Springer, pp 609–623
de Ru WG, Eloff JHP (1996) Risk analysis modelling with the use of fuzzy logic. Comput Secur 15(3):239–248
D’Agostino M, Gabbay DM, Hähnle R, Posegga J (eds) (1999) Handbook of tableau methods. Kluwer, Dordrecht
Dunn JM (1995) Positive modal logic. Studia Logica 55:301–317
Gabbay DM (1996) Labelled deductive systems. Clarendon Press, Oxford
Giunchiglia E, Lee J, Lifschitz V, McCain N, Turner H (2004) Nonmonotonic causal theories. Artif Intell 153(1–2):49–104
Goré R (1999) Tableau methods for modal and temporal logics. In: D’Agostino M, Gabbay DM, Hähnle R, Posegga J (eds) The handbook of tableau methods. Kluwer, Dordrecht
Huang C, Moraga C (2002) A fuzzy risk model and its matrix algorithm. Int J Uncertaint Fuzziness Knowl Based Syst 10(4):347–362
Lewis D (1973) Causation. J Philos 70(17):556–567
Lewis D (2000) Causation as influence. J Philos 97(4):182–197
Li N, Mitchell JC (2003) A role-based trust-management framework. In: 3rd DARPA information survivability conference and exposition (DISCEX-III 2003). IEEE Computer Society, pp 201–212
Masini A, Viganò L, Volpe M (2010) A history of until. Electron Notes Theor Comput Sci 262:189–204
Schneidewind N (2009) Software risk analysis. Int J Reliab Quality Safety Eng 16(2):117–136
Shafer G, Gillett PR, Scherl RB (2000) The logic of events. Ann Math Artif Intell 28(1–4):315–389
Singh A, Lilja DJ (2009) Improving risk assessment methodology: a statistical design of experiments approach. In: Elçi A, Makarevich OB, Orgun MA, Chefranov AG, Pieprzyk J, Bryukhomitsky YA, Örs SB (eds) Proceedings of the 2nd international conference on security of information and networks, SIN 2009, ACM, pp 21–29
Tan L, Xu S (2009) A model-checking-based approach to risk analysis in supply chain consolidations. Integr Comput Aided Eng 16(3):243–257
Terenziani P, Torasso P (1995) Time, action-types, causation: an integrated analysis. Comput Intell 11:529–552
Turner H (1999) A logic of universal causation. Artif Intell 113(1–2):87–123
Viganò L (2000) Labelled non-classical logics. Kluwer, Dordrecht
Author information
Authors and Affiliations
Corresponding author
Appendices
Appendix 1: Soundness of the system \({\fancyscript{S}}\)
To prove the soundness of the system \({\fancyscript{S}}\), we proceed in two steps: in the first step, we prove the soundness of the rules that are used in this systematic tableau construction, and in the second step, we prove the soundness of the procedure of the systematic tableau construction.
For the first step, we define that a rule (of whatever layer) is sound if every model that satisfies its premises also satisfies at least one of its conclusions when there is a forking (i.e., a meta-disjunction of formulas), or all of its conclusions when the denominator contains formulas separated by a comma (i.e., a meta-conjunction of formulas). A closing rule, that is a rule whose conclusion is CLOSED, is sound if no model satisfies its premises.
We write \(\vdash \alpha \) when a tableau ends in an exhausted state for \(\alpha \) a labeled formula of the second layer (which includes the first) or a relational formula of the form \((\vartheta , w_i) \bullet (\vartheta , w_j)\) with \(\bullet \) a relation of the second layer. For the second step, we aim at proving that if the tableau for \(X\), where \(X\) is a set of labeled and relational formulas of the second layer, is an open exhausted tableau (denoted by \(\vdash X\)), then \(X\) is satisfiable, i.e., there exists an arbitrary model \({\mathfrak M} \) such that \(\models ^{\mathfrak M} X\).Footnote 9
1.1 Soundness of the rules of the first two layers
Proof
(Theorem 3) Let \({\mathfrak M} \) be an arbitrary model with its interpretation function \(\fancyscript{I}\). The rules for the logical connectives are straightforwardly sound. If \(\vdash (\vartheta , w):\phi _1\rightarrow \phi _2\), then \(\models ^{\mathfrak M} (\vartheta , w):\phi _1\rightarrow \phi _2\), and then, by definition (of the satisfiability relation) of \(\rightarrow \), we have that \(\models ^{\mathfrak M} (\vartheta , w):\phi _1\) implies \(\models ^{\mathfrak M} (\vartheta , w):\phi _2\). This means that \(\not\models^{\mathfrak{M}} (\vartheta, w):\phi_1\) (and thus, by the satisfiability relation, \(\models ^{\mathfrak M} (\vartheta , w):\lnot \phi _1\)), or \(\models ^{\mathfrak M} (\vartheta , w):\phi _2\), which is exactly what the rule says.
If \(\vdash (\vartheta , w):\lnot \lnot \phi \), then \(\models ^{\mathfrak M} (\vartheta , w):\lnot \lnot \phi \), and then, by definition of \(\lnot \), we have that \(\not\models ^{\mathfrak M} (\vartheta , w):\lnot \phi \), which means that \(\not\models ^{\mathfrak M} (\vartheta , w):\phi \) does not hold, i.e., that \(\not\models ^{\mathfrak M} (\vartheta , w):\phi \).
If \(\vdash (\vartheta , w):\lnot (\phi _1\rightarrow \phi _2)\), then \(\models ^{\mathfrak M} (\vartheta , w):\lnot (\phi _1\rightarrow \phi _2)\), and then, by definition of \(\lnot \), we have that \(\not\models ^{\mathfrak M} (\vartheta , w):\phi _1\rightarrow \phi _2\). By definition of \(\rightarrow \), we have that \(\not\models ^{\mathfrak M} (\vartheta , w):\phi _1\) does not hold and \(\not\models ^{\mathfrak M} (\vartheta , w):\phi _2\) holds, that implies \(\models ^{\mathfrak M} (\vartheta , w):\phi _1\) and \(\models ^{\mathfrak M} (\vartheta , w):\lnot \phi _2\).
We now analyze the closing rule \((\textsc {Abs})\). Assume we are in the world \((\vartheta , w)\). If we have \(\vdash (\vartheta , w):\phi \) and \(\vdash (\vartheta , w):\lnot \phi \), then we have \(\models ^{\mathfrak M} (\vartheta , w):\phi \) and \(\models ^{\mathfrak M} (\vartheta , w):\lnot \phi \), which is not possible. Thus, the rule is sound.
We now consider the rules for the relations of the second layer.
Assume we have that \(\fancyscript{E}(\vartheta , w_i)\) and \(\fancyscript{E}(\vartheta , w_j)\). By definition of the relations \(<\) and \(=\), if two worlds \((\vartheta , w_i)\) and \((\vartheta , w_j)\) are in the model, we can have that \(\vdash (\vartheta , w_i)<(\vartheta , w_j)\), that is \(\models ^{\mathfrak M} (\vartheta , w_i) <(\vartheta , w_j)\), or we can have that \(\vdash (\vartheta ,w_i)=(\vartheta , w_j)\), that is \(\models ^{\mathfrak M} (\vartheta , w_i) = (\vartheta ,w_j)\), or we can have that \(\vdash (\vartheta , w_j) <(\vartheta , w_i)\), that is \(\models ^{\mathfrak M} (\vartheta , w_j) <(\vartheta , w_i)\). Thus, the \((=\textsc {Lin})\) rule is sound.
If we have \(\vdash (\vartheta , w_i) <(\vartheta , w_j)\), then we have that \(\models ^{\mathfrak M} (\vartheta , w_i) <(\vartheta , w_j)\). By definition of \(<\), if we have \(\models ^{\mathfrak M} (\vartheta , w_i) <(\vartheta , w_j)\), it means that \((\vartheta , w_i)\) comes before \((\vartheta , w_j)\). This can happen in two different cases. The first case is when \((\vartheta , w_i)\) is the immediate predecessor of \((\vartheta , w_j)\), that is \(\models ^{\mathfrak M} (\vartheta , w_i) \lhd (\vartheta , w_j)\). The second case is when \((\vartheta , w_i)\) comes before \((\vartheta , w_j)\) but it is not its immediate predecessor, that is \(\models ^{\mathfrak M} (\vartheta , w_i) \prec (\vartheta , w_j)\). Thus, the rule \((<)\) is sound.
Assume we have \(\vdash (\vartheta , w_i) \prec (\vartheta , w_j)\). Then we have that \(\models ^{\mathfrak M} (\vartheta , w_i) \prec (\vartheta , w_j)\). By definition of the \(\prec \) relation, there exists a new world \((\vartheta , w_k)\) such that \(\models ^{\mathfrak M} (\vartheta , w_i) \lhd (\vartheta , w_k)\) and \(\models ^{\mathfrak M} (\vartheta , w_k) <(\vartheta , w_j)\). Thus, the rule \((\prec )\) is sound.
Assume we have \(\vdash (\vartheta , w_i) <(\vartheta , w_j)\) and \(\vdash (\vartheta , w_j) <(\vartheta , w_k)\). Then we have \(\models ^{\mathfrak M} (\vartheta , w_i) <(\vartheta , w_j)\) and \(\models ^{\mathfrak M} (\vartheta , w_j) <(\vartheta , w_k)\), and then, by definition of \(<\), we have that \(\models ^{\mathfrak M} (\vartheta , w_i) <(\vartheta , w_k)\). Thus, the \((<\textsc {Trans})\) rule is sound. We argue analogously for \((\prec \textsc {Trans})\) and \((=\textsc {Trans})\).
Assume we have a world \((\vartheta , w)\) in the model. By the definition of \(=\), we have that \(\models ^{\mathfrak M} (\vartheta , w) = (\vartheta , w)\). Thus, the \((=\textsc {Refl})\) rule is sound.
Assume we have \(\vdash (\vartheta , w_i) = (\vartheta , w_j)\). Then we have \(\models ^{\mathfrak M} (\vartheta , w_i) = (\vartheta , w_j)\). By the definition of \(=\), we have that \(\models ^{\mathfrak M} (\vartheta , w_j) = (\vartheta , w_i)\). Thus, the \((=\textsc {Sym})\) rule is sound.
Assume we have \(\vdash (\vartheta , w_i) = (\vartheta , w_j)\) and \(\vdash (\vartheta , w_i) \bullet (\vartheta , w_k)\), where \(\bullet \in \{<, \lhd , \prec \}\). Then we have \(\models ^{\mathfrak M} (\vartheta , w_i) = (\vartheta , w_j)\) and \(\models ^{\mathfrak M} (\vartheta , w_i) \bullet (\vartheta , w_k)\). By the definition of \(=\), we have that \(\models ^{\mathfrak M} (\vartheta , w_j) \bullet (\vartheta , w_k)\). Thus, the \((\textsc {Subst}_2)\) rule is sound.
Assume we have \(\vdash (\vartheta , w_i)\lhd (\vartheta , w_j)\). Then we have that \(\models ^{\mathfrak M} (\vartheta , w_i)\lhd (\vartheta , w_j)\). By the definition of \(\lhd \), if we have \(\models ^{\mathfrak M} (\vartheta , w_i)\lhd (\vartheta , w_j)\), then \((\vartheta , w_i)\) is the immediate predecessor of \((\vartheta , w_j)\), which means that \((\vartheta , w_i)\) precedes the world \((\vartheta , w_j)\). Thus, we have that \(\models ^{\mathfrak M} (\vartheta , w_i)<(\vartheta , w_j)\). Therefore the rule \((\lhd <)\) is sound.
Assume we have \(\vdash (\vartheta , w_i)\prec (\vartheta , w_j)\). Then we have that \(\models ^{\mathfrak M} (\vartheta , w_i)\prec (\vartheta , w_j)\). By the definition of \(\prec \), if we have \(\models ^{{\mathfrak{M }}} (\vartheta , w_i) \prec (\vartheta , w_j)\), then there exists at least one world \((\vartheta , w_k)\) such that \(\models ^{\mathfrak M} (\vartheta , w_i)\lhd (\vartheta , w_k)\) and \(\models ^{\mathfrak M} (\vartheta , w_k)<(\vartheta , w_j)\). Then \(\models ^{\mathfrak M} (\vartheta , w_i)<(\vartheta , w_k)\) by the rule \((\lhd <)\), and using the \((<\textsc {Trans})\) rule, we have that \(\models ^{\mathfrak M} (\vartheta , w_i)<(\vartheta , w_j)\). Thus, the rule \((\prec <)\) is sound.
Assume we have \(\vdash (\vartheta , w_i)\lhd (\vartheta , w_j)\) and \(\vdash (\vartheta , w_k)\lhd (\vartheta , w_l)\) and \(\vdash (\vartheta , w_i)= (\vartheta , w_k)\). Then we have that \(\models ^{{\mathfrak{M }}} (\vartheta , w_i)\lhd (\vartheta , w_j)\) and \(\models ^{{\mathfrak{M }}} (\vartheta , w_k)\lhd (\vartheta , w_l)\) and \(\models ^{{\mathfrak{M }}} (\vartheta , w_i)= (\vartheta , w_k)\). If we apply the \((\textsc {Subst}_2)\) rule, which we have already proved sound, then we have \(\models ^{{\mathfrak{M }}} (\vartheta , w_i)\lhd (\vartheta , w_l)\). By the definition of \(\lhd \), we know that if there exists the immediate successor of a worldFootnote 10, this immediate successor is unique, \(\models ^{{\mathfrak{M }}} (\vartheta , w_j)=(\vartheta , w_l)\). Therefore, the rule \((\lhd =)\) is sound.
We now turn to the closing rules for the relations. Assume that we have \(\vdash (\vartheta , w_i)<(\vartheta , w_j)\) and \(\vdash (\vartheta , w_j)<(\vartheta , w_i)\). Then we have that \(\models ^{\mathfrak M} (\vartheta , w_i)<(\vartheta , w_j)\) and \(\models ^{{\mathfrak{M }}}(\vartheta , w_j)<(\vartheta , w_i)\). By the \((=\textsc {Lin})\) rule, which we have proved sound, if we have two worlds \((\vartheta , w_i)\) and \((\vartheta , w_j)\) in a model \({\mathfrak M} \), then we have either \(\models ^{\mathfrak M} (\vartheta , w_i)<(\vartheta , w_j)\) or \(\models ^{\mathfrak M} (\vartheta , w_j)<(\vartheta , w_i)\) or \(\models ^{{\mathfrak{M }}} (\vartheta , w_i) = (\vartheta , w_j)\) (we are not interested in this last case), but we cannot have both \(\models ^{{\mathfrak{M }}} (\vartheta , w_i)<(\vartheta , w_j)\) and \(\models ^{{\mathfrak{M }}} (\vartheta , w_j) <(\vartheta , w_i)\). Thus, the closing rule \((<\textsc {Abs})\) is sound. We proceed analogously for \((\lhd \textsc {Abs})\) and \((\prec \textsc {Abs})\), by using respectively the definitions of \(\lhd \) and \(\prec \), or by using respectively the rules \((\lhd <)\) and \((\prec <)\), and then the \((=\textsc {Lin})\) rule.
Assume that we have \(\vdash (\vartheta , w_i) = (\vartheta , w_j)\) and \(\vdash (\vartheta , w_i)<(\vartheta , w_j)\). Then we have that \(\models ^{{\mathfrak{M }}} (\vartheta , w_i) = (\vartheta , w_j)\) and \(\models ^{{\mathfrak{M }}} (\vartheta , w_i)<(\vartheta , w_j)\). By the \((<)\) rule we know that if we have two worlds \((\vartheta , w_i)\) and \((\vartheta , w_j)\), then we have one of the three cases, \(\models ^{{\mathfrak{M }}} (\vartheta , w_i) <(\vartheta , w_j)\), \(\models ^{{\mathfrak{M }}} (\vartheta , w_j)<(\vartheta , w_i)\), or \(\models ^{{\mathfrak{M }}} (\vartheta , w_i)= (\vartheta , w_j)\). Thus, we cannot have both \(\models ^{{\mathfrak{M }}} (\vartheta , w_i)<(\vartheta , w_j)\) and \(\models ^{{\mathfrak{M }}} (\vartheta , w_i) = (\vartheta , w_j)\). Therefore, the closing rule \((=\textsc {Abs})\) is true. We proved just one case of the \((= \textsc {Abs})\) rule, we argue analogously for the other two cases with the \(\lhd \) and \(\prec \) relation.
Assume that we have \(\vdash (\vartheta , w_i)\lhd (\vartheta , w_j)\) and \(\vdash (\vartheta , w_i) <(\vartheta , w_k)\) and \(\vdash (\vartheta , w_k) <(\vartheta , w_j)\). Then we have that \(\models ^{{\mathfrak{M }}} (\vartheta , w_i)\lhd (\vartheta , w_j)\) and \(\models ^{{\mathfrak{M }}} (\vartheta , w_i) <(\vartheta , w_k)\) and \(\models ^{{\mathfrak{M }}} (\vartheta , w_k) <(\vartheta , w_j)\). By definition of the \(\lhd \) relation, we know that if \(\models ^{{\mathfrak{M }}} (\vartheta , w_i)\lhd (\vartheta , w_j)\), then there exists no world \((\vartheta , w)\) such that \(\models ^{\mathfrak{M }} (\vartheta , w_i)\lhd (\vartheta , w)\) and that \(\models ^{\mathfrak{M }} (\vartheta , w)<(\vartheta , w_j)\). By the rule \((\lhd <)\), if we have \(\models ^{\mathfrak{M }} (\vartheta , w_i)\lhd (\vartheta , w)\), then we have \(\models ^{\mathfrak{M }} (\vartheta , w_i)<(\vartheta , w)\). Thus, there exists no \((\vartheta , w_k)\) such that \(\models ^{\mathfrak{M }} (\vartheta , w_i)\lhd (\vartheta , w_j)\) and \(\models ^{\mathfrak{M }} (\vartheta , w_i)<(\vartheta , w_k)\) and \(\models ^{\mathfrak{M }} (\vartheta , w_k)<(\vartheta , w_j)\). Therefore, the closing rule \((\lhd <\textsc {Abs})\) is sound.
Let’s analyze the remaining rules for the second layer. If we have \(\vdash (\vartheta , w_i):\phi \), then we have \(\models ^{\mathfrak M} (\vartheta , w_i):\phi \). Assume to also have \((\vartheta , w_j)\) such that \(\vdash (\vartheta , w_i) = (\vartheta , w_j)\), then we have \(\models ^{\mathfrak M} (\vartheta , w_i) = (\vartheta , w_j)\). By the definition of \(=\), we have that \(\models ^{\mathfrak M} (\vartheta , w_j):\phi \). Thus, the \((\textsc {Subst}_1)\) rule is sound.
If we have \(\vdash (\vartheta , w_i):\square \phi \), then we have \(\models ^{\mathfrak M} (\vartheta , w_i):\square \phi \). Assume to also have \((\vartheta , w_j)\) such that \(\vdash (\vartheta , w_i)<(\vartheta , w_j)\), then we have \(\models ^{\mathfrak M} (\vartheta , w_i)<(\vartheta , w_j)\). By definition of the \(\square \) operator, for all \((\vartheta , w_j)\) with the above condition, we then have \(\models ^{\mathfrak M} (\vartheta , w_j):\phi \). Thus, the rule \((\square )\) is sound.
If we have \(\vdash (\vartheta , w_i):\diamondsuit \phi \), then we have \(\models ^{\mathfrak M} (\vartheta , w_i):\diamondsuit \phi \). By definition of the \(\diamondsuit \) operator, we have that there exists a world \((\vartheta , w_j)\) such that \(\models ^{\mathfrak M} (\vartheta , w_i)<(\vartheta , w_j)\), and \(\models ^{\mathfrak M} (\vartheta , w_j):\phi \). Thus, the rule \((\diamondsuit )\) is sound.
If we have \(\vdash (\vartheta , w_i):{\phi _1 \, \fancyscript{C} \, \phi _2}\), then we have \(\models ^{\mathfrak M} (\vartheta , w_i):{\phi _1 \, \fancyscript{C} \, \phi _2}\). Assume that we also have a \((\vartheta , w_j)\) such that \(\vdash (\vartheta , w_j):\phi _1\) and \(\vdash (\vartheta , w_i)<(\vartheta , w_j)\). Then we have \(\models ^{\mathfrak M} (\vartheta , w_j):\phi _1\) and \(\models ^{\mathfrak M} (\vartheta , w_i)<(\vartheta , w_j)\). By definition of the \(\fancyscript{C}\) operator, for all \((\vartheta , w_j)\) with the above conditions, we have that there exists a new world \((\vartheta , w_k)\), (\(w_k\) is fresh), such that \(\models ^{\mathfrak M} (\vartheta , w_j)<(\vartheta , w_k)\) and \(\models ^{\mathfrak M} (\vartheta , w_k):\phi _2\). Thus, the rule \((\fancyscript{C})\) is sound.
If we have \(\vdash (\vartheta , w_i):{\phi _1 \, \fancyscript{P} \, \phi _2}\), then we have that \(\models ^{\mathfrak M} (\vartheta , w_i):{\phi _1 \, \fancyscript{P} \, \phi _2}\). Assume to have a \((\vartheta , w_k)\) such that \(\vdash (\vartheta , w_k):\phi _2\) and \(\vdash (\vartheta , w_i)\prec (\vartheta , w_k)\). Then we have \(\models ^{\mathfrak M} (\vartheta , w_k):\phi _2\) and \(\models ^{\mathfrak M} (\vartheta , w_i)\prec (\vartheta , w_k)\). By definition of the \(\fancyscript{P}\) operator, for all \((\vartheta , w_k)\) with the above conditions, there exists a fresh world \((\vartheta , w_j)\) such that \(\models ^{\mathfrak M} (\vartheta , w_i)<(\vartheta , w_j)\) and \(\models ^{\mathfrak M} (\vartheta , w_j)<(\vartheta , w_k)\) and \(\models ^{\mathfrak M} (\vartheta , w_j):\phi _1\). Thus, the rule \((\fancyscript{P})\) is sound.
If we have \(\vdash (\vartheta , w_i):{\phi _1 \, \fancyscript{U} \, \phi _2}\), then we have that \(\models ^{\mathfrak M} (\vartheta , w_i):{\phi _1 \, \fancyscript{U} \, \phi _2}\). By definition of the \(\fancyscript{U}\) operator, we have that \(\models ^{\mathfrak M} (\vartheta , w_i):\phi _2\) or \(\models ^{\mathfrak M} (\vartheta , w_i)<(f_{{\phi _1 \, \fancyscript{U} \, \phi _2}}(\vartheta , w_i))\) and \(\models ^{\mathfrak M} (f_{{\phi _1 \, \fancyscript{U} \, \phi _2}}(\vartheta , w_i)):\phi _2\). Thus, the rule \((\fancyscript{U}_1)\) is sound. Assume to have a \((\vartheta , w_j)\) such that \(\vdash (\vartheta , w_i)<(\vartheta , w_j)\) and \(\vdash (\vartheta , w_j)<(f_{{\phi _1 \, \fancyscript{U} \, \phi _2}}(\vartheta , w_i))\), then we have that \(\models ^{\mathfrak M} (\vartheta , w_i)<(\vartheta , w_j)\) and \(\models ^{\mathfrak M} (\vartheta , w_j)<(f_{{\phi _1 \, \fancyscript{U} \, \phi _2}}(\vartheta , w_i))\). By definition of the \(\fancyscript{U}\) operator, for all \((\vartheta , w_j)\) with the above conditions, we have that \(\models ^{\mathfrak M} (\vartheta , w_j):\phi _1\) and \(\models ^{\mathfrak M} (\vartheta , w_j):\lnot \phi _2\). Thus, the rule \((\fancyscript{U}_2)\) is sound.
We now turn to the closure rules of these operators and prove their soundness.
Assume that we have \(\vdash (\vartheta , w_i):\square \phi \) and \(\vdash (\vartheta , w_i)<(\vartheta , w_j)\) and \(\vdash (\vartheta , w_j):\lnot \phi \). Then we have that \(\models ^{\mathfrak M} (\vartheta , w_i):\square \phi \) and \(\models ^{\mathfrak M} (\vartheta , w_i)<(\vartheta , w_j)\) and \(\models ^{\mathfrak M} (\vartheta , w_j):\lnot \phi \). By definition of \(\square \), if we have \(\models ^{\mathfrak M} (\vartheta , w_i):\square \phi \), then for all \((\vartheta , w_j)\) such that \(\models ^{\mathfrak M} (\vartheta , w_i)<(\vartheta , w_j)\), we have that \(\models ^{\mathfrak M} (\vartheta , w_j):\phi \). This is in contradiction with \(\models ^{\mathfrak M} (\vartheta , w_j):\lnot \phi \). Thus, the rule \((\square \textsc {Abs})\) is sound.
Assume that we have \(\vdash (\vartheta , w):\diamondsuit \phi \) and \(\vdash (\vartheta , w):\square \lnot \phi \). Then we have that \(\models ^{\mathfrak M} (\vartheta , w):\diamondsuit \phi \) and \(\models ^{\mathfrak M} (\vartheta , w):\square \lnot \phi \). By definition of \(\diamondsuit \), if we have \(\models ^{\mathfrak M} (\vartheta , w):\diamondsuit \phi \), then there exists a world \((\vartheta , w_i)\) such that \(\models ^{\mathfrak M} (\vartheta , w)<(\vartheta , w_i)\) and \(\models ^{\mathfrak M} (\vartheta , w_i):\phi \). Instead by definition of \(\square \), if we have \(\models ^{\mathfrak M} (\vartheta , w):\square \lnot \phi \) and a world \((\vartheta , w_i)\) such that \(\models ^{\mathfrak M} (\vartheta , w)<(\vartheta , w_i)\), then \(\models ^{\mathfrak M} (\vartheta , w_i):\lnot \phi \). This is in contradiction with \(\models ^{\mathfrak M} (\vartheta , w_i):\phi \). Thus, the rule \((\diamondsuit \textsc {Abs})\) is sound.
Assume that we have \(\vdash (\vartheta , w_i):{\phi _1 \, \fancyscript{C} \, \phi _2}\). Then we have that \(\models ^{\mathfrak M} (\vartheta , w_i):{\phi _1 \, \fancyscript{C} \, \phi _2}\). Assume that we also have some \((\vartheta , w_j)\) such that \(\vdash (\vartheta , w_i)<(\vartheta , w_j)\) and \(\vdash (\vartheta , w_j):\phi _1\) and \(\vdash (\vartheta , w_j):\square \lnot \phi _2\), then we have that \(\models ^{\mathfrak M} (\vartheta , w_i)<(\vartheta , w_j)\) and \(\models ^{\mathfrak M} (\vartheta , w_j):\phi _1\) and \(\models ^{\mathfrak M} (\vartheta , w_j):\square \lnot \phi _2\). By definition of the \(\fancyscript{C}\) operator, if we have \(\models ^{\mathfrak M} (\vartheta , w_i): {\phi _1 \, \fancyscript{C} \, \phi _2}\), then for all \((\vartheta , w_j)\) such that \(\models ^{\mathfrak M} (\vartheta , w_i)<(\vartheta , w_j)\) and \(\models ^{\mathfrak M} (\vartheta , w_j):\phi _1\), we have that there exists a new \((\vartheta , w_k)\), such that \(\models ^{\mathfrak{M }} (\vartheta , w_k):\phi _2\) and \(\models ^{\mathfrak{M }} (\vartheta , w_j) <(\vartheta , w_k)\). Using the sound rule \((\square \textsc {Abs})\) we have a contradiction. Thus, the rule \((\fancyscript{C}\textsc {Abs})\) is sound.
Assume that \(\vdash (\vartheta , w_i):{\phi _1 \, \fancyscript{P} \, \phi _2}\), then we have that \(\models ^{\mathfrak M} (\vartheta , w_i):{\phi _1 \, \fancyscript{P} \, \phi _2}\). Assume to also have a world \((\vartheta , w_k)\) such that \(\vdash (\vartheta , w_i)\prec (\vartheta , w_k)\) and \(\vdash (\vartheta , w_k):\phi _2\), and \(\vdash (\vartheta , w_i)\lhd (\vartheta , w_{i+1})\), and \(\vdash (\vartheta , w_{i+1}):{\lnot \phi _1 \, \fancyscript{U} \, \phi _2}\), then we have that \(\models ^{\mathfrak M} (\vartheta , w_i)\prec (\vartheta , w_k)\), and \(\models ^{\mathfrak M} (\vartheta , w_k):\phi _2\), and \(\models ^{\mathfrak M} (\vartheta , w_i)\lhd (\vartheta , w_{i+1})\), and \(\models ^{\mathfrak M} (\vartheta , w_{i+1}):{\lnot \phi _1 \, \fancyscript{U} \, \phi _2}\). By definition of the \(\fancyscript{P}\) operator, if we have \(\models ^{\mathfrak M} (\vartheta , w_i):{\phi _1 \, \fancyscript{P} \, \phi _2}\), then, for all the worlds \((\vartheta , w_k)\) such that \(\models ^{\mathfrak M} (\vartheta , w_i)\prec (\vartheta , w_k)\) and \(\models ^{\mathfrak M} (\vartheta , w_k):\phi _2\), we have that there must exist a new world \((\vartheta , w_j)\) such that \(\models ^{\mathfrak M} (\vartheta , w_j):\phi _1\), and \(\models ^{\mathfrak M} (\vartheta , w_i)<(\vartheta , w_j)\), and \(\models ^{\mathfrak M} (\vartheta , w_j)<(\vartheta , w_k)\). By definition of \(\fancyscript{U}\) we can have two cases. The first case is when we have \(\models ^{\mathfrak M} (\vartheta , w_{i+1}):\phi _2\). This means that there is no world between \((\vartheta , w_i)\) and \((\vartheta , w_{i+1})\) where there is an occurrence of \(\phi _1\) or \(\lnot \phi _1\). The second case is when we have for all worlds \((\vartheta , w_j)\), such that \(\models ^{\mathfrak M} (\vartheta , w_i)<(\vartheta , w_j)\), and \(\models ^{\mathfrak M} (\vartheta , w_j)<(\vartheta , w_k)\), and \(\models ^{\mathfrak M} (\vartheta , w_j):\lnot \phi _1\). Both of these two cases are in contradiction with \(\models ^{\mathfrak M} (\vartheta , w_j):\phi _1\). Thus, the rule \((\fancyscript{P}\textsc {Abs})\) is sound.
Assume that \(\vdash (\vartheta , w_i):{\phi _1 \, \fancyscript{U} \, \phi _2}\), and \(\vdash (f_{{\phi _1 \, \fancyscript{U} \, \phi _2}}(\vartheta , w_i)):\phi _2\), and to also have a \((\vartheta , w_j)\) such that \(\vdash (\vartheta , w_i)<(\vartheta , w_j)\) and \(\vdash (\vartheta , w_j)<(f_{{\phi _1 \, \fancyscript{U} \, \phi _2}}(\vartheta , w_i))\), and \(\vdash (\vartheta , w_j):\lnot \phi _1\). Then we have that \(\models ^{\mathfrak M} (\vartheta , w_i):{\phi _1 \, \fancyscript{U} \, \phi _2}\), and \(\models ^{\mathfrak M} (f_{{\phi _1 \, \fancyscript{U} \, \phi _2}}(\vartheta , w_i)):\phi _2\), and \(\models ^{\mathfrak M} (\vartheta , w_i)<(\vartheta , w_j)\) and \(\models ^{\mathfrak M} (\vartheta , w_j)<(f_{{\phi _1 \, \fancyscript{U} \, \phi _2}}(\vartheta , w_i))\) and \(\models ^{\mathfrak M} (\vartheta , w_j):\lnot \phi _1\). By definition of the \(\fancyscript{U}\) operator, for all \((\vartheta , w_j)\) with the last three above conditions, we have that \(\models ^{\mathfrak M} (\vartheta , w_j):\phi _1\). This is in contradiction with \(\models ^{\mathfrak M} (\vartheta , w_j):\lnot \phi _1\). Thus, the rule \((\fancyscript{U}\textsc {Abs})\) is sound. \(\square \)
1.2 Soundness of the systematic tableau construction
We complete the soundness proof by showing that the systematic tableau construction is sound, i.e., we prove Theorem 2.
An open tableau is exhausted if it is infinite or if no rule can be applied to the formulas. We prove that if the tableau \(T\) of the set \(X\) of labeled and relational formulas of the second layer is open and exhausted, \(\vdash X\), then \(X\) is satisfied, i.e., \(\models ^{\mathfrak M} X\) for \({\mathfrak M} \) a model.
The given set of formulas \(X\) is composed by a set \(\Gamma \) of labeled formulas and a set \(\Delta \) of relational formulas, and we will thus focus on the pair \((\Gamma , \Delta )\). Assume that we build a tableau \(T\) for \(X\), and that \(T\) is open and exhausted, and call \(X^* \supseteq X\) the set of formulas produced by this tableau. \(X^*\) is composed by the set of labeled formulas \(\Gamma ^* \supseteq \Gamma \) and relational formulas \(\Delta ^* \supseteq \Delta \). As the tableau \(T\) is open and exhausted, this means that either we applied all the possible rules and all the formulas of \(X^*\) are asleep, or that some formula is awake and we have an infinite branch.
As terminology, let us say that a label \((\vartheta , w_i)\) occurs in \((\Gamma , \Delta )\), in symbols \((\vartheta , w_i)\Subset (\Gamma , \Delta )\), if there exists a \(\sigma \) such that \((\vartheta , w_i):\sigma \in \Gamma \), or there exists a \((\vartheta , w_j)\) such that \((\vartheta , w_i)\bullet (\vartheta , w_j) \in \Delta \) or \((\vartheta , w_j)\bullet (\vartheta , w_i) \in \Delta \), for \(\bullet \in \{=, <, \prec , \lhd \}\).
Starting from the open and exhausted tableau \(T\) and the sets of formulas \((\Gamma ^*, \Delta ^*)\), we define a model \({\mathfrak{M}} (\Gamma ^*, \Delta ^*) = (W, \Theta , \fancyscript{I}, {\mathfrak R} _\bullet , V)\) as follows:
-
\((\Theta , W)= \{(\vartheta , w) \mid (\vartheta , w) \Subset (\Gamma ^*, \Delta ^*)\}\), where \(\fancyscript{I}(\vartheta , w)= (\fancyscript{I}(\vartheta )\), \(\fancyscript{I}(w))= (\vartheta , w)\), and \(\Theta = \{\vartheta \mid \vartheta \Subset (\Gamma ^*, \Delta ^*)\}\), where and \(\fancyscript{I}(\vartheta )= (\vartheta )\);
-
\(((\vartheta , w_i), (\vartheta , w_j))\in {\mathfrak R} _\bullet \) iff \((\vartheta , w_i)\bullet (\vartheta , w_j)\in \Delta ^*\).
-
\(V((\vartheta , w), p)=\top \) iff \((\vartheta , w):p\in \Gamma ^*\).
We straightforwardly have that \(\models ^{{\mathfrak{M}} (\Gamma ^*, \Delta ^*)} (\Gamma ^*, \Delta ^*)\). This model satisfies the properties stated in the following two lemmas.
Lemma 2
If \((\vartheta , w_i)\bullet (\vartheta , w_j) \in (\Gamma ^*,\Delta ^*)\), then we have that \(\models ^{{\mathfrak{M}} (\Gamma ^*, \Delta ^*)} (\vartheta , w_i)\bullet (\vartheta , w_j)\).
Proof
Suppose that \((\vartheta , w_i)\bullet (\vartheta , w_j) \in (\Gamma ^*,\Delta ^*)\). By construction of \({\mathfrak{M}} (\Gamma ^*, \Delta ^*)\), this implies that \(((\vartheta , w_i),(\vartheta , w_j))\in {\mathfrak R} _\bullet \), and therefore \(\models ^{{\mathfrak{M}} (\Gamma ^*, \Delta ^*)} (\vartheta , w_i)\bullet (\vartheta , w_j)\). \(\square \)
Lemma 3
If \((\vartheta , w):\sigma \in (\Gamma ^*, \Delta ^*)\) then \(\models ^{{\mathfrak{M}} (\Gamma ^*, \Delta ^*)} (\vartheta , w):\sigma \).
Proof
We proceed by induction on the grade of \((\vartheta , w):\sigma \), i.e., on the number of the operators that compose \(\sigma \).
The base case is when \((\vartheta , w):\sigma \) is \((\vartheta , w):p\), where \(p\) is a propositional variable. If \((\vartheta , w):p \in \Gamma ^*\), then we have that \((\vartheta , w) \Subset (\Gamma ^*, \Delta ^*)\), which means that \((\vartheta , w) \in (\Theta , W)\). By the construction of \({\mathfrak{M}} (\Gamma ^*, \Delta ^*)\), we have that \(V((\vartheta , w), p)= \top \), which implies that \(\models ^{{\mathfrak{M}} (\Gamma ^*, \Delta ^*)} (\vartheta , w):p\).
Suppose that the claim holds for labeled formulas \((\vartheta , w):\sigma \) with \(n\) operators. We prove that the claim holds for formulas with \(n+1\) operators.
If \((\vartheta , w):\lnot \phi \in \Gamma ^*\), where \(\phi \) contains \(n\) operators, then \((\vartheta , w) \Subset (\Gamma ^*, \Delta ^*)\), which means that \((\vartheta , w) \in (\Theta , W)\). In \(\Gamma ^*\) there are all the formulas of the open exhausted tableau, thus, by the \((\textsc {Abs})\) rule we have that \((\vartheta, w):\phi \not\in \Upgamma^*,\), which means that \(\not\models ^{{\mathfrak{M}} (\Gamma ^*, \Delta ^*)} (\vartheta , w):\phi \), and then, by definition of \(\lnot \) and the induction hypotheses on the grade of \(\phi \) we have that \(\models ^{{\mathfrak{M}} (\Gamma ^*, \Delta ^*)} (\vartheta , w):\lnot \phi \).
If \((\vartheta , w):\phi _1\rightarrow \phi _2 \in \Gamma ^*\), where \(\phi _1\) and \(\phi _2\) contain no more than \(n\) operators, then \((\vartheta , w) \Subset (\Gamma ^*, \Delta ^*)\), which means that \((\vartheta , w) \in (\Theta , W)\). In \(\Gamma ^*\) there are all the formulas of the open exhausted tableau, thus, the given formula is asleep, and we have applied the \((\rightarrow )\) rule. From the rule, we have \((\vartheta , w):\lnot \phi _1\in \Gamma ^*\) or \((\vartheta , w):\phi _2\in \Gamma ^*\). From construction of \({\mathfrak{M}} (\Gamma ^*, \Delta ^*)\) and the induction hypothesis on the grade of \(\phi _1\) and \(\phi _2\) we have that \(\models ^{{\mathfrak{M}} (\Gamma ^*, \Delta ^*)} (\vartheta , w):\lnot \phi _1\) or \(\models ^{{\mathfrak{M}} (\Gamma ^*, \Delta ^*)} (\vartheta , w):\phi _2\), i.e., \(\models ^{{\mathfrak{M}} (\Gamma ^*, \Delta ^*)} (\vartheta , w):\phi _1\rightarrow \phi _2\) from the definition of truth.
If \((\vartheta , w):\diamondsuit \phi \in \Gamma ^*\), where \(\phi \) contains \(n\) operators, then \((\vartheta , w) \Subset (\Gamma ^*, \Delta ^*)\), which means that \((\vartheta , w) \in (\Theta , W)\). In \(\Gamma ^*\) we have all the formulas of the open exhausted tableau, thus the given formula is finished, and we have applied the \((\diamondsuit )\) rule. From the rule, we have that there exists a \((\vartheta , w_i)\in (\Theta , W)\) such that \((\vartheta , w)<(\vartheta , w_i)\in \Delta ^*\) and \((\vartheta , w_i):\phi \in \Gamma ^*\). From the construction of \({\mathfrak{M}} (\Gamma ^*, \Delta ^*)\) and the induction hypothesis on the grade of \(\phi \) we have that \(\models ^{{\mathfrak{M}} (\Gamma ^*, \Delta ^*)} (\vartheta , w_i):\phi \) and \(\models ^{{\mathfrak{M}} (\Gamma ^*, \Delta ^*)} (\vartheta , w)<(\vartheta , w_i)\), i.e., \(\models ^{{\mathfrak{M}} (\Gamma ^*, \Delta ^*)} (\vartheta , w_i):\diamondsuit \phi \) from the definition of truth.
If \((\vartheta , w):\square \phi \in \Gamma ^*\), where \(\phi \) contains no more than \(n\) operators, then \((\vartheta , w) \Subset (\Gamma ^*, \Delta ^*)\), which means that \((\vartheta , w) \in (\Theta , W)\). In \(\Gamma ^*\) we have all the formulas of the open exhausted tableau and we thus have two cases. In the first one, there was at least a \((\vartheta , w_i)\in (\Theta , W)\) such that \((\vartheta , w)<(\vartheta , w_i)\in \Delta ^*\). In the tableau \(T\), the \((\square )\) rule was applied to these formulas, and we had that \((\vartheta , w_i):\phi \in \Gamma ^*\). From the construction of \({\mathfrak{M}} (\Gamma ^*, \Delta ^*)\), Lemma 2, and the induction hypothesis on the grade of \(\phi \), we have that \(\models ^{{\mathfrak{M}} (\Gamma ^*, \Delta ^*)} (\vartheta , w_i):\phi \) and \( \models ^{{\mathfrak{M}} (\Gamma ^*, \Delta ^*)} (\vartheta , w)<(\vartheta , w_i)\), i.e., \(\models ^{{\mathfrak{M}} (\Gamma ^*, \Delta ^*)} (\vartheta , w):\square \phi \) from the definition of truth. In the second case, there was no \((\vartheta , w_i)\in (\Theta , W)\) with the above condition, so that we could not apply the \((\square )\) rule. \((\vartheta , w):\square \phi \in \Gamma ^*\), and is asleep, and thus by construction of \({\mathfrak{M}} (\Gamma ^*, \Delta ^*)\) we have that \(\models ^{{\mathfrak{M}} (\Gamma ^*, \Delta ^*)} (\vartheta , w):\square \phi \).
If \((\vartheta , w):{\phi _1 \, \fancyscript{C} \, \phi _2} \in \Gamma ^*\), where \(\phi _1\) and \(\phi _2\) contain no more than \(n\) operators, then \((\vartheta , w) \Subset (\Gamma ^*, \Delta ^*)\), which means that \((\vartheta , w) \in (\Theta , W)\). In \(\Gamma ^*\) we have all the formulas of the open exhausted tableau and we thus have two cases. In the first one, there exists at least a \((\vartheta , w_i)\in (\Theta , W)\) such that \((\vartheta , w)<(\vartheta , w_i)\in \Delta ^*\) and \((\vartheta , w_i):\phi _1 \in \Gamma ^*\). In the tableau \(T\), the \((\fancyscript{C})\) rule was applied to these formulas, and we had that there existed a new world \((\vartheta , w_j) \in (\Theta , W)\), where \((\vartheta , w_i) <(\vartheta , w_j) \in \Delta ^*\) and \((\vartheta , w_j):\phi _2 \in \Gamma ^*\). From the construction of \({\mathfrak{M}} (\Gamma ^*, \Delta ^*)\), Lemma 2, and the inductive hypothesis on the grade of \(\phi _1\) and \(\phi _2\), we have that \(\models ^{{\mathfrak{M}} (\Gamma ^*, \Delta ^*)} (\vartheta , w_i)<(\vartheta , w_j)\), \( \models ^{{\mathfrak{M}} (\Gamma ^*, \Delta ^*)} (\vartheta , w_j):\phi _2\), \(\models ^{{\mathfrak{M}} (\Gamma ^*, \Delta ^*)} (\vartheta , w)<(\vartheta , w_i)\) and \(\models ^{{\mathfrak{M}} (\Gamma ^*, \Delta ^*)} (\vartheta , w_i):\phi _1\), i.e., \(\models ^{{\mathfrak{M}} (\Gamma ^*, \Delta ^*)} (\vartheta , w_i):{\phi _1 \, \fancyscript{C} \, \phi _2}\) from the definition of truth. In the second case, there was no \((\vartheta , w_i)\in (\Theta , W)\) with the above conditions. This means that we could not apply the \((\fancyscript{C})\) rule. We have that \((\vartheta , w):{\phi _1 \, \fancyscript{C} \, \phi _2}\) is in \(\Gamma ^*\) and that is asleep, and thus by construction of \({\mathfrak{M}} (\Gamma ^*, \Delta ^*)\) we also have that \(\models ^{{\mathfrak{M}} (\Gamma ^*, \Delta ^*)} (\vartheta , w):{\phi _1 \, \fancyscript{C} \, \phi _2}\).
If \((\vartheta , w):{\phi _1 \, \fancyscript{P} \, \phi _2} \in \Gamma ^*\), where \(\phi _1\) and \(\phi _2\) contains no more than \(n\) operators, then \((\vartheta , w) \Subset (\Gamma ^*, \Delta ^*)\), which means that \((\vartheta , w) \in (\Theta , W)\). In \(\Gamma ^*\) we have all the formulas of the open exhausted tableau and we thus have two cases. In the first one, there exists a \((\vartheta , w_j)\in (\Theta , W)\) such that \((\vartheta , w)\prec (\vartheta , w_j)\in \Delta ^*\) and \((\vartheta , w_j):\phi _2 \in \Gamma ^*\). In the tableau \(T\), the \((\fancyscript{P})\) rule was applied to these formulas, and we had that there existed a new world \((\vartheta , w_i)\in (\Theta , W)\), where \((\vartheta , w_i):\phi _1\in \Gamma ^*\) and \((\vartheta , w_i)<(\vartheta , w_j)\in \Delta ^*\) and \((\vartheta , w)<(\vartheta , w_i)\in \Delta ^*\). From the construction of \({\mathfrak{M}} (\Gamma ^*, \Delta ^*)\), Lemma 2, and the inductive hypothesis on the grade of \(\phi _1\) and \(\phi _2\), we have that \( \models ^{{\mathfrak{M}} (\Gamma ^*, \Delta ^*)} (\vartheta , w_i):\phi _1\), \(\models ^{{\mathfrak{M}} (\Gamma ^*, \Delta ^*)} (\vartheta , w)<(\vartheta , w_i)\), \(\models ^{{\mathfrak{M}} (\Gamma ^*, \Delta ^*)} (\vartheta , w_i)<(\vartheta , w_j)\), \(\models ^{{\mathfrak{M}} (\Gamma ^*, \Delta ^*)} (\vartheta , w_j):\phi _2\) and \(\models ^{{\mathfrak{M}} (\Gamma ^*, \Delta ^*)} (\vartheta , w)\prec (\vartheta , w_j)\), i.e., \(\models ^{{\mathfrak{M}} (\Gamma ^*, \Delta ^*)} (\vartheta , w_i):{\phi _1 \, \fancyscript{P} \, \phi _2}\) from the definition of truth. In the second case, there was no \((\vartheta , w_j)\in (\Theta , W)\) with the above conditions. This means that we could not apply the \((\fancyscript{P})\) rule. \((\vartheta , w):{\phi _1 \, \fancyscript{P} \, \phi _2}\in \Gamma ^*\) and is asleep, and thus by construction of \({\mathfrak{M}} (\Gamma ^*, \Delta ^*)\) we have that \(\models ^{{\mathfrak{M}} (\Gamma ^*, \Delta ^*)} (\vartheta , w):{\phi _1 \, \fancyscript{P} \, \phi _2}\).
If \((\vartheta , w):{\phi _1 \, \fancyscript{U} \, \phi _2} \in \Gamma ^*\), where \(\phi _1\) and \(\phi _2\) contain no more than \(n\) operators, then \((\vartheta , w) \Subset (\Gamma ^*, \Delta ^*)\), which means that \((\vartheta , w) \in (\Theta , W)\). In \(\Gamma ^*\) we have all the formulas of the open and exhausted tableau, thus the given formula is finished and we have applied the \((\fancyscript{U}_1)\) rule. If we applied the \((\fancyscript{U}_1)\) rule in the tableau rule, we may have two cases. In the first case, \((\vartheta , w):\phi _2\in \Gamma ^*\). By the construction of \({\mathfrak M} (\Gamma ^*, \Delta ^*)\) and the induction hypothesis on the grade of \(\phi _1\) and \(\phi _2\), we have that \(\models ^{{\mathfrak{M}} (\Gamma ^*, \Delta ^*)} (\vartheta , w):\phi _2\), i.e., \(\models ^{{\mathfrak{M}} (\Gamma ^*, \Delta ^*)} (\vartheta , w):{\phi _1 \, \fancyscript{U} \, \phi _2}\) from the definition of truth. In the second case, there exists \((f_{{\phi _1 \, \fancyscript{U} \, \phi _2}}(\vartheta , w))\in (\Theta , W)\) such that \((\vartheta , w)<(f_{{\phi _1 \, \fancyscript{U} \, \phi _2}}(\vartheta , w))\in \Delta ^*\) and \((f_{{\phi _1 \, \fancyscript{U} \, \phi _2}}(\vartheta , w)):\phi _2\in \Gamma ^*\). From the construction of \({\mathfrak M} (\Gamma ^*, \Delta ^*)\) and the induction hypothesis on the grade of \(\phi _1\) and \(\phi _2\), we have that \(\models ^{{\mathfrak{M}} (\Gamma ^*, \Delta ^*)} (\vartheta , w)<(f_{{\phi _1 \, \fancyscript{U} \, \phi _2}}(\vartheta , w))\) and \(\models ^{{\mathfrak{M}} (\Gamma ^*, \Delta ^*)} (f_{{\phi _1 \, \fancyscript{U} \, \phi _2}}(\vartheta , w)):\phi _2\), i.e., \( \models ^{{\mathfrak{M}} (\Gamma ^*, \Delta ^*)} (\vartheta , w):{\phi _1 \, \fancyscript{U} \, \phi _2}\). \(\square \)
Theorem 6
If \(\models ^{\mathfrak M} X^*\) and \(X\subseteq X^*\) then \(\models ^{\mathfrak M} X\).
Proof
Suppose for the sake of contradiction that \(X^*\) is satisfiable and \(X\) is not satisfiable. As \(X\subseteq X^*\) and \(\models ^{\mathfrak M} X^*\), from the definition of satisfiability we have that \(\models ^{\mathfrak M} X^* \setminus X\) and \(\models ^{\mathfrak M} X\). This is a contradiction, because we have supposed that \(X\) is not satisfiable. \(\square \)
We are now able to prove the soundness of the systematic construction of the tableau, i.e., Theorem 2, which we can rephrase in a more detailed statement as follows:
Theorem 7
If the tableau \(T\) built by the systematic tableau construction for the set \(X\) of labeled and relational formulas of the second layer is open and exhausted, then \(X\) is satisfiable, i.e., there exists a model \({\mathfrak M} \) such that \(\models ^{\mathfrak M} X\).
Proof
Given the open and exhausted tableau \(T\), constructed from the set of formulas \(X\), we denote by \(X^*\) the set of formulas produced by \(T\). We can construct a model \({\mathfrak M} \) starting from \(X^*\). We want to prove that this model satisfies the set of formulas \(X^*\). By Lemma 2, we prove that for every relational formula such that \((\vartheta , w)\bullet (\vartheta , w^{\prime }) \in X^*\), we have that \(\models ^{\mathfrak M} (\vartheta , w)\bullet (\vartheta , w^{\prime })\). By Lemma 3, we prove that for every labeled formula \((\vartheta , w):\sigma \), such that \((\vartheta , w):\sigma \in X^*\), we have that \(\models ^{\mathfrak M} (\vartheta , w):\sigma \). We have proved that \(\models ^{\mathfrak M} X^*\). By the construction of the tableau, we know that \(X\subseteq X^*\). We can now apply Theorem 6, which says that if \(\models ^{\mathfrak M} X^*\) and \(X\subseteq X^*\), then \(\models ^{\mathfrak M} X\), and we have thus found a model \({\mathfrak M} \) that satisfies the set of formulas \(X\). \(\square \)
Appendix 2: Completeness of the system \(\fancyscript{S}\)
Let \(lab(X)= \{(\vartheta , w) \mid (\vartheta , w):\sigma \in X\} \cup \{(\vartheta , w_i) \mid (\vartheta , w_i)\bullet (\vartheta , w_j)\in X \text{ or } (\vartheta , w_j)\bullet (\vartheta , w_i)\in X \text{ for } \text{ some } w_j\}\) be the set of all labels that appear in a set \(X\) of labeled and relational formulas of the second layer. Although a branch \({\mathfrak B} \) of a tableau is defined as a set of boxes, each of which contains formulas, we often overload the notation and use \({\mathfrak B} \) to mean the set of labeled and relational formulas on the branch. Then \(lab({\mathfrak B} )\) is just the set of labels that are used on branch \({\mathfrak B} \).
A set of labels \(L\) is strongly generated if there is some (root) label, \((\vartheta , w_0)\in L\), such that every other label in \(L\) is accessible from \((\vartheta , w_0)\), and if \((\vartheta , w_0)\bullet (\vartheta , w_i)\) then \((\vartheta , w_i)\in L\). A label is accessible from another label using the accessibility relations, which in our case are \((=, <, \lhd , \prec )\).
We say that a tableau is exhausted if all appropriate tableau rules have been applied. A strongly generated set \(X\) of labeled and relational formulas of the second layer is downward exhausted if it satisfies the following conditions:
-
1.
There is no world \((\vartheta , w)\in lab(X)\) such that \((\vartheta , w):\phi \in X\) and \((\vartheta , w):\lnot \phi \in X\).
-
2.
If \((\vartheta , w):\lnot \lnot \phi \in X\), then \((\vartheta , w):\phi \in X\).
-
3.
If \((\vartheta , w):\phi _1\rightarrow \phi _2 \in X\), then \((\vartheta , w):\lnot \phi _1\in X\) or \((\vartheta , w):\phi _2\in X\).
-
4.
If \((\vartheta , w):\lnot (\phi _1\rightarrow \phi _2) \in X\), then \((\vartheta , w):\phi _1\in X\) and \((\vartheta , w):\lnot \phi _2\in X\).
-
5.
If \((\vartheta , w_i)\bullet (\vartheta , w_j) \in X\) and \((\vartheta , w_j) \bullet (\vartheta , w_z) \in X\), then \((\vartheta , w_i)\bullet (\vartheta , w_z) \in X\), where \(\bullet \in \{=, <, \prec \}\).
-
6.
If \((\vartheta , w_i)\bullet (\vartheta , w_j) \in X\), then \((\vartheta , w_i)<(\vartheta , w_j) \in X\), where \(\bullet \in \{\lhd , \prec \}\).
-
7.
If \((\vartheta , w_i)\prec (\vartheta , w_z) \in X\), then for some \((\vartheta , w_j)\in lab(X)\) we have that \((\vartheta , w_i)\lhd (\vartheta , w_j) \in X\) and \((\vartheta , w_j) <(\vartheta , w_z) \in X\).
-
8.
If \((\vartheta , w_i)<(\vartheta , w_j) \in X\), then we have that \((\vartheta , w_i)\lhd (\vartheta , w_j)\in X\) or \((\vartheta , w_i)\prec (\vartheta , w_j) \in X\).
-
9.
If \((\vartheta , w) \in lab(X)\), then we have that \((\vartheta , w)= (\vartheta , w)\in X\).
-
10.
If \((\vartheta , w_i) =(\vartheta , w_j)\in X\), then we have that \((\vartheta , w_j)= (\vartheta , w_i)\in X\).
-
11.
If \((\vartheta , w_i), (\vartheta , w_j)\in lab(X)\), then we have that \((\vartheta , w_i)<(\vartheta , w_j)\in X\) or \((\vartheta , w_i) = (\vartheta , w_j)\in X\) or \((\vartheta , w_j)<(\vartheta , w_i) \in X\).
-
12.
If \((\vartheta , w_i):\phi \in X\), and \((\vartheta , w_i)= (\vartheta , w_j)\in X\), then we have that \((\vartheta , w_j):\phi \in X\).
-
13.
If both \((\vartheta , w_i)\bullet (\vartheta , w_z)\in X\), where \(\bullet \in \{<, \lhd , \prec \}\), and \((\vartheta , w_i)= (\vartheta , w_j)\in X\), then we have that \((\vartheta , w_j)\bullet (\vartheta , w_z)\in X\).
-
14.
If \((\vartheta , w_i) \lhd (\vartheta , w_j)\in X\) and \((\vartheta , w_x) \lhd (\vartheta , w_y)\in X\) and \((\vartheta , w_i) = (\vartheta , w_x) \in X\), then we have that \((\vartheta , w_j) = (\vartheta , w_y) \in X\).
-
15.
There are no worlds \((\vartheta , w_i), (\vartheta , w_j) \in lab(X)\) such that \((\vartheta , w_i)\bullet (\vartheta , w_j) \in X\) and \((\vartheta , w_j) \bullet (\vartheta , w_i) \in X\), where \(\bullet \in \{<, \lhd , \prec \}\).
-
16.
There are no worlds \((\vartheta , w_i), (\vartheta , w_j) \in lab(X)\) such that \((\vartheta , w_i) = (\vartheta , w_j) \in X\) and \((\vartheta , w_i) \bullet (\vartheta , w_j) \in X\), where \(\bullet \in \{<, \lhd , \prec \}\).
-
17.
There are no worlds \((\vartheta , w_i), (\vartheta , w_j), (\vartheta , w_z) \in lab(X)\) such that \((\vartheta , w_i) \lhd (\vartheta , w_j) \in X\) and \((\vartheta , w_i) <(\vartheta , w_z) \in X\), and \((\vartheta , w_z) <(\vartheta , w_j) \in X\).
-
18.
If \((\vartheta , w):\square \phi \in X\), then \((\vartheta , w_i):\phi \in X\) for every \((\vartheta , w_i)\in lab(X)\) such that \((\vartheta , w)<(\vartheta , w_i)\in X\).
-
19.
If \((\vartheta , w):\diamondsuit \phi \in X\), then \((\vartheta , w_i):\phi \in X\) for some \((\vartheta , w_i)\in lab(X)\) such that \((\vartheta , w)<(\vartheta , w_i)\in X\).
-
20.
If \((\vartheta , w):{\phi _1 \, \fancyscript{C} \, \phi _2}\in X\) and \((\vartheta , w_i):\phi _1\in X\) for all \((\vartheta , w_i)\in lab(X)\) such that \((\vartheta , w)<(\vartheta , w_i)\in X\), then we have that \((\vartheta , w_j):\phi _2 \in X\), for some \((\vartheta , w_j)\in lab(X)\) such that \((\vartheta , w_i)<(\vartheta , w_j)\in X\).
-
21.
If \((\vartheta , w):{\phi _1 \, \fancyscript{P} \, \phi _2}\in X\) and for all \((\vartheta , w_j)\in lab(X)\) such that \((\vartheta , w)\prec (\vartheta , w_j)\in X\) and \((\vartheta , w_j):\phi _2\in X\), then we have that \((\vartheta , w_i):\phi _1 \in X\), for some \((\vartheta , w_i)\in lab(X)\) such that \((\vartheta , w_i)<(\vartheta , w_j)\in X\) and \((\vartheta , w)<(\vartheta , w_i)\in X\).
-
22.
If \((\vartheta , w):{\phi _1 \, \fancyscript{U} \, \phi _2} \in X\), then we have one of the two following cases. In the first case, we have that \((\vartheta , w):\phi _2 \in X\). In the second case, we have that there exists a \((f_{{\phi _1 \, \fancyscript{U} \, \phi _2}}(\vartheta , w))\in lab(X)\) such that \((f_{{\phi _1 \, \fancyscript{U} \, \phi _2}}(\vartheta , w)):\phi _2\in X\) and \((\vartheta , w)<(f_{{\phi _1 \, \fancyscript{U} \, \phi _2}}(\vartheta , w))\in X\). If \((f_{{\phi _1 \, \fancyscript{U} \, \phi _2}}(\vartheta , w))\) exists and is in \(lab(X)\) and \((f_{{\phi _1 \, \fancyscript{U} \, \phi _2}}(\vartheta , w)): \phi _2\in X\) and \((\vartheta , w)<(f_{{\phi _1 \, \fancyscript{U} \, \phi _2}}(\vartheta , w))\in X\), then for all \((\vartheta , w_i)\in lab(X)\) such that \((\vartheta , w)<(\vartheta , w_i) \in X\) and \((\vartheta , w_i) <(f_{{\phi _1 \, \fancyscript{U} \, \phi _2}}(\vartheta , w))\in X\) we have that \((\vartheta , w_i):\phi _1\in X\) and \((\vartheta , w_i):\lnot \phi _2\in X\).
-
23.
If \((\vartheta , w):\square \phi \in X\), then there is no world \((\vartheta , w_i)\in lab(X)\) such that \((\vartheta , w)<(\vartheta , w_i)\in X\) and \((\vartheta , w_i):\lnot \phi \in X\).
-
24.
There is no world \((\vartheta , w)\in lab(X)\) such that \((\vartheta , w):\diamondsuit \phi \in X\) and \((\vartheta , w):\square \lnot \phi \in X\).
-
25.
There are no worlds \((\vartheta , w), (\vartheta , w_i)\in lab(X)\) such that \((\vartheta , w):{\phi _1 \, \fancyscript{C} \, \phi _2}\in X\) and \((\vartheta , w)<(\vartheta , w_i)\in X\) and \((\vartheta , w_i):\phi _1\in X\) and \((\vartheta , w_i):\square \lnot \phi _2 \in X\).
-
26.
There are no worlds \((\vartheta , w_i), (\vartheta , w_{i+1}), (\vartheta , w_k)\in lab(X)\) such that \((\vartheta , w_i):{\phi _1 \, \fancyscript{P} \, \phi _2}\in X\) and \((\vartheta , w_i)\prec (\vartheta , w_k)\) and \((\vartheta , w_k):\phi _2\in X\) and \((\vartheta , w_i)\lhd (\vartheta , w_{i+1})\in X\), and \((\vartheta , w_{i+1}):{\lnot \phi _1 \, \fancyscript{U} \, \phi _2} \in X\).
-
27.
There are no worlds \((\vartheta , w_i), (\vartheta , w_j), (f_{{\phi _1 \, \fancyscript{U} \, \phi _2}}(\vartheta , w_i))\in lab(X)\), such that \((\vartheta , w_i):{\phi _1 \, \fancyscript{U} \, \phi _2}\in X\) and \((f_{{\phi _1 \, \fancyscript{U} \, \phi _2}}(\vartheta , w_i)):\phi _2\in X\) and \((\vartheta , w_i)<(\vartheta , w_j) \in X\) and \((\vartheta , w_j) <(f_{{\phi _1 \, \fancyscript{U} \, \phi _2}}(\vartheta , w_i))\in X\) and \((\vartheta , w_j):\lnot \phi _1\in X\).
Lemma 4
If \(X\) is a strongly generated set of labeled and relational formulas of the second layer that is downward exhausted, then \(X\) is satisfiable in a model whose possible worlds are the labels that appear in \(X\).
Proof
Suppose \(X\) is downward exhausted and let \(lab(X)\) be the set of labels that appear in \(X\). Since \(X\) is strongly generated, so is \(lab(X)\). Now, define a model \({\mathfrak M} = (W, \Theta , {\mathfrak R} _\bullet , V)\) as follows:
-
\((\Theta , W) =\{(\vartheta , w) \mid (\vartheta , w)\in lab(X)\}\).
-
\(((\vartheta , w_i), (\vartheta , w_j))\in {\mathfrak R} _\bullet \) iff \((\vartheta , w_i) \bullet (\vartheta , w_j)\in X\), where \(\bullet \in \{=, <,\) \(\lhd , \prec \}\).
-
\(V(p, (\vartheta , w))= \top \) iff \((\vartheta , w):p \in X\), for a primitive proposition \(p\) and a label \((\vartheta , w)\in lab(X)\).
If \((\vartheta , w_i)\bullet (\vartheta , w_j) \in X\), then by the construction of the model we have that \(\models ^{\mathfrak M} (\vartheta , w_i)\bullet (\vartheta , w_j)\) for where \(\bullet \in \{=, <, \lhd , \prec \}\).
We now show by induction on the formulas \(\sigma \) and the downward exhausted property that: if \((\vartheta , w):\sigma \in X\) then \(\models ^{\mathfrak M} (\vartheta , w):\sigma \) in the defined model \({\mathfrak M} \).
The base case is when \((\vartheta , w):\sigma \) is \((\vartheta , w):p\) for \(p\) a propositional variable. In this case, the result follows by construction.
We assume that the claim holds for all labeled formulas \((\vartheta , w):\sigma \) with \(n\) operators and show that it holds for labeled formulas with \(n+1\) operators.
If \((\vartheta , w):\lnot \phi \in X\), then by \((\textsc {Abs})\) we have that \((\vartheta, w):\phi\, \not\in X.\) Thus we have that \(\not\models ^{\mathfrak{M }} (\vartheta , w): \phi \), and then by definition of \(\lnot \) and the induction hypothesis, we have that \(\models ^{\mathfrak{M }} (\vartheta , w):\lnot \phi \).
If \((\vartheta , w):\phi _1\rightarrow \phi _2 \in X\), by rule \((\rightarrow )\), we have either \((\vartheta , w):\lnot \phi _1 \in X\) or \((\vartheta , w):\phi _2\in X\). By the induction hypothesis on the grade of \(\phi _1\) and \(\phi _2\), we have \(\models ^{\mathfrak M} (\vartheta , w):\lnot \phi _1\) or \(\models ^{\mathfrak M} (\vartheta , w):\phi _2\), so we conclude that \(\models ^{\mathfrak M} (\vartheta , w):\phi _1 \rightarrow \phi _2\).
If \((\vartheta , w):\square \phi \in X\), for all worlds \((\vartheta , w_i)\) such that \((\vartheta , w)<(\vartheta , w_i)\), by rule \((\square )\), we have that \((\vartheta , w_i):\phi \in X\). By the induction hypothesis on the grade of \(\phi \), we have that \(\models ^{\mathfrak M} (\vartheta , w_i):\phi \) and since \(\models ^{\mathfrak M} (\vartheta , w)<(\vartheta , w_i)\), we conclude that \(\models ^{\mathfrak M} (\vartheta , w):\square \phi \).
If \((\vartheta , w):\diamondsuit \phi \in X\), by rule \((\diamondsuit )\), we have \((\vartheta , w)<(\vartheta , w_i)\) and \((\vartheta , w_i):\phi \in X\), with \((\vartheta , w_i)\) fresh. By the induction hypothesis on the grade of \(\phi \), we have that \(\models ^{\mathfrak M} (\vartheta , w_i):\phi \) and since \(\models ^{\mathfrak M} (\vartheta , w) <(\vartheta , w_i)\), we can conclude that \(\models ^{\mathfrak M} (\vartheta , w):\diamondsuit \phi \).
If \((\vartheta , w):{\phi _1 \, \fancyscript{C} \, \phi _2}\in X\), for all worlds \((\vartheta , w_i)\), such that \((\vartheta , w_i):\phi _1\in X\) and \((\vartheta , w)<(\vartheta , w_i)\), by rule \((\fancyscript{C})\), we have that \((\vartheta , w_j):\phi _2\in X\), with \((\vartheta , w_j)\) fresh and \((\vartheta , w_i)<(\vartheta , w_j)\). By the induction hypothesis on the grade of \(\phi _2\), we have that \(\models ^{\mathfrak M} (\vartheta , w_j):\phi _2\) and since \(\models ^{\mathfrak M} (\vartheta , w_i)<(\vartheta , w_j)\), we conclude that \(\models ^{\mathfrak M} (\vartheta , w):{\phi _1 \, \fancyscript{C} \, \phi _2}\).
If \((\vartheta , w):{\phi _1 \, \fancyscript{P} \, \phi _2}\in X\), for all worlds \((\vartheta , w_j)\), such that \((\vartheta , w_j):\phi _2\in X\) and \((\vartheta , w)\prec (\vartheta , w_j)\), by rule \((\fancyscript{P})\), we have that \((\vartheta , w_i):\phi _1\in X\), with \((\vartheta , w_i)\) fresh and \((\vartheta , w_i)<(\vartheta , w_j)\) and \((\vartheta , w)<(\vartheta , w_i)\). By the induction hypothesis on the grade of \(\phi _2\), we have that \(\models ^{\mathfrak M} (\vartheta , w_i):\phi _1\) and since \(\models ^{\mathfrak M} (\vartheta , w_i)<(\vartheta , w_j)\) and \(\models ^{\mathfrak M} (\vartheta , w)<(\vartheta , w_i)\), we conclude that \(\models ^{\mathfrak M} (\vartheta , w):{\phi _1 \, \fancyscript{P} \, \phi _2}\).
Assume \((\vartheta , w):{\phi _1 \, \fancyscript{U} \, \phi _2} \in X\). By using the rule \((\fancyscript{U}_1)\), we have either \((\vartheta , w):\phi _2\in X\) or \((\vartheta , w)<(f_{{\phi _1 \, \fancyscript{U} \, \phi _2}}(\vartheta , w))\) and \((f_{{\phi _1 \, \fancyscript{U} \, \phi _2}}(\vartheta , w)):\phi _2\in X\). In the first case, by the induction hypothesis on the grade of \(\phi _2\), we have \(\models ^{\mathfrak M} (\vartheta , w):\phi _2\), we can conclude that \(\models ^{\mathfrak M} (\vartheta , w):{\phi _1 \, \fancyscript{U} \, \phi _2}\). In the second case, we have that \(\models ^{\mathfrak M} (\vartheta , w)<(f_{{\phi _1 \, \fancyscript{U} \, \phi _2}}(\vartheta , w))\) and by the induction hypothesis on the grade of \(\phi _1\) and \(\phi _2\), we have that \(\models ^{\mathfrak M} (f_{{\phi _1 \, \fancyscript{U} \, \phi _2}}(\vartheta , w)):\phi _2\). We conclude that \(\models ^{\mathfrak M} (\vartheta , w):{\phi _1 \, \fancyscript{U} \, \phi _2}\). \(\square \)
Before we prove the completeness theorem we need to show that our systematic procedure does everything that is necessary in the following sense.
Lemma 5
If \({\mathfrak B} \) is an open branch of an open and exhausted tableau built by the systematic tableau construction for system \(\fancyscript{S}\), then \({\mathfrak B} \) is closed with respect to every tableau rule in the calculus in that: every rule that could have been applied to a formula in \({\mathfrak B} \) must have been applied at some stage.
Proof
By the Fairness Lemma 1, every formula is visited at least once. The rules of the first layer are applied in the steps 5 and 6 of the while cycle. These rules were applied as soon as it was possible. So the formulas of the first layer should be asleep. If they are not asleep, it means that some main formulas of some rule have re-marked them as awake. Since \({\mathfrak B} \) is open and exhausted, and our systematic procedure is fair, the procedure visited the main formulas at some later stage.
The relational rules are applied in step 7 of the while cycle and we reason as for the first layer rules. We proceed similarly also for the rule of the second layer with the \(\diamondsuit \) operator (it was applied as soon as it was possible).
For the rule of the second layer \((\textsc {Subst}_1)\), suppose that \((\vartheta , w):\phi \) occurs in \({\mathfrak B} \) and that \((\vartheta , w_i)\) such that \((\vartheta , w)= (\vartheta , w_i)\) occurs in \({\mathfrak B} \) (and thus in \(lab({\mathfrak B} )\)). We have two cases. If \((\vartheta , w):\phi \) is asleep, then we have already applied the \((\textsc {Subst}_1)\) rule to \((\vartheta , w):\phi \) and \((\vartheta , w) = (\vartheta , w_i)\). Otherwise, if \((\vartheta , w):\phi \) is awake, then \((\vartheta , w) = (\vartheta , w_i)\) has awakened it. Since \({\mathfrak B} \) is open and exhausted, and our systematic procedure is fair, the procedure has to visit \((\vartheta , w):\phi \) at some later stage. This means that the rule \((\textsc {Subst}_1)\) has to be applied to \((\vartheta , w):\phi \) and \((\vartheta , w) = (\vartheta , w_i)\) at some later stage, since \((\vartheta , w) = (\vartheta , w_i)\) was used on the extant part of \({\mathfrak B} \).
For the rules of the second layer with the \(\square \) operator, suppose that \((\vartheta , w):\square \phi \) occurs in \({\mathfrak B} \) and that \((\vartheta , w_i)\) in \(lab({\mathfrak B} )\), such that \((\vartheta , w)<(\vartheta , w_i)\) occurs in \({\mathfrak B} \). We have two cases. If \((\vartheta , w):\square \phi \) is asleep, then we have already applied the \((\square )\) rule to \((\vartheta , w):\square \phi \) and \((\vartheta , w) <(\vartheta , w_i)\). Otherwise, if \((\vartheta , w):\square \phi \) is awake, then \((\vartheta , w) <(\vartheta , w_i)\) has awakened it. Since \({\mathfrak B} \) is open and exhausted, and our systematic procedure is fair, the procedure has to visit \((\vartheta , w):\square \phi \) at some later stage. This means that the \((\square )\) rule has to be applied to \((\vartheta , w):\square \phi \) and \((\vartheta , w) <(\vartheta , w_i)\) at some later stage, since \((\vartheta , w) <(\vartheta , w_i)\) was used on the extant part of \({\mathfrak B} \).
For the rules of the second layer with the \(\fancyscript{C}\) operator, suppose that \((\vartheta , w):{\phi _1 \, \fancyscript{C} \, \phi _2}\) occurs in \({\mathfrak B} \) and suppose to also have \((\vartheta , w_i)\) in \(lab({\mathfrak B} )\), such that \((\vartheta , w)<(\vartheta , w_i)\) and \((\vartheta , w_i):\phi _1\) also occur in \({\mathfrak B} \). We have two cases. If \((\vartheta , w):{\phi _1 \, \fancyscript{C} \, \phi _2}\) is asleep, then we have already applied the \((\fancyscript{C})\) rule to \((\vartheta , w):{\phi _1 \, \fancyscript{C} \, \phi _2}\) and the formulas of \((\vartheta , w_i)\) before. Otherwise, if \((\vartheta , w):{\phi _1 \, \fancyscript{C} \, \phi _2}\) is awake, then the formulas of \((\vartheta , w_i)\) have awakened it. Since \({\mathfrak B} \) is open and exhausted, and our systematic procedure is fair, the procedure has to visit \((\vartheta , w):{\phi _1 \, \fancyscript{C} \, \phi _2}\) at some later stage. This means that the rule \((\fancyscript{C})\) has to be applied to \((\vartheta , w):{\phi _1 \, \fancyscript{C} \, \phi _2}\) and to the formulas of \((\vartheta , w_i)\) at some later stage, since the formulas of \((\vartheta , w_i)\) were used on the extant part of \({\mathfrak B} \).
For the rules of the second layer with the \(\fancyscript{P}\) operator, suppose that \((\vartheta , w):{\phi _1 \, \fancyscript{P} \, \phi _2}\) occurs in \({\mathfrak B} \) and that \((\vartheta , w_j)\) in \(lab({\mathfrak B} )\), such that \((\vartheta , w)\prec (\vartheta , w_j)\) and \((\vartheta , w_j):\phi _2\) occur in \({\mathfrak B} \). We have two cases. If \((\vartheta , w):{\phi _1 \, \fancyscript{P} \, \phi _2}\) is asleep, then we have already applied the rule \((\fancyscript{P})\) to \((\vartheta , w):{\phi _1 \, \fancyscript{P} \, \phi _2}\) and the formulas of \((\vartheta , w_j)\) before. Otherwise, if \((\vartheta , w):{\phi _1 \, \fancyscript{P} \, \phi _2}\) is awake, then the formulas of \((\vartheta , w_j)\) have awakened it. Since \({\mathfrak B} \) is open and exhausted, and our systematic procedure is fair, the procedure has to visit \((\vartheta , w):{\phi _1 \, \fancyscript{P} \, \phi _2}\) at some later stage still. This means that the rule \((\fancyscript{P})\) has to be applied to \((\vartheta , w):{\phi _1 \, \fancyscript{P} \, \phi _2}\) and to the formulas of \((\vartheta , w_j)\) at some later stage, since the formulas of \((\vartheta , w_j)\) were used on the extant part of \({\mathfrak B} \).
For the rules of the second layer with the \(\fancyscript{U}\) operator, suppose that \((\vartheta , w):{\phi _1 \, \fancyscript{U} \, \phi _2}\) occurs in \({\mathfrak B} \). We apply the \((\fancyscript{U}_1)\) rule whenever possible. So this formula is finished, meaning that we have already applied the rule \((\fancyscript{U}_1)\) to it in the extant \({\mathfrak B} \), or it is awake and we apply the rule \((\fancyscript{U}_1)\). We can have two cases from its application. The first one is to have \((\vartheta , w):\phi _2\) in \({\mathfrak B} \) and the second one to have a \((f_{{\phi _1 \, \fancyscript{U} \, \phi _2}}(\vartheta , w))\) in \({\mathfrak B} \) such that \((\vartheta , w)<(f_{{\phi _1 \, \fancyscript{U} \, \phi _2}}(\vartheta , w))\) and \((f_{{\phi _1 \, \fancyscript{U} \, \phi _2}}(\vartheta , w)):\phi _2\). For the second case, suppose that we have a \((\vartheta , w_i)\) in \(lab({\mathfrak B} )\) such that \((\vartheta , w)<(\vartheta , w_i)\) and \((\vartheta , w_i) <(f_{{\phi _1 \, \fancyscript{U} \, \phi _2}}(\vartheta , w))\) that are also formulas in \({\mathfrak B} \). Then we apply the rule \((\fancyscript{U}_2)\), and have that \((\vartheta , w_i):\phi _1\) and \((\vartheta , w_i):\lnot \phi _2\). \(\square \)
Lemma 6
If \({\mathfrak B} \) is an open branch of an open and exhausted built by the systematic tableau construction for system \(\fancyscript{S}\), then \({\mathfrak B} \) is downward exhausted.
Proof
By Lemma 5, \({\mathfrak B} \) is closed with respect to every rule of the calculus. We now have to go through the necessary clauses to show that \({\mathfrak B} \) is downward exhausted.
Clause \(1\) is satisfied since \({\mathfrak B} \) is open. Clauses \(2\), \(3\) and \(4\) are satisfied since \({\mathfrak B} \) must be closed with respect to the classical propositional rules.
To prove that clauses \(5-17\) are satisfied, we analyze all the possible relational formulas we may have in \({\mathfrak B} \).
Assume that \((\vartheta , w_i) = (\vartheta , w_j) \in {\mathfrak B} \) and \((\vartheta , w_j) = (\vartheta , w_z) \in {\mathfrak B} \) for some \((\vartheta , w_i), (\vartheta , w_j), (\vartheta , w_z) \in lab({\mathfrak B} )\). If \((\vartheta , w_i) = (\vartheta , w_j)\) is satisfied, then the labels \((\vartheta , w_i)\) and \((\vartheta , w_j)\) represent the same world, and also for \((\vartheta , w_j) = (\vartheta , w_z)\) we have that \((\vartheta , w_j)\) and \((\vartheta , w_z)\) represent the same world. The \(=\) relation is transitive and thus \((\vartheta , w_i)\) and \((\vartheta , w_z)\) represent the same world. Thus, if \((\vartheta , w_i) = (\vartheta , w_j) \in {\mathfrak B} \) and \((\vartheta , w_j) = (\vartheta , w_z) \in {\mathfrak B} \), then by the \((=\textsc {Trans})\) rule we have that \((\vartheta , w_i) = (\vartheta , w_z) \in {\mathfrak B} \). Thus, a part of clause \(5\) is satisfied. We argue analogously for the other parts of clause \(5\), for the binary relations \(<\) and \(\prec \).
Assume that \((\vartheta , w_i) \prec (\vartheta , w_j) \in {\mathfrak B} \), for some \((\vartheta , w_i), (\vartheta , w_j) \in lab({\mathfrak B} )\). By the definition of the binary relation \(\prec \), if \((\vartheta , w_i) \prec (\vartheta , w_j)\) is satisfied, then the world represented by \((\vartheta , w_i)\) precedes the world represented by \((\vartheta , w_j)\), and there exists at least a world between them. This last consequence can be expressed with the existence of a new world that is the immediate successor of the world represented by \((\vartheta , w_i)\) and is a predecessor of the world represented by \((\vartheta , w_j)\). Thus, if \((\vartheta , w_i) \prec (\vartheta , w_j) \in {\mathfrak B} \), then by the \((\prec <)\) rule we have that \((\vartheta , w_i) <(\vartheta , w_j) \in {\mathfrak B} \). Therefore, a part of clause \(6\) is satisfied. Moreover, by the \((\prec )\) rule we have that \((\vartheta , w_i) \lhd (\vartheta , w_z) \in {\mathfrak B} \) and \((\vartheta , w_z) <(\vartheta , w_j) \in {\mathfrak B} \), where \((\vartheta , w_z)\) is a new world in \(lab({\mathfrak B} )\). Therefore, also clause \(7\) is satisfied.
Assume that \((\vartheta , w_i) \lhd (\vartheta , w_j) \in {\mathfrak B} \), for some \((\vartheta , w_i), (\vartheta , w_j) \in lab({\mathfrak B} )\). If \((\vartheta , w_i) \lhd (\vartheta , w_j)\) is satisfied, then the world represented by \((\vartheta , w_i)\) precedes the world represented by \((\vartheta , w_j)\) and there is no world between them. Thus, if \((\vartheta , w_i) \lhd (\vartheta , w_j) \in {\mathfrak B} \), then by the \((\lhd <)\) rule we have that \((\vartheta , w_i) <(\vartheta , w_j) \in {\mathfrak B} \). Therefore, the other part of clause \(6\) is satisfied.
Assume that \((\vartheta , w_i) <(\vartheta , w_j) \in {\mathfrak B} \), for some \((\vartheta , w_i), (\vartheta , w_j) \in lab({\mathfrak B} )\). By the definition of the binary relation \(<\), if \((\vartheta , w_i) <(\vartheta , w_j)\) is satisfied, then the world represented by \((\vartheta , w_i)\) precedes the world represented by \((\vartheta , w_j)\). This can happen in two cases: (1) the world represented by \((\vartheta , w_i)\) is the immediate predecessor of the world represented by \((\vartheta , w_j)\), or (2) it is not its immediate predecessor. This last case means that there exists at least another world between them, which is the definition of the \(\prec \) relation, and that \((\vartheta , w_i)\prec (\vartheta , w_j) \in {\mathfrak B} \). Thus, if \((\vartheta , w_i) <(\vartheta , w_j) \in {\mathfrak B} \), then by the \((<)\) rule we have that \((\vartheta , w_i) \lhd (\vartheta , w_j) \in {\mathfrak B} \) or \((\vartheta , w_i) \prec (\vartheta , w_j) \in {\mathfrak B} \). Therefore, clause \(8\) is satisfied.
Assume that \((\vartheta , w) \in lab({\mathfrak B} )\). By the definition of the binary relation \(=\), we have that this relation is reflexive. Thus, if \((\vartheta , w) \in lab({\mathfrak B} )\), then by the \((=\textsc {Refl})\) rule we have that \((\vartheta , w) = (\vartheta , w) \in {\mathfrak B} \). Thus, clause \(9\) is satisfied.
Assume that \((\vartheta , w_i) = (\vartheta , w_j) \in {\mathfrak B} \), for some \((\vartheta , w_i), (\vartheta , w_j) \in lab({\mathfrak B} )\). By the definition of the binary relation \(=\), if \((\vartheta , w_i) = (\vartheta , w_j)\) is satisfied, then the labels \((\vartheta , w_i)\) and \((\vartheta , w_j)\) represent the same world. Moreover, we have that this relation is symmetric. Thus, if \((\vartheta , w_i) = (\vartheta , w_j) \in {\mathfrak B} \), then by the \((=\textsc {Sym})\) rule we have that \((\vartheta , w_j) = (\vartheta , w_i) \in {\mathfrak B} \). Therefore, clause \(10\) is satisfied.
If \((\vartheta , w_i), (\vartheta , w_j)\in lab({\mathfrak B} )\), then \(\fancyscript{E}(\vartheta , w_i) \in {\mathfrak B} \) and \(\fancyscript{E}(\vartheta , w_j) \in {\mathfrak B} \). By the definition of the binary relations \(<\) and \(=\), we know that if there are two labels (that represent two worlds), then there are three cases: (1) they represent the same world, (2) a world represented by a label precedes the world represented by the other label, or (3) the inverse. Thus, if \((\vartheta , w_i), (\vartheta , w_j) \in lab({\mathfrak B} )\), then by the \((=\textsc {Lin})\) rule, we have that \((\vartheta , w_i) = (\vartheta , w_j) \in {\mathfrak B} \) or \((\vartheta , w_i) <(\vartheta , w_j) \in {\mathfrak B} \) or \((\vartheta , w_j) <(\vartheta , w_i) \in {\mathfrak B} \). Therefore, clause \(11\) is satisfied.
Assume that \((\vartheta , w_i):\phi \in {\mathfrak B} \), and \((\vartheta , w_i) = (\vartheta , w_j) \in {\mathfrak B} \) for some \((\vartheta , w_i), (\vartheta , w_j)\in lab({\mathfrak B} )\). If \((\vartheta , w_i) = (\vartheta , w_j)\) is satisfied, then the labels \((\vartheta , w_i)\) and \((\vartheta , w_j)\) represent the same world. Thus, if \((\vartheta , w_i) = (\vartheta , w_j) \in {\mathfrak B} \) and \((\vartheta , w_i):\phi \in {\mathfrak B} \), then by the \((\textsc {Subst}_1)\) rule, we have that \((\vartheta , w_j):\phi \in {\mathfrak B} \). Therefore, clause \(12\) is satisfied. We argue analogously when we have \((\vartheta , w_i) = (\vartheta , w_j) \in {\mathfrak B} \) and \((\vartheta , w_i)\bullet (\vartheta , w_z) \in {\mathfrak B} \), for some \((\vartheta , w_i), (\vartheta , w_j), (\vartheta , w_z) \in lab({\mathfrak B} )\), where \(\bullet \in \{<, \lhd , \prec \}\) and where we use the \((\textsc {Subst}_2)\) rule. Thus, clause \(13\) is satisfied.
Assume that \((\vartheta , w_i) \lhd (\vartheta , w_j)\in {\mathfrak B} \) and \((\vartheta , w_x) \lhd (\vartheta , w_y) \in {\mathfrak B} \) and \((\vartheta , w_i) = (\vartheta , w_x) \in {\mathfrak B} \), for some \((\vartheta , w_i), (\vartheta , w_j), (\vartheta , w_x), (\vartheta , w_y) \in lab({\mathfrak B} )\). If \((\vartheta , w_i) = (\vartheta , w_x)\) is satisfied, then the labels \((\vartheta , w_i)\) and \((\vartheta , w_x)\) represent the same world. Instead, if \((\vartheta , w_i) \lhd (\vartheta , w_j)\) is satisfied, then the world represented by \((\vartheta , w_i)\) precedes the world represented by \((\vartheta , w_j)\) and there is no world between them. The same holds for \((\vartheta , w_x) \lhd (\vartheta , w_y)\). In the second layer, if two worlds are in relation with each other, then they are in the same trace. Hence, we have the uniqueness of the immediate successor of a world. As \((\vartheta , w_i)\) and \((\vartheta , w_x)\) represent the same world, the immediate successor of this world is unique. Thus, \((\vartheta , w_j)\) and \((\vartheta , w_y)\) must also represent the same world. This is captured by the \((\lhd <)\) rule. Thus, if \((\vartheta , w_i) \lhd (\vartheta , w_j)\in {\mathfrak B} \) and \((\vartheta , w_x) \lhd (\vartheta , w_y) \in {\mathfrak B} \) and \((\vartheta , w_i) = (\vartheta , w_x) \in {\mathfrak B} \), then by the \((\lhd <)\) rule we have that \((\vartheta , w_j) = (\vartheta , w_y)\in {\mathfrak B} \), for some \((\vartheta , w_i), (\vartheta , w_j), (\vartheta , w_x), (\vartheta , w_y) \in lab({\mathfrak B} )\). Thus, clause \(14\) is satisfied.
Assume for the sake of contradiction that both \((\vartheta , w_i) <(\vartheta , w_j) \in {\mathfrak B} \) and \((\vartheta , w_j) <(\vartheta , w_i) \in {\mathfrak B} \), for some \((\vartheta , w_i), (\vartheta , w_j) \in lab({\mathfrak B} )\). If \((\vartheta , w_i) <(\vartheta , w_j)\) holds, then the world represented by \((\vartheta , w_i)\) precedes the world represented by \((\vartheta , w_j)\). The same holds for \((\vartheta , w_j) <(\vartheta , w_i)\), where the world represented by \((\vartheta , w_j)\) precedes the world represented by \((\vartheta , w_i)\). We have a contradiction in this case, which is captured by the \((<\textsc {Abs})\) rule, and thus \({\mathfrak B} \) is closed. This is in contradiction with having \({\mathfrak B} \) open and exhausted. We argue analogously for the relations \(\lhd \) and \(\prec \) that are captured respectively by \((\lhd \textsc {Abs})\) and \((\prec \textsc {Abs})\). If we have these contradictions, then they are all captured properly by the above closure rules. Therefore, as \({\mathfrak B} \) is open and exhausted, clause \(15\) (that represents the above closing rules) is satisfied.
Assume for the sake of contradiction that both \((\vartheta , w_i) = (\vartheta , w_j) \in {\mathfrak B} \) and \((\vartheta , w_i)<(\vartheta , w_j) \in {\mathfrak B} \), for some \((\vartheta , w_i), (\vartheta , w_j)\in lab({\mathfrak B} )\). If \((\vartheta , w_i) = (\vartheta , w_j)\) is satisfied, then the labels \((\vartheta , w_i)\) and \((\vartheta , w_j)\) represent the same world. Instead, if \((\vartheta , w_i) < (\vartheta , w_j)\) is satisfied, then the world represented by \((\vartheta , w_i)\) precedes the world represented by \((\vartheta , w_j)\). Thus, we have a contradiction, which is captured by the \((=\textsc {Abs})\) rule, and \({\mathfrak B} \) is closed. This is in contradiction with having \({\mathfrak B} \) open and exhausted. We argue analogously for \(\lhd \) and \(\prec \), where \((=\textsc {Abs})\) captures even these cases. Therefore, as \({\mathfrak B} \) is open and exhausted, clause \(16\) (that represents the \((=\textsc {Abs})\) rule) is satisfied.
Assume for the sake of contradiction that \((\vartheta , w_i) \lhd (\vartheta , w_j) \in {\mathfrak B} \), \((\vartheta , w_i) <(\vartheta , w_z) \in {\mathfrak B} \) and \((\vartheta , w_z) <(\vartheta , w_j) \in {\mathfrak B} \), for some \((\vartheta , w_i)\), \((\vartheta , w_j)\), \((\vartheta , w_z) \in lab({\mathfrak B} )\). If \((\vartheta , w_i) \lhd (\vartheta , w_j)\) is satisfied, then the world represented by \((\vartheta , w_i)\) precedes the world represented by \((\vartheta , w_j)\) and there is no world between them. Instead, if \((\vartheta , w_i) <(\vartheta , w_z)\), and \((\vartheta , w_z) <(\vartheta , w_j)\) are satisfied, then the world represented by \((\vartheta , w_z)\) is between the worlds represented by \((\vartheta , w_i)\) and \((\vartheta , w_j)\). Thus, we have a contradiction, which is captured by the \((\lhd <\textsc {Abs})\) rule, and \({\mathfrak B} \) is closed. This is in contradiction with having \({\mathfrak B} \) open and exhausted. Therefore, as \({\mathfrak B} \) is open and exhausted, clause \(17\) (that represents the \((\lhd <\textsc {Abs})\) rule) is satisfied.
Assume that \((\vartheta , w):\square \phi \in {\mathfrak B} \) and \((\vartheta , w)<(\vartheta , w_i)\in {\mathfrak B} \) for some \((\vartheta , w_i)\in lab({\mathfrak B} )\). We have to show that \((\vartheta , w_i):\phi \in {\mathfrak B} \). If \((\vartheta , w):\square \phi \in {\mathfrak B} \) and \((\vartheta , w)<(\vartheta , w_i)\in {\mathfrak B} \) and \({\mathfrak B} \) is closed with respect to the rule \((\square )\), we have that \((\vartheta , w_i):\phi \in {\mathfrak B} \). Thus, clause \(18\) is satisfied.
Clause \(19\) must be satisfied since \({\mathfrak B} \) is closed with respect to the rule \((\diamondsuit )\).
Assume that \((\vartheta , w):{\phi _1 \, \fancyscript{C} \, \phi _2}\in {\mathfrak B} \) and \((\vartheta , w)<(\vartheta , w_i)\in {\mathfrak B} \) and \((\vartheta , w_i):\phi _1\in {\mathfrak B} \) for some \((\vartheta , w_i)\in lab({\mathfrak B} )\). We have to show that there exists a \((\vartheta , w_j) \in lab({\mathfrak B} )\), such that \((\vartheta , w_j):\phi _2 \in {\mathfrak B} \) and that \((\vartheta , w_i)<(\vartheta , w_j)\in {\mathfrak B} \). If \((\vartheta , w):{\phi _1 \, \fancyscript{C} \, \phi _2} \in {\mathfrak B} \), and \((\vartheta , w)<(\vartheta , w_i)\in {\mathfrak B} \), and \((\vartheta , w_i):\phi _1\in {\mathfrak B} \) and \({\mathfrak B} \) is closed with respect to the rule \((\fancyscript{C})\), then there exists a new world \((\vartheta , w_j)\in lab({\mathfrak B} )\), such that \((\vartheta , w_i)<(\vartheta , w_j)\in {\mathfrak B} \) and \((\vartheta , w_j):\phi _2 \in {\mathfrak B} \). Thus, clause \(20\) is satisfied.
Assume that \((\vartheta , w):{\phi _1 \, \fancyscript{P} \, \phi _2}\in {\mathfrak B} \) and \((\vartheta , w)\prec (\vartheta , w_j)\in {\mathfrak B} \) and \((\vartheta , w_j):\phi _2\in {\mathfrak B} \) for some \((\vartheta , w_j)\in lab({\mathfrak B} )\). We have to show that there exists a \((\vartheta , w_i) \in lab({\mathfrak B} )\), such that \((\vartheta , w_i):\phi _1 \in {\mathfrak B} \), \((\vartheta , w)<(\vartheta , w_i) \in {\mathfrak B} \), and \((\vartheta , w_i)<(\vartheta , w_j)\in {\mathfrak B} \). If \((\vartheta , w):{\phi _1 \, \fancyscript{P} \, \phi _2} \in {\mathfrak B} \), and \((\vartheta , w)\prec (\vartheta , w_j)\in {\mathfrak B} \), and \((\vartheta , w_j):\phi _2\in {\mathfrak B} \) and \({\mathfrak B} \) is closed with respect to the rule \((\fancyscript{P})\), then there exists a new world \((\vartheta , w_i)\in lab({\mathfrak B} )\), such that \((\vartheta , w)<(\vartheta , w_i) \in {\mathfrak B} \), \((\vartheta , w_i)<(\vartheta , w_j)\in {\mathfrak B} \) and \((\vartheta , w_i):\phi _1 \in {\mathfrak B} \). Thus, clause \(21\) is satisfied.
Assume that \((\vartheta , w):{\phi _1 \, \fancyscript{U} \, \phi _2}\in {\mathfrak B} \). We have to show that we have \((\vartheta , w):\phi _2 \in {\mathfrak B} \) or that there exists \((f_{{\phi _1 \, \fancyscript{U} \, \phi _2}}(\vartheta , w)) \in lab({\mathfrak B} )\) such that \((\vartheta , w)<(f_{{\phi _1 \, \fancyscript{U} \, \phi _2}}(\vartheta , w))\in {\mathfrak B} \) and \((f_{{\phi _1 \, \fancyscript{U} \, \phi _2}}(\vartheta , w)):\phi _2 \in {\mathfrak B} \). They are satisfied as \({\mathfrak B} \) is closed with respect to the \((\fancyscript{U}_1)\) rule. When we are in the second case, we have to show that for every world \((\vartheta , w_i)\in lab({\mathfrak B} )\), such that \((\vartheta , w)<(\vartheta , w_i) \in {\mathfrak B} \) and \((\vartheta , w_i)<(f_{{\phi _1 \, \fancyscript{U} \, \phi _2}}(\vartheta , w))\in {\mathfrak B} \) we have that \((\vartheta , w_i):\phi _1\in {\mathfrak B} \) and \((\vartheta , w_i):\lnot \phi _2\in {\mathfrak B} \). This case is satisfied as \({\mathfrak B} \) is closed with respect to the rule \((\fancyscript{U}_2)\). Thus, clause \(22\) is satisfied.
Clauses \(23\)–\(27\) are satisfied since \({\mathfrak B} \) is open. \(\square \)
We can finally prove Theorem 5, which entails Corollary 1.
Proof
(Theorem 5) Suppose the tableau built for \(X\) by the systematic construction does not close. The tableau must be open and exhausted, and must contain some open branch \({\mathfrak B} \) by definition. Lemma 6 guarantees that \({\mathfrak B} \) is a downward-exhausted set. Lemma 4 guarantees that \({\mathfrak B} \) has a model \({\mathfrak M} =(lab({\mathfrak B} ), {\mathfrak R} _\bullet , V )\). Furthermore, if \((\vartheta , w):\sigma \in {\mathfrak B} \), then we have that \(\models ^{\mathfrak M} (\vartheta , w):\sigma \) and also, if \((\vartheta , w_i)\bullet (\vartheta , w_j) \in {\mathfrak B} \), then \(\models ^{\mathfrak M} (\vartheta , w_i)\bullet (\vartheta , w_j)\), where \(\bullet \in \{=, <,\lhd , \prec \}\). We can do the same for all the labeled and relational formulas in \(X\). So, for every \((\vartheta , w):\sigma \) such that \((\vartheta , w):\sigma \in X\) and \((\vartheta , w):\sigma \in {\mathfrak B} \), we have that \(\models ^{\mathfrak M} (\vartheta , w):\sigma \), and also for every relational formula \((\vartheta , w_i)\bullet (\vartheta , w_j)\), such that \((\vartheta , w_i)\bullet (\vartheta , w_j)\in X\) and \((\vartheta , w_i)\bullet (\vartheta , w_j)\in {\mathfrak B} \), we have that \(\models ^{\mathfrak M} (\vartheta , w_i)\bullet (\vartheta , w_j)\). Therefore, \(\models ^{\mathfrak M} X\). \(\square \)
Appendix 3: Soundness of the rules of the third layer
We prove Theorem 4.
Proof
(Theorem 4) Let \({\mathfrak M} \) be an arbitrary model with its interpretation function \(\fancyscript{I}\). Assume we have a world \((\vartheta , w)\). Then, by definition of the relation \(\iota \), we know that \(\models ^{\mathfrak M} (\vartheta , w)\iota (\vartheta , w)\). Thus the \((\iota \textsc {Refl})\) rule is sound. We argue analogously for \((\simeq \textsc {Refl})\).
Assume we have a trace \(\vartheta \). Then, by definition of the relation \(\sim \), we know that \(\models ^{\mathfrak M} \vartheta \sim \vartheta \). Thus the \((\sim \textsc {Refl})\) rule is sound. We argue analogously for \((\cong \textsc {Refl})\).
Assume we have \(\vdash (\vartheta , w_i)\iota (\vartheta ^{\prime }, w_j)\). Then \(\models ^{\mathfrak M} (\vartheta ,w_i)\iota (\vartheta ^{\prime }, w_j)\), and then, by definition of \(\iota \), we have that \(\models ^{\mathfrak M} (\vartheta ^{\prime }, w_j)\iota (\vartheta , w_i)\). Thus the \((\iota \textsc {Sym})\) rule is sound. We argue analogously for \((\simeq \textsc {Sym})\).
Assume we have \(\vdash \vartheta \sim \vartheta ^{\prime }\). Then we have \(\models ^{\mathfrak M} \vartheta \sim \vartheta ^{\prime }\), and then, by definition of \(\sim \), we have that \(\models ^{\mathfrak M} \vartheta ^{\prime }\sim \vartheta \). Thus the \((\sim \textsc {Sym})\) rule is sound. We argue analogously for \((\cong \textsc {Sym})\).
Assume we have \(\vdash (\vartheta , w_i)\iota (\vartheta ^{\prime }, w_j)\) and \(\vdash (\vartheta ^{\prime }, w_j)\iota (\vartheta ^{\prime \prime }, w_k)\). Then we have \(\models ^{\mathfrak M} (\vartheta , w_i)\iota (\vartheta ^{\prime }, w_j)\) and \(\models ^{\mathfrak M} (\vartheta ^{\prime }, w_j)\iota (\vartheta ^{\prime \prime }, w_k)\), and then, by definition of \(\iota \), we have that \(\models ^{\mathfrak M} (\vartheta , w_i)\iota (\vartheta ^{\prime \prime }, w_k)\). Thus the \((\iota \textsc {Trans})\) rule is sound. We argue analogously for \((\simeq \textsc {Trans})\).
Assume we have \(\vdash \vartheta \sim \vartheta ^{\prime }\) and \(\vdash \vartheta ^{\prime }\sim \vartheta ^{\prime \prime }\). Then we have \(\models ^{\mathfrak M} \vartheta \sim \vartheta ^{\prime }\) and \(\models ^{\mathfrak M} \vartheta ^{\prime }\sim \vartheta ^{\prime \prime }\), and then, by definition of \(\sim \), we have that \(\models ^{\mathfrak M} \vartheta \sim \vartheta ^{\prime \prime }\). Thus the \((\sim \textsc {Trans})\) rule is sound. We argue analogously for \((\cong \textsc {Trans})\).
Assume we have \(\vdash (\vartheta , w_i)\lhd (\vartheta ^{\prime }, w_j)\) and \(\vdash (\vartheta , w_k)\lhd (\vartheta ^{\prime \prime }, w_l)\) and \(\vdash (\vartheta , w_i) = (\vartheta , w_k)\) and \(\vdash \vartheta ^{\prime } \cong \vartheta ^{\prime \prime }\). Then we have that \(\models ^{\mathfrak{M }} (\vartheta , w_i)\lhd (\vartheta ^{\prime }, w_j)\) and \(\models ^{\mathfrak{M }} (\vartheta , w_k)\lhd (\vartheta ^{\prime \prime }, w_l)\) and \(\models ^{\mathfrak{M }} (\vartheta , w_i)= (\vartheta , w_k)\) and \(\models ^{\mathfrak{M }} \vartheta ^{\prime } \cong \vartheta ^{\prime \prime }\). If we apply the \((\textsc {Subst}_2)\) rule, then we have \(\models ^{\mathfrak{M }} (\vartheta , w_i)\lhd (\vartheta ^{\prime \prime }, w_l)\). By the definition of \(\lhd \), we know that if there exists the immediate successor of a world, this immediate successor is unique when we deal with the same trace. As we have \(\models ^{\mathfrak{M }} \vartheta ^{\prime } \cong \vartheta ^{\prime \prime }\), this means that \((\vartheta ^{\prime }, w_j)\) and \((\vartheta ^{\prime \prime }, w_l)\) are in the same trace, thus, \(\models ^{\mathfrak{M }} (\vartheta ^{\prime }, w_j)=(\vartheta ^{\prime \prime }, w_l)\). Therefore, the rule \((\lhd = \cong )\) is sound.
Assume we have \(\vdash (\vartheta , w_i):\phi \), then we have \(\models ^{\mathfrak M} (\vartheta , w_i):\phi \). Assume to also have the world \((\vartheta ^{\prime }, w_j)\) such that \(\vdash (\vartheta , w_i)\simeq (\vartheta ^{\prime }, w_j)\), then we have that \(\models ^{\mathfrak M} (\vartheta , w_i)\simeq (\vartheta ^{\prime }, w_j)\). By definition of the \(\simeq \) relation, we have that \(\models ^{\mathfrak M} (\vartheta ^{\prime }, w_j):\phi \). Thus the \((\simeq \textsc {Mon})\) rule is sound.
Assume we have \(\vdash (\vartheta , w):{\phi _1 \, \fancyscript{B} \, \phi _2}\). Then \(\models ^{\mathfrak M} (\vartheta , w):{\phi _1 \, \fancyscript{B} \, \phi _2}\). Assume to also have \((\vartheta , w_i)\) such that \(\vdash (\vartheta , w_i):\lnot \phi _1\) and \(\vdash (\vartheta , w)<(\vartheta , w_i)\) and \(\vdash (\vartheta , w_0)\lhd (\vartheta , w_i)\), then we have that \(\models ^{\mathfrak M} (\vartheta , w_i):\lnot \phi _1\) and \(\models ^{\mathfrak M} (\vartheta , w)<(\vartheta , w_i)\) and \(\models ^{\mathfrak M} (\vartheta , w_0)\lhd (\vartheta , w_i)\). Assume to also have \(\vartheta ^{\prime }\) such that \(\vdash \vartheta |_{\le w_0}\sim \vartheta ^{\prime }|_{\le w_0}\), then we have that \(\models ^{\mathfrak M} \vartheta |_{\le w_0}\sim \vartheta ^{\prime }|_{\le w_0}\), and to also have \((\vartheta ^{\prime }, w_y)\) such that \(\vdash (\vartheta ^{\prime }, w_y):\phi _2\) and \(\vdash (\vartheta , w_0)<(\vartheta ^{\prime }, w_y)\), then we have that \(\models ^{\mathfrak M} (\vartheta ^{\prime }, w_y):\phi _2\) and \(\models ^{\mathfrak M} (\vartheta , w_0)<(\vartheta ^{\prime }, w_y)\). By definition of the \(\fancyscript{B}\) operator, we then have that there exist the fresh worlds \((\vartheta ^{\prime }, w_j)\), \((\vartheta , w_x)\), \((\vartheta , w_k)\) and \((\vartheta ^{\prime }, w_h)\) such that \(\models ^{\mathfrak M} (\vartheta ^{\prime }, w_j)\iota (\vartheta , w_i)\) and \(\models ^{\mathfrak M} (\vartheta , w_0)\lhd (\vartheta ^{\prime }, w_j)\) and \(\models ^{\mathfrak M} (\vartheta ^{\prime }, w_j):\phi _1\) and \(\models ^{\mathfrak M} (\vartheta , w)<(\vartheta ^{\prime }, w_j)\) and \(\models ^{\mathfrak M} (\vartheta ^{\prime }, w_j)<(\vartheta ^{\prime }, w_y)\) and \(\models ^{\mathfrak M} (\vartheta , w_x)\iota (\vartheta ^{\prime }, w_y)\) and \(\models ^{\mathfrak M} (\vartheta , w_i)<(\vartheta , w_x)\) and \(\models ^{\mathfrak M} (\vartheta , w_x):\phi _2\) and \(\models ^{\mathfrak M} (\vartheta , w_i)<(\vartheta , w_{k})\) and \(\models ^{\mathfrak M} (\vartheta , w_{k}):\phi _2\) and \(\models ^{\mathfrak M} (\vartheta ^{\prime }, w_j)<(\vartheta ^{\prime }, w_h)\) and \(\models ^{\mathfrak M} (\vartheta , w_{k})\iota (\vartheta ^{\prime }, w_h)\) and \(\models ^{\mathfrak M} (\vartheta ^{\prime }, w_h):\lnot \phi _2\). Thus, the rule \((\fancyscript{B})\) is sound.
Assume we have \(\vdash (\vartheta , w):{\phi _1 \, \fancyscript{M} \, \phi _2}\). Then we have that \(\models ^{\mathfrak M} (\vartheta , w):{\phi _1 \, \fancyscript{M} \, \phi _2}\). Assume to also have \((\vartheta , w_i)\) such that \(\vdash (\vartheta , w_i):\lnot \phi _1\), \(\vdash (\vartheta , w)<(\vartheta , w_i)\) and \(\vdash (\vartheta , w_0)\lhd (\vartheta , w_i)\), then we have that \(\models ^{\mathfrak M} (\vartheta , w_i):\lnot \phi _1\) and \(\models ^{\mathfrak M} (\vartheta , w)<(\vartheta , w_i)\) and \(\models ^{\mathfrak M} (\vartheta , w_0)\lhd (\vartheta , w_i)\), and to also have \(\vartheta ^{\prime }\) such that \(\vdash \vartheta |_{\le w_0}\sim \vartheta ^{\prime }|_{\le w_0}\), then we have that \(\models ^{\mathfrak M} \vartheta |_{\le w_0}\sim \vartheta ^{\prime }|_{\le w_0}\), and to also have \((\vartheta , w_p)\) such that \(\vdash (\vartheta , w_p):{\phi _2 \, \fancyscript{C} \, \phi _3}\), then we have that \(\models ^{\mathfrak M} (\vartheta , w_p):{\phi _2 \, \fancyscript{C} \, \phi _3}\). Moreover, assume further to have \((\vartheta , w_r)\) such that \(\vdash (\vartheta , w_r):\phi _2\) and \(\vdash (\vartheta , w_p)<(\vartheta , w_r)\) and \(\vdash (\vartheta , w_r)<(\vartheta , w_i)\), then we have that \(\models ^{\mathfrak M} (\vartheta , w_r):\phi _2\) and \(\models ^{\mathfrak M} (\vartheta , w_p)<(\vartheta , w_r)\) and \(\models ^{\mathfrak M} (\vartheta , w_r)<(\vartheta , w_i)\), and to also have \((\vartheta ^{\prime }, w_y)\) such that \(\vdash (\vartheta ^{\prime }, w_y):\phi _3\) and \(\vdash (\vartheta , w_0)<(\vartheta ^{\prime }, w_y)\), then we have that \(\models ^{\mathfrak M} (\vartheta ^{\prime }, w_y):\phi _3\) and \(\models ^{\mathfrak M} (\vartheta , w_0)<(\vartheta ^{\prime }, w_y)\). By definition of the \(\fancyscript{M}\) operator, we then have that there exist the four fresh worlds \((\vartheta ^{\prime }, w_j)\), \((\vartheta , w_x)\), \((\vartheta , w_k)\), \((\vartheta ^{\prime }, w_h)\) such that \(\models ^{\mathfrak M} (\vartheta ^{\prime }, w_j)\iota (\vartheta , w_i)\), \(\ \models ^{\mathfrak M} (\vartheta , w_0)\lhd (\vartheta ^{\prime }, w_j)\), \(\ \models ^{\mathfrak M} (\vartheta ^{\prime }, w_j):\phi _1\), \(\ \models ^{\mathfrak M} (\vartheta , w)<(\vartheta ^{\prime }, w_j)\), \(\models ^{\mathfrak M} (\vartheta ^{\prime }, w_j)<(\vartheta ^{\prime }, w_y)\), \(\ \models ^{\mathfrak M} (\vartheta , w_x)\iota (\vartheta ^{\prime }, w_y)\), \(\ \models ^{\mathfrak M} (\vartheta , w_i)<(\vartheta , w_x)\), \(\models ^{\mathfrak M} (\vartheta , w_x):\phi _3\), \(\models ^{\mathfrak M} (\vartheta , w_i)<(\vartheta , w_{k})\), \(\models ^{\mathfrak M} (\vartheta , w_{k}):\phi _3\), \(\models ^{\mathfrak M} (\vartheta ^{\prime }, w_j)<(\vartheta ^{\prime }, w_h)\), \(\models ^{\mathfrak M} (\vartheta , w_{k})\iota (\vartheta ^{\prime }, w_h)\) and \(\models ^{\mathfrak M} (\vartheta ^{\prime }, w_h):\lnot \phi _3\). Thus, the rule \((\fancyscript{M})\) is sound.
We now turn to the closure rules of these operators and prove their soundness.
Assume we have \(\vdash (\vartheta , w):{\phi _1 \, \fancyscript{B} \, \phi _2}\), then we have that \(\models ^{\mathfrak M} (\vartheta , w):{\phi _1 \, \fancyscript{B} \, \phi _2}\). Assume to also have \((\vartheta , w_i)\) such that \(\vdash (\vartheta , w_i):\lnot \phi _1\) and \(\vdash (\vartheta , w)<(\vartheta , w_i)\) and \(\vdash (\vartheta , w_0)\lhd (\vartheta , w_i)\), then we have that \(\models ^{\mathfrak M} (\vartheta , w_i):\lnot \phi _1\) and \(\models ^{\mathfrak M} (\vartheta , w)<(\vartheta , w_i)\) and \(\models ^{\mathfrak M} (\vartheta , w_0)\lhd (\vartheta , w_i)\), and to also have \(\vartheta ^{\prime }\) such that \(\vdash \vartheta |_{\le w_0}\sim \vartheta ^{\prime }|_{\le w_0}\), then we have that \(\models ^{\mathfrak M} \vartheta |_{\le w_0}\sim \vartheta ^{\prime }|_{\le w_0}\). Assume to also have \((\vartheta ^{\prime }, w_y)\) such that \(\vdash (\vartheta ^{\prime }, w_y):\phi _2\) and \(\vdash (\vartheta , w_0)<(\vartheta ^{\prime }, w_y)\), then we have that \(\models ^{\mathfrak M} (\vartheta ^{\prime }, w_y):\phi _2\) and \(\models ^{\mathfrak M} (\vartheta , w_0)<(\vartheta ^{\prime }, w_y)\), and to also have \((\vartheta ^{\prime }, w_j)\) such that \(\vdash (\vartheta ^{\prime }, w_j):\square \phi _2\) and \(\vdash (\vartheta , w_0)\lhd (\vartheta ^{\prime }, w_j)\), then we have that \(\models ^{\mathfrak M} (\vartheta ^{\prime }, w_j):\square \phi _2\) and \(\models ^{\mathfrak M} (\vartheta , w_0)\lhd (\vartheta ^{\prime }, w_j)\). By the \((\fancyscript{B})\) rule, we have that there exists \((\vartheta ^{\prime }, w_h)\) such that \(\models ^{\mathfrak M} (\vartheta ^{\prime }, w_j)<(\vartheta ^{\prime }, w_h)\) and \(\models ^{\mathfrak M} (\vartheta ^{\prime }, w_h):\lnot \phi _2\). By the \((\square )\) rule, as for \((\vartheta ^{\prime }, w_h)\), we have \(\models ^{\mathfrak M} (\vartheta ^{\prime }, w_j)<(\vartheta ^{\prime }, w_h)\), and we then have that \(\models ^{\mathfrak M} (\vartheta ^{\prime }, w_h):\phi _2\), which is in contradiction with \(\models ^{\mathfrak M} (\vartheta ^{\prime }, w_h):\lnot \phi _2\), given by the \((\fancyscript{B})\) rule. Thus, the rule \((\fancyscript{B}\textsc {Abs}_1)\) is sound.
Assume we have \(\vdash (\vartheta , w):{\phi _1 \, \fancyscript{B} \, \phi _2}\), then we have that \(\models ^{\mathfrak M} (\vartheta , w):{\phi _1 \, \fancyscript{B} \, \phi _2}\). Assume to also have \((\vartheta , w_i)\) such that \(\vdash (\vartheta , w_i):\lnot \phi _1\) and \(\vdash (\vartheta , w)<(\vartheta , w_i)\) and \(\vdash (\vartheta , w_0)\lhd (\vartheta , w_i)\) and \(\vdash (\vartheta , w_i):\square \lnot \phi _2\), then we have that \(\models ^{\mathfrak M} (\vartheta , w_i):\lnot \phi _1\) and \(\models ^{\mathfrak M} (\vartheta , w)<(\vartheta , w_i)\) and \(\models ^{\mathfrak M} (\vartheta , w_0)\lhd (\vartheta , w_i)\) and \(\models ^{\mathfrak M} (\vartheta , w_i):\square \lnot \phi _2\), and to also have \(\vartheta ^{\prime }\) such that \(\vdash \vartheta |_{\le w_0}\sim \vartheta ^{\prime }|_{\le w_0}\), then we have that \(\models ^{\mathfrak M} \vartheta |_{\le w_0}\sim \vartheta ^{\prime }|_{\le w_0}\). Assume to also have \((\vartheta ^{\prime }, w_y)\) such that \(\vdash (\vartheta ^{\prime }, w_y):\phi _2\) and \(\vdash (\vartheta , w_0)<(\vartheta ^{\prime }, w_y)\), then we have that \(\models ^{\mathfrak M} (\vartheta ^{\prime }, w_y):\phi _2\) and \(\models ^{\mathfrak M} (\vartheta , w_0)<(\vartheta ^{\prime }, w_y)\). By the \((\fancyscript{B})\) rule, we have that there exists \((\vartheta , w_k)\) such that \(\models ^{\mathfrak M} (\vartheta , w_i)<(\vartheta , w_k)\) and \(\models ^{\mathfrak M} (\vartheta , w_k):\phi _2\). By the \((\square )\) rule, as for the world \((\vartheta , w_k)\) we have \(\models ^{\mathfrak M} (\vartheta , w_i)<(\vartheta , w_k)\), we then have that \(\models ^{\mathfrak M} (\vartheta , w_k):\lnot \phi _2\), which is in contradiction with \(\models ^{\mathfrak M} (\vartheta , w_k):\phi _2\), given by the \((\fancyscript{B})\) rule. Thus, the rule \((\fancyscript{B}\textsc {Abs}_2)\) is sound.
Assume we have \(\vdash (\vartheta , w):{\phi _1 \, \fancyscript{M} \, \phi _2}\), then we have that \(\models ^{\mathfrak M} (\vartheta , w):{\phi _1 \, \fancyscript{M} \, \phi _2}\). Assume to also have \((\vartheta , w_i)\) such that \(\vdash (\vartheta , w_i):\lnot \phi _1\) and \(\vdash (\vartheta , w)<(\vartheta , w_i)\) and \(\vdash (\vartheta , w_0)\lhd (\vartheta , w_i)\), then we have that \(\models ^{\mathfrak M} (\vartheta , w_i):\lnot \phi _1\) and \(\models ^{\mathfrak M} (\vartheta , w)<(\vartheta , w_i)\) and \(\models ^{\mathfrak M} (\vartheta , w_0)\lhd (\vartheta , w_i)\), and to also have \(\vartheta ^{\prime }\) such that \(\vdash \vartheta |_{\le w_0}\sim \vartheta ^{\prime }|_{\le w_0}\), then we have that \(\models ^{\mathfrak M} \vartheta |_{\le w_0}\sim \vartheta ^{\prime }|_{\le w_0}\). Assume to also have \((\vartheta , w_p)\) such that \(\vdash (\vartheta , w_p):{\phi _2 \, \fancyscript{C} \, \phi _3}\), then we have that \(\models ^{\mathfrak M} (\vartheta , w_p):{\phi _2 \, \fancyscript{C} \, \phi _3}\), and to also have \((\vartheta , w_r)\) such that \(\vdash (\vartheta , w_r):\phi _2\) and \(\vdash (\vartheta , w_p)<(\vartheta , w_r)\) and \(\vdash (\vartheta , w_r)<(\vartheta , w_i)\), then we have that \(\models ^{\mathfrak M} (\vartheta , w_r):\phi _2\) and \(\models ^{\mathfrak M} (\vartheta , w_p)<(\vartheta , w_r)\) and \(\models ^{\mathfrak M} (\vartheta , w_r)<(\vartheta , w_i)\). Assume to also have \((\vartheta ^{\prime }, w_y)\) such that \(\vdash (\vartheta ^{\prime }, w_y):\phi _3\) and \(\vdash (\vartheta , w_0)<(\vartheta ^{\prime }, w_y)\), then we have that \(\models ^{\mathfrak M} (\vartheta ^{\prime }, w_y):\phi _3\) and \(\models ^{\mathfrak M} (\vartheta , w_0)<(\vartheta ^{\prime }, w_y)\), and to also have \((\vartheta ^{\prime }, w_j)\) such that \(\vdash (\vartheta ^{\prime }, w_j):\square \phi _3\) and \(\vdash (\vartheta , w_0)\lhd (\vartheta ^{\prime }, w_j)\), then we have that \(\models ^{\mathfrak M} (\vartheta ^{\prime }, w_j):\square \phi _3\) and \(\models ^{\mathfrak M} (\vartheta , w_0)\lhd (\vartheta ^{\prime }, w_j)\). By the \((\fancyscript{M})\) rule, we have that there exists \((\vartheta ^{\prime }, w_h)\) such that \(\models ^{\mathfrak M} (\vartheta ^{\prime }, w_j)<(\vartheta ^{\prime }, w_h)\) and \(\models ^{\mathfrak M} (\vartheta ^{\prime }, w_h):\lnot \phi _3\). By the \((\square )\) rule, as for the world \((\vartheta ^{\prime }, w_h)\) we have \(\models ^{\mathfrak M} (\vartheta ^{\prime }, w_j)<(\vartheta ^{\prime }, w_h)\), we then have that \(\models ^{\mathfrak M} (\vartheta ^{\prime }, w_h):\phi _3\), which is in contradiction with \(\models ^{\mathfrak M} (\vartheta ^{\prime }, w_h):\lnot \phi _3\), given by the \((\fancyscript{M})\) rule. Thus, the rule \((\fancyscript{M}\textsc {Abs}_1)\) is sound.
Assume we have \(\vdash (\vartheta , w):{\phi _1 \, \fancyscript{M} \, \phi _2}\), then we have that \(\models ^{\mathfrak M} (\vartheta , w):{\phi _1 \, \fancyscript{M} \, \phi _2}\). Assume to also have \((\vartheta , w_i)\) such that \(\vdash (\vartheta , w_i):\lnot \phi _1\) and \(\vdash (\vartheta , w)<(\vartheta , w_i)\) and \(\vdash (\vartheta , w_0)\lhd (\vartheta , w_i)\), and \(\vdash (\vartheta , w_i):\square \lnot \phi _3\), then we have that \(\models ^{\mathfrak M} (\vartheta , w_i):\lnot \phi _1\) and \(\models ^{\mathfrak M} (\vartheta , w)<(\vartheta , w_i)\) and \(\models ^{\mathfrak M} (\vartheta , w_0)\lhd (\vartheta , w_i)\) and \(\models ^{\mathfrak M} (\vartheta , w_i):\square \lnot \phi _3\), and to also have \(\vartheta ^{\prime }\) such that \(\vdash \vartheta |_{\le w_0}\sim \vartheta ^{\prime }|_{\le w_0}\), then we have that \(\models ^{\mathfrak M} \vartheta |_{\le w_0}\sim \vartheta ^{\prime }|_{\le w_0}\). Assume to also have \((\vartheta , w_p)\) such that \(\vdash (\vartheta , w_p):{\phi _2 \, \fancyscript{C} \, \phi _3}\), then we have that \(\models ^{\mathfrak M} (\vartheta , w_p):{\phi _2 \, \fancyscript{C} \, \phi _3}\), and to also have \((\vartheta , w_r)\) such that \(\vdash (\vartheta , w_r):\phi _2\) and \(\vdash (\vartheta , w_p)<(\vartheta , w_r)\) and \(\vdash (\vartheta , w_r)<(\vartheta , w_i)\) we have that \(\models ^{\mathfrak M} (\vartheta , w_r):\phi _2\) and \(\models ^{\mathfrak M} (\vartheta , w_p)<(\vartheta , w_r)\) and \(\models ^{\mathfrak M} (\vartheta , w_r)<(\vartheta , w_i)\). Assume to also have \((\vartheta ^{\prime }, w_y)\) such that \(\vdash (\vartheta ^{\prime }, w_y):\phi _3\) and \(\vdash (\vartheta , w_0)<(\vartheta ^{\prime }, w_y)\), then we have that \(\models ^{\mathfrak M} (\vartheta ^{\prime }, w_y):\phi _3\) and \(\models ^{\mathfrak M} (\vartheta , w_0)<(\vartheta ^{\prime }, w_y)\). By the \((\fancyscript{M})\) rule, we have that there exists \((\vartheta , w_k)\) such that \(\models ^{\mathfrak M} (\vartheta , w_i)<(\vartheta , w_k)\) and \(\models ^{\mathfrak M} (\vartheta , w_k):\phi _3\). By the \((\square )\) rule, as for the world \((\vartheta , w_k)\) we have \(\models ^{\mathfrak M} (\vartheta , w_i)<(\vartheta , w_k)\), we then have that \(\models ^{\mathfrak M} (\vartheta , w_k):\lnot \phi _3\), which is in contradiction with \(\models ^{\mathfrak M} (\vartheta , w_k):\phi _3\), given by the \((\fancyscript{M})\) rule. Thus, the rule \((\fancyscript{M}\textsc {Abs}_2)\) is sound. \(\square \)
Rights and permissions
About this article
Cite this article
Cristani, M., Karafili, E. & Viganò, L. Tableau systems for reasoning about risk. J Ambient Intell Human Comput 5, 215–247 (2014). https://doi.org/10.1007/s12652-013-0186-7
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s12652-013-0186-7