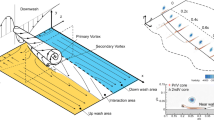
Abstract
Flow visualization experiments were conducted in a water channel and a low-speed wind tunnel at Reynolds number of 1.54 \(\times\) 104 to 1.2 \(\times\) 105 for a leading-edge extension model, which is referred to as a NASA TP-1803 model in this study. In addition, particle image velocimetry velocity measurements were taken in the water channel to obtain the quantitative information about the three-dimensional velocity field over the strake and wing surfaces. The results obtained at low, medium and high angles of attacks represent three distinct cases of interaction between the strake and wing vortices. Namely, at α = 5o and 10° the strake and wing vortices were developed over the wing surface without significant interaction noticed; at α = 20°, the strake vortex strongly interacted with the wing vortex in an intertwining manner, which was sensitive to Reynolds number; at α = 30°, the breakdown of the strake vortex took place close to the junction of the strake and the wing; thus, the interaction of the strake and the wing vortices appeared to be less significant than the case of α = 20°.
Graphic abstract

Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
In the development of a modern fighter, significant attention is drawn to its maneuverability (Herbest 1983; Kölzsch and Breitsamter 2014), which predominantly relies on the aerodynamic performance at high angle of attack. Under such a flight condition, separation vortices originated from the lifting surfaces play a key role in determining the aerodynamic characteristics (Polhamus 1966; Miau et al. 1992).
The lifting surfaces of a fighter configuration could be modeled by a delta wing planform, generically speaking. Concerning a delta wing planform at an angle of attack, the incoming freestream gets separated from the leading edges and rolled up into two large-scale counter-rotating vortices above the upper surface of the wing. The massive air gets entrained into each of the vortices and accelerated, resulting in a low-pressure center at the vortex core. This is known as the mechanism of producing the vortex lift (McMahon and Wentz 1966; Polhamus 1966; Miau et al. 1992; Kölzsch and Breitsamter 2014). In the past decades, a great deal of efforts have been contributed to understand the flow characteristics of delta wing models at high angles of attack, for which the phenomenon of vortex breakdown and control was intensively studied. A favorable design concept was referred to as the leading-edge extension (LEX) with a strake extended upstream from the leading edge of the main wing, for instance, a double-delta wing configuration (Luckring 1979a; Lamar and Frink 1981; Erickson 1982; Vigevano 1982). For such a wing planform, not only the vortex stability but also the lift can be improved greatly. Physically speaking, for a LEX configuration, the freestream flow separated from the leading edge of the strake would roll up to the upper surface of the strake. As a result, the strake vortex generated could interact with the wing vortex downstream. It is beneficial from the perspective of vortex flow control that the interaction would delay vortex breakdown above the main wing surface to higher angle of attack, thus improving the overall maneuverability. McMahon and Wentz (1966) investigated flows over the delta and double-delta wing configurations. They concluded that the principal effect of the strake on the double-delta configuration was to increase the vortex strength over the wing surface, resulting in an increase in normal force for a given angle of attack. Luckring (1979a) and Moore et al. (1979) studied the strake–wing configurations to investigate the longitudinal aerodynamic characteristics. As found, the strake could not only provide additional lift to the aircraft, but also improve the stability of the vortex structure associated with the wing. Cobleigh and Frate (1994) pointed out that the vortex generated by the strake would increase the rotation speed of the wing vortex, thus increasing the stability of the vortex.
Further insights into the physical process of vortex interaction can be learned from a number of studies reported on the strake–wing configurations. On flow over a strake and wing model, Luckring (1979b) observed that at low angle of attack the vortices originated from the strake and the wing remained separated as individual vortices over the wing surface, whereas at higher angle of attack the interaction got significant. Lamar (1980) addressed that in the interaction process, the strake and wing vortices would not merge together, but the wing vortex would be displaced away from the upper surface by the strake vortex, thus allowing the strake vortex to dominate the flow field. Based on the flow visualization results on a 76°/40° double-delta wing at α = 20o obtained in a low-speed wind tunnel, Verhaagen et al. (1995) pointed out that the interaction of the strake and wing vortices like co-rotating vortices, which would lead to one of the vortices in a helical path around the other. The findings were further confirmed by the pressure measurements on the model surface and the numerical computation. Li et al. (2013) reported the result of numerical simulation for flow over a 76°/40° double-delta wing at α = 22.5°, a case of strong interaction between the strake and wing vortices involved with the development of the cross-flow vortices. Thompson (1985) conducted a hydrogen-bubble flow visualization experiment of flows over a family of four double-delta wing models in a water towing tank and observed that whether the wing or strake vortex would be dominant in the interaction depended on the relative strengths of the two vortices and their distance in the spanwise direction. Malcolm and Nelson (1987) conducted the flow visualization experiments on a series of generic fighter configurations in a water tunnel and a wind tunnel. At high angles of attack, the interaction of the LEX and wing vortices appeared to be strongly intertwining until they both got burst near the trailing edge of the wing. Ekaterinaris et al. (1995) conducted a numerical study of flow over a 76°/40° double-delta wing at Mach number 0.22, for which the interaction of the vortices on the leeward side was examined at Reynolds number 4 \(\times\) 106. The results obtained at various angles of attack showed that as the angle of attack got higher, the vortex interaction got significant. In particular, the results of α = 19° and 22.4o illustrated that the interaction of the strake and wing vortices was featured with merging and subsequently breakdown near the trailing edge. Zhang et al. (2016) studied the interaction of strake and wing vortices over a 70°/50° double-delta by PIV. A dual-vortex structure of the strake vortices was observed. As the angle of attack increased, strake and wing vortices moved closer to each other and resulted in intensified interaction, leading to vortices merging and earlier onset of vortex breakdown.
The effect of Reynolds number in the interaction of vortices over a number of wing configurations was addressed in the literature. Watanabe et al. (2004) studied a cranked arrow wing with a center body for the Reynolds numbers in a range from 0.15 \(\times\) 106 to 1.5 \(\times\) 106 by PIV. With increasing angle of attack, the vorticity, velocity magnitude and turbulence kinetic energy in the core of the leading edge separation vortex got increased, while the radius of vortex core got decreased until the vortices breakdown. On the other hand, with increasing the Reynolds number, the radius and vorticity of the vortex core got larger and weaker, respectively, while the turbulence kinetic energy remained almost constant. Thu et al. (2012) investigated the effect of Reynolds number over a 76° /40° double-delta wing for α = 10° to 30° using a dye injection method in a water tunnel facility. With increasing Reynolds number, the trajectories of the strake and wing vortices got closer to each other and situated closer to the wing surface. But the breakdown location of the strake vortex did not change with Reynolds number. Durhasan and Karasu (2019) investigated the Reynolds number effect on different-kink-angle double-delta wing. As found, two interaction modes named the spiral and enveloping modes were observed; the spiral mode would switch to the enveloping mode as Reynolds number increased.
Despite that the experimental and numerical efforts reported in the literature have unveiled various aspects concerning the interaction of the strake and wing vortices, detailed features of the phenomenon have not been fully explored, in particular the three-dimensional aspects of the interaction process. Motivated by this consideration, this work was conducted experimentally to study the flow characteristics of a LEX model referred to as a NASA TP-1803 (Lamar and Frink 1981) model for the angles of attack up to 30°. Flow visualization experiments were conducted in a water channel and a low-speed wind tunnel, respectively. Moreover, since the Reynolds numbers of the experiments performed in the wind tunnel could be varied from 3.7 \(\times\) 104 to 1.2 \(\times\) 105, the results obtained allowed us to look into the effect of Reynolds number with regard to the interaction of the strake and wing vortices. Moreover, the three-dimensional aspects concerning the flow phenomenon of interest was examined by PIV in the water channel experiment. A reconstruction of the 3D mean flow field based on the PIV data obtained at 22 longitudinal cross-sectional planes in the region of interest enabled us to carry out further discussion on the flow phenomenon of interest for different angles of attack.
2 Methodology
2.1 Testing model
The experiments were conducted with a NASA TP-1803 model (Lamar and Frink 1981). A schematic drawing of the model is shown in Fig. 1, featuring sharp leading edges at the strake and main wings whose sweep angles were 60.6° and 44°, respectively. The experimental model was made by a 3D printer, which was subsequently sandpapered and sprayed with the water-proof paint. The model surface was finished with a 2000-grit sandpaper to ensure the model surface as smooth as possible. It is worthwhile to mention that no trip device was applied on the model surface.
It is shown in Fig. 1 that the wingspan and fuselage of the model are 182 mm and 281 mm in length, respectively; the root-chord length, C, is 108 mm, which is denoted as the reference length in this study. The blockage ratios of the model at α = 30° in the test sections of the water channel and wind wing tunnel are 3.1% and 5.6%, respectively. According to Choi and Kwon (1998), if the blockage ratios of bluff bodies in wind tunnel experiments are less than 10%, the blockage effect on the aerodynamic behaviors could be insignificant. In the present study, no further considerations were made to correct the blockage effect due to the model for α up to 30°.
2.2 Low-speed recirculating water channel
The experiments were conducted in a low-speed recirculating water channel. The test section was square in cross section, 0.6 m by 0.6 m and 2.5 m in length. The turbulence intensity measured by PIV at 1 m downstream of the inlet of the test section was about 1% for the incoming freestream velocity up to 0.1 m/s (Chou 2020). The water channel normally is operated for the freestream velocity in a range of 0.05 m/s to 0.15 m/s. Figure 2 shows a photograph of the model in the test section for the PIV measurements that the upper surface of the wing model was facing downward, because the laser sheet was introduced from the bottom of the test section.
2.3 Low-speed wind tunnel
Experiments were also performed in an open-jet low-speed wind tunnel whose test section was circular in cross section of 0.5 m in diameter and 2.5 m in length (Yu et al. 2016; Dong et al. 2019). The freestream turbulence intensity measured in the test section was less than 0.7% for the velocity in a range of 5–40 m/s (Li 2013). In this study, the experimental model was situated in an extension section of 0.4 m in length added at the end of the test section. During the experiment, no sensible vibrations were detected on the extension structure for the flow velocity up to 30 m/s. This was examined with a laser pointer situated on the extension beaming the light to a normal plate 1.8 m downstream. The amplitude of vibrations of the laser point on the wall was less than 1 mm.
2.4 Flow visualization methods
There are three methods of flow visualization employed in this study, which are briefly described below.
2.4.1 Dye injection method
For the dye injection method, the dye was prepared with the artificial food color mixed with water. The dye solution was filled in a container elevated above the model. Thus, the dye could be introduced into the test section via a plastic tube due to the gravity effect. A manual valve was used to control the exit velocity from the injection tube to be close to the freestream velocity. The density of the dye should match that of the working fluid to avoid the buoyancy effect induced. Moreover, the Reynolds number based on the diameter of the injection tube should be less than 40; otherwise, the tube could easily induce shedding vortices downstream (Zdravkovich 1997).
2.4.2 Ink-dot method
In the ink-dot method, a water-color paint was applied on the model surface in dots. Once the water-color paint dissolved in water for a certain length of time, the limiting streamlines (Lighthill 1963) on the surface were emerged, as a result of the water-color paint dragged by the action of the shear stress. Note that the limiting streamline pattern that emerged actually is equivalent to the wall shear stress pattern. In this method, care should be taken to adjust the concentration of the paint in order to optimize the length of each of the ink dots in the final appearance, which could vary in different regions depending on the magnitude of the shear stresses.
2.4.3 Oil-film method
In the wind tunnel experiment, the oil film coated on the model was made of the paraffin oil and TiO2 powder. On the other hand, in the water channel experiment the oil film applied on the model was made of the water-color paint. By this method, the secondary separation lines induced by the vortex structures over the wing surface or the location of vortex breakdown in the flow field could be identified.
2.5 Particle image velocimetry (PIV)
A two-component (2D) particle image velocimetry (PIV) was employed for velocity measurements in the water channel. It was equipped with an Argon ion laser of 5 W, Innova 70, to produce a light sheet, which was introduced into the test section to illuminate a longitudinal plane for velocity measurement. Hollow glass microspheres of 11 \(\mathrm{\mu m}\) in diameter were seeded in the flow to intensify the scattered light in the plane measured. A high-speed camera, IDT N4 series, was employed to take images of 181 \(\times\) 129 mm2 in area at a rate of 200 frames per second, for a time length of 6.3 s per measurement. The resolution of each of the images was 5.6 pixels/mm. In processing the images, a two-dimensional velocity vector was resolved within an interrogation window of 16 \(\times\) 16 pixels, which was complied with the 1/4 rule proposed by Keane and Adrian (1992). More details about this system are described in Chou (2020).
2.6 Coordinate system and the cross sections defined for PIV velocity measurements
In this study, the origin of the coordinate system is located at the leading edge of the strake where the distance from the centerline of the fuselage is 30 mm. See Fig. 3 for the origin (x, y, z) = (0, 0, 0) defined.
The PIV velocity measurements were taken at 10 longitudinal cross sections above the strake surface and 12 longitudinal cross sections above the wing surface, which are also indicated in Fig. 3. The PIV data obtained in the 22 cross-sectional planes enabled us to construct a three-dimensional view of the mean flow field of the region interested.
3 Results and discussion
3.1 Results of flow visualization
Results of flow visualization obtained with the TP-1803 model at α = 5°, 100, 20° and 30° are presented below. In this study, the Reynolds number (Re) is defined based on the freestream velocity, U0, and the root chord length of the wing, C, shown in Fig. 1.
3.1.1 Flow visualization results of the TP-1803 model at \(\alpha\) = 5° and 10°
Figure 4 presents a photograph obtained in the water channel experiment at α = 5° for Re = 1.54 \(\times\) 104 by having the oil film coated on the model surface. The formations of the strake and wing vortices are revealed from the image. While the strake vortex is developed into a sizable scale over the wing surface, the wing vortex is rather limited in region close to the leading edge. The formation of the strake vortex gets prominent at α = 10° as seen in the photograph in Fig. 5, in which the red color dye streak released from the tip of the strake reveals that the strake vortex develops into a large-scale flow structure toward the trailing edge of the wing.
The development of flow structures of the stake vortex together with the wing vortex can be further learned from Fig. 6, a photograph obtained by the oil-film method in the wind tunnel experiment at α = 10° and Re = 5.7 \(\times\) 104. It is seen that the strake vortex dominates in the inboard region above the wing surface, for which the secondary separation line induced persists to the trailing edge. Similarly, the secondary separation line induced by the wing vortex is remarkable which persists to the trailing edge of the wing as well. In viewing that the secondary separation lines associated with the flow re-attachment of the individual vortices on the wing surface are clearly distinguishable, the interaction between the vortices is referred as rather insignificant.
3.1.2 Flow visualization results of TP-1803 model at \(\alpha\)= 20°
Figure 7 presents a photograph obtained in the water channel at \(\alpha\)= 20° for Re = 1.54 \(\times\) 104. The dye released from a location near the leading edge of the strake unveils the occurrence of vortex breakdown near the trailing edge of the wing. Moreover, the interaction between the strake vortex and the wing vortex could be discerned in Fig. 8, a photograph obtained with the oil film coated on the strake surface. Interestingly seen in the photograph is that the wing vortex generated from the apex of the wing tended to roll over to the inboard side of the strake vortex, which was progressing in a three-dimensional spiraling motion. The appearance could be referred to as a spiral/coiling-type interaction in Gai et al. (2004). In the present case, the strake vortex appears to be predominant and drawing the wing vortex coiled around. The interaction can also be examined with an image in Fig. 9 obtained by the ink-dot method, in which the secondary separation line induced by the strake vortex can be identified, while the flow motion associated with the wing vortex is vaguely seen. Notably, in the mid-region on the wing surface, a large-scale spiral separation is developed. A sketch depicting an overview of this situation is given in Fig. 10. While the strake vortex is dominant over the wing surface, the large-scale spiral separation is involved with the reversed flow induced by the separated shear layer originated from the leading edge of the main wing.
As for the wind tunnel experiments performed at \(\alpha\)= 20°, Fig. 11 presents an oil-film image obtained at Re = 5.7 \(\times\) 104, whose appearance is noted somewhat different from that described in Fig. 10. Specifically, the oil-film image reveals that on the wing surface, the secondary separation lines induced by the strake and wing vortices are distinctly seen and get close to each other near the trailing edge. This appearance rather infers that the physical size of the wing vortex would be comparable to that of the strake vortex. Similar situation can be found in the literature. The numerical simulation reported in Ekaterinaris et al. (1995) and Li et al. (2013) for the 76°/40° double-delta wing models at 22.4° for Re = 4 \(\times\) 106, and 22.5° for Re = 1 \(\times\) 106, respectively, unveils a feature in common that the strake and wing vortices tended to merge near the trailing edge of the main wing. On the other hand, referring to Lamar and Frink (1981) for the wind tunnel experiments of the TP-1803 model at Reynolds numbers of 106, it was noted that through the interaction the strake and wing vortices were not merged into one vortex, but the wing vortex was displaced upward by the strake vortex. The interaction would result in higher the maximum lift coefficient and a delay in the onset of pitch-up.
Above experimental observations in the present study evidence that at \(\alpha\)= 20° the interaction between the strake and wing vortices had a significant impact on the trajectories of the vortices. Moreover, the significance of interaction appeared to be sensitive to Reynolds number.
3.1.3 Flow visualization results of TP-1803 model at \(\boldsymbol{\alpha }\)= 30°
A photograph in Fig. 12 unveils the evolution of the stake vortex at \(\alpha\)= 30° using the dye injection method, for which the experiment was performed in the water channel at Re = 1.54 \(\times\) 104. It is seen that the strake vortex persisted over the wing surface until breakdown at x/C ≈ 0.3. Moreover, a photograph in Fig. 13 which was a snapshot view of the flow at the same Reynolds number reveals that the process of vortex breakdown is of the axisymmetric type (Sarpkaya 1971).
In this case, the interaction of the strake and wing vortices appears to be less significant than that seen in the case of \(\alpha\)= 20°. This can be evidenced in Fig. 14, a photograph taken using the ink-dot method at Re = 1.54 \(\times\) 104. An overall appearance of the ink-dot pattern on the wing surface infers the development of a large-scale spanwise motion following the breakdown of the strake vortex. On the other hand, in Fig. 15, an oil-film image obtained in the wind tunnel at Re = 5.7 \(\times\) 104, which is significantly higher than that of the photograph in Fig. 14, clearly indicates the presence of a secondary separation line induced by the wing vortex. Thus, the wing vortex was actually developed over the wing surface, which persisted to the trailing edge.
3.1.4 Effect of Reynolds number
In the literature, experimental evidence indicates that the phenomenon of vortex breakdown associated with the vortex flow developed from a sharp leading-edge is insensitive to Reynolds number (Erickson 1982). Nevertheless, Gad-el-Hak and Blackwelder (1985; 1987) addressed that the effect of Reynolds number on the growth of the discrete vortices in the separated shear layer remained an issue to be investigated. Here, it is worthwhile to examine the effect of Reynolds number associated with the interaction of the strake and wing vortices developed on the present model. The oil-film flow visualization experiments were carried out in the wind tunnel for Re = 3.7 \(\times\) 104 to 1.2 \(\times\) 105. Since the time-mean flow patterns on the two sides of the center body are assumed to be symmetric, in each of the images shown below only the right wing portion is presented for discussion.
Figure 16 presents the oil-film visualization results of the model at α = 10° for Re = 3.7 \(\times\) 104 to 1.2 \(\times\) 105. In general, the flow patterns of different Reynolds numbers look alike. Nevertheless, if one would examine the spanwise locations of the secondary separation lines induced by the vortices at the chordwise location x/C = 0.9, one could see some variations due to this effect. As shown in the figure, the spanwise locations are indicated by y/s′, where y and s′ denote the spanwise distances from y = 0 to the separation line and the leading edge, respectively. As the Reynolds number increased, the secondary separation line induced by the wing vortex tended to move outboard slightly, but the secondary separation line induced by the strake vortex remained at the same location.
Apart from the observations above, the arrow indicated in each of the images highlights the appearance of multiple separation regions induced by the re-attachment of discrete vortices in the separated shear layer originated from the leading edge of the wing (Gad-el-Hak and Blackwelder 1985). Similar finding was noted in Luckring (1979b), in which the oil-film visualization images of three stake-wing configurations at α = 10° unveiled the branching of the secondary separation lines on the main wing. It was explained due to the double ridges of the oil films on the wing surface (Luckring 1979b). The experiments were performed at Re = 1.3 \(\times\) 106, which was one order of magnitude higher than those in the present study. Gursul et al. (2005) found a dual-vortex structure from a non-slender delta wing of 50° swept angle, and concluded that the dual-vortex structure was a result of vortices forming close to the wing surface and consequently interacting with the boundary layer.
The oil-film visualization results obtained in the wind tunnel at α = 20° for Re = 3.7 \(\times\) 104 to 1.2 \(\times\) 105 are presented in Fig. 17 for comparison. Discussion can be made with examining the locations of the secondary separation lines induced by the vortices at the chordwise location x/C = 0.9. First of all, it is found that with the Reynolds number increasing the interaction of the strake vortex and the wing vortex got less significant. For Re = 7.8 \(\times\) 104 and higher, the separation line induced by the wing vortex appeared to get straightened toward the trailing edge, inferring that the strake vortex had less impact in the interaction process. Also learned from the photographs at Re higher than 7.8 \(\times\) 104, the strake vortex appeared to get breakdown over the wing surface, whereas the wing vortex was kept as an organized vortical structure to the trailing edge. Verhaagen et al. (1995) reported the experimental results on a 76°/40° double-delta wing model at α = 15° and 20° and found that the breakdown of the strake vortex could be triggered by the breakdown of the wing vortex through the interaction. Gai et al. (2004) noticed that the type of interaction developed before vortex breakdown, whether the spiral/coiling or enveloping type, was dependent on Reynolds number. As Reynolds number increased, the strake and wing vortices tended to move outboard. Apart from the observations above, it is noticed in Fig. 17 that for Re = 9.7 \(\times\) 104 and 1.2 \(\times\) 105 a spiral separation developed at the wing tip as indicated by an arrow in each of the images. Conceivably, this flow structure was associated by the wing tip vortex developed.
Figure 18 presents the oil-film visualization results of the model in the wind tunnel at α = 30° for Re = 3.7 \(\times\) 104 to 1.2 \(\times\) 105. The surface patterns unveil a feature in common that the secondary separation line induced by the wing vortex persists to the trailing edge. As Reynolds number increased, the separation line tends to move outboard. This trend can be realized by examining the spanwise locations of the secondary separation lines at the chordwise location x/C = 0.9 indicated. Moreover, in each of the images of Re = 7.8 \(\times\) 104 to 1.2 \(\times\) 105, an arrow indicates the presence of a separation line at x/C = 0.3, which is attributed to breakdown of the strake vortex. The location of the separation line appears to be insensitive to the Reynolds numbers. This observation is in line with the finding of Durhasan and Karasu (2019) that for the double-delta wing models studied at α greater than 15° the breakdown location of the strake vortex would be insensitive to Reynolds number. In this case, breakdown of the strake vortex took place close to the junction of the strake and the wing; thus, the strake vortex played a less effective role in interacting with the wing vortex, compared to that seen in the case of α = 20°.
As a summary, Fig. 19 presents a plot concerning the spanwise locations of the secondary separation lines induced by the strake and wing vortices seen at the chordwise location x/C = 0.9 for all the cases studied. As aforementioned, at α = 10°, the secondary separation line induced by the strake vortex is insensitive to Re; its location stays about y/s′ = 0.11. On the other hand, the secondary separation line induced by the wing vortex moves outboard slightly as Re increased; namely, y/s′ = 0.65 for Re = 3.7 \(\times\) 104 and y/s′ = 0.74 for Re = 1.2 \(\times\) 105. At α = 20°, the spanwise distance between the strake and wing vortices appears to vary remarkably with Reynolds number. For Re = 3.7 \(\times\) 104, the normalized spanwise distance is about 0.15, whereas for Re = 1.2 \(\times\) 105 it is enlarged to 0.37. This is attributed to that the interaction between the strake and wing vortices gets weaker as Re increased. This trend is in line with the observations reported by Hebbar et al. (2000) concerning a 76°/40° double-delta wing at Re = 1.5 \(\times\) 104, 4.50 \(\times\) 104 and 7.5 \(\times\) 104. While the interaction between the strake and wing vortices was evident at low Reynolds number, it got less significant at higher Reynolds numbers. Durhasan and Karasu (2019) showed that the interaction mode could be dependent upon the Reynolds number; at Re = 1.0 \(\times\) 104, the interaction appeared as a spiral mode, whereas at Re = 2.5 \(\times\) 104 it switched to an enveloping mode. For α = 30°, it is seen in Fig. 19 that the trend of the secondary flow separation induced by the wing vortex moving outboard with Reynolds number almost coincides with that seen in the case of α = 10°. In this case, breakdown of the strake vortex took place near the junction of the strake and wing.
3.2 Results of PIV measurements
The results of PIV measurements taken in this study are reported in this section. The measurements were taken in the water channel at Re = 3.07 \(\times\) 104, for α = 10°, 20° and 30°.
3.2.1 Results of PIV measurements obtained at α = 10°
A side view of the three-dimensional flow field at α = 10° constructed from the PIV velocity measurements in the 22 cross-sectional planes is shown in Fig. 20a. Note that the plotted values have been normalized with the freestream velocity, each of which is a combination of the two velocity components in the x and z directions. In the figure, a low-speed zone near the trailing edge above the wing surface, outboard the strake vortex, is identified, which is associated with the secondary flow separation induced.
To highlight the high-velocity region measured, Fig. 20b presents a plot of the data points for which the normalized velocity values are greater than 1.05, i.e., 5% higher than the freestream velocity. While a significant number of data points are seen in region upstream of the leading edge of the wing, few data points are found in the region above the wing surface. This implies that neither the strake vortex nor the wing vortex would induce significant vortical motion over the wing surface. The PIV data also indicate that both vortices tended to stay close to the wing surface. These findings can be regarded as a complementary to the observations made in Figs. 5 and 6, whose Reynolds numbers are comparable to the present case.
3.2.2 Results of PIV measurements obtained at α = 20°
Figure 21a presents a side view of the time-mean velocity field over the model at α = 20°, based on the PIV velocity data obtained. It is noted that the non-dimensional velocity values at the cores of the strake and wing vortices are remarkably high. In this case, efforts were further made to identify the cores of the vortical structures (Earnshaw 1961; Nelson and Pelletier 2003; and Hall 1961).
The time-mean velocity distribution plots for the model at α = 20° and Re = 3.07 \(\times\) 104; a all the PIV data are included, b only the points of the normalized velocity values higher than 1.2 are plotted. Two flow visualization photographs included for comparison are duplicated from Figs. 8 and 11, respectively
In Fig. 21b, two plots are made from different view angles named the view angles 1 and 2 for the data points of which the normalized velocity values higher than 1.2 are provided. In both plots, the regions of high velocity can be identified as the cores of the strake vortex and the wing vortex. Specifically, the core of strake vortex can be identified in the streamwise region of x/C = − 0.15 to 0.52, in which the mean normalized velocity is about 1.3; downstream of x/C = 0.52, the normalized velocity is less than 1.2, but the vortex core persists. Moreover, from the view angle 2 it is seen that near the leading edge of the wing the normalized velocity is about 1.55, which is significantly greater than that in the core of the strake vortex. Nevertheless, the core of the wing vortex developed from the leading edge was much weaker than that of the strake vortex; thus, the wing vortex was in fact drawn by the strake vortex over the wing surface.
A region marked “the wing vortex” in Fig. 21a or “the vortex interaction zone” in Fig. 21b deserves attention here. Notably, this finding is explained due to the effect of stretching of the wing vortex. Owing to a strong interaction of the strake and wing vortices, the trajectory of the wing vortex gets inward and upward in a helical path, which can also be inferred by the flow visualization images included in the figure. As a result, flow in the core of the wing vortex got stretched and accelerated. Note that the two photographs included for comparison were duplicated from Figs. 8 and 11, which were obtained in the water channel tunnel at Re = 1.54 \(\times\) 104 and the wind tunnel experiment at Re = 5.7 \(\times\) 104, respectively. While the Reynolds numbers corresponding to the two photographs and that of the present case are different, the feature of strong interaction of the strake and wing vortices near the trailing edge of the wing is seen remarkably similar.
3.2.3 Results of PIV measurements obtained at α = 30°
Figure 22a presents a side view of the velocity field over the model at α = 30° based on the PIV velocity data obtained, and Fig. 22b highlights the data points of which the normalized velocity values are greater than 1.2. In either of the figures, it is seen that the breakdown location of the strake vortex is about x/C = 0.2, which almost coincides with that learned from the dye streak appearance in Fig. 12 for Re = 1.54 \(\times\) 104 and the oil-film visualization in Fig. 18 for higher Reynolds numbers. Thus, the vortex breakdown phenomenon is rather insensitive to the Reynolds numbers studied. Apart from the observations with the strake vortex, it is seen in Fig. 22b that the development of the wing vortex can be discerned with the data points of high normalized velocity extended to the mid-chord region above the wing. With the inclusion of the secondary flow separation line induced by the wing vortex marked in this figure, one could further give an estimation about the spanwise size of the wing vortex. For instance, it is about 0.04 s at x/C = 0.5 as seen from the plot, where s denotes the wingspan.
4 Conclusion
In this study, the physical aspects concerning the interaction between the strake and wing vortices developed above the TP-1803 model at α = 5°, 10°, 20° and 30° for Re from 1.54 \(\times\) 104 to 1.2 \(\times\) 105 were examined with the flow visualization methods and the PIV velocity measurements. Our findings can be summarized below.
At α = 5° and α = 10°, the interaction was deemed rather insignificant that the strake vortex and the wing vortex appeared like individual vortices over the wing surface. From the flow visualization results obtained in the water channel and wind tunnel, it is noted that the trajectories of the vortices were insensitive to the effect of Reynolds number. Specifically, the location of the strake vortex remained no change regardless of the Reynolds numbers, whereas the wing vortex moved outboard slightly as Reynolds number got higher. As indicated by the PIV measurements, both vortices were positioned near the wing surface with relatively weak strength compared to the cases of higher angles of attack.
At α = 20°, the strake vortex appeared to be predominant above the wing surface, but it got breakdown near the trailing edge. The interaction of the strake and wing vortices was so strong that the trajectory of the wing vortex was induced inboard and tended to coil around the strake vortex. As a result, the effect of stretching concerning the wing vortex near the trailing edge was evidently seen from the PIV measurements at Re = 3.07 \(\times\) 104. The effect of Reynolds number was noted remarkably from the oil-film visualization made in the wind tunnel experiments for Re = 3.7 \(\times\) 104 to 1.2 \(\times\) 105. In brief, the higher the Reynolds number, the less significant the interaction of the strake and wing vortices.
At α = 30°, the strake vortex got breakdown near the junction of the strake and wing. In this case, the interaction with the wing vortex appeared to be less significant, compared to the case of α = 20°. The location of vortex breakdown of the strake vortex appeared to be insensitive to the Reynolds numbers studied. On the other hand interestingly noted is that the trend of the secondary separation line induced by the wing vortex moving outboard with Reynolds number appeared to be almost coincide with that seen in the case of α = 10°.
Abbreviations
- x :
-
Chordwise direction
- y :
-
Spanwise direction
- z :
-
Vertical direction
- s :
-
Wingspan
- s’:
-
The spanwise distance from the origin to the leading edge of the main wing at x/C = 0.9
- C :
-
Characteristic length, i.e., the root chord length, 108 mm
- \(\mathrm{Re}\) :
-
Reynolds number based on C and U0
- U 0 :
-
Freestream velocity
- α :
-
Angle of attack
References
CK Choi, DK Kwon (1998) Wind tunnel blockage effects on aerodynamic behavior of bluff body. Wind Struct Int J; 1(4):351–364. https://doi.org/10.12989/was.1998.1.4.351
Chou MT (2020) Vortex structure analysis of aerodynamic blended wing body. Master thesis, Institute of Aeronautics and Astronautics, National Cheng Kung University. https://doi.org/10.6844/NCKU202002542
Cobleigh B, Frate J (1994) Water Tunnel Flow Visualization Study of a 4.4% Scale X-31 Forebody. NASA-TM-104276.
Dong P, Miau JJ, Zoghlami A (2019) An experimental study about drag crisis phenomenon teardrop model. J Aeronaut Astronaut Aviat 51(2):141–158. https://doi.org/10.6125/JoAAA.201906_51(2).01
Durhasan T, Karasu İ (2019) Dye visualization over double delta wing with various kink angles. J Visualization 22(4):669–681. https://doi.org/10.1007/s12650-019-00562-9
Earnshaw P (1961) An experimental investigation of the structure of a leading-edge vortex. HM Stationery Office.
Ekaterinaris JA, Coutley RL, Schiff LB, Platzer MF (1995) Numerical investigation of high incidence flow over a double-delta wing. J Aircr 32(3):457–463. https://doi.org/10.2514/3.46742
Erickson GE (1982) Water-tunnel studies of leading-edge vortices. J Aircr 19:442–448. https://doi.org/10.2514/3.57414
Gad-el-Hak M, Blackwelder RF (1985) The discrete vortices from a delta wing. AIAA J 23(6):961–962. https://doi.org/10.2514/3.9016
Gad-el-Hak M, Blackwelder RF (1987) Control of the discrete vortices from a delta wing. AIAA J 25(8):1042–1049. https://doi.org/10.2514/6.1986-1915
Gai SL, Roberts M, Barker A, Kleczaj C, Riley AJ (2004) Vortex interaction and breakdown over double-delta wings. Aeronaut J 108(1079):27–34. https://doi.org/10.1017/S0001924000004966
Gursul I, Allan M, Badcock K (2005) Opportunities for the integrated use of measurements and computations for the understanding of delta wing aerodynamics. Aerosp Sci Technol 9:181–189. https://doi.org/10.1016/j.ast.2004.08.007
Hall M (1961) A theory for the core of a leading-edge vortex. J Fluid Mech 11:209–228. https://doi.org/10.1017/S0022112061000470
Hebbar SK, Platzer MF, Fritzelas AE (2000) Reynolds number effects on the vortical-flow structure generated by a double-delta wing. Exp Fluids 28(3):206–216. https://doi.org/10.1007/s003480050380
Herbest WB (1983) Dynamics of air combat. J Aircr 20:594–598. https://doi.org/10.2514/3.44916
Keane RD, Adrian RJ (1992) Theory of cross-correlation analysis of PIV images. Appl Sci Res 49(3):191–215. https://doi.org/10.1007/BF00384623
Kölzsch A, Breitsamter C (2014) Vortex-flow manipulation on a generic delta-wing configuration. J Aircr 51:1380–1390. https://doi.org/10.2514/1.C032231
Lamar JE (1980) Analysis and design of strake-wing configurations. J Aircr 17:20–27. https://doi.org/10.2514/3.57870
Lamar JE, Frink NT (1981) Experimental and analytical study of the longitudinal aerodynamic characteristics of analytically and empirically designed strake-wing configurations at subcritical speeds. NASA-TP-1803.
Li JY (2013) Improvement on a blade performance of a vertical-axis wind turbine. Master Thesis, institute of aeronautics and astronautics, National Cheng Kung University.
Li Q, Sun D, Zhang H (2013) Detached-eddy simulations and analyses on new vortical flows over a 76/40° double delta wing. Sci China Phys Mech Astron 56(6):1062–1073. https://doi.org/10.1007/s11433-013-5105-6
Lighthill ML (1963) Introduction, boundary layer theory. In: Rosenhead L (ed) Laminar boundary layers. Chapter II. Oxford University Press, Oxford
Luckring JM (1979a) Aerodynamics of strake-wing interactions. J Aircr 16:756–762. https://doi.org/10.2514/3.58600
Luckring JM (1979b) Flow visualization studies of a general research fighter model employing a strake-wing concept at subsonic speeds. NASA-TM-80057.
Malcolm G, Nelson R (1987) Comparison of water and wind tunnel flow visualization results on a generic fighter configuration at high angles of attack. AIAA paper 1987–2423, the14th AIAA Atmospheric Flight Mechanics Conference. https://doi.org/10.2514/6.1987-2423
McMahon MC, Wentz WH (1966) An experimental investigation of the flow fields about delta and double-delta wings at low speeds.
Miau JJ, Chang RC, Chou JH, Lin CK (1992) Nonuniform motion of leading-edge vortex breakdown on ramp pitching delta wings. AIAA J 30:1691–1702. https://doi.org/10.2514/3.11125
Moore WA, Erickson GE, Lorincz DJ, Skow AM (1979) Effects of Forebody, Wing and Wing-Body-LEX Flowfields on High Angle of Attack Aerodynamics. SAE Trans, 3801–3825.
Nelson RC, Pelletier A (2003) The unsteady aerodynamics of slender wings and aircraft undergoing large amplitude maneuvers. Prog Aerosp Sci 39:185–248. https://doi.org/10.1016/S0376-0421(02)00088-X
Polhamus EC (1966) A concept of the vortex lift of sharp-edge delta wings based on a leading-edge-suction analogy. NASA-TN-D-3767, NASA Langley Research Center Hampton, VA, United States.
Sarpkaya T (1971) vortex breakdown in swirling conical flows. AIAA J 9:1792–1799. https://doi.org/10.2514/3.49981
Thompson D H (1985) A Visualization Study of the Vortex Flow Around Double-Delta Wings. Aerodynamics Report 165, Aeronautical Research Labs Melbourne (Australia).
Thu AM, Byun YH, Lee JW (2012) Dye visualization of the vortical flow structure over a double-delta wing. J Aerosp Eng 25(4):541–546. https://doi.org/10.1061/(ASCE)AS.1943-5525.0000195
Verhaagen N, Jenkins L, Kern S, Washburn A (1995) A study of the vortex flow over a 76/40-deg double-delta wing. AIAA paper 1995–650, the 33rd Aerospace Sciences Meeting and Exhibit. https://doi.org/10.2514/6.1995-650
Vigevano L (1982) Stake-Wing-Body combinations. North Atlantic Treaty Organization, Advisory Group for Aerospace Research and Development, Fluid Dynamics Panel, Von Karman Institute for Fluid Dynamics (1982) High Angle of Attack Aerodynamics. AGARD/VKI Lecture Series No. 121, Paper No. 13.
Watanabe S, Kato H, Kwak DY, Shirotake M, Rinoie K (2004) Stereoscopic PIV measurements of leading edge separation vortices on a cranked arrow wing. Meas Sci Technol 15(6):1079. https://doi.org/10.1088/0957-0233/15/6/006
Yu JM, Leu TS, Miau JJ (2016) Investigation of reduced frequency and freestream turbulence effects on dynamic stall of a pitching airfoil. J Vis 20:31–44. https://doi.org/10.1007/s12650-016-0366-6
Zdravkovich MM (1997) Flow around circular cylinders: Volume 2: Applications. Oxford University Press, Oxford. https://doi.org/10.1115/1.2819655
Zhang X, Wang Z, Gursul I (2016) Interaction of multiple vortices over a double delta wing. Aerosp Sci Technol 48:291–307. https://doi.org/10.2514/6.2015-2308
Acknowledgements
The authors would like to acknowledge the funding support by Ministry of Science and Technology, Taiwan, for this work under the project number: MOST 109-2923-H-006-001.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Chou, MT., Miau, JJ. & Chen, LY. Vortex interaction on a LEX configuration. J Vis 24, 1189–1205 (2021). https://doi.org/10.1007/s12650-021-00764-0
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s12650-021-00764-0