Structural Reynolds analogy in laminarescent boundary layers via DNS

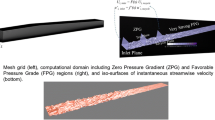
Abstract

Visualization of the thermal field in highly accelerated spatially developing turbulent boundary layers is carried out. Direct Numerical Simulation with high spatial/temporal resolution is performed in sink flow-type boundary layer by prescribing a passive scalar with a Prandtl number of 0.71. The range of the momentum thickness Reynolds number is approximately 320–432. The very strong Favorable Pressure Gradient (FPG) is imposed by a top converging shearless surface, which produces an approximately constant acceleration parameter of $K = 4.0 \times 10^{-6}$. A precursor zone is prescribed upstream of the FPG region in order to generate accurate turbulent inflow information by means of the methodology proposed by Araya et al. (J Fluid Mech 670:518–605, 2011). While evident “signatures” of the very strong FPG have been identified in the velocity field, those “signatures” are much less evident in the temperature field causing a breakdown of the Reynolds analogy provoked by the streamwise pressure gradient (or source of dissimilarity between the momentum and thermal transport). A slow decrease in the thermal boundary layer thickness, $\delta _T$, is observed in the FPG zone. Additionally, local maxima of absolute intensities of the thermal fluctuations $t'_\mathrm{RMS}$ exhibit nearly constant values (approx. 14% of $T_{\infty }$) along the composite domain. Conversely, absolute intensities of the streamwise ($u'_\mathrm{RMS}$) show increases on their local maxima, with mild decreases in the transversal components of the velocity ($v'_\mathrm{RMS}$ and $w'_\mathrm{RMS}$). Furthermore, profiles of cross-correlation $<u't'>$ at different streamwise stations depict a good collapsing level up to 4% of $\delta$ in the wall-normal direction, with peak values displacing farther from the wall in the FPG zone.

Graphical abstract