Abstract
Realization of a needle-free drug delivery device can solve needle-caused problems. Recently, attention has been given to the use of a focused liquid jet instead of the use of the existing needle-free device that generates a turbulent liquid jet. This study experimentally visualized the penetration into a gel and animal skin of a focused liquid jet with a very high speed around 200 m/s. We first examined high-speed images to evaluate the dynamics of the jet penetration into a gel. We found that the penetration depth is determined within a short time \(t_p\) (on the order of 0.01 ms). \(t_p\) is similar to \(L/V_j\), where L and \(V_j\) are, respectively, the penetration depth and the impact speed of the jet tip. We then investigated the overall shape of the penetration site represented by the length ratio \(\alpha =L/W\), where W is the width of the penetration site. Remarkably, the ratio \(\alpha\) is greater than unity for a gel, as well as for the animal skin. This suggests that the focused liquid jet can create a narrow penetration site into the target.
Graphical abstract

Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Needle-free drug delivery devices (e.g., Mitragotri 2006) have been developed over the past few decades because it can solve needle-caused problems (e.g., needle-phobia). In this device, a tube is filled with liquid, and the liquid is ejected as a jet, for example by a piston. Then, the jet impacts the skin surface and penetrates it at high speed.
One of the most significant benefits of the use of the high-speed jet is the minimization of the time needed to complete the penetration process (hereafter, the penetration time). McKeage et al. (2018) reported that the motion of the piston, as well as the penetration of a turbulent jet, is completed within on the order of 100 ms. Schramm-Baxter et al. (2004) and Taberner et al. (2012) found that the penetration depth L(t) increases rapidly at the early stage (on the order of 1 ms) and then reaches a maximum value of L within approximately 10 to 100 ms. A jet induced by an impulsive pressure change [e.g., shockwaves (Park et al. 2012; Battula et al. 2016)] has even shorter penetration time. Kato et al. (2014) used a pulsed laser with pulse duration of 350 µs to accelerate the liquid and completed the penetration in a gel, whose stiffness is similar to that of the human skin, within a few milliseconds. Tagawa et al. (2012) used a 6-ns pulsed laser to form a unique liquid jet having a focused shape and ultrahigh impact speed \(V_j\) (i.e., a focused liquid jet). This jet completed the penetration within 1 ms. Moreover, the penetration depth L of focused liquid jet could possibly be predicted at the early stage of the penetration process because the jet tip travels fast enough (\(L/V_j=0.01\hbox { ms}\) to 0.1 ms). Thus, the detailed process for determining the penetration depth (i.e., the short-term dynamics of the penetration) should be investigated with varying jet velocity and the stiffness of the target materials. In addition, there are a few studies discussing the liquid motion for the long term, which is also important.
Another important benefit for a needle-free drug delivery device is the shape of the penetration site (not only the depth L but also the width W) because it is closely related to the area of damaged skin. For the penetration depth L, Schramm-Baxter and Mitragotri (2004) used the spring-powered device to generate the turbulent liquid jet and discussed the penetration dynamics of the turbulent liquid jet into human skin. The device is targeting the larger volumes (O(0.1) mL), and the penetration depth reached 10 mm (Baxter and Mitragotri 2005). This corresponds to the depth of muscle tissue in humans, and the larger targeting volumes of the device suppose to be matched with the requirement for the intramuscular delivery, suggesting that the turbulent liquid jet is well suited for delivering antibiotics, steroids and growth hormones with regard to the performance diagram presented in Berrospe-Rodriguez et al. (2017). For the width of the penetration site W, it was found that the diffusive shape of the turbulent jet introduces spreading penetration shape (Schramm-Baxter et al. 2004; Baxter and Mitragotri 2005; Donnelly et al. 2007). For example, in Schramm-Baxter et al. (2004), the maximum width W of the penetration site was roughly twice as large as the depth L (\(L/W<\)0.5) for the intradermal drug delivery (the depth is smaller than the skin thickness T, i.e., \(L<T\)). Even in the case of complete penetration (\(L>T\)), the ratio \(\alpha =L/W\) remained less than unity. Moreover, W was much larger than the nozzle diameter D (\(D/W=O(10^{-1})\)). To minimize the invasiveness of the device, we need to reduce the area of damaged skin. Interestingly, the focused liquid jet has the potential to meet this need. Snapshots in Tagawa et al. (2013) indicate that the focused liquid jet can produce \(\alpha =L/W\approx 4\) in the gelatin, while the injected liquid volume is on the order of nano-liters. Although jets having a similar mechanism have been tested in gels (Berrospe-Rodriguez et al. 2017; Moradiafrapoli and Marston 2017; Delrot et al. 2018), there still has been little experimental investigation of the shape of the penetration site.
This study investigated the following two points for the focused liquid jet. First, we visualized the jet penetration dynamics using a high-speed imaging technique, which revealed the penetration time \(t_p\) that determines the penetration depth in the target material. Second, we investigated the shape of the penetration site using the ratio \(\alpha =L/W\). After confirming the creation of an elongated penetration site (\(\alpha >1\)) from the side view of high-speed images of gels, we conduct an experiment using animal skin.
2 Experimental method
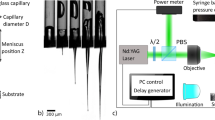
The experimental setup we used (Fig. 1) is similar to that used in previous contributions (Tagawa et al. 2012, 2013; Hayasaka et al. 2017). A glass tube (inner diameter of 500 µm) was filled with magenta ink (THC7M4N, ELECOM Co.) and irradiated by a Nd:YAG pulsed laser (Nano S PIV, Litron Lasers Co., wavelength 532 nm, pulse duration 6 ns, the size of the laser focal spot 2.6 µm (see Tagawa et al. 2016)), where the laser energy ranged within 0.6–3.0 mJ. The focused liquid jet emerged from the curved meniscus and then impacted and penetrated the target material, gelatin or hairless rat skin. The impact speed of the jet tip ranged 11 m/s\(<V_j<\)328 m/s for the gel experiment and 52 m/s\(<V_j<\)435 m/s for the skin experiment. Thus, the typical value of the jet power \(P_j\) (Schramm-Baxter and Mitragotri 2004; Moradiafrapoli and Marston 2017) was \(P_j\sim 1/8\rho \pi D_j^2V_j^3\sim\)0.04 W, where the typical values of the jet diameter \(D_j=10\, \upmu \hbox {m}\) and the jet speed \(V_j=100\hbox { m/s}\). The gel had reasonable transparency for visualizing the penetration dynamics of the jet, which is challenging for the non-transparent skin. However, the color contrast between the magenta ink and the rat skin was acceptable for image analysis. Thus, a cross-sectional image of the skin could visualize the overall shape of the penetration. A high-speed camera (FASTCAM SA-X, SA-Z, Photron Co., frame rate of \(\le\)100,000 frames per second, shutter speed of \(\sim\)0.3 µs, spatial resolution of \(\sim\)14 µm/pixel) recorded the evolution and impact of the focused liquid jet. A backlight (KL-1600 LED, OLYMPUS Co.) was used for the high-speed imaging, and a pulse generator (Model 575 Pulse/Delay Generator, BNC) triggered both the camera and pulsed laser. Hereafter, \(t=0\) indicates the timing of the start of laser irradiation. The standoff distance \(H_a\) and the position of the laser focus \(H_l\) were generally varied over the ranges 3 mm\(\le H_a\le\)10 mm and 1 mm\(\le H_l\le\)4 mm, respectively, except for data presented in Fig. 2c, d. For the gel experiment, the penetration depth L(t) and its width W(t) were measured by high-speed imaging. For the skin experiment, the penetration depth \(L_s\) and its width \(W_s\) were measured several minutes after the penetration using a digital camera (OLYMPUS TOUGH TG-620, OLYMPUS Co., with typical spatial resolution of 30 µm/pixel).
The gel concentration C was varied from 1 to 5 wt%. First, we prepared 100 g of tap water and added gel powder (Sigma-Aldrich Co., G6144). After mixing and swelling, we added hot water to the mixture until the total weight of the mixture reached 200 g. We then poured the mixture into containers (10 mm \(\times\) 10 mm \(\times\) 45 mm) after further mixing. All containers were cooled in a refrigerator at around 4 \(^\circ C\) overnight.
For the skin experiment, the skin from the back of a hairless rat (8 weeks old, SANKYO Lab Services) was used. The whole skin was cut into small pieces with a scalpel, and the surface of the cut skin was carefully wiped with ethanol. Each skin piece was pinned to a cork board to position it above the nozzle exit. The thickness of the skin measured by the vernier caliper was \(1.32\pm 0.12\) mm.
3 Results and discussion
3.1 Penetration dynamics of the focused jet
First we observed the short-term dynamics of the focused liquid jet penetration in the gel using a high-speed camera. Figure 2a shows selected image frames, and Fig. 2b presents the data analysis for the temporal penetration depth L(t), which is the distance from the gel surface to the jet tip in the gel. The temporal penetration depth L(t) increased and reached a plateau, which hereafter is referred to as the stagnation depth \(L_1\) (Fig. 2b, stage \(\textcircled {1}\)). During the penetration of the jet tip into the gel, no liquid splashed onto the gelatin surface, suggesting that the entire liquid jet penetrated the gel. The penetration depth was stable until it was struck by the jet tail having a much larger diameter than the jet tip (Fig. 2a, 8th frame, and Fig. 2b, stage \(\textcircled {2}\)). The propagation of the jet tail then increased the penetration depth further (Fig. 2b, stage \(\textcircled {3}\)). Finally, after the gel recovered elastically (Akers and Belmonte 2006; Mrozek et al. 2015), most of the jet tail rebounded off the gel–air interface (Fig. 2a, 14th frame) and retreated slightly from the greatest penetration depth. The penetration depth after relaxation is referred to as \(L_2\). Comparison of the depths \(L_1\) and \(L_2\) in Fig. 2 suggests that the jet penetration during stage \(\textcircled {1}\) is dominant for determining \(L_2\), rather than the shift during stage \(\textcircled {3}\). Note that the magnitude of the elastic response in stage \(\textcircled {3}\) possibly depends on the amount of the liquid entering the penetration site. In order to provide empirical evidence, we examined a jet having a narrower jet tail (Figs. 2c, d). In this case, stage \(\textcircled {1}\) shows a similar trend to that in Figs. 2a, b, namely, the rapid increase of L(t) to \(L_1\). In contrast, the tendency for the latter stage is very different. The impact of the jet tail deforms the gel surface (Fig. 2c, 9th frame), but it does not affect the penetration depth during stage \(\textcircled {3}\) (Fig. 2d). In this case, the final penetration depth was as \(L_2\approx L_1\).
We then observed the long-term dynamics of the focused liquid jet in the gel (Fig. 3). Figure 3a–c presents the penetration of the focused jet in 5wt% gel recorded at different frame rates (i.e., 75,000 f.p.s., 7500 f.p.s. and 500 f.p.s., respectively), offering the recording of the event for different timescales. The input energy, the standoff distance \(H_a\) and the position of the laser focus \(H_l\) are all similar to each other. We selected three cases having similar penetration depth. The analyzed temporal penetration depth L(t) for each case is also presented in Fig. 3d for full range and in Fig. 3e for the zoom-up view. Firstly, we overview the fluid dynamic events. At the very early stage (\(<O(0.1)\) ms), the temporal penetration depth is established as mentioned earlier (\(L(t)\sim L_1\), see also Fig. 3d). The jet tail enters into the penetration site (\(O(0.1)\hbox { ms}<t<O(1)\hbox { ms}\)) and bounces off the gel surface (\(>O(1)\hbox { ms}\)). This liquid bounce event could be captured for all three cases at similar timing (Fig. 3a–c). The analyzed penetration depth L(t) also reflects the effect of the liquid bounce (see Fig. 3e). Another event is the leakage of the deposited liquid from the penetration site. In comparison with the width of the penetration site at the early stage, that in O(0.1) \(\hbox {s}<t<O(1)\hbox { s}\) is remarkably thinner, possibly due to the elastic stress. Moreover, air bubble contained inside the penetration site rises and then comes off (Fig. 3b). At the later stage (\(O(1)\hbox { s}<t<O(10)\hbox { s}\)), the shape of the penetration site does not show any significant change. The important point here is that the liquid leakage does not affect the penetration depth L(t), as shown in Fig. 3d. This observation confirms our proposed relationship \(L_2\approx L_1\).
Thus, we would expect the relationship between the stagnation depth \(L_1\) and the final penetration depth \(L_2\) to be \(L_2=L_1\). Figure 4a compares \(L_2\) and \(L_1\) for various gel concentrations. The solid line shows \(L_2=\beta L_1\), where \(\beta =1.29\). All data follow a proportional trend within the magnitude of the fitting parameter \(\beta\), suggesting that the final penetration depth (\(L_2\)) is determined at the early stage of the event (\(L_1\)). Thus, we would say that the penetration time \(t_p\) is the time to reach the stagnation depth \(L_1\). As shown by the particular case shown in Fig. 2a, b, \(L_1\) is determined at t on the order of 0.01 ms. In this particular case, penetration time to reach \(L_1\) is much shorter than that found in the case of a turbulent liquid jet (approximately 10 ms to 100 ms (Schramm-Baxter et al. 2004)).
a High-speed images of the jet penetration into 5 wt% gel. b Time history of the penetration depth L(t). Circled numbers identify each stage: \(\textcircled {1}\) time interval between penetration start and plateauing of L(t), \(\textcircled {2}\) time interval between penetration of the jet tail and impact with liquid at \(L_1\) and \(\textcircled {3}\) time interval during which gel elastically recovers and the gel penetration depth becomes \(L_2\). c Penetration of jet having a narrower jet tail into 3 wt% gel. The standoff distance and the position of the laser focus are \(H_a\approx 30\) mm and \(H_l\approx 10\) mm. d Time history of the penetration depth L(t) shown in panel (c)
Penetration process in the different timescales, \(\sim\)milliseconds (a), \(\sim\)1 second (b) and \(\sim\)1 minute (c) after the injection. The gel concentration C is 5wt% for all cases. d The analyzed depth L(t) for three cases, where the color corresponds to the recording speed as indicated in (a–c). e A zoom-up view of d
3.2 Overall shape of penetration site
We expect that the focused liquid jet can produce a narrow penetration site. In the beginning, we test the relationship between the penetration depth \(L_2\) and the width of the penetration site W, which is measured when L(t) reaches to \(L_2\), for all gel concentrations (Fig. 4b). The dashed line indicates the length ratio \(\alpha =1\). Importantly, the length ratio \(\alpha =L_2/W\) is always greater than unity, meaning that the focused liquid jet produces a narrow and elongated penetration into the gel. In addition, although W increases as \(L_2\) increases, W remains similar in size for the tube diameter \(D=500\) µm.
The origin of the narrow shape of the penetration site is, indeed, led by the focused shape of the liquid jet. Here we compare the penetration process of the focused liquid jet and that of the non-focused liquid jet (the turbulent jet) in 5 wt% gel (Fig. 5). Figure 5a again shows the selected frames of the penetration process of the focused liquid jet, which is the same data with that in Fig. 3a. Figure 5b presents the penetration of the turbulent jet at the same timing as shown in Fig. 5a. The turbulent jet emerges from the flat free surface. The input laser energy, the standoff distance \(H_a\) and the laser focal point \(H_l\) are all similar to each other. Comparing Fig. 5a, b, it is quite obvious that the focused jet has the faster impact speed and leads to the deeper penetration. Figure 5c, d shows the analyzed jet speed \(V_j\) and the depth \(L_2\). The jet speed \(V_j\) for the turbulent jet is roughly one third of that for the focused liquid jet, mainly due to the loss of the flow focusing effect (Tagawa et al. 2012). Note that the large deviations of \(V_j\) at the same condition are possibly due to the cavitation-assisted jet acceleration (Kiyama et al. 2016; Hayasaka et al. 2017). The penetration depth \(L_2\) for the turbulent jet is significantly smaller than that for the focused liquid jet. This observation indicates that the focused shape of the liquid jet helps the deeper liquid delivery into a target when compared at the same input energy. Thus, it is suggested that the focused jet has the advantage for the needle-free drug injections.
The focused liquid jet could create a narrow penetration site even in the animal skin. Narrow penetration was observed in the cross-sectional image of penetrated skin (Fig. 6a), except where it scattered on the skin surface. In the extreme case, the penetrated ink can be seen even from the reverse side of the skin (Fig. 6b). The minimum velocity of the jet penetrating the skin was around 200 m/s, similar to that reported in the turbulent liquid jet (Schramm-Baxter et al. 2004). Figure 6c shows the ratio \(\alpha\) observed in the skin. All data show that \(\alpha\) was larger than unity, with an average \(\alpha\) value of around 1.91. This suggests that the focused liquid jet can create a narrow penetration site even in animal skin. Note that the magnitude of \(\alpha\) for the skin is much smaller than that for the gel (compare Figs. 4b and 6c). High-speed images (Fig. 6d) indicate that a splash at the skin surface can occur at 20 µs after the penetration. The penetration time \(t_p\sim L_s/V_j\) in this case is \(\sim\) (1 mm)/(250 m/s)\(\sim\)4 µs, which is much earlier than the timing of the splash onset, suggesting that only a part of the jet tip could penetrate in the skin and the following jets scatter on the skin surface. The possible reasons are, for example, the decrease in the momentum of the jet accompanying by the slower following jet or the existence of the outermost horny layer. The maximum \(L_s\) measured from the cross-sectional image of the skin was \(L_s\approx 1.5\) mm (see Fig. 6c), and the deliverable volume was estimated as \(\sim \pi W_s^2L_s/4\sim O(10)\) nL, consistent with the literature (Tagawa et al. 2013). This small volume in a shallow depth (\(L_s\approx 1.5\) mm, see Fig. 6c) suggests that the focused liquid jet is best suited for medical tattooing and allergy testing, rather than the injection of steroids or antibiotics (Berrospe-Rodriguez et al. 2017). Note that, this deliverable volume of liquid (\(\sim O(10)\) nL) is significantly smaller than the total liquid volume expelled by the device. This is the limitation of the current system. The further study would be addressed, which also helps to avoid the liquid scattering on the skin surface.
4 Conclusion and outlook
This study aimed to reveal the penetration dynamics of a focused liquid jet and the overall shape of the penetration site in both a gel and animal skin. High-speed images of the gel experiment captured the detailed time sequence of the short-term (Fig. 2) and the long-term dynamics of the jet penetration (Fig. 3). It was found that the penetration depth can be determined at an early stage of the penetration process. In particular, we found that the penetration time \(t_p\) for the focused liquid jet (on the order of 0.01 ms, Fig. 2a) was significantly smaller than the penetration time for the turbulent liquid jet (approximately 10 ms to 100 ms, Schramm-Baxter et al. 2004). For all gels, we confirmed the length ratio \(\alpha =L_2/W>1\), suggesting that the focused liquid jet can create narrow penetration into a small region of the target (Fig. 4b). By comparing the penetration process for the focused liquid jet and the turbulent liquid jet (Fig. 5), it was found that the focused shape of the liquid jet could offer the advantage for the needle-free drug injections. Remarkably, for the animal skin, the ratio \(\alpha\) was still greater than unity (i.e., a narrow penetration (Fig. 6)).
There are two aspects for the possible future work. For the fundamental study, the dynamic response of the gelatin gel would be an interesting topic in the field of soft matter physics. Our observation revealed that the high-speed penetration of the focused jets into the gel with different concentrations C can lead the distinguishable dynamic response of the hole (or cavity) made by the jets (see "Appendix"), while C values would not affect the overall relationships for the dimensions of the penetration site at the state of rest (i.e., \(L_1\sim L_2\)). The further understanding of this would help to improve the efficiency of the liquid delivery. For the application side, the influence of cavitation on the liquid medicine should be avoided, since the cavitation needs a high temperature to occur and can induce the shock wave upon its collapse. Thus, the other driving force of the focused liquid jet (e.g., the impact-induced liquid jet (Kiyama et al. 2016; Onuki et al. 2018)) should be explored.
References
Akers B, Belmonte A (2006) Impact dynamics of a solid sphere falling into a viscoelastic micellar fluid. J Non-Newtonian Fluid Mech 135(2–3):97–108
Battula N et al (2016) A miniature shock wave driven micro-jet injector for needle-free vaccine/drug delivery. Biotechnol Bioeng 113(11):2507–2512
Baxter J, Mitragotri S (2005) Jet-induced skin puncture and its impact on needle-free jet injections: experimental studies and a predictive model. J Control Release 106(3):361–373
Berrospe-Rodriguez C et al (2017) Toward jet injection by continuous-wave laser cavitation. J Biomed Opt 22(10):1–10
Delrot P et al (2018) Depth-controlled laser-induced jet injection for direct three-dimensional liquid delivery. Appl Phys A 124:616
Donnelly RF et al (2007) Influence of solution viscosity and injection protocol on distribution patterns of jet injectors: application to photodynamic tumour targeting. J Photochem Photobiol B 89(2–3):98–109
Hayasaka K et al (2017) Effects of pressure impulse and peak pressure of a shockwave on microjet velocity in a microchannel. Microfluid Nanofluid 21(11):166
Kato T et al (2014) Mechanics of the injected pulsejet into gelatin gel and evaluation of the effect by puncture and crack generation and growth. J Appl Phys 116(7):074901–10
Kiyama A, Tagawa Y, Ando K, Kameda M (2016) Effects of a water hammer and cavitation on jet formation in a test tube. J Fluid Mech 787:224–236
McKeage JW et al (2018) The effect of jet speed on large volume jet injection. J Control Release 280:51–57
Mitragotri S (2006) Current status and future prospects of needle-free liquid jet injectors. Nat Rev Drug Discov 68:341–6
Moradiafrapoli M, Marston JO (2017) High-speed video investigation of jet dynamics from narrow orifices for needle-free injection. Chem Eng Res Des 117:110–121
Mrozek RA et al (2015) The relationship between mechanical properties and ballistic penetration depth in a viscoelastic gel. J Mech Behav Biomed Mater 44:109–120
Onuki H, Oi Y, Tagawa Y (2018) Microjet generator for highly viscous fluids. Phys Rev Appl 9(1):014035
Ma Park et al (2012) Er:YAG laser pulse for small-dose splashback-free microjet transdermal drug delivery. Opt Lett 37(18):3894–3896
Schramm-Baxter J, Mitragotri S (2004) Needle-free jet injections: dependence of jet penetration and dispersion in the skin on jet power. J Control Release 97(3):527–535
Schramm-Baxter J et al (2004) Jet injection into polyacrylamide gels: investigation of jet injection mechanics. J Biomech 37(8):1181–1188
Taberner A et al (2012) Needle-free jet injection using real-time controlled linear Lorentz-force actuators. Med Eng Phys 34(9):1228–1235
Tagawa Y, Yamamoto S, Hayasaka K, Kameda M (2016) On pressure impulse of a laser-induced underwater shock wave. J Fluid Mech 808:5–18
Tagawa Y et al (2012) Highly focused supersonic microjets. Phys Rev X 2(3):031002–10
Tagawa Y et al (2013) Needle-free injection into skin and soft matter with highly focused microjets. Lab Chip 13(7):1357–10
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Publisher's Note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
All animal experiments were conducted in compliance with a protocol reviewed by the University Animal Care and Use Committee of TUAT (No. 27-83). We thank Y. Miyazaki for his help in conducting experiments, and financial support from Japan Society for the Promotion of Science, KAKENHI Grants 17H01246 and 16J08521, and from the Special Research Fund from the Leading Graduate School Program TUAT.
Appendix: The dynamics of the hole in gels made by the liquid jet
Appendix: The dynamics of the hole in gels made by the liquid jet
Figure 7 presents the early stage of the penetration process for different C values. It is clear that the jet propagating in the concentrated gel (Fig. 7a) stops much earlier than that in the weak gel (Fig. 7b), even if the impact speed of the jet \(V_j\) is very large. This leads the shallower penetration depth L in the concentrated gel. We can also observe that the temporal width of the penetration site in Fig. 7b is even wider than that in Fig. 7a. Although the overall trends related to the characteristic cavity dimensions L and W at the rest (e.g., the relationship \(L_1\sim L_2\) in Fig. 4) are quite similar for all C cases, the change of C can change the evolution dynamics of the penetration site dramatically. It suggests that the viscoelasticity (or the fluidity), which is change by C values, might determine the dynamics of the hole (or cavity) made by the liquid jet.
Penetration process of the jet into gels. a The impact speed of the jet \(V_j\sim\)200 m/s, the gel concentration \(C=5\hbox {wt}\%\) and the time interval between each of the frames \(\varDelta t\) is 10 µs. b\(V_j\sim\)58 m/s, \(C=2\hbox {wt}\%\) and \(\varDelta t\sim\)13 µs. The solid arrows are the guides for the jet tip in the air, and the dashed arrows are that in the gel
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Kiyama, A., Endo, N., Kawamoto, S. et al. Visualization of penetration of a high-speed focused microjet into gel and animal skin. J Vis 22, 449–457 (2019). https://doi.org/10.1007/s12650-019-00547-8
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s12650-019-00547-8