Skip to main content

Advertisement

SpringerLink
Log in

Interfacial wave motion caused by wave-mud interaction

  • Regular Paper
  • Published:
Journal of Visualization Aims and scope Submit manuscript

Abstract

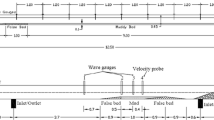
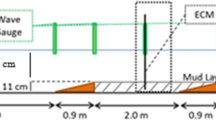
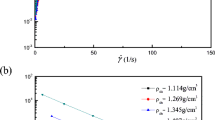
The generation of internal waves induced by surface wave in the fluid mud environment is examined via laboratory experiment in order to study its importance on surface damping. As wave propagates over soft muddy bottom, both viscous shear stress and interfacial motion contribute to energy dissipation. A fully developed fluid mud layer with a homogeneous concentration distribution is created to investigate the resulting energy dissipation for different wave heights, periods and mud densities. Visualization technique and wave gages were applied to measure interfacial motion and surface damping, respectively. Experimental results suggest that the induced interfacial amplitude depends mainly on the relative water depth, and the mode of internal oscillation was identified. Finally, based on the derived energy equation for two-layer system, we compare the relative importance of shear stress and mud motion.

Graphical Abstract

 

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Figs. 5 and 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11

Similar content being viewed by others

References

  • Aagaard T, Holm J (1989) Digitization of wave run-up using video records. J Coast Res 5:547–551

    Google Scholar 

  • Ball FK (1964) Energy transfer between external and internal gravity waves. J Fluid Mech 19:465–478

    Article  MathSciNet  MATH  Google Scholar 

  • Bonmarin P, Rochefort R et al (1989) Surface-wave profile measurement by image-analysis. Exp Fluids 7(1):17–24

    Article  Google Scholar 

  • Canny J (1986) A computational approach to edge detection. IEEE Trans Pattern Anal Mach Intell PAMI-8(6):679–698

    Google Scholar 

  • Dalrymple RA, Liu PLF (1978) Waves over soft muds: a two layer model. J Phys Oceanogr 8:1121–1131

    Article  Google Scholar 

  • de Wit PJ (1992) Liquefaction and erosion of mud due to waves and current. Tech. report 10-92. Delft Univ. Tech

  • Elgar S, Raubenheimer B (2008) Wave dissipation by muddy sea floors. Geophys Res Lett 35:L07611. doi:10.1029/2008GL033245

    Article  Google Scholar 

  • Gade HG (1958) Effects of a nonrigid, impermeable bottom on plane surface waves. J Mar Res 16:61–82

    Google Scholar 

  • Hill DF, Foda MA (1998) Subharmonic resonance of oblique interfacial waves by a progressive surface wave. Proc R Soc Lond A 454:1129–1144

    Article  MathSciNet  MATH  Google Scholar 

  • Hill DF, Foda MA (1999). Effects of viscosity and elasticity on the nonlinear resonance of internal waves. J Geophys Res 104(C5):10951–10958

    Google Scholar 

  • Lim JS (1990) Two-dimensional signal and image processing. Englewood Cliffs, NJ, Prentice Hall, pp 478–488

  • Liu PLF, Chan IC (2007) A note on the effects of a thin visco-elastic mud layer on small amplitude water-wave propagation. Coast Eng 54(3):233–247

    Article  MathSciNet  Google Scholar 

  • Maa JPY, Mehta AJ (1990) Soft mud response to water-waves. J Waterway Port Coast Ocean Eng-Asce 116(5):634–650

    Article  Google Scholar 

  • MacPherson H (1980) The attenuation of water waves over a non-rigid bed. J Fluid Mech 79:721–742

    Article  MathSciNet  Google Scholar 

  • Otsu N (1978) A threshold selection method from gray level histogram. IEEE Trans Syst Man Cybern 8:62–66

    Google Scholar 

  • Parau E, Dias F (2001) Interfacial periodic waves of permanent form with free-surface boundary conditions. J Fluid Mech 437:325–336

    Article  MathSciNet  MATH  Google Scholar 

  • Parker JR (1997) Algorithms for image processing and computer vision. New York, Wiley, pp. 23–29

  • Sakakiyama T, Bijker EW (1989) Mass-transport velocity in mud layer due to progressive waves. J Waterway Port Coast Ocean Eng-Asce 115(5):614–633

    Article  Google Scholar 

  • Scarlatos PD, Mehta AJ (1992) Instability and entrainment mechanisms at the stratified fluiid mud-water interface, nearshore and estuarine cohesive sediment transport. Pac Rim Congr 42:205–223

    Google Scholar 

  • Torres Freyermuth A, Hsu TJ (2010) On the dynamics of wave-mud interaction: a numerical study. J Geophys Res 115: C07014. doi:10.1029/2009JC005552

  • Wells JT (1983) Dynamics of coastal fluid muds in low-moderate, and high-tide-range environments. Can J Fish Aqua Sci 40:130–142

    Google Scholar 

  • Winterwerp JC, van Kesteren WGM (2004) Introduction to the physics of cohesive sediment in the marine environment. Elsevier, Amsterdam

    Google Scholar 

Download references

Acknowledgments

The authors would like to thank the National Science Council of the Republic of China, Taiwan, for financially supporting this research under Contract No. NSC. 98-2221-E-006-254–MY3 and NSC-96-2628-E-006-249-MY3.

Author information

Authors and Affiliations

  1. Department of Hydraulic and Ocean Engineering, National Cheng Kung University, No.1, Dasyue Rd, Tainan, 701, Taiwan

    Wen-Yang Hsu & Hwung-Hweng Hwung

  2. Tainan Hydraulics Laboratory, Research Center of Ocean Environment and Technology, National Cheng Kung University, 5th floor, 500, Sec.3, Anming Road, Tainan, 709, Taiwan

    Ray-Yeng Yang

  3. Division of Mathematics, General Education Center, Chienkuo Technology University, No. 1, Jieshou N. Rd, Changhua, 500, Taiwan

    Chi-Min Liu

Authors
  1. Wen-Yang Hsu
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Hwung-Hweng Hwung
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Ray-Yeng Yang
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Chi-Min Liu
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Hwung-Hweng Hwung.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Hsu, WY., Hwung, HH., Yang, RY. et al. Interfacial wave motion caused by wave-mud interaction. J Vis 15, 215–224 (2012). https://doi.org/10.1007/s12650-012-0131-4

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s12650-012-0131-4

Keywords

Search

Navigation