Experimental and analytical investigation of the response of a mud layer to solitary waves

Abstract

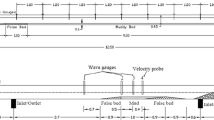
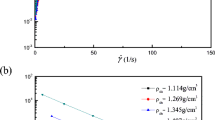
Although the different aspects of wave-mud interaction have been studied by many researchers, few studies have been conducted on the effect of solitary wave on the particle velocities formed in the layers of cohesive sediments. The main objective of the present study is to investigate different features of the mud mechanical responses to the solitary wave loadings. This paper describes a comprehensive study of solitary wave-mud interaction by means of sets of laboratory tests, in which time series of the velocity in the water and mud layers, as well as free-surface evolutions, were measured. Wave damping and several aspects of the mechanical response of the mud layer to solitary wave loadings, e.g. mud particle velocities, the ratio between positive and negative peak velocities, time shift between peak velocities in the mud and water layer and the mud movement period, were studied through nondimensional parameters. It was shown that, at higher values of the mud water content ratio, the time shifts between the peak velocities in the mud and water layers decrease, whereas the mud movement period and the ratio of the positive to the negative peaks increase. Similar trends were observed as the height of the solitary wave was increased. A viscous analytical two-layered model has been developed. Comparing to the measurements, the present model and the model of Liu and Chan (J Fluid Mech 579:467–480, 2007) presented a similar behaviour for simulating the mechanical response of mud under the action of a solitary wave and both models performed better than the model of Jiang and Zhao (J Waterw Port Coast Ocean Eng 115:345–362, 1989).

Appendix

The linearised boundary layer equations governing the system of the two-layered viscous water-mud layers are expressed as

$$ \frac{\partial {U}_{\mathrm{w}}}{\partial t}={\delta_{\mathrm{w}}}^2\frac{\partial^2{U}_{\mathrm{w}}}{\partial {z}^2} $$

(40)

$$ \frac{\partial {U}_{\mathrm{m}}}{\partial t}={\delta_{\mathrm{m}}}^2\frac{\partial^2{U}_{\mathrm{m}}}{\partial {z}^2} $$

(41)

for which, the boundary conditions are described as follows:

$$ {U}_{\mathrm{m}}=-\gamma {U}_{I,\mathrm{w}},\kern0.75em z=-{d}_N $$

(42)

$$ {U}_{\mathrm{m}}={U}_{\mathrm{w}}+\left(1-\gamma \right){U}_{I,\mathrm{w}},\kern0.75em z=0 $$

(43)

$$ {\rho}_{\mathrm{w}}{\nu}_{\mathrm{w}}\frac{\partial {U}_{\mathrm{w}}}{\partial z}={\rho}_{\mathrm{m}}{\nu}_{\mathrm{m}}\frac{\partial {U}_{\mathrm{m}}}{\partial z},\kern0.75em z=0 $$

(44)

$$ \frac{d{U}_{\mathrm{w}}}{dz}\to 0,\kern0.75em z\to \infty $$

(45)

By applying the Laplace transform to the system of the equations above, we obtain

$$ s{\overset{\sim }{U}}_{\mathrm{m}}\left(z,s\right)={\delta_{\mathrm{m}}}^2\frac{d^2{\overset{\sim }{U}}_{\mathrm{m}}\left(z,s\right)}{d{z}^2} $$

(46)

$$ s{\overset{\sim }{U}}_{\mathrm{w}}\left(z,s\right)={\delta_{\mathrm{w}}}^2\frac{d^2{\overset{\sim }{U}}_{\mathrm{w}}\left(z,s\right)}{d{z}^2} $$

(47)

$$ {\overset{\sim }{U}}_{\mathrm{m}}\left(z,s\right)=-\gamma {\overset{\sim }{U}}_{\mathrm{w}}\left(z,s\right),\kern0.75em z=-{d}_N $$

(48)

$$ {\overset{\sim }{U}}_{\mathrm{m}}\left(z,s\right)={\overset{\sim }{U}}_{\mathrm{w}}\left(z,s\right)+\left(1-\gamma \right){\overset{\sim }{U}}_{I,\mathrm{w}}(s),\kern0.75em z=0 $$

(49)

$$ {\rho}_{\mathrm{w}}{\nu}_{\mathrm{w}}\frac{d{\overset{\sim }{U}}_{\mathrm{w}}\left(z,s\right)}{dz}={\rho}_{\mathrm{m}}{\nu}_{\mathrm{m}}\frac{d{\overset{\sim }{U}}_{\mathrm{m}}\left(z,s\right)}{dz},\kern0.75em z=0 $$

(50)

$$ \frac{d{\overset{\sim }{U}}_{\mathrm{w}}\left(z,s\right)}{dz}\to 0,\kern0.75em z\to \infty $$

(51)

where $\overset{\sim }{U}$ denotes the Laplace-transformed form. The solutions for the ordinary differential equations of (46) and (47) read as follows:

$$ {\overset{\sim }{U}}_{\mathrm{w}}\left(z,s\right)={A}_{\mathrm{w}}{e}^{\sqrt{s}z}+{B}_{\mathrm{w}}{e}^{-\sqrt{s}z} $$

(52)

$$ {\overset{\sim }{U}}_{\mathrm{m}}\left(z,s\right)={A}_{\mathrm{m}}{e}^{\sqrt{s}z}+{B}_{\mathrm{m}}{e}^{-\sqrt{s}z} $$

(53)

where A_w, B_w, A_m and B_m are the constant coefficients for the transformed solutions of the water and mud layers, respectively. Applying the boundary conditions (48) to (51), the following coefficients are obtained:

$$ {A}_{\mathrm{w}}=0 $$

(54)

$$ {B}_{\mathrm{w}}=\left(\gamma -1\right){\overset{\sim }{U}}_{I,\mathrm{w}}(s)+\frac{\gamma \left(1-\gamma \right){\overset{\sim }{U}}_{I,\mathrm{w}}(s)}{\gamma +\xi }+\frac{2\gamma \xi {\overset{\sim }{U}}_{I,\mathrm{w}}(s)}{\left(\gamma -\xi \right){e}^{-\frac{\sqrt{s}}{\delta_{\mathrm{m}}}{d}_N}-\left(\gamma +\xi \right){e}^{\frac{\sqrt{s}}{\delta_{\mathrm{m}}}{d}_N}}+\frac{2\gamma \xi}{\left(\gamma +\xi \right)}\frac{\left(1-\gamma \right){\overset{\sim }{U}}_{I,\mathrm{w}}(s){e}^{-\frac{\sqrt{s}}{\delta_{\mathrm{m}}}{d}_N}}{\left(\gamma -\xi \right){e}^{-\frac{\sqrt{s}}{\delta_{\mathrm{m}}}{d}_N}-\left(\gamma +\xi \right){e}^{\frac{\sqrt{s}}{\delta_{\mathrm{m}}}{d}_N}} $$

(55)

$$ {A}_{\mathrm{m}}=\frac{\gamma \left(1-\gamma \right)}{\gamma +\xi }{\overset{\sim }{U}}_{I,\mathrm{w}}(s)-\frac{\gamma \left(\gamma -\xi \right){\overset{\sim }{U}}_{I,\mathrm{w}}(s)}{\left(\gamma -\xi \right){e}^{-\frac{\sqrt{s}}{\delta_{\mathrm{m}}}{d}_N}-\left(\gamma +\xi \right){e}^{\frac{\sqrt{s}}{\delta_{\mathrm{m}}}{d}_N}}-\gamma \frac{\left(\gamma -\xi \right)}{\left(\gamma +\xi \right)}\frac{\left(1-\gamma \right){\overset{\sim }{U}}_{I,\mathrm{w}}(s){e}^{-\frac{\sqrt{s}}{\delta_{\mathrm{m}}}{d}_N}}{\left(\gamma -\xi \right){e}^{-\frac{\sqrt{s}}{\delta_{\mathrm{m}}}{d}_N}-\left(\gamma +\xi \right){e}^{\frac{\sqrt{s}}{\delta_{\mathrm{m}}}{d}_N}} $$

(56)

$$ {B}_{\mathrm{m}}=\frac{\gamma \left(\gamma +\xi \right){\overset{\sim }{U}}_{I,\mathrm{w}}(s)}{\left(\gamma -\xi \right){e}^{-\frac{\sqrt{s}}{\delta_{\mathrm{m}}}{d}_N}-\left(\gamma +\xi \right){e}^{\frac{\sqrt{s}}{\delta_{\mathrm{m}}}{d}_N}}+\frac{\gamma \left(1-\gamma \right){\overset{\sim }{U}}_{I,\mathrm{w}}(s){e}^{-\frac{\sqrt{s}}{\delta_{\mathrm{m}}}{d}_N}}{\left(\gamma -\xi \right){e}^{-\frac{\sqrt{s}}{\delta_{\mathrm{m}}}{d}_N}-\left(\gamma +\xi \right){e}^{\frac{\sqrt{s}}{\delta_{\mathrm{m}}}{d}_N}} $$

(57)

Substituting Eqs. (54)–(57) into (52) and (53) and rewriting the equations, the followings expressions are obtained:

$$ {\overset{\sim }{U}}_{\mathrm{w}}\left(z,s\right)=\frac{\left(\gamma -1\right){\overset{\sim }{\xi U}}_{I,\mathrm{w}}(s)}{\gamma +\xi }{e}^{-\frac{\sqrt{s}}{\delta_{\mathrm{w}}}z}+\frac{2\gamma \xi {\overset{\sim }{U}}_{I,\mathrm{w}}(s)\ }{\left(\gamma -\xi \right){e}^{-\frac{\sqrt{s}}{\delta_{\mathrm{m}}}{d}_N}-\left(\gamma +\xi \right){e}^{\frac{\sqrt{s}}{\delta_{\mathrm{m}}}{d}_N}}{e}^{-\frac{\sqrt{s}}{\delta_{\mathrm{w}}}z}+\frac{2\gamma \xi}{\left(\gamma +\xi \right)}\frac{\left(1-\gamma \right){\overset{\sim }{U}}_{I,\mathrm{w}}(s){e}^{-\frac{\sqrt{s}}{\delta_{\mathrm{m}}}{d}_N}}{\left(\gamma -\xi \right){e}^{-\frac{\sqrt{s}}{\delta_{\mathrm{m}}}{d}_N}-\left(\gamma +\xi \right){e}^{\frac{\sqrt{s}}{\delta_{\mathrm{m}}}{d}_N}}{e}^{-\frac{\sqrt{s}}{\delta_{\mathrm{w}}}z} $$

(58)

$$ {\overset{\sim }{U}}_{\mathrm{m}}\left(z,s\right)=\frac{\gamma \left(1-\gamma \right)}{\gamma +\xi }{\overset{\sim }{U}}_{I,\mathrm{w}}(s){e}^{\frac{\sqrt{s}}{\delta_{\mathrm{m}}}z}-\frac{\gamma \left(\gamma -\xi \right){\overset{\sim }{U}}_{I,\mathrm{w}}(s)}{\left(\gamma -\xi \right){e}^{-\frac{\sqrt{s}}{\delta_{\mathrm{m}}}{d}_N}-\left(\gamma +\xi \right){e}^{\frac{\sqrt{s}}{\delta_{\mathrm{m}}}{d}_N}}{e}^{\frac{\sqrt{s}}{\delta_{\mathrm{m}}}z}-\gamma \frac{\left(\gamma -\xi \right)}{\left(\gamma +\xi \right)}\frac{\left(1-\gamma \right){\overset{\sim }{U}}_{I,\mathrm{w}}(s){e}^{-\frac{\sqrt{s}}{\delta_{\mathrm{m}}}{d}_N}}{\left(\gamma -\xi \right){e}^{-\frac{\sqrt{s}}{\delta_{\mathrm{m}}}{d}_N}-\left(\gamma +\xi \right){e}^{\frac{\sqrt{s}}{\delta_{\mathrm{m}}}{d}_N}}{e}^{\frac{\sqrt{s}}{\delta_{\mathrm{m}}}z}+\frac{\gamma \left(\gamma +\xi \right){\overset{\sim }{U}}_{I,\mathrm{w}}(s)}{\left(\gamma -\xi \right){e}^{-\frac{\sqrt{s}}{\delta_{\mathrm{m}}}{d}_N}-\left(\gamma +\xi \right){e}^{\frac{\sqrt{s}}{\delta_{\mathrm{m}}}{d}_N}}{e}^{-\frac{\sqrt{s}}{\delta_{\mathrm{m}}}z}+\frac{\gamma \left(1-\gamma \right){\overset{\sim }{U}}_{I,\mathrm{w}}(s){e}^{-\frac{\sqrt{s}}{\delta_{\mathrm{m}}}{d}_N}}{\left(\gamma -\xi \right){e}^{-\frac{\sqrt{s}}{\delta_{\mathrm{m}}}{d}_N}-\left(\gamma +\xi \right){e}^{\frac{\sqrt{s}}{\delta_{\mathrm{m}}}{d}_N}}{e}^{-\frac{\sqrt{s}}{\delta_{\mathrm{m}}}z} $$

(59)

whose Inverse Laplace transform leads to

$$ {U}_{\mathrm{m}}=\frac{\gamma \left(1-\gamma \right)}{\gamma +\xi }{\int}_0^t\operatorname{erfc}\left[\frac{-z}{2{\delta}_{\mathrm{m}}\sqrt{t-\tau }}\right] d\tau +\gamma \sum \limits_{n=0}^{\infty }{\left(\frac{\gamma -\xi }{\gamma +\xi}\right)}^{n+1}{\int}_0^t\frac{\partial {U}_{I,\mathrm{w}}}{\partial \tau}\left\{\operatorname{erfc}\left[\frac{\left(2n+1\right){d}_N-z}{2{\delta}_{\mathrm{m}}\sqrt{t-\tau }}\right]\right\} d\tau +\gamma \frac{\left(1-\gamma \right)}{\left(\gamma +\xi \right)}\sum \limits_{n=0}^{\infty }{\left(\frac{\gamma -\xi }{\gamma +\xi}\right)}^{n+1}{\int}_0^t\frac{\partial {U}_{I,\mathrm{w}}}{\partial \tau}\left\{\operatorname{erfc}\left[\frac{\left(2n+1\right){d}_N-z}{2{\delta}_{\mathrm{m}}\sqrt{t-\tau }}\right]\right\} d\tau -\gamma \sum \limits_{n=0}^{\infty }{\left(\frac{\gamma -\xi }{\gamma +\xi}\right)}^n{\int}_0^t\frac{\partial {U}_{I,\mathrm{w}}}{\partial \tau}\left\{\operatorname{erfc}\left[\frac{\left(2n+1\right){d}_N+z}{2{\delta}_{\mathrm{m}}\sqrt{t-\tau }}\right]\right\} d\tau -\gamma \left(1-\gamma \right)\sum \limits_{n=0}^{\infty}\frac{{\left(\gamma -\xi \right)}^n}{{\left(\gamma +\xi \right)}^{n+1}}{\int}_0^t\frac{\partial {U}_{I,\mathrm{w}}}{\partial \tau}\left\{\operatorname{erfc}\left[\frac{\left(2n+1\right){d}_N+z}{2{\delta}_{\mathrm{m}}\sqrt{t-\tau }}\right]\right\} d\tau $$

(60)

$$ {U}_{\mathrm{w}}=\left[\frac{\xi \left(\gamma -1\right)}{\gamma +\xi}\right]{\int}_0^t\operatorname{erfc}\left[\frac{z}{2{\delta}_{\mathrm{m}}\sqrt{t-\tau }}\right] d\tau -2\gamma \xi {\sum}_{n=0}^{\infty}\frac{{\left(\gamma -\xi \right)}^n}{{\left(\gamma +\xi \right)}^{n+1}}{\int}_0^t\frac{\partial {U}_{I,\mathrm{w}}}{\partial \tau}\left\{\operatorname{erfc}\left[\frac{\left(2n+1\right){d}_N+\xi z}{2{\delta}_{\mathrm{m}}\sqrt{t-\tau }}\right]\right\} d\tau -2\gamma \xi \frac{\left(1-\gamma \right)}{\left(\gamma +\xi \right)}{\sum}_{n=0}^{\infty}\frac{{\left(\gamma -\xi \right)}^n}{{\left(\gamma +\xi \right)}^{n+1}}{\int}_0^t\frac{\partial {U}_{I,\mathrm{w}}}{\partial \tau}\left\{\operatorname{erfc}\left[\frac{2n{d}_N+\xi z}{2{\delta}_{\mathrm{m}}\sqrt{t-\tau }}\right]\right\} d\tau $$

(61)