Statement of Novelty

Processes for the recovery of phosphorus from wastewater are often designed based on expert knowledge and laboratory or plant experiments, which tends to be time-consuming and costly. In the present work, we present a novel model-based approach for the analysis and optimization of phosphorus recovery processes. This is achieved by describing the thermodynamics of the complex multi-component solutions. The developed thermodynamic model uses parameters from the literature only, no adjustment with respect to phosphorus recovery processes is made. The Stuttgart process is used as an example for illustrating the capabilities of this approach, but the model could be used for other phosphorus recovery processes as well.

Introduction

Phosphorus is a key element for every living organism. Hence, phosphorus-containing substances with a high plant availability are used as agricultural fertilizers to enhance the cultivation of plants [1]. To date, the main source for these substances is rock phosphorus. However, similar to Hubbert’s peak oil predictions from 1949 [2], recent simulations indicate that rock phosphorus reserves could be exhausted within the next 100 years [3]. Making other phosphorus sources available is thus highly desirable.

The simultaneous recovery of the two nutrients phosphorus (P) and nitrogen (N) by crystallization of magnesium ammonium phosphate (MAP, MgNH4PO4·6 H2O) from wastewater or sewage sludge is an attractive alternative to rock phosphorus mining [4,5,6,7]. MAP, once an undesired by-product in wastewater treatment plants [8, 9], is nowadays used as a fertilizer [10]. Several processes were developed to produce MAP from wastewater [6, 11], including the Stuttgart process [5], which is investigated in the present work. Although the recovery of phosphorus as MAP using digested sludge from plants with chemical P-removal requires more efforts than that from plants with enhanced biological P-removal (EBPR), chemical P-removal is the main operation mode in Germany where peak effluent values of 1 mg L−1 need to be undercut at larger waste water treatment plants and much lower values are discussed even for smaller plants.

Thus, digested sewage sludge from plants with primary sedimentation and simultaneous chemical phosphorus elimination via iron-salts serves as the feed of the Stuttgart process. Essentially, digested sewage sludge is an aqueous solution with many dissolved species loaded with a solid phase [12, 13]. Hence, it is a complex multi-component, multi-phase system. Although its actual composition varies with time and location, the aqueous phase typically contains high amounts of the nonmetal ions NH4+ and PO43− [13], the metal cations Na+, K+, Mg2+ and Ca2+, and the heavy metal cations Fe3+, Al3+, Pb2+, Cu2+, Zn2+ and Ni2+ [12]; the major anions being Cl− and sulfates. The solid phase contains a plethora of insoluble organic compounds and different phosphate salts with the cations Mg2+, Ca2+, Al3+ and Fe3+. The actual composition of the sewage sludge of interest mainly depends on two factors: the source of the wastewater, i.e. whether municipal or industrial wastewater is considered—which might underlie temporal changes—and the previous process steps and operating conditions in a wastewater treatment plant. The latter encompasses e.g. measures to reduce bulky sludge via addition of aid substances and the type of thickening devices (static or mechanical) including the use of flocculants.

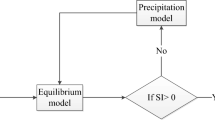
The production of MAP from such feeds is essentially a recrystallization process that consists of two major process steps: (i) dissolution of the metal phosphate salts from the solid phase into the aqueous phase and (ii) precipitation of phosphate together with Mg2+ and NH4+. This is achieved by applying several pH shifts. A scheme of the Stuttgart process, which is investigated in the present work, is presented in Fig. 1.

Fig. 1
figure 1

adopted from Ref. [25]

Scheme of the Stuttgart process (C6H8O7: citric acid, HM: heavy metal),

Full size image

In the Stuttgart process, the phosphate salts are dissolved into the aqueous phase by lowering the pH value with sulfuric acid (H2SO4). The remaining solid is removed by a filter, and only the aqueous phase is processed further. That aqueous solution usually contains less Mg2+ than PO43−, but a stoichiometric ratio is needed for maximizing the MAP precipitation. Hence, a Mg-containing salt, typically MgCl2 or MgO, is added to the aqueous solution until the molar ratio Mg2+/PO43− is slightly above 1. MAP is then precipitated by increasing the pH value with NaOH. In that process step, the precipitation of undesired salts other than MAP, e.g. iron phosphates, must be suppressed. The key difference between various processes for obtaining MAP from wastewater is the design of this suppression step. In the Stuttgart process [14], the aqueous metal cations are bound in complexes with citric acid (C6H8O7) [15,16,17]. Citrate anions of different valency form strong ion pairs (electrically neutral and non-neutral ones) with different cations and thereby prevent these ions from forming salts. However, the complexation of one mole of metal cations of the sewage sludge roughly requires one mole of citric acid, which is a rather expensive chemical, at least compared to H2SO4 and NaOH. Furthermore, not only the unwanted heavy metal cations, but also Mg2+ is complexed by citric acid, which is obviously unfavorable for the MAP precipitation. A thorough understanding of the species distributions and the extent of the complexation of the different ions is thus essential for gaining an improved understanding of the process. Moreover, a potential reduction of the required amount of citric acid is highly desirable.

The recrystallization of phosphate salts is determined by the species distribution of aqueous phosphates, which depends crucially on the pH value of the solution [18]. However, the effort for measuring species distributions in the multi-component aqueous solutions that are relevant here is high. Therefore, methods for predicting the species distributions based on models are important, but only few such studies have been presented in the literature. Ohlinger et al. [9] and Wu and Zhou [19] predicted the MAP formation as a function of pH in systems with few species, considering only the ionic species that make up MAP (Mg2+, NH4+, and PO43−). Jia et al. [20] applied a chemical equilibrium model for the optimization of ammonium removal from digested sewage sludge as MAP. They considered the species Na+, K+, Mg2+, Ca2+, NH4+ and PO43− and calculated the amount of NaOH required for raising the pH value of the sludge to 9. However, their model does not include aqueous heavy metal cations and the solid heavy metal phosphates that might precipitate together with MAP, which have a negative influence on the fertilizer qualities of the product [21]. Song et al. [22] studied the pH-dependence of the crystallization of calcium phosphate, which needs to be considered in MAP production from digested sewage sludge.

In the present work, a thermodynamic model of the MAP production from digested sewage sludge is presented. In contrast to previous studies in the literature, in our model we consider most of the major ionic constituents of the sewage sludge. The model is tested using the Stuttgart process as an example. To validate the model predictions, they are compared to experimental data from the literature for the dissolution step of the Stuttgart process. Unfortunately, such a comparison cannot be carried out for the other process steps due to a lack of experimental data. The model is used to predict the species distributions and the precipitating solids during the precipitation step of the Stuttgart process. Finally, systematic variations of process parameters are carried out, revealing some optimization potential of the Stuttgart process with respect to the amounts of employed chemicals (H2SO4, NaOH, and citric acid).

In the model, chemical equilibrium constants and solubility products for the precipitating salts are taken from the literature. An extended Debye–Hückel model [23] is used for calculating the activity coefficients of the dissolved species. The considered species are Na+, K+, Mg2+, Ca2+, Pb2+, Cu2+, Zn2+, Ni2+, Fe3+, Al3+, NH4+, Cl− as well as the different forms of phosphate ions occurring at different pH values and their many mutual combinations to salts that might precipitate from the solution. In addition, the different dissociation steps of citric acid are also considered explicitly. Other complexing agents could be included in a similar way.

Modeling and Simulation

Assumptions and Considered Species

In the present work, the aqueous phase of the sewage sludge is assumed to contain the species listed in Table 1. Insoluble organic compounds are disregarded. In the aqueous solution, chemical reactions take place, which are listed in Table 2 along with their equilibrium constants. The aqueous solution can be in thermodynamic equilibrium with one or more solid phases. It is assumed that the several solids that might precipitate from the solution form individual phases of the individual pure salts. The considered salts are listed in Table 3.

Table 1 Species considered in the model developed in the present work and their ion-specific parameters σi of the extended Debye–Hückel model taken from [23], see Eq. (3)
Full size table
Table 2 Chemical reactions considered in the developed model and their equilibrium constants at 298.15 K
Full size table
Table 3 Salts considered in the developed model and their solubility products at 298.15 K
Full size table

Thermodynamic Model

The thermodynamic model developed in the present work is conceptually similar to a model employed in a previous work for describing the crystallization sequence during the evaporation of seawater [24]. We start the model description by briefly introducing the employed normalizations of the chemical potentials. Since we only consider processes at 298.15 K and 101.3 kPa, in all following equations we drop the temperature and pressure dependence of the chemical potentials to simplify the notation.

The chemical potentials of all solutes i are normalized to infinite dilution according to Henry’s law on the molality scale as shown in Eq. (1):

$$ \mu_{i} = \mu_{i}^{0} + RT\ln \left( {\frac{{b_{i} }}{{b^{0} }}} \right) + RT\ln \gamma_{i} $$
(1)

where \(\mu_{i}^{0}\) is the reference chemical potential of solute i in the hypothetical ideal solution at a molality of 1 mol kg−1, bi is the molality of solute i, the unit molality \(b^{0} = 1\) mol kg−1 makes the second term dimensionless, and γi is the activity coefficient of solute i on the molality scale. The chemical potential of the solvent water is normalized according to Raoult as shown in Eq. (2):

$$ \mu_{{\text{W}}} = \mu_{{\text{W}}}^{0} + RT\ln a_{{\text{W}}} $$
(2)

where \(\mu_{{\text{W}}}^{0}\) is the chemical potential of pure water and aW is the activity of water.

In the present work, the activity coefficients of all ionic species are described with the extended Debye–Hückel model according to Kielland [23] as shown in Eq. (3), in which all variables are dimensionless and which only applies to 298.15 K:

$$ \ln \gamma _{i} = \frac{{ - A\, z_{i}^{2} \, \sqrt I }}{{1 + 0.3288{\mkern 1mu} \, \sigma _{i} \, \sqrt I }} $$
(3)

Here, A = 1.1658 is the Debye-Hückel constant, zi denotes the charge of ion i, and I is the ionic strength of the solution defined in Eq. (4):

$$ I = \frac{1}{2}\sum\limits_{{{\text{all}}\,i}} {\frac{{b_{i} }}{{b^{0} }}} \, z_{i}^{2} $$
(4)

In Eq. (3), σi is the so-called “distance of closest approach” parameter, which is ion-specific. Values for σi are taken from the literature and are compiled in Table 1. For some non-neutral ion pairs, no σi are available. In order to keep the model as simple as possible, σi was set to zero in these cases. Note that when setting σi to zero, the Debye–Hückel limiting law for the species i is recovered from Eq. (3). Furthermore, for the sake of simplicity, neutral ion pairs and neutral species are considered to behave ideally, i.e. γi = 1 for these components. These simplifying assumptions, and the use of an extended Debye-Hückel approach in the first place, are mainly motivated by the fact that the maximum ionic strength of the solutions studied here is about 0.2 mol kg−1. For such solutions, the present approach should be a reasonable approximation to the actual behavior of the components in solution. The water activity is modeled as shown in Eq. (5)

$$ \ln a_{{\text{W}}} = - M_{{\text{W}}} b_{0} \left( {\sum\limits_{{{\text{all}}\,i}} {\frac{{b_{i} }}{{b_{0} }}} - 2A\frac{{\sqrt {I^{3} } }}{1 + 1.2\sqrt I }} \right) $$
(5)

where MW is the molar mass of water and the sum runs over all solute species.

From the described activity coefficient model, the thermodynamic definition of pH shown in Eq. (6)

$$ {\text{pH}} = - \log_{10} \left( {\frac{{b_{{\text{H}^{ + } }} }}{{b^{0} }}\gamma_{{H^{ + } }} } \right) $$
(6)

can be evaluated straightforwardly.

The chemical equilibrium of a reaction R is characterized by its equilibrium constant KR defined in Eq. (7):

$$ K_{R} = \frac{{\prod\limits_{n} {\left( {b_{n} \gamma_{n} } \right)^{{nu_{n} }} } }}{{\prod\limits_{m} {\left( {b_{m} \gamma_{m} } \right)^{{nu_{m} }} } }} $$
(7)

Here, m are the reactants and n are the products of the reaction, bi and γi are the molality and activity coefficient on the molality scale of component i in the solution, and νi is the stoichiometric coefficient of component i in the reaction. The reactions considered in the present work and their equilibrium constants are listed in Table 2.

The only exception to Eq. (7) is the auto-protolysis of water, for which the equilibrium constant is defined in Eq. (8)

$$ K_{R} = \frac{{b_{{{\text{H}}^{ + } }} \gamma_{{{\text{H}}^{ + } }} b_{{{\text{OH}}^{ - } }} \gamma_{{{\text{OH}}^{ - } }} }}{{\left( {b^{0} } \right)^{2} a_{{\text{W}}} }} $$
(8)

because the chemical potential of water is normalized according to Raoult (cf. Eq. (2)).

In the different steps of a phosphorus recovery process, different salts precipitate from the solution or dissolve into the solution. The following inequality Eq. (9) is used to determine whether a solid salt S is present or not:

$$ K_{{{\text{SP}},S}} \ge K_{{{\text{AP,}}S}} $$
(9)

Here, \(K_{{{\text{SP}},S}}\) is the solubility product and \(K_{{{\text{AP,}}S}}\) is the so-called activity product. These properties are defined in Eqs. (10) and (11) as [38]

$$ K_{{{\text{SP}},S}} = \exp \left( { - \sum\limits_{n} {\frac{{\nu_{n} \mu_{n}^{0} }}{RT}} } \right) $$
(10)

and

$$ K_{{{\text{AP,}}S}} = \prod\limits_{n} {\left( {b_{n} \gamma_{n} } \right)^{{\nu_{n} }} \left( {a_{{\text{W}}} } \right)^{{\nu_{{{\text{W}},S}} }} } $$
(11)

Here, n are the ionic species that form salt S, νn is the stoichiometric coefficient of ion n in the salt S, and \(\mu_{n}^{0}\) is that ion’s standard chemical potential. Furthermore, bn and γn are the molality and activity coefficient of ion n in the aqueous solution, aW is the water activity in the solution, and υW,S is the number of moles of crystal water in one mole of S.

The activity product \(K_{{{\text{AP,}}S}}\) of a salt S is a formal property. It is a function of the composition of the aqueous solution. By contrast, the solubility product \(K_{{{\text{SP}},S}}\) is a constant. Equation (9) means the following: if equality between the solubility product and the activity product holds, the aqueous solution is in equilibrium with the salt S. If the greater-than sign holds, this is not the case, i.e. the solution is not saturated with the salt S. In the present work, metastability is not taken into account, i.e. if the solubility product is reached in the aqueous solution, the salt immediately precipitates. The salts considered in the present work and their solubility products, which were taken from the literature, are listed in Table 3.

Simulations of the Stuttgart Process

The developed model was used for predicting the species distributions as a function of pH in the different steps of the Stuttgart process. The initial composition of the sewage sludge used in the simulations is presented in Table 4. For the aqueous phase, the initial composition was obtained from the average values of digested sludge reported in Ref. [12] as this reference provides values for a wide range of components. To that composition, Cl− was added until the electroneutrality condition was met. For the solid phase, no detailed analysis is available in the literature. Hence, for carrying out the simulations it was assumed to comprise the PO43− salts of Mg2+, Ca2+, Al3+, and Fe3+ for the following two reasons: first, these metal ions are found to dissolve into the solution in the experiments in Ref. [25]. Second, their PO43− salts are practically insoluble in water, so that they are likely to be present in the solid phase (cf. the solubility products reported in Table 3). The amounts of these salts in the solid phase of the sewage sludge were chosen such that in the simulations of the dissolution step, the maximum metal dissolution (at low pH values) agrees with the experimental data from a sewage plant in Offenburg, Germany [25].

Table 4 Initial composition of the aqueous and solid phases of the digested sewage sludge used as input for the simulations carried out in the present work
Full size table

Starting with this initial composition of the sewage sludge, simulations were carried out for investigating the Stuttgart process, cf. Figure 1 for the process scheme. Following the experiments reported in Ref. [25], the consecutive process steps were simulated as follows: for the dissolution step, H2SO4 was added to the sewage sludge, and the pH value and the species distribution were calculated. The addition of H2SO4 was stopped at a pH value of 4. Then, mimicking the filtering process, the solid phase was simply discarded from the simulation. In the next step, MgCl2 was added to the solution until the molar ratio Mg2+/PO43− was equal to 1. Then, the complexation was carried out by adding citric acid. The amount of citric acid was stoichiometric with respect to the total amount of dissolved metal cations in solution (Mg2+, Ca2+, Al3+ and Fe3+), see Eq. (12):

$$ b_{{{\text{C}}_{6} {\text{H}}_{8} {\text{O}}_{7} }} = b_{{{\text{Mg}}^{2 + } }} + b_{{{\text{Ca}}^{2 + } }} + b_{{{\text{Al}}^{3 + } }} + b_{{{\text{Fe}}^{3 + } }} $$
(12)

As a consequence of the addition of citric acid, the pH value drops to about two. Finally, for the precipitation step, NaOH was added to the solution, and the pH value and the species distribution were calculated. NaOH is assumed to dissociate completely and was added until a pH value of 8.5 was reached. During this precipitation step, all the MAP that can potentially precipitate from solution does so.

Optimization Studies

Carrying out parameter variations in experiments is time-consuming and expensive. The model from the present work provides the opportunity for systematically studying the influence of the key parameters of the Stuttgart process by simulations and to thereby gain guidance on how the process might be optimized. In the present work, two types of variations were studied. These variations pertain the influence of the amounts of the employed chemicals H2SO4, NaOH and citric acid.

First, the pH values at which the dissolution step and the precipitation step are stopped were systematically varied in the ranges 2–5 and 6–9, respectively. All other process parameters remained unaltered. A higher pH value at the end of the dissolution step means that less H2SO4 is needed; a lower pH value at the end of the precipitation step means that less NaOH is needed. As the objective for optimization, the purity of the produced MAP was considered, since both chemicals are inexpensive and obtaining a higher quality product clearly outweighs the added cost if more H2SO4 or NaOH are needed for that purpose. The purity of MAP is defined as the mass fraction of MAP among all precipitated solids.

Second, the amount of added citric acid was varied. A potential reduction of the citric acid demand of the process is highly desirable since citric acid is the most expensive chemical used in the process. Hence, simulations were carried out in which the ratio k between the molality of citric acid and the total molality of the dissolved metal cations in solution (Mg2+, Ca2+, Al3+ and Fe3+), defined in Eq. (13) as

$$ k = \frac{{b_{{{\text{C}}_{6} {\text{H}}_{8} {\text{O}}_{7} }} }}{{b_{{{\text{Mg}}^{2 + } }} + b_{{{\text{Ca}}^{2 + } }} + b_{{{\text{Al}}^{3 + } }} + b_{{{\text{Fe}}^{3 + } }} }} $$
(13)

was varied. In the Stuttgart process as discussed in the previous section, k = 1. Again, the purity of MAP was computed, but also the total cost for the chemicals per kg of produced MAP was estimated. The cost of the individual chemicals used in these calculations are compiled in Table 5.

Table 5 Prices of chemicals used in the Stuttgart process,
Full size table

Implementation

The thermodynamic model described above was implemented in MATLAB. The process simulations and optimization studies were conducted with MATLAB as well, solving the sets of non-linear equations (mass balances and dissociation/reaction equilibria) with the MATLAB-solver fsolve.

Results and Discussion

Simulations of the Stuttgart Process

In Fig. 2, the model predictions for the dissolution step of the Stuttgart process are compared to the experimental data from Ref. [25], where the molalities of several metal cations in the aqueous phase were measured as a function of the pH value. The experimental data from Ref. [25] are compiled in Table 6 for the reader’s convenience.

Fig. 2
figure 2

Molalities of Fe3+, Al3+, Mg2+, and Ca2+ in the aqueous solution as a function of pH at 298.15 K in the dissolution step of the Stuttgart process. Lines show the predictions with the developed model, symbols are experimental data from a sewage plant in Offenburg, Germany [25], cf. Table 6. Error bars indicate the experimental uncertainties and are only shown where they exceed the symbol size

Full size image
Table 6 Experimental data for the ionic molalities of Fe3+, Al3+, Mg2+ and Ca2+ in the dissolution step of the Stuttgart process as a function of pH. The numbers shown here are averages from the series of three measurements reported in Ref. [24]
Full size table

For the initial composition of the sewage sludge, the present model yields a pH value of about 7.4, which compares favorably to the experimental data from Ref. [25], where the pH value of the digested sewage sludge (input to the Stuttgart process) is reported to be in the range 7.4–7.5. Considering that the initial composition of the sludge had to be taken from a different literature source [12], this favorable agreement is gratifying and indicates that both sources are commensurate. Moreover, the accuracy of prediction is similar to that presented by Zhou and Wu [19]. Figure 2 then shows that with decreasing pH as a result of adding H2SO4, the molalities of the ions in the aqueous phase increase due to the dissolution of phosphate salts from the solid phase of the sewage sludge. This can be explained by the combination of two effects: first, when lowering the pH value, the phosphorus species distribution in the liquid phase changes. Second, the solubility products of the metal HPO42− salts exceed those of their metal PO43− counterparts by many orders of magnitude, cf. Table 3. The combination of these two effects leads to the dissolution of the salts into the aqueous phase and, consequently, also to an increase of the metal ion concentrations. To take a specific example: the solid Ca3(PO4)2 dissolves as CaHPO4 a pH value of about 5.5, which is visible as a “kink” in the molality of Ca2+. Similar kinks in the molalities of the other ions appear in Fig. 2 whenever the dissolution of a new salt begins. At a pH value of about 3, the phosphate salts with the cations Mg2+, Ca2+ and Fe3+ are completely dissolved in the aqueous phase and hence, the molalities of these ions remain constant.

Furthermore, Fig. 2 shows good agreement between the experimental data and the model predictions. Especially the molalities of Fe3+ and Ca2+ are predicted accurately by the model. At high pH values, the model overestimates the molalities of Mg2+, while the molalities of Al3+ are underestimated for all pH values. Nonetheless, considering the simplicity of the model and the fact that no adjustable parameters were used and all calculations are entirely predictive, the overall agreement is favorable. Moreover, it must be borne in mind that the initial sludge composition and the ion molalities stem from two different literature sources, which probably also results in some discrepancies between the experimental data and the simulation results.

The next step in the Stuttgart process is the combined complexation of the heavy metal ions and the precipitation of phosphorus as MAP. We start by discussing the heavy metal complexation. Figure 3 shows the molalities of the citrate complexes of Ca2+ and Al3+ as a function of pH. Figure 4 shows a similar plot for the citrate complexes of Mg2+ and Fe3+.

Fig. 3
figure 3

Molalities of different citrate complexes of Ca2+ (___) and Al3+ (---) as a function of pH at 298.15 K as predicted by the developed model

Full size image
Fig. 4
figure 4

Molalities of different citrate complexes of Mg2+ (___) and Fe3+ (---) as a function of pH at 298.15 K as predicted by the developed model

Full size image

In the following, we only discuss Fig. 3 (Ca2+ and Al3+) because Fig. 4 (Mg2+ and Fe3+) leads to similar conclusions. At low pH values, Ca2+ and Al3+ are present as free ions. With an increase in pH, Ca2+ is first complexed by the C6H6O72− anion, while Al3+ is complexed by the C6H5O73− anion. At higher pH values, the species distribution shifts towards the C6H5O73− complex of Ca2+ and the C6H4O74− complex of Al3+. The key aspect, however, is that at high pH values, all the Al3+ is bound in the complex with C6H4O74−, but most of the Ca2+ still remains in the free form. This distinctly different behavior is likely caused by the higher valency of Al3+ compared to Ca2+: Al3+ attracts the various citrate anions much more strongly than Ca2+ does. As a consequence, the equilibrium constants of the formation reactions of the Al3+-citrate complexes are about four orders of magnitude higher than those of the Ca2+-complexes. Hence, at high pH values the complexation of the Al3+ ions is pronounced, while only some of the Ca2+ ions form citrate complexes.

A similar line of arguments holds for the comparison between Fe3+ and Mg2+ shown in Fig. 4. Note that the increase in the molality of Mg2+ when raising the pH value from 2 to about 3 in Fig. 4 is caused by the addition of MgCl2 in the same process step.

Also the other heavy metal ions (not shown in the Figures) form strong complexes with the different anions of citric acid. According to the model predictions, at a pH value of 9, there are practically no remaining free Fe3+ and Al3+ ions, more than 90% of the Cu2+, Zn2+ and Ni2+ ions and roughly 60% of the Pb2+ ions are complexed. These findings compare favorably to experimental results from the literature [26].

Moreover, again kinks in the molalities of the different Ca2+ species are visible in Fig. 3 (and in Fig. 4 for the different Mg2+ species). These kinks are caused by the precipitation of different Ca2+-containing salts, because complexation and precipitation occur simultaneously in the Stuttgart process. To discuss the precipitation in more detail, all precipitating salts are shown as a function of pH in Fig. 5.

Fig. 5
figure 5

Solid loadings (moles of solid per kg of water) of different Ca2+ and Mg2+ phosphates as well as MAP in the precipitation step of the Stuttgart process as a function of pH at 298.15 K as predicted by the developed model

Full size image

With increasing pH value, first the solubility limits of the hydrogen phosphates of Mg2+ and Ca2+ are reached, and these salts precipitate from solution. However, this changes abruptly at a pH value of 6 and above, where PO43− becomes the dominating phosphate species in solution. Since the salts containing PO43− are only sparingly soluble in aqueous solution, they start to precipitate immediately. Most notably, the desired product MAP is the main precipitating species. Ca3(PO4)2 co-precipitates with MAP, but the amounts of Ca3(PO4)2 are almost one order of magnitude lower than those of MAP. No salts of heavy metal ions precipitate since they are effectively complexed by citric acid. Hence, the process allows for obtaining MAP with high purity, the only notable contaminant being Ca3(PO4)2, which has no negative implications on the fertilizing abilities of the product. At a pH value of 8 and above, also Mg3(PO4)2 starts to precipitate, which comes along with a reduction of the MAP precipitation. Hence, too high pH values should be avoided.

Optimization Studies

Figure 6 shows the results obtained with the present model for the purity of MAP as a function of two pH values: the pH value at the end of the dissolution step and the pH value at the end of the precipitation step.

Fig. 6
figure 6

Contour plot of the achieved purity of MAP as a function of the pH of the dissolution and precipitation steps at 298.15 K. The upper right red cross indicates the operation point of the Stuttgart process as shown in Fig. 1, the lower left red cross shows the global maximum for the MAP purity. (Color figure online)

Full size image

With the operating parameters as in the Stuttgart process from Ref. [25], the maximum possible amount of MAP precipitates from solution (not shown in the Figure), and a MAP purity of about 0.72 g g−1 is achieved. The simulations suggest, however, that an increase up to about 0.80 g g−1 is possible by lowering both the pH value of the dissolution step and that of the precipitation step (but to a lesser extent). As result, more H2SO4 is needed, but approximately the same amount of NaOH is required for achieving these new pH values. Since H2SO4 is rather cheap, this seems to be a viable option.

Figure 7 shows the influence of the stoichiometric ratio k between citric acid and the dissolved metal ions, cf. Equation (13), on the price and the purity of the produced MAP.

Fig. 7
figure 7

Purity of MAP (blue symbols and lines, left axis) and costs of the process per kg of produced MAP (red symbols and lines, right axis) as a function of the stoichiometric ratio k between citric acid and the metal cations Mg2+, Ca2+, Al3+, and Fe3+ at 298.15 K. The Stuttgart process as shown in Fig. 1 is operated at k = 1. (Color figure online)

Full size image

Both the cost for the chemicals and the purity of the produced MAP increase with increasing k. The cost increases almost linearly with k; the slightly non-linear behavior at low k is caused by the fact that in this region, the amount of produced MAP increases with increasing k. For k > 0.25, all the MAP that can potentially precipitate does so. In contrast to the cost, the MAP purity increases quickly with increasing k and remains constant from k = 0.5 onwards. This plateau of the MAP purity is intriguing: it suggests that almost the same MAP purity as in the Stuttgart process (k = 1) can be achieved with k = 0.5, i.e. with a reduction of the needed amount of citric acid by 50%. As a result, also the cost per kg of produced MAP drops by almost 50%. Hence, a reduction of the use of citric acid could significantly improve the economics of the process.

Conclusions

A thermodynamic model for sewage sludge systems was developed and used for investigating the different steps of a phosphorus recovery process for MAP production, namely the Stuttgart process. The model is based on an extended Debye–Hückel approach and literature values for equilibrium constants and solubility products. All results obtained with the model are strict predictions, which were validated by comparison to available experimental data. The model can be used to gain a physico-chemical insight into the Stuttgart process and can thereby help with finding the correct ranges for the dosage of the employed chemicals. For example, the model revealed that MAP precipitation is maximized when NaOH is added in the precipitation step up to a pH value between 6.5 and 8; at lower pH, no MAP precipitates and at higher pH, other phosphate salts start to co-precipitate with MAP. Furthermore, the model can be used for process optimization. The results of calculations with systematic variations of process parameters suggest that there is room for improvement of the process with respect to product purity and cost. Most notably, the consumption of citric acid might be reduced to about half while keeping the purity of the produced MAP almost constant. Altogether, the results of the present work show that thermodynamic modeling is viable tool in the analysis and design of phosphorus recovery processes.