Abstract
The aim of this study was to determine the characteristics of shredded biomass from hay, straw and their mix in the ratio 1:1 using a sieve separator with oscillatory motion in the horizontal plane. The research was carried out according to the method described in ANSI/ASAE S424.1 standard. It was found that the geometric mean value of particle sizes x g of shredded biomass from hay, straw and their mix of dimension: 3.45, 3.21 and 2.14 mm, respectively, the greatest impact had the smallest fraction, considered to 10th percentile of cumulative weight distribution x 10 with dimensions 0.32, 0.21 and 0.06 mm, respectively. For hay, straw and mix mass relative span RS m of fines was 3.51, 4.02 and 6.19, respectively, and was negatively correlated with the distribution uniformity index I u . That was confirmed by lower values of graphic kurtosis K g , inclusive graphic skewness GS i and coefficient of uniformity C u , which correlated positively with the coefficient of gradation C g and distribution geometric standard deviation of the high GSD 1, low GSD 2 and total GSD 12 regions distributions. All of biomass particles size distributions belonged to “very poorly sorted” category and were “very fine skewed” and “leptokurtic”. Determine the suitability of the material on the basis of particle size distribution parameters for pressure agglomeration process is an invaluable practical application of this research. It was stated that mix of hay and straw is a preferable material for making pellets according to its better fragmentation. However it is less homogenous as a result of high share of fine particles at dimension under 1.65 mm. The particle size distribution of finest particles should be verified.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
Biomass size reduction process changes the particle size and shape, increases bulk density, improves flow-properties, increases porosity, and generates new surface area [1, 2]. Mani et al. [3] report that the particle size has influence on the mechanical properties of the pellets of straw from wheat, barley and corn.
The particle size distribution measurement is generally carried out by mechanical sieving utilizing a standard sieve set, which is considered as a standard procedure [4–7]. Results from particle size distribution analysis include percentage of particles retained on different sized sieves, cumulative undersize distribution, arithmetic and geometric mean dimension and associated standard deviation, and several other parameters that uniquely describe the particle size distribution [1, 6–11] and effect on the physical properties of the material used in further transformation.
The analysis of the issue shows that there are known requirements for the characteristics of the particle size distribution of material from the remains of trees and the products produced from them (briquettes, pellets). This also applies to feed granules produced from shredded plant material [12]. Even greater experience was gathered in the field of pressure agglomeration of powders for making tablets. Results of research on agricultural biomass are fragmented and explanations in the available literature are not sufficient to evaluate the fragmentation of the material. It is very important for designing handling devices and for pressure agglomeration process. Understanding the roles of particle size distribution parameters will help in better design formulation or to develop appropriate characteristics that can give improved efficiency of suitability preparation of agglomerated materials.
The aim of the study was to determine the characteristics of shredded biomass from hay, straw and their mix using a sieve separator with oscillatory motion in the horizontal plane.
Materials and Methods
For tests the biomass chopped in the forage harvester with a theoretical cutting length of 2 mm were used. The shredded material from straw, hay and mix at a mass ratio of 1:1 had a moisture 6.44 ± 0.07, 7.58 ± 0.08, and 7.96 ± 0.08%, respectively.
Plant material moisture content was carried out by drying-weighting method according to the ASAE S358.2 standard [13].
Using sieve separator (set of sieves from the below: span, dimensions of opening screens in the sequence:1.65, 5.61, 8.98, 18 and 26.9 mm) with oscillatory motion in horizontal plane, chopped biomass were separated according to the standard of ANSI/ASAE S424.1 [5]. Each sample was sieved 5 times.
For the purpose of the distribution geometric mean of particle length x g, dimensionless standard deviation s g and dimensional standard deviation s gw were determined from the following relations:
where x g is the geometric mean of biomass particle size, mm; s g is the standard deviation, dimensionless; s gw is the standard deviation, mm; m i is the mass of the material on the i-th sieve, g and x si is the geometric mean of particle length on the i-th sieve determined from the formula:
where x i is the holes diagonal of i-th sieve, mm and x (i−1) is the diagonal of sieve hole which is above the i-th sieve, mm.
The data of percentage part of cumulative undersize mass obtained from the sieve analysis are shown by a regression equation, using the equation of the Rosin–Rammler distribution [14] in the following form:
where Y is the part of mass material, finer than size x; x is the particle size, receiving from the equivalent diagonal sieve opening, mm; x R is the constant determining the size of the particles, mm and n is the constant characterizing material, which is a measure of the steepness of the curve distribution (dimensionless).
Dimensions of significance based on length and their distribution were derived from the cumulative undersize characteristics of particle dimensions original data. The following are several common particle size distribution parameters based on length were evaluated from these significant dimensions [6–8, 10, 15–17].
where I u is the uniformity index, (%); N sg is the size guide number, mm; RS m is the relative span based on length, dimensionless; C u is the coefficient of uniformity, dimensionless; C g is the coefficient of gradation, dimensionless; GS i is the inclusive graphic skewness, dimensionless; K g is the graphic kurtosis, dimensionless; n is the Rosin–Rammler distribution parameter, dimensionless; x R is the parameter or geometric mean of Rosin–Rammler dimension, mm; GSD 1, GSD 2, GSD 12 are the distribution geometric standard deviation of the high, low and total regions, respectively; and x 95, x 90, x 84, x 75, x 60, x 50, x 30, x 25, x 16, x 10, and x 5 are the corresponding particle lengths in mm at respective 95, 90, 84, 75, 60, 50, 30, 25, 16, 10, and 5% cumulative undersizes, which are also known as percentiles.
Statistical analysis was carried out with the use of a standard statistical package Statistica v.12. Statistical inferences were made at the 0.05 level of probability.
Results and Discussion
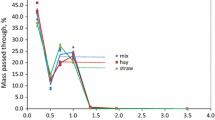
The particle size density distributions of the biomass are asymmetrical (Fig. 1), with the right-hand skewness. A positive value of graphic kurtosis K g (Table 1) is a proof of the steepness of distributions. Similar particle distribution trends were observed for hammer mill grinds of wheat, soybean meal, corn [11], alfalfa [18], wheat straw [9, 19], corn stover [6, 9], switchgrass, barley straw [19] and switchgrass [1, 9].
Inclusive graphic skewness GS i is not very high (0.47–0.67), but the graphic interpretation of density distributions (Fig. 1) allows the inference that there is a very large proportion of finest particles in the mix (hay + straw), and this distribution is similar to the exponential distribution. The other two distributions for hay and straw may be classified as log-normal distributions.
Characteristics of cumulative undersize mass show a rapid achievement of more than 90% of the biomass share with particles less than 8.98 mm, and for a mix with share obtained at a value of x 90 = 6.19 mm (Table 1).
Density distributions of shredded plant material are statistically significantly different between the types of biomass (the value of Fisher–Snedecor test is F = 30.7 with P < 0.0001).
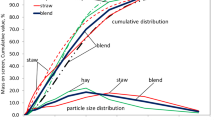
Based on own experience and knowledge from this area and methodology of research, the cumulative mass rate of shredded biomass were approximated by Rosin–Rammler model (RR). For double logarithmic RR model and after receiving a linear function, regression coefficients of equation and its assessments were calculated (Table 2).
In all cases, the evaluation of regression coefficients values are very high, both in relation to the t-Student`s test and P-value, which is not greater than 0.0003. The ratings for regression models are also high; the value of the F—Fisher–Snedecor test exceeds 300, with the critical significance level of P < 0.0001, and R2 above 96%.
Curves for the cumulative mass frequency for RR models, against the measuring points shown in Fig. 2, and the characteristic parameters of the particle size distributions are presented in Table 1. The model RR may be used for further analysis and particularly to predicting the separation of material after cutting and grinding meeting the requirements of the particle size for the production of pellets or briquettes.
The graphs (Fig. 2) and the data contained in Table 1 show that 63.2% of the biomass of mix, hay and straw meets the standards of particle size (3.2 mm, according to suggestion by Mani et al. [20]), because the values x R are 1.73, 3.64 and 3.01 mm, respectively.
The Rosin–Rammler distribution parameters n (slope) were inversely proportional to the kurtosis values (Table 1). This means that a reduced distribution parameter indicated wide distribution. This agrees with published trends [6, 9, 21]. Taking into account the original logarithmic graphical measures classification of Folk and Ward [22] all of these distributions were “very fine skewed” (0.3 ≤ GS is ≤ 1.0) and “leptokurtic” (1.11 ≤ K gs ≤ 1.50). The inclusive standard deviations (σ ig ), based on the same classification determine all mixture materials as “very poorly sorted” (2.0 ≤ σ ig ≤ 4.0 mm), which indicates that the biomass particle sizes are mixed.
Regarding the value of the geometric mean of particle size x g of shredded biomass from hay, straw and mix, with dimensions of 3.45, 3.21 and 2.14 mm, respectively, the greatest impact had finest fraction, considered to 10-th percentile of cumulative mass distribution x 10, with dimensions of 0.32, 0.21 and 0.06 mm, respectively (Table 1).
The relatively high share of fine particles in the mixture of shredded material provides greater value of RS m parameter (Table 1). Shredded material of the mix has a higher share of fine particles, because the average value of the mass share at the span of a sieves set is 6.19. The span was much greater than 1.0, which indicated a ‘borderline wide to narrow’ distribution (Table 1), and this is opposite to published trends [1, 6], especially for shredded biomass (Table 1). A method of comminute of plant biomass has influence on particle size distribution. The relative span RS m was inversely proportional to Rosin–Rammler distribution parameter n (Table 1) and this is consistent with Bitra et al. [1, 6].
The smaller mass share on the span of a sieves set, results from the fact of higher values of the distribution uniformity and the uniformity index values I u (Table 1). The greatest uniformity has mixture of shredded material from hay (I u = 1.67%) and the lowest – mix (I u = 0.30%). These parameters are linked to the values of kurtosis and skewness. If the particle size distribution is flatter (less kurtosis value) and symmetric (lower coefficient of skewness value), the mixture is more homogeneous.
The size guide number N sg for shredded material is correlated to the value of the dimensionless standard deviation (Table 3), and is 100-times value of it (Table 1).
The value of uniformity coefficient (C u ) for shredded material from hay is the smallest (10.23) and the highest is for mix (27.25), which confirms the irregularity of the particle size of that biomass. Material uniformity coefficient of <4.0 is likely to contain particles having a relatively aligned size [23]. Coefficient of uniformity above 4.0 is obtained with a larger range of particles size distribution dispersion. For this reason, all particle size distributions of shredded material must be regarded as almost uniform, which is typical for the fiber [24] and long twisted materials that are bent during transport in the shredding machine, and at the time of their separation under external load.
Coefficient of gradation for particle size distribution (C g ) is in a narrow range and is from 1.35 for hay to 1.53 for mix (Table 1). Coefficient of gradation in the range of 1–3 represents a well-graded particle size distribution [23]. It can therefore be concluded that the tested biomass material has relatively good grading particle size distribution.
Distribution geometric standard deviation of the high GSD 1, low GSD 2 and total GSD 12 regions (Table 1) are negatively correlated with the values of the geometric mean of particle size x g (Table 3). Less dispersion of the particle size is in the upper zone of the distribution than in the lower one, because values for biomass material are in the range 2.84–4.42. Distribution geometric standard deviation of the total region of the shredded material is the lowest for hay (5.67), and the largest for mix (11.79). These values correlated strongly positively with the coefficients of uniformity C u and gradation C g of particle size distribution (Table 1).
The results of variance analysis of geometric mean of particle size x g from shredded plant biomass, dimensionless standard deviation s g and dimensional one s gw are summarized in Tables 3 and 4.
In all cases, the calculated parameters of the particle size distributions are significantly different for the type of material. Geometric mean of particle size for whole mixtures are statistically significantly different between each biomass, creating separate homogeneous groups (Table 3) and the values for mix, hay and straw are 2.14, 2.96 and 3.20 mm, respectively. The standard deviations s g of the dimensionless particle size are practically poorly varied for biomass types (Table 3) and the dimensional standard deviations are consequence of the previous parameters, particularly geometric mean, therefore, that large spread of s gw values from 17.23 to 26.04 mm (Table 3) for a full sample of biomass. Bitra et al. [9] found that average geometric standard deviation (dimensionless) increased slightly from 2.5 ± 0.1 to 2.7 ± 0.1 with an increase in screen size from 12.7 to 25.4 mm and decreased to 2.6 ± 0.1 for further increase to 50.8 mm, but these figures show that the differences were not large. Geometric standard deviation (dimensionless) is therefore not a relevant evaluation criterion parameter and should be found an another indicator. All of these parameters describe the shredded biomass and depend on the material properties, conditions of agglomeration process and storage. Moreover, the particle sizes are important parameters which determine the susceptibility of biomass concentration, particle packing, moving between adjacent particles, the ability to link and create a permanent mechanical or chemical bonds and, therefore, affect the stability of the produced pellets. That requires further extended studies, taking into account mix of hay and straw as preferable material for making pellets according to its better fragmentation. However it is less homogenous as a result of high share of fine particles at dimension under 1.65 mm. The particle size distribution of finest particles should be verified, taking into account that small and medium-sized particles are desired in the granulation process [25]. Smaller particles influence the growth of the efficiency process and reduce pelleting costs. Very small particles however, may cause disturbances in the granulation process due to clogging of granulators dies.
Conclusions
-
1.
Regarding the value of the geometric mean of particle size x g of shredded biomass from hay, straw and mix, with dimensions of 3.45, 3.21 and 2.14 mm, respectively, the greatest impact had finest fraction, considered to 10-th percentile of cumulative mass distribution x 10, with dimensions of 0.32, 0.21 and 0.06 mm, respectively.
-
2.
The indicators used to evaluate the size distributions are good measures, especially in relation to evaluate the contribution of the finest particles. For hay, straw and mix the mass relative span RS m of fine fraction was 3.51, 4.02 and 6.19, respectively. It was reverse of distribution uniformity index (I u rate was 1.67, 1.12 and 0.30%, respectively), confirmed by lower values of kurtosis K g 1.14, 1.20 and 1.46, respectively, and inclusive graphic skewness GS i 0.47, 0.53 and 0.67, respectively, and the coefficient of uniformity C u 10.23, 12.83 and 27.25 respectively. That correlated positively with the coefficient of gradation C g and the distribution geometric standard deviation of the high GSD 1, low GSD 2 and total GSD 12 regions (Table 1).
References
Bitra, V.S.P., Womac, A.R., Yang, Y.T., Igathinathane, C., Miu, P.I., Chevanan, N., Sokhansanj, S.: Knife mill operating factors effect on switchgrass particle size distributions. Bioresour. Technol. 100, 5176–5188 (2009)
Drzymała, Z.: Industrial briquetting—fundamentals and methods. Studies in Mechanical Engineering. PWN-Polish Scientific Publishers, Warsaw, 13 (1993)
Mani, S., Tabil, L.G., Sokhansanj, S.: Specific energy requirement for compacting corn stover. Bioresour. Technol. 97, 1420–1426 (2006)
EL-Sayed, S.A., Mostafa, M.E.: Analysis of grain size statistic and particle size distribution of biomass powders. Waste Biomass Valor. 5, 1005–1018 (2014) doi:10.1007/s12649-014-9308-5
ASABE Standards. ANSI/ASAE S424.: Method of determining and expressing particle size of chopped forage materials by screening. ASABE, St. Joseph, MI, 791–794 (2011)
Bitra, V.S.P., Womac, A.R., Yang, Y.T., Miu, P.I., Igathinathane, C., Sokhansanj, S.: Mathematical model parameters for describing the particle size spectra of knife-milled corn stover. Biosyst. Eng. 104, 369–383 (2009)
Igathinathane, C., Pordesimo, L.O., Columbus, E.P., Batchelor, W.D., Sokhansanj, S.: Sieveless particle size distribution analysis of particulate materials through computer vision. Comput. Electron. Agric. 66, 147–158 (2009)
Allaire, S.E., Parent, L.E.: Size guide and Rosin–Rammler approaches to describe particle size distribution of granular organic-based fertilizers. Biosyst. Eng. 86, 503–509 (2003)
Bitra, V.S.P., Womac, A.R., Chevanan, N., Miu, P.I., Igathinathane, C., Sokhansanj, S., Smith, D.R.: Direct mechanical energy measures of hammer mill comminution of switchgrass, wheat straw, and corn stover and analysis of their particle size distributions. Powder Technol. 193, 32–45 (2009)
Blott, S.J., Pye, K.: Gradistat: A grain size distribution and statistics package for the analysis of unconsolidated sediments. Earth Surf. Process. Landf. 26, 1237–1248 (2001)
Pfost, H., Headley, V.: Methods of determining and expressing particle size. In: Pfost, H.B., Pickering, D. (eds.), Feed Manufacturing Technology. American Feed Manufacturers Association, Inc., Arlington, Virginia, 512–517 (1976)
Obidziński, S.: Pelletization of biomass waste with potato pulp content. Int. Agrophysics. 28, 85–91 (2014)
ASABE Standards. ASAE S358.2: Moisture measurement—forages. ASABE, St. Joseph, MI, 780–781 (2011)
Rosin, P., Rammler, E.: The laws governing the fineness of powdered coal. J. Instrum. Fuel. 7, 29–36 (1933)
Allais, I., Edoura-Gaena, R., Gros, J., Trystram, G.: Influence of egg type, pressure and mode of incorporation on density and bubble distribution of a lady finger batter. J. Food Eng. 74, 198–210 (2006)
Craig, R.F.: Craig’s soil mechanics. Spon Press, London (2004)
Igathinathane, C., Melin, S., Sokhansanj, S., Bi, X., Lim, C.J., Pordesimo, L.O., Columbus, E.P.: Machine vision based particle size distribution determination of airborne dust particles of wood and bark pellets. Powder Technol. 196, 202–212 (2009)
Yang, W., Sokhansanj, S., Crerer, W.J., Rohani, S.: Size and shape related characteristics of alfalfa grind. Can. Agr. Eng. 38, 201–205 (1996)
Mani, S., Tabil, L.G., Sokhansanj, S.: Grinding performance and physical properties of wheat and barley straws, corn stover and switchgrass. Biomass Bioenerg. 27, 339–352 (2004)
Mani, S., Tabil, L.G., Sokhansanj, S.: An overview of compaction of biomass grinds. Powder Handl. Process. 15(3), 160–168 (2003)
Jaya, S., Durance, T.D.: Particle size distribution alginate–pectin microspheres: effect of composition and methods of production. ASABE Paper No. 076022. ASABE, St. Joseph (2007)
Folk, R.L., Ward, W.C.: Brazos River bar: a study in the significance of grain size parameters. J. Sediment. Petrol. 27, 3–26 (1957)
Budhu, M.: Soil mechanics and foundations. Wiley. Danvers (2007)
Basiji, F., Safdari, V., Nourbakhsh, A., Pilla, S.: The effects of fiber length and fiber loading on the mechanical properties of wood-plastic (polypropylene) composites. J. Turk. Agric. For. 34, 191–196 (2010)
Tumuluru, J.S., Wright, C.T., Hess, J.R., Kenney, K.L.: A review of biomass densification systems to develop uniform feedstock commodities for bioenergy application. Biofuels Bioprod. Biorefining. 5(6), 683–707 (2011)
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no conflict of interest.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Lisowski, A., Kostrubiec, M., Dąbrowska-Salwin, M. et al. The Characteristics of Shredded Straw and Hay Biomass—Part 1—Whole Mixture. Waste Biomass Valor 9, 853–859 (2018). https://doi.org/10.1007/s12649-017-9835-y
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s12649-017-9835-y