Abstract
The aim of this study was to determine the characteristics of fine shredded pan fraction of biomass from sieve analyzer of oscillatory motion and as significance it was comparison the geometric mean particle size calculated according to the S319.4 standard with the arithmetic mean particle size that is assumed as half size of the last sieve 1.65 mm, according to the S424.1 standard. It was found that the finest particles size distributions are less varied between types of biomass (straw, hay and their mix) and are more aligned than particle size distributions for whole mixtures. The particles of hay were more uniform and belonged to “well sorted” category than particles of straw and mix, which were non-uniform and belonged to “moderately well sorted” category. All biomass particles size belonged to “very well sorted” category and particle size distribution were “very fine skewed” and “mesokurtic”. The geometric mean of the finest fraction particle size is almost by half smaller than the value resulting from the half value of the last sieve hole size (1.65 mm) of sieve separator with oscillatory motion in the horizontal plane, as these values are 0.45 and 0.82 mm, respectively. Assuming the 0.1 mm for a pan and the last sieve size of 1.65 mm we suggest to calculate the geometric mean (0.41 mm), which is closer to the experimental value. Application of this recommendation to the standard requires further comparative studies.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
Particles of smaller size have a greater contact area and are easier to package during compaction [1–6]. Higher surface area increases number of contact points for chemical reactions [7], which may require grinding to a nominal particle size of about 1 mm. Peleg and Mannheim [8] found that the particle size affects the material binding properties. The smaller particles have more contact area, which causes a greater bond energy per mass unit, regardless of their physicochemical properties. Biomass size reduction process changes the particle size and shape, increases bulk density, improves flow-properties, increases porosity, and generates new surface area [9].
According to MacBain and Payne [6] small and medium-sized particles are desired in the granulation process, as having a larger surface are easier to steam in the conditioning process, resulting in a better gelatinizing starch. Smaller particles influence the growth of process efficiency and reduce pelleting costs. Very small particles however, may cause disturbances in the granulation process due to clogging of granulators dies.
According to Kronbergs [10] when briquetting straw the change in the length of its particles from 20 to 1.5 mm contributed to increase in the density of briquettes by 25 %.
Mani et al. [11] report that the particle size has influence on the mechanical properties of the pellets of straw from wheat, barley and corn.
Finding acceptable mathematical functions to describe particle size distribution data may extend the application of empirical data [2]. Rosin and Rammler [12] stated their equation as a universal law of size distribution valid for all powders, irrespective of the nature of material and the method of grinding. Among at least three common size distribution functions (log-normal, Rosin–Rammler and Gaudin–Schuhmann) tested on different fertilizers, the Rosin–Rammler function was the best function based on an analysis of variance [13, 14]. Also, particle size distributions of alginate–pectin microspheres were well fit with the Rosin–Rammler model [15].
The analysis of the issue shows that there are known requirements for the characteristics of the particle size distribution of material from the remains of trees and the products produced from them (briquettes, pellets). This also applies to feed granules produced from shredded plant material [16]. Even greater experience was gathered in the field of pressure agglomeration of powders for making tablets. Through the development of the pharmaceutical industry progressed the development of the theory of shredding and compacting of mineral and biological materials [17, 18]. Results of research on agricultural biomass are fragmented and explanations in the available literature are not sufficient to evaluate the fragmentation of the material, especially the fine particle fraction. Determination of size and size distribution of the dust particles is fundamental to characterization of dust that is vital for designing handling devices and developing management strategies, e.g. prevention, control, dilution or isolation [19]. The basic problem lies in methodology calculation of the geometric mean particle size. The standard S424.1 [20] stated that a class interval between screens is calculated as a geometric mean size of particles on ith sieve (x si = (x i x i−1)0.5), but for a pan it is determined by assuming half size of last sieve, i.e. 1.65 mm/2 = 0.82 mm. Is this assumption correct, since analysis of mass distribution of all chopped forage material is based on the assumption that these distributions are logarithmic normally distributed? This question was an inspiration to test this assumption experimentally.
The aim of the study was to determine the characteristics of part of shredded biomass from hay, straw and their mix, remained on the pan after sieve selection of whole mixture biomass, called as the fine particle fraction, which was again separated by using sieve separator with oscillatory motion in the vertical plane.
Materials and Methods
For tests the biomass chopped in the forage harvester with a theoretical cutting length of 2 mm were used, intended for the production of pellets. The shredded material from straw, hay and their mix at a mass ratio of 1:1 had a moisture 6.44 ± 0.07 % 7.58 ± 0.08 % and 7.96 ± 0.08 %, respectively. Plant material moisture content was carried out by drying-weighting method according to the ASAE S358.2 [21]. For this purpose three samples of material from each plant with a mass of 20 g were weighed on the Radwag WSP 600/C scale with an accuracy of 0.01 g, and then dried to constant weight at temperature of 105 °C.
The whole mixture was separated on the sieve separator with oscillatory motion in the horizontal plane according to the ANSI/ASAE S424.1 [20] and the fine particle fraction remained on the pan was again separated by using sieve separator with oscillatory motion in the vertical plane according to the ANSI/ASAE S319.4 [22]. Because the finest particles which were sieved through a sieve with screen 1.65 mm (diagonal of the square) are close to a sphere, therefore they were separated on the sieve separator with oscillatory motion in a vertical plane.
The set of sieves from the below have dimensions of opening screens in the sequence: 0.425, 0.6, 0.85, 1.18, 1.6 and 2.36 mm, and pan on the bottom. Each type of material was sieved 5 times. A single sample of biomass used to separation in the separator was 50 g. The time of sieving was 300 s and was controlled using a stopwatch. The individual particle fractions were weighed on electronic scale with an accuracy of 0.01 g.
In order to analyses the results of particle size distribution of the biomass the log-normal distribution was used. For the purpose of the distribution geometric mean of particle length x gs, dimensionless standard deviation s gs and dimensional standard deviation s gws were determined from the following relations [22]:
where x gs is the geometric mean of biomass particle size, mm; s gs is the standard deviation, dimensionless; s gws is the standard deviation, mm; m i is the mass of the material on the i-th sieve, g and x si is the geometric mean of particle length on the i-th sieve determined from the formula:
where x i is the holes diagonal of i-th sieve, mm and x (i − 1) is the diagonal of sieve hole which is above the i-th sieve, mm.
The data of percentage part of cumulative undersize mass obtained from the sieve analysis are shown by a regression equation, using the equation of the Rosin–Rammler distribution [12] in the following form:
where Y s is the part of mass material, finer than size x; x is the particle size, receiving from the equivalent diagonal sieve opening, mm; x Rs is the constant determining the size of the particles, mm and n s is the constant characterizing material, which is a measure of the steepness of the curve distribution (dimensionless).
Dimensions of significance based on length, such as x 95s , x 90s , x 84s , x 75s , x 60s , x 50s , x 30s , x 25s , x 16s , x 10s , and x 5s describing the particle size and their distribution were derived from the cumulative undersize characteristics of particle dimensions original data. The following several common particle size distribution parameters based on length were evaluated from these significant dimensions. Uniformity index I us and size guide number N sgs [13, 23], relative span RS ms [24], coefficient of uniformity C us and coefficient of gradation C gs [25]; and inclusive graphic skewness GS is , and graphic kurtosis K gs [26, 27]; σ igs inclusive graphic standard deviation; distribution geometric standard deviation of the high region GSD 1s (between x 84s and x 50s ), distribution geometric standard deviation of the low region GSD 2s (between x 16s and x 50s ) and distribution geometric standard deviation of the total region GSD 12s (between x 84s and x 16s ) [28] were evaluated as:
where I us is the uniformity index, (%); N sgs is the size guide number, mm; RS ms is the relative span based on length, dimensionless; C us is the coefficient of uniformity, dimensionless; C gs is the coefficient of gradation, dimensionless; GS is is the inclusive graphic skewness, dimensionless; K gs is the graphic kurtosis, dimensionless; σ igs is the inclusive graphic standard deviation, mm; n s is the Rosin–Rammler distribution parameter, dimensionless; x Rs is the parameter or geometric mean of Rosin–Rammler dimension, mm; GSD 1s , GSD 2s , GSD 12s are the distribution geometric standard deviation of the high, low and total regions, respectively; and x 95s , x 90s , x 84s , x 75s , x 60s , x 50s , x 30s , x 25s , x 16s , x 10s , and x 5s are the corresponding particle lengths in mm at respective 95, 90, 84, 75, 60, 50, 30, 25, 16, 10, and 5 % cumulative undersizes, which are also known as percentiles. The parameter C gs is also known as coefficient of curvature or coefficient of concavity, the x 10s value as effective size [25], and x 50s as median diameter.
Statistical analysis was carried out with the use of a standard statistical package Statistica v.12. Statistical inferences were made at the 0.05 level of probability.
Results and Discussion
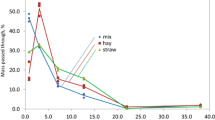
Density distribution of particle sizes of fine fraction has different characteristics (Fig. 1) than for full sample of shredded material (part 1 [29]), and differences in distributions, although statistically significant (F = 5.5, with p = 0.0077) are slight. Figure 1 presents two modal values, one for the smallest particle size of less than 0.425 mm and the second with an average geometric particle size of 0.51 mm (straw) and 0.71 mm (hay, mix). Concentration of the smallest particle size is thus distributed, but there are no longer particles in the fine particle fraction, as in the case of the whole mixture. The values of particle size distribution are summarized in Table 1.
The particle size density distributions of the biomass are asymmetrical, with the right-hand skewness (GS is = 0.34 − 0.37). A positive value of graphic kurtosis K gs (1.0 − 1.03) is a proof of the steepness of distributions. Similar particle distribution trends were observed for hammer mill grinds of wheat, soybean meal, corn [30], alfalfa [31], wheat straw [1, 32], corn stover [1, 33, 34], switchgrass, barley straw [32], switchgrass [1, 2] and giant miscanthus, giant knotweed, Virginia mallow, Spartina pectinata, Jerusalem artichoke, big bluestem, switchgrass [34]. The lowest kurtosis value (flat distribution) and coefficient of skewness value (symmetric distribution) for straw were corresponded with the biggest uniformity index value I us (5.16 %). These parameters are linked to the smallest value of uniformity coefficient C us = 5.40, what means the fine straw biomass is the most homogeneous mixture. Coefficient of gradation for particle size distribution (C gs ) is in a narrow range and is from 1.24 for straw to 1.26 for hay (Table 1). Coefficient of gradation in the range of 1–3 represents a well-graded particle size distribution [35]. Because the difference between the coefficients of skewness and kurtosis distributions of biomass are very small, taking into account the classification of Folk and Ward [27] all biomass particles size distribution were “very fine skewed” (0.3 ≤ GS is ≤ 1.0) and “mesokurtic” (0.90 ≤ K gs ≤ 1.11).
The Rosin–Rammler distribution parameters n (slope) were inversely proportional to the kurtosis values (Table 1). This means that a reduced distribution parameter indicates wide distribution. This agrees with published trends [1, 15, 33].
The relatively high share of fine particles in the mixture of shredded material provides greater value of RS ms parameter (Table 1). Shredded material of the hay has a higher share of fine particles, because the average value of the mass share at the pan of a sieves set is 2.48. The relative span RS ms was inversely proportional to Rosin–Rammler distribution parameter n s (Table 1) and this is consistent with Bitra et al. [2, 33].
The inclusive graphic standard deviations (σ igs ) descriptively classify the particulate material based on Folk and Ward [27] logarithmic original graphical measures classification [26]. The classification obtained from determined values (Table 1) for all mixture material were “very well sorted” (σ igs < 0.35 mm). It should be notice that these classifications are subjected to change when the same material of the sample are processed under different processing machine settings, such as clearance and product classification screen opening dimensions.
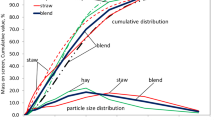
Direct values of mass fractions of fine particle from each sieve of separator with oscillatory motion in the vertical plane and the diagonal dimensions of sieve screens, were logarithmized in order to obtain linear regression, where regression coefficients were calculated and evaluated. The regression results are summarized in Table 2, and regression coefficients (x Rs , n s ) for RR models (Table 1) were calculated after antilogarithmic as well as graphs of cumulative mass frequency of fine particle fraction for hay, straw and mix (Fig. 2) were prepared. In all cases, the evaluation of regression coefficients values are very high, both in relation to the t Student's test and p value, which is not greater than 0.0001. The ratings for regression models are also high; the value of the F—Fisher–Snedecor test exceeds 100, with the critical significance level of p < 0.0001, and R2 above 86 %.
In the overall assessment of fine particles size distributions are less varied between types of biomass and are more aligned than particle size distributions for whole mixtures. Based on these results, a new conclusion may be formulated, that the value of the geometric mean of fine particle size is almost half less than the value resulting from the last half of the screen opening size of sieve (1.65 mm) separator with oscillatory motion in the horizontal plane, because these values are 0.45 mm (Table 1), and 0.82 mm, respectively. This means that the calculation of class centre as the arithmetic mean is methodically wrong and should be seeking a different, better way to determine this value. It is therefore appropriate to carry out basic research to explain this problem.
The results of variance analysis of geometric mean of fine fraction particle size x gs , dimensionless standard deviation s gw and dimensional one s gws are summarized in Tables 3 and 4.
For fine fraction geometric mean of particle size is practically the same, with total average of 0.45 mm (Table 3). The standard deviations s gs of the dimensionless particle size are practically poorly varied for biomass types (Table 3) and the dimensional standard deviations are consequence of the previous parameters, particularly geometric mean, therefore, that only slightly spread of s gws values from 1.50 to 1.58 mm for the fine fraction were received (Table 3). Bitra et al. [2] found that average geometric standard deviation (dimensionless) increased slightly from 2.5 ± 0.1 to 2.7 ± 0.1 with an increase in screen size from 12.7 to 25.4 mm and decreased to 2.6 ± 0.1 for further increase to 50.8 mm, but these figures show that the differences were not large. Geometric standard deviation (dimensionless) is therefore not a relevant discriminatory parameter and should be seeking an another indicator.
The particle size are important parameters which determine the susceptibility of biomass to compaction, density, movement between particles, possibility of their connection and creating lasting mechanical or chemical bonds, and consequently affect the durability of produced pellets.
The biomass particle size is inversely proportional to the density which results from larger contact area effects in smaller particles and better density [3–6]. Such particles in the conditioning process more easily absorb the steam and thus cause greater influence of gelatinize the starch and increase the productivity and reduce the cost and improve the agglomeration stability of the pellets. This is confirmed by studies on pellets of straw from wheat, barley, and maize [10, 11]. In addition, smaller particle size allows a better binding properties of the material because they have a higher binding energy per unit mass [8].
Abdelaziz and Hulteberg [36] concluded that smaller particle sizes would make it easier to depolymerise into smaller fragments. These low molecular weight fragments would serve as better carbon sources to be further hosted by various microbial cell factories, generating further numerous forms of value-added renewable chemicals.
The granulometry affects the bulk density and the density of the bed. Compaction of particulate material of high bulk density increases efficiency and allows for a higher density of the agglomerates is associated with less displaced air and consequently requires less compaction pressure. As in the case of density of the agglomerates, increase in bulk density reduces the energy [37].
Conclusions
The finest particles size distributions are less varied between types of biomass (straw, hay and their mix) and are more aligned than particle size distributions for whole mixtures. The particles of hay were more uniform and belonged to “well sorted” category than particles of straw and mix, which were non-uniform and belonged to “moderately well sorted” category. All biomass particles size belonged to “very well sorted” category and particle size distribution were “very fine skewed” and “mesokurtic”.
The geometric mean of particle size of the finest fraction is almost half smaller than value resulting from the half of the last sieve screen opening size (1.65 mm) because these values are 0.45 mm and 0.82 mm, respectively. Assuming the 0.1 mm for a pan and the last sieve size of 1.65 mm we suggest to calculate the geometric mean (0.41 mm), which is closer to the experimental value. Application of this recommendation to the standard requires further comparative studies.
References
Bitra, V.S.P., Womac, A.R., Chevanan, N., Miu, P.I., Igathinathane, C., Sokhansanj, S., Smith, D.R.: Direct mechanical energy measures of hammer mill comminution of switchgrass, wheat straw, and corn stover and analysis of their particle size distributions. Powder Technol. 193, 32–45 (2009)
Bitra, V.S.P., Womac, A.R., Yang, Y.T., Igathinathane, C., Miu, P.I., Chevanan, N., Sokhansanj, S.: Knife mill operating factors effect on switchgrass particle size distributions. Bioresour. Technol. 100, 5176–5188 (2009)
Kaliyan, N., More, R.V.: Strategies to improve durability of switchgrass briquettes. T. ASABE 52(6), 1943–1953 (2009)
Kaliyan, N., Morey, R.V.: Factors affecting strength and durability of densified biomass products. Biomass Bioenerg. 33(3), 337–359 (2009)
Taulbee, D., Patil, D.P., Honaker, R.Q., Parekh, B.K.: Briquetting of coal fines and sawdust part I: binder and briquetting-parameters evaluations. Int. J. Coal Prep. Util. 20(1), 1–22 (2009)
Tumuluru, J.S., Wright, C.T., Hess, J.R., Kenney, K.L.: A review of biomass densification systems to develop uniform feedstock commodities for bioenergy application. Biofuels Bioprod. Biorefin. 5(6), 683–707 (2011)
Schell, D.J., Harwood, C.: Milling of lignocellulosic biomass: results of pilot scale testing. Appl. Biochem. Biotech. 45(46), 159–168 (1994)
Peleg, M., Mannheim, C.H.: Effect of conditioners on the flow properties of powdered sucrose. Powder Technol. 7, 45–50 (1973)
Drzymała, Z.: Industrial Briquetting—Fundamentals and Methods Studies in Mechanical Engineering. PWN-Polish Scientific Publishers, Warsaw (1993)
Kronbergs, E.: Mechanical strength testing of stalk materials and compacting energy evaluation. Ind. Crop Prod. 11, 211–216 (2000)
Mani, S., Tabil, L.G., Sokhansanj, S.: Specific energy requirement for compacting corn stover. Bioresour. Technol. 97, 1420–1426 (2006)
Rosin, P., Rammler, E.: The laws governing the fineness of powdered coal. J. Instrum. Fuel. 7, 29–36 (1933)
Allaire, S.E., Parent, L.E.: Size guide and Rosin-Rammler approaches to describe particle size distribution of granular organic-based fertilizers. Biosyst. Eng. 86, 503–509 (2003)
Perfect, E., Xu, Q.: Improved parameterization of fertilizer particle size distribution. J. AOAC Int. 81, 935–942 (1998)
Jaya, S., Durance, T.D.: Particle size distribution alginate–pectin microspheres: effect of composition and methods of production. In: ASABE Paper No. 076022. ASABE, St. Joseph (2007)
Obidziński, S.: Pelletization of biomass waste with potato pulp content. Int. Agrophys. 28, 85–91 (2014)
Lisowski, A., Klonowski, J., Sypuła, M.: Using the RRSB model to predict separation of mixture used for production of pellets and briquettes. Agr. Eng. 9(115), 169–176 (2009). (article in Polish with abstract in English)
EL-Sayed, S.A., Mostafa, M.E.: Analysis of grain size statistic and particle size distribution of biomass powders. Waste Biomass Valor 5, 1005–1018 (2014). doi:10.1007/s12649-014-9308-5
Igathinathane, C., Melin, S., Sokhansanj, S., Bi, X., Lim, C.J., Pordesimo, L.O., Columbus, E.P.: Machine vision based particle size distribution determination of airborne dust particles of wood and bark pellets. Powder Technol. 196, 202–212 (2009)
ASABE Standards: ANSI/ASAE S424.1: Method of determining and expressing particle size of chopped forage materials by screening, pp. 791–794. ASABE, St. Joseph (2011)
ASABE Standards: ASAE S358.2: Moisture Measurement—Forages, pp. 780–781. ASABE, St. Joseph (2011)
ASABE Standards: ANSI/ASAE S319.4: Method of Determining and Expressing Fineness of Feed Materials by Sieving, p. 776. ASABE, St. Joseph (2011)
CFI: The CFI Guide of Material Selection for the Production of Quality Blends. Canadian Fertilizer Institute, Ottawa (1982)
Allais, I., Edoura-Gaena, R., Gros, J., Trystram, G.: Influence of egg type, pressure and mode of incorporation on density and bubble distribution of a lady finger batter. J. Food Eng. 74, 198–210 (2006)
Craig, R.F.: Craig’s Soil Mechanics. Spon Press, London (2004)
Blott, S.J., Pye, K.: Gradistat: a grain size distribution and statistics package for the analysis of unconsolidated sediments. Earth Surf. Process. Landforms 26, 1237–1248 (2001)
Folk, R.L., Ward, W.C.: Brazos River bar: a study in the significance of grain size parameters. J. Sediment. Petrol. 27, 3–26 (1957)
Hinds, W.C.: Aerosol Technology—Properties, Behavior, and Measurement of Airborne Particles. Wiley, Hoboken, NY (1982)
Lisowski, A., Kostrubiec, M., Dąbrowska-Salwin, M., Świętochowski, A.: The characteristics of shredded straw and hay biomass. Part 1: whole mixture. Waste Biomass Valor (2016). (submitted to Editor)
Pfost, H., Headley, V.: Methods of determining and expressing particle size. In: Pfost, H.B., Pickering, D. (eds.) Feed Manufacturing Technology, pp. 512–517. American Feed Manufacturers Association Inc, Arlington (1976)
Yang, W., Sokhansanj, S., Crerer, W.J., Rohani, S.: Size and shape related characteristics of alfalfa grind. Can. Agric. Eng. 38, 201–205 (1996)
Mani, S., Tabil, L.G., Sokhansanj, S.: Grinding performance and physical properties of wheat and barley straws, corn stover and switchgrass. Biomass Bioenerg. 27, 339–352 (2004)
Bitra, V.S.P., Womac, A.R., Yang, Y.T., Miu, P.I., Igathinathane, C., Sokhansanj, S.: Mathematical model parameters for describing the particle size spectra of knife-milled corn stover. Biosyst. Eng. 104, 369–383 (2009)
Lisowski, A., Figurski, R., Kostyra, K., Sypuła, M., Klonowski, J., Świętochowski, A., Sobotka, T.: Effect of maize variety and harvesting conditions on the maize chopping process, compacting susceptibility and quality of silage designed for biogas production. Ann. WULS-SGGW Agric. (Agric. Forest Eng.) 64, 25–37 (2014)
Budhu, M.: Soil Mechanics and Foundations. Wiley, Danvers (2007)
Abdelaziz, O.Y., Hulteberg, C.P.: Physicochemical characterisation of technical lignins for their potential valorisation. Waste Biomass Valor (2016). doi:10.1007/s12649-016-9643-9
Hejft, R., Obidziński, S.: Pressure agglomeration of plant materials–pelleting and briquetting (Part II). J. Res. Appl. Agric. Eng. 60(1), 19–22 (2015)
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no conflict of interest.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Lisowski, A., Kostrubiec, M., Dąbrowska-Salwin, M. et al. The Characteristics of Shredded Straw and Hay Biomass: Part 2—The Finest Particles. Waste Biomass Valor 9, 115–121 (2018). https://doi.org/10.1007/s12649-016-9747-2
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s12649-016-9747-2