Morris–Thorne-type wormhole with a cosmic string effects on harmonic oscillator problem

Abstract

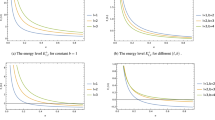
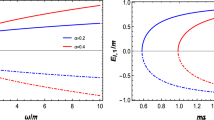
In this study, we explore quantum dynamics of non-relativistic particles within the context of a Morris–Thorne-type wormhole space-time featuring a cosmic string. Our investigation focuses on the eigenvalue solution of Schrödinger equation by utilizing the confluent Heun equation. We demonstrate that the cosmic string and the wormhole throat radius leads to significant modifications in the energy levels and wave functions of non-relativistic quantum particles. As a consequence, the degeneracy of the energy spectrum is disrupted. Subsequently, we extend our analysis to the harmonic oscillator problem, where non-relativistic particles interact harmonically within the same wormhole space-time background with a cosmic string. Employing a similar approach, we obtain the eigenvalue solution for the harmonic oscillator and analyze this solution to show the influence of the cosmic string parameter and the radius of the wormhole throat. In both scenarios, we obtain exact analytical solutions for the wave equation and specifically, we present the ground-state energy level $E_{1,m}$ and the corresponding wave function $\psi _{1,m}$ as particular cases.

Appendices

Appendix 1: The solutions of angular equations

Substituting (7) in the Eq. (8) and using the wave function (9), one will find the angular equation (12) as follows:

$$\begin{aligned} \Bigg [\frac{1}{\sin \theta }\,\frac{d}{\textrm{d}\theta }\,\Big (\sin \theta \,\frac{d}{\textrm{d}\theta }\Big )+\frac{1}{\alpha ^2\,\sin ^2 \theta }\,\frac{d^2}{\textrm{d}\phi ^2}+\ell '\,(\ell '+1)\Bigg ]\,Y(\theta ,\phi )=0. \end{aligned}$$

(43)

Let us substitute $Y (\theta ,\phi )=A(\theta )\,B(\phi )$ in the Eq. (43) and after simplification, we obtain the azimuthal equation as follows:

$$\begin{aligned} \frac{1}{\alpha ^2}\,\frac{d^2 B(\phi )}{\textrm{d}\phi ^2}+m'^2\,B(\phi )=0. \end{aligned}$$

(44)

And the polar equation

$$\begin{aligned} \Bigg [\frac{1}{\sin \theta }\,\frac{d}{\textrm{d}\theta }\,\Big (\sin \theta \,\frac{d}{\textrm{d}\theta }\Big )+\ell '\,(\ell '+1)-\frac{m'^2}{\sin ^2 \theta }\Bigg ]\,A(\theta )=0. \end{aligned}$$

(45)

Let a solution to the Eq. (44) is given by

$$\begin{aligned} B(\phi )=e^{i\,m\,\phi }. \end{aligned}$$

(46)

Substituting (46) in the Eq. (44), we obtain

$$\begin{aligned} \Big (-\frac{m^2}{\alpha ^2}+m'^2\Big )\,B(\phi )=0\Rightarrow m'=\frac{m}{\alpha }. \end{aligned}$$

(47)

For the Eq. (45), let us change a variable by $x=\cos \theta$. The equation with the function $A(\theta )$ becomes

$$\begin{aligned} \Bigg [(1-x^2)\,\frac{d^2}{\textrm{d}x^2}-2\,x\,\frac{d}{\textrm{d}x}+\ell '\,(\ell '+1)-\frac{m'^2}{1-x^2}\Bigg ]\,A(x)=0 \end{aligned}$$

(48)

which is the associated Legendre polynomials equation whose solutions are given by

$$\begin{aligned} A(x)=P^{m'}_{\ell '}(x)=(-1)^{m'}\,(1-x^2)^{m'/2}\,\frac{d^{m'}}{\textrm{d}x^{m'}}\,[P_{\ell '}(x)], \end{aligned}$$

(49)

where superscript $m'$ indicates the order and $P_{\ell '} (x)$ are polynomials of degree $\ell '$ given by

$$\begin{aligned} P_{\ell '}=\frac{1}{2^{\ell '}\,\ell '!}\,\frac{d^{\ell '}}{\textrm{d}x^{\ell '}}\,(x^2-1)^{\ell '}. \end{aligned}$$

(50)

Noted that the Legendre polynomials $P_{\ell '} (x)$ are polynomials of order $\ell '$ provided the magnetic quantum number $m'$ must have values less than or equal to $\ell '$. That is

$$\begin{aligned} \ell '\ge |m'|\quad \text{ or }\quad \ell '=|m'|+\kappa ,\quad \kappa =0,1,2,\ldots .. \end{aligned}$$

(51)

Throughout the analysis we have written $\ell '$ and $m'$ because of the presence of cosmic string in the quantum system. For $\alpha \rightarrow 1$, one will get back the standard azimuthal and polar equations which were given in many textbooks. In that case, relation (51) can be written as $\ell =(|m|+\kappa )$. Thus, one can see that the quantum numbers $(m',\ell ')$ are influenced by the topological defect of cosmic string, and these are called the effective magnetic and orbital quantum numbers, respectively.

Appendix 2: The confluent Heun equation

The standard form of the confluent Heun equation is [32, 75, 76]

$$\begin{aligned} H''(x)+\Big [\zeta +\frac{\beta +1}{x}+\frac{\gamma +1}{x-1}\Big ]\,H'(x)+\Big [\frac{\mu }{x}+\frac{\nu }{x-1} \Big ]\,H(x)=0, \end{aligned}$$

(52)

where $H(x)=H_{c}(\zeta , \beta , \gamma , \delta , \eta ;x)$ is the confluent Heun function. The parameters $\mu$ and $\nu$ given in the last term of Eq. (52) are defined as

$$\begin{aligned} \mu =\frac{1}{2}\,(\zeta +\zeta \,\beta -\beta -\beta \,\gamma -\gamma )-\eta ,\quad \nu =\frac{1}{2}\,(\zeta +\zeta \,\gamma +\beta +\beta \,\gamma +\gamma )+\delta +\eta , \end{aligned}$$

(53)

By using the Frobenius method [77], one will obtain a polynomial solution to the confluent Heun equation. Let us write the confluent Heun function as a power series around the origin,

$$\begin{aligned} H(x)=\sum ^{\infty }_{i=0}\,d_{i}\,x^{i}, \end{aligned}$$

(54)

where $d_i$ are the coefficients.

Thereby, substituting this power series in the Eq. (B.1), one will obtain the coefficient

$$\begin{aligned} d_1=-\frac{\mu }{\beta +1}\,d_0, \end{aligned}$$

(55)

with the following recurrence relation

$$\begin{aligned} d_{k+2}=\frac{1}{(k+2)(k+2+\beta )}\Bigg [\Big \{(k+1)(k+2+\beta +\gamma -\zeta )-\mu \Big \}\,d_{k+1}+(\zeta \,k+\mu +\nu )\,d_{k}\Bigg ] \end{aligned}$$

(56)

Therefore, from the Eq. (B.5), the confluent Heun series becomes a polynomial of degree n when we impose two conditions:

$$\begin{aligned} d_{n+1}=0,\quad \delta =-\zeta \,\Big [n+\frac{1}{2}\,(2+\beta +\gamma ) \Big ], \end{aligned}$$

(57)

where $n=1,2,3,\ldots ..$ But, we don’t know whether a closed expression for the energy eigenvalue will exists or not.