1 Introduction

Laser detection technology is an important means of target detection [1,2,3] and real-time monitoring [4,5,6]. Laser detection has been widely used in national defense, agriculture, geography, aerospace and more, and it has been continuously innovated in theory and technology. Laser interferometry technology can effectively address the test in complex environments such as strong energy attenuation. By reasonably adjusting the reference beam, accurate and stable laser interferometry detection information can be obtained.

Due to the random disturbance characteristics of the atmospheric turbulent medium [7, 8], the shape and area of light spots obtained by laser propagation [9, 10] in the external field are random, and the distribution of light intensity of the obtained spots is not constant and will produce a certain drift [11]. The laser propagation is also affected by weather conditions such as the temperature, humidity, air pressure and wind speed. Weather parameters are visible and easy to measure, but the intensity of atmospheric turbulence is a random comprehensive influencing factor [12], which cannot be measured by a single index. In theoretical research, it is necessary to consider the influence of fluctuations of important parameters such as the amplitude, phase and dielectric constant and summarize the statistical rule of the obtained results [13]. Finally, more intuitive parameters are used to express physical quantities such as the statistical light intensity and phase.

In this paper, through field experiments of laser echo, the shape of the light spot, area of the light spot and the intensity distribution are deeply studied to find whether the echo beam under the influence of atmospheric turbulence has a stable statistical law. This information can verify the theoretical link and lay a theoretical foundation for laser interferometry in complex environments.

2 Method

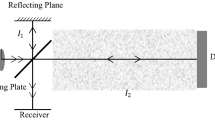
If the influence of atmosphere turbulence is considered in the laser transmission process, it will definitely undergo a laser time mutation due to the random variation of factors such as atmospheric pressure, wind speed, temperature and humidity. Under the condition of disturbance, the average intensity of laser <I> (z, \(\varrho\)) should contain the random variables of the amplitude and phase, and the wave function E(r) is

$$ E\left( r \right) = E_{0} \left( r \right)\exp \left( {\chi_{{\text{d}}} + iS_{{\text{d}}} } \right), $$
(1)

where \(\chi_{{\text{d}}}\) is the logarithmic amplitude of the random disturbance, and \(S_{{\text{d}}}\) is the phase of the random disturbance. Since the exponential part of Eq. (1) can irregularly change with time, the wave function is also a variable and can only represent the instantaneous value at a certain time. If the laser travels through a one-way distance randomly heterogeneous medium in the \(z\) direction, \(\varrho\) can be the angle coordinate, as shown in Fig. 1.

Fig. 1
figure 1

Schematic diagram of the two-channel propagation of laser through a random inhomogeneous medium

Full size image

According to \(I_{0} \left( {\varrho ,z} \right) = \left| {E_{0} \left( r \right)} \right|^{2}\), one must find the average light intensity to obtain the radiation intensity for echo. Thus,

$$ I_{0} \left( {\varrho ,z} \right) = \left| {E_{0} \left( {\varrho ,z} \right)} \right|^{2} = \frac{{\omega_{0}^{2} }}{{\omega^{2} }}\exp \left( { - \frac{{2\varrho^{2} }}{{\omega^{2} }}} \right), $$
(2)

where \(\omega_{0}\) is the beam waist radius of the laser, and \(\omega\) is the beam section radius at \(z\) of the laser transmission distance. The typical attenuation function in Eq. (2) is affected by the echo angle and section radius, respectively. When the observation angle is fixed, the light intensity significantly decreases with the decrease in beam section radius. The average intensity is as follows:

$$ I\left( {\varrho ,z} \right) = I_{0} \left( {\varrho ,z} \right)\exp \left[ {2\chi + 2\sigma_{\chi }^{2} } \right]. $$
(3)

It is approximated that \(\chi = \chi_{{\text{d}}} - \chi_{{\text{d}}}\), and the solution of \(\left( {\chi_{{\text{d}}} - \chi_{{\text{d}}} } \right)^{2}\) is \(\sigma_{\chi }^{2}\). Since atmospheric turbulence is a random disturbance medium, it is difficult to find a stable state even in windless weather, so it is more practical to adopt the statistical average method to obtain the light intensity.

The effect of the phase on the laser echo is also an important factor that cannot be ignored. If the dielectric constant is statistically expressed as the sum of the average part \(\overline{\varepsilon }\left( r \right)\) and disturbed part \(\tilde{\varepsilon }\left( r \right)\), then the phase disturbance of laser echo is

$$ \varphi_{1D} = \frac{1}{2}\left\{ {\mathop \int \limits_{0}^{z} \tilde{\varepsilon }\left( {\frac{\varrho z^{\prime}}{{2z}},z^{\prime}} \right){\text{d}}z^{\prime} + \mathop \int \limits_{z}^{0} \tilde{\varepsilon }\left[ {\frac{{\varrho \left( {2z - z^{\prime}} \right)}}{2z},z^{\prime}} \right]{\text{d}}z^{\prime}} \right\}, $$
(4)

where \(z^{\prime}\) is the integral variable. More intuitively, the variance of the two-channel function is

$$ \sigma_{\varphi D}^{2} \left( {\varrho ,z} \right) = \mathop \int \limits_{0}^{z} {\text{d}}\eta \mathop \int \limits_{0}^{\infty } \left\{ {\sigma_{\varphi }^{2} \left( \varsigma \right)\left[ {1 + e^{{ - \frac{{\varrho^{2} \eta^{2} }}{{2l_{\varepsilon }^{2} z^{2} }}}} } \right]} \right\}{\text{d}}\varsigma , $$
(5)

where \(\varrho\) and \(\varsigma\) are the transverse and longitudinal coordinates, respectively; \(l_{\varepsilon }\) denotes the inner scales of turbulence disturbance.

3 Experiment

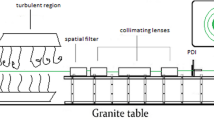
To make the obtained pulsed laser echo spot universal, the weather on the day of the experiment was selected to be clear with visibility above 12 km, and the spot collection was performed after 10 am, which was conducive to the stability of atmospheric turbulence. A laser light source with an emission wavelength of 1064 nm, an output energy of 500 mJ, a working frequency of 20 Hz and a pulse width of 1.5 ns were selected for the experiment. Here, the one-way distances of 500 m and 1500 m were listed for field experiments, and several groups of relatively stable moments and weather conditions of the field were selected, as shown in Tables 1 and 2.

Table 1 Weather conditions obtained by a laser echo spot at a 500-m one-way distance
Full size table
Table 2 Weather conditions obtained by a laser echo spot at a 1500-m one-way distance
Full size table

Among the hundreds of light spots received, eight light spots were randomly selected for observation, as shown in Figs. 2 and 3.

Fig. 2
figure 2

Echo light spot received at a one-way distance of 500 m in atmospheric turbulence

Full size image
Fig. 3
figure 3

Echo light spot received at a one-way distance of 1500 m in atmospheric turbulence

Full size image

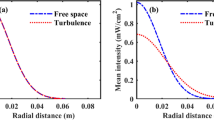
All spots were proportioned for ease of observation. In different detection distances, the area of the obtained echo spot was not identical and increased with the increase in detection distance. Observing the receiving spot, it becomes evident that the distribution of beam intensity in the section area is not constant and exhibits random fluctuations at the same receiving distance. Figures 2 and 3, and other unlisted spots at various receiving distances collectively demonstrate that the overall trend of beam intensity in the section area gradually expands from the center to the edges as the receiving distance increases. However, the shape of the light spots does not significantly change, and the region of intensity fluctuation does not have regularity. Variations in spectral intensity distribution result from factors such as atmospheric temperature, humidity, air pressure, wind speed and others. The atmospheric environment itself lacks a consistent pattern of change; hence, the experimentally obtained light spots can only be analyzed in terms of statistical distribution. The laser receiver employed in the experiment can capture 17 return faculae per second; even within that brief timespan, the intensity distribution of the spots undergoes constant changes.

While this paper presents only two detection distances of echo light spots, the intensity of these spots typically initiates from the central region and gradually diminishes toward the periphery. According to the corresponding detection distance, the intensity of the interferometric reference beam path is adjusted so that it can be coherently superimposed with the detection beam path to obtain the information of return beam interference. To achieve a noticeable interference contrast, it is essential to choose the periphery of the spot as the test area for interference at shorter distances (e.g., when the one-way distance is less than 500 m) and the center of the spot for interference testing at longer distances (e.g., when the one-way distance exceeds 1000 m). The actual selection of regions is not constant and is based on specific analyses of the atmospheric turbulence and weather conditions.

4 Results and discussion

Corresponding to the time period of echo detection of the external field, we selected 100 s between receiving time to observe the spot area and spot energy of a one-way distance of 500 m, and we obtain the variation curves in Figs. 4 and 5.

Fig. 4
figure 4

Echo spot area fluctuation curve within 100 s at a one-way distance of 500 m in atmospheric turbulence

Full size image
Fig. 5
figure 5

Echo spot energy fluctuation curve within 100 s at a one-way distance of 500 m in atmospheric turbulence

Full size image

Figure 5 shows that in the corresponding environment, the area of the spot fluctuates by 1 mm2 and changes at almost any given time. For the convenience of study, it is reasonable to assume that the average probability of a spot area is constant. Due to the instability of atmospheric turbulence, the echo spot experiences relatively severe energy fluctuation. However, as long as there is no significant change in weather conditions, the energy fluctuations within a short time range (e.g., the study time of 100 s in Fig. 5) are relatively stable on average, and the obtained interference pattern can be relatively stable.

Similarly, through the observation of the spot area and spot energy at a one-way distance of 1500 m, we obtained the fluctuation curves in Figs. 6 and 7.

Fig. 6
figure 6

Echo spot area fluctuation curve within 100 s at a one-way distance of 1500 m in atmospheric turbulence

Full size image
Fig. 7
figure 7

Echo spot energy fluctuation curve within 100 s at a one-way distance of 1500 m in atmospheric turbulence

Full size image

In Fig. 7, the spot area at the 1500 m one-way distance significantly increased compared to that at 500 m. The average spot area measured at 750 m and 1000 m was approximately 12.8 mm2 and 25.2 mm2, respectively, and the average spot area measured at 1500 m was approximately 49.5 mm2. With the increase in detection distance, the area of the laser echo spot clearly increases, and the range of change also increases. Figure 6 shows that within the same detection range, atmospheric turbulence hardly affects the area of the echo spot, and the statistical average is basically constant, which is very favorable for spot processing in the interference process. The energy of the echo light spot at 1500 m decreased by approximately 67% and 53% compared to those at 500 m and 750 m, respectively. The laser energy attenuation caused by the transmission distance is very clear, and the attenuation ratio was averaged to the unit growth distance. The unit distance energy attenuation between 750 and 1500 m was approximately 17%, while the unit distance energy attenuation between 500 and 750 m was approximately 20%. This results are consistent with the theoretical model and simulation results. In atmospheric turbulence, the detection distance is the main factor that affects the dual-channel laser transmission. As the transmission distance increases, the degree of fluctuation in dual-channel laser transmission gradually decreases.

The results show that although the echo spot area obtained in atmospheric turbulence has random disturbance, it has a relatively stable statistical law on the whole, and the spot area and disturbance range increase with the increase in the test distance. The random disturbance of echo spot energy obtained in atmospheric turbulence also has a good statistical rule, and the spot energy and disturbance range decrease with the increase in the test distance.

5 Conclusions

Atmospheric turbulence can cause random energy fluctuation of laser echo spots, and the detection distance is an important factor. With the increase in detection distance, the energy fluctuation area of the spot gradually expands from near the center to the edge. In general, the interference region with a relatively short test distance can be selected at the edge of the light spot, while that with a relatively long test distance can be selected near the central region. The distance of the interference region should refer to the specific weather conditions and intensity of atmospheric turbulence, and it is not fixed.

The cross-sectional area of the laser echo spot increases as the distance, and the range of change also increases. The spot area always randomly fluctuates, and the fluctuation range extends with the increase in test distance, but its statistical average shows good stability. The energy of the echo spot also experiences random fluctuations and decreases with the increase in test distance, but it remains statistically stable at the designated test location. These two characteristics provide convenience for the interference processing of light spots and help calibrate the attributes of the interference reference beam.