1 Introduction

Since March 2020, the world has reeled from the Coronavirus disease 2019 (COVID-19) pandemic disease. COVID-19 is a new pathogenic infection disease evolving rapidly [1]. As per the report on April 26, 2020, more than 2.92 million cases have been recorded in 210 countries and territories, 203,000 deaths, and around 829,000 people have recovered globally [2]. Millions of people are forced to remain self-isolated and under challenging conditions by national governments. The whole world is devoted to avoid the outbreak of the disease. The disease is proliferating in many countries all around the world. In the absence of proper vaccines, self-quarantine and wearing a face mask is the widely used strategy for the mitigation and control of the outbreak [3]. The \({\text{SI}}\) (susceptible–infection) model has been applied to COVID-19, and this model is used as a context for examining the nature of the pandemic. The SIR epidemic model with delay in the context of the fractional derivative with Mittag–Leffler kernel has been considered in [4], and also, a stochastic model to predict the novel coronavirus have been studied in [5]. The mathematical models have become basic tools in analyzing the spread and control of infectious disease [6]. It is important to note that the majority of classical disease models, including the Kermack–Mckendrick (1927) and Lotka– Volterra models, are used the mass action incidence rate (1926) [7]. The objective of this study is to provide a simple but effective explanatory model for the prediction of the future development of infection and for checking the effectiveness of containment and lockdown. We proposed a \({\text{SI}}\) model based on the dependent variable is a susceptible population that grows over time and difference in mortality and birth rates. The individuals are born into the simulation with no immunity (susceptible), and the infectious individuals with no treatment throughout their life, and remain in contact with the susceptible population. In \({\text{SI}}\) model, we divided size of the population \(N\) into two subgroups: the susceptible individuals (\(S\)) to the infectious individuals (\(I\)); there is a relationship between the numbers of susceptible and infectious individuals, shown by the following system of ordinary differential equations as:

$$ \dot{S} = \mu N - \beta \frac{{{\text{SI}}}}{N} - \mu S, $$
(1)
$$ \dot{I} = \beta \frac{{{\text{SI}}}}{N} - \mu I, $$
(2)

where \(\mu\) represent the birth and death rates and \(\beta\) is the friction rate between \(S\,{\text{and}} \;I\). The main aim of this paper is to specifically cite the work of [8], which deals with a similar disease system with only two stages, but we deal with \(n\)-strains of the disease of COVID-19. In Sects. 2–5, we established the global stability of a dynamical system is a difficult problem in general by using the Lyapunov functions [9]. The direct Lyapunov method is the most successful approach to the problem, allowing us to obtain the results in a straightforward manner [10, 11]. Part from the stability verification, the basic reproduction number \(R_{0}\) is the number of the secondary infections caused by an infective individual in a completely population; when \(R_{0} < 1\), the strains die, and when \(R_{0} > 1\), it persists [12, 13]. The existence and uniqueness of endemic equilibriums are demonstrated using the Lyapunov direct method [14]. Numerical simulations were run to support the analytical results that are given in Sect. 6.

2 The Structure of the model

In \({\text{SI}}\) model with one stage, we divided the size \(N\) of population into subclasses that are susceptible and infected by the disease, denoted by \(S\) and \(I\), respectively, and \(N = S + I\). The transmission to \(I\) is assumed to occur in accordance with the incidence of mass action \(\beta \frac{{{\text{SI}}}}{N}\), and the relation between \(S\) and \(I\) is given by a system of differential Eqs. (1) and (2), see Fig. 1.

Fig. 1
figure 1

Model with one strain SI

Full size image

In this model, we will discuss the stability by using the direct Lyapunov method; let us introduce the following theorem.

Theorem 2.1

(Lyapunov direct method) [15, 16] Suppose that system \(\dot{x} = f\left( {x,t} \right)\) has the origin as an equilibrium state; if there exists a continuous positive definite (p.d) function \(V(x,t):{\mathbb{R}}^{n} \to {\mathbb{R}}\), which has continuous partial derivatives and \(\dot{V}(x,t)\) is negative on a domain D containing the origin, then this origin is asymptotically stable. We note that 1. If there exists a domain D such that \(\dot{V}(x,t)\) is negative definite (n.d), then the origin is unstable. 2. If \(\dot{V}(x,t)\) is n.d, for 0 < \(\left\| {x(t)} \right\|\)< \(r\) for some \(r,\) then the origin is locally stable, and if it is n.d in the entire state space, then the origin is globally asymptotically stable.

2.1 Equilibrium points

Solving Eqs. (1) and (2), we get a disease-free equilibrium (DFE) (\(E_{0}\)) and endemic equilibrium points as:

$$ E_{0} = (S_{0} ,I_{0} ) = (N,0). $$
(3)
$$ E_{1} = (S_{1} ,I_{1} ) = (\frac{N}{{R_{0} }},(1 - \frac{1}{{R_{0} }})N),\;\;\;R_{0} = \frac{\beta }{\mu }. $$
(4)

2.2 Global stability of equilibrium points

The global stability is studied using the direct Lyapunov method for equilibrium points [15]. The global asymptotic stable of the DFE \(E_{0}\) when \(R_{0} < 1\), and for \(E_{1}\) when \(R_{0} > 1\).

Theorem 2.2

The DFE \(E_{0}\) is globally asymptotically stable when \(R_{0} < 1\).

Proof

Consider the Lyapunov function [8] of \(E_{0}\) as.

$$ V(S,I) = (S - S_{0} \ln \frac{S}{{S_{0} }}) + I $$

By derivation of Lyapunov function and using Eqs (1) and (2), we get

$$ \begin{aligned} \dot{V}(S,I) = & (1 - \frac{{S_{0} }}{S})\dot{S} + \dot{I} = (1 - \frac{{S_{0} }}{S})[\mu N - \beta \frac{{{\text{SI}}}}{N} - \mu S] + (\beta \frac{{{\text{SI}}}}{N} - \mu I) \\ = & \;\left( {2\mu N - \mu S - \mu \frac{{N^{2} }}{S}} \right) - (1 - R_{0} )\mu I \\ \end{aligned} $$
(5)

It is known that the arithmetic mean (AM) is greater than or equal the geometric mean (GM), then \(\left( {2\mu N - \mu S - \mu \frac{{N^{2} }}{S}} \right) \le 0\). Consequently, \(\dot{V}(S,I) < 0\) for, \(R_{0}\) < 1, and \(\dot{V}(S,I) = 0\) only if \(S = S_{0} ,\)\(I = I_{0} .\)

Theorem 2.3

The endemic equilibrium point \(E_{1}\) is globally stable when \(R_{0} \ge 1\).

Proof

Take a look at the Lyapunov function [8] of \(E_{1}\).

$$ V(S,I) = (S - S_{1} \ln \frac{S}{{S_{1} }}) + \left( {I - I_{1} \ln \frac{I}{{I_{1} }}} \right) $$

Also, we derivate the Lyapunov function, and using Eqs. (1) and (2), we obtain

$$ \begin{aligned} \dot{V}(S,I) = & (1 - \frac{{S_{1} }}{S})\dot{S} + (1 - \frac{{I_{1} }}{I})\dot{I} = (1 - \frac{{S_{1} }}{S})[\mu N - \beta \frac{SI}{N} - \mu S] + (1 - \frac{{I_{1} }}{I})(\beta \frac{SI}{N} - \mu I) \\ = & \;\left( {2\mu N - \mu S - \frac{{\mu N^{2} }}{{SR_{0} }}} \right) - (1 - \frac{1}{{R_{0} }})\beta S. \\ \end{aligned} $$
(6)

Therefore, \(\dot{V}(S,I) \le 0\) as \(\left( {2\mu N - \mu S - \frac{{\mu N^{2} }}{{SR_{0} }}} \right) \le 0\) from the known relation between AM and GM. And \(\dot{V}(S,I) = 0\) only if \(S = S_{1} ,\)\(R_{0} = 1.\)

2.3 The model with two infectious

The size \(N\) of population is divided into three compartments \(S,I_{1} ,I_{2}\), which denote susceptible, infected with strain 1, and with strain 2, respectively, and \(N = S + I_{1} + I_{2}\). The transmission to \(I_{i}, i = 1,2\), is assumed to occur in accordance with the incidence of mass action \(\beta_{i} \frac{{{\text{SI}}_{i} }}{N}\), see Fig. 2.

Fig. 2
figure 2

\({\text{SI}}\) model with two strains

Full size image

From this model, we get

$$ \dot{S} = \mu N - \sum\limits_{j = 1}^{2} {\beta_{j} \frac{{{\text{SI}}_{j} }}{N}} - \mu S, $$
(7)
$$ \dot{I}_{j} = \beta_{j} \frac{{{\text{SI}}_{j} }}{N} - \mu I_{j} , j = 1,2. $$
(8)

2.4 Equilibrium points

Solving Eqs (7) and (8), we get three equilibrium points, DFE equilibrium, endemic with respect to strain 1 and strain 2 as:

$$ E_{0} = (S_{0} ,I_{10} ,I_{20} ) = (N,0,0) $$
(9)
$$ \begin{aligned} E_{1} = & \;(S_{1} ,I_{{11}} ,I_{{21}} ) = (\frac{N}{{R_{1} }},(1 - \frac{1}{{R_{1} }})N,0), \\ E_{2} = & \;(S_{2} ,I_{{12}} ,I_{{22}} ) = (\frac{N}{{R_{2} }},0,(1 - \frac{1}{{R_{2} }})N), \\ \end{aligned} $$
(10)

where \(R_{1} = \frac{{\beta_{1} }}{\mu }, R_{2} = \frac{{\beta_{2} }}{\mu }, R_{0} = \max \left\{ {\frac{{\beta_{1} }}{\mu },\frac{{\beta_{2} }}{\mu }} \right\}.\)

2.5 Global Stability of equilibrium points

The direct Lyapunov method used for showing the equilibrium points are globally asymptotically stable, see Theorems (3.1–3.3).

Theorem 3.1

The DFE \(E_{0}\) is globally asymptotically stable when \(R_{j} < 1,\) for \(j = 1,2\).

Proof

Consider the Lyapunov function [8] of \(E_{0}\) as.

$$ V(S,I_{1} ,I_{2} ) = (S - S_{0} \ln \frac{S}{{S_{0} }}) + I_{1} + I_{2} $$
$$ \dot{V}(S,I_{1} ,I_{2} ) = (1 - \frac{{S_{0} }}{S})\dot{S} + \dot{I}_{1} + \dot{I}_{2} $$

Using Eqs (7) and (8), we get

$$ \dot{V} = [2\mu N - \mu S - \frac{{\mu N^{2} }}{S}] - \mu I_{1} (1 - R_{1} ) - \mu I_{2} (1 - R_{2} ). $$
(11)

As the AM is greater than or equal the GM, then \(\left( {2\mu N - \mu S - \mu \frac{{N^{2} }}{S}} \right) \le 0\). Consequently, \(\dot{V}(S,I) < 0\) for, \(R_{j} < 1\), and \(\dot{V}(S,I) = 0\) only if \(S = S_{0} ,\)\(I_{j} = I_{j0}\) for \(j = 1,2\).

Theorem 3.2

\(E_{1}\) is globally asymptotically stable.

Proof

The Lyapunov function [8] of \(E_{1}\) is.

$$ V(S,I_{1} ,I_{2} ) = (S - S_{1} \ln \frac{S}{{S_{1} }}) + \left( {I_{1} - I_{11} \ln \frac{{I_{1} }}{{I_{11} }}} \right) + I_{2} $$
$$ \dot{V}(S,I_{1} ,I_{2} ) = (1 - \frac{{S_{1} }}{S})\dot{S} + (1 - \frac{{I_{11} }}{{I_{1} }})\dot{I}_{1} + \dot{I}_{2} $$

From Eqs (7) and (8), we obtain

$$ \dot{V} = [2\mu N - \mu S - \frac{{\mu N^{2} }}{{{\text{SR}}_{1} }}] - (1 - \frac{1}{{R_{1} }})\beta_{1} S - (1 - \frac{{R_{2} }}{{R_{1} }})\mu I_{2} . $$
(12)

As the relation between the AM is greater than or equal the GM, then \(\left( {2\mu N - \mu S - \frac{{\mu N^{2} }}{{{\text{SR}}_{1} }}} \right) \le 0\). Consequently, \(\dot{V} < 0\) for, \(R_{1} > 1,\)\(R_{1} > R_{2}\) and \(\dot{V} = 0\) only if \(S = S_{1} ,\) \(I_{2} = I_{21} ,\) and \(R_{1} = 1\).

Theorem 3.3

\(E_{2}\) is globally asymptotically stable.

Proof

Consider the Lyapunov function [8] of \(E_{2}\) as.

$$ V(S,I_{1} ,I_{2} ) = (S - S_{2} \ln \frac{S}{{S_{2} }}) + I_{1} + \left( {I_{2} - I_{22} \ln \frac{{I_{2} }}{{I_{22} }}} \right) $$
$$ \dot{V}(S,I_{1} ,I_{2} ) = (1 - \frac{{S_{2} }}{S})\dot{S} + \dot{I}_{1} + (1 - \frac{{I_{22} }}{{I_{2} }})\dot{I}_{2} $$

Using Eqs (7) and (8), we have

$$ \dot{V} = [2\mu N - \mu S - \frac{{\mu N^{2} }}{{{\text{SR}}_{2} }}] - (1 - \frac{1}{{R_{2} }})\beta_{2} S - (1 - \frac{{R_{1} }}{{R_{2} }})\mu I_{1} . $$
(13)

By the relation between the arithmetic mean (AM) is greater than or equal the geometric mean (GM), then, \(\left( {2\mu N - \mu S - \frac{{\mu N^{2} }}{{{\text{SR}}_{2} }}} \right) \le 0\). Consequently, \(\dot{V} < 0\) for, \(R_{2} > 1,\)\(R_{2} > R_{1}\) and \(\dot{V} = 0\) only if \(S = S_{2} ,\) \(I_{1} = I_{12} ,\) and \(R_{2} = 1\).

2.6 The model with three infectious

We divided the size \(N\) of population into four compartments. \(S,I_{1} ,I_{2} ,I_{3}\), and \(N = S + I_{1} + I_{2} + I_{3} ,\) see Fig. 3.

Fig. 3
figure 3

\({\text{SI}}\) model with three strains

Full size image

A system of ordinary differential equations is used to derive the model:

$$ \dot{S} = \mu N - \sum\limits_{j = 1}^{3} {\beta_{j} \frac{{{\text{SI}}_{j} }}{N}} - \mu S $$
(14)
$$ \dot{I}_{j} = \beta_{j} \frac{{{\text{SI}}_{j} }}{N} - \mu I_{j} , j = 1,2,3 $$
(15)

2.7 Equilibrium points

We get four equilibrium points from solving system (14) and (15), and we obtain

$$ E_{0} = (S_{0} ,I_{10} ,I_{20} ,I_{30} ) = (N,0,0,0) $$
(16)
$$ \begin{aligned} E_{1} = & \;(S_{1} ,I_{{11}} ,I_{{21}} ,I_{{31}} ) = (\frac{N}{{R_{1} }},(1 - \frac{1}{{R_{1} }})N,0,0), \\ E_{2} = & \;(S_{2} ,I_{{12}} ,I_{{22}} ,I_{{32}} ) = (\frac{N}{{R_{2} }},0,(1 - \frac{1}{{R_{2} }})N,0) \\ \end{aligned} $$
(17)
$$ E_{3} = (S_{3} ,I_{13} ,I_{23} ,I_{33} ) = (\frac{N}{{R_{3} }},0,0,(1 - \frac{1}{{R_{3} }})N) $$
(18)

where \(R_{j} = \frac{{\beta_{j} }}{\mu }, j = 1,2,3\) are the basic reproduction ratios and \(R_{0} = \max \left\{ {\frac{{\beta_{1} }}{\mu },\frac{{\beta_{2} }}{\mu },\frac{{\beta_{3} }}{\mu }} \right\}.\)

2.8 Global stability of equilibrium points

In this section, we investigated global stability using the direct Lyapunov method, and we demonstrated that these points are globally asymptotically stable by proving the derivative of Lyapunov function is less than or equal one.

Theorem 4.1

The DFE \(E_{0}\) is globally asymptotically stable.

Proof

Consider the Lyapunov function [8] as:

$$ V(S,I_{1} ,I_{2} ,I_{3} ) = (S - S_{0} \ln \frac{S}{{S_{0} }}) + I_{1} + I_{2} + I_{3} , $$

This function is derived as follows:

$$ \dot{V}(S,I_{1} ,I_{2} ,I_{3} ) = (1 - \frac{{S_{0} }}{S})\dot{S} + \dot{I}_{1} + \dot{I}_{2} + \dot{I}_{3} $$

Using Eqs (14) and (15), we get

$$ \begin{aligned} \dot{V}(S,I_{1} ,I_{2} ,I_{3} ) = & (1 - \frac{{S_{0} }}{S})\left( {\mu N - \sum\limits_{j = 1}^{3} {\beta_{j} \frac{{SI_{j} }}{N}} - \mu S} \right) + \left( {\beta_{1} \frac{{SI_{1} }}{N} - \mu I_{1} } \right) + \left( {\beta_{2} \frac{{SI_{2} }}{N} - \mu I_{2} } \right) + \left( {\beta_{3} \frac{{SI_{3} }}{N} - \mu I_{3} } \right) \\ = & \;[2\mu N - \mu S - \frac{{\mu N^{2} }}{S}] - (\beta_{1} - \mu )I_{1} - (\beta_{2} - \mu )I_{2} - (\beta_{3} - \mu )I_{3}, \end{aligned} $$
$$ \dot{V} = [2\mu N - \mu S - \frac{{\mu N^{2} }}{S}] - (1 - R_{1} )\mu I_{1} - (1 - R_{2} )\mu I_{2} - (1 - R_{3} )\mu I_{3} . $$
(19)

As the relation between AM is greater than or equal the GM, \(\left( {2\mu N - \mu S - \mu \frac{{N^{2} }}{S}} \right) \le 0\). Consequently, \(\dot{V} < 0\) for, \(R_{j} < 1\), and \(\dot{V} = 0\) only if \(S = S_{0}\) and \(I_{j} = I_{j0}\) for \(j = 1,2,3\). The proofs of Theorems 42–4.4 are similar to the proof of Theorem 4.1.

Theorem 4.2

\(E_{1}\) is globally asymptotically stable as:

$$ \dot{V}(S,I_{1} ,I_{2} ,I_{3} ) = [2\mu N - \mu S - \frac{{\mu N^{2} }}{{SR_{1} }}] - (1 - \frac{1}{{R_{1} }})\beta_{1} S - (1 - \frac{{R_{2} }}{{R_{1} }})\mu I_{2} - (1 - \frac{{R_{3} }}{{R_{1} }})\mu I_{3} , \le 0 $$
(20)

when \(\left( {2\mu N - \mu S - \frac{{\mu N^{2} }}{{SR_{1} }}} \right) \le 0\). Consequently, \(\dot{V} < 0\) for, \(R_{1} > 1,\)\(R_{1} > R_{2}, R_{3}\) and \(\dot{V} = 0\) only if \(S = S_{1} ,\) \(I_{j} = I_{j1} ,\) for \(j = 2,3\) and \(R_{1} = 1\).

Consider the Lyapunov function [8] as:

$$ V(S,I_{1} ,I_{2} ,I_{3} ) = (S - S_{1} \ln \frac{S}{{S_{1} }}) + \left( {I_{2} + I_{3} } \right) + \left( {I_{1} - I_{11} \ln \frac{{I_{1} }}{{I_{11} }}} \right). $$

Theorem 4.3

\(E_{2}\) is globally asymptotically stable if \(R_{2} > 1\) and \(R_{2} > R_{1} ,R_{3}\); see the derivative of Lyapunov function as:

$$ \dot{V}(S,I_{1} ,I_{2} ,I_{3} ) = [2\mu N - \mu S - \frac{{\mu N^{2} }}{{SR_{2} }}] - (1 - \frac{1}{{R_{2} }})\beta_{2} S - (1 - \frac{{R_{1} }}{{R_{2} }})\mu I_{1} - (1 - \frac{{R_{3} }}{{R_{2} }})\mu I_{3}, \le 0 $$
(21)

as \(\left( {2\mu N - \mu S - \frac{{\mu N^{2} }}{{{\text{SR}}_{2} }}} \right)\le 0\). Consequently, \(\dot{V} < 0\) for, \(R_{2} > 1,\)\(R_{2} > R_{1} ,R_{3}\) and \(\dot{V} = 0\) only if \(S = S_{2} ,\) \(I_{j} = I_{j2} ,\) for \(j = 1,3\) and \(R_{2} = 1\). Also, we can use the Lyapunov function [8] as:

$$ V(S,I_{1} ,I_{2} ,I_{3} ) = (S - S_{2} \ln \frac{S}{{S_{2} }}) + \left( {I_{1} + I_{3} } \right) + \left( {I_{2} - I_{22} \ln \frac{{I_{2} }}{{I_{22} }}} \right). $$

Theorem 4.4

\(E_{3}\) is globally asymptotically stable when \(R_{3} > 1\) and \(R_{3} > R_{1} ,R_{2}\) as:

$$ \dot{V}(S,I_{1} ,I_{2} ,I_{3} ) = [2\mu N - \mu S - \frac{{\mu N^{2} }}{{{\text{SR}}_{3} }}] - (1 - \frac{1}{{R_{3} }})\beta_{3} S - (1 - \frac{{R_{1} }}{{R_{3} }})\mu I_{1} - (1 - \frac{{R_{2} }}{{R_{3} }})\mu I_{2} ,\le 0 $$
(22)

Therefore, \(\left( {2\mu N - \mu S - \frac{{\mu N^{2} }}{{{\text{SR}}_{3} }}} \right) \le 0\). Consequently, \(\dot{V}\) < 0 for, \(R_{3} > 1,\)\(R_{3} > R_{1} ,R_{2}\) and \(\dot{V} = 0\) only if \(S = S_{3} ,\) \(I_{j} = I_{j3} ,\) for \(j = 1,2\) and \(R_{3} = 1\). Let the Lyapunov function [8] be as follows:

$$ V(S,I_{1} ,I_{2} ,I_{3} ) = (S - S_{3} \ln \frac{S}{{S_{3} }}) + \left( {I_{1} + I_{2} } \right) + \left( {I_{3} - I_{33} \ln \frac{{I_{3} }}{{I_{33} }}} \right). $$

2.9 The model with \(n\)-infectious

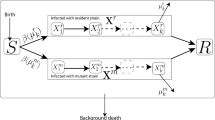
In model \(SI\) with \(n\)-strains of coronavirus that cause COVID-19, we divided the population of size \(N\) into two classes: the susceptible class, \(S\) and the infected class, \(I\). The class of \(I\) can be split into several classes noted by, \(I_{1} ,I_{2} ,...,I_{n}\) with, respectively, \(I_{1}\) is the first stage, \(I_{2}\) is the second stage, and \(I_{n}\) is the \(n\)-stage of the disease. \(N = S + I_{1} + I_{2} + ... + I_{n}\). If \(\beta_{1} , \beta_{2} ,...,\beta_{n}\) are the per capita contact rates of the infectious in respectively to \(I_{1} ,I_{2} ,...,I_{n}\). There exist rates \(\beta_{i} \frac{{SI_{i} }}{N}\) for \(i = 1,2,...,n\) which are the mass action incidence. The birth and death rate is \(\mu\), and \(\beta_{i}\) represents the transmission rate to the compartments \(I_{i}\), see the following Fig. 4.

Fig. 4
figure 4

\({\text{SI}}\) model with n-strains

Full size image

We get the following differential equations as:

$$ \dot{S} = \mu N - \sum\limits_{j = 1}^{n} {\beta_{j} } \frac{{{\text{SI}}_{j} }}{N} - \mu S $$
(23)
$$ \dot{I}_{j} = \beta_{j} \frac{{{\text{SI}}_{j} }}{N} - \mu I_{j} , j = 1,2,...,n $$
(24)

2.10 Equilibrium points

Theorem 5.1

The \(n + 1\) equilibrium points, disease-free equilibrium, endemic with respect to strain 1, and endemic with respect to strain 2,…, and endemic with respect to strain \(n\) are.

$$ E_{0} = (S_{0} ,I_{10} ,I_{20} ,...,I_{n0} ) = (N,0,0,...,0) $$
(25)
$$ E_{j} = (S_{j} ,I_{1j} ,...,I_{jj} ,...,I_{nj} ), $$
$$ S_{j} = \frac{N}{{R_{j} }}, I_{ij} = \left\{ \begin{gathered} \left( {1 - \frac{1}{{R_{j} }}} \right)N, i = j \hfill \\ 0, i \ne j \hfill \\ \end{gathered} \right. $$
(26)

where \(R_{j} = \frac{{\beta_{j} }}{\mu }\) for \(i,j = 1,2,...,n.\)

Proof

Equaling Eqs. (23) and (24) by zero:

$$ \mu N - \sum\limits_{j = 1}^{n} {\beta_{j} } \frac{{{\text{SI}}_{j} }}{N} - \mu S = 0 $$
(27)
$$ I_{j} \left( {\beta_{j} \frac{S}{N} - \mu } \right) = 0 $$
(28)

From Eq. (28), we will get two cases for \(j = 1,2,...,n\) as:

Case 1: If \(I_{j} = 0\) then, \(\beta_{j} \frac{S}{N} - \mu \ne 0\).

Case 2: If \(I_{j} \ne 0\) then, \(\beta_{j} \frac{S}{N} - \mu = 0\).

Substituting from case 1 into the equation \(N = S + I_{1} + I_{2} + ... + I_{n}\), we obtain \(E_{0}\) as in (25), and from case 2, we get

$$ S = \frac{\mu N}{{\beta_{j} }} = \frac{N}{{R_{j} }},\;\;\;R_{j} = \frac{{\beta_{j} }}{\mu } $$
(29)

From (29) into (27), we get \(E_{j}\) for \(j = 1,2,...,n\) as in (26).

2.11 The \(R_{0}\)

\(R_{0}\) is the basic reproduction number, defined as the number of secondary infections caused by an infective individual in a completely susceptible population [15]. We will obtain it by using the next-generation matrix by making the column vectors and Jacobi matrices at DFE \(E_{0} = (N,0,0,...,0)\) as:

$$ X = \left( {\begin{array}{*{20}c} {I_{1} } & {I_{2} } & {...} & {I_{n} } \\ \end{array} } \right)^{T} ,\;\;\;Y = \left( S \right),\;\;\;f = \left( {\begin{array}{*{20}c} {\beta_{1} \frac{{{\text{SI}}_{1} }}{N}} & {\beta_{2} \frac{{{\text{SI}}_{2} }}{N}} & {...} & {\beta_{n} \frac{{{\text{SI}}_{n} }}{N}} \\ \end{array} } \right)^{T} \;\;v = \left( {\begin{array}{*{20}c} {\mu I_{1} } & {\mu I_{2} } & {...} & {\mu I_{n} } \\ \end{array} } \right)^{T} . $$
$$ F = \left( {\frac{\partial f}{{\partial I}}} \right)_{(N,0,0,...,0)} = \left( {\begin{array}{*{20}c} {\beta_{1} } & 0 & \ldots & 0 \\ 0 & {\beta_{2} } & \ddots & \vdots \\ \vdots & \ddots & \ddots & 0 \\ 0 & \ldots & 0 & {\beta_{n} } \\ \end{array} } \right)\;\;{\text{and}}\;\;V = \left( {\frac{\partial v}{{\partial I}}} \right)_{(N,0,0,...,0)} = \left( {\begin{array}{*{20}c} \mu & 0 & \ldots & 0 \\ 0 & \mu & \ddots & \vdots \\ \vdots & \ddots & \ddots & 0 \\ 0 & \ldots & 0 & \mu \\ \end{array} } \right) $$
$$ R_{0} = FV^{ - 1} $$
$$ = \left( {\begin{array}{*{20}c} {\beta_{1} } & 0 & \ldots & 0 \\ 0 & {\beta_{2} } & \ddots & \vdots \\ \vdots & \ddots & \ddots & 0 \\ 0 & \ldots & 0 & {\beta_{n} } \\ \end{array} } \right) \times \frac{1}{{\mu^{n} }} \times \left( {\begin{array}{*{20}c} {\mu^{n - 1} } & 0 & \ldots & 0 \\ 0 & {\mu^{n - 1} } & \ddots & \vdots \\ \vdots & \ddots & \ddots & 0 \\ 0 & \ldots & 0 & {\mu^{n - 1} } \\ \end{array} } \right) = \left( {\begin{array}{*{20}c} {{{\beta_{1} } \mathord{\left/ {\vphantom {{\beta_{1} } \mu }} \right. \kern-0pt} \mu }} & 0 & \ldots & 0 \\ 0 & {{{\beta_{2} } \mathord{\left/ {\vphantom {{\beta_{2} } \mu }} \right. \kern-0pt} \mu }} & \ddots & \vdots \\ \vdots & \ddots & \ddots & 0 \\ 0 & \ldots & 0 & {{{\beta_{n} } \mathord{\left/ {\vphantom {{\beta_{n} } \mu }} \right. \kern-0pt} \mu }} \\ \end{array} } \right). $$

The model’s spectral radius of the next-generation matrix is \(R_{0}\); thus,

$$ R_{0} = \max \left\{ {\frac{{\beta_{1} }}{\mu },\frac{{\beta_{2} }}{\mu },...,\frac{{\beta_{n} }}{\mu }} \right\}. $$
(30)

2.12 Global stability of equilibrium points

Theorem 5.1

The DFE point \(E_{0}\) is globally asymptotically stable.

Proof

By simple iteration from strains 1, 2, and 3, we get the Lyapunov function of \(E_{0}\) as.

$$ V(S,I_{1} ,I_{2} ,...I_{n} ) = (S - S_{0} \ln \frac{S}{{S_{0} }}) + \sum\limits_{j = 1}^{n} {I_{j} } $$

We derive the Lyapunov function as:

$$ \dot{V}(S,I_{1} ,I_{2} ,...I_{n} ) = (1 - \frac{{S_{0} }}{S})\dot{S} + \sum\limits_{j = 1}^{n} {\dot{I}_{j} } $$

Using Eqs (23) and (24), we obtain

$$ \dot{V} = (1 - \frac{{S_{0} }}{S})\left( {\mu N - \sum\limits_{j = 1}^{n} {\beta_{j} } \frac{{SI_{j} }}{N} - \mu S} \right) + \sum\limits_{j = 1}^{n} {\left( {\beta_{j} \frac{{SI_{j} }}{N} - \mu I_{j} } \right)} $$
$$ = [2\mu N - \mu S - \frac{{\mu N^{2} }}{S}] - \sum\limits_{j = 1}^{n} {(1 - R_{j} )\mu I_{j} } . $$
(31)

Because the relation between the AM is greater than or equal the GM, \(\left( {2\mu N - \mu S - \mu \frac{{N^{2} }}{S}} \right) \le 0\). Consequently, \(\dot{V} < 0\) for, \(R_{j} < 1\), and \(\dot{V} = 0\) only if \(S = S_{j}\) and \(R_{j} = 1\) for \(j = 1,2,...,n\).

Theorem 5.2

The endemic equilibrium points \(E_{j}\) is globally asymptotically stable.

Proof

Also, by the simple iteration from strains 1, 2, and 3, let we consider the Lyapunov function of \(E_{j}\), for \(j = 1,2,...,n\) as:

$$ V(S,I_{1} ,...,I_{n} ) = (S - S_{j} \ln \frac{S}{{S_{j} }}) + \left( {I_{j} - I_{jj} \ln \frac{{I_{j} }}{{I_{jj} }}} \right) + \sum\limits_{\begin{subarray}{l} r = 1 \\ r \ne j \end{subarray} }^{n} {I_{r} } $$

The derivation of Lyapunov function is

$$ \dot{V}(S,I_{1} ,...,I_{n} ) = (1 - \frac{{S_{j} }}{S})\dot{S} + (1 - \frac{{I_{jj} }}{{I_{j} }})\dot{I}_{j} + \sum\limits_{\begin{subarray}{l} r = 1 \\ r \ne j \end{subarray} }^{n} {\dot{I}_{r} } $$

From Eqs (23) and (24), we get

$$ \dot{V} = (1 - \frac{{S_{j} }}{S})\left( {\mu N - \sum\limits_{m = 1}^{n} {\beta_{m} } \frac{{SI_{m} }}{N} - \mu S} \right) + (1 - \frac{{I_{jj} }}{{I_{j} }})\left( {\beta_{j} \frac{{SI_{j} }}{N} - \mu I_{j} } \right) + \sum\limits_{\begin{subarray}{l} r = 1 \\ r \ne j \end{subarray} }^{n} {\left( {\beta_{r} \frac{{SI_{r} }}{N} - \mu I_{r} } \right)} $$

Using Eqs (26), we get

$$ \begin{aligned} \dot{V} = & \mu N - \left( {S\frac{{\beta _{j} I_{j} }}{N} + \sum\limits_{\begin{subarray}{l} m = 1 \\ m \ne j \end{subarray} }^{n} S \frac{{\beta _{m} I_{m} }}{N}} \right) - \mu S - \frac{{\mu N^{2} }}{{SR_{j} }} + \frac{1}{{R_{j} }}\sum\limits_{{m = 1}}^{n} {\beta _{m} I_{m} } + \frac{{\mu N}}{{R_{j} }} + S\frac{{\beta _{j} I_{j} }}{N} - \mu I_{j} - \left( {1 - \frac{1}{{R_{j} }}} \right)S\beta _{j} + \left( {1 - \frac{1}{{R_{j} }}} \right)\mu N + \sum\limits_{\begin{subarray}{l} r = 1 \\ r \ne j \end{subarray} }^{n} {S\frac{{\beta _{r} I_{r} }}{N}} - \sum\limits_{\begin{subarray}{l} r = 1 \\ r \ne j \end{subarray} }^{n} {\mu I_{r} } \\ = & \;[2\mu N - \mu S - \frac{{\mu N^{2} }}{{{\text{SR}}_{j} }}] - (1 - \frac{1}{{R_{j} }})\beta _{j} S + \frac{1}{{R_{j} }}\left( {\beta _{j} I_{j} + \sum\limits_{\begin{subarray}{l} m = 1 \\ m \ne j \end{subarray} }^{n} {\beta _{m} I_{m} } } \right) - \mu I_{j} - \sum\limits_{\begin{subarray}{l} r = 1 \\ r \ne j \end{subarray} }^{n} {\mu _{r} I_{r} } ; \\ \end{aligned} $$

by replacing \(m\) by \(r\), we get,

$$ \dot{V} = [2\mu N - \mu S - \frac{{\mu N^{2} }}{{{\text{SR}}_{j} }}] - (1 - \frac{1}{{R_{j} }})\beta_{j} S - \sum\limits_{\begin{subarray}{l} r = 1 \\ r \ne j \end{subarray} }^{n} {\left( {1 - \frac{{R_{r} }}{{R_{j} }}} \right)\mu_{r} I_{r} } $$
(32)

Since the relation between the AM is greater than or equal the GM, \(\left( {2\mu N - \mu S - \frac{{\mu N^{2} }}{{{\text{SR}}_{j} }}} \right) \le 0\). Consequently, \(\dot{V} < 0\) for, \(R_{j} > 1\), and \(R_{j} > R_{r} ,\) and \(\dot{V} = 0\) only if \(S = S_{j} ,\)\(R_{j} = 1,\)\(I_{r} = I_{ij} ,\) for \(i \ne j.\)

3 Numerical simulations

The numerical simulations are performed by using the Maple program to illustrate the analytic results. It is demonstrated that if \(R_{0} < 1\), we note that the only one strain dies out (Fig. 5); if \(R_{0} > 1\), then the strain persists (Fig. 6). When \(R_{j} < 1,\) both the two strains die out (Fig. 7); also when \(R_{j} > 1,\) the two strains persist (Fig. 8), for \(j = 1,2\). Since \(R_{j} < 1\), all strains die out (Fig. 9), and if \(R_{j} > 1\), then all three strains persist (Fig. 10), when \(j = 1,2,3\).

Fig. 5
figure 5

Disease-free equilibrium: The strains die out, and the parameter values are as follows: \(\beta = 0.2, \mu = 0.5, N = 100, R_{0} = \left( {{\beta \mathord{\left/ {\vphantom {\beta \mu }} \right. \kern-0pt} \mu }} \right) = 0.4\)

Full size image
Fig. 6
figure 6

Endemic equilibrium: The strain persists, and the parameter values are as follows: \(\beta = 0.6, \mu = 0.4,\,\,\,N = 100,\,\,\,\,R_{0} = \left( {{\beta \mathord{\left/ {\vphantom {\beta \mu }} \right. \kern-0pt} \mu }} \right) = 1.5\,\,\,\)

Full size image
Fig. 7
figure 7

Disease-free equilibrium: All strains die out. Values of parameter are: \(\begin{gathered} \beta_{1} = 0.6,\,\,\,\beta_{2} = 0.1,\,\,\,\mu = 0.75,\,\,\,N = 50,\,\,\,R_{1} = \left( {{{\beta_{1} } \mathord{\left/ {\vphantom {{\beta_{1} } \mu }} \right. \kern-0pt} \mu }} \right) = 0.8,\,\,\,R_{2} = \left( {{{\beta_{2} } \mathord{\left/ {\vphantom {{\beta_{2} } \mu }} \right. \kern-0pt} \mu }} \right) = 0.133, \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,R_{0} = \max \left\{ {R_{1} ,R_{2} } \right\} = 0.8\,\,\,\,\, \hfill \\ \end{gathered}\)

Full size image
Fig. 8
figure 8

Endemic equilibrium: All strains persist. Values of parameter are: \(\begin{gathered} \beta_{1} = 0.6,\,\,\,\beta_{2} = 0.7,\,\,\,\mu = 0.44,\,\,\,N = 100,\,\,\,R_{1} = \left( {{{\beta_{1} } \mathord{\left/ {\vphantom {{\beta_{1} } \mu }} \right. \kern-0pt} \mu }} \right) = 1.36,\,\,\,R_{2} = \left( {{{\beta_{2} } \mathord{\left/ {\vphantom {{\beta_{2} } \mu }} \right. \kern-0pt} \mu }} \right) = 1.59 \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,R_{0} = \max \left\{ {R_{1} ,R_{2} } \right\} = 1.59\,\, \hfill \\ \end{gathered}\)

Full size image
Fig. 9
figure 9

Disease-free equilibrium: Strains die out, and the parameter values are: \(\begin{gathered} \beta_{1} = 0.53,\,\,\,\,\,\beta_{2} = 0.54,\,\,\,\,\,\,\,\beta_{3} = 0.000054,\,\,\,\,\,\,\mu = 0.65,\,\,\,N = 20,\,\,\, \hfill \\ R_{1} = \left( {{{\beta_{1} } \mathord{\left/ {\vphantom {{\beta_{1} } \mu }} \right. \kern-0pt} \mu }} \right) = 0.815,\,\,\,R_{2} = \left( {{{\beta_{2} } \mathord{\left/ {\vphantom {{\beta_{2} } \mu }} \right. \kern-0pt} \mu }} \right) = 0.830,\,\,\,\,R_{3} = \left( {{{\beta_{3} } \mathord{\left/ {\vphantom {{\beta_{3} } \mu }} \right. \kern-0pt} \mu }} \right) = .000083,\,\,\,\,\,\,\, \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,R_{0} = \max \left\{ {R_{1} ,R_{2} ,R_{3} } \right\} = 0.830\,\, \hfill \\ \end{gathered}\)

Full size image
Fig. 10
figure 10

Endemic equilibrium: All strains persist, and the parameter values are: \(\begin{gathered} \beta_{1} = 0.6,\,\,\,\beta_{2} = 0.19,\,\,\,\beta_{3} = 0.7,\,\,\,\,\,\,\,\mu = 0.15,\,\,\,N = 40 \hfill \\ R_{1} = \left( {{{\beta_{1} } \mathord{\left/ {\vphantom {{\beta_{1} } \mu }} \right. \kern-0pt} \mu }} \right) = 4,\,\,\,\,\,\,\,R_{2} = \left( {{{\beta_{2} } \mathord{\left/ {\vphantom {{\beta_{2} } \mu }} \right. \kern-0pt} \mu }} \right) = 1.26,\,\,\,\,R_{3} = \left( {{{\beta_{3} } \mathord{\left/ {\vphantom {{\beta_{3} } \mu }} \right. \kern-0pt} \mu }} \right) = 4.66, \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,R_{0} = \max \left\{ {R_{1} ,R_{2} ,R_{3} } \right\} = 4.66 \hfill \\ \end{gathered}\)

Full size image

4 Conclusion

In this paper, we consider a system of differential equations to the model \(SI\) of \(n -\) strain coronaviruses. The \(n -\) basic reproduction ratios \(R_{1}\), \(R_{2}\), …, \(R_{n}\) which are the threshold quantities of the population dynamics are determined. We note that the global stabilities of each equilibrium points depend on the basic reproduction ratios and were determined by using Lyapunov functions. In this model with n-strains, for \(j = 1,2,...,n\), when \(R_{j}\) < 1, the system has only DFE \(E_{0}\), which is a globally asymptotically stable, that is, all strains die out. When \(R_{j}\) > 1, the equilibrium points \(E_{j}\) are a globally asymptotically stable, and all strains persist. Numerical simulations, using the Maple program, were carried out to support the analytic results to show the effect of all strains.