1 Introduction

Nuclear physics has many main objectives in the previous decades, for instance the research of quark–gluon plasma (QGP). From hadronic matter to quark–gluon plasma (QGP), there exists a search for the phase transition that utilized high energy for collisions of heavy ions and began in the mid-1980s with experiments at CERN’s superproton synchrotron (SPS) in Europe, and Brookhaven’s alternating gradient synchrotron (AGS) in the USA [1]. Also, there are many works investigated the hadron at extreme conditions as in Refs. [3,4,5,6,7,8,9].

Many efforts have been devoted to compute heavy quarkonia’s binding energy and dissociation temperatures. In Ref. [10], the energy levels and decay widths of heavy quarkonium in a quark–gluon plasma are calculated. The implications of their results for heavy quarkonium reduction in heavy ion collisions are also discussed. In Ref. [11], the authors computed the entropy and effective string tension of the moving in the strongly coupled plasma, using a deformed anti-de Sitter/Reissner–Nordstrom black hole metric, that has a heavy quark–antiquark pair, and employed chemical potentials. In [12], charmonium and bottomonium S-wave states are explained using AdS/QCD from the bottom up, the researchers measured masses, decay constants and current spectral functions of heavy vector mesons. In Ref. [13], the authors study the existence of charmonium states in QGP; in the Bjorken boost-invariant expansion, the plasma equation of motion is used by employing Cornell potential. In Ref. [14], the thermal width and potential of heavy quarkonia were researched by the authors, and they discovered that at low unconfined temperatures the magnetic field can cause a significant thermal fluctuation of the thermal width. In Ref. [15], to characterize their travel inside the quark–gluon plasma, the authors employed coupled transport equations for open heavy flavour and quarkonium states. Furthermore, the nuclear modification factor of all bottomonia states in addition to the azimuthal angular anisotropy coefficient was computed. In Ref. [16], the authors investigated the emergence of heavy quarkonium inside a quark–gluon plasma (QGP) in the real time and employed the lowest Landau level approximation with the strong magnetic field limit; the heavy quark complex potential is used. In Ref. [17], a magnetized hot quark–gluon plasma medium is considered; the authors estimated quarkonium state dissociation, and they mapped the quarkonium properties at limited baryonic chemical potential utilizing the quasi-particle Debye mass.

In the description of quark–gluon plasma, thermodynamic properties are crucial of strange quark matters [18]. In Ref. [19], within the domain of nonrelativistic quantum mechanics, the asymptotic iteration method is employed to derive the energy spectrum of the general molecular potential; they calculated thermodynamic properties.

The fractional calculus has recently received attention in various domains of physics that feature nonlinear, complicated phenomena, such as in Refs. [20,21,22,23]. For the explanation of significant energy spectra and complex mechanisms of the standard model in high-energy physics, such as in Ref. [24], the author used conformable fractional of the Nikiforov–Uvarov (CF–NU) method and employed the radial Schrödinger equation and temperature-dependent potential to calculate the energy eigenvalues and corresponding functions. Also, the effect of fractional-order parameter is discussed on heavy quarkonium masses in a hot QCD medium. In Ref. [25], the author used fractional Schrödinger equation, and the wave function is calculated using the Laplace and Fourier transforms, and then stated in terms of the Mittag-Leffler function.

The aim of this work is to study the effect of fractional nonrelativistic model in the binding energy, the dissociation temperature and thermodynamic properties which are not considered in recent other works.

The paper is organized as follows: In Sect. 2, the exact solution of the N-dimensional Schrödinger equation with the two-body potential in SCQGP of heavy quarkonium using GFD is deduced. In Sect. 3, the variation of heavy quarkonium binding energy and mass spectra at finite temperature is introduced. In Sect. 4, the results and discussion are written. In Sect. 5, the conclusion is introduced.

2 The exact solution of the N-dimensional Schrödinger equation with the two-body potential in SCQGP of heavy quarkonium using GFD

2.1 Theoretical method

In this section, the Schrödinger equation (SE) for two particles interacting via two-body potential in the N-dimensional space is shown in Refs. [2, 27, 28].

$$\begin{aligned} \left[ \frac{\text {d}^{2}}{\text {d}r^{2}}+\left( \frac{N-1}{r}\right) \frac{\text {d}}{\text {d}r}-\frac{L(L+N-2)}{r^{2}} +2\mu _{q\overline{q}}\left( E_{nl}-V(r)\right) \right] \psi _{nl}(r)=0, \end{aligned}$$
(1)

where L, \(\ N\), and \({\mu } _{q\overline{q}}\) are the angular momentum quantum number, the dimensionality number and reduced mass, respectively; \({\mu }_{q\overline{q}}=\frac{M_\text {q}M_{\overline{q}}}{M_\text {q}+M_{\overline{q}}}\). Setting the following wave function in Eq. (1)

$$\begin{aligned} \psi _{nl}(r)=r^{\frac{1-N}{2}}R _{nl}(r). \end{aligned}$$
(2)

We get

$$\begin{aligned} \left[ \frac{\text {d}^{2}}{\text {d}r^{2}}+2\mu _{q\overline{q}} \left( E_{nl}-V(r)\right) -\frac{\left( L+ \frac{N-2}{2}\right) ^{2}-\frac{1}{4}}{r^{2}}\right] R _{nl}(r)=0. \end{aligned}$$
(3)

Then, we can write Eq. (3) in dimensionless units by taking \(z=A\) r, \(\mu =A\) \(\mu ^{^{\prime }},\) \(E_{nl}\) \(=A\) \(E_{nl}^{^{\prime }}\) and \(A=1\)  \(\text {MeV}\) for the quarkonium particle; then, we obtain

$$\begin{aligned} \left[ A^{2}\frac{\text {d}^{2}}{\text {d}z^{2}} +2 A\mu ^{^{\prime }}(AE_{nl}^{^{\prime }}-V(z))- A^{2}\frac{\left( L+\frac{N-2}{2}\right) ^{2}- \frac{1}{4}}{z^{2}}\right] R_{nl}(z)=0, \end{aligned}$$
(4)

we can write Eq. (4) in the fractional form as in [26], if \(M_\text {q}=M_{\overline{q}}= m^{^{\prime }}\).

$$\begin{aligned} \left[ D^{\alpha }D^{\alpha }+m^{^{\prime }}(E_{nl}^{^{\prime }}-\frac{1}{A} V(z))-\frac{\left( L+\frac{N-2}{2}\right) ^{2}-\frac{1}{4}}{z^{^{2\alpha }}} \right] R_{nl}(z)=0. \end{aligned}$$
(5)

.

Here,

$$\begin{aligned} D^{\alpha }R_{nl}(z)= & {} \left( \frac{\Gamma (\beta )}{\Gamma (\beta -\alpha +1)}\right) \text { }z^{1-\alpha }\frac{\text {d}R}{\text {d}z} \nonumber \\ D^{\alpha }D^{\alpha }R_{nl}(z)= & {} \left( \frac{\Gamma (\beta )}{\Gamma (\beta -\alpha +1)}\right) ^{2}\left[ z^{2-2\alpha }\frac{\text {d}^{2}R}{\text {d}z^{2}}+(1-\alpha )z^{1-2\alpha }\frac{\text {d}R}{\text {d}z}\right] \end{aligned}$$
(6)

Then, we can write Eq. (5) in the fractional differential model using Eq. (6) [26, 27].

$$\begin{aligned} \left[ \left( \frac{\Gamma (\beta )}{\Gamma (\beta -\alpha +1)}\right) ^{2}\left[ z^{2-2\alpha }\frac{ \text {d}^{2}}{\text {d}z^{2}}+(1-\alpha )z^{1-2\alpha }\frac{\text {d}}{\text {d}z}\right] +m^{^{\prime }}\left( E_{nl}^{^{\prime }}-\frac{1}{A}V(z)\right) -\frac{\left( L+\frac{N-2}{2} \right) ^{2}-\frac{1}{4}}{z^{2\alpha }}\right] R_{nl}(z)=0, \end{aligned}$$
(7)

by diving Eq. (7) on \((\frac{\Gamma (\beta )}{\Gamma (\beta -\alpha +1)})^{2}z^{2-2\alpha }\); then, we get

$$\left[ {\frac{{{\text{d}}^{2} }}{{{\text{d}}z^{2} }} + (1 - \alpha )z^{{ - 1}} \frac{{\text{d}}}{{{\text{d}}z}} + \left( {\frac{{\Gamma (\beta )}}{{\Gamma (\beta - \alpha + 1)}}} \right)^{{ - 2}} z^{{2\alpha - 2}} \left[ {m^{\prime}(E^{\prime}_{{nl}} - \frac{1}{A}V(z)) - \frac{{\left( {L + \frac{{N - 2}}{2}} \right)^{2} - \frac{1}{4}}}{{z^{{2\alpha }} }}} \right]} \right]R_{{nl}} (z) = 0.$$
(8)

By taking the following wave function in Eq. (8),

$$\begin{aligned} R(z)= & {} z^{\frac{-B}{2}}\varphi (z), \nonumber \\ B= & {} (1-\alpha ); \end{aligned}$$
(9)

then, we get the following equation

$$\frac{{{\text{d}}^{2} \varphi (z)}}{{{\text{d}}z^{2} }} + \left[ {\left( {\frac{B}{2}} \right)\left( {1 - \frac{B}{2}} \right)z^{{ - 2}} + \left( {\frac{{\Gamma (\beta )}}{{\Gamma (\beta - \alpha + 1)}}} \right)^{{ - 2}} z^{{2\alpha - 2}} \left[ {m^{\prime}\left( {E^{\prime}_{{nl}} - \frac{1}{A}V(z)} \right) - \frac{{\left( {L + \frac{{N - 2}}{2}} \right)^{2} - \frac{1}{4}}}{{z^{{2\alpha }} }}} \right]} \right]\varphi (z) = 0$$
(10)
$$\frac{{{\text{d}}^{2} \varphi (z)}}{{{\text{d}}z^{2} }} + \left[ {\left( {\frac{{\Gamma (\beta )}}{{\Gamma (\beta - \alpha + 1)}}} \right)^{{ - 2}} z^{{2\alpha - 2}} \left( {m\prime \left( {E^{\prime}_{{nl}} - \frac{1}{A}V(z)} \right)} \right) + \left( {\left( {\frac{B}{2}} \right)\left( {1 - \frac{B}{2}} \right) - \left( {\frac{{\Gamma (\beta )}}{{\Gamma (\beta - \alpha + 1)}}} \right)^{{ - 2}} \left( {L(L + N - 2) + \frac{{N^{2} - 4N + 3}}{4}} \right)} \right)z^{{ - 2}} } \right]\varphi (z) = 0.$$
(11)

where V(z) is the two-body potential represented by the following as in Ref. [2].

$$\begin{aligned} V(z)=\frac{AQ}{4\pi \text { }z^{\alpha }}(\cos (k_{i}^{^{\prime }}\text { } z^{\alpha })+\frac{1}{\sqrt{3}}\sin (k_{i}^{^{\prime }}\text { }z^{\alpha }))\exp [-k_{r}^{^{\prime }}\text { }z^{\alpha }], \end{aligned}$$
(12)

where \(k_{i}=A\) \(k_{i}^{^{\prime }}\), \(k_{r}=A\) \(k_{r}^{^{\prime }}\), and \(A=1\)  \(\text {MeV}.\)

Fig. 1
figure 1

The potential V(z) is drawn between the quark and antiquark as a function of a distance (z), for different values of fractional parameter \(\alpha\) at T= 175MeV

Full size image
Fig. 2
figure 2

The potential V(z) is drawn as a function of a distance (z) for different values of temperature, \(\alpha =0.5\) (left panel), \(\alpha =1\) at (right panel)

Full size image

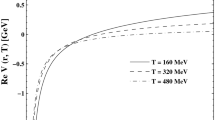
In Fig. 1, the potential V(z) between a quark and an anti-quark is shown as a consequence of distance z at finite temperatures (\(T=175 \text {MeV}\)), for different values of \(\alpha\)= 0.4, 0.6, and 0.8. We observe that an increase in the fractional parameter (\(\alpha\)) results in a decrease in the peak curve’s positive part; like the Cornell potential, the attitude of the potential satisfies both screening and confinement type forces. This conduct is compatible with [2]. Figure 2 (left panel) shows the conduct of the potential V(z) between a quark and an anti-quark as a consequence of distance z at finite value of the fractional parameter (\(\alpha =0.5\)), for different values of temperatures \(T=175,\) 250,  and 300  \(\text {MeV}\). It is obvious that the increase in the temperature leads to a decrease in the peak curve’s positive part; also, Fig. 2 (right panel) shows the same behaviour at \(\alpha =1\), for various values of temperatures \(T=175,\) 250,  and 300  \(\text {MeV}\). It shows a high level of concordance in terms of quality with comparable results in [1, 2].

As in [18], with \(Q=-q^{2}\) for quarkonium, substituting Eq. (12) in the form of Taylor expansion into Eq. (7) and rearranging, we obtain

$$\left[ {\frac{{{\text{d}}^{2} }}{{{\text{d}}z^{2} }} + \left( {\frac{{\Gamma (\beta )}}{{\Gamma (\beta - \alpha + 1)}}} \right)^{{ - 2}} z^{{2\alpha - 2}} \left[ {\left( {m^{\prime } E_{{nl}}^{\prime } - \frac{{m^{\prime } Q}}{{4\pi z^{\alpha } }}} \right) - \frac{{m^{\prime } Q}}{{4\pi }}\left( {\frac{{k_{i}^{\prime } }}{{\sqrt 3 }} - k_{r}^{\prime } } \right) - \frac{{m^{\prime } Q}}{{8\pi }}\left( {\frac{{k_{r}^{{\prime 2}} }}{2} - \frac{{k_{i}^{{\prime 2}} }}{2} - \frac{{k_{r}^{{\prime 2}} k_{i}^{{\prime 2}} }}{{\sqrt 3 }}} \right)z^{\alpha } - \frac{{m^{\prime } Q}}{{8\pi }}\left( {\frac{{k^{\prime } k_{i}^{\prime } }}{{2\sqrt 3 }} - \frac{{k_{i}^{{\prime 3}} }}{{6\sqrt 3 }} - \frac{{k_{i}^{{\prime 3}} }}{6} - \frac{{k_{i}^{{\prime 2}} k^{\prime } }}{{\sqrt 2 }}} \right)z^{{2\alpha }} - \frac{{m^{\prime } Q}}{{8\pi }}\frac{{k_{i}^{{\prime 4}} }}{{12}} - \frac{{k_{r}^{{\prime 2}} k_{i}^{{\prime 2}} }}{2} - \frac{{k_{i}^{\prime } k_{r}^{{\prime 3}} }}{{3\sqrt 3 }} + \frac{{k_{i}^{{\prime 2}} k_{r}^{\prime } }}{{3\sqrt 3 }}z^{{3\alpha }} } \right] + \left( {\left( {\frac{B}{2}} \right)\left( {1 - \frac{B}{2}} \right) - \left( {\frac{{\Gamma (\beta )}}{{\Gamma (\beta - \alpha + 1)}}} \right)^{{ - 2}} \left( {L(L + N - 2) + \frac{{N^{2} - 4N + 3}}{4}} \right)} \right)z^{{ - 2}} } \right]\varphi _{{nl(Z)}} = 0.$$
(13)

The analytical exact iteration method (AEIM) needs constructing the following ansatz for the wave function, by using generalized fractional of the analytical exact iteration method (CFAEIM) in Refs. [27, 28, 52].

$$\begin{aligned} \varphi _{nl(Z)}=f_{n}(z)\exp [g_{l}(z)], \end{aligned}$$
(14)

where

$$f_{n} (z) = \left\{ {\begin{array}{*{20}l} {1,\quad } \hfill & {n = 0} \hfill \\ {\Pi _{{i = 1}}^{n} (z^{\alpha } - \alpha _{i}^{n} ),\quad } \hfill & {n = 1,2,3,...} \hfill \\ \end{array} } \right\}$$
(15)

and

$$\begin{aligned} \ g_{l}(z)= & {} \frac{-1}{2}\frac{\alpha _{1}}{A^{2\alpha }}z^{2\alpha }-\frac{ \beta _{1}}{A^{\alpha }}z^{\alpha }+\delta _{1} \ln \left[ {\frac{z}{A}} \right] ^{\alpha } \nonumber \\ r= & {} \frac{z}{A},0<\alpha \le 1, \alpha _{1}, \beta _{1}>0. \end{aligned}$$
(16)

The Laguerre polynomials are clearly equal to \(f_{n}(z)\). From Eq. (14), we obtain.

$$\begin{aligned} \varphi ^{^{\prime \prime }}(z)=(g_{l}^{^{\prime \prime }}(z)+g_{l}^{\prime ^{2}}(z)+\frac{f_{n}^{^{\prime \prime }}(z)+2\text { }f_{n}^{^{\prime }}(z) \text { }g_{l}^{\prime }(z)}{f_{n}(z)})\varphi (z). \end{aligned}$$
(17)

By substituting from Eqs. (15), and (16), into Eq. (17), we get the following formula.

$$\varphi ^{\prime\prime}(z) = \left( \begin{gathered} \frac{{\alpha ^{2} \alpha _{1}^{2} }}{{A^{{4\alpha }} }}Z^{{4\alpha - 2}} + 2\frac{{\alpha ^{2} {\text{ }}\alpha _{1}^{2} {\text{ }}\beta _{1} }}{{A^{{3\alpha }} }}Z^{{3\alpha - 2}} + \left( {\frac{{\alpha ^{2} {\text{ }}\beta _{1}^{2} }}{{A^{{2\alpha }} }} - \frac{{2\alpha ^{2} \alpha _{1} {\text{ }}\delta _{1} + \alpha (2\alpha - 1)\alpha _{1} }}{{A^{{2\alpha }} }}} \right)Z^{{2\alpha - 2}} \hfill \\ - \left( {\frac{{2\alpha ^{2} {\text{ }}\beta _{1} \delta _{1} + \alpha (\alpha - 1)\beta _{1} }}{{A^{\alpha } }}} \right)Z^{{\alpha - 2}} + \left( {\alpha ^{2} \delta _{1}^{2} - \alpha {\text{ }}\delta _{1} } \right)Z^{{ - 2}} \hfill \\ \end{gathered} \right)\varphi (z).$$
(18)

When the equivalent powers on both sides of Eqs. (13, 18) are compared, at (n = 0) we get \(\varepsilon _{0l}\) as follows.

$$\varepsilon _{{0l}} = \frac{Q}{{4\pi }}\left( {\frac{{k^{\prime}_{i} }}{{\sqrt 3 }} - k^{\prime}_{r} } \right) + \frac{1}{{m\prime A^{{2\alpha }} }}\left( {\frac{{\Gamma (\beta )}}{{\Gamma (\beta - \alpha + 1)}}} \right)^{2} \left[ {\alpha _{1} (\alpha (2\alpha - 1) + \;2\alpha ^{2} (\delta _{1} + 0)) - \alpha ^{2} {\text{ }}\beta _{1}^{2} } \right],$$
(19)

where

$$\begin{aligned} \alpha _{1}=\left[ \frac{m^{^{\prime }}Q\text { }A^{4\alpha }}{4\pi \alpha ^{2}}\left( \frac{\Gamma (\beta )}{\Gamma (\beta -\alpha +1)}\right) ^{-2}\left( \frac{k_{r}^{\prime 2}\text { }k_{i}^{^{\prime }}}{2\sqrt{3}}-\frac{k_{i}^{^{\prime }3}}{6\sqrt{3} }-\frac{k_{r}^{^{\prime }3}}{6}-\frac{k_{r}^{^{\prime }}\text { } k_{i}^{^{\prime }2}}{2}\right) \right] ^{\frac{1}{2}}, \end{aligned}$$
(20)

and

$$\begin{aligned} \beta _{1}= & {} \frac{\text { }A^{\alpha }}{8\alpha }\sqrt{\frac{m^{^{\prime }}\text { }Q}{\pi }}*\left( \frac{\Gamma (\beta )}{\Gamma (\beta -\alpha +1)}\right) ^{-1}*\left( \frac{\left( \frac{k_{r}^{^{\prime }2}}{2}-\frac{k_{i}^{^{\prime }2}}{2}-\frac{ k_{i}^{^{\prime }}\text { }k_{r}^{^{\prime }}}{\sqrt{3}}\right) }{\left( \frac{ k_{r}^{^{\prime }2}\text { }k_{i}^{^{\prime }}}{2\sqrt{3}}-\frac{ k_{i}^{^{\prime }3}}{6\sqrt{3}}-\frac{k_{r}^{^{\prime }3}}{6}-\frac{ k_{r}^{^{\prime }}\text { }k_{i}^{^{\prime }2}}{2}\right) ^{\frac{1}{2}}}\right) . \end{aligned}$$
(21)
$$\begin{aligned} \delta _{1,2}= & {} \frac{1}{2\alpha }\left[ 1\pm \sqrt{1+\left( \frac{\Gamma (\beta )}{\Gamma (\beta -\alpha +1)}\right) ^{-2}(4L(L+N-2)+(N^{2}-4N+3))+2B\left( 1-\frac{B}{2}\right) }\right] \end{aligned}$$
(22)

Then, Eq. (22) can be written as follows:

$$\begin{aligned} \delta _{1,2}=\frac{1}{2\alpha }[1\pm l^{^{\prime }}], \end{aligned}$$
(23)

where

$$\begin{aligned} l^{^{\prime }}= & {} \sqrt{1+\left( \frac{\Gamma (\beta )}{\Gamma (\beta -\alpha +1)} \right) ^{-2}(4L(L+N-2)+(N^{2}-4N+3))+2B\left( 1-\frac{B}{2}\right) }. \end{aligned}$$
(24)
$$\varepsilon _{{0l}} = {\text{ }}\frac{Q}{{4\pi }}\left( {\frac{{k_{r}^{\prime } }}{{\sqrt 3 }} - k_{r}^{\prime } } \right) - \frac{Q}{{16\pi }}\left[ {\frac{{\left( {\frac{{k_{r}^{2} }}{2} - \frac{{k_{i}^{2} }}{2} - \frac{{k_{i} {\text{ }}k_{r} }}{{\sqrt 3 }}} \right)^{2} }}{{\left( {\frac{{k_{r}^{2} {\text{ }}k_{i} }}{{2\sqrt 3 }} - \frac{{k_{i}^{3} }}{{6\sqrt 3 }} - \frac{{k_{r}^{3} }}{6} - \frac{{k_{r} {\text{ }}k_{i}^{2} }}{2}} \right)}}} \right]{\text{ }} + \left( {\frac{{\Gamma (\beta )}}{{\Gamma (\beta - \alpha + 1)}}} \right)k^{\prime } \left[ {\frac{{k^{\prime } Q}}{{4\pi \alpha ^{2} }}\left( {\frac{{k_{r}^{2} {\text{ }}k_{i} }}{{2\sqrt 3 }} - \frac{{k_{i}^{3} }}{{6\sqrt 3 }} - \frac{{k_{r}^{3} }}{6} - \frac{{k_{r} {\text{ }}k_{i}^{2} }}{2}} \right)} \right]^{{\frac{1}{2}}} {\text{ }}*\left[ {\alpha (2\alpha - 1) + \alpha \left( {1 + \sqrt {\begin{array}{*{20}c} {1 + \left( {\frac{{\Gamma (\beta )}}{{\Gamma (\beta - \alpha + 1)}}} \right)^{{ - 2}} (4L(L + N - 2)} \\ { + (N^{2} - 4N + 3)) + 2B\left( {1 - \frac{B}{2}} \right)} \\ \end{array} } } \right.} \right]{\text{ }}$$
(25)

The iteration method is then done several times. As a consequence, the exact energy formula for any state in the N-dimensional space is expressed as follows, for any arbitrary n state.

$$\begin{aligned} E_{nl}= & {} \frac{Q}{4\pi }\left( \frac{k_{i}}{\sqrt{3}}-k_{r}\right) -\frac{Q}{16\pi }\left[ \frac{(\frac{k_{r}^{2}}{2}-\frac{k_{i}^{2}}{2}-\frac{k_{i}\text { }k_{r}}{ \sqrt{3}})^{2}}{\left( \frac{k_{r}^{2}\text { }k_{i}}{2\sqrt{3}}-\frac{k_{i}^{3}}{6 \sqrt{3}}-\frac{k_{r}^{3}}{6}-\frac{k_{r}\text { }k_{i}^{2}}{2}\right) }\right] \nonumber \\{} & {} +\frac{\left( \frac{\Gamma (\beta )}{\Gamma (\beta -\alpha +1)}\right) }{m}\left[ \frac{m \text { }Q\text { }}{4\pi \alpha ^{2}}\left( \frac{k_{r}^{2}\text { }k_{i}}{2\sqrt{3}} -\frac{k_{i}^{3}}{6\sqrt{3}}-\frac{k_{r}^{3}}{6}-\frac{k_{r}\text { }k_{i}^{2} }{2}\right) \right] ^{\frac{1}{2}} \nonumber \\{} & {} *[\alpha (2\alpha -1)+2n+\alpha \left[ 1+\sqrt{\begin{array}{c} 1+(\frac{\Gamma (\beta )}{\Gamma (\beta -\alpha +1)})^{-2}(4L(L+N-2) \\ +(N^{2}-4N+3))+2B\left( 1-\frac{B}{2}\right) \end{array} }\right] . \end{aligned}$$
(26)

We can get the special case at \(\alpha =\beta =1\), as in [2]

$$\begin{aligned} E_{nl}= & {} \frac{Q}{4\pi }\left( \frac{k_{i}}{\sqrt{3}}-k_{r}\right) -\frac{Q}{16\pi }\left[ \frac{\left( \frac{k_{r}^{2}}{2}-\frac{k_{i}^{2}}{2}-\frac{k_{i}\text { }k_{r}}{ \sqrt{3}}\right) ^{2}}{\left( \frac{k_{r}^{2}\text { }k_{i}}{2\sqrt{3}}-\frac{k_{i}^{3}}{6 \sqrt{3}}-\frac{k_{r}^{3}}{6}-\frac{k_{r}\text { }k_{i}^{2}}{2}\right) }\right] \nonumber \\{} & {} +\frac{1}{m}\left[ \frac{m\text { }Q\text { }A^{4\alpha }}{4\pi \alpha ^{2}}\left( \frac{ k_{r}^{2}\text { }k_{i}}{2\sqrt{3}}-\frac{k_{i}^{3}}{6\sqrt{3}}-\frac{ k_{r}^{3}}{6}-\frac{k_{r}\text { }k_{i}^{2}}{2}\right) \right] ^{\frac{1}{2}} \nonumber \\{} & {} *2(1+\text { }n)+\sqrt{1+4L(L+N-2)+(N^{2}-4\text { }N+3)}. \end{aligned}$$
(27)

Also, the corresponding wave function for any n state as follows.

$$\begin{aligned} \varphi _{nl(Z)}= & {} N_{nl}\text { }_{i=1}^{n}(Z^{\alpha }-\alpha _{i}^{n})\nonumber \\{} & {} *\exp \left[ -\left[ \frac{m\text { }Q\text { }A^{3\alpha }}{32\pi \alpha ^{2}} \left( \frac{\Gamma (\beta )}{\Gamma (\beta -\alpha +1)}\right) ^{-2}\left( \frac{k_{r}^{2}\text { }k_{i}}{2\sqrt{3}}-\frac{k_{i}^{3}}{6\sqrt{3}}-\frac{k_{r}^{3}}{6}-\frac{ k_{r}\text { }k_{i}^{2}}{2}\right) \right] ^{\frac{1}{2}}\right] Z^{2\alpha } \nonumber \\{} & {} *\exp \left[ -\frac{\text { }1}{8\alpha }\sqrt{\frac{m^{^{\prime }}\text { }Q}{ \pi }}*\left( \frac{\Gamma (\beta )}{\Gamma (\beta -\alpha +1)}\right) ^{-1}*\left( \frac{(\frac{k_{r}^{^{\prime }2}}{2}-\frac{k_{i}^{^{\prime }2}}{2}-\frac{ k_{i}^{^{\prime }}\text { }k_{r}^{^{\prime }}}{\sqrt{3}})}{\left( \frac{ k_{r}^{^{\prime }2}\text { }k_{i}^{^{\prime }}}{2\sqrt{3}}-\frac{ k_{i}^{^{\prime }3}}{6\sqrt{3}}-\frac{k_{r}^{^{\prime }3}}{6}-\frac{ k_{r}^{^{\prime }}\text { }k_{i}^{^{\prime }2}}{2}\right) ^{\frac{1}{2}}}\right) \text { } Z^{\alpha }\right] \nonumber \\{} & {} *\left( \frac{Z}{A}\right) ^{\frac{1}{2}\left[ 1\pm \sqrt{1+\left( \frac{\Gamma (\beta )}{ \Gamma (\beta -\alpha +1)}\right) ^{-2}(4L(L+N-2)+(N^{2}-4N+3))+2B\left( 1-\frac{B}{2}\right) } \right] }, \end{aligned}$$
(28)

Here,

$$\begin{aligned} k_{i}^{^{\prime }}= & {} \frac{k_{s}}{2} \nonumber \\ k_{r}^{^{\prime }}= & {} \frac{\sqrt{3}k_{s}}{2}. \end{aligned}$$
(29)

Also,

$$\begin{aligned} k_{s}^{2}= & {} \frac{M_\text {q}\omega _{p}^{2}}{g_{c}\left( \frac{\partial p}{\partial n} _\text {f}\right) } \nonumber \\ \omega _{p}^{2}= & {} \frac{\frac{4}{3}\alpha _{o}n_{of}}{M_\text {q}}. \end{aligned}$$
(30)

The temperature-dependent running coupling constant in SCQGP is supplied by [32].

$$\begin{aligned} \alpha _{s}(T)=\left( \frac{6\pi }{(33-2\text { }n_\text {f})\ln \left( \frac{T}{\Lambda _{T}}\right) } \right) \left( 1-\frac{3(153-19n_\text {f})\ln (2\ln (\frac{T}{\Lambda _{T}}))}{(33-2\text { } n_\text {f})^{2}\ln \left( \frac{T}{\Lambda _{T}}\right) }\right) . \end{aligned}$$
(31)

The colour degrees of freedom are included in \(g_{c}\), the number density corresponding to the specific flavour is denoted by \(n_\text {f}\), the quark mass is denoted by m, and \((\frac{\partial p}{\partial n}_\text {f})\) is provided by [33]. Equation (26) gives the expression for binding energy of the quarkonium.

3 Variation of heavy quarkonium binding energy and mass spectra at finite temperature

The mass spectra of heavy quarkonia are estimated in this section for states \(J/\Psi\), \(\chi _\text {c}\)  \(\gamma ,\) and \(\chi _\text {b}\) for both charmonium (\(c\overline{c})\) and bottomonium (\(b \overline{b})\) systems, using Eq. (26) in the N-dimensional space for any state at finite temperature. Here \(m=M_{c}\) for charmonium and \(m =M_\text {b}\) for bottomonium mesons. Figures 3, 4, 5, 6, 10, 11, 12, 13, 14 and 15 demonstrate the variation of binding energy with temperature for different states of quarkonia. The mass spectra of heavy quarkonia was determined according to the following formula [28, 34, 52].

$$\begin{aligned} M=2M_\text {q}+E_{nl}^{N}. \end{aligned}$$
(32)

Substituting from Eq. (26) into Eq. (32), the mass spectra for different states of heavy quarkonia as a temperature-dependent variable are supplied by

$$\begin{aligned} M= & {} 2M_\text {q}+\frac{Q}{4\pi }\left( \frac{k_{i}}{\sqrt{3}}-k_{r}\right) -\frac{Q}{16\pi }\left[ \frac{(\frac{k_{r}^{2}}{2}-\frac{k_{i}^{2}}{2}-\frac{k_{i}\text { }k_{r}}{ \sqrt{3}})^{2}}{(\frac{k_{r}^{2}\text { }k_{i}}{2\sqrt{3}}-\frac{k_{i}^{3}}{6 \sqrt{3}}-\frac{k_{r}^{3}}{6}-\frac{k_{r}\text { }k_{i}^{2}}{2})}\right] \nonumber \\{} & {} +\frac{\left( \frac{\Gamma (\beta )}{\Gamma (\beta -\alpha +1)}\right) }{m}\left[ \frac{m \text { }Q\text { }}{4\pi \alpha ^{2}}\left( \frac{k_{r}^{2}\text { }k_{i}}{2\sqrt{3}} -\frac{k_{i}^{3}}{6\sqrt{3}}-\frac{k_{r}^{3}}{6}-\frac{k_{r}\text { }k_{i}^{2} }{2}\right) \right] ^{\frac{1}{2}} \nonumber \\{} & {} *[\alpha (2\alpha -1)+2n+\alpha \left[ 1+\sqrt{ \begin{array}{c} 1+\left( \frac{\Gamma (\beta )}{\Gamma (\beta -\alpha +1)}\right) ^{-2}(4L(L+N-2) \\ +(N^{2}-4N+3))+(2B)(1-\frac{B}{2}) \end{array} }\right] . \end{aligned}$$
(33)

4 Results and discussion

4.1 Heavy quarkonium dissociation temperature in the N-dimensional space

This condition is weakly bound when the quarkonium’s binding energy is lower than the melting point, and it can be destroyed by thermal fluctuations by transferring energy. The dissociation temperature is defined as the lowest temperature at which no ringing structure can be seen, and it does not have to be the binding energy. The dissociation of quarkonia has reached zero. There has been a substantial percentage work done to define dissociation temperatures for various states of quarkonia. In Ref. [35], the upper and the minimum bounds for dissociation temperatures were calculated by \(E_\text {bin}=T\) and \(E_\text {bin}=3T\) conditions. In Ref.  [36], making use of the opportunity, the high temperature at which quarkonium states dissociate was established by the researchers. \(\Gamma (T)\ge 2E_\text {bin}(T)\), In Refs. [28, 37], the authors employed the condition of vanishing binding energy to estimate the dissociation temperature in various states for heavy quarkonium. In this work, the condition \(E_\text {bin}(T)=T\) is used to get the dissociation temperatures for various states of heavy quarkonium. Tables 1, 2 and 3 describe the dissociation temperature in various states.

Fig. 3
figure 3

(Left panel) Binding energy of \(J/\Psi\) as a variation of temperature T is shown at N=3. (Right panel) Binding energy of \(\chi _{c}\) as a variation of temperature T is shown at N=3, for \(\alpha =\beta\) =1, 0.5, and 0.7

Full size image
Fig. 4
figure 4

(Left panel) Binding energy of \(\gamma\) as a variation of temperature T is shown at N=3. (Right panel) Binding energy of \(\chi _{b}\) as a variation of temperature T is shown at N=3, for \(\alpha =\beta\) =1, 0.4, and 0.6 at N=3

Full size image

In Fig. 3 (left panel) and 3 (right panel), the variation in heavy quarkonia’s binding energy (\(J/\psi\)) is plotted via temperature for \(1\text {S}\) and \(1\text {P}\) states, respectively. It is worth noting that with the increase in the temperature the binding energy becomes weaker, and an increase in the value of \(\alpha\) and \(\beta\) makes the curve higher. Also, our results are compatible with the other literatures such as [36, 38,39,40]. Figure 3 (right panel) shows the same behaviour for 1 S and 1P states. Figure 4 (left panel) shows the form of the binding energy of \(\gamma (1S)\) meson in a three-dimensional space. It is worth noting that the binding energy rises as the temperature decreases (in units of \(T_\text {c}\)), and an increase in the value of \(\alpha\) and \(\beta\) makes the curve higher. Figure 4 (right panel) shows the variation of binding energy of \(\chi (2b)\), when values of parameters \(\alpha\) and \(\beta\) increase, and then, the behaviour of curve gets close to curve at \(\alpha =\beta =1\).

Fig. 5
figure 5

(Left panel) Binding energy of \(J/\Psi\) as a variation of temperature T is shown at N = 3. (Right panel) Binding energy of \(\chi _{c}\) as a variation of temperature T is shown at N = 3, for \(\alpha =\beta\) =0.5, 0.7, and 0.9

Full size image
Fig. 6
figure 6

(Left panel) Binding energy of \(\gamma\) as a variation of temperature T is shown at N=3. (Right panel) Binding energy of \(\chi _\text {b}\) as a variation of temperature T is shown at N = 3, for \(\alpha =\beta\) =0.5, 0.7, and 0.9

Full size image

In Fig. 5 (left panel) and 5 (right panel), variation of binding energy for heavy quarkonia \(J/\psi\) at 1S state is plotted at dimensionality number N=3 for \(\alpha =\beta\) =0.5, 0.7, and 0.9. It is observable that binding energy increases with the increase in (\(\alpha , \beta\)). Also. our results are compatible with [28]. Figure 5(right panel) exhibits the behaviour of heavy quarkonia’s binding energy \(\chi _\text {c}\) at \(1\text {P}\) state. We observe that the curves have the same behaviour. In Fig. 6 (left panel) and 6 (right panel), the variation of binding energy for bottomonium \(\gamma\) and \(\chi _\text {b}\) meson is shown for \(1\text {S}\) and \(1\text {P}\) states, respectively. Also, at dimensionality number N=3 for \(\alpha =\beta\) = 0.5, 0.7, and 0.9. it is distinguished that an increase in \(\alpha , \beta\) leads to an increase in the binding energy value.

4.2 Thermodynamic properties

Calculating a system’s partition function, which is a temperature-dependent variable, is at the core of researching its thermodynamic properties. It is commonly referred to as the distribution function, and if it is determined, other thermodynamic properties can be derived using it. We obtained thermodynamic properties by using the two-body potential in SCQGP, and the partition function is provided by \(Z=\sum _{n=0}^{\infty }\exp [-\beta _{s} E_{nl}]\), where \(\beta _{s} =\frac{1}{KT}\), and K is the Boltzmann constant. When the principal quantum number n is around 0 and 1, 2,..., the quantity can be represented by use of an integral, as in [41,42,43], where the partition function and thermodynamic properties are presented as follows:

4.2.1 Partition function

Here, \(Z=\sum _{n=0}^{\infty }\exp [-\beta _{s} E_{nl}]\); by using Taylor expansion, then we get

$$\begin{aligned} Z=\frac{\exp [A_{1}-A_{2}+A_{3}*A_{4}]\beta _{s}}{(1+\exp [-2A_{3}])} \end{aligned}$$
(34)

where

$$\begin{aligned} \ A_{1}= & {} \frac{Q}{4\pi }\left( \frac{k_{i}}{\sqrt{3}}-k_{r}\right) \end{aligned}$$
(35)
$$\begin{aligned} A_{2}= & {} \frac{Q}{16\pi }\left[ \frac{(\frac{k_{r}^{2}}{2}-\frac{k_{i}^{2}}{2}-\frac{ k_{i}\text { }k_{r}}{\sqrt{3}})^{2}}{(\frac{k_{r}^{2}\text { }k_{i}}{2\sqrt{3}} -\frac{k_{i}^{3}}{6\sqrt{3}}-\frac{k_{r}^{3}}{6}-\frac{k_{r}\text { }k_{i}^{2} }{2})}\right] \end{aligned}$$
(36)
$$\begin{aligned} A_{3}= & {} \frac{\left( \frac{\Gamma (\beta )}{\Gamma (\beta -\alpha +1)}\right) }{m}\left[ \frac{m \text { }Q\text { }A^{4\alpha }}{4\pi \alpha ^{2}}\left( \frac{k_{r}^{2}\text { }k_{i} }{2\sqrt{3}}-\frac{k_{i}^{3}}{6\sqrt{3}}-\frac{k_{r}^{3}}{6}-\frac{k_{r} \text { }k_{i}^{2}}{2}\right) \right] ^{\frac{1}{2}}. \end{aligned}$$
(37)
$$\begin{aligned} A_{4}= & {} \left[ \alpha (2\alpha -1)+2n+\alpha \left( 1+\sqrt{1+\left( \frac{\Gamma (\beta )}{ \Gamma (\beta -\alpha +1)}\right) ^{-2}(4L(L+N-2)+(N^{2}-4N+3))+(2B)(1- \frac{B}{2})}\right) \right] . \end{aligned}$$
(38)
Fig. 7
figure 7

(Left panel) The partition function (Z) is shown as a function of \(\beta _{s}\), for different values of \(\alpha\), and \(\beta\) at N=3. (Right panel) The partition function (Z) is shown as a function of \(\beta _{s}\), for different values of dimensionality number N at \(\alpha =\beta =0.7\)

Full size image

In Fig. 7 (left panel) and 7 (right panel), the partition function (Z) is sensitive at the highest values of \(\beta _{s}\), as we can see. The variety of \(\beta _{s} =0.0035\)  \(\text {MeV}^{-1}\) to \(0.0065 \text {MeV}^{-1}\) in accordance to \(T=150\) to \(300 \text {MeV}\). That is the temperature range where charmonium dissolves into its constituents as charm quarks. Also, it is noted that with the increase in values of \(\alpha\) and \(\beta\) then conduct of the curve becomes higher. The conduct of Z is compatible with [19], wherein the authors plot the exact partition function as a function of \(\beta _{s}\) with different values of \(V_\text {max}\) and the semiclassical partition function. In addition, in Fig. 7 (right panel), the partition function increases as values of \(\beta _{s}\) increase, as we can see. The partition function’s behaviour will have an impact on additional observables to be discussed later. It is worth noting that binding energy depends on dimensionality number and that Z increases with the increase in the dimensionality number (N).

4.2.2 Mean energy U

$$\begin{aligned} {U(}\beta _{s} )=-\frac{\partial }{\partial (\beta _{s} )}\ln Z(\beta _{s} ). \end{aligned}$$
(39)
Fig. 8
figure 8

(Left panel) The mean energy (U) is shown as a function of \(\beta _{s}\) for different values of \(\alpha\), and \(\beta\) at N=3. (Right panel) The mean energy is shown as a function of \(\beta _{s}\), for different values of dimensionality number N at \(\alpha =\beta =0.9\)

Full size image

In Fig. 8 (left panel) and 8 (right panel), internal energy (U) decreases as \(\beta _{s}\) rises. In Fig. 8 (left panel), by increasing values of \(\alpha\) and \(\beta\) then curves become higher. In Fig. 8 (right panel), by raising the dimensionality number, values of U shift to higher values; many other theoretical works have the same behaviour as in [41]. For HCL, the internal energy rises as N rises as in [44], and thermodynamic properties are computed in a magnetic cosmic string background for a neutral particle, by using the nonrelativistic Schrödinger–Pauli equation. The authors also observed that when temperature and angular quantum number rise, internal energy rises. Thus, internal energy behaves in a consistent manner. It indicates when \(\beta _{s}\) and the vibration quantum number increases. Also, U decreases monotonically \((V_{max})\). Other studies including such in [41, 44, 45] do not consider this effect.

4.2.3 Specific heat C

$$\begin{aligned} C\mathbf {(}\beta _{s} )=\frac{\partial (U)}{\partial T}=-K\beta _{s} ^{2}\frac{ \partial (U)}{\partial \beta _{s}} \end{aligned}$$
(40)
Fig. 9
figure 9

(Left panel) The specific heat (C) is shown as a function of \(\beta _{s}\) for different values of \(\alpha\), and \(\beta\) at N=3. (Right panel) C is shown as a function of \(\beta _{s}\), for different values of dimensionality number N at \(\alpha =\beta = 0.9\)

Full size image

Figure 9 (left panel) and 9 (right panel) shows that the specific heat (C) decreases as \(\beta _{s}\) increases, and it moves to higher values when parameters \(\alpha ,\beta\) increase. Moreover, as shown in Fig. 9 (right panel), the dimensionality number raises the specific heat to higher values. The behaviour of the specific heat is investigated in [41, 43, 44, 46] that Schrödinger equation is used. With these efforts, we discovered a qualitative agreement.

4.2.4 Free energy

$$\begin{aligned} {F(}\beta _{s})=-\frac{1}{\beta _{s}}\ln Z(\beta _{s}). \end{aligned}$$
(41)
Fig. 10
figure 10

(Left panel) The free energy (F) is shown as a function of \(\beta _{s}\) for different values of \(\alpha\), and \(\beta\) at N=3. (Right panel) F is shown as a function of \(\beta _{s}\), for different values of dimensionality number N at \(\alpha =\beta =0.7\)

Full size image

Figure 10 (left panel) and 10 (right panel) shows that when \(\beta _{s}\) rises, it leads to rises in the free energy (F). In addition, as shown in Fig. 10 (left panel), the free energy increases as parameters \(\alpha\) and \(\beta\) increases; also, as shown in Fig. 10 (right panel), the free energy increases as N increases. In [45], free energy is studied for strange quark matter and the authors reached the same conclusion. In [44], the free energy is calculated for a neutral particle and has the same behaviour; it decreases as the temperature rises. In the current work, we note heavy quarks have accord in terms of quality [44, 45].

4.2.5 Entropy

$$\begin{aligned} S\mathbf {(}\beta _{s} )=K\ln Z(\beta _{s} )-K\beta _{s} \frac{\partial }{\partial \beta _{s} } \ln Z(\beta _{s} ). \end{aligned}$$
(42)
Fig. 11
figure 11

(Left panel) The entropy (S) is shown as a function of \(\beta _{s}\) for different values of \(\alpha\), and \(\beta\) at N=3. (Right panel) S is shown as a function of \(\beta _{s}\), for different values of dimensionality number N at \(\alpha =\beta =0.8\)

Full size image

In Fig. 11 (left panel) and 11 (right panel), the behaviour of entropy decreases with increasing \(\beta _{s}\). Additionally, when \(\alpha ,\beta\) increase, the entropy shifts to higher levels, and shifts to higher levels as dimensionality number increases. In Refs. [43,44,45, 47], for the light quark, the strange quark, and natural particles, the authors observe that entropy increases as temperature rises. For the charm quark, they got the same result. Furthermore, there has been no change in the phase transition in the temperature interval indicating melts below the critical temperature for heavy quarks; this is compatible with Ref. [48].

Fig. 12
figure 12

(Left panel) Binding energy \(J/\psi\) is shown as a function of temperature for different values of dimensionality number N at T=175 MeV and \(\alpha =\beta =0.7\). (Right panel) Binding energy of \(\chi _\text {c}\) is shown as a function of temperature for different values of dimensionality number N, T=175 MeV and \(\alpha =\beta =0.6\)

Full size image
Fig. 13
figure 13

(Left panel) Binding energy of \(\gamma\) is shown as a function of temperature, for different values N at T=175 MeV and \(\alpha =\beta =0.8\). (Right panel) Binding energy of \(\chi _\text {b}\) is shown as a function of temperature for different values of N, at T=175 MeV and \(\alpha =\beta =0.9\)

Full size image

In Fig. 12 (left panel), the variation of binding energy for heavy quarkonia \(J/\psi\) at 1S state is plotted at \(\alpha =\beta =0.7\) for different values of dimensionality number N. It should be observed that the binding energy depends on dimensionality number and increases with the increase in N. Our results are compatible with Ref. [28]. Figure 12 (right panel) exhibits the behaviour of heavy quarkonia’s binding energy \(\chi _\text {c}\) at \(1\text {P}\) state. We observe that the curve becomes higher with the increase in N. In Fig. 13 (left panel) and 13 (right panel), variation of binding energy for bottomonium \(\gamma\) and \(\chi _\text {b}\) meson is shown for 1S and \(1\text {P}\) states, respectively. And for different values of N at \(\alpha =\beta\) =0.8, and 0.9. It is distinguished that an increase N leads to an increase in binding energy value.

Fig. 14
figure 14

(Left panel) Binding energy \(J/\psi\) is shown as a function of temperature for different values of \(\alpha\), and \(\beta\) at N = 4 and T = 175 MeV. (Right panel) Binding energy of \(\chi _\text {c}\) is shown as a function of temperature for different values of \(\alpha\), and \(\beta\) at N=4 and T=175 MeV

Full size image
Fig. 15
figure 15

(Left panel) Binding energy of \(\gamma\) is shown as a function of temperature for different values of \(\alpha\), and \(\beta\) at N=4 and T=175 MeV. (Right panel) Binding energy of \(\chi _{b}\) is shown as a function of temperature for \(\alpha\), and \(\beta\) at N=4 and T=175 MeV

Full size image

In Fig. 14 (left panel), the variation of binding energy for heavy quarkonia \(J/\psi\) at 1S state is plotted at dimensionality number N = 4 for \(\alpha =\beta\) =0.5, 0.7, and 0.9. It is observable that the binding energy increases with the increase in \(\alpha , \beta\). Also, at N=4 we note that the behaviour of curves gets higher. Our results are compatible with Ref. [28]. Figure 14 (right panel) exhibits the behaviour of heavy quarkonia’s the binding energy \(\chi _\text {c}\) at \(1\text {P}\) state. We observe that the curves have the same behaviour. In Fig. 15 (left panel) and 15 (right panel), the variation of binding energy for bottomonium \(\gamma\) and \(\chi _\text {b}\) meson is shown for \(1\text {S}\) and \(1\text {P}\) states, respectively. Also, at dimensionality number N=4 for \(\alpha =\beta\) = 0.5, 0.7, and 0.9. It is distinguished that an increase in \(\alpha , \beta\) leads to an increase in the binding energy value.

Fig. 16
figure 16

(Left panel) The mass spectra of charmonium is shown as a function of temperature for 1 S and 1P states at \(\alpha =\beta =0.6\). (Right panel) The mass spectra of bottomonium is shown as a function of temperature for 1 S and 1P states at \(\alpha =\beta =0.8\)

Full size image

In Fig. 16 (left panel) and 16 (right panel), the temperature-dependent behaviour of heavy quarkonia mass spectra is investigated (in units of \(T_\text {c}\)) utilizing two values of quark mass for \(1\text {S}\) and \(1\text {P}\) states (charmonium \(c\overline{c}\) and bottomonium \(b\overline{b})\). And at \(\alpha =\beta\) =0.6, and 0.8 and T=175 MeV, high mass spectra of heavy quarkonia result from rising quark mass, which correspond with [49]. Also, an increase in the dimension number gets the curve becomes higher.

Fig. 17
figure 17

(Left panel) Dependence of \(J/\psi\) binding energy on temperature in three-dimensional space. (Right panel) Dependence of \(\gamma\) binding energy on temperature in three-dimensional space

Full size image
Fig. 18
figure 18

(Left panel) Dependence of \(J/\psi\) binding energy on temperature. (Right panel) Dependence of \(\gamma\) binding energy on temperature in four-dimensional space

Full size image

In Fig. 17 (left panel) and 17 (right panel), in three-dimensional space, the binding energy of charmonium and bottomonium mesons is displayed in this diagram for 1 S and 1P states, and for charmonium and bottomonium, respectively. It is worth noting that the binding energy rises as dissociation temperature decreases. And also fractional parameter \((\alpha )\) has an important effect on increase binding energy. In Fig. 18, in four-dimensional space, the binding energy of \(J/\psi\) and \(\gamma\) mesons is plotted. It is noticeable that \((\alpha )\) has an important effect on increase binding energy. And also curves become higher by increasing N.

Fig. 19
figure 19

(Left panel) Binding energy \(J/\psi\) is shown as a function of temperature for different values of \(\alpha\), and \(\beta\) at N=5 and T=175 MeV. (Right panel) Binding energy of \(\chi _\text {c}\) is shown as a function of temperature for different values of \(\alpha\), and \(\beta\) at N=5 and T=175 MeV

Full size image
Fig. 20
figure 20

(Left panel) Binding energy of \(\gamma\) is shown as a function of temperature for different values of \(\alpha\), and \(\beta\) at N = 5 and T = 175 MeV. (Right panel) Binding energy of \(\chi _\text {b}\) is shown as a function of temperature for \(\alpha\), and \(\beta\) at N = 5 and T = 175 MeV

Full size image

In Fig. 19 (left panel), variation of binding energy for heavy quarkonia \(J/\psi\) at 1S state is plotted at dimensionality number N = 5 for \(\alpha =\beta\) = 0.5, 0.7, and 0.9. It is observable that binding energy increase with the increase in \(\alpha , \beta\). Also, at N = 5 we note that the behaviour of curves get higher. Figure 19 (right panel) exhibits the behaviour of heavy quarkonia’s binding energy \(\chi _\text {c}\) at \(1\text {P}\) state. We observe that the curves have the same behaviour. In Fig. 20 (left panel) and 20(right), variation of binding energy for bottomonium \(\gamma\) and \(\chi _\text {b}\) meson is shown for \(1\text {S}\) and \(1\text {P}\) states, respectively. Also, at dimensionality number N=5 for \(\alpha =\beta\) = 0.5, 0.7, and 0.9. It is distinguished that, an increase in \(\alpha , \beta\) leads to an increase in binding energy value.

Table 1 Dissociation temperature (\(T_\text {D}\)) with \(T_\text {c}=175\text {MeV}\) for the quarkonium states using \(M_\text {c}=1710\text {MeV}\) and \(\ M_\text {b}=5050\text {MeV}\) at \(N=3\)
Full size table
Table 2 Dissociation temperature (\(T_\text {D}\)) with \(T_\text {c}=175\text {MeV}\) for the quarkonium states using \(M_\text {c}=1710\text {MeV}\) and \(\ M_\text {b}=5050\text {MeV}\) at \(N=4\)
Full size table
Table 3 Dissociation temperature (\(T_\text {D}\)) with \(T_\text {c}=175\text {MeV}\) for the quarkonium states using \(M_{c}=1710\text {MeV}\) and \(\ M_\text {b}=5050\text {MeV}\) at \(N=5\)
Full size table

In Table 1, the dissociation temperature has been computed for the ground state also the first and the second excited states of heavy quarkonia including such charmonium\((c\overline{c})\), and bottomonium \((b\overline{b})\) at \(N=3\), \(M_{c}=1710\)  \(\text {MeV}\) and \(\ M_{b}\) \(=5050\)  \(\text {MeV}\) as in [2], for different values of fractional parameter \(\alpha\) = 0.5, 0.7, and 0.9. It is worth noting that at N=3 the states are dissociated around values 1.472 \(T_\text {c}\) to 1.51 \(T_\text {c}\), 1.64 \(T_\text {c}\) to 1.75 \(T_\text {c}\), 0.9 \(T_\text {c}\) to 1.221 \(T_\text {c}\), and 1.2 \(T_\text {c}\) to 1.292 \(T_\text {c}\), respectively, for the following states \(J/\psi\), \(\chi _\text {c}\), \(\gamma\), and \(\chi _\text {b}\).

From Table 1, we lead to the conclusion that states melt around the critical temperature and that stimulated charmonia states exist at higher temperatures. The dissociation temperature is determined by the Debye screening mass selected. The influence of fractional parameter \(\alpha\) on dissociation temperature is shown by Debye screening mass. We note that an increase in \(\alpha\) leads to an increase in the dissociation temperature for states. Values of states \(J/\psi\) and \(\chi _\text {c}\) are agreed quantitatively when compared to [28, 38]. The value of \(\gamma\) is smaller values when compared to some literature as an instance [28, 36]. The values of \(\chi _{b}\) agree [50, 51].

In Tables 2 and 3, the dissociation temperatures of heavy quarkonia for several states including such charmonium\((c \overline{c})\) and bottomonium \((b\overline{b})\) have been computed at \(N=4, 5\) and the critical temperatures \(T_\text {c}=175\)  \(\text {MeV}\), also at \(M_\text {c}=1710\) \(\text {MeV}\), and \(\ M_\text {b}\) \(=5050\)  \(\text {MeV}\) as in Ref. [2], for different values of fractional parameter \(\alpha\) = 0.5, 0.7, and 0.9. It is worth noting that at N=4 the states are dissociated around values 1.52 \(T_\text {c}\) to 1.553 \(T_\text {c}\), 1.76 \(T_\text {c}\) to 1.831 \(T_{c}\), 1.23 \(T_\text {c}\) to 1.42 \(T_\text {c}\), and 1.294 \(T_\text {c}\) to 1.392 \(T_\text {c}\), respectively, for the following states \(J/\psi\), \(\chi _\text {c}\), \(\gamma\), and \(\chi _\text {b}\). It is worth noting that there has been a rise in distinct quarkonium states, increasing \(\alpha\) causes an increase in the dissociation temperature. Table 3 shows that at N=5 the states are dissociated around values 1.593 \(T_\text {c}\) to 1.642 \(T_\text {c}\), 1.862 \(T_\text {c}\) to 1.93 \(T_\text {c}\), 1.51 \(T_\text {c}\) to 1.62 \(T_\text {c}\), and 1.42 \(T_\text {c}\) to 1.54 \(T_\text {c}\), respectively, for the following states \(J/\psi\), \(\chi _\text {c},\)  \(\gamma\), and \(\chi _\text {b}\). It is worth noting that increasing \(\alpha\), \(\beta\) causes an increase in the dissociation temperature. Finally, we conclude from the above two tables that fractional parameter \(\alpha\) has a great effect on the dissociation temperatures that were not accounted in previous studies; also, an increase in the dimensionality number causes an increase in the dissociation temperature.

5 Comparison with other recent models

In Ref. [64], by employing the Nikiforov–Uvarov method to solve the radial Schrodinger equation with the extended Cornell potential at finite temperature, the temperature-dependent energy, mass spectra, and the temperature-dependent energy eigenvalue expansion are used to determine the thermodynamic quantities such as free energy \(F(\beta )\), mean energy \(U(\beta )\), specific heat \(C(\beta )\), entropy \(S(\beta )\), and magnetic susceptibility \(\chi (\beta )\) in terms of canonical partition function \(Z(\beta )\) for quarkonia (charmonium and bottomonium) and have been computed at \(\beta =15 GeV^{-1}\). They noted that mass spectra values for bottomonium rise for all values of n when the temperature (T) decreases and \((\beta )\) increases, but at significantly greater values. Except for the free energy function and specific heat, it can be observed that all of them reach their stable values at a suitably large \(\beta\) value and decreases. The entropy decreases rapidly as \(\beta\) increases, and magnetic susceptibility efficiency decreases rapidly. Then, except for free energy, temperature has a beneficial impact on all thermal properties. These calculations are consistent with our results.

In Ref. [65], the analytical exact iteration approach (AEIM) was used to solve the N-dimensional radial Schrodinger equation, which generalizes the Cornell potential to finite temperature and chemical potential. In N-dimensional space, the authors calculated the binding energies and mass spectra of heavy quarkonia such as charmonium and bottomonium mesons. Also, the dissociation temperatures for several states of heavy quarkonia are computed in three dimensions. They observed that when temperature rises, the binding energy becomes weaker. They estimate the dissociation temperature for various states of heavy quarkonia from the constraint \(E_\text {bin} = 0\), since the state is dissociated when its binding energy vanishes. They determined the dissociation temperatures for the ground and excited states at dimensionality number \(N = 3, 4, 5\), and it is noted that the states dissociate around \(1.3 T_{c}\). Also, these calculations are comptible with our results

In Ref. [66], the authors used the N-dimensional radial Schrodinger equation in which the Cornell potential is extended by including the quadratic potential and its inverse of quadratic potential. The authors employed Nikiforov–Uvarov (NU) method to calculate the energy eigenvalues and wave functions in N-dimensional space. They calculated mass of spectra and thermodynamic properties of heavy quarkonia such that \(F(\beta )\), \(U(\beta )\), \(C(\beta )\), and \(S(\beta )\), and they noted that the heavy quarkonia mass spectra such as charmonium and bottomonium increase with increasing dimensional number due to the increasing binding energy. They plotted thermodynamic properties at \(T = 0.154\) to \(0.250 \text {GeV}\) which represents the range of temperature which charmonium melts to its constituents as charm quark. They discovered that as the temperature rises, the internal energy, specific heat, and entropy decrease. Also, internal energy, the free energy, the specific heat, and the entropy shift to higher values by increasing dimensional number. We found that results of Ref. [66] are consistent with our results

In Ref. [67], recent lattice investigations of string breaking in QCD with dynamical quarks establish the heavy quark potential’s in-medium temperature dependence. Comparing this to the binding energies of various quarkonium states, in heated matter, there are two collective forms of quarkonium dissociation. The authors found hadronic in-medium effects for \(T < T_{c}\), relating to the approach to chiral symmetry restoration and string tension red, resulting in a lower string-breaking threshold. As a result, the highly excited quarkonium states are dissociated such as \((\psi \acute{}, \chi _{c}, and \chi \acute{}_{b}\) through decay into open charm or beauty. Lower states are more tightly bound such as \(J/\Psi\), \(\gamma\), and \(\chi _{b}\) that survive up to or beyond \(T_{c}\). Colour screening in a deconfined medium will thus be used to dissociate them.

In [59], the authors investigated the energy levels of charmonium and bottomonium above the phase transition temperature using the colour-singlet free energy \(F_{1}\) and internal energy \(U_{1}\) determined by Kaczmarek et. al [60] in quenched QCD. In this model, based on a variational principle, they discover that the \(Q\bar{Q}\) potential contains just the \(Q\bar{Q}\) internal energy \(U_{Q Q\bar{}}\), which can be calculated by removing the gluon internal energy contributions from the total \(U_{1}\). Such a \(U_{Q Q\bar{}}\) potential leads to weakly bound \(J/\psi\) and \(\eta _{c}\) at temperatures above the phase transition temperature and they become unbound at \(1.62 T_{c}\). The \(\chi _{c}\), \(\eta \acute{c}\), and \(\psi \acute{}\) states are found to be unbound in the quark–gluon plasma. In this potential model, \(\gamma\), \(\eta _{b}\), \(\gamma \acute{}\), and \(\chi _{b}\) are bound at temperatures above \(\hbox {T}_{c}\), \(\gamma\), and \(\eta _{b}\) dissociates spontaneously at 4.1 \(\hbox {T}_{c}\), \(\chi _{b}\) at \(1.18 T_{c}\), and \(\gamma \acute{}\) and \({\eta _{b}}\acute{}\) at \(1.38T_{c}\).

6 Conclusions

The two-body potential in SCQGP is produced using the fractional analytical iteration method to solve the N-dimensional radial Schrodinger equation. Using a generalized fractional derivative, the fractional binding energy and wave function have been determined in the N-dimensional space, where the fractional parameter \(0<\alpha \le 1\). The influence of fractional parameter on binding energy, mass spectra, and thermodynamic properties of heavy quarkonium (charmonium and bottomonium) for different states was investigated.

Furthermore, in the current work, we get a special case of the binding energy in the N-dimensional space at \(\alpha =1\) as in Ref. [2]. In comparison with GFD–AEIM data, the influence of fractional parameters of SCQGP in this work is investigated. We go into the conclusion that fractional parameter has a crucial role in SCQCD in improving quarkonium masses and binding energy wherein fractional parameter causes an effect on the behaviour of curves for binding energy and mass spectra for different heavy quarkonium states. In addition, at a finite temperature, the dissociation temperature for various states of heavy quarkonia has been computed by comparing our results with the existing literature. From the figures, by increasing the fractional parameter value and then binding energy, mass spectra appear to change to higher values. And it is compatible with many works such as in [2, 43, 52].

We also applied the present results to calculate thermodynamic properties such as partition function, internal energy, specific heat, entropy, and free energy. We computed and plotted thermodynamic properties in the fractional form, we found that our results are compatible with other works and the physical behaviour of thermodynamic properties is compatible with experimental data. We also observed that when \(\beta _{s}\) increases, internal energy, specific heat, and entropy decrease. Many works, for example [28, 44, 45, 47], do not discuss the thermodynamic properties of heavy quarkonium. And note the crucial effect of fractional parameter and dimensionality number on the behaviour of thermodynamic properties.

Also in the current work, a higher-dimensional space (N = 3, 4, 5) is evaluated. Dimensionality number has a significant impact on how binding energy, mass spectra, and thermodynamic properties behave for heavy quarkonia for \(N\ge 3\). From the figures, by changing dimensionality number values then binding energy, mass spectra, and thermodynamic properties appear to change to higher values. And we showed the degree of conformity of our results with previous works such as in  Refs. [43, 52].

We intend to expand our research in the future to include the influence of external magnetic fields on heavy meson properties that will provide extra details about quark–gluon plasma as in Refs. [68, 69].