1 Introduction

In 1979, Hayashi and Shirafuji succeeded in obtaining a gravitational theory which is formulated on the Weitzenböck space–time, and which is characterized by both the vanishing curvature tensor due to the absolute parallelism geometry (\({\text{AP}} - {\text{geometry}}\)) and by the torsion tensor formed of four parallel vector fields. This theory is called new general relativity (\({\text{NGR}}\)), and has been extensively explored in the literature [1,2,3,4,5,6,7,8]. Blixt et al. studied the Hamiltonian and primary constraints of the new general relativity [3]. Jiménez and Dialektopoulos revisited the number and nature of new general relativity perturbative degrees of freedom around the flat Minkowski background from a different perspective, and extended it to include cubic interactions [6]. Guzmán and Khaled created a classification of the principal constraints in the parametric method for the new general theory of relativity [7]. The field equations of \({\text{NGR}}\) contains three free parameters \(d_{1} ,d_{2} ,\,{\text{and}}\,\,d_{3}\), as seen in Sect. 3. Several years after the emergence of this theory, specifically in 1996, Mikhail et al. succeeded to find cosmological models based on this theory. These models depend on the theoretical free parameters and are not interpreted based on the change of these parameters [9]. These models built on this theory think that the expansion of the current Universe could be well described by solving the field equations in the presence of dust within the framework of spatially flat Robertson–Walker space–time (\({\text{RW}}\)), which gives a decelerating expansion with a constant deceleration parameter. From 1998, the experimental efforts to confirm this, however, led to the discovery that the current Universe is in fact accelerating [10,11,12,13]. In 2003, Caldwell et al. discussed some scenarios of the Universe where it will eventually re-collapse and end with a Big Crunch, or expand forever, becoming increasingly cold and empty [14]. At the end of the search, Caldwell et al. found the consequences that follow if the dark energy is phantom energy, in which the sum of the pressure and energy density is negative. The positive phantom energy density becomes infinite in finite time, overcoming all other forms of matter in such a way that the gravitational repulsion rapidly brings the epoch of cosmic structure to a close. The phantom energy rips apart the Milky Way, solar system, Earth, and ultimately the molecules, atoms, nuclei, and nucleons of which it composed, before the death of the Universe in the Big Rip [14]. Since that astonishing discovery, many cosmologists have resorted to explaining the evolution of the universe using a deceleration parameter that varies with cosmic time [15,16,17,18,19]. The main objective of this article, according to the modern data of the evolution of the universe, is to find cosmological models that depend on NGR field equations under the conditions on the free parameters of the field equations for this theory. In this article, we review cosmological models that end with the Big Rip and others that end with the Big Crunch. To crystallize this article, in Sect. 2 we provide a brief summary of \({\text{AP}} -\)geometry. Section 3 reviews the general formalism of the \({\text{NGR}}\) theory. The Big Bang–Big Rip model as well as energy conditions in the \({\text{NGR}}\) theory is discussed in Sect. 4. Also, the Big Bang–Big Crunch model and energy conditions in the \({\text{NGR}}\) theory are discussed in Sect. 5, with conditions on the effective potential. Special solutions of NGR field equations are found in Sect. 6. The purpose of this article is clarified by a number of Figures and Tables. Finally, the conclusions linked to this article are outlined in Sect. 7.

2 A brief summary of \({\text{AP}} -\)geometry

In what follows, a review of the \({\text{AP}}\)-geometry is undertaken. The building of the conventional absolute parallelism geometry \({\text{AP}}\) is defined completely in the 4-dimensions by a tetrad vector \(\lambda_{i}^{\,\,\gamma }\) (\(i = 1,\,2,\,3,\,4\)) indicating the vector number, and (\(\gamma = 1,\,2,\,3,4\)) indicating the coordinate component. These four vectors satisfy the normalization condition [20]:

$$ \lambda_{i}^{\,\,\gamma } \lambda_{i\,\alpha } = \delta_{\alpha }^{\,\,\gamma } ,\;{\text{and}}\;\lambda_{i}^{\,\,\alpha } \lambda_{j\,\alpha } = \delta_{i\,j} . $$
(1)

One constructs the following symmetric tensors:

$$ g_{\alpha \beta } = \eta_{ij} \,\lambda_{i\alpha } \lambda_{j\beta } , $$
(2)

where \(\eta_{ij} = diag( + 1,\, - 1,\, - 1,\, - 1)\).

At any point in the \({\text{AP}}\) geometry, one can define the Riemannian space, at which the symmetric tensor (2) plays the following metric tensor:

$$ ds^{2} = g_{\alpha \beta } dx^{\alpha } dx^{\beta } . $$
(3)

The generalization of the partial differentiation in the Riemannian space is defined for the covariant vectors as follows:

$$ A_{\beta ;\gamma } = A_{\beta ,\gamma } - \left\{ {\mathop {}\limits_{\beta \,\,\,\,\,\gamma }^{\alpha } } \right\}A_{\alpha } , $$
(4)

where

$$ \left\{ {\mathop {}\limits_{\alpha \,\,\,\,\beta }^{\gamma } } \right\} = g^{\gamma \varepsilon } (g_{\alpha \varepsilon \,,\beta } + g_{\beta \varepsilon \,,\alpha } - g_{\alpha \beta \,,\varepsilon } )/2. $$
(5)

One can define the non-symmetric connection \(\Gamma_{\,\,\,\,\alpha \beta }^{\gamma }\) as follows:

$$ \Gamma_{\,\,\,\,\alpha \beta }^{\gamma } = \lambda_{i}^{\,\,\gamma } \lambda_{i\,\alpha \,,\beta } = - \lambda_{i\,\alpha } \lambda_{i\,,\,\beta }^{\,\,\gamma } $$
(6)

This is the consequence of the following absolute parallelism condition:

$$ \lambda_{i\,\alpha \,|\,\beta } = \lambda_{i\,\alpha \,,\,\beta } - \Gamma_{\,\,\,\,\alpha \beta }^{\gamma } \,\lambda_{i\,\gamma } . $$
(7)

Using the affine connection (6), one can define the following third-order tensors:

$$ \Lambda_{\,\,\,\,\alpha \beta }^{\gamma } = \Gamma_{\,\,\,\,\alpha \beta }^{\gamma } - \Gamma_{\,\,\,\,\beta \alpha }^{\gamma } = - \Lambda_{\,\,\beta \alpha }^{\gamma } , $$
(8)
$$ \gamma_{\,\,\,\,\,\alpha \beta }^{\gamma } = \Gamma_{\,\,\,\,\alpha \beta }^{\gamma } - \left\{ {\mathop {}\limits_{\alpha \,\,\,\,\,\,\,\beta }^{\gamma } } \right\} = \lambda_{i}^{\,\,\gamma } \lambda_{i\,\alpha \,;\,\beta } = - \lambda_{i\,\alpha } \lambda_{i\,;\,\beta }^{\,\gamma } , $$
(9)

where \(\Lambda_{\,\,\,\alpha \beta }^{\gamma }\) is the torsion tensor, and \(\gamma_{\,\,\,\,\alpha \beta }^{\,\gamma }\) is the contortion tensor. Both can be related by:

$$ \gamma_{\alpha \mu \nu } = \frac{1}{2}\left( {\Lambda_{\alpha \mu \nu } + \Lambda_{\nu \mu \alpha } - \Lambda_{\mu \alpha \nu } } \right), $$
(10)

Contracting (8) and (10), one gets:

$$ C_{\alpha } = \Lambda_{\,\,\alpha \beta }^{\beta } = \gamma_{\,\,\,\alpha \beta }^{\beta } , $$
(11)

which is called a basic vector.

From the above tensors, one can define another third-order tensor given by:

$$ t_{\alpha \mu \nu } = \frac{1}{2}\left( {\Lambda_{\alpha \mu \nu } - \Lambda_{\mu \alpha \nu } } \right) - \frac{1}{6}\left( {g_{\nu \alpha } C_{\mu } + g_{\mu \nu } C_{\alpha } } \right) + \frac{1}{3}g_{\alpha \mu } C_{\nu } , $$
(12)

with the axial vector:

$$ a_{\mu } = \frac{1}{6}\varepsilon_{\mu \nu \rho \sigma } \Lambda^{\nu \rho \sigma } , $$
(13)

where \(\varepsilon_{\mu \nu \rho \sigma } = \sqrt { - g} \,\,\delta_{\mu \nu \rho \sigma }\) is the Levi–Civita symbol, and \(g\) is the determinant of the metric tensor.

In the following section, we will briefly review the derivation of field equations for \({\text{NGR}}\) to investigate the effect of the parameters of this theory on the Big Rip–Big Crunch models.

3 General formalism of the new general relativity theory

In this section we will be concerned with the \({\text{NGR}}\) theory introduced in [1] that is defined by a local and parity-preserving quadratic form of the torsion. These theories are obviously formulated in a Weitzenbock space and have been extensively explored in the literature. From Hayashi and Shirafuji [1], the Lagrangian function for the \({\text{NGR}}\) takes the following form:

$$ \ell = \lambda \left( {\frac{R}{16\pi \,G} + d_{1} \,t^{\alpha \mu \nu } \,t{}_{\alpha \mu \nu }\, + d_{2} \,C^{\alpha } C_{\alpha } + d_{3} \,a^{\alpha } \,a_{\alpha } } \right) $$
(14)

where \(d_{1} ,\,d_{2} ,\,d_{3}\) are the dimensionless free parameters, \(R\) is the Ricci scalar, and \(G\) is the Newtonian constant.

\({\text{NGR}}\) with the gravitational Lagrangian (14) well describes all the observed gravitational phenomena in the identical level as the general relativity \(({\text{GR}})\). It is important to mention the criteria governing the \(NGR\) Lagrangian: Global Lorentz invariance, diffeomorphisms invariance that is at most quadratic in the torsion and no higher than second order field equations.

From a variational principle for the Lagrangian function (1), Hayashi and Shirafuji were able to obtain the field equations in the form [1] (we have chosen the unit system such that \(8\pi \,G = 1\)),

$$ G^{\mu \nu } + 2\,F_{\,\,\,\,\,\,\,\,\,\,|\lambda }^{\mu \nu \lambda } - 2C_{\lambda } F^{\mu \nu \lambda } + 2H^{\mu \nu } - g^{\mu \nu } L^{\prime} = T^{\mu \nu } , $$
(15)

where \(G^{\mu \nu }\) is the Einstein tensor defined by:

$$ G^{\mu \nu } = R^{\mu \nu } - \frac{1}{2}g^{\mu \nu } R, $$
(16)

with \(R^{\mu \nu }\) being the Ricci tensor, and:

$$ F^{\mu \nu \lambda } = d_{1} (t^{\mu \nu \lambda } - t^{\mu \lambda \nu } ) - d_{2} (g^{\mu \nu } C^{\lambda } - g^{\mu \lambda } C^{\nu } ) - \frac{{d{}_{3}}}{3}\varepsilon^{\mu \nu \lambda \rho } a_{\rho } = - F^{\mu \lambda \nu } , $$
(17)
$$ H^{\mu \nu } = \Lambda^{\rho \sigma \mu } F_{\rho \sigma }^{\,\,\,\,\nu } - \frac{1}{2}\Lambda^{\nu \rho \sigma } F_{\,\,\,\,\rho \sigma }^{\mu } = H^{\nu \mu } , $$
(18)
$$ L^{\prime} = \ell /\lambda , $$
(19)

and the material energy momentum tensor \(T^{\mu \nu }\) is defined as follows:

$$ T^{\mu \nu } = \frac{1}{\lambda }\frac{{\delta \,\ell_{m} }}{{\delta \,b_{\,\,\,\nu }^{\alpha } }}b^{\alpha \mu } , $$
(20)

where \(\ell_{m}\) denotes the Lagrangian density of the material fields.

We can notice that Eqs. (1–7) are reduced to the original \({\text{GR}}\) equations when \(d_{1} = d_{2} = d_{3} = 0\).

The field equations for the Friedmann–Robertson–Walker (\({\text{FRW}}\)) metric [21]:

$$ ds^{2} = - \,dt^{2} + \frac{{16\,a^{2} (t)}}{{(4 + k\,r^{2} )^{2} }}\left( {dr^{2} + r^{2} (d\theta^{2} + \sin^{2} \theta \,d\phi^{2} )} \right), $$
(21)

are obtained as follows [9]:

$$ 3YH^{2} + \frac{3B\,k}{{a^{2} }} = \rho , $$
(22)
$$ 2Y\,\dot{H} + 3Y\,H^{2} + \frac{Bk}{{a^{2} }} = - P, $$
(23)

where the dot denotes differentiation with respect to the cosmic time \(t\), \(k\) is the curvature constant (\(k = 0,1, - 1\)), \(a(t)\) is an unknown function which is called the scale factor, \(H(t)\) is the Hubble parameter which is defined through \(H(t) = \dot{a}/a\), here \(\rho\) and \(P\) are the proper energy density and pressure respectively, and the new parameters \(Y\) and \(B\) are given by \(Y = 1 - 3\,d_{2}\),\(B = 1 + (4/3)\,d_{3}\).

Equations (22) and (23) are reduced to the original \({\text{GR}}\) at \(d_{2} = d_{3} = 0\).

The equation of state for this model is given by:

$$ \omega = \frac{P}{\rho } = - \frac{{a^{2\,} (2Y\,\dot{H} + 3Y\,H^{2} ) + Bk}}{{3Y\,a^{2} H^{2} + 3B\,k}}. $$
(24)

The solutions found for Eqs. (22) and (23) are given by the following table [9] (Table 1).

Table 1 Solutions of the field equations
Full size table

These solutions involve the two parameters \(d_{2}\) and \(d_{3}\) characterizing the field equations of the NGR, where \(\beta\), \(\gamma\) and \(\delta\) are the constants of integration.

In the next section, we will study the effect of the parameters \(Y\) and \(B\) on the Big Rip universe as well as on the energy conditions.

4 The Big Bang–Big Rip model and energy conditions in \({\text{NGR}}\)

The field Eqs. (22) and (23) have three unknowns, namely \(\rho ,\,P\) and \(a\).So, in order to obtain the unique solution, we need one physically reasonable relation among the variables. Consequently, we assume a quadratic deceleration parameter of the form [19]:

$$ q = (8n^{2} - 1) - 12nt + 3t^{2} , $$
(25)

where \(n\) is a free parameter given from observations.

The relation between the Hubble parameter and the deceleration parameter is given by [22]:

$$ q + 1 = dH^{ - 1} /dt. $$
(26)

The deceleration parameter (26) represents the Big bang–Big Rip–Big Crunch model. It has a singularity at \(t = 0,\,2n\) and \(4n\). Also, the universe begins with the Big Bang and ends with the Big Crunch with the same value \(q = 8n^{2} - 1\). The deceleration parameter behavior has been discussed before in most of the literature; for example, see Refs. [23,24,25,26,27,28].

From Eqs. (25) and (26), one obtains:

$$ H = \frac{{\dot{a}}}{a} = \frac{1}{t\,(t - 2n)\,(t - 4n)}, $$
(27)

and its derivative is given by:

$$ \dot{H} = - \,\frac{{8n^{2} - 12n\,t + 3\,t^{3} }}{{t^{2} \,(t - 2n)^{2} \,(t - 4n)^{2} }}. $$
(28)

Integration of Eq. (17) leads to:

$$ a(t) = \frac{{\left( {t\,(t - 4n)} \right)^{{{1 \mathord{\left/ {\vphantom {1 {8n^{2} }}} \right. \kern-0pt} {8n^{2} }}}} }}{{\left( {t - 2n} \right)^{{{1 \mathord{\left/ {\vphantom {1 {4n^{2} }}} \right. \kern-0pt} {4n^{2} }}}} }}. $$
(29)

In order to study the physical behavior of the model, we substitute from Eqs. (27–29) in (22–24) to get:

$$ \rho = \frac{3Y}{{t^{2} (t - 2n)^{2} (t - 4n)^{2} }} + \frac{{3Bk(t - 2n)^{{{1 \mathord{\left/ {\vphantom {1 {2n^{2} }}} \right. \kern-0pt} {2n^{2} }}}} }}{{(t(t - 4n))^{{{1 \mathord{\left/ {\vphantom {1 {4n^{2} }}} \right. \kern-0pt} {4n^{2} }}}} }}, $$
(30)
$$ P = - \,\left( {\frac{{Y(16n^{2} + 3 - 24nt + 6t^{2} )}}{{t^{2} (t - 2n)^{2} (t - 4n)^{2} }} + \frac{{Bk(t - 2n)^{{{1 \mathord{\left/ {\vphantom {1 {2n^{2} }}} \right. \kern-0pt} {2n^{2} }}}} }}{{(t(t - 4n))^{{{1 \mathord{\left/ {\vphantom {1 {4n^{2} }}} \right. \kern-0pt} {4n^{2} }}}} }}} \right), $$
(31)
$$ \rho - \frac{P}{\omega } = \frac{1}{\omega }\,\left( {\frac{{Y(3\,\,\omega + 16n^{2} + 3 - 24nt + 6t^{2} )}}{{t^{2} (t - 2n)^{2} (t - 4n)^{2} }} + \frac{{Bk(3\omega + 1)\,(t - 2n)^{{{1 \mathord{\left/ {\vphantom {1 {2n^{2} }}} \right. \kern-0pt} {2n^{2} }}}} }}{{(t(t - 4n))^{{{1 \mathord{\left/ {\vphantom {1 {4n^{2} }}} \right. \kern-0pt} {4n^{2} }}}} }}} \right). $$
(32)

One can study the energy conditions using Eq. (32), which gives the Dominant Energy Condition \(({\text{DEC}})\)\(\rho + P \ge 0\), the Null Energy Condition \(({\text{NEC}})\)\(\rho - P \ge 0\), as well as the Strong Energy Condition \(({\text{SEN}})\) \(\rho + 3P \ge 0\).

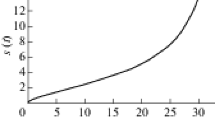
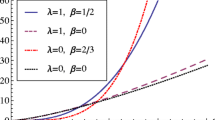
To study the physical quantities of our model, we take \(n = 0.5\). Now, as per the different values of the parameters \(Y\) and \(B\), we have different cosmological fluids. These are discussed in the subcases as follows. We use different values for the pair of parameters (\(Y,\,B\)) when \((Y,\,B) = (1,\,1)\), which represents the original GR. Figures 1, 2, 3 and 4 represent the behavior of the proper energy density \(\rho\) against cosmic time \(t\). Behavior patterns for the flat, open, and closed universes are similar (i.e., the curves are identical). All the discussed models have singularity at \(t = 0,{\text{and}}\,1\): The universe begins with the Big Bang at \(t = 0\) and ends with the Big Rip at \(t = 1\). The choice of the parameter values \(Y\,{\text{and}}\,B\) is important as it is determined to accept the model. Accordingly, we can accept the models \((Y = B = 1),\,(Y = 1,B = 0)\), \((Y = 1,B = - 1)\), \((Y = 0,B = 1)\) and \((Y = 0,B = - 1,k = 1)\) because they achieve the weak energy condition \((WEC)\,\,\rho \ge 0\). One can reject the models \((Y = - 1,\,\,B = 1)\), \((Y = - 1,B = 0)\), \((Y = - 1,B = - 1)\),\((Y = 0,B = 1,k = 1)\) and \((Y = 0,B = - 1,k = 1)\) for incompatibility with the \((WEC)\,\)

Fig. 1
figure 1

Dynamics of the proper energy density \(\rho\) against cosmic time \(t:0 \to 1\) for \((Y = 1,B = 0),\,\,(Y = 1,\,B = - 1)\), \((Y = B = 1)\) and \(k = 1,0, - 1\)

Full size image
Fig. 2
figure 2

Dynamics of the proper energy density \(\rho\) against cosmic time \(t:0 \to 1\) for \((Y = - 1,\,\,B = 0),\,\,(Y = - 1,B = - 1),\) \((Y = - 1,\,\,B = 1)\) and \(k = 1,\,0, - 1\)

Full size image
Fig. 3
figure 3

Dynamics of the proper energy density \(\rho\) against cosmic time \(t:0 \to 1\) for \((Y = 0,B = 1\,)\)

Full size image
Fig. 4
figure 4

Dynamics of the proper energy density \(\rho\) against cosmic time \(t:0 \to 1\) for \((Y = 0,\,B = - 1)\)

Full size image

In Fig. 5, we plot the dynamics of the pressure \(P\) against cosmic time \(t\) for the flat, open, and closed universe. The pressure diverges at the beginning and the end of the universe, but exhibits the same behaviors (i.e., the curves are identical) for spatially closed, flat, and open universes for the models \((Y = B = 1)\), \((Y = 1,B = - 1)\) and \((Y = 1,B = 0)\). In Fig. 6, we plot the dynamics of \({\text{DEC}}\) against cosmic time \(t\) for the flat, open, and closed universe. It is clear from the curve that \({\text{DEC}}\) is fulfilled only with the acceleration of the universe until it reaches the Big Rip. In Figs. 7 and 8, we plot the dynamics of \(({\text{NEC}})\) against cosmic time \(t\) for the models \((Y = B = 1),\,(Y = 1,\,B = - 1)\),\((Y = 1,\;B = 0)\). It is clear from the curve that \(({\text{NEC}})\) is fulfilled for these models.

Fig. 5
figure 5

Dynamics of the pressure \(P\) against cosmic time \(t:0 \to 1\) for \((Y = B = 1),\,\,(Y = 1,\,B = - 1),\)\((\,Y = 1,\,B = 0)\) and \(k = 1,0, - 1\)

Full size image
Fig. 6
figure 6

Dynamics of the \(({\text{DEC}})\) \(\rho + P\) against cosmic \(t:0 \to 1\) for \((Y = B = 1),\,(Y = 1,B = 0),\,(Y = 1,\,B = - 1),\) \((Y = 0,B = - 1)\,,(Y = 0,B = 1)\) and \(k = 1,0, - 1\)

Full size image
Fig. 7
figure 7

Dynamics of the \(({\text{NEC}})\) \(\rho - P\) against cosmic time \(t:0 \to 1\) for \((Y = 1,\,B = - 1),\,(Y = 1,\,B = 0)\), \((Y = B = 1)\) and \(k = 1,\,0, - 1\)

Full size image
Fig. 8
figure 8

Dynamics of the \(({\text{NEC}})\) \(\rho - P\) against cosmic time \(t:0 \to 1\) for \(\,\,(Y = 0,\,B = 1)\,\,,\,(\,Y = 0,\,B = - 1)\) and \(k = 1,\,0, - 1\)

Full size image

In Fig. 9, we plot the dynamics of \({\text{SEC}}\) against cosmic time \(t\) for the flat, open, and closed universe. In the models \((Y = B = 1),\,(Y = 1,\,B = 0),\,(Y = 1,\,B = - 1),\) \((Y = 0,\,B = 1),\,(Y = 0,\,B = - 1)\), \({\text{SEC}}\) is violated and the curves are identical. In Fig. 10, we plot the dynamics of the equation of the state parameter \(\omega\) against cosmic time \(t\) for the models \((Y = B = 1)\,\,{\text{and}}\,\,(Y = 1,B = - 1)\). The flat, open, and closed universe moves from the phase of radiation \(\omega = 1/3\) to the dust stage \(\omega = 0\), and then to the quintessence stage \(- 1/3 < \omega < - 1\), the vacuum energy stage \(\omega = - 1\), and ends with Phantom Universe \(\omega < - 1\) at the Big Rip \(t = 1\).

Fig. 9
figure 9

Dynamics of the \(({\text{SEC}})\) against cosmic time \(t:0 \to 1\) for \((Y = B = 1),\,(Y = 1,\,B = 0),\,(Y = 1,\,B = - 1),\) \((Y = 0,\,B = 1),\,(Y = 0,\,B = - 1)\) and \(k = 1,0, - 1\)

Full size image
Fig. 10
figure 10

Dynamics of the equation of state \(\omega\) against cosmic time \(t:0 \to 1\) for \((Y = B = 1),\,\,\,(Y = 1,\,B = - 1)\) and \(k = 1,\,0, - 1\)

Full size image

The cosmological models studied in this Section represent the Big Bang–Big Rip model under the values of the parameters \(n,\,Y,\,{\text{and}}\,B\). In the following Section, we will discuss models for the rebound of the universe after the Big Rip until it reaches the Big Crunch, without addressing the causes of the rebound that may affect quantum gravity; for more, see Ref. [29].

5 The Big Bang–Big Crunch model and energy conditions in \({\text{NGR}}\)

In this Section we look at the behavior of the universe after the Big Rip. We will study the physically acceptable models obtained in the previous Section. As previously mentioned, the Big Rip of the universe occurs when \(t = 2n = 1\), then the universe rebounds until it collapses on itself by what is called the Big Crunch when \(t = 4n = 2\). With the same previous steps used in the previous Section, the evolutionary behavior of both the proper energy density and pressure of the fluid can be studied using Eqs. (30–32). In Figs. 11, 12 and 13, we plot the dynamic evolution of the proper energy density with respect to cosmic time. Figures 11, 12 and 13 represent the evolution of the universe from the moment of the Big Bang to the Big Crunch (that is,\(t:0 \to 2\)). We note that the energy density is a positive value in the two phases, that is, it meets the \({\text{WEC}}\) for the models \((Y = B = 1),\,\,(Y = 1,\,B = 0),(Y = 1,\,B = - 1)\), \((Y = 0,\,B = 1)\) and \((Y = 0,\,B = - 1)\).We also note that the universe has a singularity at both the Big Bang \(t = 0\), Big Rip \(t = 1\), and Big Crunch \(t = 2\). In Fig. 14, we plot the dynamic evolution of the pressure of the fluid with respect to cosmic time. The pressure has a positive value and enters to a negative value at \(t:0 \to 1\) for the models \((Y = B = 1),\,\,(Y = 1,\,B = 0),(Y = 1,\,B = - 1)\), and its behavior is reversed in the second stage. In Fig. 15, we plot the dynamics of \(DEC\) against cosmic time \(t\). \({\text{DEC}}\) has a positive value and enters to a negative value at \(t:0 \to 1\) for the models \((Y = B = 1),\,\,(Y = 1,\,B = 0),(Y = 1,\,B = - 1)\),\((Y = 0,\,B = - 1),\) and \((Y = 0,\,B = 1)\) its behavior is reversed in the second stage at \(t:1 \to 2\) and the curves are identical. One can notice that the models \((Y = B = 1),\,\,(Y = 1,\,B = - 1)\) and \((Y = 1,B = 0)\) satisfy the \({\text{NEC}}\) in both the first and second stages of the evolution of the universe, as is clear in Fig. 16. In Fig. 17, we plot the dynamics of \(NEC\) against cosmic time \(t\). \({\text{NEC}}\) has a negative value and enters to a positive value at \(t:0 \to 1\) for the models \((Y = 0,\,B = - 1),(Y = 0,\,B = 1)\), and its behavior is reversed in the second stage. In Fig. 18, we plot the dynamic evolution of the \({\text{SEC}}\) with respect to cosmic time. \(SEC\) has a positive value and enters to a negative value at \(t:0 \to 1\) for the models \((Y = B = 1),\,\,(Y = 1,\,B = 0),(Y = 1,\,B = - 1)\), and its behavior is reversed in the second stage. In Fig. 19, we plot the dynamics of the equation of state \(\omega\) against cosmic time \(t\). The scenario of the evolution of the universe with the state parameter in relation to the models proposed in this paper sees that the universe passes through several stages from the moment of the Big Bang until it ends in the Big Crunch. In the first stage, the universe began with the radiation stage \(\omega = 1/3\), then moved to the dust stage \(\omega = 0\), and then proceeded to the quintessence stage \(- 1/3 < \omega < - 1\), the vacuum energy stage \(\omega = - 1\), and ends with Phantom Universe \(\omega < - 1\) at the Big Rip \(t = 1\). In the second stage, the expansion of the universe regresses in the opposite way, as it begins with a Phantom Universe phase and ends with a radiation phase.

Fig. 11
figure 11

Dynamics of the proper energy density \(\rho\) against cosmic time \(t:0 \to 2\) for \((Y = B = 1),\)\((Y = 1,\,B = 0),\,\,(Y = 1,\,B = - 1)\) and \(k = 1,\,0, - 1\)

Full size image
Fig. 12
figure 12

Dynamics of the proper energy density \(\rho\) against cosmic time \(t:0 \to 2\) for \((Y = 0,\,B = 1)\)

Full size image
Fig. 13
figure 13

Dynamics of the proper energy density \(\rho\) against cosmic time \(t:0 \to 2\) for \((Y = 0,\,B = - 1)\)

Full size image
Fig. 14
figure 14

Dynamics of the pressure \(P\) against cosmic time \(t:0 \to 2\) for \((Y = B = 1\,)\,,\,\,(\,Y = 1,\,B = - 1)\) and \((Y = 1,\,B = 0)\)

Full size image
Fig. 15
figure 15

Dynamics of the \(({\text{DEC}})\) \(\rho + P\) against cosmic time \(t:0 \to 2\) for \((Y = 1,\,B = - 1),\,(Y = 1,\,B = 0),(Y = B = 1),\) \((Y = 0,\,\,B = - 1\,)\,,\) \((Y = 0,\,\,B = 1\,)\,\) and \(k = 1,\,0, - 1\)

Full size image
Fig. 16
figure 16

Dynamics of the \(({\text{NEC}})\) \(\rho - P\) against cosmic time \(t:0 \to 2\) for \((Y = 1,\,B = - 1),\,(Y = 1,\,B = 0),(Y = B = 1)\) and \(k = 1,\,0, - 1\)

Full size image
Fig. 17
figure 17

Dynamics of the \(({\text{NEC}})\) \(\rho - P\) against cosmic \(t:0 \to 2\) for \((Y = 0,B = 1)\), \((Y = 0,B = - 1)\) and \(k = 1,\,0, - 1\)

Full size image
Fig. 18
figure 18

Dynamics of the \(({\text{SEC}})\) \(\rho + 3P\) against cosmic time \(t:0 \to 2\) for \((Y = B = 1\,),\,\,(\,Y = 1,\,B = - 1),\)\((Y = 1,\,B = 0)\) and \(k = 1,\,0, - 1\)

Full size image
Fig. 19
figure 19

Dynamics of the equation of state \(\omega\) against cosmic time \(t:0 \to 2\) for \((Y = B = 1\,),\,\,(\,Y = 1,\,B = - 1),\) \((Y = 1,\,B = 0)\) and \(k = 1,\,0, - 1\)

Full size image

The Friedmann Eq. (22) can be rewritten as follows:

$$ \dot{a}^{2} + \frac{Bk}{Y} - \frac{{a{}^{2}\rho }}{3Y} = \dot{a}^{2} + V_{{{\text{eff}}}} (a) = 0, $$
(33)

where \(V_{{{\text{eff}}}} (a)\) is the effective potential, and \(\dot{a}^{2}\) is the analog of kinetic energy.

The continuity (or conservation of energy–momentum) equation in \({\text{NGR}}\) is given by [9]:

$$ \dot{\rho } = - \,3\,H(\rho + P). $$
(34)

Substituting \(P = \omega \rho\) in Eq. (34), one gets:

$$ \dot{\rho } = - \,3\,H(1 + \omega )\rho , $$
(35)

Integrating this Equation, one obtains:

$$ a{}^{2}\rho = \,\,a{}^{ - (1 + 3\,\omega )}. $$
(36)

Therefore, the effective potential is given by:

$$ V_{{{\text{eff}}}} (a) = \frac{Bk}{Y} - \frac{1}{{3Ya{}^{(1 + 3\,\omega )}}}, $$
(37)

where \(a(t)\) is given by Eq. (29).

The Eq. (37) gives the relationship between the effective potential and cosmic time. Now let’s test some special cases. In Fig. 20, we plot the effective potential against cosmic time \(t\). We note that in cases of the flat, closed, and open models, when \(\omega = 1/3\), the effective potential for the \((Y = B = 1\,)\,\) model exhibits different behaviors, but the effective potential converges to the curvature constant at the very late times of the universe, strictly speaking, \(V_{{{\text{eff}}}} \to k\). But for the \((\,Y = 1,\,B = - 1)\) model, the effective potential converges to the inverse of the curvature constant at the very late times of the universe, strictly speaking, \(V_{{{\text{eff}}}} \to - k\) as shown in Fig. 21. In the \((\,Y = 1,\,B = - 1)\) model, the effective potential converges to the same value at the very late times of the universe, strictly speaking, \(V_{{{\text{eff}}}} \to 0\) as shown in Fig. 22. In Figs. 23, 24 and 25, we note that in cases of the flat, closed, and open models, when \(\omega = - 1/3\), the effective potential has a constant value in all the considered models in this paper. In Figs. 26, 27 and 28, we note that in cases of the flat, closed, and open models, when \(\omega = - 1\), the effective potential converges to the same value at the very late times of the universe for the model \((\,Y = 1,\,B = 1)\), strictly speaking, \(V_{{{\text{eff}}}} :k \to \infty\), while the effective potential for the model \(\,(\,Y = 1,\,B = - 1)\) changes as follows \(V_{{{\text{eff}}}} : - k \to \infty\).

Fig. 20
figure 20

Effective potentials against cosmic time \(t:0 \to 1\) when \(\omega = 1/3\) for \((Y = B = 1)\)

Full size image
Fig. 21
figure 21

Effective potentials against cosmic time \(t:0 \to 1\) when \(\omega = 1/3\) for \((Y = 1,\,B = - 1)\)

Full size image
Fig. 22
figure 22

Effective potentials against cosmic time \(t:0 \to 1\) \(\omega = 1/3\) for \((Y = 1,\,B = 0)\) and \(k = 1,\,0, - 1\)

Full size image
Fig. 23
figure 23

Effective potentials against cosmic time \(t:0 \to 1\) when \(\omega = - 1/3\) for \((Y = B = 1)\)

Full size image
Fig. 24
figure 24

Effective potentials against cosmic time \(t:0 \to 1\) when \(\omega = - 1/3\) for \((Y = 1,\,B = - 1)\)

Full size image
Fig. 25
figure 25

Effective potentials against cosmic time \(t:0 \to 1\) when \(\omega = - 1/3\) for \((Y = 1,\,B = 0)\) and \(k = 1,\,0, - 1\)

Full size image
Fig. 26
figure 26

Effective potentials against cosmic time \(t:0 \to 1\) when \(\omega = - 1\) for \((Y = B = 1)\)

Full size image
Fig. 27
figure 27

Effective potentials against cosmic time \(t:0 \to 1\) when \(\omega = - 1\) for \((Y = 1,\,\,B = - 1)\)

Full size image
Fig. 28
figure 28

Effective potentials against cosmic time \(t:0 \to 1\) when \(\omega = - 1\) for \((Y = 1,\,\,B = 0)\,\,\,\) and \(k = 1,\,0, - 1\)

Full size image

We will discuss the previous Figures in the discussion section.

6 Special solutions of the \({\text{NGR}}\) field equations

In this section, we test the field parameters on some special solutions. In the case of a flat universe, the field Eqs. (22–23) can be written as follows:

$$ \dot{H} + \frac{3}{2}(1 + \omega )\,H = 0, $$
(38)

Note that the previous equation does not depend on the field parameters.

Integrating Eq. (38), one gets:

$$ H = \frac{2}{3}(1 + \omega )^{ - 1} \,t^{ - 1} , $$
(39)

and

$$ a(t) = t^{2/3(1 + \omega )} . $$
(40)

In Table 2, we find the special solutions from Eq. (40)

Table 2 Special solutions of the field equations
Full size table

7 Conclusions

In this article, we have discussed the solution of the \({\text{NGR}}\) field equations in view of the absolute Parallelism geometry and studied the effect of the field parameters \(d_{1} ,\,d_{2} ,\,d{}_{3}\) on the proposed models. The exact solutions are analyzed for flat, open, and closed universes. The qualitative behavior of energy density \(\rho\) and pressure \(P\) is examined. Also, the energy conditions for these models have been discussed. We have also discussed the evolutionary behavior of the effective potential of the models proposed in this article. The observations for the various universes discussed above are as follows:

  • All the suggested models in this article have a singularity at \(t = 0,\,1,\,2\) for \(n = 1/2\). The choice of the parameter \(n\) is important as it determines the singularity.

  • Some of the suggested models are compatible with the positivity condition of energy density \(\rho \ge 0\) within the cosmic time interval of \(t \in [0,\,2]\), under the condition \(d_{2} \le 1/3\). We accept the flat, closed, and open universe in this article for the previous reason.

  • The field equations of \({\text{NGR}}\) are reduced to the original \({\text{GR}}\) at \(d_{1} = \,d_{2} , = d{}_{3} = 0\).

  • Model \(Y = 1,\,B = 1\) represents the original \(GR\) for the Big Bang–Big Rip model within the cosmic time interval of \(t \in [0,\,1]\), and the Big Rip–Big Crunch model within the cosmic time interval of \(t \in [1,\,2]\).

  • In the considered models, \({\text{WEC}}\) is satisfied, but \({\text{NEC}},\) \({\text{DEC}}\), and \({\text{SEC}}\) are violated of energy bounds. It is also interesting to mention here that the violation of these energy bounds ensures the existence of the instabilities, which is an interesting feature of modified gravity that supports the cosmic acceleration due to dark energy. In order to explain the late-time cosmic acceleration with \(\omega = - 1\), \({\text{DEC}}\,\,{\text{and}}\,\,{\text{SEC}}\) need to be violated since \(P = \omega \rho\). Such a violation of \({\text{DEC}}\,\,{\text{and}}\,\,{\text{SEC}}\) is confirmed from Table 2, and therefore ensures the cosmological viability of our models \((Y = B = 1)\), \((Y = 1,\,B = - 1)\) and \((Y = 1,\,\,B = 0).\)

  • The energy conditions are linear relationships consisting of energy density and pressure constructed from Raychaudhuri equation. They are important tools to understand the behavior of time-like or space-like curves and singularities [30]. The energy conditions applied to the proposed cosmological models are given in Table 3. Also, the ranges of the effective potential are given in Table 4.

  • It is clear from Table 4 that the effective potential for our cosmological models is affected by the values of the parameters of the field equations.

  • In the case \(\omega :1/3 \to - 1\) and \(Y = B = 1\), the effective potential ranges from \(\infty\) \(\to\) \(k\) \(\to\) \(\infty\) for all values of \(a\). In the case \(Y = 1,B = - 1\), the effective potential ranges from \(\infty\) \(\to\) \(- k\) \(\to\) \(\infty\) for all values of \(a\). Also, in the case \(Y = 1,B = 0\), the effective potential ranges from \(\infty\) \(\to\) \(0\) \(\to\) \(\infty\) for all values of \(a\). This means that the entire expansion history is considered in these models. The evolutionary behavior of the effective potential is affected by the value of parameter \(B\), whether it is positive or negative.

  • The Radiation, Dust, Dark energy, vacuum, and Phantom universe are obtained from the field equations without effect from the field parameters, see Table 2.

  • By comparing the special solutions in Table 2 with the previous solutions in Table 1, we find that they are identical.

  • Finally, we find that the cosmological models are affected by the value of the field parameters. The acceptable conditions for these parameters are: \(d_{1} \,\,{\text{and}}\,d_{3} \in R\), \(d_{2} \le 1/3\).

Table 3 Energy conditions for our cosmological models
Full size table
Table 4 Effective potential for our cosmological models
Full size table