1 Introduction

Due to its application in industry and technology, non-Newtonian liquid issues in fluid mechanics have captured the attention of many researchers. According to Bingham’s earlier rheological properties [1], fluids can be classified into Newtonian and non-Newtonian groups depending on shear stress. In past few years, engineers and scientists have become increasingly interested in physical issues involving Newtonian fluids [2,3,4,5,6]. Non-Newtonian fluids have physical features that differ from Newtonian fluids in that they display a nonlinear connection between shear stress and share rate. Furthermore, the viscosity of a non-Newtonian fluid does not kept constant with shear rate and is modified by a number of factors. Non-Newtonian fluids include emulsions, slurries, polymer melts, solutions and foams. Many scholars have explored non-Newtonian fluids in recent years due to their extensive applications in the cosmetic, nuclear reactors, pharmaceutical, cooling systems, and chemical fields, such as oils, chemicals, the production of paints, cleansers and syrups. Furthermore, heat transfer with non-Newtonian fluids is a broad topic that cannot be covered in its fullness in this study due to the wide variety of fluids of relevance. So, to fully understand non-Newtonian liquids and all of their uses, it is necessary to study their flow behavior in great detail. Therefore, engineers, physicists, and mathematicians confront a special challenge when it comes to non-Newtonian fluid mechanics. Non-Newtonian liquids are complicated, and no one constitutive equation can encompass all of their properties [7,8,9]. In a number of studies, non-Newtonian fluids have been addressed via a range of models [10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25]. In light of non-Newtonian fluid’s widespread use, various academics presented non-Newtonian models, such as power-law model [11], viscoelastic type [13,14,15], Brinkman model [12], Powell-Eyring type [16,17,18], Jeffrey model [19], Casson model [20,21,22] and Maxwell type [23,24,25].

One of the major models in the series of these non-Newtonian fluids is the Williamson fluid model, which was first presented by Williamson [26]. By discussing pseudoplastic materials and developing a fluid model for non-Newtonian fluids, he pioneered work that was later known by his name. Due of its vital uses, numerous scholars [27,28,29,30] have been employing this model to highlight the real behavior of fluids for the past few years. The Cattaneo-Christov heat transfer model is a modified version of the Fourier law that is used to compute the properties of a heat flux model while taking into consideration the relaxation time for heat flux dispersion across the physical model [31]. As a result, various academics [32, 33] have done more research on the most important properties of this model.

It is important to note that, based on a thorough analysis of the previously mentioned review of the literature, no in-depth investigation of a dissipative non-Newtonian Williamson fluid caused by a stretching sheet subjected to a magnetic field and variable properties with thermal radiation under the Cattaneo-Christov fluxes phenomenon condition has been carried out. Therefore, the exploration of the relationship between Cattaneo-Christov fluxes and variable fluid parameters in a magnetohydrodynamic radiative and reactive non-Newtonian Williamson fluid is the novel aspect of the current work. Additionally, the effects of slip velocity and the viscous dissipation phenomenon on the rates of heat mass transfer are explored. The suggested model’s governing equations are represented and made simplified employing the proper dimensionless transformations. The shooting technique is then used to solve the modeled equations. To further understand how the various governing factors affect velocity, temperature, and concentration, graphs are created for each of the parameters.

2 Physical model and mathematical formulation

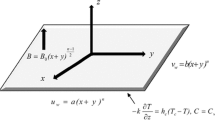
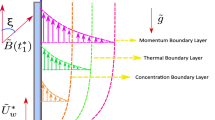
To design a flow model, we consider a two-dimensional non-Newtonian Williamson fluid flow with thermal radiation, a magnetic field, a chemical reaction, and the Cattaneo-Christov heat flux phenomena. This model was chosen because it accurately describes a significant number of non-Newtonian models, perhaps the plurality, over a broad range of shear rates. We use a Cartesian coordinate system in which u is assigned to the x-axis and v to the y-axis. The fluid flow is subsequently constrained by the elastic sheet stretching and an effective magnetic force with strength B that is assigned vertically, as shown in Fig. 1.

Fig. 1
figure 1

Problem description

Full size image

Moreover, the magnetic Reynolds number is thought to be exceedingly low in order to eliminate the magnetic field of induction. Assume that \(T, T_{\text {w}}, C\) and \(C_{\text {w}}\) to demonstrate the Williamson fluid temperature, fluid temperature on the sheet, fluid concentration and the fluid concentration on the sheet, respectively. Additionally, \(T_{\infty }, C_{\infty }\) determine the temperature of the unconstrained stream and the concentration of the ambient fluid particles, respectively. The present analysis also assumes chemical reactions between fluid particles and the phenomenon of viscous dissipation. On the other hand, the slip velocity phenomenon occurs on a rough elastic sheet that is subjected to thermal radiation with \(q_{\text {r}}\) radiative heat flux.

Herein, we posited that the fluid thermal conductivity \(\kappa\) and the diffusion coefficient D can be listed as follows [34, 35]:

$$\begin{aligned} \mu= \mu _{\infty }e^{-\alpha \theta }, \end{aligned}$$
(1)
$$\begin{aligned} \kappa= \kappa _{\infty }(1+\varepsilon _{1}\theta ), \end{aligned}$$
(2)
$$\begin{aligned} D= D_{\infty }(1+\varepsilon _{2} \phi ), \end{aligned}$$
(3)

where \(\alpha\) is the viscosity parameter, \(\mu _{\infty }\) is the ambient fluid viscosity, \(\kappa _{\infty }\) is the ambient fluid conductivity, \(\varepsilon _{2}\) is the variable diffusion parameter, \(D_{\infty }\) is the ambient fluid diffusivity and \(\varepsilon _{1}\) is the thermal conductivity parameter. Here, it is important to note that White and Majdalani [36] developed a formula for viscosity that is temperature-dependent. The empirical finding that the relationship between fluid viscosity and temperature is exponential forms the basis for this equation. Therefore, in our investigation of viscosity, we follow them. We picked a thermal conductivity that is linearly associated with temperature in order to follow Dandapat et al. [37] in this regard. In light of these assumptions, the simulated flow problem is demonstrated using the equations below [38]:

$$\begin{aligned}{} & {} \frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}=0, \end{aligned}$$
(4)
$$\begin{aligned}{} & {} u \frac{\partial u}{\partial x}+v \frac{\partial u}{\partial y}=\frac{1}{\rho _{\infty }}\frac{\partial }{\partial y} \left\{ \mu \frac{\partial u}{\partial y}+ \mu \frac{\Gamma }{\sqrt{2}}\left( \frac{\partial u}{\partial y}\right) ^{2}\right\} -\frac{\sigma \,B^{2}}{\rho _{\infty }}u, \end{aligned}$$
(5)
$$\begin{aligned}{} & {} \begin{aligned}&u \frac{\partial T}{\partial x}+v \frac{\partial T}{\partial y}+\gamma _{1}\Phi _{E}=\frac{1}{\rho _{\infty } c_{\text {p}}}\frac{\partial }{\partial y}\Big {(}\kappa \frac{\partial T}{\partial y}\Big {)}-\frac{1}{\rho _{\infty } c_{\text {p}}}\frac{\partial q_{\text {r}}}{\partial y} \\ {}&\quad +\frac{\mu }{\rho _{\infty } c_{\text {p}}}\left\{ \left( \frac{\partial u}{\partial y}\right) ^{2}+\frac{\Gamma }{\sqrt{2}}\left( \frac{\partial u}{\partial y}\right) ^{3}\right\} , \end{aligned} \end{aligned}$$
(6)
$$\begin{aligned}{} & {} \begin{aligned} u \frac{\partial C}{\partial x}+v \frac{\partial C}{\partial y}+\gamma _{2}\Phi _{C}=\frac{\partial }{\partial y}\Big {(}D\frac{\partial C}{\partial y}\Big {)}-k_{1}\left( C-C_{\infty }\right) , \end{aligned} \end{aligned}$$
(7)

where \(\Gamma , \rho _{\infty }, B, k_{1}, D, \gamma _{1}, \gamma _{2}, \sigma\) and \(c_{\text {p}}\) denote the Williamson time constant, the density away from the sheet, the magnetic field strength, the reaction rate, the diffusion coefficient, the amount of time it takes for the heat flow to cool down, the duration of time it takes for the mass flux to relax, the electrical conductivity and the specific heat at constant pressure. The followings are the supportive physical boundaries [30]:

$$\begin{aligned} u= & {} a x+\frac{\lambda _{1}}{\mu _{\infty }}\left( \mu \frac{\partial u}{\partial y}+\mu \frac{\Gamma }{\sqrt{2}}\left( \frac{\partial u}{\partial y}\right) ^{2}\right) , \quad v=0, \quad T\nonumber \\= & {} T_{\rm{w}}, \quad C=C_{\rm{w}} \quad \text{ at } \quad y=0, \end{aligned}$$
(8)
$$\begin{aligned} u\rightarrow & {} 0, \quad T \rightarrow T_{\infty }, \quad C \rightarrow C_{\infty }, \quad \text{ at } \quad y \rightarrow \infty , \end{aligned}$$
(9)

where [39]:

$$\begin{aligned} \Phi _{E}= & {} u^{2} \frac{\partial ^{2} T}{\partial x^{2}}+v^{2} \frac{\partial ^{2} T}{\partial y^{2}}+u \frac{\partial u}{\partial x} \frac{\partial T}{\partial x}+v \frac{\partial v}{\partial y} \frac{\partial T}{\partial y}+u \frac{\partial v}{\partial x} \frac{\partial T}{\partial y}\nonumber \\{} & {} +v \frac{\partial u}{\partial y} \frac{\partial T}{\partial x}+2 u v \frac{\partial ^{2} T}{\partial x \partial y}, \end{aligned}$$
(10)
$$\begin{aligned} \Phi _{C}= & {} u^{2} \frac{\partial ^{2} C}{\partial x^{2}}+v^{2} \frac{\partial ^{2} C}{\partial y^{2}}+u \frac{\partial u}{\partial x} \frac{\partial C}{\partial x}+v \frac{\partial v}{\partial y} \frac{\partial C}{\partial y}+u \frac{\partial v}{\partial x} \frac{\partial C}{\partial y}\nonumber \\{} & {} +v \frac{\partial u}{\partial y} \frac{\partial C}{\partial x}+2 u v \frac{\partial ^{2} C}{\partial x \partial y}. \end{aligned}$$
(11)

Now, we used the dimensionless quantities indicated below to achieve the non-dimensional form of the aforementioned governing equations [40]:

$$\begin{aligned}{} & {} u=a x f^{\prime }(\eta ), \quad v=-\sqrt{a \nu _{\infty }} f(\eta ), \quad \eta =y \sqrt{\frac{a}{\nu _{\infty }}}, \quad \theta (\eta )\nonumber \\{} & {} \quad =\frac{T-T_{\infty }}{T_{\rm{w}}-T_{\infty }}, \quad \phi (\eta )=\frac{C-C_{\infty }}{C_{\rm{w}}-C_{\infty }}, \end{aligned}$$
(12)

where f is the dimensionless stream function, \(\theta\) is the dimensionless temperature and \(\phi\) is the dimensionless concentration. When the final postulate is considered, equation (4) is proven, and the remaining equations along with the boundary conditions are converted to the following form:

$$\begin{aligned}{} & {} \left( \left( 1+W_{e} f^{\prime \prime } \right) f^{\prime \prime \prime }-\alpha \theta ^{\prime } f^{\prime \prime }\left( 1+ \frac{W_{e}}{2}f^{\prime \prime }\right) \right) e^{-\alpha \theta }\nonumber \\{} & {} \qquad -f'^{2}+ff''-M f'=0, \end{aligned}$$
(13)
$$\begin{aligned}{} & {} \frac{1}{\text {Pr}}\left( (1+R+\varepsilon _{1}\theta )\theta ''+\varepsilon _{1}\theta '^{2}\right) + f \theta ^{\prime }- D e_{1}\left( f f^{\prime } \theta ^{\prime }+f^{2} \theta ^{\prime \prime }\right) \nonumber \\{} & {} \qquad + Ec\left( f''^{2}+\frac{W_{e}}{2}f''^{3}\right) e^{-\alpha \theta }=0, \end{aligned}$$
(14)
$$\begin{aligned}{} & {} \frac{1}{\text {Sc}}\left( (1+\varepsilon _{2}\phi )\phi ''+\varepsilon _{2}\phi '^{2}\right) +f \phi ^{\prime }-D e_{2}\left( f f^{\prime } \phi ^{\prime }+f^{2} \phi ^{\prime \prime }\right) \nonumber \\{} & {} \qquad -K \phi =0. \end{aligned}$$
(15)
$$\begin{aligned}{} & {} f=0, \quad f^{\prime }=1+\lambda \left( f''+\frac{W_{e}}{2}f''^{2}\right) e^{-\alpha \theta }, \quad \theta =1, \quad \phi \nonumber \\{} & {} \quad =1 \quad \text{ at } \quad \eta =0, \end{aligned}$$
(16)
$$\begin{aligned}{} & {} f^{\prime }\rightarrow 0, \quad \theta \rightarrow 0, \quad \phi \rightarrow 0 \quad \text{ at } \quad \eta \rightarrow \infty , \end{aligned}$$
(17)

where \(W_{e}=\Gamma x\sqrt{\frac{2a^{3}}{\nu _{\infty }}}\), \(M=\frac{\sigma B^{2}}{a \rho _{\infty }}\), \(R=\frac{16 \sigma ^{*}T_{\infty }^{3}}{3k^{*}\kappa _{\infty }}\), \(\lambda =\lambda _{1}\sqrt{\frac{a}{\nu _{\infty }}}\), \(D e_{1}=\gamma _{1} a\), \(Ec=\frac{u_{\rm{w}}^{2}}{c_{\text {p}}(T_{\rm{w}}-T_{\infty })}\), \(D e_{2}=\gamma _{2} a\), \(K=\frac{k_{1}}{a}\) and \({\text {Pr}}=\frac{\mu _{\infty } c_{\text {p}}}{\kappa _{\infty }}\) are the local Weissenberg number, the magnetic number, the radiation parameter, the slip velocity parameter, the thermal Deborah number, the Eckert number, the Deborah number which related to the mass transfer field, the chemical reaction parameter and the Prandtl number. Here, it is important to note that the Eckert number (Ec) and the Williamson parameter (We) are both still dependent on the length scale (x), and are hence referred to as local parameters. Since these parameters are functions of x and undergo local changes during the flow activity, it is imperative to remember that the presented governing equations only apply to locally similar solutions [41]. As a result, we have provided accurate values for We and Ec for the current problem, which applies to the flow study for all values of y and for a specific value of x. Additionally, the local Nusselt number \({\text {Nu}}_{x}\), the local Sherwood number \({\text {Sh}}_{x}\), and the drag force coefficient in terms of \({\text {Cf}}_{x}\) are determined by:

$$\begin{aligned}{} & {} {\text {Cf}}_{x}{\text {Re}}^{\frac{1}{2}}=- \left( f''(0)+\frac{W_{e}}{2}f''^{2}(0)\right) e^{-\alpha \theta (0)},\quad \frac{{\text {Nu}}_{x}{\text {Re}}^{\frac{-1}{2}}}{1+R}\nonumber \\{} & {} \quad =-\theta '(0),\quad {\text {Sh}}_{x}{\text {Re}}^{\frac{-1}{2}}=-\phi '(0) \end{aligned}$$
(18)

where \({\text {Re}}=\frac{u_{\rm{w}} x}{\nu _{\infty }}\) is the local Reynolds number.

3 Validation of numerical scheme

In this study, a non-Newtonian Williamson model was presented, and we employed the shooting technique to obtain a numerical solution. The shooting methodology advantages from using quick and flexible methods for solving initial value problems. Furthermore, this approach greatly enhances numerical nonlinearity distribution and stability as compared to other approaches. Therefore, we evaluated the current findings to those of other research published in the literature [42]. A comparison is performed for the values of the skin-friction coefficient \({\text {Cf}}_{x}{\text {Re}}^{\frac{1}{2}}\) when \(M=\lambda =\alpha =0\). This comparison is made using a shooting technique for different Weissenberg numbers \(W_{e}=0.0, 0.1, 0.2\) and 0.3. The findings shown in Table 1 are found to be in good agreement. Additionally, the obtained data demonstrates that the proposed technique is both effective and dependable.

Table 1 Comparison of \({\text {Cf}}_{x}{\text {Re}}^{\frac{1}{2}}\) with the results of Nadeem et al. [42] when \(\lambda =\alpha =M=0\)
Full size table

4 Results and discussion

The simulation studies of a non-Newtonian Williamson fluid over a stretching surface are presented in this section. The momentum field considers the slip velocity phenomenon, the energy equation includes the viscous dissipation and thermal radiation effects, and the mass transport equation includes the chemical process. Via the shooting approach, the governing equations are numerically solved using supported dimensionless transformation. This section discusses the graphical effects of physical dimensionless amounts on complicated profiles. The impact of the magnetic number M on the Williamson flow velocity \(f'(\eta )\), temperature \(\theta (\eta )\), and concentration \(\phi (\eta )\) profiles is shown in Fig. 2. In the boundary layer region, the velocity profile as well as the thickness of the boundary layer shows a declining pattern with progressive M values. Physically, as the magnetic field grows, the force known as Lorentz encourages higher fluid resistance, which results in the fluid flow velocity being slowed down. Because the Lorentz force is created, the magnetic parameter has the opposite effect on both temperature and concentration profiles as observed from Fig. 2-b.

Fig. 2
figure 2

(a) \(f'(\eta )\) for picked M, (b) \(\theta (\eta )\) and \(\phi (\eta )\) for picked M

Full size image

The velocity, temperature, and concentration profiles for the viscosity parameter \(\alpha\) are shown in Fig. 3. It’s worth noting that \(\alpha\) has a greater impact on velocity profiles than on temperature or concentration profiles. Increases in the viscosity parameter \(\alpha\) result in decreases in the velocity profile \(f'(\eta )\) and associated boundary layer thickness, whereas the temperature \(\theta (\eta )\) and concentration \(\phi (\eta )\) fields show the opposite tendency. Physically, high Williamson viscosity causes the fluid to become more viscous and resist motion, which reduces the thickness of the boundary layer and the velocity profile.

Fig. 3
figure 3

(a) \(f'(\eta )\) for picked \(\alpha\), (b) \(\theta (\eta )\) and \(\phi (\eta )\) for picked \(\alpha\)

Full size image

Figure 4 shows the velocity, temperature, and concentration for the slip velocity parameter \(\lambda\). When the slip velocity parameter is increased, both the temperature \(\theta (\eta )\) and concentration \(\phi (\eta )\) profiles increase, and as a result, the thermal boundary layer thickness increases. With the same parameter, however, the reverse tendency is observed for both the velocity distribution \(f'(\eta )\) and the sheet velocity \(f'(0)\). Physically, the sheet roughness affects the slip velocity phenomenon. As a result, as the slip velocity parameter increases, the sheet roughness also increases, adding to the impedance to fluid motion.

Fig. 4
figure 4

(a) \(f'(\eta )\) for picked \(\lambda\) (b) \(\theta (\eta )\) and \(\phi (\eta )\) for picked \(\lambda\)

Full size image

The influence of the local Weissenberg number \(W_{e}\) on Williamson fluid velocity, Williamson fluid temperature, and Williamson fluid concentration is depicted in Fig. 5. The graph illustrates that raising the local Weissenberg number \(W_{e}\) causes temperature and concentration distribution to rise, whereas the same value of \(W_{e}\) causes fluid velocity to decrease.

Fig. 5
figure 5

(a) \(f'(\eta )\) for picked \(W_{e}\), (b) \(\theta (\eta )\) and \(\phi (\eta )\) for picked \(W_{e}\)

Full size image

The impact of the thermal conductivity parameter \(\varepsilon\) has been depicted in Fig. 6. The larger values of \(\varepsilon\) correspond to a broader temperature distribution \(\theta (\eta )\) and a marginal increase in the concentration field \(\phi (\eta )\), but an increase in the same parameter results in a little decrease in the velocity graphs \(f'(\eta )\).

Fig. 6
figure 6

(a) \(f'(\eta )\) and \(\phi (\eta )\) for picked \(\varepsilon\), (b) \(\theta (\eta )\) for picked \(\varepsilon\)

Full size image

The effect of the thermal Deborah number \(D e_{1}\) on velocity distribution, temperature distribution and concentration distribution is depicted in Fig. 7. The Deborah number is a rheological term that describes the fluidity of materials under specified flow circumstances. Low-relaxation-time materials flow freely and exhibit quick stress decay as a result. The fluid motion \(f'(\eta )\) scarcely improves with the bigger \(D e_{1}\) parameter, but the concentration profiles \(\phi (\eta )\) are slightly reduced. Furthermore, extended values of the thermal Deborah number \(D e_{1}\) reduce both the thickness of the thermal region and the profiles of temperature \(\theta (\eta )\). Physically, we can say that the system displays a nonconducting trait at increasing thermal Deborah numbers, which causes the heat distribution to become more constrained.

Fig. 7
figure 7

(a) \(f'(\eta )\) and \(\phi (\eta )\) for picked \(D e_{1}\), (b) \(\theta (\eta )\) for picked \(D e_{1}\)

Full size image

Figure 8 depicts the dimensionless velocity, dimensionless concentration, and thermal profiles for different Eckert number Ec estimates. It is evident that as the Eckert number is increased, the dimensionless velocities \(f'(\eta )\) diminish modestly while the dimensionless concentration \(\phi (\eta )\) stretches slightly. Furthermore, the increase in Eckert number Ec obviously improves both the temperature profile and the thickness of the thermal region. In terms of physics, we can state that the system exhibits a highly conducting property when the Eckert number is raised, resulting in a more distributed fluid temperature.

Fig. 8
figure 8

(a) \(f'(\eta )\) and \(\phi (\eta )\) for picked Ec, (b) \(\theta (\eta )\) for picked Ec

Full size image

Figure 9 shows the effect of the Deborah number \(D e_{2}\), which is related to mass transfer, and the chemical reaction parameter K on Williamson fluid concentration. Because both the concentration characteristics \(\phi (\eta )\) and the concentration boundary thickness of the Williamson fluid decrease when both the chemical reaction parameter and the Deborah number increase, the mass transfer rate increases as well.

Fig. 9
figure 9

(a) \(\phi (\eta )\) for picked \(D e_{2}\), (b) \(\phi (\eta )\) for picked K

Full size image

From an engineering standpoint, we now concentrate on the fluctuations of physical quantities of interest. For all regulating factors of our model, the local skin-friction \({\text {Cf}}_{x}({\text {Re}}_{x})^{\frac{1}{2}}\), the local Nusselt number \(\frac{{\text {Nu}}_{x}{\text {Re}}_{x}^{\frac{-1}{2}}}{1+R}\), and the local Sherwood number \({\text {Sh}}_{x}{\text {Re}}_{x}^{\frac{-1}{2}}\) are introduced in Table 2. The skin friction coefficient improves as the magnetic number increases, although the values of the local Nusselt number show the opposite tendency. Likewise, a higher magnetic field strength causes the values of the local Sherwood number to be reduced more. Skin friction coefficient values decrease when the viscosity parameter, slip velocity parameter, and local Weissenberg number increase, lowering both the local Nusselt number and the local Sherwood number. The skin friction coefficient and the local Nusselt number, respectively, grow and shrink uniformly with the thermal Deborah number and the Eckert number. Furthermore, increasing the chemical reaction parameter or the Deborah number increases the rate of mass transfer, while increasing the thermal conductivity parameter reduces it significantly.

Table 2 Values for  \({\text {Cf}}_{x}(Re_{x})^{\frac{1}{2}}\), \(\frac{{\text {Nu}}_{x}{\text {Re}}_{x}^{\frac{-1}{2}}}{1+R}\) and \({\text {Sh}}_{x}{\text {Re}}_{x}^{\frac{-1}{2}}\) for various values of M, \(\alpha\), \(\lambda\), \(\varepsilon\), \(W_{e}\), \(D e_{1}\), Ec, \(De_{2}\) and K with \({\text {Pr}}=3.0\), \({\text {Sc}}=0.7\), \(\varepsilon _{2}=0.2\) and \(R=0.5\)
Full size table

5 Conclusions

We investigated laminar steady MHD dissipative Williamson fluid flow subjected to Cattaneo-Christov heat mass fluxes. The existence of chemical reaction, slip velocity and thermal radiation influences the flow with varying conductivity and diffusivity. By hiring the shooting method, the numerical solutions for the suggested problem are evaluated. The following are the main findings of the current study. In light of the results, the viscosity and slip velocity parameters diminish the velocity profile, whereas an increase in the Deborah number results in a little increase in the velocity profile. Also, while the Deborah number and chemical parameter raise it, the Sherwood number falls as the Eckert number increases. Likewise, a concentration field expands for increasing slip and viscosity parameters, whereas it shrinks for increasing chemical reaction and Deborah number. On the other hand, both the viscous dissipation phenomena and the thermal conductivity parameter slow down the rate of heat transmission. Further, with the magnetic effect present, the skin friction coefficient is more significant. Finally, in future, we want to build on this investigation by examining how varying heat and mass flux alter the flow characteristics through porous media.