1 Introduction

The dual property played by PbO as a modifier and/or former in the glass networks makes it to have a high effect on the construction of the host network. The bonding types of Pb and O determine its role as a former or modifier in the host glass system network [1, 2]. At low concentration, PbO can act as a former with both PbO3 and PbO4 as structural units [1, 3,4,5]. Increasing its concentration collapses its character as a former accompanied by an increase in the modifier role. This dual property can adapt the physical properties of PbO to match a given technological requirements such as x-ray and γ ray absorbers [6]. Borate oxide (B2O3) is an excellent glass former and is composed of two structural units namely BO3 and BO4. The planner trigonal of BO3 can be linked together via bridging oxygen atoms to form micro-domains boroxol rings [7]. The other component, BO4, is considered as a minor building block. Furthermore, introduction of a suitable modifier in the structural network of B2O3 can transform BO3 to BO4 to produce bridging oxygen (BO) [8]. Moreover, BO4 could be changed into BO3 and associates oxygen dangling bond structural defect or non-bridging oxygen (NBO). The ratio (BO3/BO4), which depends on the annealing temperature and/or concentration of modifier oxide [9, 10], changes the physical properties of its host network. Chromium is a paramagnetic transition metal; when introduced in a network, it can affect the insulating strength of the host glass and could be used in cathode materials in rechargeable batteries [11, 12]. These unique properties of chromium take place due to its presence in the structural network with various oxidation states. These oxidation states are Cr3+ (which act as a modifier), Cr4+, Cr5+, and Cr6+ (which act as a former with \({\text{Cr}}_{4}^{2 - }\) as a building block) [13, 14]. The multivalence of chromium ions that can exist in the host network depends on the modifier–former ratio, mobility of the modifier, size of the ions, and their field strength.

The previous measurements of neutron diffraction [15] on GeO2 introduced in PbO have indicated that the structure of GeO2 consists of GeO4 and GeO6 together with GeO5 units. These structural properties of GeO2 make it exhibit high ionic conductivity and become a good candidate in solid electrolyte applications [16]. The former search [17] was proposed to clarify the effect of substitution of Cr2O3 with GeO2 on the structure using FTIR and variation in optical dispersion of 25B2O3–73.8PbO–xGeO2–(1.2–x)Cr2O3 glass system. Owing to the importance of applications of Cr2O3 in cathode materials [18] and GeO2 as a high conductivity oxide [19], the present work is intended to have a comprehensive and detailed study on the electrical conductivity mechanisms and dielectric characteristics in the composition 25B2O3–73.8PbO–xGeO2–(1.2-x)Cr2O3 glass system under a given frequency and temperature ranges. Calculations of ac conductivity of the investigated samples and comparing it with the current electrical conduction theories are presented. The theory of compensation law (Mayer–Neldel) is linked to the expression of relaxation time to analyze the dependence of the determined OLPT conduction mechanism. Furthermore, the dielectric parameters of Cole–Cole diagrams are also presented and discussed.

2 Experimental details

A samples of lead borate bulk glass of compositions 25B2O3–73.8PbO–xGeO2–(1.2 − x) Cr2O3 where x ≤ 1.2 mol. % as listed in Table 1 are fabricated by a melt quenching technique using rhodium crucibles at temperature 1173–1273 K for sufficient time to ensure a complete homogeneity of the melted mixture. To remove the thermal strains, the mixture was transferred onto stainless steel mold at around 623 K. More details about preparation conditions are found elsewhere [17]. In the present work, the dc conductivity (σdc) is measured using the two-probe method in sandwich configuration and in the temperature range 303–393 K. The output current is measured using A Keithley-610C electrometer. The reproducibility of the presented measurements for the investigated fresh samples was acceptable. On the other hand, in the case of ac conductivity (σac) an impedance analyzer model Schlumberger Solartron 1260 is used to measure the resistance Rac, dielectric permittivity components over a frequency range 0.1 kHz–5 MHz.

Table 1 Glass compositions in mole %, ratio \(GeO_{2} /\left[ {GeO_{2} + Cr_{2} O_{3} } \right]\), the values of thermal activation energy of dc conduction, ΔEdc, pre-exponential factor, σo, polaron hopping energy, WH0, polaron radius, rp, decay parameter, α, for investigated samples as a function of composition
Full size table

3 Results and discussion

The structural phase of as-prepared samples has been identified using an X-ray diffraction (XRD) computerized system (model: Philips EXPERT-MPDUG PW-3040 diffractometer with Cu Kα radiation source) in the 2θ range 10–90° as seen in Fig. 1. The broad hump in the range 12–42° is well constituted in this figure only in the short-range order (SRO) for all analyzed samples. The films investigated do not present mid-range order (MRO) pattern. The better flattening of this SRO crest and the lack of MRO details suggest that the intro of GeO2 in the amorphous state of lead borate at the expense of Cr2O3 may be compensated in the matrix void space, going to cause a static disorder change in the form of bond angle distributions and some bond correlated distances.

Fig. 1
figure 1

XRD pattern of 25B2O3–73.8PbO–xGeO2-(1.2 − x) Cr2O3 (0 ≤ x ≤ 1.2 mol. %)

Full size image

3.1 Electrical conduction

3.1.1 DC Conductivity

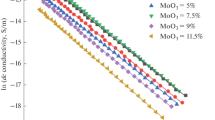
The variation of dc conductivity due to substituting of Cr2O3 with GeO2 in lead borate host network is measured in the temperature (T) range 303–393 K as shown in Fig. 2. In this figure and for each sample, there is one mechanism of conduction satisfying the thermally activated conductivity relation [20],

$$\sigma_{{{\text{dc}}}} = \sigma_{0} \exp \, \left( { - \frac{{\Delta E_{{{\text{dc}}}} }}{{K_{{\text{B}}} T}}} \right)$$
(1)

where σ0 is theS pre-exponential factor, KB is Boltzmann’s constant, T is temperature and ΔEdcis the thermal activation energy of conduction and is calculated from the slope of ln σdc = f (1/T) in Eq. 1. It should be noted that the conduction mechanism in the studied temperature range is argued to excitation of carriers from the extended states of the valence band to the extended states in the conduction band with an activation energy ΔEdc. Calculated values of electrical quantities for examined bulk samples are recorded in Table 1. Figure 3 displays that increasing GeO2 ions content from 0.0 to 0.6 mol % at the expense of Cr2O3 decreases the value of ΔEdc from 0.96 eV to 0.45 eV. Furthermore, when GeO2 > 0.6 mol %, the activation energy increases again from 0.45 to 0.91 eV with an anomalous composition at x = 0.6 mol % (GeO2/[GeO2 + Cr2O3] = 0.5). The same tendency is also seen for the calculated pre-exponential factor in a Table 1. This trend could be investigated and analyzed as follows: The ionic conductivity of oxides occurs when applying an electric field which moves the modifier ions between two energy positions which are separated by an energy barrier, ΔEdc, in the network. During its motion, the ions move through paths that are considered as a grouping of both bridging [BO] and non-bridging oxygen [NBO] atoms as illustrated in Fig. 4 [21]. Applying an electric field makes ions to move and do work by pushing oxygen atoms out word. In the previous work on the same compositions [17], the peaks which represents the intensity of [BO3] and [BO4] of the measured IR spectrum are deconvoluted for each sample to obtain the value of N4 (which represents the ratio of BO4 tetrahedral units to the total concentration of boron atoms [22, 23]) in the studied glass. The obtained values of N4 in the previous work [17] are added to Fig. 3 of the present work as a function of composition. Regarding Fig. 3 the decrease of activation energy, ΔEdc, against composition up to x = 0.6 mol % means increasing the number of formed bonds which reduces the density of structural defects and increases the compactness of the investigated samples. This leads to an increase in the number of bridging oxygens as confirmed by the trend of N4 in Fig. 3. Furthermore, when x > 0.6 mol % the valence of Cr2O3 ions transforms to lower values accompanied by an increase of the valence of GeO2 [24]. This increases the density of dissociated bonds and lead to the formation of dangling bonds or non-bridging Oxygen and to a decrease of the sample compactness and increasing value of ΔEdc shown in Fig. 4.

Fig. 2
figure 2

Dependence of the dc conductivity on the applied temperature for studied compositions. The numbers in the legend refer to the compositions of the samples as in Table 1

Full size image
Fig. 3
figure 3

Dependence of activation energy ∆Edc (solid circles) and density of bridging Oxygen (N4) (open circles) [17], on the ratio GeO2/[GeO2 + Cr2O3]

Full size image
Fig. 4
figure 4

Representative figure displays the role played by modifier ions in the ionic conductivity. The symbols in the diagram have the following meaning, BO = Bridging Oxygen, NBO = Non-bridging Oxygen, O = Oxygen, and B = Boron [21]

Full size image

3.1.2 AC electrical conductivity

The measured total conductivity σtot (ω, T) at a specific frequency ω and a temperature T can be written as:

$$\sigma_{{{\text{tot}}}} (\omega ,T) \, = \sigma_{{{\text{dc }} + }} \sigma_{{{\text{ac}}}} \left( \omega \right)$$
(2)

where σac (ω) is the frequency dependent conductivity. Measurements of alternating current conductivity (ac) are obtained for the investigated bulk samples in the frequency range 100 Hz–1.0 MHz using an oscillating voltage with 1.0 Vrms.

Figure 5 shows the frequency dependence of measured total conductivity in the temperatures range 303–393 K. It should be mentioned that for clearing up purposes, not all the noted temperature data are considered in the figure. Furthermore, Fig. 5 displays that for any composition and at any temperature the trend of the curve is mostly composed of two components. The first component lies in the low-frequency range where f ≤ 3.0 kHz where the total conductivity shows an independent on frequency and temperature dependent and represents the dc conductivity portion. This dc region is followed by another "crossover" region where the total conductivity shows an increase linearly against frequency when f ≥ 3 kHz.

Fig. 5
figure 5

Total conductivity dependence on frequency at different isotherms for all studied glass compositions

Full size image

The dependence of ac conductivity on frequency could be analyzed by considering a power law [24]:

$$\sigma_{{{\text{ac}}}} = A\omega^{{\text{s}}}$$
(3)

A is a pre-exponential factor, and s is a power exponent, \(s = \frac{{{\text{d}}\ln \sigma \left( \omega \right)}}{{{\text{d}}\ln \omega }}\). The value of s indicates the type of ac conduction mechanism in amorphous materials [24]. Several models [20, 25,26,27] based on hopping or tunneling electrons (polarons) have been developed to explain the frequency and temperature dependence of ac conductivity. In these models, it is usually expected that pair approximation holds, i.e., the dielectric loss occurs due to localization of moved carriers between pairs of sites. Regarding the quantum mechanical tunneling (QMT) model [25], the power exponent s might be calculated as \(s = 1 - 4/\ln (1/\omega \tau_{0} )\), that is, in the QMT models it does not depend on the temperature but is frequency dependent. In the non-overlapping small polaron tunneling (NSPT) [25], s can be evaluated using \(s = 1 - 4/\ln (1/\omega \tau_{0} ) - W_{{\text{H}}} /K_{{\text{B}}} T\), where WH is the polaron hopping energy. This means that s depends on temperature and applied frequency. On the other hand, the model which relates the relaxation variable WM with the separation of hopping sites R is the correlated barrier hopping (CBH) [26]. In this model, frequency exponent s could be determined by the following relation \(s = 1 - (6K_{{\text{B}}} T/[W_{{\text{M}}} + K_{{\text{B}}} T\ln (\omega \tau_{0} )]\), where s decreases with increasing temperature.

Alternatively, the mechanism for the polaron tunneling model proposed by Long [27] is called overlapping large polaron tunneling (OLPT). In this model, the ac conductivity can be evaluated by the following expression:

$$\sigma_{{{\text{ac}}}} \left( \omega \right) = \frac{{\pi^{4} }}{12}e^{2} \left( {K_{{\text{B}}} T} \right)^{2} \left[ {N\left( {E_{{\text{F}}} } \right)} \right]^{2} \frac{{\omega R_{{\upomega }}^{4} }}{{2\alpha K_{{\text{B}}} T + W_{{{\text{H}}0}} r_{{\text{p}}} /R_{{\upomega }}^{2} }}$$
(4)

In this model, the polaron wells of two sites are joined together and reduce the value of polaron hopping energy [28, 29],

$$W_{{\text{H}}} = W_{{{\text{H}}0}} \left( {1 - \frac{{r_{{\text{p}}} }}{R}} \right)$$
(5)
$$W_{{{\text{H}}0}} = \frac{{e^{2} }}{{4\varepsilon_{{\text{p}}} r_{{\text{p}}} }}$$
(6)

rp is the polaron radius and εp is the dielectric constant [27]. It is assumed again that \(W_{{{\text{H}}0}}\) is constant for all sites, where the separation \(R\) is a random variable. For the distance of tunneling at a frequency \(\omega\):

$$R_{{\upomega }} = \frac{1}{4\alpha }\left[ {\ln \left( {\frac{1}{{\omega \tau_{0} }}} \right) - \frac{{W_{{{\text{H}}0}} }}{{K_{{\text{B}}} T}}} \right] + \left\{ {\left[ {\ln \left( {\frac{1}{{\omega \tau_{0} }}} \right) - \frac{{W_{{{\text{H}}0}} }}{{K_{{\text{B}}} T}}} \right]^{2} + \frac{{8\alpha r_{{\text{p}}} W_{{{\text{H}}0}} }}{{K_{{\text{B}}} T}}} \right\}^{\frac{1}{2}}$$
(7)

where α is the decay parameter of the restricted electron wave function. Then, the frequency exponent s is estimated as:

$$s = 1 - \frac{{4 + 6\beta W_{H0} r_{p}^{\prime } /R_{\omega }^{\prime 2} }}{{R_{\omega }^{\prime } \left[ {1 + \left( {\beta W_{H0} r_{p}^{\prime } /R_{\omega }^{\prime 2} } \right)} \right]^{2} }}$$
(8)

where the reduced quantities \(R^{\prime}_{{\upomega }} = 2\alpha R_{{\upomega }}\), \(r^{\prime}_{{\text{p}}} = 2\alpha \, r_{{\text{p}}}\), and \(\beta = 1/K_{{\text{B}}} T\) are used. As shown in Eq. 8, in the OLPT model s shows both frequency and temperature dependence. The value of s decreases from unity against the increase in temperature. For high values of \(r^{\prime}_{{\text{p}}}\), s remains to decrease with increasing temperature. In the case of small values of \(r^{\prime}_{{\text{p}}}\), s displays a minimum at a given temperature and then increases with increasing temperature. Figure 6 shows the behavior of the function s = f(T) for QMT, NSPT, CBH, and OLPT models evaluated in studied temperature range together through the values of the parameters ω = 104 s−1, \(\tau_{0}\) = 10–12 s. For sake of comparison, the investigated experimental data of the present power exponent s are inserted in Fig. 6 for compositions 2, 5, and 6 mol % as an example (see Table 1). The comparison clarified that the OLPT is the greatest pronounced and probable conduction model for the considered samples in the considered temperature range. Values of the parameters WH0, rp, and 1/α obtained by fitting the frequency exponent s to OLPT models shown in Fig. 6 are listed in Table 1. In the literature, OLPT model as a conduction mechanism is observed for other compositions such as ZnS chalcogenide materials [30], semiconducting silver vanadate glasses [31], and NaZnPO4 [32].

Fig. 6
figure 6

Dependence of the frequency power exponent, s, as a function of temperature for the considered samples obtained from slopes of Fig. 5. Solid curves indicate the values of s evaluated using the models: QMT, NSPT, CBH. The dashed arc signifies the OLPT model (Eq. 8), which clarifies a reasonable good fit with the experimental results (symbols) of samples 2, 5, and 6 mol. % as an example. The symbols have the same meaning as in Fig. 2

Full size image

Another examination for the OLPT model comes from the temperature dependence of the measured σac. Figure 7 shows such plots in the studied frequency range for samples with compositions x = 0.0, 0.4, 0.8, and 1.2 mol. %. (The other studied compositions have the same trend.) Values of \(\tau_{0}\), ɛ and N(EF) used in the fitting process for the examined samples are presented in Table 2. It should be noted that values of dielectric constant, ɛ, used in the fitting process are taken from the Cole–Cole diagram, sec. 3.4 of the present work. In Fig. 7, it is detected that in the frequency range f > 0.1 kHz and T < 333 K the fitting (solid lines) seems to be suitable in the low-temperature range and departs from the experimental σac trend in the high-temperature region.

Fig. 7
figure 7

Dependence of the measured σac for the studied samples with x = 0.0, 0.4, 0.8, and 1.2 mol % on the temperature at different frequencies. The open circles denote experimental values of σac. The solid curves are the greatest fits to σac using OLPT model (Eq. 4) while the dashed curves are the best fitting using the MN rule (Eq. 12)

Full size image
Table 2 characteristic relaxation time, τ0, optical dielectric constant, ε∞, density of states at Fermi level, N(EF), characteristic temperatures, \(T_{0}^{ + }\), and normal pre-exponential factors, \(\sigma_{00}^{ + }\) for considered samples as a function of composition
Full size table

3.2 Enhancing OLPT model by MN rule

In thermal processes, Mayer–Neldel (MN) rule [33] identified that the ac electrical conductivity can be stated as:

$$\sigma = \sigma_{0} \exp \left( { - \frac{{\Delta E_{{{\text{ac}}}} }}{{K_{{\text{B}}} T}}} \right)$$
(9)

The pre-exponential factor σ0 is linked with the thermal activation energy of conduction ΔEac in the form:

$$\sigma_{0} = \sigma_{00} \exp \left( {\frac{{\Delta E_{{{\text{ac}}}} }}{{K_{{\text{B}}} T_{0} }}} \right)$$
(10)

where \(\sigma_{00}\) is a constant and T0 is a MN characteristic temperature. For the considered ac conductivity, the process for obtaining the MN graph is defined as follows: the parameters associated with the exponential factor σ0(ω) and the activation energy ΔEac are obtained from plots of the ac conductivity versus the temperature (see Fig. 7). The activation energy is evaluated from the slope of the straight regression line in the resulting plot. However, the factor, σ00 can be evaluated from the intercept of the regression line extrapolation at 1/T = 0 (see Fig. 8). In this figure, the symbols are experimental data while the solid lines are the best fit data with fitting parameter R2 ≈ 0.99. The data points shown in Fig. 8 follow the logarithmic form of Eq. 10:

$$\ln \sigma_{0} (\omega ) = \sigma_{00}^{ \pm } + \frac{{\Delta E_{{{\text{ac}}}} }}{{K_{{\text{B}}} T_{0}^{ \pm } }}$$
(11)
Fig. 8
figure 8

Normal Meyer–Neldel (MN) rule for bulk studied glass samples. The symbols correspond to the experimental data and the solid lines are least-squares straight line fits. The numbers between parentheses are the compositions of the studied samples see Table 1

Full size image

\(\sigma \, _{00}^{ \pm }\) and \(T_{0}^{ \pm }\) are constants. The superscript signs indicate the normal and inverted MN rule, respectively. Indeed, Fig. 8 indicates that the experimental data obey the normal MN rule. The values of \(\sigma_{00}^{ \pm }\) and \(T_{0}^{ \pm }\) for studied bulk samples are listed in Table 2.

The modified formula of σac(ω) of the OLPT model built on the MN rule could be given as:

$$\sigma_{{{\text{ac}}}} \left( \omega \right) = \frac{{\pi^{4} }}{12\zeta }e^{2} \left( {\frac{{K_{{\text{B}}} T}}{\zeta }} \right)^{2} \left[ {N\left( {E_{{\text{F}}} } \right)} \right]^{2} \frac{{\omega R_{\omega }^{4} }}{{2\alpha (K_{{\text{B}}} T/\zeta ) + W_{{{\text{H}}0}} r_{{\text{p}}} /R_{{\upomega }}^{2} }}$$
(12)

where \(\zeta = \frac{{T_{0}^{ + } - T}}{{T_{0}^{ + } }}\).

The tunneling distance at a frequency \(\omega\) is given by the following formula:

$$R_{\omega } = \frac{1}{4\alpha }\left[ {\ln \left( {\frac{1}{{\omega \tau_{0} }}} \right) - \frac{{W_{{{\text{H}}0}} }}{{K_{{\text{B}}} T/\zeta }}} \right] + \left\{ {\left[ {\ln \left( {\frac{1}{{\omega \tau_{0} }}} \right) - \frac{{W_{{{\text{H}}0}} }}{{K_{{\text{B}}} T/\zeta }}} \right]^{2} + \frac{{8\alpha r_{{\text{p}}} W_{{{\text{H}}0}} }}{{K_{{\text{B}}} T/\zeta }}} \right\}^{\frac{1}{2}}$$
(13)

The exponent s can then be evaluated in terms of MN rule as:

$$s = 1 - \frac{{4 + 6\beta^{\prime}W_{H0} r_{p}^{\prime } /R_{\omega }^{\prime 2} }}{{R_{\omega }^{\prime } \left[ {1 + \left( {{{\beta^{\prime}W_{H0} r_{p}^{\prime } } \mathord{\left/ {\vphantom {{\beta^{\prime}W_{H0} r_{p}^{\prime } } {R_{\omega }^{\prime 2} }}} \right. \kern-\nulldelimiterspace} {R_{\omega }^{\prime 2} }}} \right)} \right]^{2} }}$$
(14)

where \(\beta^{\prime} = \zeta /K_{{\text{B}}} T\)

It should be noted that Eqs. 12 and 14 differ from Eqs. 4 and 8 due to the presence of MN rule factor (ζ) in the previous equations. It is useful to see the effect of the ζ factor (i.e.\(T_{0}^{ + }\)) on the ac conductivity and the frequency exponent s. These have been evaluated numerically using the parameters characterizing samples. The trend of exponent s with temperature calculated using the MN rule (Eq. 14) is shown in Fig. 9. However, this figure illustrates that the trend of the exponent s calculated using the MN rule as evidenced by this rule fits in the higher temperature region and diverges with decreasing temperature.

Fig. 9
figure 9

Frequency exponent s for all presented compositions as a function of temperature. The hard curves are the best fit for (OLPT) model (Eq. 8) while the dashed lines trends are the fits of the data to the MN rule (Eq. 14). The symbols have the same meaning as in Fig. 2

Full size image

Additional fitting is achieved to the experimental data of σac as a function of temperature with the ac conductivity calculated using Eq. 12 and is shown also in Fig. 9. The figure shows the theoretical values of s calculated using Eq. 12 together with that evaluated by Eq. 14 (MN). Indeed, this figure indicates that in the low-temperature region (T < 350 K) OLPT model shows a good fit while in the high-temperature region (T > 350 K) MN rule (Eq. 12) gives a good fit, concerning OLPT, using values of \(T_{0}^{ + }\). The good fitting for T < 350 and after 350 with two different conduction mechanisms in Fig. 9 could be explained as follows: In the first region which lies in temperature range T < 350 K has a low activation energy. If the conduction process involves an activation energy which is small compared with the excitation energy, the conduction mechanism will obey tunnelling or hopping mechanism depending on the studied composition [34] (OLPT model in the present case). Furthermore, as the temperature of the system increases to higher temperatures (> 350 k in the present case), the activation energy becomes large compared to excitation energy; therefore, the system will produce infrared vibrations or photons [35] and the conduction mechanism transforms to thermal mechanism which obeys the MN mechanism.

3.3 Dielectric dispersion

In this section, the two components of the dielectric constant ε1 and dielectric loss ε2, parameters are calculated for investigated bulk samples in the considered ranges of temperature and frequency. Figure 10 shows the graphical relations of the calculated values of ε1, ε2 versus the applied frequency at different isotherms in the temperature range, 303–393 K. According to Debye model [36], the decrease in ε1 with increasing frequency could be attributed to the role played by polarizability and relaxation polarization. At higher values of frequency, the dipoles are not able to oscillate with the applied high frequency so that the oscillations begin to be behind those of the field and the orientation polarization stopped up. This behavior is accompanied by the appearance of loss peak as shown in ε2-lnω relation in Fig. 10. Furthermore, in the non-Debye model, the transition time τ0 is calculated by applying τ0 = 1/ωp to the obtained data in Fig. 10, as shown by τ0 shifting toward high frequency. The evaluated values of τ0 for studied samples are listed in Table 2. The decrease in ε2 with frequency is argued to the fact that at low frequencies, the high values of ε2 are due to the migration of ions in the material. At reasonable frequencies, the trend of ε2 is due to the influence of ion jump, conduction loss of ions migration, and ion polarization loss. At higher frequencies, ions vibrations may be considered as the only source of dielectric loss.

Fig. 10
figure 10

Frequency dependence of the real (ε1), imaginary (ε2) dielectric constants for the studied samples with compositions x = 0.0, 0.4, 0.8, and 1.2 mol.%

Full size image

Indeed, the dielectric constants of a solid depend on the applied frequency where this dependence is found to decrease from a static value εs at low frequency toward a smaller value of optical value ε∞ at higher frequencies. The difference between εs and ε∞ is ascribed to the dipole polarization [36]. In this case, the relation between εs, ε∞, and complex dielectric constant, ε*, is related as follows:

$$\varepsilon^{*} - \varepsilon_{\infty } = \frac{{\varepsilon_{s} - \varepsilon_{\infty } }}{{1 + \left( {i\omega \tau_{0} } \right)^{1 - \alpha } }}\quad 0 \, \le \, \alpha \, \le \, 1$$
(15)

where α is a characteristic of a specific material; in the current study, the value is a property of a particular material (α ~ 0.4–0.5), with the value α = 0 for Debye relaxation. The Cole–Cole equation's real and imaginary parts are:

$$\left. \begin{gathered} \varepsilon^{\prime} = \varepsilon_{\infty } + \left( {\varepsilon_{{\text{s}}} - \varepsilon_{\infty } } \right)\frac{{1 + \left( {\omega \tau_{0} } \right)^{1 - \alpha } \sin \left( {\frac{1}{2} \propto \pi } \right)}}{{1 + 2\left( {\omega \tau_{0} } \right)^{1 - \alpha } \sin \left( {\frac{1}{2} \propto \pi } \right)\left( {\omega \tau_{0} } \right)^{{2\left( {1 - \alpha } \right)}} }} \hfill \\ \varepsilon^{\prime\prime} = \left( {\varepsilon_{{\text{s}}} - \varepsilon_{\infty } } \right)\frac{{1 + \left( {\omega \tau_{0} } \right)^{1 - \alpha } \cos \left( {\frac{1}{2} \propto \pi } \right)}}{{1 + 2\left( {\omega \tau_{0} } \right)^{1 - \alpha } \sin \left( {\frac{1}{2} \propto \pi } \right)\left( {\omega \tau_{0} } \right)^{{2\left( {1 - \alpha } \right)}} }} \hfill \\ \end{gathered} \right\}$$
(16)

The dependence of ε2 on ε1 is obtained by applying the Cole–Cole model [37]. Figure 11 shows such dependence for the investigated samples in the studied temperature range. After extrapolating the fitted values to the real-axis (ε1- axis), the plot shows that at lower frequencies the experimental points near the dashed semicircles give different values of the static dielectric constant εs as listed in Table 2. At higher frequencies, all the data at different temperatures converge in one point that denotes a single value of optical dielectric constant, ε∞.

Fig. 11
figure 11

Cole–Cole plots for the considered compositions at x = 0.0, 0.2, 0.6, 1.0 and, 1.2 and at temperatures 303, 333, 363, and 393 K. The dashed curves are the fitting of Cole–Cole equations (Eq. 16) to the measured values of ε1 and ε2

Full size image

4 Conclusions

An inclusive study of electric and dielectric properties due to the addition of GeO2 at the expense of Cr2O3 in the lead borate host network in the temperature 303–393 K and frequency 100 Hz–1.0 MHz range permits us to draw the following conclusions:

The anomalous point observed at x = 0.6 mol % in the dependence of dc activation energy on composition is argued to the formation of bridging and non-bridging oxygen bonds formed due to the role played by Cr2O3 and GeO2 ions in the PbO–B2O3 network. The dominant dc conduction mechanism is due to the transition between extended states of valence and conduction bands. The graphical plot of measured σtotal against frequency is mostly composed of two regions. The former lies in the low-frequency range and shows independence on frequency and temperature dependence. This dc region is followed by another "crossover" region to high-frequency dispersion where σtotal increases linearly against ω. The evaluated values of the power exponent s of the ac conductivity formulation showed a decrease against the increase in temperature. The evaluated values of s for the investigated samples have been examined concerning current conduction models and showed that overlapping large polaron tunneling (OLPT) is the best probable conduction model for the investigated samples over the studied temperature and frequency ranges. The normal MN parameters (\(\sigma_{00}^{ + }\) and \(T_{0}^{ + }\)) are evaluated and used to fit the measured ac conductivities of the considered samples. A suitable fitting is noticed in the high-temperature region with a deviation in the low-temperature range. Arc form of the Cole–Cole diagram leads to one value of optical dielectric constant,\(\varepsilon_{\infty }\), and different values for the static dielectric constant \(\varepsilon_{{\text{s}}}\) throughout the temperature range, 303–393 K.