State-selective differential and total cross sections for single-electron capture in $He^{+}$–He collisions

Abstract

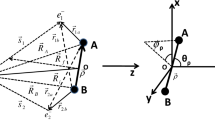
Theoretical investigations on state-selective total and angular differential cross sections for single-electron capture in collision of $He^{+}$ with ground state helium atom has been presented within the framework of four-body distorted-wave model in the energy range of 30–4000 keV. In this model, distortions in the initial channel related to the Coulomb continuum states of the target and the active electron in the field of residual projectile ion are included. Here, the electron in the projectile plays the role of screening of the projectile ion. In this formalism, the dielectronic interaction $\frac{1}{r_{12}}$ explicitly appears in the perturbation potential $V_{i}$ of the prior form of transition amplitude. Moreover, we include the interaction of the projectile with the passive electron in the target in both prior and post forms of the transition amplitude. The main purpose of the present study is to investigate the relative importance of this interaction to the state-selective total as well as projectile angular-differential cross sections with impact energies. The angular-differential cross sections (DCS) for ground-state transfer exhibit an oscillatory structure at intermediate energies. This oscillatory structure demonstrates the analogy of atomic de Broglie’s matter-wave scattering with Fraunhofer-type diffraction of light waves. The present theoretical results are compared with the available experimental data as well as few theoretical calculations. We find that our computed results, particularly in the prior form, indicate better agreement with the experimental data than that of the post form. Post-prior discrepancy of the total cross sections does not exceed 25% throughout the energy range considered.

Appendices

Appendices

Using the integral representation for the confluent hypergeometric function

$$\begin{aligned} {_{_{1}}}F_{_{1}}(i\alpha ;1;z)=\frac{1}{2\pi i}\oint d\tau \tau ^{i\alpha -1}(\tau -1)^{-i\alpha }\exp {(z\tau )}, \end{aligned}$$

(9)

the transition amplitude of Eq. (3) in the main text may be written as

$$\begin{aligned} \mathscr {T}_{if}^{\mp }= & {} \frac{N_{i}}{(2\pi i)^{2}}\oint _{\Gamma _{1}} dt_{1} t_{1}^{i\alpha _{1}-1}(t_{1}-1)^{-i\alpha _{1}}\nonumber \\&\oint _{\Gamma _{2}} dt_{2}t_{2}^{-i\alpha _{2}-1}(t_{2}-1)^{i\alpha _{2}} \mathscr {J}^{(\mp )}, \end{aligned}$$

(10)

where

$$\begin{aligned} \mathscr {J}^{(+)}=Z_{T}^{*}(Z_{P}\mathscr {I}_{R}-\mathscr {I}_{x_{1}}-\mathscr {I}_{x_{2}})+\mathscr {I}_{R}^{\prime } \end{aligned}$$

(11a)

and

$$\begin{aligned} \mathscr {J}^{(-)}=Z_{T}^{*}(\mathscr {I}_{R}-\mathscr {I}_{x_{1}})+(\mathscr {I}_{r_{12}}-\mathscr {I}_{s_{2}})+\mathscr {I}_{R}^{\prime }, \end{aligned}$$

(11b)

in which the form of $\mathscr {I}_{S}$($S=R, x_{1}, x_{2}, r_{12}, s_{2}$) reads

$$\begin{aligned} \mathscr {I}_{S}= & {} N_{b}\int \int \int d\vec {s}_{1}d\vec {s}_{2}d\vec {R}\exp {(i\vec {q}.\vec {R}+i\vec {v}.\vec {s}_{2}t_{1}-i\vec {k}_{i}.\vec {R}t_{2})}\nonumber \\&\frac{1}{S}\exp {(-\beta _{2}x_{2}-\lambda _{1}s_{1}-\lambda _{2}s_{2}-\epsilon R-\delta _{i}r_{12})}, \end{aligned}$$

(12)

where $\beta _{2}=\delta _{2}$, $\lambda _{1}=\gamma _{1}+Z_{P}$, $\lambda _{2}=\gamma _{2}-ivt_{1}$, $\epsilon =\epsilon _{i}-ik_{i}t_{2}$, $\epsilon _{i}, \delta _{i}\rightarrow 0$.

The value of $\epsilon _{i}=2\delta _{2}$ for the evaluation of $\mathscr {I}_{R}^{\prime }$. The $\delta _{2}$ ($\gamma _{1}$ and $\gamma _{2}$) are the orbital component of the initial (final) bound state wavefunctions. The constant $N_{b}$ originates from the initial ($\phi _{P}(\vec {s}_{1}$) and $\phi _{T}(\vec {x}_{2})$) and final ($\phi _{f}(\vec {s}_{1}, \vec {s}_{2})$) bound-state wavefunctions.

The integral over $\vec {S}$

$$\begin{aligned} \int d\vec {S} \exp {(-\sigma S - i\vec {q}.\vec {S})}=-4\pi \frac{\partial }{\partial \sigma }\left\{ \frac{1}{q^{2}+\sigma ^{2}}\right\} , \end{aligned}$$

(13)

applying the integral identity

$$\begin{aligned} \exp {(-\xi x_{i})}=-\frac{1}{2\pi ^{2}}\frac{\partial }{\partial \xi }\int d\vec {k}. \frac{e^{i\vec {k_{i}}.\vec {x}_{i}}}{(k^{2}+\xi ^{2})}, \end{aligned}$$

(14)

employing the expression

$$\begin{aligned} \frac{1}{S}=\frac{1}{2\pi ^{2}}\int d\vec {q} \frac{\exp {(i\vec {q}.\vec {S}})}{q^{2}} \end{aligned}$$

(15)

for $S=(\vec {x}_{1}, \vec {r}_{12})$, applying Feynman parameterization integral

$$\begin{aligned} \frac{1}{A^{n}B^{m}}=\frac{(n+m-1)!}{(n-1)!(m-1)!}\int _{0}^{1} dt \frac{t^{n-1}(1-t)^{m-1}}{[At+B(1-t)]^{n+m}}, \end{aligned}$$

(16)

and applying the integral representation of three denominator integral of Lewis [40], the Eq. (10) may be reduced as

$$\begin{aligned} \mathscr {T}_{if}^{(-)}= & {} 64\pi ^{3}\left[ Z_{T}\left\{ \frac{2}{\lambda _{1}^{3}}\frac{\partial ^{2}\mathscr {I}_{S}}{\partial \delta _{2} \partial \gamma _{2}}\bigg |_{\delta _{i}, \epsilon _{i}\rightarrow 0}-\frac{\partial ^{4}\mathscr {I}^{\prime }_{S}}{\partial \delta _{2}\partial \gamma _{1}\partial \gamma _{2}\partial \epsilon _{i}} \bigg |_{\delta _{i}, \epsilon _{i}\rightarrow 0}\right\} \right. \nonumber \\&\left. +\left\{ \frac{\partial ^{4}\mathscr {I}^{\prime }_{S}}{\partial \epsilon _{i}\partial \gamma _{1}\partial \gamma _{2}\partial \delta _{i}} \bigg |_{\delta _{i}, \epsilon _{i}\rightarrow 0}- \frac{2}{\lambda _{1}^{3}}\frac{\partial ^{2}\mathscr {I}_{S}}{\partial \delta _{2} \partial \epsilon _{i}}\bigg |_{\epsilon _{i}, \delta _{i}\rightarrow 0}\right\} \right] \end{aligned}$$

(17)

and

$$\begin{aligned} \mathscr {T}_{if}^{(+)}= & {} 64 Z_{T}\pi ^{3}\left[ \frac{2Z_{P}}{\lambda _{1}^{3}}\frac{\partial ^{2}\mathscr {I}_{S}}{\partial \delta _{2} \partial \gamma _{2}}\bigg |_{\epsilon _{i}, \delta _{i}\rightarrow 0} - \frac{\partial ^{4}\mathscr {I}^{\prime }_{S}}{\partial \delta _{2}\partial \gamma _{1}\partial \gamma _{2}\partial \epsilon _{i}}\bigg |_{\epsilon _{i}, \delta _{i}\rightarrow 0}\right. \nonumber \\&\left. -\frac{\partial ^{2}\mathscr {I}_{S}}{\partial \delta _{2} \partial \epsilon _{i}}\bigg |_{\epsilon , \delta _{i}\rightarrow 0}\right] . \end{aligned}$$

(18)

To evaluate the $V_{S}(R)$ i.e., $\mathscr {I}_{R}^{\prime }$ for both the prior and post forms, the operator may be written as

$$\begin{aligned}&\frac{128\pi ^{3}}{\lambda _{1}^{3}}\left[ -Z_{P}\frac{\partial ^{2}\mathscr {I}_{S}}{\partial \delta _{2}\partial \gamma _{2}}\bigg |_{\delta _{i},\epsilon _{i}\rightarrow 0}-\beta _{2}Z_{P}\frac{\partial ^{3}\mathscr {I}_{S}}{\partial \delta _{2}\partial \gamma _{2}\partial \epsilon _{i}}\bigg |_{\epsilon \ne 0, \delta _{i}\rightarrow 0}\right. \nonumber \\&\qquad \left. +Z_{P}\frac{\partial ^{2}\mathscr {I}_{S}}{\partial \delta _{2}\partial \gamma _{2}}\bigg |_{\epsilon _{i}\ne 0, \delta _{i}\rightarrow 0}\right] , \end{aligned}$$

(19)

where, $\mathscr {I}_{S}=\int _{0}^{\infty }k dy$, $\mathscr {I}_{S}^{\prime }=\int _{0}^{1}dt \int _{0}^{\infty }\frac{k}{\Delta } ds$,

and

$$\begin{aligned} \Delta ^{2}=\lambda _{1}^{2}(1-t), k=[\sigma _{0}+\sigma _{1}t_{1}+\sigma _{2}t_{2}+\sigma _{3}t_{1}t_{2}]^{-1}. \end{aligned}$$

Here $\sigma _{0}$, $\sigma _{1}$, $\sigma _{2}$ and $\sigma _{3}$ are functions of the momentum vectors, the orbital components of bound state, the velocity, the integration variables (t and s) and the projectile scattering angle. $\mathscr {I}_{S}$ in Eqs. (17)–(19) contain one-dimensional Lewis integral, wheras $\mathscr {I}_{S}^{\prime }$ in this equations contain two-dimensional integrals such as Lewis and Feynman integral. The Lewis integral with infinite upper limit and the Feynmen integral from 0 to 1 have been performed numerically by Gauss-Legendre quadrature method. It is mentioned that for the terms $\frac{1}{r_{12}}$ and $\frac{1}{x_{1}}$ in the perturbation potential, an additional one-dimensional integral over $t\epsilon (0,1)$ is needed.

Table 1 Positions of first dark and bright, and second dark and bright in the angular-differential cross sections along with the effective aperture radius $\rho$ calculated by the Fraunhofer diffraction (FD) theory and full width at half maximum (FWHM) at different impact energies

Fig. 1

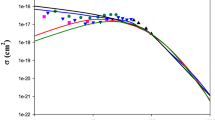
Ground state total cross sections as a function of laboratory incident energy E (keV) for the reaction $He^{+}+He(1s^{2})\rightarrow He(1s^{2})+He^{+}$. Theory: The full and dashed dark lines represent the results of present DW-4B method in prior and post forms using complete perturbation potential. The dashed blue lines represents the prior DW-4B without $V_{S}(R)$. The dotted green line represent the results of Gao et al. [31] using semi-classical atomic-orbital close-coupling method (SCAOCC); red dash-dotted line, CDW-4B results of Mancev [4]; violet dash-dotted line, dCTMC results of Guo et al. [33]. Experiments : filled triangle, results of Guo et al. [33], filled circle DuBois [42] and filled red square, results of de Castro Faria et al. [43]

Fig. 2

Cross sections for single-electron transfer to final state $He(1s2s {^{1}}{} \mathbf{S}$, $1s2p {^{1}}{} \mathbf{P}$ and $1s3s {^{1}}{} \mathbf{S} )$ as a function of the projectile energy. Theory: The full and dashed dark lines represent the prior and post results; dashed blue line, prior results without $V_{s}(R)$; dash-dotted violet line, results of Winter and Lin [36]; dotted red line, Hildenbrand et al. [37]; dotted green line SCAOCC results of Gao et al. [31]. Experiments: filled square, results of Okasaka et al. [34]; filled circle, results of Hippler et al. [35] and filled triangle, results of Muller and Heer et al. [44]

Fig. 3

Differential cross sections as a function of projectile scattering angle $\theta _{P}$ (radian) in the laboratory frame of reference for single electron transfer to the ground state in $He^{+}$–He collisions at 30, 100, 240, 600 and 2520 keV. Theory: The full and dashed curves represent the present result in prior form with and without $V_{S}(R)$; red dotted curve, SCAOCC results [31]; blue dotted curve, CDW-BIS results [25]. Experiments: filled dark circle, results of Sch$\ddot{o}$ffler et al. [25] and filled red circle, results of Guo et al. [33]

Fig. 4

Ground state transfer angular-differential cross sections weighted by $\sin {\theta _{p}}$ as a function of projectile scattering angle at impact energies 30, 100, 240, 600 and 2520 keV. Theory: The full and dashed curve represents the present prior results with and without $V_{S}(R)$ in the perturbation potential; green dotted curve, results of Gao et al. [31]. Experiments: filled dark circle, results of Sch$\ddot{o}$ffler et al. [25] and filled red circle, results of Guo et al. [33]