1 Introduction

The relationship between mean and variance has been extensively analyzed for various quantities, including crop yields, population size, and crime frequency [1,2,3,4,5]. Taylor formalized the relationship in his seminal paper [6], and his formula of \(\sigma \propto \mu ^\alpha\), where \(\sigma\) and \(\mu\) denote the standard deviation and mean of a given phenomenon, respectively, is known as Taylor’s law. Taylor’s law was initially applied in the field of ecology, including in Taylor’s original study of organisms within a particular area [7, 8]. However, owing to the explosive increase in available data and the rapid expansion of computational power, Taylor’s law has more recently been observed and analyzed for many kinds of social phenomena, including temporal fluctuations in population, temporal or regional fluctuations in crime reports, and the variation in sales of products in retail stores [3, 9, 10].

Taylor’s law describes the extent to which the variation of a quantity increases with the mean, which is governed by the scaling exponent \(\alpha\). If the quantity follows a Poisson distribution, the scaling exponent \(\alpha\) should be 0.5, since, in this case, the variance \(\sigma ^2\) should be equal to the mean \(\mu\). A scaling exponent greater than 0.5 suggests a larger increase in the variation of the quantity with its mean than would be expected for a quantity following a Poisson distribution, i.e., a quantity that is randomly determined.

For store management, understanding or predicting the nature of fluctuations in product sales through Taylor’s law can be helpful. For example, knowledge of such fluctuations can be used for stock optimization [10]. Fukunaga et al. empirically showed Taylor’s law in the sales of products in various product categories, suggesting a cross-over in the law in which there is a transition of the scaling exponent [11]. They report that Taylor’s law for product sales can have two asymptotic scaling exponents, \(\alpha = 0.5\) and 1, where the \(\alpha = 0.5\) exponent is applicable for a sufficiently small value of mean sales, and the \(\alpha = 1\) exponent is applicable for a sufficiently large value. Fukunaga et al. analyzed the sales of the 10 most frequently purchased products in various product categories using data from approximately 150 convenience stores in Kawasaki city, Japan, and describe the relationships they found between sales features and product categories. For example, they found that Taylor’s law for the sales of a weekly magazine exhibited specific features according to the day of the week, reflecting the fact that stores generally begin selling magazines on a specific day.

However, the effect of product brand, as opposed to product category, on Taylor’s law for product sales has not heretofore been closely examined. We would expect that the way of selling or purchasing products depends in large measure on the product brand and that such a relationship cannot be explained only by the category to which the brand belongs. There are several reasons for this: The sales of brands in the same category are likely to influence the sales of one another given the cannibalization effect; for example, the sales of a brand A product may be suppressed if a brand B product in the same category is discounted by the store, because many customers will purchase the brand B product in place of brand A. There are other brand-related factors that generate differences in the ways in which products are sold or purchased; for example, promotions featuring free samples [12, 13]. Stores may discount or conduct promotional campaigns more frequently for certain brands than for others, or other brands may engender customer loyalty to the extent that the customer’s purchase intention for the brand is rarely affected by a discount on the brands. Thus, a branded product can be significantly influenced by others in the same product category and substantially differ in the ways in which they are purchased or sold. The aim of this study was to determine the following: (1) whether Taylor’s law can be observed in the sales of various product brands, and (2) whether the nature of Taylor’s law for product sales depends not only on the product category but also on the product brand.

2 Method

2.1 Data

In conducting our study, we analyzed POS (Point-of-Sale) data provided by True Data Inc., which summarizes customer purchase behavior for 54 brands in eight categories of products sold in supermarkets in the Greater Tokyo Area from January 1, 2017, to June 30, 2020 (see Table 1).

POS data record information on product and store when an item is sold. These same data have previously been used for a variety of purposes, including an analysis of consumer preferences for genetically modified foods [14] and the prediction of future restaurant sales [15].

Table 1 Categories and brands belonging to each category
Full size table

2.2 Taylor’s Law for Product Sales

Taylor’s law is a scaling law connecting the mean (\(\mu\)) and standard deviation (\(\sigma\)) of a particular quantity

$$\begin{aligned} \sigma \propto \mu ^\alpha , \end{aligned}$$
(1)

where \(\alpha\) is a constant referred to as the scaling exponent. The equation can also be written as

$$\begin{aligned} \log \sigma = \alpha \log {\mu } + \beta , \end{aligned}$$
(2)

where \(\beta\) denotes a constant. If we plot the standard deviation against the mean of a quantity with a logarithmic scale on both the vertical and horizontal axes, we can observe a linear relationship with the slope \(\alpha\) when the examined quantity conforms to Taylor’s law.

As noted earlier, a previous study of Taylor’s law for product sales [11] found a cross-over in which a scaling exponent of 0.5 was observed when mean product sales were sufficiently small, and a scaling exponent of 1.0 was observed when mean product sales were sufficiently large. This previous study suggested several reasons for the emergence of such a cross-over. The authors of the study considered three random variables S, N, and X representing the total sales volume of a product, the number of consumers who would buy the product, and the number of units of the product that each consumer purchases, respectively. By assuming that the purchase behaviors of consumers are independent and identical, i.e., \(X_1,...,X_N\) are i.i.d., they derived the following equation for the standard deviation of the total sales volume S:

$$\begin{aligned} \sigma _S = \sqrt{\frac{\sigma _X^2}{\mu _X}\mu _S+\mathrm{CV}(N)^2\mu _S^2}, \end{aligned}$$
(3)

where \(\sigma _A\) and \(\mu _A\) denote the standard deviation and mean of random variable A, respectively, and \(\mathrm{CV}(A)\) denotes the coefficient of variation \(\sigma _A/\mu _A\). For \(\mu _S \gg 1\), the equation can be written as

$$\begin{aligned} \sigma _S \approx \mathrm{CV}(N)\cdot \mu _S, \end{aligned}$$
(4)

i.e., Taylor’s law with scaling exponent 1, whereas for \(\mu _S \approx 0\), we have

$$\begin{aligned} \sigma _S \approx \sqrt{\frac{\sigma _X^2}{\mu _X}}\mu _S^{0.5}, \end{aligned}$$
(5)

which is Taylor's law with scaling exponent 0.5. We can determine the cross-over point \(\mu _C\) as the intersection of Eqs. (4) and (5), that is, as

$$\begin{aligned} \mu _C = \frac{\sigma _X^2}{\mu _X}\mathrm{CV}(N)^{-2}. \end{aligned}$$
(6)

We examined whether we could observe Taylor’s law and its cross-over for sales for each of the various brands in the POS data. To do so, we first calculated the standard deviation of the total sales volume S in each store and for all stores combined. The value of S was calculated for each day’s sales in a week and for weekly sales. Thus, a \(\sigma _S\) and \(\mu _S\) pair was derived (i) for each day of the week and in each store, (ii) weekly in each store, (iii) for each day of the week and in all stores, and (iv) weekly and in all stores. We then plotted these \(\sigma _S\) and \(\mu _S\) pairs to examine Taylor’s law with a cross-over for product sales.

In addition, we evaluated the features of Taylor’s law and its cross-over for each brand’s sales based on the coefficients of \(\mu _S\) and \(\mu _S^2\) in Eq. (3). We determined these coefficients \(C_1 = \sigma _X^2/\mu _X\) and \(C_2=\mathrm{CV}(N)\) by fitting the data of \(\sigma _{S_i}\) and \(\mu _{S_i}\) for the sales of the focal brand to Eq. (3). More precisely, we estimated \(C_1\) and \(C_2\) using ordinary least squares, minimizing the error function

$$\begin{aligned} E = \sum _i \left( \log \sigma _{S_i} - \log \sqrt{C_1\mu _{S_i} + C_2 \mu _{S_i}^2 }\right) ^2, \end{aligned}$$
(7)

where \(S_i\) denotes the total sales S calculated from the data, and took the logarithm of both \(\sigma _{S_i}\) and \(\sqrt{C_1\mu _{S_i} + C_2 \mu _{S_i}^2}\) according to Eq. (3). Estimation of \(C_1\) and \(C_2\) was conducted numerically using the Levenberg–Marquardt method, where we restricted \(C_1\) and \(C_2\) to positive values; their initial values were both set in the range 0–3. We also derived the cross-over point \(\mu _C\) [Eq. (6)] using the estimated values of \(C_1\) and \(C_2\). Note that we cannot directly calculate X or N from POS data, because the data do not tell us about customers who did not purchase a certain item, i.e., \(X=0\), cannot be seen, and we cannot know the actual distribution of X or N based on the data. Therefore, neither \(C_1=\sigma _X^2/\mu _X\) nor \(\mathrm{CV}(N)\) can be directly calculated from the data. In contrast, the estimated values of \(C_1\) and \(C_2\) can be regarded as providing information on the unobservable random variables X and N, which represent the number of items that an individual would purchase and the number of customers that a store would have, respectively.

3 Results

Fig. 1
figure 1

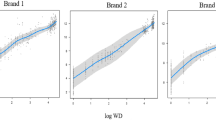
Scatter plot of \(\sigma _S\) versus \(\mu _S\) for brand “Coca Cola” belonging to category Cola. Both vertical and horizontal axes are logarithmically scaled. The meaning of each marker is shown in the legend. The solid curve is the theoretical curve (Eq. (3)) with the estimated coefficients \(C_1=\sigma _X^2/\mu _X=4.091\) and \(C_2=\mathrm{CV}(N)=0.328\). The vertical dashed line represents the cross-over point \(\mu _C\) derived from \(C_1\) and \(C_2\)

Full size image
Fig. 2
figure 2

Same as Fig. 1 but for brand “UCC” belonging to category Coffee. The estimated coefficients were \(C_1=\sigma _X^2/\mu _X=4.651\) and \(C_2=\mathrm{CV}(N)=0.732\)

Full size image

For many of the brands analyzed, we observed Taylor’s law and its cross-over in the relationship between the standard deviation \(\sigma _S\) and mean \(\mu _S\) of total product sales S. We show examples of plots of \(\sigma _S\) against \(\mu _S\) for brands “Coca Cola” in category Cola (Fig. 1), “UCC” in Coffee (Fig. 2), and “Top” and “New Beads” in Laundry Detergent (Figs. 3, 4), where both the horizontal and vertical axes are logarithmically scaled. In each figure, the theoretical curve given by Eq. (3) with the numerically estimated coefficients \(C_1\) and \(C_2\) is shown as a solid line. Additionally, the cross-over point \(\mu _C\) is indicated by a dashed line. If Eq. (3) exactly holds between \(\sigma _S\) and \(\mu _S\), then, as the theoretical curve suggests, we may observe that \(\sigma _S\) increases almost linearly with \(\mu _S\) with slope 0.5 (slope 1) when \(\mu _S\) is sufficiently smaller (larger) than \(\mu _C\). Such a linear relationship with different slopes is continuously altered from one to the other around \(\mu _C\) when both the horizontal and vertical axes are logarithmically scaled. Figures 1, 2, and 3 exhibit linearities between \(\sigma _S\) and \(\mu _S\) similar to the linearity in the theoretical curve. In each of these figures, we plotted \(\sigma _S\) and \(\mu _S\) for various items of the same brand; for example, in the figure for “Coca Cola” (Fig. 1), we plotted these values for Coca Cola 1.5 L, Coca Cola Zero 300 mL, Coca Cola Orange Vanilla 500 mL, etc. Interestingly, the linearities showing Taylor’s law with a cross-over appear to be generally determined by the brand, regardless of the difference in items of the same brand. Some deviations of the plots from the theoretical curve can be mainly attributed to the differences in stores where the brand’s products are sold, such as differences in their location, or in the way in which total product sales S is calculated. Note that we calculated S both weekly and for each day of the week and showed the resulting \(\sigma _S\) and \(\mu _S\) in a single figure.

Fig. 3
figure 3

Same as Fig. 1 but for brand “Top” belonging to category Laundry Detergent. The estimated coefficients were \(C_1=\sigma _X^2/\mu _X=0.996\) and \(C_2=\mathrm{CV}(N)=1.511\)

Full size image
Fig. 4
figure 4

Same as Fig. 1 but for brand “New Beads” belonging to Laundry Detergent. The estimated coefficients were \(C_1=\sigma _X^2/\mu _X=0.479\) and \(C_2=\mathrm{CV}(N)=2.084\)

Full size image

Some brands exhibited specific features in their Taylor’s law with cross-over. Figure 4 for the brand “New Beads” in the Laundry Detergent category demonstrates a version of Taylor’s law in which the cross-over is not uniquely determined; that is, several linear relationships between \(\sigma _S\) and \(\mu _S\) appear to co-exist for the range of \(\mu _S\) around 1–10. A possible reason for such an unclear cross-over is the difference in the location of the stores or the day of the week on which we focused in the calculation of S. For example, if an item of a particular brand is discounted in a store every weekend, then the behavior of consumers in the store on weekdays would be expected to differ from that on weekends. In such a situation, the total sales S of a brand would behave as if it is composed of the S from several brands possessing different features, which is presumably reflected in the unclear cross-over in Fig. 4. As another example, the plots in Fig. 3 for brand “Top” in category Laundry Detergent show two separate clusters. One cluster is within the range of \(\mu _S\) from \(10^{-2}\) to \(10^0\), which is smaller than \(\mu _C\), whereas the other is around \(\mu _S=10^1\), which is greater than \(\mu _C\). This suggests that the increase in \(\sigma _S\), i.e., the fluctuation of S with \(\mu _S\), in the latter cluster is more significant than that in the former cluster. We could expect that the difference in the ways of selling and purchasing on weekdays and weekends may also generate such clusters.

Fig. 5
figure 5

Scatter plot of coefficients \(\mathrm{CV}(N)\) and \(\sigma _X^2/\mu _X\). The vertical and horizontal axes are both logarithmically scaled. The meaning of each marker is shown in the legend

Full size image

Figure 5 shows the estimated values of the coefficients \(C_1=\sigma _X^2/\mu _X\) and \(C_2=\mathrm{CV}(N)\) of respectively \(\mu _S\) and \(\mu _S^2\) [Eq. (3)] for all the brands analyzed. The coefficients of brands belonging to the same category are plotted relatively close to each other. Because N denotes the number of customers in a store on a day or in a week, the estimated value of \(\mathrm{CV}(N)\) obtained by comparing the data to the theoretical curve represents the degree of fluctuation in the number of consumers that each store is supposed to have. By contrast, the estimated value of \(\sigma _X^2/\mu _X\) represents the extent to which the number of items purchased by a customer fluctuates; if X simply follows a Poisson distribution, this value is equal to 1. All brands of Japanese Tea exhibited high values of \(\sigma _X^2/\mu _X\), each well above 1. The value of \(\mathrm{CV}(N)\) of brands belonging to the Laundry Detergent category was higher than those of brands belonging to other categories. In the Instant Noodles category, the values of \(\mathrm{CV}(N)\) of all brands were relatively high. Thus, from the estimated values of \(\mathrm{CV}(N)\) and \(\sigma _X^2/\mu _X\), we can infer that the number of customers purchasing brands in the Laundry Detergent and Instant Noodles categories in each store tends to fluctuate significantly, whereas the fluctuation in the number of purchased items per customer largely varies in the category of Japanese Tea. In the Coffee category, the \(\sigma _X^2/\mu _X\) values of all brands are similar, whereas those of \(\mathrm{CV}(N)\) are relatively dispersed, indicating that the degree of fluctuation in the number of customers significantly depends on the brand. Regarding the difference in brands, “New Beads” exhibited an interesting feature: the \(\mathrm{CV}(N)\) value of the “New Beads” brand is the highest, while its \(\sigma _X^2/\mu _X\) value is the lowest among brands in the Laundry Detergent category, indicating a large fluctuation in the number of customers and a suppressed fluctuation in the number of items per consumer for the brand.

Fig. 6
figure 6

Each vertical line segment shows the range of \(\mu _S\) for each brand, \([\mu _S^{\mathrm{{low}}}, \mu _S^{\mathrm{{high}}}]\), where \(\mu _S^{\mathrm{{high}}}\) and \(\mu _S^{\mathrm{{low}}}\) denote the maximum and minimum values of \(\mu _S\), respectively. Quantiles and the mean of \(\mu _S\) and cross-over point \(\mu _C\) for each brand are shown by a square, circle, and cross, respectively. Different colors represent different categories, as also shown at the top of the figure

Full size image
Fig. 7
figure 7

Normalized \(\mu _C\) of each brand. Different colors represent different categories, as also shown at the top of the figure

Full size image

To capture the overall dispersion of the plots of \(\sigma _S\) and \(\mu _S\) in the range of \(\mu _S\) greater or less than the cross-over point \(\mu _C\), we summarize the distributions of \(\mu _S\) for all brands in Fig. 6 and the relative values of \(\mu _C\) against these distributions, called normalized \(\mu _C\), in Fig. 7. Here, the normalized \(\mu _C\) was calculated as

$$\begin{aligned} \text {Normalized }\mu _C = \displaystyle \frac{\mu _C - \mu _S^{\mathrm{{low}}}}{{\mu _S^{\mathrm{{high}}}} - \mu _S^{\mathrm{{low}}}}, \end{aligned}$$

where \(\mu _S^{\mathrm{{high}}}\) (\(\mu _S^{\mathrm{{low}}}\)) is the highest (lowest) value of \(\mu _S\). Therefore, if the normalized \(\mu _C\) is greater than 0.5, the region where \(\mu _S\) is less than \(\mu _C\) is larger than the other region. The former region was called the Poisson area in a previous study [11], since \(\sigma _S\propto \mu _S^{0.5}\) asymptotically holds in this region for the theoretical curve, whereas the latter region is called the non-Poisson area, corresponding to \(\sigma _S\propto \mu _S\). Figure 6 suggests a dependence of the distribution of \(\mu _S\) and the value of \(\mu _C\) on product category. The values of \(\mu _S\) of brands in the Japanese Tea (Laundry Detergent) category are, overall, distributed over a greater (smaller) range than those in the other categories. It also seems that \(\mu _C\) of brands in the same category have similar values, particularly for the categories of Japanese Tea, Beer, Liquor, Cola, Coffee, and Carbonated Flavor. In Fig. 7, the normalized \(\mu _C\) of brands in these categories, excluding Japanese Tea, tend to be greater than those of the other categories. Although we can observe tendencies in the distribution of \(\mu _S\) and the value of \(\mu _C\) according to category, these values also vary among brands in the same category. For example, “Asahi Off”, “Mets Cola”, “Wonda”, “Sprite”, and “Real Gold” have significantly higher \(\mu _C\) compared to other brands in their respective categories, indicating wide Poisson areas in their plots of \(\sigma _S\) against \(\mu _S\). Thus, each brand is expected to possess features that cannot be explained solely by its category.

Fig. 8
figure 8

Coefficient of determination R of each brand. Different colors represent different categories, as also shown at the top of the figure

Full size image

We evaluated the deviation of the plots of \(\sigma _S\) and \(\mu _S\) from the theoretical curve for all brands using the coefficient of determination R: \(R = 1 -{\sum _i\left( {y_i}-\hat{y_i}\right) ^2}/{\sum _i\left( {y_i}-\bar{y_i}\right) ^2}\), where \(y_i=\log \sigma _{S_i}\), and \(\bar{y_i}\) and \(\hat{y_i}\) denote the mean of \(y_i\) and estimated value of \(y_i\) obtained from Eq. (3), respectively. For most brands, the value of R exceeded 0.9, suggesting that the dispersion of the plots against the theoretical curve is not large (Fig. 8). However, the cross-overs of Taylor’s law can still be unclear, even though R takes a large value exceeding 0.9. We also observed a dependence of R on the categories. The values of R of brands belonging to the Beer and Liquor categories were consistently high, whereas those of Japanese Tea, Instant Noodles, and Coffee were relatively low. Thus, as confirmed by the plots of \(\sigma _S\) versus \(\mu _S\) shown in the Supplementary Information for each of the brands, Taylor’s law of product sales can be observed relatively clearly for many of the Beer and Liquor brands.

4 Discussion

We examined whether Taylor’s law of product sales can be observed for brands by analyzing POS data from 72 Japanese supermarkets. Our empirical analyses showed that product sales for many brands follow Taylor’s law with cross-over, as suggested in a previous study [11] on product sales in convenience stores. We also evaluated differences in the features of Taylor’s law for brands and categories, which were not precisely examined in the previous study, based on various statistics related to Taylor’s law and its cross-over, including the estimated values of \(\sigma _X^2/\mu _X\) and \(\mathrm{CV}(N)\) obtained by fitting our data to the theoretical curve, the coefficient of determination R regarding the fitting, the distribution of \(\mu _S\), and the relative value of the cross-over point \(\mu _C\) to the distribution of \(\mu _S\). Our analysis showed that some characteristics of Taylor’s law could be attributed to the method of selling and purchasing for each brand or category. For most categories, brands belonging to the same category exhibited similar values in their statistics. However, we also confirmed meaningful variations in the statistics for brands in the same category, which may be generated by features that are specific to each brand, such as the price and labels of the brand.

Our results suggest that, for some brands, the assumption that each consumer purchases a certain item completely randomly, e.g., so that the number of items per consumer X follows a Poisson distribution, is not suitable for practical data. We estimated \(\sigma _X^2/\mu _X\) by fitting the data of the standard deviation and mean of the total sales volume to the theoretical curve. However, the previous study analyzed Taylor’s law for product sales under the assumption that \(\sigma _X^2/\mu _X=1\). This was based on the general and feasible postulations that the count X of purchased items of a single customer in a given time unit follows a Poisson distribution or that the parameter of such a Poisson distribution follows a gamma distribution [11, 16,17,18]. We did not assume \(\sigma _X^2/\mu _X=1\); rather, we estimated \(\sigma _X^2/\mu _X\) to find that, for many of the brands in the categories of Japanese Tea and Instant Noodles, the value was significantly greater than 1, indicating that the fluctuation of X is greater than would be expected if a customer purchases an item completely randomly, i.e., where X follows a Poisson distribution. Note that we could not directly calculate \(\sigma _X^2/\mu _X\) from the POS data, since such data are recorded only when a purchase is actually made, that is, the data do not provide purchase information for consumers who did not purchase a certain product, even though they had the potential to do so, i.e., \(X_i=0\).

The cases in which \(\sigma _X^2/\mu _X\) exceeds 1 may be attributable to changes in the selling price. For example, the \(\sigma _X^2 / \mu _X\) of brands belonging to the Japanese Tea category was significantly greater than 1. Nearly all small-sized Japanese Tea products are popular, inexpensive, and frequently discounted. The price effect, i.e., a large fluctuation in the number of purchased items per customer, X, might explain the large \(\sigma _X^2 / \mu _X\) that we found. That is, the lower the price of a product, the more a consumer will purchase the product, which can generate a large value of X, sometimes leading to a large \(\sigma _X\), as well. In addition, the difference in days of the week or in the locations of stores can also contribute to an increased variation in X; large sales may be seen in specific stores or on specific days, such as weekends.

Some brands exhibited specific features in their Taylor’s law as compared to other brands in the same category. For example, “Mets Cola” and “Real Gold” had a significantly higher value of normalized \(\mu _C\), i.e., a wider range of Poisson area, than other brands in their respective categories. “Mets Cola” and “Real Gold” have very specific characteristics. The former is labeled as Food for Specified Health Uses (Tokuho in Japanese), whereas the latter is an energy drink, and both of them tend to be more expensive than the other brands in their categories. One possible reason for their large Poisson areas could be that consumers rarely purchase these products in bulk and not many consumers purchase them at all. Such features could be expected to lead to small values for mean total sales \(\mu _S\), with the restriction of the value of \(\sigma _S\) growing rapidly with \(\mu _S\) for such a small \(\mu _S\). “New Beads” in the Laundry Detergent category also has a specific feature. Its \(\sigma _X^2/\mu _X\) and \(\mathrm{CV}(N)\) values are the highest and lowest, respectively, in its category, indicating a small fluctuation in the number of items purchased by individual consumers and a large fluctuation in the number of consumers who are likely to purchase the product. Consumers who buy “New Beads” may be sensitive to price, as the brand is generally inexpensive. Thus, \(\mathrm{CV}(N)\) becomes large seemingly, because many consumers purchase it on a specific day, which may be when it is discounted.

In future work, we plan to develop a clearer picture of Taylor’s law with cross-over for the sales of individual brands by plotting \(\sigma _S\) against \(\mu _S\) only for total sales on a particular day, e.g., Sunday, or only for stores located in a particular region. This was not possible in the present study because of the limited size of the dataset. In addition, we plan to investigate more precisely the dependence of Taylor’s law on product categories by collecting sales data for a wider variety of brands and categories.