Sublinear Computational Time Modeling by Momentum-Space Renormalization Group Theory in Statistical Machine Learning Procedures

Abstract

We review sublinear computational time modeling using momentum-space renormalization group approaches in the statistical machine learning algorithms. The modeling scheme has been proposed and the basic frameworks have been briefly explained in a short note (Tanaka et al. in J. Phys. Soc. Jpn, 87(8), Article ID: 085001, 2018). We present their detailed formulations and some numerical experimental results of sublinear computational time modeling based on the momentum-space renormalization scheme.

1 Introduction

Probabilistic graphical models have useful applications in statistical machine learning theory, and many authors are investigating their applications in artificial intelligent computational systems [1, 2]. Realizations of statistical machine learning systems with probabilistic graphical models entail massive computational time. For avoiding such problems, some statistical–mechanical techniques have been introduced, for example, advanced mean-field methods including belief propagations [3,4,5,6,7,8]. However, it is very difficult to reduce the computational time to the sublinear time for each system size in such advanced mean-field methods although they can achieve the linear computational time modeling. Recent research in data sciences has helped understand the necessity to treat high-dimensional state vectors, and it is necessary to achieve novel sublinear computational time modeling schemes in probabilistic graphical models. Sublinear computational time modeling is used to reduce the computational time for solving the given problem to the order of sublinear time with respect to the system size.

The renormalization group (RG) theory [9,10,11,12,13] is one of important theories in statistical mechanics. The RG theory was introduced to investigate a universality class of phase transitions in probabilistic graphical models by considering spatially coarse-graining procedures. The RG scheme can be divided to two kinds: real-space renormalization group (RSRG) schemes and momentum-space renormalization group (MSRG) schemes. MSRG schemes are implemented in the spectrum space of the Fourier transformations in the probabilistic graphical model and have produced many successful results in combination with perturbation techniques.

Recently, the present authors have proposed applications of RG techniques to achieve sublinear computational time modeling schemes in the statistical machine learning theory. In physics, it is well known that the RG scheme is typically used to capture critical phenomena characterized by certain diverging statistical quantities, particularly, the correlation length. It might seem that the achievements of the sublinear time computational time modeling in the statistical machine learning theory are far from the standard physical applications of the RG schemes, because the statistical models for data sciences have finite sizes and no critical phenomena are expected. However, it has become necessary to treat many high-dimensional state vectors in recent data sciences and it is important to achieve to reduce the computational time in the statistical models containing such high-dimensional state vectors. The present authors have considered introducing RG techniques to systematically reduce the system size in the statistical model while applying the statistical machine learning schemes, systematically. One way to accomplish them is to apply the RSRG scheme to probabilistic image segmentations, in which a Potts model is employed as a prior probability [14]. The other one is to introduce the momentum-space renormalization scheme to probabilistic noise reductions, in which a Gaussian graphical model is introduced as a prior probability [15]. The most important aspect of the statistical machine learning algorithms is how the computational time of the estimation of hyperparameters from data vectors should be reduced. One of familiar and practical estimation schemes involving hyperparameters is the expectation-maximization (EM) algorithm [16, 17]. However, the EM algorithm needs some commutations of statistical quantities in the massive probabilistic graphical model. Two of the works by the present authors applied the RG approaches to estimate the hyperparameters by means of the EM algorithm.

The present paper is not an original paper but a review paper of the sublinear computational time modeling using the MSRG approaches in the EM algorithm for statistical machine learning system based on the Gaussian graphical models which has been published as a short note paper [15] and their background formulations. In the present paper, we provide their detailed formulations and some numerical experimental results of the sublinear computational time modeling based on the momentum-space renormalization scheme. Their essential part of the sublinear computational time modeling scheme has been proposed and the most important numerical experimental results have been shown as the above short note paper. In Sect. 2, we present the sublinear computational time modeling of statistical machine learning systems for probabilistic noise reductions by introducing the momentum-space renormalization schemes. Section 3 shows practical schemes of the sublinear computational time EM algorithm. In Sect. 4, statistical performance analysis of the hyperparameter estimations using the sublinear computational time EM algorithm is given. In Sect. 5, we mention some concluding remarks.

2 Momentum-Space Renormalization Group Scheme of Gaussian Graphical Model

In this section, we review fundamental formulations of momentum-space renormalization group approaches in Gaussian graphical models. Gaussian graphical models are sometimes referred also to as Gaussian–Markov random fields [4, 18,19,20,21,22,23,24], and are familiar probabilistic graphical models for Bayesian noise reduction systems with the EM algorithm. In noise reductions of image processing in particular, the graphical structures are usually square grid graphs and then unitary matrices based on discrete Fourier transformations are useful. Although scale transformations in the MSRG approaches are achieved through the wave-number space in the discrete Fourier transformations, we mention that they differ from low-pass filters in conventional signal processing.

Now we consider images on the square grid graph with the periodic boundary conditions for the abscissa and the ordinate. In the position vector for each pixel of the present square grid graph, the abscissa and the ordinate are denoted by x and y, respectively, such that the position vector of the pixel is denoted by (x, y). The periodic boundary conditions for the abscissa and ordinate mean that $x=M$ and $y=N$ are interpreted as $x=0$ and $y=0$, respectively. We introduce the set of all the pixels by a notation $V(M,N)={\{(x,y) |x=0,1,{\ldots },M-1; y=0,1,{\ldots },N-1 \}}$. We remark that V(M, N) can be regarded as an ordered set by considering the two-dimensional position vector (x, y) as

$$\begin{aligned} {\varvec{r}}_{i} \equiv \left( (i-1){\mathrm{mod}}(M), \left\lfloor {\frac{i-1}{M}}\right\rfloor \right) \qquad (i=1,2,3,{\ldots },MN), \end{aligned}$$

(1)

where the notation ${\lfloor }a{\rfloor }$ is the floor function defined by ${\lfloor }a{\rfloor }{\equiv }a-a\,{\mathrm{mod}}\,1$.

We define the state variables $f_{x,y}$ and $g_{x,y}$ ($(x,y){\in }V(M,N)$) of a light intensity at each pixel (x, y), in the original images and the degraded images. The state variable $f_{x,y}$ and $g_{x,y}$ take any real values in the interval $(-{\infty },+{\infty })$. The state vector ${\varvec{f}}$ and ${\varvec{g}}$ are defined by ${\varvec{f}} \equiv {(f_{x,y}|(x,y){\in }V(M,N))}$ and ${\varvec{g}} \equiv { (g_{x,y}|(x,y){\in }V(M,N))}$, respectively.

We consider a prior probability density function ${\rho }^{(M,N)}{({\varvec{f}} |{\alpha },{\gamma })}$ defined by

$$\begin{aligned} {\rho }^{(M,N)}{\left( {\varvec{f}}\big |{\alpha },{\gamma }\right) }\equiv & {} {\frac{1}{Z_{M,N}({\alpha },{\gamma })}} {\exp }\left( -{\frac{1}{2}}{\alpha }{\sum _{\{x,y\}{\in }V(M,N)}} {\left( {\left( f_{x,y}-f_{x+1,y}\right) }^{2} +{\left( f_{x,y}-f_{x,y+1}\right) }^{2}\right) } \right. \nonumber \\&\left. -{\frac{1}{2}}{\gamma }{\sum _{(x,y){\in }V(M,N)}}{f_{x,y}}^{2} \right) , \end{aligned}$$

(2)

for original images ${\varvec{f}}$. Here $Z_{M,N}({\alpha },{\gamma })$ is a normalization constant of ${\rho }^{(M,N)}({\varvec{f}}|{\alpha },{\gamma })$, which is defined by

$$\begin{aligned} Z_{M,N}({\alpha },{\gamma })\equiv &\, {} {\left( {\prod _{(x,y){\in }V(M,N)}} {\int _{-{\infty }}^{+{\infty }}} dz_{x,y}\right) } \nonumber \\&{\times }\, {\exp }\left( -{\frac{1}{2}}{\alpha }{\sum _{\{x,y\}{\in }V(M,N)}} {\left( {\left( z_{x,y}-z_{x+1,y}\right) }^{2} +{\left( z_{x,y}-z_{x,y+1}\right) }^{2} \right) }\right. \nonumber \\&\left. -\,{\frac{1}{2}}{\gamma }{\sum _{(x,y){\in }V(M,N)}}{z_{x,y}}^{2} \right) . \end{aligned}$$

(3)

Degraded images ${\varvec{g}}$ are generated from a given original image ${\varvec{f}}$ according to the following conditional probability density function:

$$\begin{aligned}&{\rho }^{(M,N)}({\varvec{g}}|{\varvec{f}},{\beta }) = {\sqrt{ {\left( {\frac{{\beta }}{2{\pi }}}\right) }^{|MN|} }} {\exp }\left( -{\frac{1}{2}}{\beta } {\sum _{(x,y){\in }V(M,N)}} {\left( g_{x,y}-f_{x,y} \right) }^{2} \right) . \end{aligned}$$

(4)

Here, we remark that ${\alpha }$ and ${\beta }$ are referred to as hyperparameters in the statistical machine learning theory. ${\alpha }$ is an interaction between the nearest neighbour pairs of pixels. Equation (4) means that the additive white Gaussian noise is assumed as a degradation process, and ${\beta }$ corresponds to the inverse of the variance of the additive White Gaussian noise.

The prior probability density function ${\rho }^{(M,N)}({\varvec{f}}|{{\widehat{\alpha }}},{{\widehat{\gamma }}})$ in Eq. (2) can be rewritten as

$$\begin{aligned} {\rho }^{(M,N)}({\varvec{f}}|{\alpha },{\gamma })= & {} {\sqrt{ {\frac{ {\det { {\left( {\gamma }{\varvec{I}}(M,N)+{\alpha }{\mathrm{C}}(M,N)\right) }}} }{ (2{\pi })^{MN} }} }} {\exp }{\left( {\frac{1}{2}} {\varvec{f}}^{\mathrm{{T}}} {\left( {\gamma }{\varvec{I}}(M,N)+{\alpha }{\varvec{C}}(M,N)\right) } {\varvec{f}} \right) }. \end{aligned}$$

(5)

Here ${\varvec{C}}(M,N)$ and ${\varvec{I}}(M,N)$ denote an $MN\,{\times }\,MN$ matrix whose $(x,y|x',y')$-components ${\langle }x,y\big |{\varvec{C}}(M,N)\big |x',y'{\rangle }$ and ${\langle }x,y\big |{\varvec{I}}(M,N)\big |x',y'{\rangle }$ ($(x,y){\in }V(M,N)$, $(x',y'){\in }V(M,N)$) are defined by the following two-dimensional representations as

$$\begin{aligned} {\langle }x,y\big |{\varvec{C}}(M,N)\big |x',y'{\rangle }\equiv & \,{} 4{\delta }_{x',x}{\delta }_{y',y} -{\delta }_{x',x-1}{\delta }_{y',y} -{\delta }_{x',x+1}{\delta }_{y',y} -{\delta }_{x',x}{\delta }_{y',y-1} -{\delta }_{x',x}{\delta }_{y',y+1} \nonumber \\&(x,x'=0,1,{\ldots },M-1;y,y'=0,1,{\ldots },N-1), \end{aligned}$$

(6)

and

$$\begin{aligned} {\langle }x,y\big |{\varvec{I}}(M,N)\big |x',y'{\rangle }\equiv & {} \,{\delta }_{x',x}{\delta }_{y',y} \,(x,x'=0,1,{\ldots },M-1;y,y'=0,1,{\ldots },N-1), \end{aligned}$$

(7)

respectively. Here, we remark that ${\langle }x,y |{\varvec{C}}(M,N) |x',y'{\rangle }$ refers to the $(i,i')$-elements $({\varvec{C}}(M,N))_{i,i'}$ of the matrix ${\varvec{C}}(M,N)$ for the relationships ${\varvec{r}}_{i}=(x,y)$ and ${\varvec{r}}_{i'}=(x',y')$ by Eq. (1). Moreover, ${\langle }x,y|{\varvec{I}}(M,N) |x',y'{\rangle }$ denotes the $(i,i')$-elements $({\varvec{I}}(M,N))_{i,i'}$ of matrix ${\varvec{I}}(M,N)$ in similar arguments. Hereafter, we use similar representations for the elements of the other matrix.

We introduce an $MN\,{\times }\,MN$ unitary matrix ${\varvec{U}}(M,N)$ and its conjugate matrix ${\varvec{U}}^{\dag }(M,N)$ as follows:

$$\begin{aligned} {\langle }x,y\big |{\varvec{U}}(M,N)\big |k,l{\rangle }\equiv & {} {\frac{1}{{\sqrt{MN}}}} {\exp }\left( -i{\frac{2{\pi }kx}{M}}-i{\frac{2{\pi }ly}{N}}\right) , \end{aligned}$$

(8)

$$\begin{aligned} {\langle }k,l\big | {\varvec{U}}^{\dag }(M,N)\big |x,y{\rangle }\equiv & {} {\frac{1}{{\sqrt{MN}}}} {\exp }\left( +i{\frac{2{\pi }kx}{M}}+i{\frac{2{\pi }ly}{N}}\right) . \end{aligned}$$

(9)

where ${\varvec{U}}^{\dag }(M,N)\equiv {\overline{{\varvec{U}}(M,N)}}^{\mathrm{{T}}}$ is the adjoint matrix of ${\varvec{U}}(M,N)$. We can confirm the following relations for ${\varvec{U}}(M,N)$ and ${\varvec{U}}^{\dag }(M,N)$:

$$\begin{aligned}&{\sum _{(k,l){\in }W(M,N)}} {\langle }x,y\big |{\varvec{U}}(M,N)\big |k,l{\rangle } {\langle }k,l\big |{\varvec{U}}^{\dag }(M,N)\big |x',y'{\rangle }\nonumber \\&\quad = {\delta }_{x,x'}{\delta }_{y,y'} \,((x,y),(x',y'){\in }V(M,N)), \end{aligned}$$

(10)

$$\begin{aligned}&{\sum _{(x,y){\in }V(M,N)}} {\langle }k,l\big |{\varvec{U}}^{\dag }(M,N)\big |x,y{\rangle } {\langle }x,y\big |{\varvec{U}}(M,N)\big |k',l'{\rangle }\nonumber \\&\quad = {\delta }_{k,k'}{\delta }_{l,l'} \,((k,l),(k',l'){\in }W(M,N)), \end{aligned}$$

(11)

where

$$\begin{aligned} W(M,N)\equiv & {} \left\{ (k,l)\Big | k=-\left\lfloor {\frac{M-1}{2}}\right\rfloor , -\left\lfloor {\frac{M-1}{2}}\right\rfloor+1,{\ldots }, +\left\lfloor {\frac{M}{2}}\right\rfloor , \right. \nonumber \\&\left. \quad l=-\left\lfloor {\frac{N-1}{2}}\right\rfloor, -\left\lfloor{\frac{N-1}{2}}\right\rfloor+1,{\ldots }, +\left\lfloor {\frac{N}{2}}\right\rfloor \right\} . \end{aligned}$$

(12)

We remark that W(M, N) can be also regarded as an ordered set by considering the two-dimensional wave-number-dependent vector (k, l) as

$$\begin{aligned} {\varvec{p}}_{i} \equiv \left( -\left\lfloor {\frac{M-1}{2}}\right\rfloor + (i-1){\mathrm{mod}}(M), -\left\lfloor {\frac{N-1}{2}}\right\rfloor +\left\lfloor {\frac{i-1}{M}}\right\rfloor \right) \quad (i=1,2,3,{\ldots },MN), \end{aligned}$$

(13)

in the similar arguments for Eqs. (1). Equations (10) and (11) mean that ${\varvec{U}}(M,N){\varvec{U}}^{\dag }(M,N) ={\varvec{U}}^{\dag }(M,N){\varvec{U}}(M,N)={\varvec{I}}(M,N)$, where ${\varvec{I}}(M,N)$ is an $MN\,{\times }\,MN$ identity matrix such that we have ${\varvec{U}}^{\dag }(M,N)={\varvec{U}}^{-1}(M,N)$. We confirm that ${\varvec{C}}(M,N)$ is diagonalized by the unitary matrix ${\varvec{U}}(M,N)$ as follows:

$$\begin{aligned} {\varvec{C}}(M,N)={\varvec{U}}(M,N){\varvec{\Lambda }}(M,N){\varvec{U}}^{\dag }(M,N), \end{aligned}$$

(14)

where

$$\begin{aligned}&{\langle }k,l\big |{\varvec{\Lambda }}(M,N)\big |k',l'{\rangle } \equiv {\delta }_{k,k'} {\delta }_{l,l'} {\lambda }{\left( {\frac{2{\pi }k}{M}} ,{\frac{2{\pi }l}{N}}\right) }, \end{aligned}$$

(15)

$$\begin{aligned}&{\lambda }{\left( {\frac{2{\pi }k}{M}} ,{\frac{2{\pi }l}{N}}\right) } \equiv 4-2{\cos }\left( {\frac{2{\pi }k}{M}}\right) -2{\cos }\left( {\frac{2{\pi }l}{N}}\right) . \end{aligned}$$

(16)

The prior probability density function can be rewritten as

$$\begin{aligned} R^{(M,N)}{\left( {\varvec{f}}\big |{\alpha },{\gamma }\right) }= & {} {\sqrt{ {\frac{1}{(2{\pi })^{MN}}} {\prod _{(k,l){\in }W(M,N)}} {\left( {\gamma } +{\alpha } {\lambda }{\left( {\frac{2{\pi }k}{M}} ,{\frac{2{\pi }l}{N}}\right) } \right) } }} \nonumber \\&{\times }\, {\exp }\left( -{\frac{1}{2}} {\sum _{(k,l){\in }W(M,N)}} {\varvec{f}}^{\mathrm{{T}}}{\varvec{U}}^{\dag }(M,N) \big |k,l{\rangle } \right. \nonumber \\&\left. {\times }\, {\left( {\gamma } +{\alpha } {\lambda }{\left( {\frac{2{\pi }k}{M}} ,{\frac{2{\pi }l}{N}}\right) } \right) } {\langle }k,l\big | {\varvec{U}}(M,N){\varvec{f}} \right) . \end{aligned}$$

(17)

Here we remark that ${\varvec{U}}(M,N){\varvec{f}}$ and ${\varvec{f}}^{\mathrm{{T}}}{\varvec{U}}^{\dag }(M,N)$ are the column vector and row vector, respectively. Also ${\langle }k,l| {\varvec{U}}(M,N){\varvec{f}}$ and ${\varvec{f}}^{\mathrm{{T}}}{\varvec{U}}^{\dag }(M,N) |k,l{\rangle }$ are their i-th elements $\left( {\varvec{U}}(M,N){\varvec{f}}\right) _{i}$ and $\left( {\varvec{f}}^{\mathrm{{T}}}{\varvec{U}}^{\dag }(M,N)\right) _{i}$ with the relationship ${\varvec{p}}_{i}=(k,l)$ as per Eq. (13).

Now we introduce a new state vector ${\varvec{F}}$ as

$$\begin{aligned} {\varvec{F}} \equiv {\left( F{\left( {\frac{2{\pi }k}{M}},{\frac{2{\pi }l}{N}}\right) } = {\langle }k,l\big | {\varvec{U}}(M,N){\varvec{f}} \Big |(k,l){\in }W(M,N)\right) }, \end{aligned}$$

(18)

and a prior probability density function ${\rho }^{(M,N)}{ ({\varvec{F}}|{\alpha },{\gamma })}$ for the state vector ${\varvec{F}}$:

$$\begin{aligned} R^{(M,N)}{\left( {\varvec{F}}\big |{\alpha },{\gamma }\right) }= & {} {\sqrt{ {\frac{1}{(2{\pi })^{MN}}} {\prod _{(k,l){\in }W(M,N)}} {\left( {\gamma } +{\alpha } {\lambda }{\left( {\frac{2{\pi }k}{M}} ,{\frac{2{\pi }l}{N}}\right) } \right) } }} \nonumber \\&{\times }\, {\exp }\left( -{\frac{1}{2}} {\sum _{(k,l){\in }W(M,N)}} \left( {\gamma } \right. \right. \nonumber \\&\left. \left. +\,{\alpha } {\lambda }{\left( {\frac{2{\pi }k}{M}} ,{\frac{2{\pi }l}{N}}\right) } \right) F{\left( {\frac{2{\pi }k}{M}},{\frac{2{\pi }l}{N}}\right) } F{\left( -{\frac{2{\pi }k}{M}},-{\frac{2{\pi }l}{N}}\right) } \right) . \end{aligned}$$

(19)

By introducing a new state variable in a subspace as

$$\begin{aligned} {{\tilde{F}}}{\left( {\left( {\frac{2{\pi }k}{M}}\right) }{\left( {\frac{M}{m}}\right) }, {\left( {\frac{2{\pi }l}{N}}\right) }{\left( {\frac{N}{n}}\right) }\right) } \equiv F{\left( {\frac{2{\pi }k}{M}},{\frac{2{\pi }l}{N}}\right) } {}{\left( (k,l){\in }W(m,n)\right) }, \end{aligned}$$

(20)

the marginal probability density function $R^{(m,n)} {( {\{ {{\tilde{F}}}{({\frac{2{\pi }k}{m}},{\frac{2{\pi }l}{n}})} |(k,l){\in }W(m,n)\}} |{\alpha },{\gamma })}$ in the momentum-space can be calculated as follows:

$$\begin{aligned}&R^{(m,n)} {\left( {\left\{ {{\tilde{F}}}{\left( {\frac{2{\pi }k}{m}},{\frac{2{\pi }l}{n}}\right) } \Big |(k,l){\in }W(m,n)\right\} } |{\alpha },{\gamma }\right) } \nonumber \\&\quad \equiv \, {\left( {\prod _{(k,l){\in }W(M,N)}} {\int } dF{\left( {\frac{2{\pi }k}{M}},{\frac{2{\pi }l}{N}}\right) } \right) } \nonumber \\&\qquad {\times }\, {\left( {\prod _{(k,l){\in }W(m,n)}} {\delta }{\left( F{\left( {\frac{2{\pi }k}{M}},{\frac{2{\pi }l}{N}}\right) } - {{\tilde{F}}}{\left( {\frac{2{\pi }k}{m}},{\frac{2{\pi }l}{m}}\right) } \right) } \right) } R^{(M,N)}{\left( {\varvec{F}}\big |{\alpha },{\gamma }\right) } \nonumber \\&\quad =\, {\sqrt{ {\frac{1}{(2{\pi })^{mn}}} {\prod _{(k,l){\in }W(m,n)}} {\left( {\gamma } +{\alpha } {\lambda }{\left( {\frac{2{\pi }k}{M}} ,{\frac{2{\pi }l}{N}}\right) } \right) } }} \nonumber \\&\qquad {\times }\, {\exp }\left( -{\frac{1}{2}} {\sum _{(k,l){\in }W(m,n)}} {\left( {\gamma } +{\alpha } {\lambda }{\left( {\frac{2{\pi }k}{M}} ,{\frac{2{\pi }l}{N}}\right) } \right) } {{\tilde{F}}}{\left( {\frac{2{\pi }k}{m}},{\frac{2{\pi }l}{n}}\right) } {{\tilde{F}}}{\left( -{\frac{2{\pi }k}{m}},-{\frac{2{\pi }l}{n}}\right) } \right) . \end{aligned}$$

(21)

We remark that the high-frequency modes are not ignored but are marginalized. Only low-frequency modes are rescaled or extended to recover the same frequency range as that of the original probabilistic Gaussian graphical model. The marginalization is referred to as the “trace Out” in the RG techniques in the physics. Again, we remark again that the present algorithm does the trace out; rather, it merely rescales instead of just ignoring the high-frequency modes. We consider that it is based on the standard RG.

Now we set new positive integers m and n with $m{\le }M$ and $n{\le }N$, respectively, and introduce the following scale transformation from the state vectors ${\varvec{f}}$ in the space V(M, N) to the new state vectors ${\varvec{{\tilde{f}}}} = {({{\tilde{f}}}_{x,y} |(x,y){\in }V(m,n))}$

$$\begin{aligned} {{\tilde{f}}}_{x,y} \equiv {\sum _{(k,l){\in }W(m,n)}} {\langle }x,y\big |{\varvec{U}}(m,n)\big |k,l{\rangle } {{\tilde{F}}}{\left( {\left( {\frac{2{\pi }k}{M}}\right) }{\left( {\frac{M}{m}}\right) }, {\left( {\frac{2{\pi }l}{N}}\right) }{\left( {\frac{N}{n}}\right) }\right) } {}((x,y){\in }V(m,n)), \end{aligned}$$

(22)

such that

$$\begin{aligned} {\varvec{{\tilde{f}}}} \equiv {\varvec{U}}^{\dag }(m,n){\varvec{B}}(m,n|M,N){\varvec{U}}(M,N){\varvec{f}}, \end{aligned}$$

(23)

where

$$\begin{aligned}&{\langle }k',l'\big |{\varvec{B}}(m,n|M,N)\big |k,l{\rangle } \equiv {\delta }_{k,k'} {\delta }_{l,l'} \,{\left( (k',l'){\in }W(m,n), (k,l){\in }W(M,N)\right) }, \end{aligned}$$

(24)

$$\begin{aligned}&{\langle }k,l\big |{\varvec{U}}(m,n)\big |x,y{\rangle } \equiv {\frac{1}{{\sqrt{mn}}}} {\exp }{\left( -i{\frac{2{\pi }kx}{m}}-i{\frac{2{\pi }ly}{n}} \right) } \nonumber \\&\quad {\left( (x,y){\in }V(m,n),(k,l){\in }W(m,n)\right) }, \end{aligned}$$

(25)

and ${\varvec{U}}^{\dag }(m,n)\equiv {\overline{{\varvec{U}}(m,n)}}^{\mathrm{{T}}}$ is the adjoint matrix of ${\varvec{U}}(m,n)$. Equation (23) is one of MSRG transformations and is visualized as Fig. 1. Some examples obtained by applying the MSRG transformation in Eq. (23) to the original images ${\varvec{f}}^{*}$ in Fig.2 are shown in Figs. 3, 4 and 5.

Fig. 1

Visualization of the MSRG transformation of the prior probability density function of Eq. (26)

Fig. 2

Original images ${\varvec{f}}^{*}$ ($M=N=256$). a Parrots. b Couple. c Mandrill

Fig. 3

Reduced images ${\varvec{{\tilde{f}}}}^{*} \equiv {\varvec{U}}^{\dag }(m,n){\varvec{B}}(m,n|M,N){\varvec{U}}(M,N){\varvec{f}}^{*}$ for $m=n=192$, such that ${\frac{m}{M}}={\frac{n}{N}}={\frac{3}{4}}$ for each original image ${\varvec{f}}^{*}$ in Fig. 1. a Parrots. b Couple. c Mandrill

Fig. 4

Reduced images ${\varvec{{\tilde{f}}}}^{*} \equiv {\varvec{U}}^{\dag }(m,n){\varvec{B}}(m,n|M,N){\varvec{U}}(M,N){\varvec{f}}^{*}$ for $m=n=128$, such that ${\frac{m}{M}}={\frac{n}{N}}={\frac{1}{2}}$ for each original image ${\varvec{f}}^{*}$ in Fig. 1. a Parrots. b Couple. c Mandrill

Fig. 5

Reduced images ${\varvec{{\tilde{f}}}}^{*} \equiv {\varvec{U}}^{\dag }(m,n){\varvec{B}}(m,n|M,N){\varvec{U}}(M,N){\varvec{f}}^{*}$ for $m=n=64$, such that ${\frac{m}{M}}={\frac{n}{N}}={\frac{1}{4}}$ for each original image ${\varvec{f}}^{*}$ in Fig. 1. a Parrots. b Couple. c Mandrill

We assume that the prior probability density function of ${\varvec{{\tilde{f}}}}$ is given as

$$\begin{aligned} {\rho }^{(m,n)}{\left( {\varvec{{\tilde{f}}}}\big |{\alpha },{\gamma }\right) }= & {} {\sqrt{ {\frac{1}{(2{\pi })^{mn}}} {\prod _{(k,l){\in }W(m,n)}} {\left( {\gamma } +{\alpha } {\lambda }{\left( {\frac{2{\pi }k}{M}} ,{\frac{2{\pi }l}{N}}\right) } \right) } }} \nonumber \\&{\times }\, {\exp }\left( -{\frac{1}{2}} {\sum _{(k,l){\in }W(m,n)}} {\varvec{{\tilde{f}}}}^{\mathrm{{T}}}{\varvec{U}}^{\dag }(m,n) \big |k,l{\rangle } \right. \nonumber \\&\left. {\times }\, {\left( {\gamma } +{\alpha } {\lambda }{\left( {\frac{2{\pi }k}{M}} ,{\frac{2{\pi }l}{N}}\right) } \right) } {\langle }k,l\big | {\varvec{U}}(m,n){\varvec{{\tilde{f}}}} \right) . \end{aligned}$$

(26)

The conditional probability density function ${\rho }^{(M,N)}({\varvec{g}}|{\varvec{f}},{\beta })$ in Eq. (4) can be rewritten as

$$\begin{aligned} {\rho }^{(M,N)}({\varvec{g}}|{\varvec{f}},{\beta })&= {\sqrt{ {\left( {\frac{{\beta }}{2{\pi }}}\right) }^{MN} }} \nonumber \\&\quad {\times } {\exp }\left( -{\frac{1}{2}}{\beta } {\sum _{(k,l){\in }W(M,N)}} {\left( {\varvec{g}}- {\varvec{f}}\right) }^{\mathrm{{T}}} {\varvec{U}}^{\dag }(M,N)\big |k,l{\rangle } {\langle }k,l\big |{\varvec{U}}(M,N) {\left( {\varvec{g}} - {\varvec{f}} \right) } \right) . \end{aligned}$$

(27)

Now we introduce a new state vector ${\varvec{F}}$ as

$$\begin{aligned} {\varvec{G}} \equiv {\left( G{\left( {\frac{2{\pi }k}{M}},{\frac{2{\pi }l}{N}}\right) } = {\langle }k,l\big | {\varvec{U}}(M,N){\varvec{g}} \Bigg |(k,l){\in }W(M,N)\right) } \qquad {\left( (k,l){\in }W(M,N)\right) }, \end{aligned}$$

(28)

and the conditional probability density function ${\rho }^{(M,N)}({\varvec{g}}|{\varvec{f}},{\beta })$ in Eq. (4) can be regarded as the conditional probability density function $R^{(M,N)}({\varvec{G}}|{\varvec{F}},{\beta })$ in the momentum-space:

$$\begin{aligned}&R^{(M,N)}({\varvec{G}}|{\varvec{F}},{\beta }) = {\sqrt{ {\left( {\frac{{\beta }}{2{\pi }}}\right) }^{MN} }} \nonumber \\&\quad {\times }\, {\exp }\left( -{\frac{1}{2}}{\beta } {\sum _{(k,l){\in }W(M,N)}} {\left( G{\left( {\frac{2{\pi }k}{M}},{\frac{2{\pi }l}{N}}\right) } - F{\left( {\frac{2{\pi }k}{M}},{\frac{2{\pi }l}{N}}\right) } \right) } \right. \nonumber \\&\quad \left. {\times }\, {\left( G{\left( -{\frac{2{\pi }k}{M}},-{\frac{2{\pi }l}{N}}\right) } - F{\left( -{\frac{2{\pi }k}{M}},-{\frac{2{\pi }l}{N}}\right) } \right) } \right) . \end{aligned}$$

(29)

We introduce the scale transformation

$$\begin{aligned} {{\tilde{G}}}{\left( {\left( {\frac{2{\pi }k}{M}}\right) }{\left( {\frac{M}{m}}\right) }, {\left( {\frac{2{\pi }l}{N}}\right) }{\left( {\frac{N}{n}}\right) }\right) } \equiv G{\left( {\frac{2{\pi }k}{M}},{\frac{2{\pi }l}{N}}\right) } \end{aligned}$$

(30)

in the momentum-space, and the marginal probability density function $R^{(m,n)}{({( {{\tilde{G}}}{({\frac{2{\pi }k}{m}},{\frac{2{\pi }l}{n}})} \big |(k,l){\in }W(m,n))} | {\{ {{\tilde{F}}}{({\frac{2{\pi }k}{m}},{\frac{2{\pi }l}{n}})} \big |(k,l){\in }W(m,n)\}},{\beta })}$ in the momentum space can be calculated as follows:

$$\begin{aligned}&R^{(m,n)}{\left( {\left( {{\tilde{G}}}{\left( {\frac{2{\pi }k}{m}},{\frac{2{\pi }l}{n}}\right) } \Big |(k,l){\in }W(m,n)\right) } \Bigg | {\left\{ {{\tilde{F}}}{\left( {\frac{2{\pi }k}{m}},{\frac{2{\pi }l}{n}}\right) } \Big |(k,l){\in }W(m,n)\right\} },{\beta }\right) } \nonumber \\&\quad \equiv {\left( {\prod _{(k,l){\in }W(M,N){\setminus }W(m,n)}} {\int } dG{\left( {\frac{2{\pi }k}{M}},{\frac{2{\pi }l}{N}}\right) } {\int } dF{\left( {\frac{2{\pi }k}{M}},{\frac{2{\pi }l}{N}}\right) } \right) } \nonumber \\&\qquad {\times }\, {\left( {\prod _{(k,l){\in }W(m,n)}} {\delta }{\left( G{\left( {\frac{2{\pi }k}{M}},{\frac{2{\pi }l}{N}}\right) } - {{\tilde{G}}}{\left( {\frac{2{\pi }k}{m}},{\frac{2{\pi }l}{n}}\right) } \right) } \right) } \nonumber \\&\qquad {\times }\, {\left( {\prod _{(k,l){\in }W(m,n)}} {\delta }{\left( F{\left( {\frac{2{\pi }k}{M}},{\frac{2{\pi }l}{N}}\right) } - {{\tilde{F}}}{\left( {\frac{2{\pi }k}{m}},{\frac{2{\pi }l}{n}}\right) } \right) } \right) } R^{(M,N)}({\varvec{G}}|{\varvec{F}},{\beta }) \nonumber \\&\quad =\, {\sqrt{ {\left( {\frac{{\beta }}{2{\pi }}}\right) }^{mn} }} {\exp }\left( -{\frac{1}{2}}{\beta } {\sum _{(k,l){\in }W(m,n)}} {\left( {{\tilde{G}}}{\left( {\frac{2{\pi }k}{m}},{\frac{2{\pi }l}{n}}\right) } - {{\tilde{F}}}{\left( {\frac{2{\pi }k}{m}},{\frac{2{\pi }l}{n}}\right) } \right) } \right. \nonumber \\&\qquad \left. {\times }\, {\left( {{\tilde{G}}}{\left( -{\frac{2{\pi }k}{m}},-{\frac{2{\pi }l}{n}}\right) } - {{\tilde{F}}}{\left( -{\frac{2{\pi }k}{m}},-{\frac{2{\pi }l}{n}}\right) } \right) } \right) . \end{aligned}$$

(31)

We introduce the following scale transformation from the state vector ${\varvec{g}}$ in the space V(M, N) to new state vectors ${\varvec{{\tilde{g}}}} = { ({{\tilde{g}}}_{x,y} |(x,y){\in }V(m,n))}$

$$\begin{aligned} {{\tilde{g}}}_{x,y} \equiv {\sum _{(k,l){\in }W(m,n)}} {\langle }x,y\big |{\varvec{U}}(m,n)\big |k,l{\rangle } {{\tilde{G}}}{\left( {\frac{2{\pi }k}{m}},{\frac{2{\pi }l}{n}}\right) } \qquad ((x,y){\in }V(m,n)), \end{aligned}$$

(32)

such that

$$\begin{aligned} {\varvec{{\tilde{g}}}} \equiv {\varvec{U}}^{\dag }(m,n){\varvec{B}}(m,n|M,N){\varvec{U}}(M,N){\varvec{g}}. \end{aligned}$$

(33)

Some examples obtained by applying the MSRG transformation in Eq. (33) to degraded images ${\varvec{g}}$ in Fig. 6 are shown in Figs. 7, 8 and 9.

Fig. 6

Degraded images ${\varvec{g}}^{*}$ generated from the original images ${\varvec{f}}^{*}$ in Fig. 2 by according to the additive white Gaussian noise with average 0 and variance $1/{\beta }^{*}=40^{2}$ ($M=N=256$). a Parrots. b Couple. c Mandrill

Fig. 7

Reduced images ${\varvec{{\tilde{g}}}}^{*} \equiv {\varvec{U}}^{\dag }(m,n){\varvec{B}}(m,n|M,N){\varvec{U}}(M,N){\varvec{g}}^{*}$ for $m=n=192$, such that ${\frac{m}{M}}={\frac{n}{N}}={\frac{3}{4}}$ for each degraded image ${\varvec{g}}^{*}$ in Fig. 6. a Parrots. b Couple. cMandrill

Fig. 8

Reduced images ${\varvec{{\tilde{g}}}}^{*} \equiv {\varvec{U}}^{\dag }(m,n){\varvec{B}}(m,n|M,N){\varvec{U}}(M,N){\varvec{g}}^{*}$ for $m=n=128$, such that ${\frac{m}{M}}={\frac{n}{N}}={\frac{1}{2}}$ for each degraded image ${\varvec{g}}^{*}$ in Fig. 6. a Parrots. b Couple. c Mandrill

Fig. 9

Reduced images ${\varvec{{\tilde{g}}}}^{*} \equiv {\varvec{U}}^{\dag }(m,n){\varvec{B}}(m,n|M,N){\varvec{U}}(M,N){\varvec{g}}^{*}$ for $m=n=64$, such that ${\frac{m}{M}}={\frac{n}{N}}={\frac{1}{4}}$ for each degraded image ${\varvec{g}}^{*}$ in Fig. 6. a Parrots. b Couple. c Mandrill

Moreover, we introduce the conditional probability density function of the degraded image ${\varvec{{\tilde{g}}}}\equiv {({{\tilde{g}}}_{x,y}| (x,y){\in }V(m,n))}$, where the original image ${\varvec{{\tilde{f}}}}$ given in the reduced space V(m, n), is assumed to satisfy

$$\begin{aligned} {\rho }^{(m,n)}({\varvec{{\tilde{g}}}} | {\varvec{{\tilde{f}}}},{\beta })&= {\sqrt{ {\left( {\frac{{\beta }}{2{\pi }}}\right) }^{mn} }} \nonumber \\&\quad {\times }\, {\exp }\left( -{\frac{1}{2}}{\beta } {\sum _{(k,l){\in }W(m,n)}} {\left( {\varvec{{\tilde{g}}}}-{\varvec{{\tilde{f}}}} \right) }^{\mathrm{{T}}} {\varvec{U}}^{\dag }(m,n)\big |k,l{\rangle } {\langle }k,l\big |{\varvec{U}}(m,n) {\left( {\varvec{{\tilde{g}}}}-{\varvec{{\tilde{f}}}} \right) } \right) . \end{aligned}$$

(34)

3 Momentum-Space Renormalization Group Approaches in EM Algorithm

In this section, we provide a practical scheme of the EM algorithm in the MSRG approaches. The fundamental framework is based on the maximization of marginal likelihood. We first formulate the probability density function of ${\varvec{{\tilde{g}}}}$ and regard it as a marginal likelihood function of ${\alpha }$, ${\beta }$ and ${\gamma }$.

Under some assumptions in the previous section, the marginal likelihood ${\rho }^{(m,n)}({\varvec{{\tilde{g}}}} | {\alpha },{\beta },{\gamma })$ in the space V(m, n) is defined by

$$\begin{aligned} {\rho }^{(m,n)}({\varvec{{\tilde{g}}}} | {\alpha },{\beta },{\gamma }) \equiv {\int } {\rho }^{(m,n)}({\varvec{{\tilde{g}}}} | {\varvec{{\tilde{f}}}},{\beta }) {\rho }^{(m,n)}({\varvec{{\tilde{f}}}} | {\alpha },{\gamma }) {\text {d}}{\varvec{{\tilde{f}}}}. \end{aligned}$$

(35)

Our proposed framework is designed to achieve the estimation of the hyperparameters ${\alpha }$, ${\beta }$ and ${\gamma }$ by maximizing ${\rho }^{(m,n)}{({\varvec{{\tilde{g}}}} \Big |{\alpha },{\beta },{\gamma })}$ as follows:

$$\begin{aligned}&{\left( {\frac{1}{mn}}\right) } {\ln }{\left( {\rho }^{(m,n)}{\left( {\varvec{{\tilde{g}}}} \big | {\alpha },{\beta },{\gamma }\right) } \right) } = -{\frac{1}{2}} {\ln }{\left( {\frac{2{\pi }}{{\beta }}} \right) } \nonumber \\&\qquad +\,{\frac{1}{2mn}} {\sum _{(k,l){\in }W(m,n)}} {\ln }{\left( {\gamma } +{\alpha } {\lambda }{\left( {\frac{2{\pi }k}{M}},{\frac{2{\pi }l}{N}}\right) } \right) } \nonumber \\&\qquad -\,{\frac{1}{2mn}} {\sum _{(k,l){\in }W(m,n)}} {\ln }{\left( {\beta }+{\gamma } +{\alpha } {\lambda }{\left( {\frac{2{\pi }k}{M}},{\frac{2{\pi }l}{N}}\right) } \right) } \nonumber \\&\qquad -\,{\frac{1}{2mn}} {\sum _{(k,l){\in }W(m,n)}} {\varvec{{\tilde{g}}}}^{\mathrm{{T}}}{\varvec{U}}^{\dag }(m,n)\big | k,l{\rangle } {\frac{ {\beta } {\left( {\gamma } +{\alpha } {\lambda }{\left( {\frac{2{\pi }k}{M}},{\frac{2{\pi }l}{N}}\right) } \right) } }{ {\left( {\beta }+{\gamma } +{\alpha } {\lambda }{\left( {\frac{2{\pi }k}{M}},{\frac{2{\pi }l}{N}}\right) } \right) } }} {\langle }k,l\big | {\varvec{U}}(m,n){\varvec{{\tilde{g}}}}. \end{aligned}$$

(36)

Estimates of hyperparameters, ${{\widehat{\alpha }}}_{m,n}({\varvec{g}})$, ${{\widehat{\beta }}}_{m,n}({\varvec{g}})$ and ${{\widehat{\gamma }}}_{m,n}({\varvec{g}})$, are determined so as to maximize the marginal likelihood ${\rho }^{(m,n)}{({\varvec{{\tilde{g}}}} ={\varvec{U}}^{\dag }(m,n){\varvec{B}}(m,n|M,N){\varvec{U}}(M,N){\varvec{g}} | {\alpha },{\beta },{\gamma })}$ with respect to ${\alpha }$, ${\beta }$ and ${\gamma }$, respectively, as follows:

$$\begin{aligned}&{\left( {{\widehat{\alpha }}}_{m,n}({\varvec{g}}), {{\widehat{\beta }}}_{m,n}({\varvec{g}}), {{\widehat{\gamma }}}_{m,n}({\varvec{g}})\right) } \nonumber \\&\quad = {\arg }{\max _{{\left( {\alpha },{\beta },{\gamma }\right) }}} {\rho }^{(m,n)}{\left( {\varvec{{\tilde{g}}}} ={\varvec{U}}^{\dag }(m,n){\varvec{B}}(m,n|M,N){\varvec{U}}(M,N){\varvec{g}} \Big |{\alpha },{\beta },{\gamma }\right) }. \end{aligned}$$

(37)

By considering the extremum conditions of ${\rho }^{(m,n)}{({\varvec{{\tilde{g}}}} ={\varvec{U}}^{\dag }(m,n){\varvec{B}}(m,n|M,N){\varvec{U}}(M,N){\varvec{g}} |{\alpha },{\beta },{\gamma })}$ with respect to ${\alpha }$, ${\beta }$ and ${\gamma }$, the simultaneous deterministic equations for the estimates of hyperparameters, ${{\widehat{\alpha }}}_{m,n}({\varvec{g}})$, ${{\widehat{\beta }}}_{m,n}({\varvec{g}})$ and ${{\widehat{\gamma }}}_{m,n}({\varvec{g}})$, are derived as follows:

$$\begin{aligned}&{\frac{1}{2mn}} {\sum _{(k,l){\in }W(m,n)}} {\frac{ {\lambda }{\left( {\frac{2{\pi }k}{M}},{\frac{2{\pi }l}{N}}\right) } }{ {{\widehat{\gamma }}}_{m,n}({\varvec{g}}) +{{\widehat{\alpha }}}_{m,n}({\varvec{g}}) {\lambda }{\left( {\frac{2{\pi }k}{M}},{\frac{2{\pi }l}{N}}\right) } }} \nonumber \\&\quad = {\frac{1}{2mn}} {\sum _{(k,l){\in }W(m,n)}} {\frac{{\lambda }{\left( {\frac{2{\pi }k}{M}},{\frac{2{\pi }l}{N}}\right) }}{{{\widehat{\beta }}}_{m,n}({\varvec{g}}) +{{\widehat{\gamma }}}_{m,n}({\varvec{g}}) +{{\widehat{\alpha }}}_{m,n}({\varvec{g}}) {\lambda }{\left( {\frac{2{\pi }k}{M}},{\frac{2{\pi }l}{N}}\right) } }} \nonumber \\&\qquad +\,{\frac{1}{2mn}} {\sum _{(k,l){\in }W(m,n)}} {\varvec{{\tilde{g}}}}^{\mathrm{{T}}}{\varvec{U}}^{\dag }(m,n)\big |k,l{\rangle } \nonumber \\&\qquad {\times }\, {\frac{{{\widehat{\beta }}}_{m,n}({\varvec{g}})^{2} {\lambda }{\left( {\frac{2{\pi }k}{M}},{\frac{2{\pi }l}{N}}\right) }}{{\left( {{\widehat{\beta }}}_{m,n}({\varvec{g}})+{{\widehat{\gamma }}}_{m,n}({\varvec{g}} ) +{{\widehat{\alpha }}}_{m,n}({\varvec{g}}) {\lambda }{\left( {\frac{2{\pi }k}{M}},{\frac{2{\pi }l}{N}}\right) } \right) }^{2}}} {\langle }k,l\big |{\varvec{U}}(m,n){\varvec{{\tilde{g}}}}, \end{aligned}$$

(38)

$$\begin{aligned}&{\frac{1}{2mn}} {\sum _{(k,l){\in }W(m,n)}} {\frac{1}{ {{\widehat{\gamma }}}_{m,n}({\varvec{g}}) +{{\widehat{\alpha }}}_{m,n}({\varvec{g}}) {\lambda }{\left( {\frac{2{\pi }k}{M}},{\frac{2{\pi }l}{N}}\right) } }} \nonumber \\&\quad = {\frac{1}{2mn}} {\sum _{(k,l){\in }W(m,n)}} {\frac{1}{{{\widehat{\beta }}}_{m,n}({\varvec{g}}) +{{\widehat{\gamma }}}_{m,n}({\varvec{g}}) +{{\widehat{\alpha }}}_{m,n}({\varvec{g}}) {\lambda }{\left( {\frac{2{\pi }k}{M}},{\frac{2{\pi }l}{N}}\right) } }} \nonumber \\&\qquad +\,{\frac{1}{2mn}} {\sum _{(k,l){\in }W(m,n)}} {\varvec{{\tilde{g}}}}^{\mathrm{{T}}}{\varvec{U}}^{\dag }(m,n)\big |k,l{\rangle } \nonumber \\&\qquad {\times }\, {\frac{{{\widehat{\beta }}}_{m,n}({\varvec{g}})^{2} }{{\left( {{\widehat{\beta }}}_{m,n}({\varvec{g}}) +{{\widehat{\gamma }}}({\varvec{g}}) +{{\widehat{\alpha }}}({\varvec{g}}) {\lambda }{\left( {\frac{2{\pi }k}{M}},{\frac{2{\pi }l}{N}}\right) } \right) }^{2}}} {\langle }k,l\big |{\varvec{U}}(m,n){\varvec{{\tilde{g}}}}, \end{aligned}$$

(39)

$$\begin{aligned}&{\frac{1}{{{\widehat{\beta }}}_{m,n}({\varvec{g}})}} = {\frac{1}{mn}} {\sum _{(k,l){\in }W(m,n)}} {\frac{1}{{{\widehat{\beta }}}_{m,n}({\varvec{g}})+{{\widehat{\gamma }}}_{m,n}({\varvec{g}}) +{{\widehat{\alpha }}}_{m,n}({\varvec{g}}) {\lambda }{\left( {\frac{2{\pi }k}{M}},{\frac{2{\pi }l}{N}}\right) } }} \nonumber \\&\qquad +{\frac{1}{mn}} {\sum _{(k,l){\in }W(m,n)}} {\varvec{{\tilde{g}}}}^{\mathrm{{T}}}{\varvec{U}}^{\dag }(m,n)\big |k,l{\rangle } \nonumber \\&\qquad {\times } {\frac{ {\left( {{\widehat{\gamma }}}_{m,n}({\varvec{g}}) +{{\widehat{\alpha }}}_{m,n}({\varvec{g}}) {\lambda }{\left( {\frac{2{\pi }k}{M}},{\frac{2{\pi }l}{N}}\right) } \right) }^{2}}{ {\left( {{\widehat{\beta }}}_{m,n}({\varvec{g}})+{{\widehat{\gamma }}}_{m,n}({\varvec{g}}) +{{\widehat{\alpha }}}_{m,n}({\varvec{g}}) {\lambda }{\left( {\frac{2{\pi }k}{M}},{\frac{2{\pi }l}{N}}\right) } \right) }^{2}}} {\langle }k,l\big |{\varvec{U}}(m,n){\varvec{{\tilde{g}}}}. \end{aligned}$$

(40)

The practical algorithm to solve Eqs. (38), (39) and (40) with respect to ${{\widehat{\alpha }}}_{m,n}({\varvec{g}})$, ${{\widehat{\beta }}}_{m,n}({\varvec{g}})$ and ${{\widehat{\gamma }}}_{m,n}({\varvec{g}})$ is given as follows:

4 Hyperparameter Estimation and Noise Reduction Algorithm

Step 1: :

Input a given data point ${\varvec{g}}$ and the set of positive integers (m, n). Compute ${{\tilde{G}}}(k,l)$ using

$$\begin{aligned}&{{\tilde{G}}}(k,l) \Leftarrow {\frac{1}{\sqrt{mn}}} {\sum _{(x,y){\in }V(m,n)}} {\varvec{g}}^{\mathrm{{T}}}{\varvec{B}}^{\mathrm{{T}}}(m,n|M,N)\big |x,y{\rangle } {\exp }{\left( -i{\frac{2{\pi }kx}{m}}-i{\frac{2{\pi }ly}{n}}\right) } \nonumber \\&\quad {\left( (k,l){\in }W(m,n) \right) }. \end{aligned}$$

(41)

Set ${\alpha }(t)$, ${\beta }(t)$ and ${\gamma }(t)$ as initial values, and $t{\Leftarrow }0$.

Step 2: :

Update t by $t{\Leftarrow }t+1$ and compute u, v and ${\beta }(t)$ from ${\alpha }(t-1)$, ${\beta }(t-1)$ and ${\gamma }(t-1)$ as follows:

$$\begin{aligned}&u \Leftarrow {\frac{1}{2mn}} {\sum _{(k,l){\in }W(m,n)}} {\frac{{\lambda }{\left( {\frac{2{\pi }k}{M}},{\frac{2{\pi }l}{N}}\right) }}{{\left( {\beta }(t-1)+{\gamma }(t-1) +{\alpha }(t-1) {\lambda }{\left( {\frac{2{\pi }k}{M}},{\frac{2{\pi }l}{N}}\right) } \right) } }} \nonumber \\&\quad +{\frac{1}{2mn}} {\sum _{(k,l){\in }W(m,n)}} |{{\tilde{G}}}(k,l)|^{2} {\frac{{\beta }(t-1)^{2} {\lambda }{\left( {\frac{2{\pi }k}{M}},{\frac{2{\pi }l}{N}}\right) }}{{\left( {\left( {\beta }(t-1) +{\gamma }(t-1)+{\alpha }(t-1) {\lambda }{\left( {\frac{2{\pi }k}{M}},{\frac{2{\pi }l}{N}}\right) } \right) } \right) }^{2}}}, \end{aligned}$$

(42)

$$\begin{aligned}&v \Leftarrow {\frac{1}{2mn}} {\sum _{(k,l){\in }W(m,n)}} {\frac{1}{{\left( {\beta }(t-1) +{\gamma }(t-1) +{\alpha }(t-1) {\lambda }{\left( {\frac{2{\pi }k}{M}},{\frac{2{\pi }l}{N}}\right) } \right) } }} \nonumber \\&\quad +{\frac{1}{2mn}} {\sum _{(k,l){\in }W(m,n)}} |{{\tilde{G}}}(k,l)|^{2} {\frac{{\beta }(t-1)^{2} }{{\left( {\left( {\beta }(t-1)+{\gamma }(t-1) +{\alpha }(t-1) {\lambda }{\left( {\frac{2{\pi }k}{M}},{\frac{2{\pi }l}{N}}\right) } \right) } \right) }^{2}}}, \end{aligned}$$

(43)

$$\begin{aligned}&{\beta }(t) \Leftarrow \left( {\frac{1}{mn}} {\sum _{(k,l){\in }W(m,n)}} {\frac{1}{{\left( {\beta }(t-1)+{\gamma }(t-1) +{\alpha }(t-1) {\lambda }{\left( {\frac{2{\pi }k}{M}},{\frac{2{\pi }l}{N}}\right) } \right) } }} \right. \nonumber \\&\left. \quad +{\frac{1}{mn}} {\sum _{(k,l){\in }W(m,n)}} |{{\tilde{G}}}(k,l)|^{2} {\frac{ {\left( ({\gamma }(t-1) +{\alpha }(t-1) {\lambda }{\left( {\frac{2{\pi }k}{M}},{\frac{2{\pi }l}{N}}\right) } \right) }^{2}}{{\left( {\beta }(t-1)+{\gamma }(t-1) +{\alpha }(t-1) {\lambda }{\left( {\frac{2{\pi }k}{M}},{\frac{2{\pi }l}{N}}\right) } \right) }^{2}}} \right) ^{-1}. \end{aligned}$$

(44)

Step 3: :

Repeat the following updates for ${\alpha }(t)$ and ${\gamma }(t)$ until they converge:

$$\begin{aligned}&\left( \begin{array}{cccc} {\alpha }(t)\\ {\gamma }(t)\\ \end{array} \right) \Leftarrow \left( \begin{array}{cccc} {\varvec{\alpha }}(t) \left( {\frac{1}{2mnu}} {\displaystyle { {\sum _{(k,l){\in }W(m,n)}} }} {\frac{ {\lambda }{\left( {\frac{2{\pi }k}{M}},{\frac{2{\pi }l}{N}}\right) } }{ {\left( {\gamma }(t) +{\alpha }(t) {\lambda }{\left( {\frac{2{\pi }k}{M}},{\frac{2{\pi }l}{N}}\right) } \right) } }} \right) ^{1/2}\\ {\gamma }(t) \left( {\frac{1}{2mnv}} {\displaystyle { {\sum _{(k,l){\in }W(m,n)}} }} {\frac{1}{ {\left( {\gamma }(t) +{\alpha }(t) {\lambda }{\left( {\frac{2{\pi }k}{M}},{\frac{2{\pi }l}{N}}\right) } \right) } }} \right) ^{1/2}\\ \end{array} \right) . \end{aligned}$$

(45)

Step 4: :

Set ${{\widehat{\alpha }}}_{m,n}({\varvec{g}}){\Leftarrow }{\alpha }(t)$, ${{\widehat{\beta }}}_{m,n}({\varvec{g}}){\Leftarrow }{\beta }(t)$, ${{\widehat{\gamma }}}_{m,n}({\varvec{g}}){\Leftarrow }{\gamma }(t)$. Go to Step 5 if ${{\widehat{\alpha }}}_{m,n}({\varvec{g}})$, ${{\widehat{\beta }}}_{m,n}({\varvec{g}})$ and ${{\widehat{\gamma }}}_{m,n}({\varvec{g}})$ converge, and return to Step 2 otherwise.

Step 5: :

Repeat the following update rule until ${\varvec{{\widehat{f}}}}{\left( {\varvec{{\widehat{\alpha }}}_{m,n}({\varvec{g}})},{\widehat{\beta }}_{m,n}({\varvec{g}}),{{\widehat{\gamma }}}({\varvec{g}})\right) }$ converges:

$$\begin{aligned}&{\varvec{{\widehat{f}}}}{\left( {\varvec{{\widehat{\alpha }}}}_{m,n}({\varvec{g}}),{\widehat{ \beta }}_{m,n}({\varvec{g}}),{{\widehat{\gamma }}}({\varvec{g}})\right) } \Leftarrow {\frac{1}{4{{\widehat{\alpha }}}_{m,n}({\varvec{g}})+{{\widehat{\beta }}}_{m,n}({\varvec{ g}})+{{\widehat{\gamma }}}_{m,n}({\varvec{g}})}} \nonumber \\&\quad {\times }\, \left( {{\widehat{\beta }}}_{m,n}({\varvec{g}}){\varvec{g}} +\left( {{\widehat{\gamma }}}_{m,n}({\varvec{g}}){\varvec{I}}(M,N)\right. \right. \nonumber \\&\quad \left. \left. +\,{{\widehat{\alpha }}}_ {m,n}({\varvec{g}}){\left( 4{\varvec{I}}(M,N)-{\varvec{C}}(M,N)\right) }\right) {\varvec{{\widehat{f}}}}{\left( {\varvec{{\widehat{\alpha }}}_{m,n}({\varvec{g}})}, {\widehat{ \beta }}_{m,n}({\varvec{g}}),{\widehat{\varvec{\gamma }}}\right) } \right) . \end{aligned}$$

(46)

Some restored results ${\varvec{{\widehat{f}}}}{\left( {\varvec{{\widehat{\alpha }}}_{m,n}}({\varvec{g}}^{*}),{{\widehat{\beta }}}_{m,n}({\varvec{g}}^{*}),{{\widehat{\gamma }}}({\varvec{g}}^{*})\right) }$ obtained by applying the above algorithm to degraded images ${\varvec{g}}^{*}$ in Fig. 6 are shown in Figs. 10, 11, 12 and 13. Computational times in the estimation processes of hyperparameters, ${{\widehat{\alpha }}}_{m,n}({\varvec{g}})$, ${{\widehat{\beta }}}_{m,n}({\varvec{g}})$ and ${{\widehat{\gamma }}}_{m,n}({\varvec{g}})$, in the numerical experiments for the degraded images ${\varvec{g}}^{*}$ in Fig. 6 are also shown in Fig. 14. Numerical experimental results of the logarithm of the signal-to-noise ratio $10{\log }_{10}{( {\frac{ {\mathrm{Var}}{\left[ {\varvec{f}}^{*}\right] } }{ {\Vert {\varvec{{\widehat{f}}}}(n,n)-{\varvec{f}}^{*}\Vert }^{2} }} )}$(dB) for the degraded images ${\varvec{g}}^{*}$ in Fig. 6 are shown in Fig. 15. Here, ${\mathrm{Var}}{ [{\varvec{f}}^{*}]}$ is a variance of the light intensities for each colour, red, green and blue, on all the pixels in the original image ${\varvec{f}}^{*}$

Fig. 10

Restored images ${\varvec{{\widehat{f}}}}(M,N)$ for the degraded images ${\varvec{g}}^{*}$ in Fig. 6, such that $m=M$ and $n=N$. a Parrots. b Couple. c Mandrill

Fig. 11

Restored images ${\varvec{{\widehat{f}}}}(m,n)$ for the degraded images ${\varvec{g}}^{*}$ in Fig. 6 in the case of $m=n=256$ such that ${\frac{m}{M}}={\frac{n}{N}}={\frac{3}{4}}$. a Parrots. b Couple. c Mandrill

Fig. 12

Restored images ${\varvec{{\widehat{f}}}}(m,n)$ for the degraded images ${\varvec{g}}^{*}$ in Fig. 6 in the case of $m=n=256$ such that ${\frac{m}{M}}={\frac{n}{N}}={\frac{1}{2}}$. a Parrots. b Couple. c Mandrill

Fig. 13

Restored images ${\varvec{{\widehat{f}}}}(m,n)$ for the degraded images ${\varvec{g}}^{*}$ in Fig. 6 in the case of $m=n=64$ such that ${\frac{m}{M}}={\frac{n}{N}}={\frac{1}{4}}$. a Parrots. b Couple. c Mandrill

Fig. 14

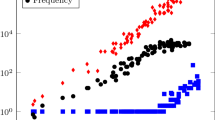
Computational times for the estimation processes of hyperparameters, ${{\widehat{\alpha }}}_{n,n}({\varvec{g}})$, ${{\widehat{\beta }}}_{n,n}({\varvec{g}})$ and ${{\widehat{\gamma }}}_{n,n}({\varvec{g}})$, in the numerical experiments for the degraded images ${\varvec{g}}^{*}$ in Fig. 6. a Parrots. b Couple. c Mandrill

Fig. 15

Logarithm of the signal-to-noise ratio $10{\log }_{10}{( {\frac{ {\mathrm{Var}}{\left[ {\varvec{f}}^{*}\right] } }{ {\Vert {\varvec{{\widehat{f}}}}(n,n)-{\varvec{f}}^{*}\Vert }^{2} }} )}\hbox {(dB)}$. The red, green and blue circles correspond to the results for each light colour intensity. a Parrots. b Couple. c Mandrill

5 Statistical Performance Estimation of Gaussian Graphical Model

In this section, we estimate the statistical performance of our framework of the maximization of the renormalized marginal likelihood ${\rho }^{(m,n)}({\varvec{{\tilde{g}}}}|{\alpha },{\beta },{\gamma })$ in Eq. (36) with Eq. (33). In the present Bayesian inference method, we assume that the data vectors ${\varvec{g}}$ are generated from the conditional probability density function ${\rho }^{(M,N)}({\varvec{g}} | {\varvec{f}},{\beta }^{*})$ in Eq. (4), under the assumption that a parameter vector ${\varvec{f}}={\varvec{f}}^{*}$ is given.

$$\begin{aligned} {\left\{ \begin{array}{ll}{\begin{array}{cc} {{\overline{\alpha }}}_{m,n}({\varvec{f}}^{*}) \equiv {\displaystyle {\int }} {{\widehat{\alpha }}}_{m,n}({\varvec{g}}) {\rho }^{(M,N)}({\varvec{g}} | {\varvec{f}}={\varvec{f}}^{*},{\beta }^{*}) {\text {d}}{\varvec{g}}, \\ {{\overline{\beta }}}_{m,n}({\varvec{f}}^{*}) \equiv {\displaystyle {\int }} {{\widehat{\beta }}}_{m,n}({\varvec{g}}) {\rho }^{(M,N)}({\varvec{g}} | {\varvec{f}}={\varvec{f}}^{*},{\beta }^{*}) {\text {d}}{\varvec{g}}, \\ {{\overline{\gamma }}}_{m,n}({\varvec{f}}^{*}) \equiv {\displaystyle {\int }} {{\widehat{\gamma }}}_{m,n}({\varvec{g}}) {\rho }^{(M,N)}({\varvec{g}} | {\varvec{f}}={\varvec{f}}^{*},{\beta }^{*}) {\text {d}}{\varvec{g}}. \end{array}} \end{array}\right. } \end{aligned}$$

(47)

Equation (47) provides the statistical average of the hyperparameters in the EM algorithm with respect to the probability density function ${\rho }^{(M,N)}({\varvec{g}} | {\varvec{f}}={\varvec{f}}^{*},{\beta }^{*})$. For example, suppose that we generate D degraded images ${\varvec{g}}^{(1)}({\varvec{f}}^{*}),{\varvec{g}}^{(2)}({\varvec{f}}^{*}), {\ldots },{\varvec{g}}^{(D)}({\varvec{f}}^{*})$ from the given original image ${\varvec{f}}^{*}$, and calculate the estimates of hyperparameters for each degraded image ${\varvec{g}}^{(d)}({\varvec{f}}^{*})$ ($d=1,2,{\ldots },D$). Then we can estimate the statistical average of the estimates in the EM algorithm by the sample average of the estimates obtained by applying the EM algorithm to each degraded image ${\varvec{g}}^{(d)}({\varvec{f}}^{*})$. Equation (47) can be regarded as the statistical average of estimates in the EM algorithm with respect to the infinite number of degraded images generated from the probability density function ${\rho }^{(M,N)}({\varvec{g}} |{\varvec{f}}={\varvec{f}}^{*},{\beta }^{*})$ as follows:

$$\begin{aligned} {\left\{ \begin{array}{ll}{\begin{array}{cc} {{\overline{\alpha }}}_{m,n}({\varvec{f}}^{*}) \simeq {\frac{1}{D}} {\displaystyle {\sum _{d=1}^{D}}} {{\widehat{\alpha }}}_{m,n}{\left( {\varvec{g}}^{(d)}({\varvec{f}}^{*})\right) }, \\ {{\overline{\beta }}}_{m,n}({\varvec{f}}^{*}) \simeq {\frac{1}{D}} {\displaystyle {\sum _{d=1}^{D}}} {{\widehat{\beta }}}_{m,n}{\left( {\varvec{g}}^{(d)}({\varvec{f}}^{*})\right) }, \\ {{\overline{\gamma }}}_{m,n}({\varvec{f}}^{*}) \simeq {\frac{1}{D}} {\displaystyle {\sum _{d=1}^{D}}} {{\widehat{\gamma }}}_{m,n}{\left( {\varvec{g}}^{(d)}({\varvec{f}}^{*})\right) }. \end{array}} \end{array}\right. } \end{aligned}$$

(48)

The detailed analysis for the EM algorithm in the case of $M=m$ and $N=n$ appears in Ref. [20].

We consider the average of the logarithm of the renormalized marginal likelihood ${\ln }{({\rho }^{(m,n)}{({\varvec{{\tilde{g}}}}= {\varvec{U}}^{\dag }(m,n){\varvec{B}}(m,n|M,N){\varvec{U}}(M,N){\varvec{g}} \Big |{\alpha },{\beta },{\gamma })})}$ in the probability density function ${\rho }^{(M,N)}({\varvec{g}}|{\varvec{f}}^{*},{\beta }^{*})$ as follows:

$$\begin{aligned}&L_{m,n}{\left( {\alpha },{\beta },{\gamma }\big | {\beta }^{*},{\varvec{f}}^{*}\right) } \equiv {\frac{1}{mn}} {\int } {\rho }^{(M,N)}({\varvec{g}}|{\varvec{f}}={\varvec{f}}^{*},{\beta }^{*}) \nonumber \\&\quad {\times } {\ln }{\left( {\rho }^{(m,n)}{\left( {\varvec{{\tilde{g}}}}= {\varvec{U}}^{\dag }(m,n){\varvec{B}}(m,n|M,N){\varvec{U}}(M,N){\varvec{g}} \Big |{\alpha },{\beta },{\gamma }\right) } \right) } {\text {d}}{\varvec{g}} \end{aligned}$$

(49)

By substituting Eq. (36) to Eq. (49), we can obtain the expression of $L_{m,n}{({\alpha },{\beta },{\gamma }| {\beta }^{*},{\varvec{f}}^{*})}$ in terms of the original image ${\varvec{f}}^{*}$ as follows:

$$\begin{aligned} L_{m,n}{\left( {\alpha },{\beta },{\gamma }\big | {\beta }^{*},{\varvec{f}}^{*}\right) }= & {} {\int } {\rho }^{(M,N)}({\varvec{g}} | {\varvec{f}}={\varvec{f}}^{*},{\beta }^{*}) \left( -{\frac{1}{2}} {\ln }{\left( {\frac{2{\pi }}{{\beta }}} \right) } \right. \nonumber \\&+\,{\frac{1}{2mn}} {\sum _{(k,l){\in }W(m,n)}} {\ln }{\left( {\gamma } +{\alpha } {\lambda }{\left( {\frac{2{\pi }k}{M}},{\frac{2{\pi }l}{N}}\right) } \right) } \nonumber \\&-\,{\frac{1}{2mn}} {\sum _{(k,l){\in }W(m,n)}} {\ln }{\left( {\beta }+{\gamma } +{\alpha } {\lambda }{\left( {\frac{2{\pi }k}{M}},{\frac{2{\pi }l}{N}}\right) } \right) } \nonumber \\&-\,{\frac{1}{2mn}} {\sum _{(k,l){\in }W(m,n)}} {\varvec{g}}^{\mathrm{{T}}}{\varvec{U}}^{\dag }(M,N) {\varvec{B}}^{\mathrm{{T}}}(m,n|M,N)\big |k,l{\rangle } \nonumber \\&\left. {\times }\, {\frac{ {\beta } {\left( {\gamma } +{\alpha } {\lambda }{\left( {\frac{2{\pi }k}{M}},{\frac{2{\pi }l}{N}}\right) } \right) } }{ {\left( {\beta }+{\gamma } +{\alpha } {\lambda }{\left( {\frac{2{\pi }k}{M}},{\frac{2{\pi }l}{N}}\right) } \right) } }} {\langle }k,l\big | {\varvec{B}}(m,n|M,N){\varvec{U}}(M,N){\varvec{g}} \right) \nonumber \\= & {} -{\frac{1}{2}} {\ln }{\left( {\frac{2{\pi }}{{\beta }}} \right) } \nonumber \\&+\,{\frac{1}{2mn}} {\sum _{(k,l){\in }W(m,n)}} {\ln }{\left( {\gamma } +{\alpha } {\lambda }{\left( {\frac{2{\pi }k}{M}},{\frac{2{\pi }l}{N}}\right) } \right) } \nonumber \\&-\,{\frac{1}{2mn}} {\sum _{(k,l){\in }W(m,n)}} {\ln }{\left( {\beta }+{\gamma } +{\alpha } {\lambda }{\left( {\frac{2{\pi }k}{M}},{\frac{2{\pi }l}{N}}\right) } \right) } \nonumber \\&-\,{\frac{1}{2mn}} {\int } {\rho }^{(M,N)}({\varvec{g}} | {\varvec{f}}={\varvec{f}}^{*},{\beta }^{*}) \nonumber \\&{\times }\, \left( {\sum _{(k,l){\in }W(m,n)}} {\varvec{g}}^{\mathrm{{T}}}{\varvec{U}}^{\dag }(M,N) {\varvec{B}}^{\mathrm{{T}}}(m,n|M,N)\big |k,l{\rangle } \right. \nonumber \\&\left. {\times }\, {\frac{ {\beta } {\left( {\gamma } +{\alpha } {\lambda }{\left( {\frac{2{\pi }k}{M}},{\frac{2{\pi }l}{N}}\right) } \right) } }{ {\left( {\beta }+{\gamma } +{\alpha } {\lambda }{\left( {\frac{2{\pi }k}{M}},{\frac{2{\pi }l}{N}}\right) } \right) } }} {\langle }k,l\big | {\varvec{B}}(m,n|M,N){\varvec{U}}(M,N){\varvec{g}} \right) \nonumber \\= & -{\frac{1}{2}} {\ln }{\left( {\frac{2{\pi }}{{\beta }}} \right) } +{\frac{1}{2mn}} {\sum _{(k,l){\in }W(m,n)}} {\ln }{\left( {\gamma } +{\alpha } {\lambda }{\left( {\frac{2{\pi }k}{M}},{\frac{2{\pi }l}{N}}\right) } \right) } \nonumber \\&-\,{\frac{1}{2mn}} {\sum _{(k,l){\in }W(m,n)}} {\ln }{\left( {\beta }+{\gamma } +{\alpha } {\lambda }{\left( {\frac{2{\pi }k}{M}},{\frac{2{\pi }l}{N}}\right) } \right) } \nonumber \\&-\,{\frac{1}{2mn}} {\int } {\rho }^{(M,N)}({\varvec{g}}|{\varvec{f}}={\varvec{f}}^{*},{\beta }^{*}) \nonumber \\&{\times }\, \left( {\sum _{(k,l){\in }W(m,n)}} {\left( {\varvec{g}}-{\varvec{f}}^{*}\right) }^{\mathrm{{T}}} {\varvec{U}}^{\dag }(M,N) {\varvec{B}}^{\mathrm{{T}}}(m,n|M,N)\big |k,l{\rangle } \right. \nonumber \\&\left. {\times }\, {\frac{ {\beta } {\left( {\gamma } +{\alpha } {\lambda }{\left( {\frac{2{\pi }k}{M}},{\frac{2{\pi }l}{N}}\right) } \right) } }{ {\left( {\beta }+{\gamma } +{\alpha } {\lambda }{\left( {\frac{2{\pi }k}{M}},{\frac{2{\pi }l}{N}}\right) } \right) } }} {\langle }k,l\big | {\varvec{B}}(m,n|M,N){\varvec{U}}(M,N){\left( {\varvec{g}}-{\varvec{f}}^{*}\right) } \right) {\text {d}}{\varvec{g}} \nonumber \\&-\,{\frac{1}{2mn}} {\int } {\rho }^{(M,N)}({\varvec{g}}|{\varvec{f}}={\varvec{f}}^{*},{\beta }^{*}) {\text {d}}{\varvec{g}} \nonumber \\&{\times }\, \left( {\sum _{(k,l){\in }W(m,n)}} {\left( {\varvec{f}}^{*}\right) }^{\mathrm{{T}}}{\varvec{U}}^{\dag }(M,N) {\varvec{B}}^{\mathrm{{T}}}(m,n|M,N)\big |k,l{\rangle } \right. \nonumber \\&\left. {\times }\, {\frac{ {\beta } {\left( {\gamma } +{\alpha } {\lambda }{\left( {\frac{2{\pi }k}{M}},{\frac{2{\pi }l}{N}}\right) } \right) } }{ {\left( {\beta }+{\gamma } +{\alpha } {\lambda }{\left( {\frac{2{\pi }k}{M}},{\frac{2{\pi }l}{N}}\right) } \right) } }} {\langle }k,l\big | {\varvec{B}}(m,n|M,N){\varvec{U}}(M,N){\varvec{f}}^{*} \right) . \end{aligned}$$

(50)

By integrating the fourth and fifth term of Eq. (50) with respect to ${\varvec{g}}$, we obtain

$$\begin{aligned} L_{m,n}{\left( {\alpha },{\beta },{\gamma }\big | {\beta }^{*},{\varvec{f}}^{*}\right) }&\equiv {\frac{1}{mn}} {\int } {\rho }^{(M,N)}({\varvec{g}}|{\varvec{f}}={\varvec{f}}^{*},{\beta }^{*}) \nonumber \\&\quad {\times }\, {\ln }{\left( {\rho }^{(m,n)}{\left( {\varvec{{\tilde{g}}}}= {\varvec{U}}^{\dag }(m,n){\varvec{B}}(m,n|M,N){\varvec{U}}(M,N){\varvec{g}} \Big |{\alpha },{\beta },{\gamma }\right) } \right) } {\text {d}}{\varvec{g}} \nonumber \\&= -{\frac{1}{2}} {\ln }{\left( {\frac{2{\pi }}{{\beta }}}\right) } +{\frac{1}{2mn}} {\sum _{(k,l){\in }W(m,n)}} {\ln }{\left( {\frac{ {\gamma }+{\alpha } {\lambda }{\left( {\frac{2{\pi }k}{M}},{\frac{2{\pi }l}{N}}\right) } }{ {\beta }+{\gamma } +{\alpha } {\lambda }{\left( {\frac{2{\pi }k}{M}},{\frac{2{\pi }l}{N}}\right) } }} \right) } \nonumber \\&\quad -\,{\frac{1}{2mn}} {\sum _{(k,l){\in }W(m,n)}} {\frac{ {\beta } {\left( {\gamma } +{\alpha } {\lambda }{\left( {\frac{2{\pi }k}{M}},{\frac{2{\pi }l}{N}}\right) } \right) } }{ {\beta }^{*} {\left( {\beta }+{\gamma } +{\alpha } {\lambda }{\left( {\frac{2{\pi }k}{M}},{\frac{2{\pi }l}{N}}\right) } \right) } }} \nonumber \\&\quad -\,{\frac{1}{2mn}} {\sum _{(k,l){\in }W(m,n)}} ({\varvec{f}}^{*})^{\mathrm{{T}}}{\varvec{U}}^{\dag }(N) {\varvec{B}}^{\mathrm{{T}}}(m,n|M,N)|k,l{\rangle } \nonumber \\&\quad {\times }\, {\frac{ {\beta } {\left( {\gamma } +{\alpha } {\lambda }{\left( {\frac{2{\pi }k}{M}},{\frac{2{\pi }l}{N}}\right) } \right) } }{ {\beta }+{\gamma } +{\alpha } {\lambda }{\left( {\frac{2{\pi }k}{M}},{\frac{2{\pi }l}{N}}\right) } }} {\langle }k,l|{\varvec{B}}(m,n|M,N){\varvec{U}}(M,N){\varvec{f}}^{*}. \end{aligned}$$

(51)

The statistical averages for the estimates of the hyperparameters are given as

$$\begin{aligned}&{\left( {{\overline{\alpha }}}_{m,n}({\varvec{f}}^{*}), {{\overline{\beta }}}_{m,n}({\varvec{f}}^{*}), {{\overline{\gamma }}}_{m,n}({\varvec{f}}^{*})\right) } = {\arg }{\max _{({\alpha },{\beta },{\gamma })}} L_{m,n}{\left( {\alpha },{\beta },{\gamma }\big | {\beta }^{*},{\varvec{f}}^{*}\right) }. \end{aligned}$$

(52)

The statistical performance of our proposed scheme is given by

$$\begin{aligned} D_{m,n}{\left( {\beta }^{*},{\varvec{f}}^{*}\right) }&\equiv {\frac{1}{N^{2}}} {\int } {\left\| {\varvec{f}}- {\varvec{{\widehat{f}}}}{\left( {{\overline{\alpha }}}_{m,n}({\varvec{f}}^{*}), {{\overline{\beta }}}_{m,n}({\varvec{f}}^{*}), {{\overline{\gamma }}}_{m,n}({\varvec{f}}^{*})\big |{\varvec{g}}\right) }\right\| }^{2} \nonumber \\&\quad {\times }\, {\rho }^{(M,N)}({\varvec{g}}|{\varvec{f}}={\varvec{f}}^{*},{\beta }^{*}) {\text {d}}{\varvec{g}} \nonumber \\&= {\frac{1}{MN}} {\sum _{(k,l){\in }W(M,N)}} {\frac{1}{{\beta }^{*}}} {\left( {\frac{ {{\overline{\beta }}}_{m,n}({\varvec{f}}^{*}) }{ {{\overline{\beta }}}_{m,n}({\varvec{f}}^{*}) +{{\overline{\gamma }}}_{m,n}({\varvec{f}}^{*}) +{{\overline{\alpha }}}_{m,n}({\varvec{f}}^{*}) {\lambda }{\left( {\frac{2{\pi }k}{M}},{\frac{2{\pi }l}{N}} \right) }}} \right) }^{2} \nonumber \\&\quad +\, {\frac{1}{MN}} {\sum _{(k,l){\in }W(M,N)}} ({\varvec{f}}^{*})^{\mathrm{{T}}}{\varvec{U}}(M,N)|k,l{\rangle } \nonumber \\&\quad {\times }\, {\left( {\frac{{{\overline{\gamma }}}_{m,n}({\varvec{f}}^{*}) +{{\overline{\alpha }}}_{m,n}({\varvec{f}}^{*}) {\lambda }{\left( {\frac{2{\pi }k}{M}},{\frac{2{\pi }l}{N}}\right) } }{{{\overline{\beta }}}_{m,n}({\varvec{f}}^{*}) +{{\overline{\gamma }}}_{m,n}({\varvec{f}}^{*}) +{{\overline{\alpha }}}_{m,n}({\varvec{f}}^{*}) {\lambda }{\left( {\frac{2{\pi }k}{M}},{\frac{2{\pi }l}{N}}\right) } }} \right) }^{2} {\langle }k,l|{\varvec{U}}(M,N){\varvec{f}}^{*}, \end{aligned}$$

(53)

where

$$\begin{aligned}&{{\widehat{f}}}_{x,y} {\left( {\alpha },{\beta },{\gamma }\big |{\varvec{g}}\right) } = {\int } f_{x,y}{\rho }^{(M,N)}({\varvec{f}}|{\varvec{g}}, {\alpha },{\beta },{\gamma }) {\text {d}}{\varvec{f}}, \end{aligned}$$

(54)

$$\begin{aligned}&{\rho }^{(M,N)}({\varvec{f}}|{\varvec{g}},{\alpha },{\beta },{\gamma }) \equiv {\frac{ {\rho }^{(M,N)}({\varvec{g}}|{\varvec{f}},{\beta }) {\rho }^{(M,N)}({\varvec{f}}|{\alpha },{\gamma })}{{\rho }^{(M,N)}({\varvec{g}}|{\alpha },{\beta },{\gamma })}}. \end{aligned}$$

(55)

Statistical averages of logarithm of the signal-to-noise ratio, $10{\log }_{10}{( {\frac{ {\mathrm{Var}}[{\varvec{f}}^{*}] }{D_{n,n}({\beta }^{*},{\varvec{f}}^{*})}} )}$(dB) ($m=n$) in Eq. (53) for the original images ${\varvec{f}}^{*}$ in Fig. 3 are shown in Fig. 16. Statistical averages of the hyperparameters, ${{\overline{\alpha }}}_{n,n}({\varvec{f}}^{*})$, ${{\overline{\beta }}}_{n,n}({\varvec{f}}^{*})$ and ${{\overline{\gamma }}}_{n,n}({\varvec{f}}^{*})$, are shown in Figs. 17, 18 and 19, respectively. Flows of estimates of the hyperparameters, ${( {{\overline{\alpha }}}_{n,n}({\varvec{f}}^{*}), {{\overline{\beta }}}_{n,n}({\varvec{f}}^{*}))}$ and ${( {{\overline{\alpha }}}_{n,n}({\varvec{f}}^{*}), {{\overline{\gamma }}}_{n,n}({\varvec{f}}^{*}))}$, in the momentum-space renormalization transformation in the EM algorithm of the Gaussian graphical model for the original images ${\varvec{f}}^{*}$ in Fig. 3 are shown in Figs. 20 and 21. These flows in Fig. 20 are drawn by plotting ${\left( {{\overline{\alpha }}}_{n,n}({\varvec{f}}^{*}), {{\overline{\beta }}}_{n,n}({\varvec{f}}^{*})\right) }$ in Figs. 17 and 18 and the flows in Fig. 21 are drawn by plotting ${\left( {{\overline{\alpha }}}_{n,n}({\varvec{f}}^{*}), {{\overline{\gamma }}}_{n,n}({\varvec{f}}^{*})\right) }$ from Figs. 17 and 19.

Fig. 16

Statistical average of the logarithm of the signal-to-noise ratio, $10{\log }_{10}{( {\frac{ {\mathrm{Var}}[{\varvec{f}}^{*}] }{D_{n,n}({\beta }^{*},{\varvec{f}}^{*})}} )}\hbox {(dB)}$ ($m=n$) in Eq. (53) for the original images in Fig. 3. The red, green and blue circles correspond to the results for each light colour intensity. a Parrots. b Couple. c Mandrill

Fig. 17

Statistical average ${{\overline{\alpha }}}_{n,n}={{\overline{\alpha }}}_{n,n}({\varvec{f}}^{*})$ in Eq. (52) for the original images in Fig. 3. The red, green and blue circles correspond to the results for each light colour intensity. a Parrots. b Couple. c Mandrill

Fig. 18

Statistical average ${{\overline{\beta }}}_{n,n}={{\overline{\beta }}}_{n,n}({\varvec{f}}^{*})$ in Eq. (52) for the original images in Fig. 3. The red, green and blue circles correspond to the results for each light colour intensity. a Parrots. b Couple. c Mandrill

Fig. 19

Statistical average ${{\overline{\gamma }}}_{n,n}={{\overline{\gamma }}}_{n,n}({\varvec{f}}^{*})$ in Eq. (52) for the original images in Fig. 3. The red, green and blue circles correspond to the results for each light colour intensity. a Parrots. b Couple. c Mandrill

Fig. 20

Flows of $({{\overline{\alpha }}}_{n,n}({\varvec{f}}^{*}), {{\overline{\beta }}}_{n,n}({\varvec{f}}^{*}))$ in the MSRG transformations in the EM algorithm of the Gaussian graphical model for the original images in Fig. 3. The red, green and blue circles correspond to the results for each light colour intensity. a Parrots. b Couple. c Mandrill

Fig. 21

Flows of $({{\overline{\alpha }}}_{n,n}({\varvec{f}}^{*}), {{\overline{\gamma }}}_{n,n}({\varvec{f}}^{*}))$ in the MSRG transformations in the EM algorithm of the Gaussian graphical model for the original images in Fig. 3. The red, green and blue circles correspond to the results for each light colour intensity. a Parrots. b Couple. c Mandrill

For the limits of ${\frac{n}{N}}{\rightarrow }+0$ and ${\frac{m}{M}}{\rightarrow }+0$, ${\rho }^{(m,n)}{({\varvec{{\tilde{f}}}}\big |{\alpha },{\gamma })}$ in Eq. (26) and ${\rho }^{(m,n)}{({\varvec{{\tilde{g}}}}| {\varvec{{\tilde{f}}}},{\alpha },{\beta })}$ in Eq. (34), are reduced to ${\rho }^{(m,n)}{({\varvec{{\tilde{f}}}} |{\alpha }=0,{\gamma })}$ and ${\rho }^{(m,n)}{ ({\varvec{{\tilde{g}}}}| {\varvec{{\tilde{f}}}},{\beta })}$, respectively. This means that the joint probability density function ${\rho }^{(m,n)}{({\varvec{{\tilde{f}}}},{\varvec{{\tilde{g}}}} |{\alpha },{\beta },{\gamma })}$ has a fixed point at ${( 0, {\beta }, {\gamma })}$ in the scale transformations in Eqs. (23) and (33). In ${\frac{n}{N}}>{\frac{1}{4}}$ and ${\frac{m}{M}}>{\frac{1}{4}}$, the estimates, ${{\widehat{\alpha }}}_{m,n}({\varvec{g}})$, ${{\widehat{\beta }}}_{m,n}({\varvec{g}})$ and ${{\widehat{\gamma }}}_{m,n}({\varvec{g}})$ are located along the flow by MSRG transformation. In ${\frac{n}{N}}<{\frac{1}{4}}$ and ${\frac{m}{M}}<{\frac{1}{4}}$, they leave from the flow. In Fig. 9, it is seen that the noise in the reduced image ${\varvec{{\tilde{g}}}}$ is hardly recognized for ${\frac{n}{N}}={\frac{1}{4}}$ and ${\frac{m}{M}}={\frac{1}{4}}$. In fact, the hyperparameter ${\beta }$ corresponds to the inverse of the variance in the additive white Gaussian noise, and then ${{\widehat{\beta }}}_{m,n}({\varvec{g}})$ rapidly increases although ${{\widehat{\alpha }}}_{m,n}({\varvec{g}})$ and ${{\widehat{\gamma }}}_{m,n}({\varvec{g}})$ remain near the renormalization flow within the limit of ${\frac{n}{N}}{\rightarrow }+0$ and ${\frac{m}{M}}{\rightarrow }+0$.

6 Concluding Remarks

In the present review paper, we have summarized the MSRG approaches for the Gaussian graphical models in a finite-size square grid graph. We have provided the formulations and a practical algorithm for noise reduction applications in image processing using the Bayesian sublinear computational time modeling. Moreover, we derive also the statistical performance schemes of the above systems. from the statistical–mechanical point of view. The estimated results of the hyperparameters are first located along the flow of the MSRG transformations in the region ${\frac{mn}{MN}}>{ ({\frac{1}{4}})}^{2}$. However, the sublinear modeling cannot recognize the noise in the reduced image ${\varvec{{\tilde{g}}}}$ in the region ${\frac{mn}{MN}}<{({\frac{1}{4}})}^{2}$ and then the estimate of the hyperparameter ${\beta }$, which corresponds to the inverse of the variance in the additive white Gaussian noise, goes to infinity with ${\frac{mn}{MN}}$ decreasing in the region.

We consider finite-size system only, and our formulation is within the discrete Fourier transformation. However, if we consider a system size with infinity as the limit, such that $M{\rightarrow }+{\infty }$ and $N{\rightarrow }+{\infty }$, the state vector ${\varvec{f}}$ would be composed of an infinite number of components. At this stage, $f_{x,y}$ is a function of x and y which are any real number in $(-{\infty }+{\infty }$, and which can then be rewritten as f(x, y). ${\rho }{({\varvec{f}}|{\alpha },{\gamma })}$ is a functional of ${\varvec{f}}={\{f(x,y) |(x,y){\in }(-{\infty },+{\infty })^{2}\}}$ and is given by

$$\begin{aligned}&{\rho }{\left( {\varvec{f}}\big |{\alpha },{\gamma }\right) } \propto {\exp }\left( -{\frac{1}{2}}{\alpha } {\int _{-{\infty }}^{+{\infty }}} {\int _{-{\infty }}^{+{\infty }}} {\left( {\left( {\frac{{\partial }}{{\partial }x}}f(x,y)\right) }^{2} + {\left( {\frac{{\partial }}{{\partial }y}}f(x,y)\right) }^{2} \right) }{\text {d}}x{\text {d}}y \right. \nonumber \\&\quad \left. -{\frac{1}{2}}{\gamma } {\int _{-{\infty }}^{+{\infty }}} {\int _{-{\infty }}^{+{\infty }}} {f(x,y)}^{2}{\text {d}}x{\text {d}}y \right) , \end{aligned}$$

(56)

instead of Eq. (2). For the probability density function in Eq. (56), the integral ${\int }({\cdots }){\text {d}}{\varvec{f}}$ means a functional integral. This is a starting point of the statistical field theory in the physics [25,26,27]. Big data sciences are characterized by extremely large dimensional state vectors, and we expect that the statistical field theory should provide powerful applications in such cases.Indeed, this theory is one of the most exciting research paradigms for sublinear computational time modeling in the data sciences.