The component outage model for power systems using availability approximations

Abstract

The traditional outage models with constant failure rates do not truly reflect the environmental and operating conditions nor the effect of repair operations on power systems. This paper proposes two useful approximations for the availability function based only on the first three of the lifetime distribution. We compare the availability function of a power transformer using the numerical inverse of the transformed availability function. It also suggests methods to verify the effectiveness of the approaches. Finally, it outlines the proposed approximations to validate the efficacy of the approximations.

1 Introduction

Power systems components and reliability are crucial in planning and managing the energy sector. There has been an ever-increasing need for accurate outage models for the reliability assessment of such systems. Although models using simulation and other reliability tools have previously appeared, Markov models have proved useful and are still widely used in reliability models. Although this is the case, most models use their analysis’s constant failure rates from outdated statistical data. While these models can be considered initial approximations, their predictions should not be considered safe reliability measures of sophisticated and sensitive systems such as power systems. The ageing of power systems leads to a bathtub failure rate. While short-term reliability may accept a constant failure rate, summing plays a key role in long-timescale problems and must be incorporated into the model. Besides, system maintenance significantly affects failure rates. Earlier models allowed the concepts of good as new or bad as old maintenance. It should also be noted that power systems enjoy maintenance actions. At the same time, power systems enjoy maintenance actions that fall between these two categories and can be referred to as general repairs [1]. These maintenance actions have an apparent impact on the failure rate. What is more, operating conditions profoundly affect the failure rates of the systems. Hence, there is a need for accurate outage models with varying failure rates.

Components are subject to deterioration over time due to ageing. Manufacturers tend to ignore this fact as they focus solely on reliability. Recently Zheng et al. [2] considered the importance measures of components in a smart electric power grid system in terms of availability functions. Alvarez-Alvarado et al. [3] presented a comprehensive reliability model for production capability with the help of a new mathematical formulation derived from the concept of the Markov chain, which predicts that the component deteriorates by ageing. On the other hand, Alvarez-Alvarado et.al. [4] used Markov Chains to model the component’s lifetime to achieve repair rates. Moreover, a close review of the relevant literature reveals that preventive maintenance outage problems are gaining importance. For instance, Abiri-Jahromi et al. [5] have addressed the issue of preventive maintenance interruption planning, allowing thermal units to create maintenance interruption models based on cost/benefit analysis of maintenance tasks. Similarly, Hou et al. [6] proposed a Continuous-time Markov chain model using outage and repair rates. They concluded that their model is more efficient, especially in small-scale or reliable power systems. Martorell et al. [7] presented a new age-dependent reliability model in another study. The model includes surveillance and maintenance effectiveness related to new nuclear power plants. This model can support life management and life extension programs by improving or optimizing new nuclear power plants. Preventive maintenance components (PM) is a system that provides a solution when the deterioration level of a component reaches a critical point. Recently Javed et al. [8] proposed a sizing approach for an off-grid power system to supply a minimum power threshold during power disruption events. The use of maintenance policy has shown that complex multi-unit systems have significant potential to reduce service costs. An optimal maintenance period can be determined when planned preventive maintenance is carried out for the entire system. Moreover, Shafiee and Finkelstein [9] compared individual care policies based on age and condition without planned care. In a lifetime, deteriorating systems appear in every field. A study by Wang et al. [10] discussed the bridge resistance and concluded that over time, the bridge reliability deteriorates and causes economic losses due to road freight volumes. He presented a new model for the degradation process and revealed the properties that did not decrease during the process. Auto-correlation is also included in the said model. Time-dependent reliability is sensitive to selecting the type of deterioration early in the service life. It has become less sensitive to deterioration as the service time increases.

Ji et al. [11] proposed an alternative renewal process-based component outage model with a staircase function in an attempt to identify the impact of transition on the failure rate. However, their success was limited to the transformed availability function for two steps using the staircase function and steady-state availability for the general N-step staircase function. Our motivation is that, although their approach gives a viable alternative to transient failure rate outage models, the all-important function could not be obtained. In this paper, we propose two failure rate outage models. In line with the purposes of the present study, two approximations are introduced to calculate the availability function based on the first three moments of the failure time and repair distribution. Availability measure confrontations require the explicit form of the failure time and repair distributions. This fundamental assumption may not work in several practical applications, such as reliability, queuing, and inventory problems. At best, one might own the statistical characteristics of the underlying distributions. There are several cases where the moments of distributions are easily obtained, but the underlying theoretical distribution is not available in a closed function. As in the case of power systems, efficient estimators of the moments could be obtained from the observed historical data. Therefore, our approximations make a significant contribution. Our methods are robust in choosing distributions and parameters and are easy to implement.

The layouts of the present paper are as follows: In Sect. 2, we introduce the basics of alternating processes and availability functions. Section 3 presents the two approximations for the availability function that recapitulate some availability function results when the staircase function approximates the time-varying failure rate. Section 4 is devoted to using the ageing failure rate of a transformer as a vehicle of illustration to compute the availability function explicitly. Finally, the concluding remarks are presented in Sect. 5.

2 Availability function and some approximations

Consider an alternating renewal process, with up and down states denoted by U and D respectively. Let the sequence independently specify the duration of the two states and identically distributed random variables $U_n$ and $D_n$, and we define the Z by $Z=U+D$.

2.1 Notations

$F_U$, $f_U$::

The distribution and the density function, respectively, of the up times U.

$F_D$, $f_D$::

The distribution and the density function, respectively, of the down times D.

$F_Z$, $f_Z$::

The distribution and the density function, respectively, of the $Z=U+D$.

$M_U(t)$::

The renewal function of the process $U_n$.

$M_D(t)$::

The renewal function of the process $D_n$.

A(t)::

The availability function of the process $Z_n=U_n+D_n$.

$\mu _{{rU}}$::

The r-order central moments of the up times U, for $r=1,2,\ldots$,

$$\begin{aligned} \mu _{{rU}}=E\big [\,U^r\,\big ]. \end{aligned}$$

$\mu _{{rD}}$::

The r-order central moments of the down times D, for $r=1,2,\ldots$,

$$\begin{aligned} \mu _{{rD}}=E\big [\,D^r\,\big ]. \end{aligned}$$

$\mu _{{rZ}}$::

The r-order central moments of $Z=U+D$, for $r= 1,2,\ldots$,

$$\begin{aligned} \mu _{{rZ}}=E\big [\,Z^r\,\big ]. \end{aligned}$$

$f*g$::

The convolution between the functions f and g,

$$\begin{aligned} \big (f*g\big )(t)=\int _0^t\, f(t-v)g(v)dv,\quad \text {for \,}\, t\ge 0. \end{aligned}$$

$f^{*}$::

The Laplace transform of a function f,

$$\begin{aligned} f^*(s)=\int _0^{\infty }\, e^{-st}f(t)\,dt,\quad \text {for \,}\, s\ge 0. \end{aligned}$$

Remark 1

The corresponding renewal functions of the up and down states as well as the availability function is known to satisfy the following integral equations [12]:

$$\begin{aligned} M_D(t)=&\,F_{Z}(t)+\int _0^t M_D(t-x) \,dF_{Z}(x), \nonumber \\ M_U(t)=&\,F_{U}(t)+\int _0^t M_U(t-x) \, dF_{Z}(x), \nonumber \\ A(t)=&\,\big [ \, 1 - F_{U}(t)\,\big ]+ \int _0^t A(t-x)\, dF_Z(x). \end{aligned}$$

Remark 2

Applying Laplace transform on both sides of the above equations yield [13]:

$$\begin{aligned} M_D^*(s)=&\,\frac{f_U^*(s)\,f_D^*(s)}{s\Big (1-f_U^*(s)\,f_D^*(s)\Big )}, \nonumber \\ M_U^*(s)=&\,\frac{f_U^*(s)}{s\Big (1-f_U^*(s)\,f_D^*(s)\Big )}, \nonumber \\ A^*(s)=&\,\frac{1-f_{U}^*(s)}{s\Big (1-f_{Z}^*(s)\Big )}. \end{aligned}$$

(1)

It is also well known that the availability and renewal functions are related through the following:

$$\begin{aligned} A(t)= M_D(t)-M_U(t)+1. \end{aligned}$$

The steady-state availability A is given by:

$$\begin{aligned} A=&\lim _{t\rightarrow \infty } A(t)=\frac{\mu _{{1U}}}{\mu _{{1U}} + \mu _{{1D}}}. \end{aligned}$$

The availability function can be expressed in terms of the renewal functions of the number of failures and repairs. Since there is extensive literature available on approximations of renewal functions (see for example [14,15,16]). Arunachalam et al. in [13] found two approximations to the availability function. These are nonparametric because they do not require the explicit form of the distribution functions $F_U$, $F_D$ and $F_Z$ and require only their first three moments. These approximations are given by:

Proposition 1

(Approximation 1) Suppose that the first two raw moments $\mu _{{1U}}$, and $\mu _{{2U}}$ of the up times and $\mu _{{1D}}$, and $\mu _{{2D}}$ of the down times exist and are known. Then we have the following approximation to the availability function A(t):

$$\begin{aligned} A_1(t)= \frac{\mu _{{1U}}}{\mu _{{1U}}+\mu _{{1D}}}+\frac{\mu _{{1D}}}{\mu _{{1U}}+\mu _{{1D}}}\,\, e^{s_0t}, \end{aligned}$$

(2)

where

$$\begin{aligned} s_0=-\frac{2\, \mu _{{1Z}}\, \mu _{{1D}}}{\mu _{{1U}}\,\mu _{{2 Z}}-\mu _{{1 Z}}\,\mu _{{2U}}}. \end{aligned}$$

(3)

Proposition 2

(Approximation 2) Suppose that the first two raw moments $\mu _{{1U}}$, and $\mu _{{2U}}$ of the up times as well as the first three moments $\mu _{{1Z}}$, $\mu _{{2Z}}$ and $\mu _{{3Z}}$ of the sum of the up and down times exist and are known. Then the availability function A(t) can be approximated by:

$$\begin{aligned} A_2(t)= \frac{2\mu _{{1Z}}^2\,e^{s_1t}+2\mu _{{1U}}\mu _{{1Z}}\,\big (1-e^{s_2t}\big ) -\mu _{{2Z}}\big (e^{s_1t}-e^{s_2t}\big )}{2\mu _{{1Z}}^2}, \end{aligned}$$

(4)

where

$$\begin{aligned} s_1=&-\frac{\,6\big (\mu _{{2Z}}-2\mu _{{1Z}}^2\big )\,\mu _{{1Z}}}{2\mu _{{3Z}}\mu _{{1Z}}-3\mu _{{2Z}}^2}, \end{aligned}$$

(5)

$$\begin{aligned} s_2=&-\frac{6\big (\mu _{{2Z}}-2\mu _{{1U}}\mu _{{1Z}}\big )\,\mu _{{1Z}}}{2\mu _{{3Z}}\mu _{{1Z}}-3\mu _{{2Z}}^2+6\mu _{{2Z}}\mu _{{1Z}}\mu _{{1U}}-6\mu _{{2U}}\mu _{{1Z}}^2}. \end{aligned}$$

(6)

The proofs of the above assertions are given in [13].

3 A component outage model with transient failure rate

If a component is working after some initial time and an outage occurs, then the component is repaired and must return to the working state when the repairs are completed. The component’s state after the repair is the same as the initial state. If $U_n$ represents the time of working of the component for the nth time, and $D_n$ denotes the repair duration for the nth time, then the nth renewal period can be expressed as $Z_n = U_n + D_n$. Renewal takes place when the component returns to the working state after repair. In addition, we can suppose that the different renewal periods are independent and identically distributed. All the results presented in this section are shown in the Appendix. We suppose that the density function for the random variable $D_n$ is given by:

$$\begin{aligned} f_D(t)=\mu e^{-\mu t}, \quad \text {if}\quad t\geqslant 0. \end{aligned}$$

(7)

3.1 Staircase with two steps

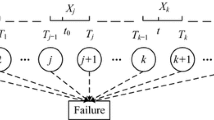
If the staircase functions with two steps are used to approximate the component ageing failure rate in a model of a lifetime (Fig. 1, left), that is, if U represents the component lifetime where $\lambda (t)$ is its failure rate, we can consider that,

$$\begin{aligned} \lambda (t)={\left\{ \begin{array}{ll} \lambda _1, &{} \text {if}\quad 0=t_0\le t <t_1,\\ \lambda _2,&{} \text {if}\quad t_1\ge t, \end{array}\right. } \end{aligned}$$

(8)

and we suppose that U has a partial exponential comportment in each one of the intervals $[0,t_1)$ and $[t_1,\infty )$, then, the availability function Laplace transform is,

Fig. 1

Aging failure rates. Left: Two steps. Right: n steps

$$\begin{aligned} A^(s)=\frac{(s+\mu )\Big [e^{t_1(s+\lambda _1)}\big (s+\lambda _2\big )+\lambda _1-\lambda _2\Big ]}{s\Big [e^{t_1(s+\lambda _1)}\big (s+\lambda _1+\mu \big ) \big (s+\lambda _2\big )+\mu \big (\lambda _1-\lambda _2\big )\Big ]}. \end{aligned}$$

In general, it is not possible to calculate the inverse Laplace transform with analytical methods, and then it will have resorted to the approximations (2) and (4). In many cases, it is only interesting to know how the steady availability function is, and that is:

$$\begin{aligned} A:=\lim \limits _{t\rightarrow \infty }A(t)=\frac{\mu \Big (\lambda _2-\big (\lambda _2-\lambda _1\big )e^{-\lambda _1t_1}\Big )}{\lambda _2\big (\mu +\lambda _1\big )-\mu \big (\lambda _2-\lambda _1\big )e^{-\lambda _1t_1}}. \end{aligned}$$

3.2 General case: Staircase with n steps

If $n\ge 1$, a partition $\big \{t_0,t_1,t_{n-1},t_n\big \}$ of the interval $[0,\infty ]$ is constructed (Fig. 1, right), with

$$\begin{aligned} 0=t_0<t_1<\cdots<t_{n-1}<t_n=\infty , \end{aligned}$$

and thus is defined $\lambda$ by,

$$\begin{aligned} \lambda (t)={\left\{ \begin{array}{ll}\lambda _1, &{}\text {if}\quad t_{0}\le t< t_1,\\ \lambda _2, &{}\text {if}\quad t_{1}\le t< t_2,\\ &{}\vdots \\ \lambda _n, &{}\text {if}\quad t_{n-1}\le t< t_n, \end{array}\right. } \end{aligned}$$

(9)

and it is supposed that U has a partial exponential comportment in each one of the intervals $[t_{k-1},t_{k}),k=0,\ldots ,n-1$ and $[t_{n-1},\infty )$.

In this case, we will use Eqs. (2) and (4), to approximate the availability function A(t), for which it is necessary to establish explicit formulas for $\mu _{{rU}}$, $\mu _{{rD}}$ and $\mu _{{rZ}}$, $r=1,2,3$, which will be deducted in the Appendix.

4 Numerical illustration of an actual transformer

The Weibull distribution function generally represents failure times of electronic and power systems whose failure rate curves are tub-shaped. Ji et al. [11] considered the parameters of the Weibull distribution failure rate as a vehicle of illustration for the components for a 230/115 kV,200MVA transformer [11]. These values and their total are presented in Table 1.

Table 1 Failure rate for a transformer

The repair times are assumed to be exponentially distributed with $\mu =$ 18/years. The ageing of the fault rate for the transformer leakage (Weibull(3.57, 15.98)) was approximated, as in [11]. We now move on to analyse four different values of n and $\lambda (t)$ values [11], which yield the following models and by using results obtained in Eqs. (3), (5), (6) and in the Appendix, and we obtained moments values and also the constants $s_0, s_1$ and $s_2$ are summarized in the Table 2.

model 1: $n=7.$ :

$$\begin{aligned} \lambda (t)={\left\{ \begin{array}{ll} 0.01, &{} \text { if }\quad 0\le t<10,\\ 0.12, &{} \text { if }\quad 10\le t<15,\\ 0.26, &{} \text { if }\quad 15\le t<20,\\ 0.5, &{} \text { if }\quad 20\le t<25,\\ 0.85, &{} \text { if }\quad 25\le t<30,\\ 1.34, &{} \text { if }\quad 30\le t<35,\\ 1.62, &{} \text { if }\quad 35\le t<\infty . \end{array}\right. } \end{aligned}$$

model 2: $n=3.$ :

$$\begin{aligned} \lambda (t)={\left\{ \begin{array}{ll} 0.01, &{} \text { if }\quad 0\le t<10,\\ 0.36, &{} \text { if }\quad 10\le t<25,\\ 0.64, &{} \text { if }\quad 25\le t<\infty . \end{array}\right. } \end{aligned}$$

model 3: $n=1$, small.:

$$\begin{aligned} \lambda (t)= 0.005,\ \text { if }\quad \ 0\le t<\infty . \end{aligned}$$

model 4: $n=1$, large.:

$$\begin{aligned} \lambda (t)= 1.07, \ \text { if }\quad \ 0\le t<\infty . \end{aligned}$$

Table 2 The values moments and coefficient values for Models 1–4

Fig. 2

Distribution functions for the Models 1–4 and the Weibull(3.57,15.98)

Fig. 3

Approximation 1 for the Availability functions in Models 1–4

Fig. 4

Approximation 2 for the Availability functions in Models 1–4

According to (12), the graphs of the distribution functions of the approximations and the Weibull distribution (3.57, 15.98) graphic are given in Figure 2. While the distribution functions in Models 1 and 2 are quite acceptable, those in Models 3 and 4 are not. However, we will use them for comparison.

Now, using the formulas (2) and (4), we will present approximate results of the availability function over time (Tables 3 and 4), as well as their corresponding graphs (Figs. 3 and 4). It is important to note that the current study attempts to provide the approximate calculation of the availability functions for the different models, as Ji et al. [11], only present the results for the steady-state availability. It is observed from the tables and figures that our results match those of Ji et al. [11]. The values of steady availability found by Ji et al. are 0.9957, 0.9948, 0.9998, and 0.9445, which correspond to Models 1, 2, 3, and 4, respectively, and coincide with the values found here, in three significative digits. The presented approximations calculated for values much larger than $t = 50$, the results of the availability functions would be much closer to the values of the steady availabilities. (See Appendix B: Tables 3 and 4).

5 Concluding remarks

This paper proposes two useful approximations to evaluate availability functions numerically. They efficiently assess and give exact values for the commonly used exponential lifetime distributions. These approximations are non-parametric because one does not necessarily know the underlying failure time distributions. This aspect makes approximations a convenient tool for reliability practitioners. As approximation 2 involves the third moment $\mu _{3Z}$ of the total time, the method will be robust even for highly skewed lifetime distributions. Furthermore, the approximations provide exact values when the underlying distributions are exponential, approximating the time-varying failure rate by piece-wise constant failure rates. Then, computing the availability functions using their approximations is bound to yield accurate results. Finally, such a procedure eliminates the need for computationally expensive Monte Carlo simulation. The proposed moment-based approximation is particularly useful for practitioners to calculate the availability function when there is no knowledge of the form of the distribution function. We have mentioned only some distributions and plan to consider some frequently used distributions in power systems. In this paper, we have considered only the first two moments, considering that higher-order moments require additional parameters, which could increase the estimation error.

Appendices

Appendix A Appendix: Analytic derivations

1.1 A.1 Staircase with two steps

1.1.1 A.1.1 Distribution function of the ${\textbf{U}}$

If the ageing failure rate is given by (8) and we suppose that U has partial exponential comportment in each one of the intervals $[0,t_1)$ and $[t_1,\infty )$, so if $U\le t_1$, U has a truncated exponential distribution with rate $\lambda _1$, while if $U> t_1$, U has a delayed exponential distribution with rate $\lambda _2$. That is:

$$\begin{aligned} P(U\leqslant t\,\big |\, U\le t_1)&={\left\{ \begin{array}{ll}0, &{}\text {if}\quad t<0,\\ \frac{1-e^{-\lambda _1 t}}{1-e^{-\lambda _1 t_1}},&{} \text {if}\quad t\in [0,t_1),\\ 1, &{}\text {if}\quad t\ge t_1. \end{array}\right. }\\ P(U\leqslant t\,\big |\, U> t_1)&={\left\{ \begin{array}{ll}0, &{}\text {if}\quad t<t_1,\\ 1-e^{-\lambda _2 (t-t_1)}, &{}\text {if}\quad t\ge t_1. \end{array}\right. } \end{aligned}$$

Additionally,

$$\begin{aligned} P(U\le t_1)=&1-e^{-\lambda _1t_1},\\ P(U>t_1)=&1-P(U\le t_1)=e^{-\lambda _1t_1}. \end{aligned}$$

Then,

$$\begin{aligned} F_U(t):=P(U\le t)&=P(U\le t\mid U\le t_1)P(U<t_1)+P(U\le t\mid U> t_1)P(U\ge t_1)\nonumber \\&= {\left\{ \begin{array}{ll}\left( \frac{1-e^{-\lambda _1t}}{1-e^{-\lambda _1t_1}}\right) (1-e^{-\lambda _1t_1})+0\cdot e^{-\lambda _1t_1}, &{}\text {if}\quad t<t_1,\\ 1 \cdot (1-e^{-\lambda _1t_1})+\left( 1-e^{-\lambda _2(t-t_1)}\right) e^{-\lambda _1t_1}, &{}\text {if}\quad t\ge t_1,\end{array}\right. }\nonumber \\&={\left\{ \begin{array}{ll}1-e^{-\lambda _1t}, &{}\text {if}\quad t<t_1,\\ 1-e^{-\lambda _2 t+(\lambda _2-\lambda _1)t_1}, &{}\text {if}\quad t\ge t_1.\end{array}\right. } \end{aligned}$$

(10)

By deriving the above result, it is obtained the lifetime density function:

$$\begin{aligned} f_U(t)&:= {\left\{ \begin{array}{ll}\lambda _1e^{-\lambda _1t}, &{}\text {if}\quad 0\le t<t_1,\\ \lambda _2e^{-\lambda _2 t+(\lambda _2-\lambda _1)t_1}, &{}\text {if}\quad t\ge t_1.\end{array}\right. } \end{aligned}$$

1.1.2 A.1.2 Laplace transform of the availability function for the process $\mathbf {\{Z_n\}}$

$$ \begin{aligned} & f_{U}^{*} (s) = \int_{0}^{{t_{1} }} {e^{{ - st}} } \lambda _{1} e^{{\lambda _{1} t}} dt + \int_{{t_{1} }}^{\infty } {e^{{ - st}} } \lambda _{2} e^{{ - \lambda _{2} t + (\lambda _{2} - \lambda _{1} )t_{1} }} dt \\ & = \frac{{e^{{ - st_{1} - \lambda _{1} t_{1} }} \left[ {\lambda _{1} e^{{st_{1} + \lambda _{1} t_{1} }} \left( {s + \lambda _{2} } \right) + s\left( {\lambda _{2} - \lambda _{1} } \right)} \right]}}{{\left( {s + \lambda _{1} } \right)\left( {s + \lambda _{2} } \right)}}, \\ & {\text{and}},\quad f_{D}^{*} (s) = \frac{\mu }{{s + \mu }}. \\ \end{aligned} $$

As U and D are independents, and $Z=U+D$,

$$\begin{aligned} f_Z^*(s)&=(f_U*f_D )^*(s)=\big (f_U^*(s)\big )\big (f_D^*(s)\big )\\&=\frac{\mu e^{-st_1-\lambda _1t_1}\Big [\lambda _1e^{st_1+\lambda _1t_1}\big (s+\lambda _2\big )+s\big (\lambda _2-\lambda _1\big )\Big ]}{\big (s+\lambda _1\big )\big (s+\lambda _2\big )\big (s+\mu \big )}. \end{aligned}$$

Then, by (1),

$$\begin{aligned} A^*(s)&= \frac{1-f_U^*(s)}{s\big (1-f_Z^*(s)\big )}\\&=\frac{(s+\mu )\Big [e^{t_1(s+\lambda _1)}\big (s+\lambda _2\big )+\lambda _1-\lambda _2\Big ]}{s\Big [e^{t_1(s+\lambda _1)}\big (s+\lambda _1+\mu \big )\big (s+\lambda _2\big )+\mu \big (\lambda _1-\lambda _2\big )\Big ]}. \end{aligned}$$

1.1.3 A.1.3 Moments for U, D and Z

$$\begin{aligned} \mu _{{1U}}&=\int _0^{t_1} t\,\lambda _1 e^{\lambda _1t}\, dt +\int _{t_1}^{\infty } t\, \lambda _2e^{-\lambda _2 t+(\lambda _2-\lambda _1)t_1}\,dt\\&\quad =\frac{e^{-\lambda _1t_1}\big (\lambda _1-\lambda _2\big )}{\lambda _1\lambda _2}+\frac{1}{\lambda _1},\\ \mu _{{2U}}&=\int _0^{t_1} t^2\,\lambda _1 e^{\lambda _1t}\, dt +\int _{t_1}^{\infty } t^2\, \lambda _2e^{-\lambda _2 t+(\lambda _2-\lambda _1)t_1}\,dt\\&\quad =\frac{2e^{-\lambda _1t_1}\Big [\lambda _1\lambda _2t_1\big (\lambda _1-\lambda _2\big )\Big ]}{\lambda _1^2\lambda _2^2}+\frac{2}{\lambda _1^2},\\ \mu _{{3U}}&=\int _0^{t_1} t^3\,\lambda _1 e^{\lambda _1t}\, dt +\int _{t_1}^{\infty } t^3\, \lambda _2e^{-\lambda _2 t+(\lambda _2-\lambda _1)t_1}\,dt\\&\quad =\frac{3e^{-\lambda _1t_1}\Big [\lambda _1^2\lambda _2^2t_1^2\big (\lambda _1-\lambda _2\big )+2\lambda _1\lambda _2t_1\big (\lambda _1^2-\lambda _2^2\big ) +2\lambda _1^3-2\lambda _2^3\Big ]}{\lambda _1^3\lambda _2^3}+\frac{6}{\lambda _1^3},\\ \mu _{{1D}}&=\int _0^{\infty } t\,\mu e^{\mu t}\, dt =\frac{1}{\mu },\\ \mu _{{2D}}&=\int _0^{\infty } t^2\,\mu e^{\mu t}\, dt =\frac{2}{\mu ^2},\\ \mu _{{3D}}&=\int _0^{\infty } t^3\,\mu e^{\mu t}\, dt =\frac{6}{\mu ^3},\\ \mu _{{1Z}}&=\mu _{{1U}}+\mu _{{1D}}\\&\quad =\frac{e^{-\lambda _1t_1}\big (\lambda _1-\lambda _2\big )}{\lambda _1\lambda _2}+\frac{1}{\lambda _1}+\frac{1}{\mu },\\ \mu _{{2Z}}&=\mu _{{2U}}+2\mu _{{1U}}\mu _{{1D}}+\mu _{{2D}}\\&\quad =\frac{2e^{-\lambda _1t_1}\Big [\lambda _1\lambda _2\mu t_1\big (\lambda _1-\lambda _2\big ) +\lambda _1^2\big (\mu +\lambda _2\big )-\lambda _2^2\big (\mu +\lambda _1\big )\Big ]}{\lambda _1^2\,\lambda _2^2\,\mu }\\&\quad \quad +\frac{2}{\lambda _1\mu }+\frac{2}{\lambda _1^2}+\frac{2}{\mu ^2},\\ \mu _{{3Z}}&=\mu _{{3U}}+3\mu _{{2U}}\mu _{{1D}}+3\mu _{{1U}}\mu _{{2D}}+\mu _{{3D}}\\&\quad =\frac{3e^{-\lambda _1t_1}}{\lambda _1^3\,\lambda _2^3\,\mu ^2}\left[ \lambda _1^2\,\lambda _2^2\,\mu ^2 t_1 ^2 \big (\lambda _1-\lambda _2\big ) +2\lambda _1\lambda _2\mu t_1+\Big ( \lambda _1^2 \big (\mu +\lambda _2\big ) - \lambda _2^2 \big (\mu +\lambda _1\big )\Big ) \right. \\&\quad \quad \quad \quad \quad \quad \left. +2\Big ( \lambda _1^3\big (\lambda _2^2+\lambda _2\mu +\mu ^2\big ) - \lambda _2^3\big (\lambda _1^2+\lambda _1\mu +\mu ^2\big ) \Big ) \right] \\&\quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad +\frac{6}{\lambda _1\mu ^2} +\frac{6}{\lambda _1^2\,\mu }+\frac{6}{\lambda _1^3} +\frac{6}{\mu ^3}. \end{aligned}$$

1.1.4 A.1.4 The steady state availability for the renewal process $\mathbf {Z_n}$

$$\begin{aligned} A&=\lim _{t\rightarrow \infty } A(t)\\&=\frac{\mu _{{1U}}}{\mu _{{1U}} + \mu _{{1D}}},\,\, \text {by (2)}\\& =\frac{\mu \Big (\lambda _2-\big (\lambda _2-\lambda _1\big )e^{-\lambda _1t_1}\Big )}{\lambda _2\big (\mu +\lambda _1\big )-\mu \big (\lambda _2-\lambda _1\big )e^{-\lambda _1t_1}}. \end{aligned}$$

This model can be improved by increasing the number of steps, and the renew process theory can be used to calculate an analytical solution for the availability function because the failure rate is constant by intervals.

1.2 A.2 Staircase with three steps

1.2.1 A.2.1 Distribution Function ${F_U}$

If the aging failure rate is given by

$$\begin{aligned} \lambda (t)={\left\{ \begin{array}{ll}\lambda _1, &{}\text {if}\quad 0\le t< t_1,\\ \lambda _2, &{}\text {if}\quad t_{1}\le t< t_2,\\ \lambda _3, &{}\text {if}\quad t \ge t_2, \end{array}\right. } \end{aligned}$$

and U has a partial exponential comportment in each one of the intervals $[0,t_1]$, $(t_1,t_2]$ and $(t_2,\infty )$, so if $U\le t_1$, U has a truncated exponential distribution with rate $\lambda _1$; if $t_1<U\le t_2$, U has a truncated exponential distribution with rate $\lambda _2$; while if $U>t_2$, U has a delayed exponential distribution with rate $\lambda _3$. Besides $F_U$ is like as (10) in $[0,t_2)$. That is:

$$\begin{aligned} P(U\leqslant t\,\big |\, U\le t_1)&={\left\{ \begin{array}{ll}0, &{}\text {if}\quad t<0,\\ \frac{1-e^{-\lambda _1 t}}{1-e^{-\lambda _1 t_1}},&{} \text {if}\quad t\in [0,t_1),\\ 1, &{}\text {if}\quad t\ge t_1. \end{array}\right. }\\ P(U\leqslant t\,\big |\,t_1<U\le t_2)&={\left\{ \begin{array}{ll}0, &{}\text {if}\quad t<t_1,\\ \frac{1-e^{-\lambda _2 (t-t_1)}}{1-e^{-\lambda _2 (t_2-t_1)}},&{} \text {if}\quad t\in [t_1,t_2),\\ 1, &{}\text {if}\quad t\ge t_2. \end{array}\right. }\\ P(U\leqslant t\,\big |\, U> t_2)&={\left\{ \begin{array}{ll}0, &{}\text {if}\quad t<t_2,\\ 1-e^{-\lambda _3 (t-t_2)}, &{}\text {if}\quad t\ge t_2. \end{array}\right. } \end{aligned}$$

Similarly to (10), it is obtained:

$$\begin{aligned} P(U\leqslant t)&={\left\{ \begin{array}{ll}1-e^{-\lambda _1t}, &{}\text {if}\quad t<t_1,\\ 1-e^{-\lambda _2 t+(\lambda _2-\lambda _1)t_1}, &{}\text {if}\quad t_1\le t<t_2,\end{array}\right. } {and then,} P(U\le t_1)&=1-e^{-\lambda _1t_1},\\ P(t_1<U\le t_2)&=P(U\leqslant t_2)-P(U\leqslant t_1)\\&=\big (1-e^{-\lambda _2 t_2+(\lambda _2-\lambda _1)t_1} \big )-\big (1-e^{-\lambda _1t_1}\big )\\&=e^{-\lambda _1t_1}\big (1-e^{-\lambda _2 ( t_2-t_1)}\big ),\\ P( U> t_2)&=1-P(U\le t_2)\\&=e^{-\lambda _2 t_2+(\lambda _2-\lambda _1)t_1)}. \end{aligned}$$

So, if $t\ge t_2$,

$$\begin{aligned} P(U\le t)&= P(U\leqslant t\,\big |\, U\le t_1)P(U\le t_1)+P(U\leqslant t\,\big |\,t_1<U\le t_2)P(t_1<U\le t_2)\\&\quad \quad + P(U\leqslant t\,\big |\, U> t_2) P( U> t_2)\\ {}&=1\cdot \big (1-e^{-\lambda _1t_1}\big )+1\cdot \big (e^{-\lambda _1t_1}\big (1-e^{-\lambda _2 ( t_2-t_1)}\big )\big )\\&\quad \quad +\big (1-e^{-\lambda _3 (t-t_2)}\big )\big (e^{-\lambda _2 t_2+(\lambda _2-\lambda _1)t_1)}\big )\\&=1-e^{-\lambda _3t+(\lambda _2-\lambda _1)t_1+(\lambda _3-\lambda _2)t_2}. \end{aligned}$$

Therefore,

$$\begin{aligned} F_U(t)&={\left\{ \begin{array}{ll}1-e^{-\lambda _1t}, &{}\text {if}\quad t<t_1,\\ 1-e^{-\lambda _2 t+(\lambda _2-\lambda _1)t_1}, &{}\text {if}\quad t_1\le t< t_2,\\ 1-e^{-\lambda _3t+(\lambda _2-\lambda _1)t_1+(\lambda _3-\lambda _2)t_2}, &{}\text {if}\quad t\ge t_2, \end{array}\right. } \end{aligned}$$

(11)

and by deriving the above result:

$$\begin{aligned} f_U(t)&={\left\{ \begin{array}{ll}\lambda _1e^{-\lambda _1t}, &{}\text {if}\quad t<t_1,\\ \lambda _2e^{-\lambda _2 t+(\lambda _2-\lambda _1)t_1}, &{}\text {if}\quad t_1\le t< t_2,\\ \lambda _3e^{-\lambda _3t+(\lambda _2-\lambda _1)t_1+(\lambda _3-\lambda _2)t_2}, &{}\text {if}\quad t\ge t_2, \end{array}\right. } \end{aligned}$$

1.3 A.3 General case: Staircase with ${\textbf{n}}$ steps

1.3.1 A.3.1 Distribution function ${F_U}$

If the aging failure rate function $\lambda (t)$ is given by (9) and U has a partial exponential comportment in each one of the intervals $(t_{k-1},t_k]$, $k=1,\ldots ,n$, then by means of an inductive procedure, from (10) and (11), it is obtained the component lifetime distribution function as:

$$\begin{aligned} F_U(t)&={\left\{ \begin{array}{ll}0, &{}\text {if}\quad t<t_0,\\ 1-e^{-\lambda _k t+\sum \limits _{i=1}^{k}\big (\,\lambda _i -\lambda _{i-1}\big )t_{i-1} },&{}\text {if}\quad t_{k-1}\le t <t_k,\,k=1,\ldots ,n,\end{array}\right. } \end{aligned}$$

(12)

where $\lambda _0=0$. So, the component lifetime density function is:

$$\begin{aligned} f_U(t)&={\left\{ \begin{array}{ll}0, &{}\text {if}\quad t<t_0,\\ \lambda _ke^{-\lambda _k t+\sum \limits _{i=1}^{k}\big (\,\lambda _i -\lambda _{i-1}\big )t_{i-1} },&{}\text {if}\quad t_{k-1}\le t <t_k,\,k=1,\ldots ,n.\end{array}\right. } \end{aligned}$$

1.3.2 A.3.2 Moments for U, D and Z

$$\begin{aligned} \mu _{{1U}}&=\int _0^{\infty }t\,f_U(t)\,dt=\sum \limits _{k=1}^n\,\int _{t_{k-1}}^{t_k}\,t\, \lambda _ke^{-\lambda _k t+\sum \limits _{i=1}^{k}\big (\,\lambda _i -\lambda _{i-1}\big )t_{i-1} }\,dt\,,\\ \text {and,} \int _{t_{k-1}}^{t_k}\,t\,f_U(t)\,dt\,&=e^{\,\,\sum \limits _{i=1}^k \big (\lambda _i-\lambda _{i-1}\big )t_{i-1}}\Big [t_{k-1}e^{-\lambda _k t_{k-1}}- t_{k}e^{-\lambda _k t_{k}}\Big .\\&\quad \quad \quad \quad \quad \quad \Big .+\frac{e^{-\lambda _k t_{k-1}}}{\lambda _k} - \frac{e^{-\lambda _k t_{k}}}{\lambda _k}\Big ]\\&=e^{\,\,\sum \limits _{i=1}^k\big (\lambda _i-\lambda _{i-1}\big )t_{i-1}}\Big [t_{k-1}e^{-\lambda _k t_{k-1}}- t_{k}e^{-\lambda _k t_{k}}\Big ]\\&\quad \quad \quad \quad \quad \quad +e^{\,\,\sum \limits _{i=1}^k\big (\lambda _i-\lambda _{i-1}\big )t_{i-1}}\left[ \frac{e^{-\lambda _k t_{k-1}}}{\lambda _k} - \frac{e^{-\lambda _k t_{k}}}{\lambda _k}\right] . \end{aligned}$$

Also,

$$\begin{aligned} e^{\,\,\sum \limits _{i=1}^k\big (\lambda _i-\lambda _{i-1}\big )t_{i-1}}\Big [t_{k-1}e^{-\lambda _k t_{k-1}}- t_{k}e^{-\lambda _k t_{k}}\Big ]\\ =t_{k-1}e^{\,\,\sum \limits _{i=1}^k\big (\lambda _i-\lambda _{i-1}\big )t_{i-1}-\lambda _kt_{k-1}}- t_{k}e^{\,\,\sum \limits _{i=1}^k\big (\lambda _i-\lambda _{i-1}\big )t_{i-1}-\lambda _kt_{k}}\\ =t_{k-1}e^{\,\,\sum \limits _{i=1}^{k-1}\big (\lambda _i-\lambda _{i-1}\big )t_{i-1}-\lambda _{k-1}t_{k-1}}- t_{k}e^{\,\,\sum \limits _{i=1}^k\big (\lambda _i-\lambda _{i-1}\big )t_{i-1}-\lambda _kt_{k}}. \end{aligned}$$

It is defined,

$$\begin{aligned} a(k):=t_{k}e^{\,\,\sum \limits _{i=1}^k\big (\lambda _i-\lambda _{i-1}\big )t_{i-1}-\lambda _kt_{k}} \text {\,\,if\,\,}k=1,\ldots ,n,\quad \text { and}\quad a(0):=0. \end{aligned}$$

Then,

$$\begin{aligned} \sum _{k=1}^n \,\big (a(k-1)-a(k)\big )=a(0)-a(n)=0, \end{aligned}$$

in fact,

$$\begin{aligned} a(n)=\lim \limits _{t_n\rightarrow \infty }t_{n}e^{\,\,\sum \limits _{i=1}^n\big (\lambda _i-\lambda _{i-1}\big )t_{i-1}-\lambda _nt_{k}}\\ =\lim \limits _{t_n\rightarrow \infty }t_{n}e^{\,\,-\lambda _n\big (t_n-t_{n-1}\big )+\sum \limits _{i=1}^{n-1}\big (\lambda _i-\lambda _{i-1}\big )t_{i-1}} =0. \end{aligned}$$

So,

$$\begin{aligned} \mu _{{1U}}&=\sum \limits _{k=1}^n\,\frac{1}{\lambda _k}\left[ e^{-\lambda _k t_{k-1}} - e^{-\lambda _k t_k} \right] e^{\,\,\sum \limits _{i=1}^k\big (\lambda _i-\lambda _{i-1}\big )t_{i-1}}, \\ \text {Similarly,} \mu _{{2U}}&=2\sum \limits _{k=1}^n\,\,\frac{1}{\lambda _k^2}\Big [\big (1+\lambda _k t_{k-1}\big )\,e^{\,-\lambda _kt_{k-1}}-\big (1+\lambda _k t_{k}\big )\,e^{\,-\lambda _kt_{k}}\Big ]\, e^{\,\,\sum \limits _{i=1}^k\big (\lambda _i-\lambda _{i-1}\big )t_{i-1}}, \text {and,} \mu _{{3U}}&=3\sum \limits _{k=1}^n\,\,\frac{1}{\lambda _k^3}\Big [\big (2+2\lambda _k t_{k-1}+\lambda _k^2 t_{k-1}^2\big )\,e^{\,-\lambda _kt_{k-1}}\Big .\\ {}&\qquad \qquad \qquad \qquad \Big . -\big (2+2\lambda _k t_{k}+\lambda _k^2 t_{k}^2\big )\,e^{\,-\lambda _kt_{k}}\Big ]\, e^{\,\,\sum \limits _{i=1}^k\big (\lambda _i-\lambda _{i-1}\big )t_{i-1}}. \end{aligned}$$

Guoqiang Ji et al. [11] have given explicit expressions for the steady state availability for the general as were as the particular case of $n=2$. Otherwise,

$\mu _{{1D}}=1/\mu$, $\mu _{{2D}}=2/\mu ^2$ and $\mu _{{3D}}=6/\mu ^3$ and $\mu _{{1Z}}$, $\mu _{{2Z}}$ and $\mu _{{3Z}}$ are easily obtained, by

$$\begin{aligned} \mu _{{1Z}}&= \mu _{{1U}}+ \mu _{{1D}},\\ \mu _{{2Z}}&=\mu _{{2U}}+2\mu _{{1U}}\mu _{{1D}}+\mu _{{2D}},\\ \mu _{{3Z}}&=\mu _{{3U}}+3\mu _{{2U}}\mu _{{1D}}+3\mu _{{1U}}\mu _{{2D}}+\mu _{{3D}}. \end{aligned}$$

Appendix B: Appendix: Results of the availability functions

See Tables 3 and 4.

Table 3 Values for the approximation 1, in the different models

Table 4 Values for the approximation 2, in the different models