1 Introduction

For successful merchandising decisions in traditional space management, a specific tool called a planogram is widely used by retailers. It illustrates the layout of the products on the fixtures. Creating effective visual plans is very important for supporting the retailers’ decisions related to shelf space allocation. It allows for maximizing the store profits [5, 30] and, consequently, more effective functioning of the entire organization. The retail shelf space allocation problem (SSAP) is well-known in the literature. The examination of software applications in assortment and shelf space management, as well as quantitative models, has been presented by Hübner and Kuhn [27].

In this research, we formulate the SSAP according to the merchandising rules that specify vertical and horizontal groups of products and the division of the products based on sales potentials. Merchandising generalizes any techniques or practices of visual representation of products in the retail store. Dependencies between the customers’ buying behaviour, product categorization, shelf location, and visual representation of them can be found in the research of Anic et al. [1], Desrochers and Nelson [17], Elbers [19].

The research by Gabrielli and Cavazza [22] deepened the knowledge about placing products at the end of an aisle. They studied brand appreciation on low, medium, and high levels. They concluded that the location of the product to be exposed is very powerful for brand recognition. Bianchi-Aguiar et al. [6] studied the categorization of product families and allocating them into blocks as well as a multi-level hierarchical structure. They proposed a method of decomposing the main problem into sub-problems and applying specific methods to solve them. Düsterhöft et al. [18] studied various shelf segments of different attractiveness with the aim of appropriately assigning available shelf space between lots of brands, considering optimum replenishment decisions. The concept of shelf segments of flexible size (named “virtual”) was defined by Czerniachowska [10], Czerniachowska and Hernes [12] and Czerniachowska et al. [15, 16]. Several types of segments with regard to product types included local or regional and convenience or complementary products. Other types of segments allocated near the aisles included products, taking into account store customer traffic flow. The research by Czerniachowska [10] most widely explains the evidence regarding shelf levels and shelf segment usage in the SSAP models and gives a wide variety of solution tricks specifically to this problem. Metaheuristics [10, 15, 16] and hyper-heuristics [12] were adopted to solve the SSAP with shelf segments.

The objective of this paper is to present a real retail shelf space allocation model and to develop efficient heuristic algorithms that can allow for obtaining good practical results in a very short time, the ideas of which can also be used in other shelf space allocation models. The mathematical model, which was first presented in Czerniachowska and Hernes [13] includes vertical product allocation constraints as well as horizontal categories grouping, which are very important in visual merchandising.

One of the key limitations of the SSAP literature is not taking into account merchandising rules based on the frequency of product movement and product price. In the model by Czerniachowska and Hernes [13], a method of dividing products and allocating them to different vertical shelf levels based on their sales potential is proposed. Valenzuela and Raghubir [36] concluded that cheaper brands should be located on the bottom shelves, and the best place for luxury brands is on the top shelves. Therefore, in the model, Czerniachowska and Hernes [13] differentiated products based on their sales potential in order to locate them correctly on the bottom or top shelves.

In many studies, different approaches have been developed for shelf space allocation. Because of the NP-hard nature of the shelf space allocation problem, heuristic algorithms are needed for the solution of large instances of real-world problems. On this basis, many approaches have been proposed, including:

There are two concepts taken into account in this paper: capping and nesting. Capping means an allocation of a product on top of another product with a rotation of the product on the top in order to push in more products on the shelf if there is no space to duplicate a product row one more time on the first product orientation. Nesting means an allocation of a product into another product, such as a basket or a plate.

2 Paper contributions

We develop heuristics and test them on different practical problem instances of different sizes and compare our solution with the CPLEX solver. The proposed techniques may be used to allow retailers to make category management decisions faster and to obtain higher profits. The proposed methods construct solutions incrementally, which has the following advantages:

  • Only feasible candidate solutions are considered. Hence, no repair operator is required as opposed to metaheuristics (e.g. [8,9,10,11, 15, 16, 20, 21, 24,25,26, 28, 29, 31,32,33,34,35]), such as evolutionary algorithms, in which random local search, crossover, and mutation operations can turn a correct solution into an infeasible one.

  • If constraints cannot be satisfied, the user can be notified to change the product grouping method, increase the minimum category size and tolerance, reassign sales potentials, etc.

  • Each step filters out infeasible candidate solutions, so in the following steps, the search space is smaller than in the case of non-deterministic algorithms, such as evolutionary algorithms.

  • The proposed heuristics are better than the neighbourhood search approaches (e.g. [4], low-level heuristics (e.g. [2] or simulated annealing (e.g. [ 2, 4, 7, 12, 37] because they do not need an initial solution to start with or neighbourhood preferences for constructing a possible solution.

  • The proposed approach presents considerable competitiveness over metaheuristics and hyper-heuristics proposed by other researchers, as in the proposed approach, the total number of product allocations could be calculated and compared to the general case. This is extremely valuable in case of time-saving while processing large datasets.

In the experiments, the proposed method was tested on data sets that were generated on the basis of real-life data. In the tests, the heuristics found the solution for 11 SSAP instances for which CPLEX was not able to find one, which motivates the use of heuristics and suggests further development towards hybrid methods.

The paper is organized as follows. Problem formulation and its mathematical model are presented in Sect. 3. A detailed description of proposed heuristics is presented in Sect. 4. Next, in Sect. 5, the results of computational experiments are presented. The article is concluded in Sect. 6.

3 Statement of the problem

3.1 Creation of a planogram

The Shelf Space Allocation Problem (SSAP) consists in constructing a planogram that is divided horizontally into categories and vertically into subcategories. The problem can be formulated as follows [13]: there is a given number of products \(P\) that must be displayed on \(S\) shelves of a planogram. The products \(1,...,P\) are assigned to \(K\) product categories. On the planogram, there are also initially assigned spaces for the \(K\) product categories, i.e., the minimum possible size of the category allowing it to be visually attractive for the customers. The problem is to define the appropriate shelf space for each product category \(K\) with regard to the quantity of each product with the objective of maximizing retailers’ profit.

Products \(1,...,P\) are divided into \(K\) categories based on their types (product families) and into \(G\) subcategories based on their sales potential. Each category is vertical, i.e., the products are placed on all shelves \(i\)\((i = 1,...,S)\) within one category \(k\)\((k = 1,...,K)\). In this paper, we assume that more general categories (such as milk) can be extended to the vertical spaces allocated to more specific categories (such as yoghurt and cheese). This follows the practice observed in real-life applications.

The sales potential subcategory \(g\)\((g = 1,...,G)\) is horizontal, i. e. the products are placed on one shelf \(i\)\((i = 1,...,S)\) within one subcategory \(g\)\((g = 1,...,G)\), but the same sales potential subcategory \(g\)\((g = 1,...,G)\) exists in all categories \(k\)\((k = 1,...,K)\). The higher the sales potential subcategory of the product, the more expensive it is and, therefore, the better level position on the shelf it receives. Obviously, the eye-level shelf for branded or expensive products is the best option.

The products with the lowest sales potential are located on the lowest shelf but can also be located on higher shelves. On the other hand, the products with the highest sales potential are located on the highest shelf (at eye level) and can’t be located on other shelves. Products of the same category \(k\)\((k = 1,...,K)\) must be located together. This means that the category can’t be split or interrupted with products from another category.

3.2 Planogram rules for categories and sales potential subcategories

Table 1 shows the rules for allocating products on shelves. Products from category A and subcategory 10 can be allocated to the shelves for categories A, B, C and subcategories 10, 20, 30. Products from category C and subcategory 30 can’t be allocated to the shelves for other categories and subcategories. Another example, B20 can be placed in B20, B30, C20, C30. Sales potentials are assigned with the interval 10 for practical reasons. For example, if in the general assortment set, products are assigned to 10 and 20 sales subcategories, but one seasonal or promotional shelf is added only for 2-week intervals, it is easier to assign seasonal or promo products to 15 sales potential without the reassignment of the general assortment. Figures 1 and 2 present possible category sizes on the shelves with different sales potentials. The borderline between the categories may be flexible (Fig. 1) or strict (Fig. 2).

Table 1 Categories and sales potential subcategory allocation rules
Full size table
Fig. 1
figure 1

Possible categories and sales potential subcategory allocation with the flexible border between vertical categories

Full size image
Fig. 2
figure 2

Possible categories and sales potential subcategory allocation with the strict border between vertical categories

Full size image

3.3 Explanation of other parameters used in the model

In the remaining part of the paper, the following notation is used. Due to a large number of problem parameters, in the given paper, subscripts are used for variable indexes. Superscripts are set for a variable’s clarification and mustn’t be interpreted as indexes.

A parameter defining the minimum category size is the \(m_{k}\) per cent of the shelf length, i.e., each category must exist on the planogram, and the products in this category must be noticeable. The coefficient \(t_{k}\) per cent of the shelf length limits the maximum category size tolerance between shelves in the category. This parameter is used to create visually attractive vertical category shapes with a well-defined border between the categories.

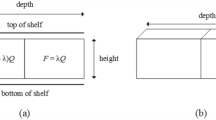
Each shelf \(i\)\((i = 1,...,S)\) has a different length capacity \(s_{i}^{l}\), shelf height \(s_{i}^{h}\), shelf depth capacity \(s_{i}^{d}\), product weight bound \(s_{i}^{b}\), and shelf sales potential subcategory \(s_{i}^{g}\). In the analyzed model, all shelves are assigned to each of the categories; a subcategory \(g\)\((g = 1,...,G)\) is assigned to the shelf, and products from each subcategory \(g\) \((g = 1,...,G)\) are also allocated to a certain category \(k\)\((k = 1,...,K)\) (Figs. 1, 2).

In the given problem, the product \(j\) has width \(p_{j}^{w}\), height \(p_{j}^{h}\), depth \(p_{j}^{d}\), and weight \(p_{j}^{b}\). Out-of-stock situations are avoided by the retailer with the control of the supply limit parameter of the product \(p_{j}^{s}\), which indicates the maximum possible number of product items displayed. The product item profit \(p_{j}^{u}\) characterizes the profit gained from the product if it is displayed. The category of the product is expressed by \(p_{j}^{k}\), and its sales potential subcategory is \(p_{j}^{g}\).

Generally, each product is placed on the shelf in the front orientation, but for some products, the secondary side orientation (90 degrees) is also available. Binary parameters of a product \(p_{j}^{{o_{1} }}\) and \(p_{j}^{{o_{2} }}\) reflect if the front and side orientation are available for the product \(j\). For the front orientation,\(p_{j}^{{o_{1} }}\) we take product width \(p_{j}^{w}\) as the width of the product on the shelf and depth \(p_{j}^{d}\) as the depth of the product on the shelf. For side orientation,\(p_{j}^{{o_{2} }}\) we take its depth \(p_{j}^{d}\) as the width of the product on the shelf and width \(p_{j}^{w}\) as the depth of the product on the shelf.

$$p_{j}^{{o_{1} }} = \left\{ {\begin{array}{*{20}l} {1,} \hfill & {{\text{if front orientation is available for the product }}j} \hfill \\ {0,} \hfill & {{\text{otherwise}}} \hfill \\ \end{array} } \right.,\,j = 1,...,P.$$
$$p_{j}^{{o_{2} }} = \left\{ {\begin{array}{*{20}l} {1,} \hfill & {{\text{if side orientation is available for the product }}j} \hfill \\ {0,} \hfill & {{\text{otherwise}}} \hfill \\ \end{array} } \right.,\,j = 1,...,P.$$

To ensure a substitution effect, the products are grouped into clusters \(p_{j}^{l}\). If the product is out-of-stock or delisted from the assortment, the customer can choose a similar product (with the same characteristics, functions, and tastes) from another brand. Moreover, when one product is delisted, to prevent the loss of profit, retailers ensure the availability of another substitutive product on the shelf. Cluster parameter \(p_{j}^{l}\) means the similar substitution product group. Products from the same cluster must be placed together on the same shelf next to one another.

3.4 Product item representation

In this paper, we take into account not only the facings of the products but also cappings and nestings, which is an extension with respect to models typically used in the literature, which only consider facings. Capping means that products, such as rectangular packages, can be put on top of each other in a rotated orientation. Nesting means that products, such as buckets, can be put inside each other. Depending on the product package’s physical characteristics, cappings can be placed above the facings of the product rotated 90 degrees (e.g., tea boxes), and nesting is placed inside the facings (e.g., bowls or plates). To describe the product nesting possibilities, the nesting coefficient \(p_{j}^{n}\) \(\left( {p_{j}^{n} < 1} \right)\) signifies additional height for one nested item (e.g., the additional bowl height if bowls are placed inside each other). Regular products that can’t be nested \(p_{j}^{n} = 0\) because products that can’t be nested are represented as another row of facings.

The lower \(f_{j}^{\min }\) and upper \(f_{j}^{\max }\) bounds of facings of the products that should be placed on the shelves are defined by the retailer at the store. Furthermore, the lower \(c_{j}^{\min }\) and upper \(c_{j}^{\max }\) bounds of side cappings per position can also be restricted for each product. The parameter \(c_{j}^{\max }\) means the maximum number of cappings that can actually be placed above the facings sequence of items without destroying them because of the weight of the capping items. The mandatory number of sequences of facings in one capped group is \(\left\lceil {p_{j}^{h} /p_{j}^{w} } \right\rceil\) for products with front orientation and \(\left\lceil {p_{j}^{h} /p_{j}^{d} } \right\rceil\) for products with secondary side orientation, which describes the possibility of holding up the cappings above. Let’s consider an example. If more than \(c_{j}^{\max }\) tea boxes are put above the tea box facings sequence, the boxes on the bottom level may be broken or destroyed, or tea boxes on the top level could fall off the shelf.

The lower \(n_{j}^{\min }\) and upper \(n_{j}^{\max }\) bounds of the side nestings per position can also be restricted for each product. The parameter \(n_{j}^{\max }\) indicates the maximum number of nestings that can actually be placed above one facing item without destroying it. Let’s consider another example. If more than \(n_{j}^{\max }\) the bowls are put inside the lower bowl on the shelf, the lowest bowl may be broken or destroyed, or the bowls on the top level could fall off the shelf. The multi-shelf product placement possibility is defined by the minimum \(s_{j}^{\min }\) and the maximum \(s_{j}^{\max }\) number of shelves on which it can be placed. Based on the introductory definitions of facings, cappings and nestings above, the total number of items of the product is the sum of facings \(f_{ij}\), cappings \(c_{ij}\) and nesting numbers \(n_{ij}\) of a product. All of the aforementioned parameters (\(f_{ij}\),\(c_{ij}\),\(n_{ij}\)) represent the number of product items. Figures 3 and 4 represent the cappings and nestings allocation methods.

Fig. 3
figure 3

Cappings allocation

Full size image
Fig. 4
figure 4

Nestings allocation

Full size image

3.5 The idea of a solution to the problem

In this paper, the number of facings in the vertical dimension is not considered. It is assumed that shelf height and product supply limit is given only for one topmost sequence of facings with capping or nesting on it, i.e., only one horizontal sequence of facings is analyzed. The same case goes with the depth of the products and the depth of the shelf, which is also given for one front sequence of facings. If the depth of the investigated part of the shelf is exceeded, and if the product could be placed on both front and side orientations, it is possible to rotate it so that it could fit the depth limitations.

Based on the above-mentioned suppositions, in order to solve the problem, the task is to calculate the number of facings \(f_{ij}\), cappings \(c_{ij}\) and nestings \(n_{ij}\) of a product \(j\) which is allowed to be placed on the shelf \(i\) with regard to different constraints which, for clearness, can be grouped into 4 classes: shelf constraints, product constraints, multi-shelves constraints, and category constraints, in order to maximize the total retailer’s profit.

3.6 Problem formulation

Given the assumptions stated above, the shelf space management problem can be summarized as a following non-linear integer programming model. The model was first presented by Czerniachowska and Hernes [13].

$$\max \sum\limits_{j = 1}^{P} {\sum\limits_{i = 1}^{S} {x_{ij} p_{j}^{u} (f_{ij} + c_{ij} + n_{ij} )} }$$
(1)
$$x_{{ij}} = \left\{ {\left\{ {\begin{array}{*{20}l} {1,{\text{ }}} \hfill & {{\text{if product }}j{\text{ is put to the shelf }}i} \hfill \\ {0,} \hfill & {{\text{otherwise}}} \hfill \\ \end{array} } \right.} \right\},j = 1, \ldots ,P,\;i = 1, \ldots ,S.$$

\(f_{ij}\)—the number of facings of the product \(j\)\((j = 1,...,P)\) on the shelf \(i\)\((i = 1,...,S)\).\(c_{ij}\)—the number of cappings of the product \(j\)\((j = 1,...,P)\) on the shelf \(i\)\((i = 1,...,S)\).\(n_{ij}\)—the number of nestings of the product \(j\)\((j = 1,...,P)\) on the shelf \(i\)\((i = 1,...,S)\).

$$y_{{ij}}^{{o_{1} }} = \left\{ {\begin{array}{*{20}l} {1,} \hfill & {{\text{if product }}j{\text{ is put to the shelf }}i{\text{ on front orientation}}} \hfill \\ {0,} \hfill & {{\text{otherwise}}} \hfill \\ \end{array} } \right\},\;j = 1,...,P,i = 1,...,S.$$
$$y_{{ij}}^{{o_{2} }} = \left\{ {\begin{array}{*{20}l} {1,} \hfill & {{\text{if product }}j{\text{ is put to the shelf }}i{\text{ on side orientation}}} \hfill \\ {0,} \hfill & {{\text{otherwise}}} \hfill \\ \end{array} } \right\},\;j = 1, \ldots ,P,\;i = 1, \ldots ,S.$$

The formula (1) multiplies the profit from one product item \(p_{j}^{u}\) by the number of the product items \((f_{ij} + c_{ij} + n_{ij} )\), thereby representing the total profit gained by the retailer.

3.7 Shelf constraints

$$\sum\limits_{j = 1}^{P} {f_{ij} \left(y_{ij}^{{o_{1} }} p_{j}^{w} + y_{ij}^{{o_{2} }} p_{j}^{d} \right)} \le s_{i}^{l} ,i = 1,...,S$$
(2)
$$x_{ij} \left( {p_{j}^{h} + \left\lceil {\frac{{c_{ij} x_{ij} }}{{\max \left( {\left\lfloor {\frac{{f_{ij} (y_{ij}^{{o_{1} }} p_{j}^{w} + y_{ij}^{{o_{2} }} p_{j}^{d} )}}{{p_{j}^{h} }}} \right\rfloor ,1} \right)}}} \right\rceil \cdot \left( {y_{ij}^{{o_{1} }} p_{j}^{w} + y_{ij}^{{o_{2} }} p_{j}^{d} } \right) + \left\lceil {\frac{{n_{ij} x_{ij} }}{{\max \left( {f_{ij} ,1} \right)}}} \right\rceil \cdot p_{j}^{h} p_{j}^{n} } \right) \le s_{i}^{h} ,$$
$$j = 1,...,P,i = 1,...,S$$
(3)
$$x_{ij} \left( {y_{ij}^{{o_{1} }} p_{j}^{d} + y_{ij}^{{o_{2} }} p_{j}^{w} } \right) \le s_{i}^{d} ,j = 1,...,P,i = 1,...,S$$
(4)
$$\sum\limits_{j = 1}^{P} {\left( {f_{ij} + c_{ij} + n_{ij} } \right)p_{j}^{b} } \le s_{i}^{b} ,i = 1,...,S$$
(5)

Constraint (2) restricts the shelf length. Constraint (3) assures that the height of each product on a shelf satisfies the shelf height limit. Capped products with front orientation (\(p_{j}^{{o_{1} }} = 1\)) are placed in a way that their width results in additional height to the facings of the product. Capped products with side orientation (\(p_{j}^{{o_{2} }} = 1\)) are placed in such a way that their depth results in additional height to the facings of the product. The total height equals the sum of the product height, cappings (Fig. 3) height and nestings (Fig. 4) height. Constructions \(x_{ij} /\max (f_{ij} ,1)\) are used for omitting cases with the division by 0 if a product is not placed on the shelf. Constraint (4) restricts the shelf depth limit. Constraint (5) imposes the shelf weight limit.

3.8 Product constraints

$$\sum\limits_{i = 1}^{S} {x_{ij} } \ge s_{j}^{\min } ,j = 1,...,P$$
(6)
$$\sum\limits_{i = 1}^{S} {x_{ij} } \le s_{j}^{\max } ,j = 1,...,P$$
(7)
$$\sum\limits_{i = 1}^{S} {\left( {f_{ij} + c_{ij} + n_{ij} } \right) \le p_{j}^{s} ,\;j = 1,...,P}$$
(8)
$$\sum\limits_{i = 1}^{S} {f_{ij} } \ge f_{j}^{\min } ,j = 1,...,P$$
(9)
$$\sum\limits_{i = 1}^{S} {f_{ij} } \le f_{j}^{\max } ,j = 1,...,P$$
(10)
$$c_{ij} \ge c_{j}^{\min } ,j = 1,...,P,i = 1,...,S$$
(11)
$$c_{ij} \le c_{j}^{\max } \cdot \left\lfloor {\frac{{f_{ij} \left( {y_{ij}^{{o_{1} }} p_{j}^{w} + y_{ij}^{{o_{2} }} p_{j}^{d} } \right)}}{{p_{j}^{h} }}} \right\rfloor ,\;j = 1, \ldots ,P,\;i = 1, \ldots ,S$$
(12)
$$n_{ij} \ge n_{j}^{\min } ,j = 1,...,P,i = 1,...,S$$
(13)
$$n_{ij} \le n_{j}^{\max } f_{ij} ,j = 1,...,P,i = 1,...,S$$
(14)
$$c_{ij} \cdot n_{ij} = 0,j = 1,...,P,i = 1,...,S$$
(15)

Constraints (6) and (7) restrict for the multi-shelf products, the minimum and the maximum number of shelves where these products should be placed. Constraint (8) imposes the available supply limit for a product. Constraints (9) and (10) impose the product facings lower and upper bound. Constraints (11) and (12) provide the lower and upper bounds of cappings per position. Constraint (12) ensures that the number of product facings is enough for the capping, i.e., the product may be capped. Constraints (13) and (14) guarantee the lower and upper bounds of nestings per facing position. Constraint (15) ensures the presentation of either cappings or nestings for a product, but not both of them at the same time.

3.9 Multi-shelves constraints

$$y_{ij}^{{o_{1} }} \cdot y_{ij}^{{o_{2} }} = 0,j = 1,...,P,i = 1,...,S$$
(16)
$$y_{ij}^{{o_{1} }} + y_{ij}^{{o_{2} }} = 1,j = 1,...,P,i = 1,...,S$$
(17)
$$\mathop {\max }\limits_{i = 1,...,S} (y_{ij}^{{o_{1} }} ) \ne \mathop {\max }\limits_{i = 1,...,S} (y_{ij}^{{o_{2} }} ),j = 1,...,P$$
(18)
$$y_{ij}^{{o_{1} }} \le p_{j}^{{o_{1} }} ,j = 1,...,P,i = 1,...,S$$
(19)
$$y_{ij}^{{o_{2} }} \le p_{j}^{{o_{2} }} ,j = 1,...,P,i = 1,...,S$$
(20)
$$\forall (a,b: \left| {a - b} \right| \ne 1 \wedge a < b, a,b = 1,...,S)[x_{aj} \cdot x_{bj} = 0],j = 1,...,P$$
(21)
$$\forall \left( {a,b:p_{a}^{l} = p_{b}^{l} , a,b = 1,...,P} \right)\left[ {x_{ia} = x_{ib} } \right],\;i = 1,...,S$$
(22)

For multi-shelf products, the requirement is to put the product on all shelves in the same orientation in order to make it noticeable in the same way on all the shelves. Constraints (16)–(17) indicate that only one orientation (front or side) is available for each product. Constraint (18)ensures the same orientation of the product on all shelves. Constraints (19)–(20) ensure the possibility of the front or side orientation, respectively. Constraint (21) allows the product to be placed only on adjacent shelves. Constraint (22) ensures that the products in the same cluster are placed together on the same shelf.

3.9.1 Category constraints

$$\left( {\sum\limits_{\begin{subarray}{l} j = 1, \\ p_{j}^{k} = k \end{subarray} }^{P} {f_{ij} (y_{ij}^{{o_{1} }} p_{j}^{w} + y_{ij}^{{o_{2} }} p_{j}^{d} )} \ge \left[ {s_{i}^{l} \cdot m_{k} } \right]} \right) \vee \left( {\sum\limits_{\begin{subarray}{l} j = 1, \\ p_{j}^{k} = k \end{subarray} }^{P} {f_{ij} } = 0} \right),\;i = 1,...,S,k = 1,...,K$$
(23)
$$\mathop {\max }\limits_{i = 1,...,S} \left( {\sum\limits_{\begin{subarray}{l} j = 1, \\ p_{j}^{k} = k \end{subarray} }^{P} {f_{ij} \left( {y_{ij}^{{o_{1} }} p_{j}^{w} + y_{ij}^{{o_{2} }} p_{j}^{d} } \right)} } \right) - \mathop {\min }\limits_{i = 1,...,S} \left( {\sum\limits_{\begin{subarray}{l} j = 1, \\ p_{j}^{k} = k \end{subarray} }^{P} {f_{ij} \left( {y_{ij}^{{o_{1} }} p_{j}^{w} + y_{ij}^{{o_{2} }} p_{j}^{d} } \right)} } \right) \le \left[ {\mathop {\max }\limits_{i = 1,...,S} (s_{i}^{l} ) \cdot t_{k} } \right],k = 1,...,K$$
(24)
$$x_{ij} \le \min (\max (s_{i}^{g} - p_{j}^{g} ,0),1),j = 1,...,P,i = 1,...,S$$
(25)

Constraint (23) guarantees the minimum category size if the products of this category exist on the shelf. Constraint (24) restricts the category tolerance between different shelves of the category in order to form the border between neighbouring categories. \(\left[ {...} \right]\) denotes rounding to the nearest integer. Constraint (25) ensures the allocation of the products based on their sales potential subcategories. Products with lower sales potential can be placed on shelves with greater sales potential. Products with greater sales potential cannot be placed on shelves with lower sales potential.

3.9.2 Integrity constraints

$$x_{ij} \cdot s_{i}^{l} \cdot \left( {\frac{{y_{ij}^{{o_{1} }} }}{{p_{j}^{w} }} + \frac{{y_{ij}^{{o_{2} }} }}{{p_{j}^{d} }}} \right) \ge f_{ij} ,\;j = 1,...,P,\;i = 1,...,S$$
(26)
$$x_{ij} \le f_{ij} \cdot \left( {y_{ij}^{{o_{1} }} + y_{ij}^{{o_{2} }} } \right),\;j = 1,...,P,\;i = 1,...,S$$
(27)
$$c_{ij} \le x_{ij} \cdot c_{j}^{\max } \cdot \left\lfloor {\frac{{f_{ij} (y_{ij}^{{o_{1} }} p_{j}^{w} + y_{ij}^{{o_{2} }} p_{j}^{d} )}}{{p_{j}^{h} }}} \right\rfloor ,j = 1,...,P,i = 1,...,S$$
(28)
$$n_{ij} \le x_{ij} \cdot n_{j}^{\max } \cdot f_{ij} ,j = 1,...,P,i = 1,...,S$$
(29)

Constraints (26) and (27) ensure that when a product is placed on a shelf, the number of facings is non-zero and vice versa. Constraint (28) signifies capping relationships. Constraint (29) guarantees nesting relationships.

3.9.3 Decision variables

$$x_{ij} \in \{ 0,1\} j = 1,...,P,i = 1,...,S$$
(30)
$$f_{ij} = \{ f_{j}^{\min } ...f_{j}^{\max } \} j = 1,...,P,i = 1,...,S$$
(31)
$$c_{ij} = \left\{ {c_{j}^{\min } ...c_{j}^{\max } \cdot \left\lfloor {\frac{{f_{ij} (y_{ij}^{{o_{1} }} p_{j}^{w} + y_{ij}^{{o_{2} }} p_{j}^{d} )}}{{p_{j}^{h} }}} \right\rfloor } \right\},\;j = 1,...,P,\;i = 1,...,S$$
(32)
$$n_{ij} = \{ n_{j}^{\min } ...n_{j}^{\max } \cdot f_{j}^{\max } \} j = 1,...,P,i = 1,...,S$$
(33)
$$y_{ij}^{{o_{1} }} \in \{ 0,1\} j = 1,...,P,i = 1,...,S$$
(34)
$$y_{ij}^{{o_{2} }} \in \{ 0,1\} j = 1,...,P,i = 1,...,S$$
(35)

The binary decision variable (30) shows if the product \(j\) is placed on the shelf \(i\). Decision variables (31)–(33) represent the number of facings, cappings and nestings of the product \(j\) on the shelf \(i\), which are integers bounded by the given upper bound values. Binary decision variables (34)–(35) show if the product \(j\) is placed on the shelf \(i\) in the front or side orientation accordingly.

4 New SSAP heuristics

In this section, we propose heuristics that can be applied to the variety of SSAP instances with different product and shelf constraints specific to each shelf.

4.1 Main steps

The proposed algorithm can be represented along these lines. The main goal of this algorithm is to create all possible product allocations with regard to all constraints. In the beginning, the algorithm does not specify the number of facings, cappings and nestings. It only determines if the product can be placed on the shelf. Next, the numeric values for facings, cappings and nestings are found based on the allocations received from the first procedures of the algorithm. Among the received allocations with facings, cappings and nestings specified, the most profitable solution is selected.

figure a

Below the following notations are used. “Product sequence” means the sequence of products on one shelf with no regard as to which level this shelf will be situated (\(s_{1}\), \(s_{2}\) or \(s_{3}\)). “Shelf sequence” means the simultaneous sequences for all of the shelves (\(s_{1}\), \(s_{2}\) and \(s_{3}\)), created on the basis of the product sequences, the level of each shelf is known.

4.1.1 Main procedure GenerateProductOnShelfAllocations

This procedure selects the products from each category \(\{ j:p_{j}^{k} = k, \, j = 1,...,P,k = 1,...,K\}\) and generates possible product to shelf allocations (whether a product is placed on the shelf or not) with regard to the constraints. All the sequential steps of the remaining procedures are explained below.

4.1.2 GenerateTernaryValues procedure

This procedure constructs all sequences consisting of those product orientations which are allowed by product orientation constraints. The number of sequences is limited because, while generating, many allocations are excluded by the constraints which determine if a given product can be placed on the shelf or not. The allocations that do not satisfy all constraints can be excluded, which substantially reduces the number of generated sequences with respect to all possible ternary sequences.

According to the constraint (19) for the products with possible front orientation (\(p_{j}^{{o_{1} }} = 1\)) it generates ternary allocations using ‘0’s and ‘1’s. The number of such sequences is \(\left| {\{ j:p_{j}^{k} = k, \, p_{j}^{{o_{1} }} = 1,j = 1,...,P,k = 1,...,K\} } \right|\). E.g., 01,010—there are 5 products in the category, the 2nd and the 4th product is put on the shelf in front orientation. In this sequence, the following notations are used: 0—not placed, 1—front orientation, 2—side orientation.

Because the side orientation is the secondary one, all products have a front orientation (\(p_{j}^{{o_{1} }} = 1\)), but only a few of them have the additional side orientation (\(p_{j}^{{o_{2} }} = 1\)). Next, the procedure generates ternary allocations using ‘0’s and ‘2’s for products with possible side orientation (\(p_{j}^{{o_{2} }} = 1\)) according to the constraint (20). The number of such sequences is \(\left| {\{ j:p_{j}^{k} = k, \, p_{j}^{{o_{2} }} = 1,j = 1,...,P,k = 1,...,K\} } \right|\). For example, if the sequence is 20110—there are 5 products in the category, the 1st product is put on the shelf in the side orientation, the 3rd and the 4this put on the shelf in the front orientation.

Obviously, this procedure generates sequences in a way that excludes duplications, i.e., ternary sequences must be generated for each product considering its orientation.

4.1.3 GenerateProductSequences procedure

According to the constraint (22), all cluster products must be put together on the shelf, so this procedure excludes the incorrect sequences from the set of ternary sequences. Only correct sequences are left so that.

$$\begin{array}{*{20}l} {\forall \left( {k:k = 1,...,K} \right)\left[ {\sum\limits_{\begin{gathered} j,a = 1,...,P, \hfill \\ p_{j}^{k} = k, \hfill \\ p_{j}^{l} = p_{a}^{l} , \hfill \\ j \ne a \hfill \\ \end{gathered} } {x_{ij} = \left| {\{ j:p_{j}^{k} = k,\;p_{j}^{l} = p_{a}^{l} ,\;j \ne a,j,\;a = 1,...,P\} } \right|} } \right] \vee } \hfill \\ { \vee \forall \left( {k:k = 1,...,K} \right)\left[ {\sum\limits_{\begin{gathered} j,a = 1,...,P, \hfill \\ p_{j}^{k} = k, \hfill \\ p_{j}^{l} = p_{a}^{l} , \hfill \\ j \ne a \hfill \\ \end{gathered} } {x_{ij} = 0} } \right]} \hfill \\ \end{array} ,i = 1,...,S,$$
(36)

Which means that cluster products may be placed on the shelf together or may not be placed on the shelf at all.

In order to differentiate cluster and non-cluster products, the next parameter is defined.

$$z_{j} = \mathop {\min }\limits_{j,a = 1,...,P} \left(\left| {\{ j:p_{j}^{k} = k,p_{j}^{l} = p_{a}^{l} ,j \ne a\} } \right| - 1,1\right)$$
$$z_{j} = \left\{ \begin{gathered} 1,{\text{ if product }}j{\text{ is in a cluster}} \hfill \\ 0,{\text{ otherwise}} \hfill \\ \end{gathered} \right\},j = 1,...,P.$$

Claim. In this step, the number of possible product on shelf allocations equals:

$$\begin{array}{*{20}l} {\forall \left( {k:k = 1,...,K} \right)\left( {\prod\limits_{\begin{subarray}{l} j = 1,...,P, \\ p_{j}^{k} = k, \\ z_{j} = 0 \end{subarray} } {\left( {p_{j}^{{o_{1} }} + p_{j}^{{o_{2} }} + 1} \right)} \cdot \mathop {\max }\limits_{a = 1,...,P} \left( {\prod\limits_{\begin{gathered} j = 1,...,P, \hfill \\ p_{j}^{k} = k, \hfill \\ z_{j} = 1, \hfill \\ p_{j}^{l} = p_{a}^{l} , \hfill \\ j \ne a \hfill \\ \end{gathered} } {\left( {p_{j}^{{o_{1} }} + p_{j}^{{o_{2} }} + 1} \right)} } \right)} \right)} \hfill \\ { \, \uparrow \, \uparrow } \hfill \\ {\text{ non - cluster products cluster products}} \hfill \\ \end{array}$$
(37)

Proof. For non-cluster products, take the total possible variations with repetitions. For cluster products, calculate variations with repetitions only for one product in a cluster (because cluster products cannot be placed separately).

4.1.4 GenerateShelfValues procedure

This procedure constructs sequences for products that must be allocated on shelves taking into account the sales potentials subcategory constraint (25). It generates sequences specifically for each shelf on the basis of the sequences from the procedure GenerateProductSequences, i.e., for each shelf \(i\)\((i = 1,...,S)\), only ternary sequences are left so that \((p_{j}^{g} \le s_{i}^{g} )\).

4.1.5 GenerateShelfSequences procedure

From the sequences generated by the procedure GenerateShelfValues, this procedure excludes the ones that do not satisfy the minimum and maximum shelf number limit (constraints (6)–(7)). In order to take into account how many shelves the product can be allocated on, a parameter is provided.\(s_{j}^{real}\)—the real number of shelves to which a product can be allocated considering the shelf and the product sales potential subcategory \(s_{i}^{g}\) and \(p_{j}^{g}\), the maximum number of shelves, which it can be allocated on is \(s_{j}^{\max }\).

$$s_{j}^{real} = \min \left( {\sum\limits_{\begin{subarray}{l} i = 1,...,S \\ p_{j}^{g} \le s_{i}^{g} \end{subarray} } {1,s_{j}^{\max } } } \right),j = 1,...,P$$

Claim. The number of possible product on shelf allocations with regard to the minimum and the maximum number of shelves (constraints (6)–(7)) for the multi-shelf products and sales potentials subcategory (constraint (25)) equals:

$$\begin{gathered} \forall \left( {k:k = 1,...,K} \right)\left( {\prod\limits_{\begin{subarray}{l} j = 1,...,P \\ p_{j}^{k} = k, \\ z_{j} = 0 \end{subarray} } {(p_{j}^{{o_{1} }} + p_{j}^{{o_{2} }} + 1)^{{s_{j}^{real} }} \cdot \mathop {\max }\limits_{a = 1,...,P} \left( {\prod\limits_{\begin{gathered} j = 1,...,P \hfill \\ p_{j}^{k} = k, \hfill \\ z_{j} = 1, \hfill \\ p_{j}^{l} = p_{a}^{l} , \hfill \\ j \ne a \hfill \\ \end{gathered} } {\left( {p_{j}^{{o_{1} }} + p_{j}^{{o_{2} }} + 1} \right)^{{\min \left( {s_{j}^{real} } \right)}} } } \right)} } \right) \hfill \\ \, \uparrow \, \uparrow \hfill \\ {\text{ non - cluster products cluster products}} \hfill \\ \end{gathered}$$
(38)

Proof. For non-cluster products, take all the possible variations with repetitions from (37), leave only those where the product sales potential subcategory does not exceed the shelf sales potential subcategory \((p_{j}^{g} \le s_{i}^{g} )\). For cluster products, leave only those where the minimal sales potential subcategory in the cluster does not exceed the shelf sales potential subcategory:

\(\begin{array}{*{20}l} {\forall \left( {k:k = 1,...,K} \right)\forall \left( {j,a = 1,...,P:p_{j}^{k} = k,z_{j} = 1,p_{j}^{l} = p_{a}^{l} ,j \ne a} \right)} \hfill \\ {\left[ {s_{j}^{real} = \mathop {\min }\limits_{\begin{gathered} j,a = 1,...,P, \hfill \\ p_{j}^{k} = k, \hfill \\ z_{j} = 1, \hfill \\ p_{j}^{l} = p_{a}^{l} \hfill \\ j \ne a \hfill \\ \end{gathered} } (s_{j}^{real} ) = \mathop {\min }\limits_{\begin{gathered} j,a = 1,...,P, \hfill \\ p_{j}^{k} = k, \hfill \\ z_{j} = 1, \hfill \\ p_{j}^{l} = p_{a}^{l} \hfill \\ j \ne a \hfill \\ \end{gathered} } \left( {\min \left( {\sum\limits_{\begin{subarray}{l} i = 1,...,S \\ p_{j}^{g} \le s_{i}^{g} \end{subarray} } {1,s_{j}^{\max } } } \right)} \right)} \right]} \hfill \\ \end{array}\).

If the products in a cluster have different sales potential subcategories, they must be put on the shelf with the sales potential subcategory equal or greater than the maximum sales potential subcategory in the cluster. If a product is placed on the shelf, it cannot be placed on another shelf, so we sum up only those sequences where \(\sum\limits_{\begin{subarray}{l} i = 1,...,S \\ p_{j}^{g} \le s_{i}^{g} \end{subarray} }^{{}} 1 \le s_{j}^{\max }\).

Claim. The total number of possible product on shelf allocations considering all categories equals:

$$\begin{gathered} \prod\limits_{{k = 1}}^{K} {\left( {\prod\limits_{\begin{subarray}{l} j = 1,...,P \\ p_{j}^{k} = k, \\ z_{j} = 0 \end{subarray} } {\left( {p_{j}^{{o_{1} }} + p_{j}^{{o_{2} }} + 1} \right)^{{s_{j}^{{real}} }} \cdot \mathop {\max }\limits_{{a = 1,...,P}} } \left( {\prod\limits_{\begin{gathered} j = 1,...,P \hfill \\ p_{j}^{k} = k, \hfill \\ z_{j} = 1, \hfill \\ p_{j}^{l} = p_{a}^{l} , \hfill \\ j \ne a \hfill \\ \end{gathered} } {\left( {p_{j}^{{o_{1} }} + p_{j}^{{o_{2} }} + 1} \right)^{{s_{j}^{{real}} }} } } \right)} \right)} \hfill \\ {\text{ }} \uparrow {\text{ }} \uparrow \hfill \\ {\text{ non - cluster products cluster products}} \hfill \\ \end{gathered}$$
(39)

Proof. The total number of possible products on shelf allocations considering all categories is a multiplication of previously found values for each category (formula (38)).

Claim. The total number of product allocations in a general case is

$$(3^{P} )^{S} = 3^{PS}$$
(40)

Number 3 represents the possible allocations of the product: (1) if it is not placed on the shelf, (2) if it is placed on the shelf in the front orientation, (3) if it is placed on the shelf in the side orientation. All products may be placed on all shelves simultaneously.

Claim. The total number of product allocations in a general case that takes categories into account is:

$$\left( {\prod\limits_{\begin{subarray}{l} k = 1, \ldots ,K \\ p_{j}^{k} = k \end{subarray} } {3^{{\left| {\left\{ {j:p_{j}^{k} = k, \, j = 1, \ldots ,P} \right\}} \right|}} } } \right)^{S} = \prod\limits_{\begin{subarray}{l} k = 1, \ldots ,K \\ p_{j}^{k} = k \end{subarray} } {3^{{\left| {\left\{ {j:p_{j}^{k} = k, \, j = 1, \ldots ,P} \right\}} \right|}} } = 3^{PS}$$
(41)

In this formula, the total number of products \(P\) equals the sum of the number of products in each category, i.e. \(P = \sum\limits_{\begin{subarray}{l} k = 1,...,K \\ p_{j}^{k} = k \end{subarray} }^{{}} {\left| {\{ j:p_{j}^{k} = k, \, j = 1,...,P\} } \right|}\).

Claim. The total number of product allocations in our case, which takes the current constraints into account, can be reduced to:

$$\prod\limits_{k = 1}^{K} {\left( {\prod\limits_{\begin{subarray}{l} j = 1,...,P \\ p_{j}^{k} = k, \\ z_{j} = 0 \end{subarray} } {\left( {p_{j}^{{o_{1} }} + p_{j}^{{o_{2} }} + 1} \right)^{{s_{j}^{real} }} \cdot \mathop {\max }\limits_{a = 1,...,P} \left( {\prod\limits_{\begin{gathered} j = 1,...,P \hfill \\ p_{j}^{k} = k, \hfill \\ z_{j} = 1, \hfill \\ p_{j}^{l} = p_{a}^{l} , \hfill \\ j \ne a \hfill \\ \end{gathered} } {\left( {p_{j}^{{o_{1} }} + p_{j}^{{o_{2} }} + 1} \right)^{{s_{j}^{real} }} } } \right)} } \right)}$$
(42)

The next steps of the procedure are as follows:

  1. 1.

    Exclude from the generated sequences the sequences with an incorrect orientation (constraints (16)–(18)).

  2. 2.

    Exclude from the generated sequences the sequences where the shelf depth limit is exceeded (constraint (4)).

  3. 3.

    Generate sequences with regard to the next shelf constraint (21). After this step, shelf permutations may be reduced. The number of shelf permutations may be left the same if there are no products allocated to multiple shelves in the given category.

  4. 4.

    From the generated set of sequences, exclude ones where the total width of facings lower bound on one shelf exceeds the total width of facings upper bound. Leave only those sequences that satisfy category tolerance between different shelves (constraint (24)).

    $$\begin{gathered} \forall \left( {k:k = 1,...,K} \right)\mathop {\max }\limits_{\begin{subarray}{l} i,a = 1,...,S, \\ i \ne a \\ p_{j}^{k} = k \end{subarray} } \left( {x_{ij} f_{j}^{\min } \left( {y_{ij}^{{o_{1} }} p_{j}^{w} + y_{ij}^{{o_{2} }} p_{j}^{d} } \right)} \right) - x_{aj} f_{j}^{\max } \left( {y_{aj}^{{o_{1} }} p_{j}^{w} + y_{j}^{{o_{2} }} p_{j}^{d} } \right) \le \hfill \\ \le \left[ {\mathop {\max }\limits_{i = 1,...,S} (s_{i}^{l} ) \cdot t_{k} } \right] \hfill \\ \end{gathered}$$
    (43)
  5. 5.

    Based on the \(\{ f_{j}^{\min } ...f_{j}^{\max } \}\) if, in the result, the empty shelves are not expected within the category, at this step, the sequences with all ‘0’s (empty shelf) and consequently the sequences with all ‘1’s or ‘2’s (all products are put on this shelf) can be excluded.

  6. 6.

    Based on the assumption provided in step (5), get single shelf sequences and exclude empty and full shelves from them. In this step, we obtain the shelf sequences, which combine sequences for all shelves.

4.1.6 GenerateProductWidthSequences procedure

This procedure calculates the product sequence. The main steps of such a procedure are as follows:

figure b

4.1.7 FindSpaceCategory procedure

In this procedure, the remaining length for a category is calculated based on the constraint (23). The same actions are done for weight.

The following notations will be used.\(b_{j}^{bin}\)—binary (0/1) value for the product \(j\)\((j = 1,...,P)\) in the current category in the sequence.\(b_{j}^{ter}\)—ternary (0/2) value for the product \(j\)\((j = 1,...,P)\) in the current category in the sequence.\(c_{k}^{l\min }\)—the minimum length of the category \(k\)\((k = 1,...,K)\).\(c_{k}^{l\max }\)—the maximum length of the category \(k\)\((k = 1,...,K)\).\(c_{k}^{b\min }\)—the minimum weight of the category \(k\)\((k = 1,...,K)\).\(c_{k}^{b\max }\)—the maximum weight of the category \(k\)\((k = 1,...,K)\).\(c_{k}^{h}\)—the height of the category \(k\)\((k = 1,...,K)\).\(c_{k}^{d}\)—the depth of the category \(k\)\((k = 1,...,K)\).\(r_{j}\)—the number of remaining available items of the product \(j\)\((j = 1,...,P)\).

$$x_{ij} = \max \left( {b_{j}^{bin} ,b_{j}^{ter} ,1} \right)\sqrt {b^{2} - 4ac} ,\;j = 1, \ldots ,P,\;i = 1, \ldots ,S$$
(44)
$$y_{ij}^{{o_{1} }} = \left\{ {\begin{array}{*{20}l} {1,} \hfill & {\max \left( {b_{j}^{bin} ,b_{j}^{ter} } \right) = 1} \hfill \\ {0,} \hfill & {{\text{otherwise}}} \hfill \\ \end{array} } \right\},\;j = 1, \ldots ,P,\;i = 1, \ldots ,S$$
(45)
$$y_{ij}^{{o_{2} }} = \left\{ {\begin{array}{*{20}l} {1,} \hfill & {\max \left( {b_{j}^{bin} ,b_{j}^{ter} } \right) = 2} \hfill \\ {0,} \hfill & {{\text{otherwise}}} \hfill \\ \end{array} } \right\},\;j = 1,...,P,\;i = 1,...,S$$
(46)
$$c_{k}^{l\min } = \sum\limits_{\begin{subarray}{l} j = 1, \\ p_{j}^{k} = k \end{subarray} }^{P} {x_{ij} f_{j}^{\min } \left( {y_{ij}^{{o_{1} }} p_{j}^{w} + y_{ij}^{{o_{2} }} p_{j}^{d} } \right)} ,\;k = 1,...,K$$
(47)
$$c_{k}^{l\max } = s_{i}^{l} - (K - 1) \cdot \left[ {s_{i}^{l} \cdot m_{k} } \right],\;i = 1, \ldots ,S,\;k = 1, \ldots ,K$$
(48)
$$c_{k}^{b\min } = \sum\limits_{\begin{subarray}{l} j = 1, \\ p_{j}^{k} = k \end{subarray} }^{P} {x_{ij} \left( {f_{j}^{\min } + c_{j}^{\min } + n_{j}^{\min } } \right)p_{j}^{b} ,\;k = 1,...,K}$$
(49)
$$c_{k}^{b\max } = \left[ {\frac{{c_{k}^{l\max } \cdot s_{i}^{b} }}{{s_{i}^{l} }}} \right],\;i = 1,...,S,\;k = 1,...,K$$
(50)
$$c_{k}^{h} = s_{i}^{h} ,\;i = 1, \ldots ,S,\;k = 1, \ldots ,K$$
(51)
$$c_{k}^{d} = s_{i}^{d} ,\;i = 1, \ldots ,S,\;k = 1, \ldots ,K$$
(52)

The formula (44) indicates if the product is put on the shelf in the investigated category in the current product sequence. Formulas (45) and (46) show if the product is put on the shelf in the investigated category in the front (45) or side (46) orientation. Formulas (47) and (48) represent the minimum and maximum category length on the shelf calculated on the facings from the given product sequence. Formulas (49) and (50) calculate the minimum and the maximum category weight. The category’s height (51) and depth (52) equal the corresponding shelf values.

4.1.8 CreateItems procedure

We model the problem as a knapsack with internal sections, each section of which is dedicated to the product of the defined type. Because all the products, according to the generated sequence, must be placed into the knapsack, each section must exist. The goal is to define the number of items of each product \((f_{j}^{\max } + c_{j}^{\max } + n_{j}^{\max } )\) and in consequence, the size of the section.

In this procedure, the items which will be later put in the knapsack are created in the following way. We have a bounded 0–1 knapsack, the set and the number of items \((f_{j}^{\max } + c_{j}^{\max } + n_{j}^{\max } )\) which can be put into it is known. For each product in the current product sequence, we check if it is capped \((c_{j}^{\max } > 0)\) or nested \((n_{j}^{\max } > 0)\). If not, we add all \(f_{j}^{\max }\) items to the set. The number of items that are added to the set is calculated with regard to the supply limit (constraint (8)), lower and upper bound of product facings (constraints (9) and (10)), cappings per position (constraints (11) and (12)), nestings per facing (constraints (13) and (14)). The available number of nests per face is also under the control of the height limit (constraint (3)). The products that are added to the items are marked with a \(groupID\) given at the step of item creation. One capped (nested) item is assigned a \(groupID\). The separate items which are included in this capped (nested) group have the same \(groupID\). This means that separate items and capped (nested) items cannot be taken simultaneously. Therefore, the items which can be taken simultaneously have different \(groupID\), otherwise capped (nested) items, and corresponding not capped (not nested) items have the same \(groupID\), which means that we can take either capped (nested) or not capped (not nested) items in the same group, but not both of them.

4.1.9 FindWidthLB procedure

We represent the knapsack as a knapsack with sections inside; in each section, different number of product items of the given type can be put. The total knapsack size is fixed; we modify only the size of the interior sections. In order to solve the knapsack problem later, this procedure defines the step \(step_{p}\) with which the section size will be increased or decreased, i.e., the greatest common divisor \(gcd\) for each product in the category, i.e., the smallest item width of the given product type in the item set. From the previous procedure where items have been created, it is known that items may be represented as single product facing or merged from some facings with capping above or nestings inside. So, the width of an item (both for capped and nested ones) and weight (only for capped items) will be different. Therefore, in this case,\(gcd\) equals the minimum width of the product in the group with the same index \(j\), i.e., all products with the same index \(j\) have width divisible by the minimum width in the group.

In the next listing, the following notations are used:\(step_{j}\)—\(gcd\) of items in the group with the same \(j\)\((j = 1,...,P)\).\(start_{j}\)—start width of the knapsack for items with index \(j\)\((j = 1,...,P)\).\(end_{j}\)—end width of the knapsack for items with index \(j\)\((j = 1,...,P)\).\(t\)—input parameter, a common multiple for \(step_{p}\), used to take not one \(gcd\) but \(t \cdot gcd\) of the product \(j\)\((j = 1,...,P)\) in order to perform local search faster.

The future width dimension for the product \(j\) will be [0, \(start_{j}\), \(start_{j} + step_{j}\) … \(end_{j}\)].

4.1.10 GenerateVariableWidths procedure

In this procedure, we define the multisection knapsacks variants of the total section number \(\left| {\{ j:p_{j}^{k} = k, \, j = 1,...,P,k = 1,...,K\} } \right|\). The widths of sections vary from \(start_{j}\) to \(end_{j}\) with the step \(step_{j}\). All generated solutions are saved for later analysis.

4.1.11 CalculateProfit procedure

In this procedure, we sort items by profit in non-ascending order. Next, we add items to the knapsack section one by one if its width does not exceed the section size, supply limit \(p_{j}^{s}\) of the product \(j\) (also summing up cappings and nestings) is satisfied, and \(groupID\) for capped and nested items is the same.

4.1.12 CalculateTotals procedure

After the items have been chosen for each section of the knapsack, this procedure calculates facings, cappings, nestings, profit, width, weight, height, depth of each section of the knapsack.

4.1.13 OutputWidths procedure

In this procedure, we create a quality report for each width of the sections of the knapsack. Obviously, for each knapsack section size, different variants of totals will appear. Thus, for each binary \(b_{j}^{bin}\) or ternary \(b_{j}^{ter}\) value of product allocations, for each total knapsack width and weight, take items set with maximum profit.

4.1.14 GetMaxProfitSolution procedure

This procedure selects the sequence with the appropriate numbers of facings \(f_{ij}\), cappings \(c_{ij}\) and nestings \(n_{ij}\) for the given product, which gives the maximum total profit. This is the best solution for the given product.

4.2 Proposed heuristics explanation

All heuristics described in this paper combine generated product sequences from 4.1.3 (GenerateProductSequences procedure), shelf sequences from 4.1.5 (GenerateShelfSequences procedure) and category totals (profit, width, weight, binary or ternary values of product allocations) from 4.1.14 (GetMaxProfitSolution procedure). All heuristics search only for an appropriate solution based on a formula (42). Figure 5 illustrates common and distinct steps in all proposed heuristics.

Fig. 5
figure 5

Heuristics steps

Full size image

5 Computational Experiment

The computational experiments evaluate the performance of the solutions of the developed heuristics for the presented shelf space allocation problem. As there is neither real-world data available due to commercial confidentiality nor any benchmark found in literature or available from open sources, simulated test problems were generated. All of their data is based on real-life data.

The computational experiments were implemented in Visual C# 2015 and MS SQL Server 2014.

Language: Visual C# 2015

Microsoft Visual Studio Community 2015

Version 14.0.25431.01 Update 3

Microsoft.NET Framework

Version 4.6.01055

Microsoft SQL Server Management Studio12.0.2269.0

An optimal (or maximum feasible in some cases) solution to compare with has been found using commercial solver IBM ILOG CPLEX Optimization Studio Version: 12.7.1.0.

5.1 Heuristics performance

Some of the advantages of the presented algorithms are:

  • Lack of randomly selected elements, so there is no need to run it several times;

  • Data is visible in each step and can be easily checked;

  • The coefficient parameters that can also be easily estimated while watching the data.

Table 2 summarizes the number of solutions found by all heuristics where the heuristics solution was the best (most profitable) feasible solution among those that were found by a given heuristic. Heuristic \(H_{3}\) was the best among all of them, finding the maximum solution in 20 cases. But as we see in Table 3, other heuristics found the maximum feasible solution also in cases where \(H_{3}\) cannot achieve this. So there is definitely a necessity for other implemented ones. Compared to the CPLEX solver, heuristics found the solution in 34 cases while CPLEX in 23 cases only. In Table 3, we do not differentiate which of these solutions was better. Table 3 presents the total number of feasible solutions received. This observation proves the necessity of the heuristics because, clearly, instances for which CPLEX did not find a feasible solution do exist.

Table 2 Number of solutions found by Heuristics where Heuristics solution is a maximum feasible solution
Full size table
Table 3 Number of solutions found by Heuristics and by CPLEX Solver
Full size table

In order to estimate the performance of the heuristics, the following notations will be used.

\(U_{h}\)—the profit of the heuristics (calculated in formula (1)).

\(U_{o}\)—the profit of the CPLEX solution.

\(U_{h} /U_{o}\)—the profit ratio of the heuristics to the optimal (or maximum feasible in some cases) solution.

Table 4 presents the quality of solutions found by heuristics compared to the CPLEX solver and to the results reported by Czerniachowska and Hernes [13]. It could be observed that the average profit ratio of the best heuristic is 95.25%, with minimal and maximal values of 87.78% and 99.84%, respectively. Not bad, but this situation should be improved in the future. As we remember from 4.1.13 we took items set with maximum profit for each equal width and weight. At this step, the less profitable sequences were excluded, only the best ones for each width and weight were taken, but later these best ones were excluded because of not satisfy other constraints. As we see, the CPLEX solver created a better solution on the basis of a not profitable sequence. So in future research, the method of including the worst sequences without increasing their number so much should be proposed. Nevertheless, as we see, there are some advantages of the proposed approach. In 11 cases, heuristics found the solution, but CPLEX did not because there were few sequences to be analyzed, so taking the best sequences in 4.1.13 helped to create a feasible solution fast. It could be noticed that there was no reverse situation where CPLEX found the solution, but heuristics did not. In 11 cases, the solution was found neither by heuristics nor by CPLEX. This case illustrates a situation from the real world where retailers order something that cannot be implemented, e.g., there are too many products in the category that they cannot be placed in beautiful columns, it is better to divide them in some other way, minimum category size or category tolerance should be changed, the shelf weight or length does not fit, or the sales potentials of the products are incorrect so that on there are too many products one shelf and too few on another. All these errors are visible and could be analyzed at each described step. As we remember, if product sequences ( 4.1.3) or shelf sequences ( 4.1.5) could not be generated, there is no reason to waste time trying to find the solution to this data. In such a situation, a hint should be given to space planners explaining what constraint is not met and why and what should be corrected. The same thing happens if we receive too many sequences in one category and too few in another. As we see, the profit ratio does not depend on product number or on the shelf length, compared to the previous research. Based on the nature of the problem, CPLEX could find the solution neither for small instances (15 products) nor for large instances (50 products). This depends on the category parameters, such as tolerance and minimum category size, as well as the number of possible product and shelf sequences to be generated. If the input data is too complicated, the solution could not be found by CPLEX, if the input data is less complicated, the solution could be found, but in this case, heuristics would be slightly worse.

Table 4 The quality of the heuristics solution compared to CPLEX and the latest research
Full size table

Comparing the obtained quality results with the results by Czerniachowska and Hernes [13], we can observe that the minimum and average profit ratios of the proposed heuristics are a bit higher. The minimum profit ratio is 87.78% (Table 4) compared to 86.80% of the mentioned research. The average profit ratio is 95.25% (Table 4) compared to 94.57% of the mentioned research. The maximum profit ratio is the same and equals 99.84%. The standard deviation of the proposed heuristics is 3.93% (Table 4) compared to 4.17%, which makes them more stable.

The processing time for searching for the maximum feasible solution, which on average varies from 16.79 up to 54.55 s comparing all heuristics. The heuristic \(H_{5}\) was the fastest. The heuristic \(H_{6}\) was the slowest.

Table 5 compares the total time of execution of heuristics in the proposed approach and in the research by Czerniachowska and Hernes [13]. Total time for our approach means the sum of execution times of all 6 heuristics. The total time for the research by Czerniachowska and Hernes [13] means the sum of execution times of both 2 heuristics that they proposed. We used such a measure of the total time because we needed to run all 6 heuristics before we got the answer or decided which heuristics was the best.

Table 5 Total time of execution of heuristics in the proposed approach and in the research by Czerniachowska and Hernes [13]
Full size table

Comparing the achieved time results with the results by Czerniachowska and Hernes [13], we can notice that proposed heuristics, on average, found the solution slower (15.36 min), compared to 10.82 min in previous research. But total time combines the time of all 6 heuristics. On average, the execution time of one heuristics is less than a minute, so it is faster than the average execution time of a single heuristics in the previous research. The time limit for CPLEX was set to 2 min because it is slightly more than the average execution time of a single heuristics in our research. But in most cases, CPLEX spent for solution significantly less than 2 min.

The heuristic \(H_{1}\) is used for initial space searching when neither the solution range nor approximate profit for each category is known. The heuristic \(H_{2}\) is used for the improvement of the solution, which was found by the heuristic \(H_{1}\). Steering parameters of the heuristic \(H_{2}\) help to improve the total solution because they improve the partition solutions for each category. The heuristic \(H_{3}\) is also used for the improvement of the solution, which was found by heuristic \(H_{1}\), but it is used when there are too many results to check that heuristic \(H_{2}\) cannot do this in a reasonable time. The heuristics \(H_{4}\), \(H_{5}\), \(H_{6}\) are appropriate for large instances and can process a large amount of data very fast. They differ from each other by steering parameters, grouping methods, and sorting order.

Table 6 shows the total number of product allocations in the general case (formulas (40) or (41)) and the total number of product allocations of the proposed solution by authors (formula (42)) calculated on the basis of the test data. As can be observed, there is a huge difference between the general case and our method. It should be highlighted that in our proposed heuristics, only data that satisfy all the constraints is taken in each step. That is why the reduction in the number of solutions is so visible and so high.

Table 6 The total number of product allocations in the general case compared to the proposed solution
Full size table

6 Conclusion

This paper focuses on the SSAP in order to maximize the total profit. Retailers are looking for expert solutions or advice on how to differentiate and allocate products while minimizing lost revenue, maximizing profit, find a balance between meeting customer needs and multiple inputs. Based on the NP-hard nature of the problem examined, which is an extension of a knapsack problem and is difficult to be solved, there is a growing interest of scientists in developing heuristics and metaheuristics for the SSAP.

We proposed 6 heuristics and gave detailed practical algorithms with enough explanation, which are ready to be implemented in other category management problems. The first 3 heuristics are better for small instances. The last 3 ones are designed especially for large instances, as they process large amounts of data in a very short time. Examples of implementation and changing steering parameters are also included. The new practicable mathematical model was developed with the objective of maximizing the retailer’s profit, which takes into account merchandising visual products display, i.e., horizontal products grouped into categories and vertical shelf levels based on the products’ values and sales potentials.

To examine the performance of the proposed heuristics, 45 test cases were investigated. Among them, heuristics found solutions in 34 cases while CPLEX in 23 only. The profit ratio of the developed heuristics in the best case on average is 95.25%, with its minimal and maximal values 87.78% and 99.84%, accordingly.

The main characteristics which differentiate the proposed solution techniques from the previous ones are the lack of randomly generated or randomly selected elements and the fact that data in all described steps is visible and can be easily analyzed or adjusted by the coefficient steering parameters. In 11 cases where a solution was not found, the bits of advice of changing data could be given to category planners, i.e., changing the product grouping method, increase the minimum category size and tolerance, and reassign sales potentials. Very frequently, it occurs that the category planner cannot estimate if the solution exists. In the simplest case, the proposed steps of product and shelf sequence generation help him with this task. This detail also differentiates our research from the previous ones because it has a method of checking constraints quickly. The next steps could show which category does not meet constraints if the solution is not found. Heuristics execute in a couple of seconds or minutes, depending on the instance and heuristic type. A shorter calculation time is achieved because, in the beginning, we reduce the search space, generating only the possible product and shelf sequences, and then only the correct single parts of the future solution are taken, excluding the combinations which do not satisfy the constraints. So in all steps of the proposed algorithm, only the correct parts of the constructed solutions are considered. In most metaheuristics, there are random local searches, crossovers, and mutation operations that can make a correct solution infeasible, and thus, repair procedures have to be used. For example, Czerniachowska [10] developed a correction and solution improvement procedure in order to obtain the appropriate solution after each GA step. She also excluded a shelf with large packaged products from GA implementation and adopted dynamic programming to solve it optimally. Thus, different methods were used for solution correction. But in the current research, the heuristics generate only appropriate solutions which do not need to be corrected.

As for the limitation of the proposed heuristic approach, there is no solution component evaluation while composing the whole solution. For example, in a genetic algorithm, highly rated components can be selected for crossover and solution creation at further steps. In the proposed approach, we can control the number of solutions generated and evaluate the total solution.

The results of the research can be used, for example, in order to implement a shelf space allocation module in retail information systems. There are several interesting, practically relevant questions and directions available for future investigation. We recommend the shelf space allocation model with included constraints of store layout for future research. It would be interesting and practically relevant to expand the proposed mathematical model with the goal of maximizing customer traffic. In addition, the model should consider clockwise or anti-clockwise customer direction.