1 Introduction

In the perishable food supply chains (PFSC) there are continuous changes in the quality of the product from the moment it leaves the farm until it reaches the consumer, generating losses. It is estimated that one third of food production worldwide is wasted or damaged [22]. In developing countries, post-harvest losses often exceed 50% [53]. Fresh food consumers demand better organoleptic properties and a greater variety, however the perishable nature of fresh food makes logistics and their quality management difficult [5, 33].

The location of the actors and production, transformation, commercials and distribution facilities make up the configuration of the supply chain (SC) which governs logistic flows. Due to the geographic dispersion, the intensity and frequency of flows between these facilities, a series of modeling techniques have been developed to achieve better performance measures in food supply chain (FSC). The modeling about FSC uses different strategies, from purely conceptual to those developed through operations research with simulation or optimization techniques [48]. If the interest is to achieve the best performance measures, optimization models are formulated which are often more complex in the search for solutions [2, 20].

Logistics integrates the companies with their suppliers, processing plants, distribution centers and customers [10, 21]. The optimization models allow to establish the location of the PFSC´s facilities, as well as to determine its operation. The flows in the PFSC have particularities that are derived from configuration of the supply chain (SC). When the SC design (SCD) is established with an emphasis on logistics, the Logistics Network Design (LND) concept appears [19]. As in the SCD, the LND includes strategic decisions such as the definition of capacity, number and location of collection centers, processing plants and distribution centers [32, 40]. The duration and conditions of logistics operations have a significant impact on the performance of a logistics network for fresh agricultural products.

The configurations of the LND lead to duration of transport time, storage, processing and distribution. Therefore, when making decisions about LND´s configurations is necessary to evaluate the affects for delivery time and product quality must be taken into account [11, 28], they identified various internal factors (strengths and weaknesses) and external factors (opportunities and threats) of Indian agri-food supply chain (AFSC) to make a strategic analysis which need to be addressed in designing of Indian AFSC, where the small farm holding farmers is a major weakness of Indian agriculture system. In this direction, the problems of logistics in a supply chain management in most of the research is done on decentralized control strategy only. Its necessary to compare the centralized and decentralized supply chains to find out which type of supply chain is more advantageous in terms of performance [41]. Perishable products require careful handling throughout their supply chain, which requires reefer vehicles and cold storage facilities. They need to move fast in the supply chain as their longer stay would cause more energy consumption and higher perishability losses leading to increased cost and carbon footprints. Thus, is necessary development sustainable freight transportation (SFT) and cold-chain for perishable food products [50].

There are several investigations that study how to take advantage of the food waste generated in the FSCs. Walia and Sanders [51] study the problem of food waste in the US and its ecological cost, discusses public policy and private action to curb food waste or toward hunger alleviation. Eisenhandler and Tzur [13] analyze the collecting food donations from suppliers in the food industry and delivering them to food relief agencies that serve individuals in need, the model has emphasis in simultaneous vehicle routing and resource allocation decisions, with the aim of maximizing the total amount distributed and achieving equity in the allocation. On the same way, Dubey and Tanksale [12] evaluated the role that Food banks play to ensure food security through surplus food recovery and redistribution to economically deprived and marginalized people, identifying challenges and barriers that impede their growth, 14 barriers through literature review were established. Traceability systems in PFSC become a mechanism that, when implemented, also allows the reduction of waste and food losses [23, 27].

The logistics flows in the PFSC are influenced by a series of factors such as supply, demand, storing operations, transformation, storage and distribution, having all an effect on one side to food security [2, 3] and the other hand location of facilities [43]. There are different study on urban demand in retailers, some authors have been concerned with studying competitive vs. collaborative markets, they find an improvement in logistics performance when forming demand clusters [1]. Other have focus on the differences of consumption habits between races and purchasing practices in neighborhoods of cities, they study the importance of race and culture in food consumption [56].

Some institutions such as CFS consider as the four pillars of food security are availability, access, utilization and stability [8], while others what food security includes the sufficient and stable availability of food supply, prompt and permanent access to them in quantity, quality and safety [9, 24]. The balance of logistics flows derived from supply and demand could affect food security, given its effect on availability and access [37, 38]. The PFSC there is an imbalance between supply and demand, there are periods of high and low supply to the which the demand does not respond in the same way, this affects the balance and therefore the logistic flows in the chain [34]

For the evaluation of the performance of the SC, a series of metrics have been proposed which can be classified into efficiency, responsiveness, reliability, flexibility, quality, in the process and the parties involved [6, 25]. For the PFSC there is a need to include quality, useful life, logistic performance and losses, as well as the access and the availability, elements from food security [5, 39]. Research works are found in developed countries, future research in developing countries should focus on reducing losses and increasing food availability and access [54]. It is found that the models leave out key actor such as processors, supermarkets and retailers [46]. Esmizadeh and Mellat Parast [17] conducted a systematic literature review to examine several logistics network designs and evaluate their performance with respect to cost, quality, delivery, flexibility, and resilience. They pose that each network has its own strengths: a hub-and-spoke network has economies of scale to reduce delivery costs, and routing flexibility to mitigate the effects of disruptions, a cross-docking network provides lower inventory cost; and a pick-up and delivery network provides lower delivery time. They suggest considering a hybrid logistics model in situations where firms need to emphasize cost and resilience. As well as organizations need to be aware of the trade-off among different competitive priorities if they intend to address multiple competitive priorities such as cost and service quality in their logistics system.

Therefore, the LND of food (FLND) presents greater challenges, given the problems they face in the real complex systems, including the multiplicity of decisions, scales, levels, periods, objectives and undoubtedly the multiple parties interested [29]. The use of integrated approaches and models in PFSC is limited; the models do not incorporate their inherent characteristics [25], such as the incidence of the cold chain, shelf life, organoleptic attributes or freshness and innocuity [3, 44]. There is a need to include the behavior of temperature in the useful life of food, as well as in transport, inventories and demand [49]. The main challenge is to develop models that can be solved on real-world size problems, for foods that are not linked to cold chains or that are exposed to a wider range of temperatures [11].

Studies show interest of retailers in improving their performance by responding to different consumer cultures, however availability and access can be affected by competition factors that lead to monopolies and oligopolies [18], then the question arises on how retailers are preserved downstream of the SC and to distribute the power of the market [1].

There is a lack of research on modeling and optimization methods for PFSC management [30]. In this context, its necessary to develop models which represent the features of PFSC on deficit periods, listed above which should have multiobjective functions that permit improve performance of PFSC, such as, the decrease of the perishable food losses and average lead time, as well as the increase on inclusion of the retailed storekeepers attended which should allow to guarantee availability and access, elements of food security in PFSC.

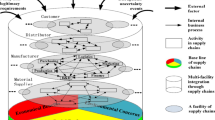
In Fig. 1, the constitutive elements of the logistics network are presented; it entails logistics flows and the factors that affect food security. The continuous arrows represent the food flow, while the dotted represents the information. In the upper part of Fig. 1, the actors are presented in orange color, whose when producing, marketing, demanding and consuming, generate the food flows, represented by green color. The performance of the logistics network can be measured by efficiency, costs, prices, responsiveness and quality which have been shown in the lower part of the figure in blue. A good flow performance contributes to availability and access, hence to food security.

Fig. 1
figure 1

Logistics network and its relationship with flows and food security

Full size image

The document has been organized in three parts. The methodological design which includes the model configuration design of PFSC. The case study was applied in perishable fruit supply chain. Last Section shows the results and their discussion, followed by the conclusions.

2 Methodological design

2.1 Model design

The use of optimization models allows establishing efficiency boundaries, when proposing, validating and implementing their derived configuration. A multi-objective, multi-product and multi-level model was defined for the location of facilities (collection and distribution centers-wholesaler) from food for moments of deficit in the PFSC. For the construction of the model, a review of the literature on models of logistics networks, localization, perishable food supply chain was made, from which the variables, parameters, objective functions and constrains used by researchers for models in FSC were identified. The other hand, the mono-objective mixed linear programming optimization model was taken from Orjuela-Castro et al. [35]. The model was applied to a fruits perishable supply chain (PFrSC). For the parameterization of the models, information was obtained through two strategies. On the one hand, with information from studies and reports from public institutions, on the other hand, surveys were applied to the different actors in the fruit chain.

The model has three objective that permit minimize the losses, the lead time and maximize the attention of retailed food storekeepers which affect the food safety, the available and the access food. Therefore, the model pretends:

  1. 1.

    Redundancy in customer service flows is guaranteed, in such a way that customers are served by all distribution channels, this to minimize the lack of a product in case of disruptions in any arc. With this the availability of food is strengthened

  2. 2.

    It seeks to maximize the number of customers served, thus, guarantees better availability of products and improves access to them by consumers

  3. 3.

    Different types of waste are reduced and so improve food availability.

On the other hand, the model responses to the different characteristics of fresh perishable food supply chain, it considers the losses derived from the impacts caused by changes in temperature (T0) and relative humidity (RH), in mountainous environment of developing countries which use transport without refrigeration and with improper handling of the fresh food.

2.2 Model configuration design of the PFSC

The multi-objective mathematical model proposed for the PFSC includes different thermal floors and their impact on the perishability of different types of food. The perishability is calculated on three approaches, the loss of food by manipulation in the storage nodes, the loss of food due to climatic changes and relative humidity derived from the different thermal floors. The proposed model addresses the problem of the logistics network setting, considering an environment where the demand is greater than the supply and food security must be guaranteed, in this sense, it seeks to minimize losses, decrease the average time of service, and maximize the number of customers served.

The model establishes the location of the collection and distribution centers (wholesalers), considers each municipality of producers, suppliers, as well as the transformation nodes, marketplaces, hypermarkets and shopkeepers as customers which allows a clearer identification of the Problem components to solve, Fig. 2.

Fig. 2
figure 2

Location and flow connections

Full size image

An important element in food sustainability is to involve a significant number of suppliers and minimize the oligopoly or monopoly [7]. The existence of big number of retail storekeepers decreases food risk [1]. The PFSC presents seasonality in the supply and generating periods of deficit. In coherence with the performance measures of this research, in a scenario with scarcity, three objective functions are proposed, the reduction of losses, maximize the number of clients attended and minimize the response time or attention (Lead time). In a PFSC with shortage, different customers must be attended and the intermediate nodes through which it must pass established. Below is the formulation for the supply deficit model.

2.2.1 Main sets and index

  • FARM = Areas of agricultural production, index i

  • SC = Possible location areas of the storage centers, index j

  • DC = Possible location areas of distribution centers, index k

  • FOODS = Types of perishable foods, index f

  • MARKET = Market places, index p

  • STORE = Consolidated stores, index t

  • HYPERM = Hypermarkets, index h

  • C = Centers of productive transformation, index c

  • DT = set of all possible destinations, index d, DT = (SC ∪ DC ∪ MARKET ∪ STORE ∪ HYPERM ∪ C)

  • \(\mathrm{DI}\,=\,\) set of intermediate and final destinations, index d3, DI = (DC ∪ MARKET ∪ STORE ∪ HYPERM ∪ C)

  • \(\mathrm{OT}\,=\,\) set of all possible origins, index o, OT = (FARM ∪ SC ∪ DC)

  • \(\mathrm{OIJ}\,=\,\) set of all possible origins up to link 2, index o2, OIJ = (FARM ∪ SC)

  • \(\mathrm{DF}\,=\,\) Set of final destinations, index d2, DF = (MARKET ∪ STORE ∪ HYPERM ∪ C)

2.2.2 Main parameters

  • \({\mathrm{OFI}}_{\mathrm{fi}}\,=\,\) Quantity of perishable food type f produced by the agricultural production area i

  • \({\mathrm{CF}}_{\mathrm{j}}\,=\,\) Fixed cost of the central storage located in j

  • \({\mathrm{CG}}_{\mathrm{k}}\,=\,\) Fixed cost of the wholesale center located in k

  • \({\mathrm{CT}}_{\mathrm{od}}\,=\,\) Transport cost between the origin \(\mathrm{o }\in \mathrm{ OT}\) to destination d ∈ DTOT{o}

  • \({\mathrm{CAM}}_{\mathrm{j}}\,=\,\) Maximum capacity of the storage center located in zone j j

  • \({\mathrm{CAL}}_{\mathrm{j}}\,=\,\) Minimum capacity of collection centers located in zone j

  • \({\mathrm{CTL}}_{\mathrm{k}}\,=\,\) Minimum capacity of wholesale centers

  • \({\mathrm{CP}}_{\mathrm{f}}\,=\,\) Cost of loss of perishable food type f

  • \({\mathrm{DN}}_{\mathrm{fd}2}\,=\,\) Demand at final destination d2,of the type of perishable good f ∈ FDF{d2}

  • \({\upbeta }_{\mathrm{fd}}\,=\,\) Percentage of food f that is lost, due to handling in storage at node o2 ∈ OT.

  • \({\mathrm{DIN}}_{\mathrm{od}} \,=\,\)  = Distance between the origin o ∈ OT to destiny d ∈ DTOT{o}

  • \({\mathrm{TN}}_{\mathrm{od}} \,=\,\) Loss percentage due to temperature change between the origin to destiny

  • \({\mathrm{HN}}_{\mathrm{od}}\,=\,\) Loss percentage due to relative humidity change between the the origin to destiny

2.2.3 Decision variables

The decision variables are presented below.

2.2.3.1 Opening variables

\(BOSC_{j} = \left\{ {\begin{array}{*{20}l} 1 \hfill & {If\,a\,storagecente\,R\,is\,opened\,in\,the\,area\,j \in SC} \hfill \\ 0 \hfill & {On\,the\,contrary} \hfill \\ \end{array} } \right\}\)

\(BOCD_{k} = \left\{ {\begin{array}{*{20}l} 1 \hfill & {If\,a\,distribution\,center\,\left( {wholesale} \right)\,is\,opened\,in\,the\,area\,k \in DC} \hfill \\ 0 \hfill & {On\,the\,contrary} \hfill \\ \end{array} } \right\}\)

\(BPD2_{d2} = \left\{ {\begin{array}{*{20}l} 1 \hfill & {If\,the\,final\,client\,is\,attended\,d2 \in DF} \hfill \\ 0 \hfill & {On\,the\,contrary} \hfill \\ \end{array} } \right\}\)

2.2.3.2 Flow variables

Those assigned holds those of flow and excess,

$$\begin{aligned} &{W\mathrm{N}}_{fod}=\mathrm{Amount\, of \,the \,type \,of \,perishable \,food} \,f \,to \,send \,from \,o to \,d. \quad\forall \,o\,\in \,OT, \,\forall \,d\,\in \,DT, \,\forall \,f\,\in\, F\\ &{SFI}_{fi}=\mathrm{Amount \,of \,the \,type \,of \,perishable \,food} \,f\,\in \,F \,overbid \,from \,the \,agricultural \,production \,area \,i\, {\varvec{i}}, \,\,\forall \,i\,\in \,\mathrm{FARM}\\ &{SFID}_{fd2}=\mathrm{Amount \,of \,the \,type \,of \,perishable \,food} \,f \,in \,the \,final \,destination \,d2, \,\,\forall \,\forall \,d2\,\in\, DF;\,\,\forall \,f\,\in \,FDF\,\left\{d2\right\}\end{aligned}$$

2.2.4 Objective function

$$\mathrm{Minimize \,Z}\,=\, F(OBJ1,OBJ2,-OBJ3)$$

Food total loses

This function considers the amount of food that is lost in all flows from origin to destinations due to changes in temperature and relative humidity between them, it also considers the amount of food that is lost due to handling for storage in intermediate centers.

$$\begin{aligned}OBJ1&=MIN Z1\\ &=\sum_{o \in OT}\sum_{d\in DT}\sum_{f\in \left(FOT\left\{o\right\}\cap FDT\left\{d\right\}\right)}{WN}_{fod}*\left({TN}_{od}+H{N}_{od}\right)\\ &\quad +\sum_{j\in \left\{SC\cup \mathrm{DC}\right\}}\sum_{f\in FOT\left\{j\right\}}\sum_{d3\in DIF\left\{f\right\}}W{N}_{fjd3}*\left({\beta }_{fj}\right) \\ &\quad +\sum_{d2\in DF}\sum_{f\in FDF\left\{d2\right\}}\sum_{k\in OTF\left\{f\right\}}W{N}_{fkd2}*\left(1-{TN}_{kd2}-{HN}_{kd2}\right)*{\beta }_{fd2}\end{aligned}$$

Estimated average time of service

For each one of the final clients \(d2\in DF\) the mean time of attention is given by the balanced average of the average time of attention that each of the three links has, that is, the producers, Collection Centers (CA, consolidation) and the wholesale or distribution centers (CM). It was necessary to establish the average time of attention in each link, it is important that food arrives soon even if there are few, short supply times contribute to food security, if the food arrive the consumer faster increases availability and reduces losses. See Appendix.

$$OBJ2=MIN Z2=\sum_{d2\in DF}{LTD2E}_{d2}*\frac{{DNT}_{d2}}{\sum_{d2\in DF}{DNT}_{d2}}$$

Number of clients attended

When there is deficit supply, it is important to guarantee the availability and access at the food in the different market’s channels, even in small quantities, so that coverage can be provided to a greater number of customers, prioritizing the retailed food storekeepers so to avoid the hypermarkets monopolies, if food safety it don't want to be affect.

$$OBJ3=MAX Z3=\sum_{d2\in DF}{BPD2}_{d2}$$

2.2.5 Constrains

It includes the constraints of Flow Balance for all the links, the capacity and opening control for the collection centers and wholesale or distribution centers.

2.2.5.1 Flow balance

This is for supply and demand or distribution.

  • In Production Zones

The set of constraints guarantees the flow balance for each agricultural area i, for each perishable food available f, for this purpose it requires that the supply of each production area i of each of the available food f be sent to all the nodes of destination d,

$${OFI}_{fi} =\sum_{d\in DTF\left\{f\right\}}W{N}_{fid} \forall i \in \mathrm{FARM},\forall f\in FI\left\{i\right\} .$$

  • In storage/distribution centers

Storage centers (SC):


The set of constraints guarantees the balance of flows for each available perishable food f, at each storage center j; everything sent to the storage center, less what is lost in shipping, it must be equal to everything that goes out, plus what is lost in the storage facility due to manipulation.

$$\sum_{i\in IF\left\{f\right\}}W{N}_{fij}\left(1-{TN}_{ij}-{HN}_{ij}\right)=\sum_{d3\in DIF\left\{f\right\}}W{N}_{fjd3}*\left(1+{\beta }_{fj}\right) \forall j\in SC, \forall f\in FJ\left\{j\right\}$$

Distribution centers (DC):


This set of constraints guarantees the flow balance for each available perishable food f, on all distribution centers k.

$$\sum_{o2\in OIJF\left\{f\right\}}W{N}_{fo2k}*\left(1-{TN}_{o2k}-{HN}_{o2k}\right)=\sum_{d2\in DFF\left\{f\right\}}W{N}_{fkd2}*\left(1+{\beta }_{fk}\right) \forall k\in DC, \forall f\in FK\left\{k\right\}$$
2.2.5.2 Capacity and opening control for CA and CM

Storage centers (CA):

This set of constraints ensures that if a storage center j is opened, it must have a flow bounded by a minimum and a maximum

$${CAL}_{j}*{BOSC}_{j}\le \sum_{i\in AGRI}\sum_{f\in (FI\left\{i\right\}\cap FJ\left\{j\right\})}W{N}_{fij}\le {CAM}_{j}*{BOSC}_{j} \forall j\in SC$$

Distribution centers (CM):

This set of constraints ensures that if a distribution centers k is opened, it must have a flow bounded by a minimum and a maximum

$${CTL}_{k}*{BOCD}_{k} \le \sum_{o2\in OIJ}\sum_{f\in (FOIJ\left\{o2\right\}\cap FK\left\{k\right\})}W{N}_{fo2k}\le {CTM}_{k}*{BOCD}_{k} \forall k\in DC$$
2.2.5.3 Demand in links

These constraints guarantee that the proportion of demand for each of the possible types of suppliers is met at the upper and lower limits for each one of the served clients, avoiding the monopoly of the strongest players, if it is forced to send all clients since all suppliers at the PFSC.


Minimum and maximum demand for the first link per food (agricultural production areas)


This set of constraints ensures that the amount of end-customer demand directly satisfied by agricultural production zones, will be bounded by a maximum and minimum.

$${DN}_{fd2}*{\alpha i}_{fd2}*\left(1+{\beta }_{fd2}\right)*{\gamma d2}_{fd2}*{BPD2}_{d2} \le \sum_{i\in IF\left\{f\right\}}W{N}_{fid2}*\left(1-{TN}_{id2}-{HN}_{id2}\right)\le {DN}_{fd2}*{\alpha i}_{fd2}*\left(1+{\beta }_{fd2}\right)*{BPD2}_{d2} \forall d2\in DF, \forall f\in FDF\left\{d2\right\}$$

Minimum and maximum demand for the second link (distribution centers)


This set of constraints ensures that the amount of end-customer demand directly satisfied by storage centers, will be bounded by a maximum and minimum.

$${DN}_{fd2}*{\alpha j}_{fd2}*\left(1+{\beta }_{fd2}\right)* {\gamma d2}_{fd2}*{BPD2}_{d2}\le \sum_{j\in JF\left\{f\right\}}W{N}_{fjd2}*\left(1-{TN}_{jd2}-{HN}_{jd2}\right)\le {DN}_{fd2}*{\alpha j}_{fd2}*\left(1+{\beta }_{fd2}\right)*{BPD2}_{d2} \forall d2\in DF, \forall f\in FDF\left\{d2\right\}$$

Minimum and maximum demand for the third link (distribution centers)


This set of constraints ensures that the amount of end-customer demand directly satisfied by the distribution centers, will be bounded by a maximum and a minimum.

$${DN}_{fd2}*{\alpha k}_{fd2}*\left(1+{\beta }_{fd2}\right)* {\gamma d2}_{fd2}*{BPD2}_{d2}\le \sum_{k\in KF\left\{f\right\}}W{N}_{fkd2}*\left(1-{TN}_{kd2}-{HN}_{kd2}\right)\le {DN}_{fd2}*{\alpha k}_{fd2}*\left(1+{\beta }_{fd2}\right)*{BPD2}_{d2}\quad \forall d2\in DF, \forall f\in FDF\left\{d2\right\}$$
2.2.5.4 Implications of seasonality

  • Flow and opening relationships

These three sets of constraints ensure that only flows to destinations that have been opened are sent.

$$\begin{aligned}&W{N}_{fij}\le {CAM}_{j}*{BOSC}_{j} \forall j\in SC,i\in \mathrm{FARM},f\in (FI\left\{i\right\}\cap FJ\left\{j\right\})\\ &W{N}_{fo2k}\le {CTM}_{k}*{BOCD}_{k} \forall k\in DC ,\forall o2\in OIJ,f\in (FOIJ\left\{o2\right\}\cap FK\left\{k\right\})\\ &W{N}_{fod2}\le {DN}_{fd2}*{BPD2}_{d2 } \forall d2\in DF, \forall o \in OT \forall f\in (FDF\left\{d2\right\}\cap FOT\left\{o\right\})\end{aligned}$$

  • Definition of estimated lead time

This constrains is used to calculate the supply time to all end customers, it is calculated as a weighted supply time in each of the three channels by the volume served by that channel. The first component is the average supply time of the flows that go direct from the farms to the clients, weighted by the percentage of demand served through this channel. The second component is the average supply time of the flows that go from the storage centers to the customers, weighted by the percentage of demand served by this channel. The last component is the average supply time of the flows that go from the distribution centers to the customers, weighted by the percentage of demand served by this channel.

$$\begin{aligned}{LTD2E}_{d2}&=\left[\frac{\sum_{f\in FDF\left\{d2\right\} }\sum_{i\in IF\left\{f\right\}}{LTD}_{id2}*{W\mathrm{N}}_{fid2}}{{DNT}_{d2}}\right]\\ &\quad+\left[\left(\frac{\sum_{f\in FDF\left\{d2\right\} }\sum_{j\in JF\left\{f\right\}}\left[{LTJE}_{j}+{SERV}_{j}+{LTD}_{jd2}\right]*{W\mathrm{N}}_{fjd2}}{{DNT}_{d2}}\right)\right]\\ &\quad+\left[\left(\frac{\sum_{f\in FDF\left\{d2\right\} }\sum_{k\in KF\left\{f\right\}}\left[{LTKE}_{k}+{SERV}_{k}+{LTD}_{kd2}\right]*{W\mathrm{N}}_{fkd2}}{{DNT}_{d2}}\right)\right]\forall d2\in DF\end{aligned}$$

2.3 Solution strategy of the multi objective PFSC

To solve the multi objective for PFSC, it is necessary to optimize the three proposed objective functions systematically and simultaneously, to determine the set of points that correspond to the best solutions, known as a set of non-dominated solutions or Pareto front. A point or solution x ∈ X, dominates another point x * ∈ X, if it meets the following two conditions [26].

  • Fi (x) ≤ Fi (x*), for all objective i

  • Fi(x) < Fi (x*, for at least one objective i.

One of the most used exact optimization multi-objective approaches to find the set of solutions, is ε-constraint. Each of the objective functions separately is optimized while all the other objective functions are incrementally restricted [52]. This technique is used whenever the computational time of the base model allows it, even in a combinatorial optimization problem it is used for validation of instances [4, 57].

As the PFSC Model design configuration is linear at all its constraints and in the objective function, as well as, the binary variables are only related to the process of opening or closing nodes, the computational complexity of the model allows the implementation of the solution technique ε-constraint, through at a script in AMPL.

3 Case study: the Perishable Fruit Supply Chain Cundinamarca-Bogotá, Colombia

The models were applied in a real case of the Perishable Fruit Supply Chain (PFrSC), due the level of consumption in Bogota and the level of production of its main supplier, Cundinamarca-Colombia (Fig. 5). Through the application of the characterization methodology from Orjuela Castro et al. [37, 38], the behavior of the PFrSC was established. Colombia has 32 departments, of which Cundinamarca is the third most populated in the country with 2.800.000 inhabitants, not including Bogotá, capital of Colombia. Cundinamarca has 116 municipalities in a region of 22.623 km2 located in the center of the country's Andean eastern mountain range, this permits a variety of thermal floors and a production of a wide variety of food. The department supplies more than 60% of the food consumed in Bogotá [36], the most populated city in the country with 7.743.955 inhabitants by 2020, is located in the center of the department with 20 localities and 1.775 km2.

The surveys were carried out for five fruits, three from warm climate (mango, orange and tangerine) and two from cold climate (strawberry and blackberry). The primary information survey included qualitative and quantitative data used later as information in the modeling phases. The qualitative data allowed establishing the behavior of the market competition, the relationships of the actors and the negotiation culture in the PFrSC. With the quantitative data the information was organized in order to establish the flows. As unit of analysis the farmers, wholesale merchants, retailers, agribusiness, hypermarkets, sellers in market squares and shopkeepers were used. The study was realized in the Colombia Cundinamarca-Bogotá region.

The data obtained with primary information was supplemented with secondary information. We analyzed documents issued by national and international institutions, government, and unions which issue official statistics in the agricultural sector. For the supply, information was provided by the Ministry of Agriculture 2006–2019, Municipal Agricultural Evaluations (EVA by its initials in Spanish–Agronet). For the demand in Bogotá, the information was obtained of the different institutional documents, such as the national surveys [14,15,16] as well as of studies from Development Secretariat of Bogotá, 2006–2009 and data from FAO, WTO, and TRADE-MAP.

The primary information was taken on field in two different periods, in 2014–2015 (Group GICALyT Universidad Distrital), 2016–2017 (Group SEPRO Universidad Nacional). In 2014–2015, the surveys were carried out in Bogotá for 9 wholesalers of Corabastos, one agroindustry, 2 hypermarkets, and 54 shopkeepers from different locations in Bogotá, 25 surveys into 13 public and private marketplaces in the city of Bogotá and 16 food transporters. The surveys contain 132 parameters, the numbers of questions asked by actor were: for wholesalers and hypermarkets 120, transporters 48, agroindustry 132, shopkeepers and dwellers 76. The surveys carried out during 2016–2017 were: 10 for transporters that carry food from Corabastos to stores, 66 in eleven marketplaces and 228 in store retailers. The numbers of questions were, transporters 48, wholesalers 63, shopkeepers 64 and food vendors 72. The previous study was complemented with studies from the Office of the Mayor of Bogotá and the Universidad Distrital between 2005 and 2009, through which the food consumption was stablished, at 9 localities, they found that the consumption of citrus is between 56.5 and 126.9 g per inhabitant per day, with an average of 84.88 g. This figure is used in the optimization models, as well as the population and its growth as projected by the Secretariat of District Planning [42] (Fig. 3).

Fig. 3
figure 3

Population density in Bogotá

Full size image

There are different studies of the demand by government institutions, according to the survey [16] in average 63.1% of the surveyed population consumes fruits, with a lower 57.5 and superior of 68.7 percent limit. This same [14], shows that 32.1% consume fruit daily, 54.4% weekly and 4.9% monthly. Map shows the population density of Bogotá, and the location of the possible distribution centers (stars). The blue points show the public marketplaces distributed throughout the territory in the city of Bogotá.

The Multi-objective, multi-product and multi-echelons model for the location of facilities allows to establish new settings in the PFrSC, according to the three established performance measures. The initial purpose was to determine how and where storage centers (Cundinamarca) and distribution centers (Bogotá) should be located. Then by reconfiguring the PFSC, determine the amount and location of the facilities, then was evaluated how was affected the actors placing them in performance measures. The scenarios that included three optimization objectives with deficit was modeled, searching the efficient (Pareto) boundaries.

4 Results

For the deficit model, 24 of the 54 municipalities of Cundinamarca which produce the six fruits under study, were taken. In the model, three performance measures were evaluated. Graphs are presented for the performance measures derived from the Pareto border points. To obtain the border 260,020 runs were performed in AMPL, applying e-constraints, the total of variables in each run were 2401, 33 binary and 2368 linear, 422 equality constraints and 1514 with inequality. The solutions were obtained through Gurobi 7.5.0. Figure 4 shows the results of the three objective functions plotted in Matlab.

Fig. 4
figure 4

Pareto borders

Full size image

The points, in orange in Fig. 4, represent the Pareto Border, set of non-dominated points, the objective function represented with the number of clients served is a discrete value, it is identified that for each level of this objective function, there are points that belong to the Pareto border. For the lowest values of the number of clients served, the supply times and the lowest losses are available, as the number of customers served at the border increases, solutions with greater losses and longer delivery times appear. It is identified that the objective function associated with losses is more sensitive to the increase in the number of customers served, than at the time of supply which is explained, since the delivery time is an average based on these flows and the average absorbs the variations. In Fig. 4, point A is a point of the Pareto border; it has the best value of the number of customers, the shortest delivery time and the greatest loss. On the other hand, the point B has the least number of clients attended, the lowest loss and not the lowest lead time, this shows the tradeoff between the objectives.

Given that there are 974 non-dominated points that form the efficiency frontiers, there would be an equal number of the performance measures, x,y,z points, each one giving rise to a possible setting. Therefore, to perform an analysis that allows the best decision making for the stakeholders, the settings were made for the extremes, that is, three settings where each objective is optimal and another one that search of the balance between the three measures of performance. For determine the latter, the median of the values taken by the objectives in the efficiency frontier was taken; found when applying e-constraints. The non-dominated point that was close to it was then sought, the set of points for the objective functions proposed. The optimal value by each objective have been highlighted in yellow, as seen in the Table 1, there isn’t an optimal point x, y, z for all objectives, this is due for classic multiobjective model tradeoff phenomenon.

Table 1 Optimal of the three objective functions
Full size table

Below are the collection centers in Cundinamarca (right side of the graphs) and distribution centers open in Bogotá (left side) for each setting. The objectives of minimizing the losses and the lead time and maximization of the claimants served generate different locations of the storage centers and wholesalers (distribution), to see Table 2 and Fig. 5.

Table 2 Location of collection centers (Cundinamarca) and distribution (Bogotá D.C). deficit model
Full size table
Fig. 5
figure 5

Collection centers (CC, Cundinamarca) and wholesale distribution center (WD, Bogotá), for median of Obj 1, 2 and 3

Full size image

As well as can be seen into Table 1, for each optimal objective a particular configuration is obtained, the LND selected it is the one median of objectives 1, 2 and 3 looking for the balance between the three, Fig. 4.

In Figs. 6 and 7 is show the flow between the production centers I, the collection centers j, wholesale distribution centers k, Neighborhood stores t, Marketplaces p, Hypermarkets h and Fruits Industries c, for each the objectives and for warm and cold climates fruits, respectively.

Fig. 6
figure 6

Flow tons/year, based on objectives, warm climate fruits

Full size image
Fig. 7
figure 7

Flows tons/year, based on objectives, cold climate fruits

Full size image

For the case of warm climate fruits, Fig. 6, the optimization of the first objective, loss minimization, achieves largest flow between i-j-k-t echelons, this behavior also occurs in the objective with the medians. Also, is important to note that into the other two objectives, maximize the number of clients and minimize the overage service time, the flow from production centers i is homogeneously distributed to collection centers j and the wholesale centers k.

From elsewhere, for the case of cold climate fruits, Fig. 7, the optimization of the third objective, maximize the number of clients, achieves largest flow between i-j-k-t echelons, this behavior also occurs in the second objective, minimize the overage service time. While, for the other two cases, loss minimization and with the medians of the three objectives, the flow from production centers i is homogeneously distributed to collection centers j and the wholesale centers k.

4.1 Discussion

An appropriate setting of the PFSC generates a decrease of the losses and improving the response capacity. On its behalf, the existence of intermediate nodes which allow the consolidation of orders and the conservation of food, is a fundamental element in the performance of the PFSC. It is imperative to find mechanisms that counteract the imbalances between supply and demand and which tend to mitigate effects on food security [33]. Some options during times of deficit can include a large number of retailers in supply of food available, this contributes to non-disappearing the stores avoiding monopolies, therefore this contributes to food security.

As it is a multi-objective model, there are Pareto boundaries for each performance measures. As there are multiple non-dominated solutions, to decide which should be the right LND with respect to the three objectives evaluated, government institutions and unions should bring together the different actors of the PFSC and apply multi-goal models. This is because actors have different interests and therefore make decisions based on various performance measures, prioritizing them in a different way, an effect of the tradeoffs found. Whereby, for this conflict is necessary that the governments and unions should promote meeting between stakeholders so that they reconcile their interests.

The multi-objective model of optimization designed exceeds what is found in the literature by including on the one hand the effects of temperature and relative humidity, a recommendation raised by van der Vorst et al. [49]. Contemplating the different thermal floors and the means used to transport food in mountainous areas, the geographical region where the case study is applied, in developing countries, brings the model closer to a better representation of reality for the PFSC, a deficiency manifested in the studies of Goetschalckx et al. [20], Akkerman et al. [3], Soto-Silva et al. [44, 45] and Sanabria et al. [43].

The design of a multi-objective and multilevel model that includes all the echelons of the PFSC from production to consumption, responds to the call of authors such as van der Vorst et al. [47], Manzini and Accorsi [25], Yu and Nagurney [55] and Orjuela-Castro and Adarme-Jaimes [31], in this way our study include supply, distribution and demand, with an integral approach of the chain, since they contain all its links.

There are several studies that show the need to allow plurality at the ends of the perishable food chains, in the field of producers [7], and in the field of retailers [1]. This investigation contributes to this last case, when developing a model for moments of deficit of fruit supply. The inclusion of a big number of retailers (shopkeepers and neighborhood merchants) counteracts the monopolies of large stores, avoiding the risk of guaranteeing competition. The modeling of this proposal in this model allows the demonstration of its validity.

5 Conclusions

The multi-objective optimization model designed, showed as the making of different strategic decisions leads to individual’s configurations which depend on efficiency, response capacity or quality, generating specifics logistics operation for the perishable food supply chain (PFSC).

Its application to the perishable fruit supply chain (PFrSC) makes it possible to establish that the actors could move to efficient borders from the established performance measures.

Multiobjective models allow evaluating tradeoffs, the decision makers are immersed in to decide between these three performance measures. In accordance with the performance measures for the PFrSC efficiency, response capacity and quality, studied in this research, three objectives have been established for the model, minimization of losses and response times (lead time) and maximization of participation of retailers in periods of deficit.

The seasonality of some fruits generates problems of shortage at different periods of time which unbalances the logistics flows. When the model is run, the results reflect that the effects on the setting with the three objectives generate equilibrium the flows between the echelons.

As future work, the model can be expanded, if the other elements of pillars of food safety, stability and utility are considered, not contemplated into account in this research.