Optimal ordering policy for deteriorating items with power-form stock dependent demand under two-warehouse storage facility

Abstract

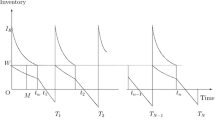
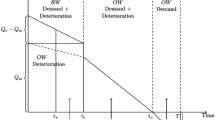
In realistic world, there usually exist various factors that induce the retailer to order more items than the capacity of his Own-warehouse (OW). Therefore, for the retailer, it is very practical to determine whether or not to rent other warehouse and what order policy to adopt if other warehouse is indeed needed. For the stock dependent demand pattern, retailer has his own warehouse to display the items and may hire another warehouse of the larger capacity, treated as rented warehouse (RW) to storage the excess inventory. In this paper, an inventory model with power form stock-dependent demand rate is developed. The demand rate is assumed to be a polynomial form of current inventory level in Own-warehouse. It is also assumed that retailer first fulfills the demand (depending upon the stock displayed in the OW) directly from the RW until the inventory level in the RW reaches to the zero level, after that, demand is fulfilled from OW. As a consequence, no item is transferred from RW to OW, therefore no transfer cost (neither fixed nor variable) is considered between RW and OW. It is considered that the deterioration rate per unit items in the RW and OW are different due to different preservation environments, as a consequence the holding costs per unit item in RW and OW are also different. Proposed model is illustrated with some numerical example along with some sensitivity analysis of parameters.

Appendix

Proof of Theorem 1: For the sake of convenience, let us suppose that

$$ \matrix{ {f(q) = \left( {p - c} \right)q\left( {\alpha \beta + \theta {q^{{\left( {1 - \beta } \right)}}}} \right) + S\alpha \left( {1 - \beta } \right)\quad {\mathrm{and}}} \\ {g(q) = \frac{{\left( {{h_o} + d\theta + p\theta } \right)}}{{\left( {2 - \beta } \right)}}{q^{{\left( {2 - \beta } \right)}}}} \\ }<!end array> $$

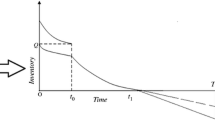
The graphs of the f(q) and g(q) are given in Fig. 5.

Fig. 5

 

For single warehouse inventory system, it is seen that the optimal quantity q^* for TP(q) to be maximum satisfies

$$ \left( {p - c} \right)q * \left( {\alpha \beta + \theta {{\left( {q * } \right)}^{{\left( {1 - \beta } \right)}}}} \right) + S\alpha \left( {1 - \beta } \right) = \frac{{\left( {{h_o} + d\theta + p\theta } \right)}}{{\left( {2 - \beta } \right)}}{\left( {q * } \right)^{{\left( {2 - \beta } \right)}}} $$

(30)

$$ {\mathrm{i}}.{\mathrm{e}}.{\mathrm{f}}\left( {{\mathrm{q}}*} \right) = {\mathrm{g}}\left( {{\mathrm{q}}*} \right) $$

(31)

Since M ≥ 0, we have

$$ \left( {p - c} \right)W\left( {\alpha \beta + \theta {W^{{\left( {1 - \beta } \right)}}}} \right) + S\alpha \left( {1 - \beta } \right) \geqslant \frac{{\left( {{h_o} + d\theta + p\theta } \right)}}{{\left( {2 - \beta } \right)}}{W^{{\left( {2 - \beta } \right)}}} $$

$$ i.e.f\left( W \right)\geqslant g\left( W \right) $$

(32)

from Eqs. 31 and 32 and the Fig. 5, we can easily observe that q* ≥ W. in contrast, if W ≤ q*, it can also be easily seen from Fig. 5 that f(W) ≥ g(W), i.e. M ≥ 0. This completes the proof of theorem 1.

Proof of Theorem 2: We have from Eq. 27

$$ \matrix{ {T{P_2}\left( {{T_r}} \right) = \frac{1}{T}\left[ {\left( {p + d} \right)W{e^{{ - \theta {T_r}}}} - \frac{{\left( {p\theta + {h_o} + d\theta } \right)}}{{\left( {2 - \beta } \right)\left( {\alpha + \theta {W^{{\left( {1 - \beta } \right)}}}} \right)}}{W^{{\left( {2 - \beta } \right)}}}{{\left\{ {1 - \theta \left( {1 - \beta } \right){T_r}} \right\}}^{{\frac{{\left( {2 - \beta } \right)}}{{\left( {1 - \beta } \right)}}}}}} \right.} \hfill \\ {+ \left( {p - c} \right)\alpha {W^{\beta }}\left( {{T_r} - \frac{{\theta \beta }}{2}T_r^2} \right) - \left( {c + d} \right)W - \left( {c + d} \right)\frac{{\gamma \alpha }}{{\delta + 1}}{W^{\beta }}T_r^{{\delta + 1}} - } \hfill \\ {\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,{h_o}W\left( {{T_r} - \frac{\theta }{2}T_r^2} \right) - {h_r}\alpha {W^{\beta }}\left( {\frac{1}{2}T_r^2 - \frac{{\theta \beta }}{3}T_r^3 + \frac{{\gamma \delta }}{{\left( {\delta + 1} \right)\left( {\delta + 2} \right)}}T_r^{{\delta + 2}} + } \right.} \hfill \\ {\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left. {\left. {\frac{{\theta \beta \gamma }}{{\left( {\delta + 1} \right)\left( {\delta + 3} \right)}}T_r^{{\delta + 3}} + \frac{1}{2}{{\left( {\frac{\gamma }{{\delta + 1}}} \right)}^2}T_r^{{2\delta + 2}}} \right) - {S_1}} \right]} \hfill \\ }<!end array> $$

By the necessary condition of optimality, the optimal value of $T_r^{ * }$ of T_r for the maximization of TP₂(T_r), must satisfy $\frac{{d\left[ {T{P_2}\left( {{T_r}} \right)} \right]}}{{d{T_r}}} = 0$. For assuring the existence of $T_r^{ * }$, we first differentiate $\frac{{d\left[ {T{P_2}\left( {{T_r}} \right)} \right]}}{{d{T_r}}}$ with respect to T _r i.e. $\frac{{{d^2}\left[ {T{P_2}\left( {{T_r}} \right)} \right]}}{{dT_r^2}}$.

For the maximization of TP ₂(T _r ), $\frac{{{d^2}\left[ {T{P_2}\left( {{T_r}} \right)} \right]}}{{dT_r^2}} < 0$, for the optimal value $T_r^{ *}\;of\;{T_r}$. Hence $T_r^{ * }$ is the global maximum point of TP₂(T_r) in the interval (0, T) when M ≥ 0.

Proof of Theorem 3: Based on results of theorem (2), the average total profit function reaches its maximum at the point ${{\mathrm{T}}_{\mathrm{r}}} = T_r^{ * }$ in the interval [0, T] if M ≥ 0. This indicates that when M ≥ 0, the maximum average total profit $T{P_2}({T_r})$, for the inventory system with two warehouse should be greater than $T{P_2}(0)$. From Eqs. 9 and 27, we see that $T{P_2}(0) = T{P_1}(W)$.

Thus, $T{P_2}(T_r^{*}) > T{P_1}(W),\,if\,M \geqslant 0.$

From theorem (1), the optimal ordering quantity q*, of the single-warehouse system is greater than or equal to W when M ≥ 0. Therefore, for single-warehouse inventory system with capacity restriction, the optimal ordering quantity q* = W, and the corresponding maximal average profit is TP₁(W). Hence it concludes the theorem.