Fuzzy production inventory model for deteriorating items with shortages under the effect of time dependent learning and forgetting: a possibility / necessity approach

Abstract

This study investigates the effects of learning and forgetting on the production lot size problems allowing shortages for the infinite planning horizon. Items deteriorate while they are in storage, and both demand and deterioration rates are arbitrary function of time. This paper extends the work of Alamri and Balkhi (Int. J. Prod. Econ. 107:125–138, 2007) by assuming the shortages in production lot size model subject to the effects of learning and forgetting in fuzzy environment. The system is subject to learning in the production stage and to forgetting while production ceased so that the optimal manufactured quantity for any given cycle is dependent on the instantaneous production rate. All cost are taken constants or fuzzy in nature. Hence two models are introduced separately with constant and fuzzy cost. A closed form for the total relevant costs is derived, that minimizes total cost of the underlying inventory system. Model with fuzzy costs is formulated as to optimize the possibility/ necessity measure of the fuzzy goal of the objective function. When costs are imprecise, optimistic and pessimistic equivalent of fuzzy objective function is obtained by using credibility measure of fuzzy event by taking fuzzy expectation. The models are illustrated with three examples as well as their numerical verifications are also given.

Appendices

Appendix A: Expected value operator

1.1 Possibility/necessity in fuzzy environment

Any fuzzy subset á of $\Re$ (where $\Re$ represents a set of real numbers) with membership function ${\mu_{{\widetilde{\text{a}}}}}\left( {\text{x}} \right):\Re \to \left[ {0,{1}} \right]$ is called a fuzzy number. Let $\widetilde{\text{a}}$ and $\widetilde{\text{b}}$ be two fuzzy quantities with membership functions ${\mu_{{\widetilde{\text{a}}}}}$ (x): and ${\mu_{{\widetilde{\text{b}}}}}$ (x) respectively. Then according to Liu and Lwamura [30], Maiti and Maiti [21]

Where the abbreviation ‘Pos’ represents possibility and ‘Nes’ represents necessity and ‘*’ is any of the relations >, <, =, ≤, ≥.

The dual relationship of possibility and necessity requires that

$$ {\text{Nes}}\left( {\widetilde{\text{a}}*\widetilde{\text{b}}} \right) = 1 - {\text{Pos}}\left( {\overline {\widetilde{\text{a}} * \widetilde{\text{b}}} } \right) $$

Also necessity measures satisfy the condition

$$ {\text{Min}}\left( {{\text{Nes}}\left( {\widetilde{\text{a}} * \widetilde{\text{b}}} \right)} \right),\;{\text{Nes}}\left( {\overline {\widetilde{\text{a}} * \widetilde{\text{b}}} } \right) = 0 $$

The relationships between possibility and necessity measures satisfy also the following conditions (cf. Dubois and Prade (1997)):

$$ \left. {{\text{Pos}}\left( {\widetilde{\text{a}} * \widetilde{\text{b}}} \right) \geqslant {\text{Nes}}\left( {\widetilde{\text{a}} * \widetilde{\text{b}}} \right),{\text{Nes}}\left( {\widetilde{\text{a}} * \widetilde{\text{b}}} \right) > 0} \right) \Rightarrow {\text{Pos}}\left( {\widetilde{\text{a}} * \widetilde{\text{b}}} \right) = 1\,{\text{and}}\,{\text{Pos}}\left( {\widetilde{\text{a}} * \widetilde{\text{b}}} \right) < 1 \Rightarrow {\text{Nes}}\left( {\widetilde{\text{a}} * \widetilde{\text{b}}} \right) = 0 $$

If $\widetilde{\text{a}}$, and $\widetilde{\text{c}} = {\text{f}}\left( {\widetilde{\text{a}},\widetilde{\text{b}}} \right)$ where f: $\Re \times \Re \to \Re$ be a binary Operation, then membership function ${\mu_{{\widetilde{\text{c}}}}}$ of $\widetilde{\text{c}}$ is defined as

Recently based on possibility measure and necessity measure, the third set function Cr, called credibility measure, analyzed by Liu and Liu [27] is as follows:

$$ {\text{Cr}}\left( {\widetilde{\text{A}}} \right) = \frac{1}{2}\left[ {{\text{Pos}}\left( {\widetilde{\text{A}}} \right) + {\text{Nes}}\left( {\widetilde{\text{A}}} \right)} \right]\,{\text{for}}\,{\text{any}}\,\widetilde{\text{A}}\,{\text{in}}\,{{2}^{\Re }} $$

Where ${2^{\Re }}$ is the power set of $\Re$.

It is easy to check that Cr satisfies the following conditions:

• i* Cr (Ø) = 0 and ${\text{Cr}}\left( \Re \right) = 1$;

• ii* ${\text{Cr}}\left( {\widetilde{\text{A}}} \right) \leqslant {\text{Cr}}\left( {\widetilde{\text{B}}} \right)$ whenever A, B in ${2^{\Re }}$ and ${\text{A}} \subseteq {\text{B}}$

Thus Cr is also a fuzzy measure defined on $\left( {\Re, {2^{\Re }}} \right)$. Besides, Cr is self dual, i.e. ${\text{Cr}}\left( {\widetilde{\text{A}}} \right) = 1 - {\text{Cr}}\left( {{{\widetilde{\text{A}}}^{\text{c}}}} \right)$ for any $\widetilde{\text{A}}$ in ${2^{\Re }}$.

In this Paper, based on the credibility measure the following form is defined as

$$ {\text{Cr}}\left( {\widetilde{\text{A}}} \right) = \left[ {\rho {\text{Pos}}\left( {\widetilde{\text{A}}} \right) + \left( {1 - \rho } \right){\text{Nes}}\left( {\widetilde{\text{A}}} \right)} \right] $$

(cf. Liu and Liu [27]) for any $\widetilde{\text{A}}$ in ${2^{\Re }}$ and 0 < ρ < 1. It also satisfies the above condition.

1.2 Triangular fuzzy number

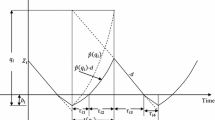
Triangular fuzzy number (TFN) ($\widetilde{\text{a}}$) (see Fig. 1) is the fuzzy number with the membership function ${\mu_{{\widetilde{\text{A}}}}}$(x), a continuous mapping: ${\mu_{{\widetilde{\text{A}}}}}\left( {\text{x}} \right) = \Re \to \left[ {0,1} \right]$,

$$ {\mu_{{\widetilde{\text{A}}}}}\left( {\text{x}} \right) = \left\{ {\matrix{ 0 \hfill &{{\text{for}} - \infty < x < {{\text{a}}_1}} \hfill \\ {\frac{{{\text{x}} - {{\text{a}}_1}}}{{{{\text{a}}_2} - {{\text{a}}_1}}}} \hfill &{{\text{for}}\;{{\text{a}}_1} \leqslant {\text{x}} \leqslant {{\text{a}}_2}} \hfill \\ {\frac{{{{\text{a}}_3} - {\text{x}}}}{{{{\text{a}}_3} - {{\text{a}}_2}}}} \hfill &{{\text{for}}\;{{\text{a}}_2} \leqslant {\text{x}} \leqslant {{\text{a}}_3}} \hfill \\ 0 \hfill &{{\text{for}}\;{{\text{a}}_3} \leqslant {\text{x}} \leqslant \infty } \hfill \\ }<!end array> } \right. $$

Lemma 1

The expected value of triangular fuzzy number $\widetilde{\text{A}} = \left( {{{\text{a}}_{{1}}},{{\text{a}}_{{2}}},{{\text{a}}_{{3}}}} \right)$ is ${\text{E}}\left( {\widetilde{\text{A}}} \right) = \frac{1}{2}\left[ {\left( {1 - \rho } \right){{\text{a}}_1} + {{\text{a}}_2} + \rho {{\text{a}}_3}} \right]$

Proof 1

Let $\widetilde{\text{A}} = \left( {{{\text{a}}_{{1}}},{{\text{a}}_{{2}}},{{\text{a}}_{{3}}}} \right)$ be a triangular fuzzy number. Then

$$ \begin{array}{*{20}{c}} {{\text{Pos}}\left( {\widetilde{{\text{A}}} \geqslant {\text{r}}} \right) = \left\{ {\begin{array}{*{20}{c}} 1 \hfill & {{\text{if}}\,{\text{r}} \leqslant {{{\text{a}}}_{2}}} \hfill \\ {\frac{{{{{\text{a}}}_{2}} - {\text{r}}}}{{{{{\text{a}}}_{2}} - {{{\text{a}}}_{1}}}}} \hfill & {{\text{if}}\,{{{\text{a}}}_{2}} \leqslant {\text{r}} \leqslant {{{\text{a}}}_{3}}} \hfill \\ 0 \hfill & {{\text{if}}\:{\text{r}} \geqslant {{{\text{a}}}_{3}}} \hfill \\ \end{array} } \right.} \\ {{\text{Nes}}\left( {\widetilde{{\text{A}}} \geqslant {\text{r}}} \right) = \left\{ {\begin{array}{*{20}{c}} 1 \hfill & {{\text{if }}\,{\text{r}} \leqslant {{{\text{a}}}_{1}},} \hfill \\ {\frac{{{{{\text{a}}}_{3}} - {\text{r}}}}{{{{{\text{a}}}_{2}} - {{{\text{a}}}_{1}}}}} \hfill & {{\text{if}}\,{{{\text{a}}}_{1}} \leqslant {\text{r}} \leqslant {{{\text{a}}}_{2}}} \hfill \\ 0 \hfill & {{\text{if}}\,{\text{r}} \geqslant {{{\text{a}}}_{2}}} \hfill \\ \end{array} } \right.} \\ \end{array} $$

The credibility measure for TFN can be defined as

$$ \begin{array}{*{20}{c}} {{\text{Cr}}\left( {\widetilde{{\text{A}}} \geqslant {\text{r}}} \right) = \left\{ {\begin{array}{*{20}{c}} 1 \hfill & {{\text{if}}\:{\text{r}} \leqslant {{{\text{a}}}_{1}}} \hfill \\ {\frac{{{\text{x}} - {{{\text{a}}}_{1}}}}{{{{{\text{a}}}_{2}} - {{{\text{a}}}_{1}}}} - \frac{{\left( {1 - \rho } \right){\text{r}}}}{{{{{\text{a}}}_{2}} - {{{\text{a}}}_{1}}}}} \hfill & {{\text{if}}\:{{{\text{a}}}_{1}} \leqslant {\text{r}} \leqslant {{{\text{a}}}_{2}}} \hfill \\ {\frac{{{{{\text{a}}}_{3}} - {\text{x}}}}{{{{{\text{a}}}_{3}} - {{{\text{a}}}_{2}}}}} \hfill & {{\text{if}}\:{{{\text{a}}}_{2}} \leqslant {\text{r}} \leqslant {{{\text{a}}}_{3}}} \hfill \\ 0 \hfill & {{\text{if }}\:{\text{r}} \geqslant {{{\text{a}}}_{3}}} \hfill \\ \end{array} } \right.} \\ {\underline {{\text{Cr}}} \left( {\widetilde{{\text{A}}} \leqslant {\text{r}}} \right) = \left\{ {\begin{array}{*{20}{c}} 0 \hfill & {{\text{if}}\:{\text{r}} \leqslant {{{\text{a}}}_{1}}} \hfill \\ {\rho \frac{{{\text{r}} - {{{\text{a}}}_{1}}}}{{{{{\text{a}}}_{2}} - {{{\text{a}}}_{1}}}}} \hfill & {{\text{if}}\:{{{\text{a}}}_{1}} \leqslant {\text{r}} \leqslant {{{\text{a}}}_{2}}} \hfill \\ {\frac{{{{{\text{a}}}_{3}} - \rho {{{\text{a}}}_{2}} - \left( {1 - \rho } \right){\text{r}}}}{{{{{\text{a}}}_{3}} - {{{\text{a}}}_{2}}}}} \hfill & {{\text{if}}\:{{{\text{a}}}_{2}} \leqslant {\text{r}} \leqslant {{{\text{a}}}_{3}}} \hfill \\ 1 \hfill & {{\text{if }}\:{\text{r}} \geqslant {{{\text{a}}}_{3}}} \hfill \\ \end{array} } \right.} \\ \end{array} $$

Based on the credibility measure, Liu and Liu [26, 27] presented the expected value operator of a fuzzy variable as follows:

Let $\widetilde{\text{X}}$ be a normalized fuzzy variable. The expected value of the fuzzy variable $\widetilde{\text{X}}$ is defined by

$$ {\text{E}}\left( {\widetilde{\text{X}}} \right) = \int_0^{\infty } {\left( {\widetilde{\text{X}} \geqslant {\text{r}}} \right){\text{dr}} - \int_{{ - \infty }}^0 {{\text{Cr}}\left( {\widetilde{\text{X}} \leqslant {\text{r}}} \right){\text{dr}}} } $$

When the right hand side of (7) is of form ∞-∞, the expected value can not be defined. Also, the expected value operation has been proved to be linear for bounded fuzzy variable, i.e., for any two bounded fuzzy variables $\widetilde{\text{X}}$ and $\widetilde{\text{Y}}$, we have ${\text{E}}\left[ {{\text{a}}\widetilde{\text{X}} + {\text{b}}\widetilde{\text{Y}} = {\text{aE}}\left( {\widetilde{\text{X}}} \right) + {\text{bE}}\left( {\widetilde{\text{Y}}} \right)} \right.$ for any real numbers a and b. Then

$$ \matrix{ {{\text{E}}\left( {\widetilde{\text{A}}} \right) = \int_0^{\infty } {{\text{Cr}}\left( {\widetilde{\text{A}} \geqslant {\text{r}}} \right){\text{dr}} - \int_{{ - \infty }}^0 {{\text{Cr}}\left( {\widetilde{\text{A}} \leqslant {\text{r}}} \right){\text{dr}}} } } \\ { = \int_0^{{{{\text{a}}_1}}} {{\text{Cr}}\left( {\widetilde{\text{A}} \geqslant {\text{r}}} \right){\text{dr}} + \int_{{{{\text{a}}_1}}}^{{{{\text{a}}_2}}} {{\text{Cr}}\left( {\widetilde{\text{A}} \geqslant {\text{r}}} \right){\text{dr}} + \int_{{{{\text{a}}_2}}}^{{{{\text{a}}_3}}} {{\text{Cr}}\left( {\widetilde{\text{A}} \geqslant {\text{r}}} \right){\text{dr}} + \int_{{{{\text{a}}_3}}}^{{{{\text{a}}_4}}} {{\text{Cr}}\left( {\widetilde{\text{A}} \leqslant {\text{r}}} \right){\text{dr}}} } } } } \\ { = \frac{1}{{{ }2}}\left[ {\left( {1 - \rho } \right){{\text{a}}_1} + {{\text{a}}_2} + \rho {{\text{a}}_3}} \right]} \\ }<!end array> $$

1.3 Single programming problem under fuzzy expected value model

A general single-objective mathematical programming problem with fuzzy parameters in the objective function is of the following form:

$$ \matrix{ {\text{Max}} \hfill &{{\text{f}}\left( {{\text{u}},\widetilde{\xi }} \right)} \hfill \\ {{\text{Subject}}\,{\text{to}}\,{{\text{g}}_{\text{j}}}\left( {{\text{u}},\widetilde{\xi }} \right) \leqslant 0,} \hfill &{{\text{j}} = 1,2,\; \ldots \ldots {\text{k}},} \hfill \\ }<!end array> $$

Where u and $\widetilde{\xi }$ are decision vector and fuzzy vector respectively. To convert the fuzzy objective and constraints to their crisp equivalents, Liu and Liu [27] proposed a new method to convert the problem into an equivalent single-objective fuzzy expected value model i.e. the equivalent crisp model is:

$$ \matrix{ {{\text{E}}\left[ {{\text{f}}\left( {{\text{u}},\widetilde{\xi }} \right)} \right]} \hfill &{} \hfill \\ {{\text{Subject}}\,{\text{to}}\,{\text{E}}\left[ {{{\text{g}}_{\text{j}}}\left( {{\text{u}},\widetilde{\xi }} \right)} \right] \leqslant 0,} \hfill &{{\text{j}} = 1,2,\; \ldots {\text{k}},} \hfill \\ }<!end array> $$

Appendix B: Checking the approximation of Zj

We have from Eqs. (37), (40) and (41)

$$ {\widehat{\text{t}}_{{1{\text{j}}}}} = {{\text{t}}_{{11}}}{\left( {{\beta_{\text{j}}} + {{\text{Q}}_{\text{j}}}} \right)^{{ - \left( {{\text{r}} + {l_{\text{j}}}} \right)}}} $$

(B.1)

$$ {\widehat{\text{t}}_{{1{\text{j}}}}}{\left( {{\beta_{\text{j}}} + {{\text{Q}}_{\text{j}}} + {{\text{Z}}_{\text{j}}}} \right)^{{{l_{\text{j}}}}}} = {{\text{t}}_{{11}}} $$

(B.2)

$$ {l_{\text{j}}} = {{{{\text{r}}\log \left( {{\beta_{\text{j}}} + {{\text{Q}}_{\text{j}}}} \right)}} \left/ {{\log \left[ {{{{1 + {{\text{Z}}_{\text{j}}}}} \left/ {{\left( {{\beta_{\text{j}}} + {{\text{Q}}_{\text{j}}}} \right)}} \right.}} \right]}} \right.} $$

(B.3)

Respectively, Substituting (A.1) in (A.2) we obtain

$$ \matrix{ {{{\left( {{\beta_{\text{j}}} + {{\text{Q}}_{\text{j}}} + {{\text{Z}}_{\text{j}}}} \right)}^{{{l_{\text{j}}}}}}{{\left( {{\beta_{\text{j}}} + {{\text{Q}}_{\text{j}}}} \right)}^{{ - \left( {{\text{r}} + {l_{\text{j}}}} \right)}}} = 1} \hfill \\ { \Rightarrow \left( {{\beta_{\text{j}}} + {{\text{Q}}_{\text{j}}} + {{\text{Z}}_{\text{j}}}} \right){{\left( {{\beta_{\text{j}}} + {{\text{Q}}_{\text{j}}}} \right)}^{{{{{ - \left( {{\text{r}} + {l_{\text{j}}}} \right)}} \left/ {{{l_{\text{j}}}}} \right.}}}} = 1} \hfill \\ { \Rightarrow \left( {{\beta_{\text{j}}} + {{\text{Q}}_{\text{j}}} + {{\text{Z}}_{\text{j}}}} \right){{\frac{{\left( {{\beta_{\text{j}}} + {{\text{Q}}_{\text{j}}}} \right)}}{{\left( {{\beta_{\text{j}}} + {{\text{Q}}_{\text{j}}}} \right)}}}^{{{{{ - \left( {\text{r}} \right)}} \left/ {{{l_{\text{j}}}}} \right.}}}} = 1} \hfill \\ { \Rightarrow {{\left( {{\beta_{\text{j}}} + {{\text{Q}}_{\text{j}}}} \right)}^{{{{{ - \left( {\text{r}} \right)}} \left/ {{{l_{\text{j}}}}} \right.}}}} + {{\text{Z}}_{\text{j}}}{{\frac{{\left( {{\beta_{\text{j}}} + {{\text{Q}}_{\text{j}}}} \right)}}{{\left( {{\beta_{\text{j}}} + {{\text{Q}}_{\text{j}}}} \right)}}}^{{{{{ - \left( {\text{r}} \right)}} \left/ {{{l_{\text{j}}}}} \right.}}}} = 1} \hfill \\ { \Rightarrow {{{{{\text{Z}}_{\text{j}}}}} \left/ {{\left( {{\beta_{\text{j}}} + {{\text{Q}}_{\text{j}}}} \right)}} \right.} = \left\{ {{{1} \left/ {{{{\left( {{\beta_{\text{j}}} + {{\text{Q}}_{\text{j}}}} \right)}^{{{{{ - \left( {\text{r}} \right)}} \left/ {{{l_{\text{j}}}}} \right.}}}}}} \right.}} \right\}{{{ - 1 \cong 1}} \left/ {{{{\text{t}}_{{1{\text{j}}}}}}} \right.}} \hfill \\ }<!end array> $$

(B.4)

where t_1j = t₁₁(β_j + 1)^−r. Note here that our goal is to suggest an approximation form of Z_j, which depends upon the value of l_j, where these two values are somehow difficult to estimate. In the last relation, the value of t_1j is considered as a constant only for approximation purpose, elsewhere, t_1j is the time needed to produce the first unit in cycle j, which is measured in units of time/unit. This approximation is simply our suggestion to overcome the inadequacy in the assumption that the value of total forgetting is fixed. Therefore substituting (A.4) in (A.3), the forgetting slope can be rewritten as

$$ {l_j} = {{{{\text{r}}\log \left( {{\beta_{\text{j}}} + {{\text{Q}}_{\text{j}}}} \right)}} \left/ {{\log \left[ {1 + {{1} \left/ {{{{\text{t}}_{{1{\text{j}}}}}}} \right.}} \right]}} \right.} $$

(B.5)

As the approximation of Z_j/(β_j + Q_j) by 1/t_1j produces very close results for the parameters suggested in Tables 2, 3, 4 and 5.