Introduction

The dynamics of optical dromion propagation across trans–continental and trans–oceanic distances is of paramount importance in telecommunications industry [1,2,3,4,5,6,7,8,9,10]. The rising demand for fast Internet communications is occurring on a daily basis [11,12,13,14,15,16,17,18,19,20]. However, there are several measures and means that are being continuously adopted to control and suppress the Internet bottleneck effect. One of the most important mechanisms to meet this vital requirement is to consider fractional temporal evolution that would trigger a traffic signaling effect at junction points such as in Hawai’i, USA, so that the Internet traffic can be smoothed out and signal flow would be streamlined.

The current paper studies the Internet bottleneck effect control for optical dromions that are governed by the nonlinear Schrödinger’s equation (NLSE) [21,22,23,24,25,26,27,28,29,30]. This is the model that will be addressed in the paper by the aid of the enhanced modified tanh expansion approach [31,32,33,34,35,36,37,38]. The retrieved optical dromions are exhibited in the rest of the paper along with their supporting numerical simulations. The details are inked in the rest of the paper after a succinct introduction to the model along with its technical features.

Governing model

The following integrable (2+1)-dimensional NLS system of equations is studied by Radha and Lakshmanan [19]:

$$\begin{aligned} \begin{aligned}&{i {p}_{t}}={{p}_{xy}}+pq, \\&{{q}_{x}}=2{{\left( {{\left| p \right| }^{2}} \right) }_{y}}. \\ \end{aligned} \end{aligned}$$
(1)

In [20], the optical dromion solutions of the above system are studied using the extended modified auxiliary equation mapping method. Additionally, exact solutions to the integrable (2 + 1)-dimensional NLS system are investigated in [21]. Moreover, three novel techniques are addressed for studying the analytic solutions to the integrable generalized (2+1)-dimensional NLS system of equations in [22].

In this article, our aim is to apply the enhanced modified extended tanh method (eMETEM) to obtain numerous optical dromions when applied to the considered nonlinear Schrödinger equation. This represents a novel addition to the literature. The proposed technique offers notable advantages in generating a multitude of optical dromions [23]. Here, the proposed method is applied to the generalized integrable (2+1)-dimensional conformable nonlinear Schrödinger (NLS) system of equations to construct different novel optical dromions. Thus, the following generalized (2+1)-dimensional conformable nonlinear Schrödinger (NLS) system is considered:

$$\begin{aligned} \begin{aligned}&i\frac{{{\partial }^{\theta }}p}{\partial {{t}^{\theta }}}+{{\beta }_{1}}{{p}_{xy}}+{{\beta }_{2}}pq=0, \\&{{\beta }_{3}}{{q}_{x}}+{{\beta }_{4}}{{\left( {{\left| p \right| }^{2}} \right) }_{y}}=0,\,\,\,0<\theta \le 1. \\ \end{aligned} \end{aligned}$$
(2)

In this context, \(\theta\) represents the conformable fractional order, while \({{\beta }_{1}},{{\beta }_{2}},{{\beta }_{3}},\) and \({{\beta }_{4}}\) are real constants. The operator \(\frac{{{\partial }^{\theta }}.}{\partial {{t}^{\theta }}}\) denotes the conformable fractional derivative. Fractional calculus has emerged as a powerful tool for representing a wide range of physical phenomena. Unlike traditional integer-order models, modern fractional-order models provide increased adaptability and flexibility. In this work, we aim to analyze the fundamentals of conformable derivatives, which serve as a significant form for grasping the dynamics of diverse physical processes. The application of conformable derivatives extends across various fields including physics, engineering, finance, and biology, highlighting their potential as valuable analytical tools for complex systems [21, 22].

Definition 1.1

Let \(p:(0,\infty )\rightarrow R\). The conformable derivative of order \(\theta\) can be introduced as follows:

$$\begin{aligned} {{L}_{\theta }}\left( p \right) \,(x)=\underset{a\rightarrow 0}{\mathop {\lim }}\,\frac{p(x+a{{x}^{1-\theta }})-p(x)}{a}, \end{aligned}$$
(3)

for all \(x>0\) and \(\theta \in (0,1]\) [23].

Mathematical analysis

In this section, several new conformable optical dromions to the current model are constructed using the enhanced modified tanh expansion method. Let’s assume that the following series represents the solution of the present equation:

$$\begin{aligned} H(\varsigma )=\sum \limits _{i=0}^{N}{{{a}_{i}}}F{{(\varsigma )}^{i}}+\sum \limits _{j=N+1}^{2N}{{{b}_{j-N}}}F{{(\varsigma )}^{N-j}}, \end{aligned}$$
(4)

where \({{a}_{0}},{{a}_{1}},\ldots ,{{a}_{N}}\), \({{b}_{0}},{{b}_{1}},\ldots ,{{b}_{N}}\) are arbitrary constants that need to be found later, and N is a balancing constant. F(ς) satisfies the following first-order ordinary differential equation (ODE):

$$\begin{aligned} F(\varsigma {)}'=\lambda \mp F{{(\varsigma )}^{2}}. \end{aligned}$$
(5)

Now, the solutions of the above Eq. (5) with parameter \(\lambda\) are introduced as follows:

Dark soliton solution:

$$\begin{aligned} F_{1}^{\pm }(\varsigma )=\pm \sqrt{\pm \lambda }\tanh \left( \sqrt{\pm \lambda }\left( \varsigma +\gamma \right) \right) .~ \end{aligned}$$
(6)

Singular soliton solution:

$$\begin{aligned} F_{2}^{\pm }(\varsigma )=\pm \sqrt{\pm \lambda }\coth \left( \sqrt{\pm \lambda }\left( \varsigma +\gamma \right) \right) .~ \end{aligned}$$
(7)

Dark soliton solution:

$$\begin{aligned} F_{3}^{\pm }(\varsigma )=\mp \frac{\lambda -\sqrt{\pm \lambda }\tanh \left( \sqrt{\pm \lambda }\left( \varsigma +\gamma \right) \right) }{1\mp \sqrt{\pm \lambda }\tanh \left( \sqrt{\pm \lambda }\left( \varsigma +\gamma \right) \right) }. \end{aligned}$$
(8)

Straddled soliton solution:

$$\begin{aligned} F_{4}^{\pm }(\varsigma )=\mp \frac{\sqrt{\pm \lambda }\left( 5-4\cosh \left( 2\sqrt{\pm \lambda }\left( \varsigma +\gamma \right) \right) \right) }{3+4\sinh \left( 2\sqrt{\pm \lambda }\left( \varsigma +\gamma \right) \right) }.~ \end{aligned}$$
(9)

Straddled soliton solution:

$$\begin{aligned} F_{5}^{\pm }(\varsigma )=\mp \frac{\varepsilon \sqrt{\pm \lambda \left( {{A}^{2}}+{{B}^{2}} \right) }-A\sqrt{\pm \lambda }\cosh \left( 2\sqrt{\pm \lambda }\left( \varsigma +\gamma \right) \right) }{A\sinh \left( 2\sqrt{\pm \lambda }\left( \varsigma +\gamma \right) \right) +B}.~~ \end{aligned}$$
(10)

Straddled soliton solution:

$$F_{6}^{ \pm } (\varsigma ) = \mp \varepsilon \sqrt { \pm \lambda }\, \left[ {1 - \frac{{2A}}{{\left( {A + \cosh \left( {2\sqrt { \pm \lambda } \left( {\varsigma + \gamma } \right)} \right) \pm \varepsilon \sinh \left( {2\sqrt { \pm \lambda } \left( {\varsigma + \gamma } \right)} \right)} \right)}}} \right].$$
(11)

Dark soliton solution:

$$\begin{aligned} F_{7}^{\pm }(\varsigma )=\pm \frac{\sqrt{\mp \lambda }\left( 1-\tanh \left( \sqrt{\pm \lambda }\left( \varsigma +\gamma \right) \right) \right) }{1+\sqrt{\pm \lambda }\tanh \left( \sqrt{\pm \lambda }\left( \varsigma +\gamma \right) \right) }.~ \end{aligned}$$
(12)

Straddled soliton solution:

$$\begin{aligned} F_{8}^{\pm }(\varsigma )=\mp \frac{\sqrt{\mp \lambda }\left( 4-5\cosh \left( 2\sqrt{\mp \lambda }\left( \varsigma +\gamma \right) \right) \right) }{3+5\sinh \left( 2\sqrt{\mp \lambda }\left( \varsigma +\gamma \right) \right) }.~ \end{aligned}$$
(13)

Straddled soliton solution:

$$\begin{aligned} F_{9}^{\pm }(\varsigma )=\mp \frac{\varepsilon \sqrt{\mp \lambda \left( {{A}^{2}}+{{B}^{2}} \right) }-A\sqrt{\mp \lambda }\cosh \left( 2\sqrt{\mp p}\left( \varsigma +\gamma \right) \right) }{A\sinh \left( 2\sqrt{\mp \lambda }\left( \varsigma +\gamma \right) \right) +B}.~ \end{aligned}$$
(14)

In this study, we explore the scenario where \({F}'(\varsigma )=\lambda - F{{(\varsigma )}^{2}}\) as defined in Eq. (5). By incorporating Eq. (4) and its derivatives into the governing model, a polynomial in terms of powers of \(F(\varsigma )\) is derived. We then organize terms with similar powers of \(F(\varsigma )\) and set each coefficient to zero, resulting in a set of algebraic equations.

Application to the Model

In this section, different forms of optical solutions to the generalized integrable (2+1)-dimensional (NLS) system of equations are analyzed utilizing the present approach. Here, we begin with the following transformations:

$$\begin{aligned} \begin{aligned}&p(x,y,t)=H(\varsigma ){{e}^{i\psi (x,t)}}, \\&q(x,y,t)=G(\varsigma ), \\&\varsigma ={{g}_{1}}x+{{h}_{1}}y+{{c}_{1}}\frac{{{t}^{\theta }}}{\theta },\psi (x,t)={{g}_{2}}x+{{h}_{2}}y+{{c}_{2}}\frac{{{t}^{\theta }}}{\theta }. \\ \end{aligned} \end{aligned}$$
(15)

Here, \({{g}_{1}}\) and \({{g}_{2}}\) represent the wave speed, while \({{h}_{1}}\) and \({{h}_{2}}\) denote the wave number and the frequency of the optical dromions, respectively. By inserting the above transformations into Eq. (2), we obtain the following real and imaginary parts, respectively:

$$\begin{aligned}{} & {} ({{c}_{1}}+{{\beta }_{1}}({{g}_{1}}{{h}_{2}}+{{g}_{2}}{{h}_{1}})){H}'=0, \end{aligned}$$
(16)
$$\begin{aligned}{} & {} -{{c}_{2}}H-{{\beta }_{1}}{{g}_{2}}{{h}_{2}}H+{{\beta }_{1}}{{g}_{1}}{{h}_{1}}{H}''+{{\beta }_{2}}HG=0, \end{aligned}$$
(17)

and

$$\begin{aligned} {{\beta }_{3}}{{g}_{1}}{G}'+{{\beta }_{4}}{{h}_{1}}{{H}^{2}}^{\prime }=0. \end{aligned}$$
(18)

Integrating Eq. (18), the following constraints are derived:

$$\begin{aligned} G=\frac{{{\beta }_{4}}{{h}_{1}}}{{{\beta }_{3}}{{g}_{1}}}{{H}^{2}}. \end{aligned}$$
(19)

By solving Eq. (16), we obtain

$$\begin{aligned} {{c}_{1}}=-{{\beta }_{1}}({{g}_{1}}{{h}_{2}}+{{g}_{2}}{{h}_{1}}). \end{aligned}$$
(20)

Inserting Eq. (20) into Eq. (17), we obtain

$$\begin{aligned} -({{c}_{2}}+{{\beta }_{1}}{{g}_{2}}{{h}_{2}})H+{{\beta }_{1}}{{g}_{1}}{{h}_{1}}{H}''-\frac{{{h}_{1}}{{\beta }_{2}}{{\beta }_{4}}}{{{g}_{1}}{{\beta }_{3}}}{{H}^{3}}=0. \end{aligned}$$
(21)

In Eq. (21), implementing the balancing principle between \({H}''\) and \({{H}^{3}}\), we obtain \(N=1\). Thus, from Eq. (4) the following is obtained:

$$\begin{aligned} H(\varsigma )={{a}_{0}}+{{a}_{1}}F(\varsigma )+{{b}_{1}}\frac{1}{F(\varsigma )}. \end{aligned}$$
(22)

Substituting Eq. (22) and its derivative into Eq. (21), and then setting the coefficients of the corresponding powers of \({{F}^{N}}(\varsigma )\) to zero yields a set of nonlinear equations:

$$\begin{aligned} {{\left( F(\varsigma ) \right) }^{0}}:&-{{a}_{0}}{{c}_{2}}-{{a}_{0}}{{g}_{2}}{{h}_{2}}{{\beta }_{1}}-\frac{a_{0}^{3}{{h}_{1}}{{\beta }_{2}}{{\beta }_{4}}}{{{g}_{1}}{{\beta }_{3}}}\nonumber \\ & \quad -\frac{6{{a}_{0}}{{a}_{1}}{{b}_{0}}{{h}_{1}}{{\beta }_{2}}{{\beta }_{4}}}{{{g}_{1}}{{\beta }_{3}}}=0,~ \end{aligned}$$
(23)
$$\begin{aligned} {{\left( F(\varsigma ) \right) }^{1}}:&-{{a}_{1}}{{c}_{2}}-2p{{a}_{1}}{{g}_{1}}{{h}_{1}}{{\beta }_{1}}-{{a}_{1}}{{g}_{2}}{{h}_{2}}{{\beta }_{1}}\nonumber \\& \quad -\frac{3a_{0}^{2}{{a}_{1}}{{h}_{1}}{{\beta }_{2}}{{\beta }_{4}}}{{{g}_{1}}{{\beta }_{3}}}-\frac{3a_{1}^{2}{{b}_{0}}{{h}_{1}}{{\beta }_{2}}{{\beta }_{4}}}{{{g}_{1}}{{\beta }_{3}}}=0, \end{aligned}$$
(24)
$$\begin{aligned}{} & {} {{\left( F(\varsigma ) \right) }^{2}}:-\frac{3{{a}_{0}}a_{1}^{2}{{h}_{1}}{{\beta }_{2}}{{\beta }_{4}}}{{{g}_{1}}{{\beta }_{3}}}=0,~ \end{aligned}$$
(25)
$$\begin{aligned}{} & {} {{\left( F(\varsigma ) \right) }^{3}}:2{{a}_{1}}{{g}_{1}}{{h}_{1}}{{\beta }_{1}}-\frac{a_{1}^{3}{{h}_{1}}{{\beta }_{2}}{{\beta }_{4}}}{{{g}_{1}}{{\beta }_{3}}}=0,~ \end{aligned}$$
(26)
$$\begin{aligned}{} & \left( \frac{1}{F(\varsigma )} \right) :-{{b}_{0}}{{c}_{2}}-2p{{b}_{0}}{{g}_{1}}{{h}_{1}}{{\beta }_{1}}-{{b}_{0}}{{g}_{2}}{{h}_{2}}{{\beta }_{1}}\nonumber \\ & \quad -\frac{3a_{0}^{2}{{b}_{0}}{{h}_{1}}{{\beta }_{2}}{{\beta }_{4}}}{{{g}_{1}}{{\beta }_{3}}}-\frac{3{{a}_{1}}b_{0}^{2}{{h}_{1}}{{\beta }_{2}}{{\beta }_{4}}}{{{g}_{1}}{{\beta }_{3}}}=0, \end{aligned}$$
(27)
$$\begin{aligned}{} & {} \left( \frac{1}{F{{(\varsigma )}^{2}}} \right) :-\frac{3{{a}_{0}}b_{0}^{2}{{h}_{1}}{{\beta }_{2}}{{\beta }_{4}}}{{{g}_{1}}{{\beta }_{3}}}=0,~ \end{aligned}$$
(28)
$$\begin{aligned}{} & {} \left( \frac{1}{F{{(\varsigma )}^{3}}} \right) :2{{p}^{2}}{{b}_{0}}{{g}_{1}}{{h}_{1}}{{\beta }_{1}}-\frac{b_{0}^{3}{{h}_{1}}{{\beta }_{2}}{{\beta }_{4}}}{{{g}_{1}}{{\beta }_{3}}}=0.~ \end{aligned}$$
(29)

Result 1,2,3,4:

$$\begin{aligned}{} & {} {{a}_{0}}=0,{{a}_{1}}=\pm \frac{\left( {{c}_{2}}+{{g}_{2}}{{h}_{2}}{{\beta }_{1}} \right) \sqrt{{{\beta }_{3}}}}{4\sqrt{2}p{{h}_{1}}\sqrt{{{\beta }_{1}}}\sqrt{{{\beta }_{2}}}\sqrt{{{\beta }_{4}}}},\nonumber \\{} & {} {{a}_{2}}=\pm \frac{\left( {{c}_{2}}+{{g}_{2}}{{h}_{2}}{{\beta }_{1}} \right) \sqrt{{{\beta }_{3}}}}{4\sqrt{2}{{h}_{1}}\sqrt{{{\beta }_{1}}}\sqrt{{{\beta }_{2}}}\sqrt{{{\beta }_{4}}}},{{g}_{1}}=-\frac{{{c}_{2}}+{{g}_{2}}{{h}_{2}}{{\beta }_{1}}}{8p{{h}_{1}}{{\beta }_{1}}}. \end{aligned}$$
(30)

Result 5,6:

$$\begin{aligned}{} & {} {{a}_{0}}=0,{{a}_{1}}=\pm \frac{\left( {{c}_{2}}+{{g}_{2}}{{h}_{2}}{{\beta }_{1}} \right) \sqrt{{{\beta }_{3}}}}{\sqrt{2}p{{h}_{1}}\sqrt{{{\beta }_{1}}}\sqrt{{{\beta }_{2}}}\sqrt{{{\beta }_{4}}}},\nonumber \\{} & {} {{a}_{2}}=0,{{g}_{1}}=-\frac{{{c}_{2}}+{{g}_{2}}{{h}_{2}}{{\beta }_{1}}}{2p{{h}_{1}}{{\beta }_{1}}}. \end{aligned}$$
(31)

Result 7,8:

$$\begin{aligned}{} & {} {{a}_{0}}=0,{{a}_{1}}=0,{{a}_{2}}=\pm \frac{\left( {{c}_{2}}+{{g}_{2}}{{h}_{2}}{{\beta }_{1}} \right) \sqrt{{{\beta }_{3}}}}{\sqrt{2}{{h}_{1}}\sqrt{{{\beta }_{1}}}\sqrt{{{\beta }_{2}}}\sqrt{{{\beta }_{4}}}},{{g}_{1}}\nonumber \\{} & {} =-\frac{{{c}_{2}}+{{g}_{2}}{{h}_{2}}{{\beta }_{1}}}{2p{{h}_{1}}{{\beta }_{1}}}. \end{aligned}$$
(32)

By substituting the functions \(F_{i}^{-}(\varsigma )\), where \(i=1,\ldots ,9\), along with Eqs. (30)–(32) into Eq. (22), we obtain the solutions of Eq. (2) by plugging the solutions (6)–(14) above into \(p_{i}^{-}(x,t)\) and \(q_{i}^{-}(x,t)\), where \(i=1,\ldots ,9\). Here, we utilize the result given in (32) to derive the following conformable optical dromions:

Dark soliton solutions:

$$\begin{aligned} p_{1}^{-}(x,t)=\pm \frac{\left( {{c}_{2}}+{{g}_{2}}{{h}_{2}}{{\beta }_{1}} \right) \sqrt{{{\beta }_{3}}}}{\sqrt{2\lambda {{\beta }_{1}}{{\beta }_{2}}{{\beta }_{4}}}{{h}_{1}}}\tanh \left[ \sqrt{\lambda }\left( \gamma +\varsigma \right) \right] {{\text {e}}^{\text {i}\left( \frac{{{t}^{\theta }}{{c}_{2}}}{\theta }+x{{g}_{2}}+y{{h}_{2}} \right) }},~ \end{aligned}$$
(33)

and

$$\begin{aligned} q_{1}^{-}(x,t)=\mp \frac{\left( {{c}_{2}}+{{g}_{2}}{{h}_{2}}{{\beta }_{1}} \right) }{{{\beta }_{2}}}\tanh {{\left[ \sqrt{\lambda }\left( \gamma +\varsigma \right) \right] }^{2}}, \end{aligned}$$
(34)

where \(\varsigma ={{h}_{1}}y-\frac{\left( {{c}_{2}}+{{g}_{2}}{{h}_{2}}{{\beta }_{1}} \right) }{2\lambda {{h}_{1}}{{\beta }_{1}}}x-\frac{{{\beta }_{1}}{{t}^{\theta }}}{\theta }\left( {{g}_{2}}{{h}_{1}}-\frac{{{h}_{2}}\left( {{c}_{2}}+{{g}_{2}}{{h}_{2}}{{\beta }_{1}} \right) }{2\lambda {{h}_{1}}{{\beta }_{1}}} \right) .\)

Singular soliton solutions:

$$\begin{aligned} p_{2}^{-}(x,t)=\pm \frac{\left( {{c}_{2}}+{{g}_{2}}{{h}_{2}}{{\beta }_{1}} \right) \sqrt{{{\beta }_{3}}}}{\sqrt{2\lambda {{\beta }_{1}}{{\beta }_{2}}{{\beta }_{4}}}{{h}_{1}}}\coth \left[ \sqrt{\lambda }\left( \gamma +\varsigma \right) \right] {{\text {e}}^{\text {i}\left( \frac{{{t}^{\theta }}{{c}_{2}}}{\theta }+x{{g}_{2}}+y{{h}_{2}} \right) }}, \end{aligned}$$
(35)

and

$$\begin{aligned} q_{2}^{-}(x,t)=\mp \frac{\left( {{c}_{2}}+{{g}_{2}}{{h}_{2}}{{\beta }_{1}} \right) }{{{\beta }_{2}}}\coth {{\left[ \sqrt{\lambda }\left( \gamma +\varsigma \right) \right] }^{2}}.~~ \end{aligned}$$
(36)

Dark soliton solutions:

$$p_{3}^{ - } (x,t) = \mp \frac{{\left( {c_{2} + g_{2} h_{2} \beta _{1} } \right)\sqrt {\beta _{3} } \left( { - \lambda + \sqrt \lambda \tanh \left[ {\sqrt \lambda \left( {\gamma + } \right)} \right]} \right)}}{{\lambda h_{1} \sqrt {2\beta _{1} \beta _{2} \beta _{4} } \left( {1 - \sqrt \lambda \tanh \left[ {\sqrt \lambda \left( {\gamma + } \right)} \right]} \right)}}e^{{{\text{i}}\left( {\frac{{t^{\theta } c_{2} }}{\theta } + xg_{2} + yh_{2} } \right)}} ,$$
(37)

and

$$\begin{aligned} q_{3}^{-}(x,t)=\pm \frac{\left( {{c}_{2}}+{{g}_{2}}{{h}_{2}}{{\beta }_{1}} \right) {{\left( -\lambda +\sqrt{\lambda }\tanh \left[ \sqrt{\lambda }\left( \gamma +\varsigma \right) \right] \right) }^{2}}}{\lambda {{\beta }_{2}}{{\left( 1-\sqrt{\lambda }\tanh \left[ \sqrt{\lambda }\left( \gamma +\varsigma \right) \right] \right) }^{2}}}.~ \end{aligned}$$
(38)

Straddled soliton solutions:

$$p_{4}^{ - } (x,t) = \mp \frac{{\left( {5 - 4\cosh \left[ {2\sqrt \lambda \left( {\gamma + \varsigma } \right)} \right]} \right)\left( {c_{2} + g_{2} h_{2} \beta _{1} } \right)\sqrt {\beta _{3} } }}{{\sqrt {2\lambda \beta _{1} \beta _{2} \beta _{4} } h_{1} \left( {3 + 4\sinh \left[ {2\sqrt \lambda \left( {\gamma + \varsigma } \right)} \right]} \right)}}e^{{{\text{i}}\left( {\frac{{t^{\theta } c_{2} }}{\theta } + xg_{2} + yh_{2} } \right)}} ,~$$
(39)

and

$$\begin{aligned} q_{4}^{-}(x,t)=\mp \frac{{{\left( 5-4\cosh \left[ 2\sqrt{\lambda }\left( \gamma + \right) \right] \right) }^{2}}\left( {{c}_{2}}+{{g}_{2}}{{h}_{2}}{{\beta }_{1}} \right) }{{{\left( 3+4\sinh \left[ 2\sqrt{\lambda }\left( \gamma + \right) \right] \right) }^{2}}{{\beta }_{2}}}.~ \end{aligned}$$
(40)

Straddled soliton solutions:

$$p_{5}^{ - } (x,t) = \pm \frac{{\left( {\sqrt {\left( {A^{2} + B^{2} } \right)\lambda } - A\sqrt \lambda \cosh \left[ {2\sqrt \lambda \left( {\gamma + } \right)} \right]} \right)\left( {c_{2} + g_{2} h_{2} \beta _{1} } \right)\sqrt {\beta _{3} } }}{{\lambda \sqrt {2\beta _{1} \beta _{2} \beta _{4} } h_{1} \left( {B + A\sinh \left[ {2\sqrt \lambda \left( {\gamma + } \right)} \right]} \right)}}e^{{{\text{i}}\left( {\frac{{t^{\theta } c_{2} }}{\theta } + xg_{2} + yh_{2} } \right)}} ,~$$
(41)

and

$$q_{5}^{ - } (x,t) = \pm \frac{{\left( {\sqrt {\left( {A^{2} + B^{2} } \right)\lambda } - A\sqrt \lambda \cosh \left[ {2\sqrt \lambda \left( {\gamma + } \right)} \right]} \right)^{2} \left( {c_{2} + g_{2} h_{2} \beta _{1} } \right)}}{{\lambda \left( {B + A\sinh \left[ {2\sqrt \lambda \left( {\gamma + } \right)} \right]} \right)^{2} \beta _{2} }},$$
(42)

where A and B are arbitrary constants.

Straddled soliton solutions:

$$p_{6}^{ - } (x,t) = \mp \frac{{\left( {1 - \frac{{2A}}{{A + \cosh \left[ {2\sqrt \lambda \left( {\gamma + } \right)} \right] + \sinh \left[ {2\sqrt \lambda \left( {\gamma + } \right)} \right]}}} \right)\left( {c_{2} + g_{2} h_{2} \beta _{1} } \right)\sqrt {\beta _{3} } }}{{\sqrt {2\lambda \beta _{1} \beta _{2} \beta _{4} } h_{1} \left( {B + A\sinh \left[ {2\sqrt \lambda \left( {\gamma + } \right)} \right]} \right)}}e^{{{\text{i}}\left( {\frac{{t^{\theta } c_{2} }}{\theta } + xg_{2} + yh_{2} } \right)}} ,~$$
(43)

and

$$q_{6}^{ - } (x,t) = \pm \frac{{\left( {c_{2} + g_{2} h_{2} \beta _{1} } \right)}}{{\beta _{2} }}\left( {1 - \frac{{2A}}{{A + \cosh \left[ {2\sqrt \lambda \left( {\gamma + } \right)} \right] + \sinh \left[ {2\sqrt \lambda \left( {\gamma + } \right)} \right]}}} \right)^{2} .$$
(44)
Fig. 1
figure 1

The comparison of dark plot of \({{\left| {{p}_{1}}(x,t) \right| }^{2}}\) for \(\theta =1\) and \(\theta =0.5\), where \({{h }_{2}}=0.2,{{h}_{1}}=0.6,{{\beta }_{1}}y==1,{{\beta }_{2}}={{\beta }_{3}}=0.7,{{\beta }_{4}}=0.9,{{g}_{2}}=0.9,{{\beta }_{2}}=0.1,{{c}_{2}}=-0.5,\lambda =0.8,\gamma =0.3,\) and \(\theta =1\)

Full size image
Fig. 2
figure 2

The wave plots of \({\text {Im}}({{p}_{1}}(x,t))\), where \({{h }_{2}}=0.2,{{h}_{1}}=0.6,{{\beta }_{1}}=y=1,{{\beta }_{2}}={{\beta }_{3}}=0.7,{{\beta }_{4}}=0.9,{{g}_{2}}=0.9,{{\beta }_{2}}=0.1,{{c}_{2}}=-0.5,\lambda =0.8,\gamma =0.3,\) and θ= 1

Full size image
Fig. 3
figure 3

The comparison of bright plots of \({\text {Re}}({{q}_{1}}(x,t))\) for θ= 1 and θ= 0.5, where h2 = 0.2, h1 = 0.6,  β1= y = 1,  β2 = β3 = 0.7,  β4 = 0.9, g2 = 0.9,  β2 = 0.1, c2 = − 0.5, λ = 0.8, γ = 0.3, and θ= 1

Full size image
Fig. 4
figure 4

The multi-bright plots of \({{\left| {{p}_{5}}(x,t) \right| }^{2}}\), where h2 = 0.2, h1 = 0.6,  β1= y = 1,  β2 = β3 = 0.7,  β4 = 0.9, g2 = 0.9,  β2 = 0.1, c2 = − 0.5, λ = − 0.5, γ = 0.3, and θ= 1

Full size image
Fig. 5
figure 5

The mixed dark-bright plots of \({\text {Re}}({{p}_{5}}(x,t))\), where \({{h }_{2}}=0.2,{{h}_{1}}=0.6,{{\beta }_{1}}=y=1,{{\beta }_{2}}={{\beta }_{3}}=0.7,{{\beta }_{4}}=0.9,{{g}_{2}}=0.9,{{\beta }_{2}}=0.1,{{c}_{2}}=-0.5,\lambda =-0.1,\gamma =0.3,\) and \(\theta =1\)

Full size image
Fig. 6
figure 6

The multi-dark and mixed dark-bright plots of \({\text {Re}}({{q}_{5}}(x,t))\) and \({\text {Im}}({{q}_{5}}(x,t))\), where \({{h }_{2}}=0.2,{{h}_{1}}=0.6,{{\beta }_{1}}=y=1,{{\beta }_{2}}={{\beta }_{3}}=0.7,{{\beta }_{4}}=0.9,{{g}_{2}}=0.9,{{\beta }_{2}}=0.1,{{c}_{2}}=-0.5,\lambda =-0.1,\gamma =0.3,\) and \(\theta =1\)

Full size image
Fig. 7
figure 7

The effect of the conformable parameter on \({{\left| {{p}_{1}}(x,t) \right| }^{2}}\) and \({\text {Re}}({{p}_{1}}(x,t))\), where \({{h }_{2}}=0.2,{{h}_{1}}=0.6,{{\beta }_{1}}=y=1,{{\beta }_{2}}={{\beta }_{3}}=0.7,{{\beta }_{4}}=0.9,{{g}_{2}}=0.9,{{\beta }_{2}}=0.1,{{c}_{2}}=-0.5,\lambda =0.8,\gamma =0.3,\) and \(\theta =1\)

Full size image
Fig. 8
figure 8

The effect of the conformable parameter on \({\text {Im}}({{p}_{5}}(x,t))\) and \({\text {Re}}({{p}_{5}}(x,t))\), where \({{h }_{2}}=0.2,{{h}_{1}}=0.6,{{\beta }_{1}}=y=1,{{\beta }_{2}}={{\beta }_{3}}=0.7,{{\beta }_{4}}=0.9,{{g}_{2}}=0.9,{{\beta }_{2}}=0.1,{{c}_{2}}=-0.5,\lambda =-0.1,\gamma =0.3,\) and \(\theta =1\)

Full size image

Results and discussion

In this section, we have carefully chosen specific values for the physical parameters to showcase the importance of the present conformable Schrödinger equation system. To grasp the features of the innovative optical solutions and communicate their physical relevance, a variety of graphs have been employed. In this investigation, we examine how the conformable order derivative \(\theta\) and the time parameter t impact the current optical dromions. This exploration is visualized through a series of two-dimensional and three-dimensional plots depicted in Figs. 1, 2, 3, 4, 5, 6, 7, and 8, both in graph (a) and graph (b).

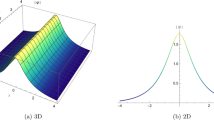
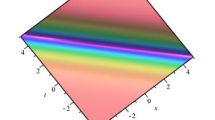
Figures 1, 2, 3, 4, 5, 6, 7, and 8 address the contour, 3D, and 2D plots of the imaginary part, real part, and square of the modulus of the optical dromions. Figure 1a,b represent the comparison of the effect of the parameter of the conformable derivative on the dark optical soliton solution \({{\left| {{p}_{1}}(x,t) \right| }^{2}}\), while the comparison of the effect of the parameter of the conformable derivative on the dark optical soliton solution \({\text {Im}}({{p}_{1}}(x,t))\) is depicted in Fig. 2a,b. The dark and multi-dark soliton solutions have various applications in optical fiber systems, including pulse shaping, wavelength division multiplexing, and high-capacity data transmission. By manipulating the parameters governing the propagation of dark solitons, engineers can design optical fiber systems tailored to specific communication needs. However, the presence of multiple bell-shaped solitons suggests that the system supports the existence of multiple coherent structures that propagate without changing their shape or speed. In Fig. 4a and Fig. 6a, multi-bright and multi-dark soliton solutions are depicted, respectively. However, the mixed dark-bright and dark-bright optical soliton solutions are illustrated in Fig. 5a and Fig. 6b, respectively. Further, the imaginary part of \({{p}_{1}}(x,t)\) is wave optical soliton solution from Fig. 2a.

In Fig. 1a,b, the comparison of dark soliton solutions \({{\left| {{p}_{1}}(x,t) \right| }^{2}}\) for \(\theta =1\) and \(\theta =0.5\) is illustrated. Thus, Fig. 5 indicates that increasing the value of the conformable parameter influences the dynamic of the soliton to move to the right-hand side, as well as the same behavior can be observed in Fig. 3a,b for the real part of \({{q}_{1}}(x,t)\). Furthermore, the behavior of the topological aspects of the soliton solutions with changes in the time parameter t is depicted in Figs. 2b, 4b, and 5b. Finally, the behavior of the topological aspects of various soliton solutions with changes in the conformable derivative \(\theta\) is illustrated in Fig. 8a,b, respectively. Perhaps the functions of the solutions exhibit similarities, yet their solution sets diverge. These distinct solution sets exert significant influence on wave profiles, underscoring the novelty of our study. Moreover, the obtained results are unprecedented and defy comparison with any previously published research. The depicted figures provide a dynamic portrayal of various soliton solutions, ranging from periodic and bright to singular, combo bright-dark, and dark optical solitons, respectively. Notably, these reported solutions bear physical significance; for example, the profile of a laminar jet mirrors the hyperbolic secant, while the calculation of magnetic moment and special relativity rapidity involves the hyperbolic tangent. Similarly, the hyperbolic cotangent finds application in the Langevin function for magnetic polarization.

Conclusion

The current paper recovered optical dromions that came with fractional temporal evolution. The enhanced modified tanh expansion approach is the adopted scheme that retrieved the optical dromions that are presented in the paper. The results are surely usable in telecommunication industry towards performance enhancement purposes. These results ae interesting and can later be applied with additional models that would yield furthermore interesting and applicable results. Later, the model would be addressed with Fokas–Lenells equation, Schrödinger–Hirota equation and several other models. This is just a tip of the iceberg and the avalanche of the upcoming results would be disseminated all across the board after the recovered results are aligned with the pre-existing ones [24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44].