Introduction

Infrared imaging systems are widely used in many industrial applications, particularly in surveillance and the military. Its good response can be achieved in either total darkness, dust, smoke, light fog, rain, or snow [1,2,3]. In military applications the optical system is exposed to harsh environments, so the image quality of the optical system should be maintained over the wide operating temperature range and also, the target detection with suitable resolution and long range over a wide field of view. Few materials are transparent in the infrared region rather than in the visible band, such as germanium (Ge), zinc selenide (ZnSe), zinc sulfide (ZnS), and chalcogenide glasses. In addition to the rareness of these materials, the relative changes of their refractive indices with respect to the temperature changes are very high. The temperature fluctuations lead to great changes in their indices as well as their physical parameters, such as radii and thickness. Additionally, the housing dimensions will change the separations between the optical elements. These changes lead to a focus shift, which is called thermal aberration. So the compensation of this focus shift “athermalization” and achromatization with correcting high-order aberration due to the large aperture and wide field of view for the optical system is important and challenging. There are many techniques for athermalization. The mechanical active technique requires a movement of the optical element(s), whereas the optical passive can be achieved by selecting different materials with different thermal expansions and different changes of refractive indices with temperature (dn/dT). The last one is preferred, as it is more reliable, more stable, compact, and lightweight [3,4,5,6]. However, uncooled FPA detectors have many advantages such as being lightweight, compact, low power consumption, and good reliability. Unfortunately, the sensitivity is quite small and it has a quite high noise equivalent temperature difference (NETD). To overcome these disadvantages, the F-number, which expresses the input power of the light acquired by the lens of the optical system, should be less than 2 [1, 2]. Meanwhile, the optical design by Dong Janing worked at F-number 2.2, which is not preferred for uncooled F.P.A [4]. Moreover, Jing Wang’s design has two diffractive surfaces. It will affect badly on the transmission of the optical system due to decreasing of the diffractive efficiency. This design suffers from a manufacturing difficulty for the first lens as the aspheric and diffractive are on different surfaces [5], Jiang Lun designed an objective lens with F-number 1, but the optical system designed for low Nyquist frequency “17 lp” for low detector resolution “30 µm.” This MTF performance indicates that the high-order aberrations are not well corrected [6].

Design principle

The single lens power is given by

$$ \emptyset = \left( {n - 1} \right)\left( {\frac{1}{{r_{1} }} - \frac{1}{{r_{2} }}} \right) $$
(1)

where n is the index of refraction and r1 and r2 are the radii of the lens.

The change of the lens power with temperature can be derived as

$$ \frac{d\emptyset }{{dT}} = \frac{dn}{{dT}}\left( {\frac{1}{{r_{1} }} - \frac{1}{{r_{2} }}} \right) + \left( { - \frac{1}{{r_{1} }} + \frac{1}{{r_{2} }}} \right)\alpha \left( {n - 1} \right) $$
(2)

where \(\frac{1}{r}\frac{dr}{{dT}} = \alpha\)is the thermal expansion coefficient of the glass.

$$ {\text{hence}} \frac{d\emptyset }{{dT}} = \left( {\frac{{\frac{dn}{{dT}}}}{n - 1} - \alpha } \right)\left( {\frac{1}{{r_{1} }} - \frac{1}{{r_{2} }}} \right)\left( {n - 1} \right) = \emptyset \left( {\frac{{\frac{dn}{{dT}}}}{n - 1} - \alpha } \right) $$
(3)
$$ {\text{so that }} \frac{d\emptyset }{{dT}} = \emptyset \beta $$

\(\beta = \left[ {\left[ {\left( {dn/dT} \right)/\left( {n - 1} \right)} \right] - \alpha } \right]\)is the thermo-optical coefficient of the lens.

For single lens in the housing, the defocus will be

$$ \frac{d\emptyset }{{dT}} = \emptyset \left( {\beta - \alpha_{h} } \right) $$
(4)

where \(\alpha_{h}\) is the thermal expansion coefficient of the housing.

For an optical system consisting of many lenses (k), there are two cases.

  1. (a)

    For k lens in contact

The total power of k elements is

$$ \emptyset = \left( {\frac{1}{{h_{1} }}} \right) \mathop \sum \limits_{i = 1}^{k} h_{i} \emptyset_{i} $$
(5)

The achromatic condition is given by

$$ \Delta f_{\lambda } = \left( {\frac{1}{{h_{1} \emptyset }}} \right)^{2} \mathop \sum \limits_{i = 1}^{k} h_{i}^{2} \frac{1}{v}_{i} \emptyset_{i} = 0 $$
(6)

The athermalizion condition is also given by

$$ \Delta f_{T} = \left( {\frac{1}{{h_{1} \emptyset }}} \right)^{2} \mathop \sum \limits_{i = 1}^{k} h_{i}^{2} (\beta_{i} \emptyset_{i} ) + \alpha_{h} {\text{\O }} = 0 $$
(7)

where hi is the paraxial ray height at the ith lens and vi is the Abbe number of the ith lens.

  1. (b)

    For k separated elements

It can be athermalized as multiple lens groups individually, and the residual thermal aberration can be shared between these groups [7].

The power of the refractive optical element that has a diffractive surface (hybrid element) is

$$ \emptyset_{{{\text{tot}}}} = \emptyset_{{{\text{refractive}}}} + \emptyset_{{{\text{diffractive}}}} $$

Material properties and material section

Table 1 shows the most commonly used materials in the infrared region with their physical properties. Germanium is the most common material used. As shown, germanium has a large Abbe number and, hence, its dispersive power is very low, so it is convenient for achieving low chromatic aberration. Additionally, it has a high refractive index, which is good for correcting spherical aberration. So germanium is a preferred material for designing optical systems in the LWIR region. Unfortunately, it has high dn/dT, which will cause high thermal aberration. With the aid of the athermal chart (Fig. 1), a good combination of materials can be used for fabricating athermalized and achromatized optical systems [8].

Table 1 Some IR materials transparent in λ = 8–12 µm spectral band
Full size table
Fig. 1
figure 1

Athermal chart for most common IR materials

Full size image

Optical design

In this work, a compact optical system with a wide field of view (12.2°) and low relative aperture (F/#1.1) is presented. Its focal length is 120 mm. The optical system consists of four lenses. The materials used were hybrid aspheric–diffractive germanium for the first lens, Gasir 5 for the second lens with a conic surface, the third lens was zinc selenide, and the fourth one was aspheric Gasir 1. As the Knoop hardness for germanium is 780 kg/mm2, the first lens is of germanium to bear the harsh environment. The system has a large aperture and wide field of view, as well as it is athermalized. Also, it is achromatized for secondary spectrum “max- color shift is 7 µ” and well corrected for higher-order aberrations (nearly diffraction limit performance as will be shown later) over a temperature range extended from − 40 to + 65 °C. Moreover, the system is relatively compact (140 mm). The system resolution that is compatible with an uncooled focal plane array detector (FPA) 1280 × 1024 has a pixel pitch 17 µm.

In this optical system, the ratio between the center thickness and diameter was considered the manufacturing process to prevent lens damage. Also, the minimum edge thickness after adding 1 mm over the clear aperture for the housing is 3 mm for the finished lens. The aspheric lens has one aspheric surface to prevent the manufacturing risk. The system is optimized for aluminum housing with thermal expansion 23 × 10−6 c−1. Figure 2 shows the optical system layout, and Table 2 lists the optical system data.

Fig. 2
figure 2

Optical system layout

Full size image
Table 2 The optical design data
Full size table

Aspheric coefficient

1st surface

4th -1.393216E-008

6th 5.090586E-014

8th -2.6295252E-016

 

10th 5.9882394E-020

  

8th surface

4th 3.7451177E-007

6th 9.8297086E-011

8th 7.420309994E-014

With respect to the diffractive element, which is known as a binary element, the focal length formula is given by [4,5,6].

$$ f = \frac{{ r_{m}^{2} }}{2m\lambda } $$
(8)

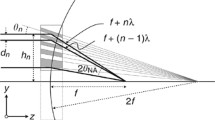
where rm is the radius of m zone.

The radii of the different steps on a binary surface (diffractive surface) that adds a phase shift by m (2\(\pi\)), are shown in Fig. 3.

Fig. 3
figure 3

Diffractive rings on the 1st surface X (mm)

Full size image

The main advantages of the diffractive element are the correction of the chromatic aberration and aid in athermalization, where the thermal expansion coefficient and dispersion of the diffractive element are sign opposite to that of the refractive element [5].

System evaluation

Spot diagram and encircled energy

Spot diagram and encircled energy are good ways to evaluate the optical system performance. Spot diagram is a representation of the energy distribution of a point source object at the image plane. It simulates the ray distribution at the image plane by tracing bundles of rays through the optical system. The RMS spot diameter represents about 68% of the concentrated energy [9]. The spot diagrams of the system from − 40 to + 65 °C are shown in Figs. 4a, b, and c. The maximum RMS radius of the spot diagram at full field of view is less than 10 µm, which is less than the pixel pitch (17 µm) over the whole temperature range. Figure 5a, b, and c shows the encircled energy graphs from − 40 to + 65 °C. More than 80% of the energy fall on 17 µm over the temperature range. The system performance is considered nearly diffraction limit and stable over the total temperature range.

Fig. 4
figure 4

a Spot diagram at + 20 °C, b Spot diagram at + 65 °C, c Spot diagram at − 40 °C

Full size image
Fig. 5
figure 5

a Encircled energy at + 20 °C, b Encircled energy at + 65 °C, c Encircled energy at − 40 °C

Full size image

Modulation transfer function (MTF) curves

The MTF curve is an important criterion and good indication for expressing the optical system performance, especially for the image forming system. It represents the contrast modulation transfer through the optical system. It can be expressed as [10].

\({\text{MTF = }}\frac{{\text{image modulation}}}{{\text{object modulation }}}{\text{ modulation = }}\frac{{I_{{{\text{max}}}} - I_{{{\text{min}}}} }}{{I_{{{\text{max}}}} { + }I_{{{\text{min}}}} }}\) where Imax is the maximum intensity Imin is the minimum intensity

For thermal imaging system, the detector’s thermal sensitivity shou be considered. As thermal sensitivity (expressed as NETDFootnote 1) increases, the threshold contrast for the target at different spatial frequencies (MRTDFootnote 2**) will increase. It can be expressed as:

\({\text{MRTD = }}\frac{{{\text{NETD}}}}{{{\text{MTF}}}}{ }\). The NETD for uncooled detectors is quite large. So, the MTF of the optical system needs to reach the diffraction limit, at low F-number, as possible [10,11,12]. Figure 6a, b, and c shows that the MTF of the optical system is nearly diffraction limitednd very well corrected for aberrations over the total range of temperature and full field.

Fig. 6
figure 6

a MTF curve at + 20 °C, b MTF curve at − 40 °C, c MTF curve at + 65 °C

Full size image

Strehl ratio

Strehl ratio is one of the most meaningful ways of expressing the optical system performance. It represents the ratio between the peak diffraction intensities of an aberrated wavefront and a perfect wavefront. In this optical system, the Strehl ratio is not less than 0.95 over the whole temperature range at all field points. Figure 7a, b, and c shows the on-axis Strehl ratio over the temperature range.

Fig. 7
figure 7

a On-axis Strehl ratio at + 20 °C, b On-axis Strehl ratio at − 40 °C, c On-axis Strehl ratio at + 65 °C

Full size image

In IR imaging, the system should be calibrated from the inherent emission, which is called nonuniformity correction. This can be achieved by adding a shutter between the optics and detector. Recently, several uncooled detectors are shutterless and use software techniques for this calibration.

Also, some field stops could be added to restrict the outfield stray light to reduce the incoming noise [13].

Anti-reflection coating

The refractive indices of infrared materials are high “larger than 2,” and this leads to high loss of the incident wave energy due to the high reflection. For example, the refractive index of germanium is 4 and the transmittance from one Ge lens is about 40%. For the whole system introduced in this paper, the total transmittance is only 6.6% of the incident wave energy. To increase the transmittance of the system, the anti-reflection coating is a must. The rareness of materials transpare in IR makes the design of coating challenge. As the optical system consists of four different materials, each material has either double-layer film coating of optical thickness \(t_{i} = \frac{{\delta_{i} \lambda_{0} }}{{2\pi n_{i} }}\). The condition for the double layer is a positive value [14]. The designs for four lens materials are shown in Table 3. Figure 8a, b, c, and d shows the reflectance of the lens after coating.

Table 3 Coating configuration for optical design materials
Full size table
Fig. 8
figure 8

a The energy loss of germanium lens after anti-reflection coating for 8 mm thickness, b The energy loss of Gasir 5 lens after anti-reflection coating for 15.5 mm thickness, c The energy loss of gasir lens after anti reflection coating for 8 mm thickness, d The energy loss of ZnSe lens after anti-reflection coating for 5.5 mm thickness

Full size image

n1, n2, and ns are the refractive indices of the first layer, second layer, and lens, respectively. ti is the geometrical thickness of the film, and δ is the phase thickness of the film.

Also, as the materials used have high absorption coefficient (Table 4), the absorption due to materials should be taken into consideration. The transmittance of the lens after absorption loss is T = e−αt where α is the absorption coefficient and t is the medium thickness.

Table 4 The absorption coefficient for the used material
Full size table

By applying this coating configuration (considering the absorption loss of lenses), the transmittance of the whole system is enhanced to 75.58% at 8 µm, 94.08% at 10 µm and 81.57% at 12 µm at the center of the optical system. In spite of, the diffraction efficiency for the Kinoform surface (Binary 2) is 99.8%, but this transmittance will decrease around 1% due to the manufacturing process depending on the manufacturing tools and accuracy [15, 16].

On the front germanium lens, diamond-like carbon (DLC) protective layer could be added on the front surface to stand the harsh condition.

Conclusion

A well-corrected and optical passive athermalized optical system has been designed. The optical system is considered to work in harsh environments. The system has large aperture “109 mm,” wide field of view “12.2°,” and is relatively compact “140 mm.” With the applicable lowest number of aspheric and diffractive surfaces, the system is well corrected for higher-order aberration and nearly diffraction-limited performance. The Strehl ratio reached 0.95% at 20 °C. Also, the choosing of the optical material “using athermal chart” with the only one diffractive surface saves the system to be athermalized and achromatized for the secondary spectrum. The system performance is stable over the temperature range from − 40 °C to + 65 °C. The good MTF of the system will overcome the low sensitivity of the uncooled detector that is inversely proportional to MRTD. By applying the anti-reflection coating on the lenses, the transmittance of the system is enhanced to reach 94.04% at 10 µm at the center of the optical system. The optical system was optimized and evaluated by ZEMAX software.