A Class of Mutualistic Systems Having an Almost Periodic Global Attractor

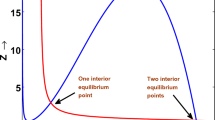
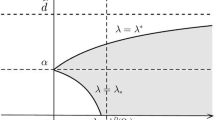
Abstract

We propose a general almost periodic model to describe a mutualistic interaction between two seasonal species when climate-mediated shifts change their population dynamics. In the modeling process, we use almost periodic functions as parameters of the model to describe a loss of synchronicity in the population dynamics of the mutualistic species. We also consider that the benefit granted for each species from the interaction with the partner species is modeled by a family of increasing bounded functions, which describe the fact that the maximum benefit received for each species is reached in high abundance of the partner species. We prove that there is a unique almost periodic globally stable solution of the model, when some conditions over the parameters of the model proposed are satisfied. Numerical simulations of the solutions of the model show significant differences between solutions within the periodic and the almost periodic framework. Forecasting asynchronous arrivals of species can help to decision makers to design species conservation strategies.

Appendix A: Almost Periodic Functions and Cooperative Systems

In this first part, we summarize some well known basic facts about the almost periodic functions and cooperative systems. Almost periodic functions are nowadays a very active theme. We give here only a very basic introduction to the topic and refer the reader to [29, 32] for much more details.

Definition 1

A function $\phi \in \textrm{C}^0(\mathbb {R})$ is almost periodic if, for all $\epsilon >0$ there exists a set of real numbers $T(\epsilon )\subseteq \mathbb {R}$ altogether with a length $l(\epsilon )>0$ such that for any interval of length $l(\epsilon )$, there exists at least one point $\tau \in T(\epsilon )$ contained in that interval such that

$$\begin{aligned} \left| \phi (x+\tau )-\phi (x)\right| <\epsilon \end{aligned}$$

for each $x\in \mathbb {R}$. We will call numbers in $T(\epsilon )$ translation numbers and the number $l(\epsilon )$will be called a length for $T(\epsilon )$.

The above collection of all almost periodic functions will be denoted by $AP(\mathbb {R})$ which is a Banach space endowed with the usual $\sup -$norm. It is possible to associate to an almost periodic function $\varphi$ its unique Fourier series:

$$\begin{aligned} \varphi \sim \sum _{n\in \mathbb {N}} a(\lambda _n) e^{i\lambda _n x}. \end{aligned}$$

The exponents $\lambda _n$ are called the frequencies of $\phi$.

Typical examples of almost periodic functions are $\sin t+\sin \sqrt{2}t$ which is almost periodic since it is a trigonometric polynomial presents a finite number of Fourier frequencies. Another example which is not quasi periodic is for instance $\sum _{k=1}^\infty \frac{1}{k^2}\cos \frac{t}{k^2}$.

Another well-known result in this area is that, for every almost periodic function there exists the mean value

$$\begin{aligned} \mathcal {M}[\phi ]: = \lim _{T\rightarrow \infty } \frac{1}{T} \int _{0}^{T} \phi (x) dx. \end{aligned}$$

This is a bounded linear functional, $\mathcal {M}:AP(\mathbb {R}) \rightarrow \mathbb {R}$, having the following properties:

• 1. $\phi \ge 0$ implies $\mathcal {M}[\phi ]\ge 0$.

• 2. The Parseval equality holds:

  $$\begin{aligned} \mathcal {M}\left[ \left| \phi \right| ^2\right] = \sum _{n\in \mathbb {N}} \left| a(\lambda _n)\right| ^2. \end{aligned}$$

Now we review some aspects about cooperative systems, for a brief introduction to cooperative systems see [33]. For two points $x, y \in \mathbb {R}^2$ denote the partial order $u \le v \; \text {if}\; u_i \le v_i \; \text {for each} \; i$, also denote $u<v$ if $u\le v$ and $u\ne v$. Let $f,g:\mathbb {R}\times D\subseteq \mathbb {R}^3\rightarrow \mathbb {R}$ be a couple of differentiable and almost periodic functions on the first variable. We consider the system:

$$\begin{aligned} \begin{aligned} x'(t)&=f(t,x(t),y(t)),\\ y'(t)&=g(t,x(t),y(t)), \end{aligned} \end{aligned}$$

(A1)

where we suppose that f(t, x, y), g(t, x, y) are both uniformly almost periodic with respect to $(x,y)\in C$ for every compact $C\subseteq D$, i.e., the set of translation numbers, $\tau (\epsilon )$, is independent of $(x,y)\in C$.

More specifically, if f have generalized Fourier expansions,

$$\begin{aligned} f(t,x,y) \sim {\overline{f}}(x,y) + \sum _{n=0}^\infty a(f, \lambda _n) \cos (\lambda _nt) + b(f, \lambda _n) \sin (\lambda _nt), \end{aligned}$$

f is uniformly almost periodic, whenever the frequencies $\lambda _n$ do not depend on (x, y), see [32] Chapter VI.

Definition 2

System (A1) is said to be of cooperative type if for all $t\in \mathbb {R}$, $x\in (a(t),A(t))$, $y\in (b(t),B(t))$ we have

$$\begin{aligned}f_{y}(t,x,y)\ge 0, \; g_{x}(t,x,y)\ge 0.\end{aligned}$$

We will say that (a(t), b(t)) are a subsolution pair if

$$\begin{aligned} a'(t)\le &\, {} f(t,a(t),b(t)), \end{aligned}$$

(A2)

$$\begin{aligned} b'(t)\le &\, {} g(t,a(t),b(t)). \end{aligned}$$

(A3)

For every $t\in \mathbb {R}$. A super-solution (A(t), B(t)) is defined similarly with the reversing inequalities. We will say that a sub-solution (a(t), b(t)) and a supersolution (A(t), B(t)) are ordered if $a(t)\le A(t)$ and $b(t)\le B(t)$ for all $t\in \mathbb {R}$.

A cooperative system is a monotone dynamical system in the sense that the Poincare map preserves a partial ordering on $R^{n}$. When $n=2$, every solution of (A1) is eventually monotone. Typically in this type of systems, the solutions converge asymptotically to equilibrium [34, 35]. An important feature for cooperative system (A1) related to almost periodic orbits was established in [27], Theorem 2. Explicitly the following result holds.

Theorem 2

Consider an ordered pair of a subsolution pair (a(t), b(t)) and a supersolution pair (A(t), B(t)) of the system (A1) such that $a(t)<A(t),$ and $b(t)<B(t)$. Suppose that there is no equilibrium point $(x_0,y_0)$ such that $a(t)\le x_0\le A(t)$ and $b(t)\le y_0\le B(t)$. If the system is cooperative type, then it has an almost periodic solution satisfying $a(t)\le x(t)\le A(t)$ and $b(t)\le x(t)\le B(t)$ for all $t\in \mathbb {R}$. Furthermore, if $(\underline{x}(t),\underline{y}(t)),({\overline{x}}(t),{\overline{y}}(t))$, denote the minimal and maximal almost periodic solutions having initial data satisfying $a(0)<x(0)<A(0)$ and $b(0)<y(0)<B(0)$. Then any solution of (A1), converges to the product of strips $(\underline{x}(t),{\overline{x}}(t))\times (\underline{y}(t),{\overline{y}}(t))$.

In a degenerate case, we could have a stable equilibrium, instead of a genuine almost periodic orbit.