Dynamical Analysis of a Model for Secondary Infection of the Dengue

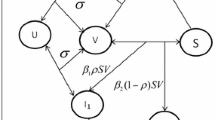
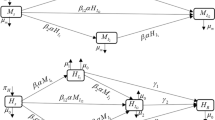
Abstract

Dengue disease is a major public health problem in the world with a fast spreading rate. Human migration has contibute to spread of the different serotypes of dengue virus, incrementing the risk of dengue hemorrhagic fever and dengue shock syndrome. The disease immunological response is complex, with severe disease linked to the antibody-dependent enhancement. In this work we propose a system of differential equations to model the impact of human migration on the spread of two serotypes of dengue virus between two regions where only one of the serotypes was initially present. When the individuals to the other region they can contract a different serotype. Using the next generation matrix method, the basic reproductive number $R_0$ is calculated and disease-free equilibrium stability is determined. In addition, conditions are obtained that guarantee the existence of an endemic equilibrium. These results provide conditions to predict an epidemic outbreak of dengue hemorrhagic due to a secondary infection of dengue.

Appendices

Appendix A: Positive Invariant Set $\Gamma$

We will see that the vector field on the boundary of $\Gamma$ does not point to the exterior of the region.

It can be seen that in the hyperplanes $S_i=0$, $I_i=0$, $R_i=0$, $I_{ij}=0$, $Z{ij}=0$, $U_i=0$, $V_i=0, \; i,j=1,2$ the components $S_i$, $I_i$, $R_i$, $I_{ij}$, Z ij, $U_i$, $V_i$ of vector field are positive and therefore the vector field points to the interior of $\Gamma$.

Now, adding components of the human and vector population in system (1) we get

$$\begin{aligned} \dfrac{dN_h}{dt}=\mu \left( \dfrac{\Lambda _1+\Lambda _2}{\mu } -N_h\right) \; \text{ y } \; \dfrac{dN_v}{dt}=\mu \left( \dfrac{\Omega _1+\Omega _2}{\nu } -N_v\right) , \end{aligned}$$

Using Gronwall inequality we have

$$\begin{aligned} \limsup \limits _{t \rightarrow \infty } N_h(t) \le \dfrac{\Lambda _1+\Lambda _2}{\mu } \; \text{ and } \; \limsup \limits _{t \rightarrow \infty } N_v(t) \le \dfrac{\Omega _1+\Omega _2}{\nu } . \end{aligned}$$

Also

$$\begin{aligned} \dfrac{dN_h}{dt}<0 \text{ and } \dfrac{dN_v}{dt}<0 \text{ for } N_h>\dfrac{\Lambda _1+\Lambda _2}{\mu } \text{ and } \dfrac{\Omega _1+\Omega _2}{\nu }, \text{ respectively }. \end{aligned}$$

This shows that the solutions of system (1) remain in the set $\Gamma .$

Appendix B: Existence of an Endemic Equilibrium Point

An endemic equilibrium point $P_3$ exists, if the conditions of the following propositions are satisfied.

Proposition 7

The values $I_{12}^*$, $I_{21}^*$, $I_2^*$ and $S_2^*$ are positive if

i):

$0<I_2^*<\dfrac{(m_{21}+\mu )(\gamma _1+\mu )\left( \mu \nu (\alpha (I_1^*+I_{21}^*)+\nu )+\alpha \beta _{21}\rho _1\Omega _1\right) I_{21}^*}{\alpha \beta _{21}\gamma _2m_{21} \rho _1 \Omega _1 (I_1^*+I_{21}^*)},$ and

ii):

$\dfrac{R_{01} S_1^*}{S_{01}}-1<\frac{\alpha I_1^*}{\nu }<\frac{R_{01} S_1^*}{S_{01}}, \text{ and } 0<I_1^*<r_{01}.$

where $r_{01}$ is the positive root of quadratic polinomial $N_1$ (it is described in the proof).

Proof

From (2)

$$\begin{aligned} I_{12}^*=\frac{h_{02}I_2^*+h_{01}}{m_{21}\alpha \beta _{21}\gamma _2 \rho _1 \Omega _1(I_1^*+I_{21}^*)}. \end{aligned}$$

where

$$\begin{aligned} h_{02}=&-\alpha \beta _{21}\gamma _2m_{21} \rho _1 \Omega _1 (I_1^*+I_{21}^*)<0,\\ h_{01}=&(m_{21}+\mu )(\gamma _1+\mu )\left( \mu \nu (\alpha (I_1^*+I_{21}^*)+\nu ) +\alpha \beta _{21}\rho _1\Omega _1\right) I_{21}^*>0. \end{aligned}$$

Then $I_{12}^*>0,$ if $h_{02}I_2^*>-h_{01}$, which is hypothesis i).

On the other hand, since

$$\begin{aligned} I_{21}^*=-\dfrac{ I_1^*\nu (\gamma _1+\mu )}{\nu (\gamma _1+\mu )I_1^*-\beta _1 \Omega _1S_1^*}\left( I_1^*+\frac{\nu }{\alpha }-\dfrac{\beta _1\Omega _1S_1^*}{(\gamma _1+\mu )\nu }\right) >0, \end{aligned}$$

if $\dfrac{\beta _1\Omega _1S_1^*}{(\gamma _1+\mu )\nu }-\dfrac{\nu }{\alpha }<I_1^* <\dfrac{\beta _1\Omega _1S_1^*}{(\gamma _1+\mu )\nu }.$ Substituting $R_{01}=\frac{\alpha \beta _1 S_{01}^* U_{01}^*}{(\gamma _1+\mu )\nu }$ in $\dfrac{\beta _1\Omega _1S_1^*}{(\gamma _1+\mu )\nu }$, we have $\dfrac{R_{01} S_1^*}{S_{01}}-1<\frac{\alpha I_1^*}{\nu }<\frac{R_{01} S_1^*}{S_{01}},$ which is hypothesis ii).

By (2) we have that the sign of $I_2^*$ and $S_2^*$ are given by the sign of $N_1$ and $N_2$. Since $N_2=\alpha \beta _{21}\gamma _2 m_{21}\rho _1\Omega _1(I_1^*+I_{21}^*)(\mu +m_{12}) \Big (I_1^*\left( \alpha I_{21}^*(\gamma _1+\mu ) (\mu +m_{21}) (\beta _{12} \rho _2\Omega _2+\mu \nu ) (\beta _{21}\rho _1\Omega _1+\mu \nu )+\beta _{21} \gamma _2\mu \nu ^2 m_{21}\rho _1 \Omega _1 \right) +I_{21}^*\left( \alpha I_{21}^* (\gamma _1+\mu ) (\mu +m_{21}) (\beta _{12} \rho _2 \Omega _2+\mu \nu ) (\beta _{21} \rho _1 \Omega _1+\mu \nu )+\mu \nu ^2 (\mu (\gamma _1+\mu ) (\beta _{12} \rho _2 \Omega _2+\mu \nu )+m_{21} ((\gamma _1+\mu ) (\beta _{12} \rho _2 \Omega _2+\mu \nu ) +\beta _{21} \gamma _2 \rho _1 \Omega _1)) \right) \Big )>0,$

then $I_2^*>0$ and $S_2^*>0$ if $N_1>0.$

Note that $N_1=h_{12}I_1^*{^2}+h_{11}I_1^*+h_{10}$ where

$$\begin{aligned} h_{12}= & {} -\alpha \beta _{12} \beta _{21} \gamma _1 \gamma _2 m_{12} m_{21} \rho _1\rho _2\Omega _1 \Omega _2,\\ h_{11}= & {} \alpha I_{21}^* (m_{12} (\mu (\gamma _1+\mu ) (\gamma _2+\mu ) (\beta _{12} \rho _2\Omega _2+\mu \nu ) (\beta _{21} \rho _1\Omega _1+\mu \nu )+\beta _{12} m_{21} \rho _2\Omega _2 \left( \beta _{21} \rho _1\Omega _1 (\mu (\gamma _1+\gamma _2) -\gamma _1 \gamma _2+\mu ^2)+\mu \nu (\gamma _1+\mu ) (\gamma _2+\mu )\right) +\mu \nu m_{21} (\gamma _1+\mu ) (\gamma _2+\mu ) (\beta _{21} \rho _1\Omega _1+\mu \nu ))+\mu (\gamma _1+\mu ) (\gamma _2+\mu ) (\mu +m_{21}) (\beta _{12} \rho _2\Omega _2+\mu \nu ) (\beta _{21} \rho _1\Omega _1+\mu \nu ))+\beta _{21} \gamma _2 \mu \nu ^2 m_{21} \rho _1\Omega _1 (\gamma _2+\mu ) (\mu +m_{12}),\\ h_{10}= & {} \mu I_{21}^*\Big ( \alpha I_{21}^* (m_{12} (\beta _{12} \rho _2\Omega _2 (\beta _{21} \rho _1\Omega _1 ((\gamma _1+\mu ) (\gamma _2+\mu )+m_{21} (\gamma _1+\gamma _2+\mu ))+\nu (\gamma _1+\mu ) (\gamma _2+\mu ) (\mu +m_{21}))+\nu (\gamma _1+\mu ) (\gamma _2+\mu ) (\mu +m_{21}) (\beta _{21} \rho _1\Omega _1+\mu \nu ))+(\gamma _1+\mu ) (\gamma _2+\mu ) (\mu +m_{21}) (\beta _{12} \rho _2\Omega _2+\mu \nu ) (\beta _{21} \rho _1\Omega _1+\mu \nu ))+\nu ^2 (\gamma _2+\mu ) (\mu +m_{12}) (\mu (\gamma _1+\mu ) (\beta _{12} \rho _2\Omega _2+\mu \nu )+m_{21} ((\gamma _1+\mu ) (\beta _{12} \rho _2\Omega _2+\mu \nu )+\beta _{21} \gamma _2 \rho _1\Omega _1)) \Big ). \end{aligned}$$

Furthermore, $N_1=h_{12}(I_1^*-r_{00})(I_1^*-r_{01}),$ where

$r_{00}=\frac{-h_{11}+\sqrt{h_{11}^2-4h_{12}h_{10}}}{2h_{12}}$ and $r_{01}=\frac{-h_{11}-\sqrt{h_{11}^2-4h_{12}h_{10}}}{2h_{12}}.$

Since

$$\begin{aligned} h_{12}<0 \text{ and } h_{10}>0, \end{aligned}$$

then $N_1>0$ if $0<I_1^*<r_{01}$, which is hypothesis ii). Therefore $I_2^*>0$ and $S_2^*>0.$ $\square$

Now, we will show that the polynomial equations of system (3) can have a positive solution. The quartic and constant coefficients of system (3) are

$$\begin{aligned} e_4=&\alpha ^2\nu ^2\rho ^2\beta _{21}^2(m_{12}+\mu )(m_{21}+\mu )^2 (\gamma _1+\mu )^4(\gamma _2+\mu )((m_{21}+\mu )\nu +\beta _2\rho _2),\\ f_4=&-\alpha ^2\Omega _1^2\beta _1^3\mu (m_{12}+\mu )(m_{21}+\mu ) (\mu \nu +\beta _{12}\rho _2\Omega _2)(m_{21}\beta _1\mu (\gamma _2+\mu )\nu \\&+\beta _1\mu ^2(\gamma _2+\mu )\nu +\beta _2\beta _{21}\gamma _2\rho _1\Omega _2(m_{12}+\mu )),\\ e_0=&-\beta _1^2 \mu (\mu +m_{12}) (a_0-a_1 S_1) (b_0+b_1 S_1)S_1^2,\\ f_0=&I_1^2\beta _{21}^2\rho ^2\nu (\gamma _1+\mu )(c_2I_1^2+c_1 I_1+c_0), \end{aligned}$$

where

$$\begin{aligned} a_1= & {} \alpha \beta _1\Omega _1(m_{21}+\mu )(\mu \nu +\beta _{12}\rho _2\Omega _2),\\ a_0= & {} \nu ^2\left( \mu \nu (m_{21}+\mu )(\gamma _1+\mu )+\beta _{12}\rho _2\Omega _2(m_{21}+\mu )(\gamma _1+\mu )+m_{21}\beta _{21}\gamma _2\rho _1\Omega _1\right) ,\\ b_1= & {} \alpha \Omega _1\left( \beta _1\mu \nu (m_{21}+\mu )^2(\gamma _2+\mu )+\beta _2\Omega _2(\beta _1\mu (m_{21}+\mu )(\gamma _2+\mu )+m_{12}m_{21}\beta _{21}\gamma _2\rho _1)\right) ,\\ b_0= & {} -m_{21}^2\nu ^2(\gamma _2+\mu )(\mu \nu (\gamma _1+\mu )+\beta _{21}\gamma _2\rho _1\Omega _1)+m_{21}(-\beta _2 \Omega _2(\mu \nu ^2 (\gamma _1+\mu ) (\gamma _2+\mu ) -\alpha \beta _{21}\gamma _2 \Lambda _2 \rho _1 \Omega _1)-\mu \nu ^2 (\gamma _2+\mu ) (\beta _{21} \gamma _2 \rho _1 \Omega _1+2 \mu \nu (\gamma _1+\mu ))) -\mu ^2\nu ^2(\gamma _1+\mu )(\gamma _2+\mu )(\mu \nu +\beta _2\Omega _2),\\ c_2= & {} -\alpha (m_{12}+\mu )(m_{21}+\mu )(\gamma _1+\mu )^2(\mu \nu +\beta _{12}\rho _2\Omega _2)((m_{21}+\mu )(\gamma _2+\mu )\nu +\beta _2\gamma _2\Omega _2),\\ c_1= & {} -\alpha (\gamma _1+\mu )\left( \mu (2\mu (m_{21}+\mu )(\gamma _2+\mu )(\mu (\gamma _1+\mu )+m_{21}(\gamma _1-\gamma _2+\mu ))\nu ^3 +\nu \Omega _2(\beta _2\gamma _2\mu (\nu (\mu (\gamma _1+\mu )+m_{21} (\gamma _1-\gamma _2+\mu ))-\alpha \Lambda _1 (\mu +m_{21})) +\beta _{12}(m_{21}+\nu )(\gamma _2+\mu )(2\mu (\gamma _1+\mu )+m_{21} (2 \gamma _1-\gamma _2+2\mu ))\nu \rho _2)+\beta _{12}\beta _2 \gamma _2 \rho _2 \Omega _2^2 (\mu +m_{21})(\nu (\gamma _1+\mu )-\alpha \Lambda _1)+m_{12}(\beta _{12}\beta _2 \gamma _2\rho _2 \Omega _2^2 (\mu +m_{21})(\nu (\gamma _1+\mu )-\alpha \Lambda _1)+ \nu \Omega _2 (\beta _2 \gamma _2\mu (\nu (\mu (\gamma _1+\mu )+m_{21}(\gamma _1-\gamma _2+\mu ))-\alpha \Lambda _1 (\mu +m_{21}))+\beta _{12} \nu \rho _2(\mu +m_{21}) (2\mu (\gamma _1+\mu )(\gamma _2+\mu )+m_{21}(\gamma _1 (\gamma _2+2 \mu )-(\gamma _2-2 \mu )(\gamma _2+\mu ))))+2 \mu \nu ^3 (\gamma _2+\mu ) (\mu +m_{21}) (\mu (\gamma _1+\mu )+m_{21} (\gamma _1-\gamma _2+\mu ))))\right) . \end{aligned}$$

And the expression $c_0$ is given below in the proof of Proposition 9.

Since $e_4>0$ and $f_4<0$, in order to have a positive solution, it is enough to find conditions to have $e_0<0$ and $f_0>0$.

Proposition 8

$e_0<0$ if any of the following conditions are satisfied:

• $b_0\ge 0$ and $S_1<\dfrac{a_0}{a_1},$

• $b_0< 0$ and $\Big (-\dfrac{b_0}{b_1}<S_1 \text{ and } S_1<\dfrac{a_0}{a_1}\Big ) \text{ or } \Big (-\dfrac{b_0}{b_1}>S_1 \text{ and } S_1>\dfrac{a_0}{a_1}\Big ).$

Proof

Remember that

$$\begin{aligned} e_0=-\beta _1^2 \mu (\mu +m_{12}) (a_0-a_1 S_1) (b_0+b_1 S_1)S_1^2. \end{aligned}$$

Since $a_0>0$ , $a_1>0$ and $b_1>0$ then,

$$\begin{aligned} a_0-a_1 S_1>0, \text{ if } S_1<\dfrac{a_0}{a_1}, \end{aligned}$$

and

$$\begin{aligned} b_0+b_1 S_1>0, \text{ if } b_0\ge 0 \text{ or } b_0<0 \text{ and } S_1>-\dfrac{b_0}{b_1}. \end{aligned}$$

On the other hand, $a_0-a_1 S_1<0, \text{ if } S_1>\dfrac{a_0}{a_1},$

and

$$\begin{aligned} b_0+b_1 S_1<0 \text{ if } b_0<0 \text{ and } S_1<-\dfrac{b_0}{b_1}. \end{aligned}$$

$\square$

Proposition 9

$f_0>0,$ if the following conditions are satisfied:

• $\gamma _1+\mu \ge \gamma _2$ and $\alpha >-\dfrac{c_{00}}{c_{01}},$

• $0<I_1<r_{02}.$

Proof

Since

$$\begin{aligned} f_0=I_1^2\beta _{21}^2\rho ^2\nu (\gamma _1+\mu )(c_2I_1^2+c_1I_1+c_0), \end{aligned}$$

we are going to show that the expression

$$\begin{aligned} c_2I_1^2+c_1I_1+c_0 \end{aligned}$$

(B1)

is positive. Since

$$\begin{aligned} c_0=c_{00}+c_{01}\alpha , \end{aligned}$$

where

$$\begin{aligned} c_{01}= & {} \beta _2\gamma _2\nu \Lambda _1\Omega _2(m_{12}+\mu )\Big (\mu \nu \left( \mu (\gamma _1+\mu )+m_{21} (\gamma _1-\gamma _2+\mu )\right) +\beta _{12}\rho _2\Omega _2(m_{21}+\nu )(\gamma _1+\nu )\Big ),\\ c_{00}= & {} -\mu \nu ^3\left( \mu (\gamma _1+\mu )+m_{21}(\gamma _1-\gamma _2+\mu )\right) \Big (\beta _{12}\rho _2\Omega _2\left( m_{12} ((\gamma _1+\mu ) (\gamma _2+\mu )+m_{21} (\gamma _1+\gamma _2+\mu )) +(\gamma _1+\mu ) (\gamma _2+\mu ) (\mu +m_{21} \right) +\nu (m_{12}+\mu )(\gamma _2+\mu )\left( \mu (\gamma _1+\mu )+m_{21} (\gamma _1-\gamma _2+\mu )\right) \Big ). \end{aligned}$$

If $\gamma _1+\mu \ge \gamma _2$ then

$$\begin{aligned} c_{01}>0 \text{ and } c_{00}<0. \end{aligned}$$

Thus

$$\begin{aligned} c_0>0 \text{ if } \alpha >-\dfrac{c_{00}}{c_{01}}. \end{aligned}$$

Since $c_2<0,$ the parabola corresponding to the expression (B1) opens downwards. Therefore

$$\begin{aligned} c_2I_1^2+c_1I_1+c_0=c_2( I_1-r_{02})(I_1-r_{03})>0 \text{ if } 0<I_1<r_{02}, \end{aligned}$$

where $r_{02}$ is the positive root of (B1) $\square$

Appendix C: Global Stability of the Disease-Free Equilibrium

We define the following function to demonstrate the global stability of the equilibrium point $P_0$:

$$\begin{aligned} f(x,&y)=(F-T)x-\mathcal {F}+\mathcal {T}\\ =&\begin{pmatrix} -(\gamma _1+\mu ) &{}\beta _1S_{01}^* &{}0 &{}0\\ \alpha U_{01}^* &{}-\nu &{}0 &{}0\\ 0 &{}0 &{}-(\gamma _2+\mu ) &{}\beta _2 S_{02}^*\\ 0 &{}0 &{}\alpha U_{02}^* &{}-\nu \\ \end{pmatrix} \begin{pmatrix} I_1\\ V_1\\ I_2\\ V_2\\ \end{pmatrix}-\begin{pmatrix} \beta _1S_1V_1\\ \alpha I_1 U_1\\ \beta _2S_2V_2\\ \alpha I_2U_2\ \end{pmatrix} + \begin{pmatrix} (\gamma _1+\mu )I_1 \\ \nu V_1\\ (\gamma _2+\mu )I_2 \\ \nu V_2\\ \end{pmatrix}, \\ =&\begin{pmatrix} \beta _1S_{01}^*V_1-(\gamma _1+\mu )I_1 \\ \alpha I_1 U_{01}^*-\nu V_1\\ \beta _2S_{02}^*V_2-(\gamma _2+\mu )I_2 \\ \alpha I_2 U_{02}^*-\nu V_2\\ \end{pmatrix}-\begin{pmatrix} \beta _1S_1V_1\\ \alpha I_1U_1\\ \beta _2S_2V_2\\ \alpha I_2 U_2\ \end{pmatrix}+ \begin{pmatrix} (\gamma _1+\mu )I_1 \\ \nu V_1\\ (\gamma _2+\mu )I_2 \\ \nu V_2\\ \end{pmatrix},\\ =&\begin{pmatrix} \beta _1V_1(S_{01}^*-S_1) \\ \alpha I_1(U_{01}^*-U_1)\\ \beta _2V_2(S_{02}^*-S_2) \\ \alpha I_2(U_{02}^*-U_2)\\ \end{pmatrix}. \end{aligned}$$

From the above, we note that $f(x,y)\ge 0$, for (x, y) in $\Gamma .$

We will built a Lyapunov function following Shuai and van den Driessche technique [26, 27]. For this, we consider the following matrix.

$$\begin{aligned} T^{-1}F=\begin{pmatrix} 0 &{} \frac{\beta _1 S_{01}^*}{\gamma _1+\mu }&{}0 &{}0\\ \dfrac{\alpha U_{01}^*}{\nu }&{}0 &{}0 &{}0\\ 0 &{}0 &{}0 &{}\frac{\beta _2 S_{02}^*}{\gamma _2+\mu }\\ 0 &{}0 &{}\frac{\alpha U_{02}^*}{\nu } &{}0\\ \end{pmatrix}. \end{aligned}$$

The characteristic polynomial of $T^{-1}F$ is,

$$\begin{aligned} \left( \lambda ^2-\frac{\alpha \beta _1 S_{01}^* U_{01}^*}{(\gamma _1+\mu )\nu }\right) \left( \lambda ^2-\frac{\alpha \beta _2 S_{02}^* U_{02}^*}{(\gamma _2+\mu )\nu } \right) =0. \end{aligned}$$

Therefore the spectral radius of $T^{-1}F$ is equal to

$$\begin{aligned} R_0=max(\sqrt{R_{01}},\sqrt{R_{02}}). \end{aligned}$$

where

$$\begin{aligned} R_{01}=\frac{\alpha \beta _1 S_{01}^* U_{01}^*}{(\gamma _1+\mu )\nu } \text{ and } R_{02}=\frac{\alpha \beta _2 S_{02}^* U_{02}^*}{(\gamma _2+\mu )\nu }. \end{aligned}$$

If $w=(w_1,w_2,w_3,w_4)$ is a left eigenvector associated with the eigenvalue $R_0$ of $T^{-1}F$ then it satisfies the following equations.

$$\begin{aligned}&w_1=\frac{\alpha U_{01}^*}{R_0 \nu }w_2, \end{aligned}$$

(C2)

$$\begin{aligned}&w_3=\dfrac{\alpha U_{02}^*}{R_0 \nu }w_4, \end{aligned}$$

(C3)

$$\begin{aligned}&\Big (R_0-\dfrac{R_{01}}{R_0}\Big )w_2=0, \end{aligned}$$

(C4)

$$\begin{aligned}&\Big (R_0-\dfrac{R_{02}}{R_0}\Big )w_4=0. \end{aligned}$$

(C5)

We have three cases $R_0=\sqrt{R_{01}}$ or $R_0=\displaystyle \sqrt{R_{02}}$ with $\displaystyle \sqrt{R_{01}} \ne \sqrt{R_{02}}$. And $R_0=\displaystyle \sqrt{R_{01}}=\sqrt{R_{02}}$

Case $R_0=\sqrt{R_{01}}>\sqrt{R_{02}}.$

From (C4), $\Big (R_0-\dfrac{R_{01}}{R_0}\Big )=\Big (\sqrt{R_{01}}-\sqrt{R_{01}}\Big )=0.$

From (C5), $\Big (R_0-\dfrac{R_{02}}{R_0}\Big )=\dfrac{1}{\sqrt{R_{01}}}\Big (R_{01}-R_{02}\Big )\ne 0$ if $R_{01} \ne R_{02}.$ Therefore $w_4=0.$

Taking $w_2=1$ and substituting in (C2) and (C3) we have

$$\begin{aligned} w^T=\Big (\dfrac{\alpha U_{01}^*}{R_0\nu },1,0,0 \Big ). \end{aligned}$$

Since $x^T=\left( I_1,V_1,I_2,V_2\right) ,$ we define the Lyapunov function as

$$\begin{aligned} Q_1(x)=w^T T^{-1} x=\dfrac{\alpha U_{01}^*I_1}{R_0 \nu (\gamma _1+\mu )}+\dfrac{V_1}{\nu }. \end{aligned}$$

It is clear that $Q_1(x)\ge 0$ and $Q_1(x)=0$ if and only if $x=0.$

Moreover,

$$\begin{aligned} \begin{aligned} \dot{Q_1}=&\dfrac{\alpha U_{01}^*\dot{I}_1}{R_0\nu (\gamma _1+\mu )}+\dfrac{\dot{V}_1}{\nu },\\ =&\dfrac{\alpha U_{01}^*}{R_0\nu (\gamma _1+\mu )}\Big (\beta _1 S_1V_1-I_1(\gamma _1+\mu )\Big )+\dfrac{1}{\nu }\Big (\alpha I_1U_1-\nu V_1\Big ),\\ =&\dfrac{\alpha U_{01}^*}{R_0\nu (\gamma _1+\mu )}\Big (\beta _1 S_{01}^*V_1-I_1(\gamma _1+\mu )-(S_{01}^*-S_1)\beta _1V_1\Big )\\&+\dfrac{1}{\nu }\Big (\alpha I_1U_{01}^*-\nu V_1-(U_{01}^*-U_1)\alpha I_1\Big ),\\ =&\dfrac{\alpha \beta _1S_{01}^* U_{01}^*}{\nu (\gamma _1+\mu )}\dfrac{V_1}{R_0}-\dfrac{\alpha U_{01}^*I_1}{R_0 \nu }+\dfrac{\alpha U_{01}^*I_1}{\nu }-V_1-A_1,\\ =&(R_0-1)V_1+(R_0-1)V_1\dfrac{\alpha U_{01}^*I_1}{R_0 \nu }-A_1,\\ =&(R_0-1)(V_1+\dfrac{\alpha U_{01}^* I_1}{R_0 \nu })-A_1. \end{aligned} \end{aligned}$$

where $A_1=\left( S_{01}^*-S_1\right) \frac{\alpha U_{01}^*\beta _1V_1}{R_0\nu (\gamma _1+\mu )}+\left( U_{01}^*-U_1\right) \dfrac{\alpha I_1}{\nu }\ge 0$, since $(x,y) \in \Gamma .$

Therefore $\dot{Q_1}<0$ if $R_0<1.$

Case $R_0=\sqrt{R_{02}}>\sqrt{R_{01}}.$

In the same way as above, we have that the Lyapunov function is

$$\begin{aligned} Q_2(x)= & {} w^T T^{-1} x=\dfrac{\alpha U_{02}^*I_2}{R_0 \nu (\gamma _2+\mu )}+\dfrac{V_2}{\nu } \; \text{ and } \\ \dot{Q_2}= & {} (R_0-1)(V_2+\dfrac{\alpha U_{02}^* I_2}{R_0 \nu })-A_2<0, \; \text{ if } R_0<1 , \end{aligned}$$

where $A_2=\left( S_{02}^*-S_2\right) \frac{\alpha U_{02}^*\beta _2V_2}{R_0\nu (\gamma _2+\mu )}+\left( U_{02}^*-U_2\right) \dfrac{\alpha I_2}{\nu }\ge 0$, since $(x,y) \in \Gamma .$

Case $R_0=\sqrt{R_{01}}=\sqrt{R_{02}}.$

The left eigenvector associated with the eigenvalue $R_0$ of $T^{-1}F$ is

$$\begin{aligned} w^T=\Big (\dfrac{\alpha U_{01}^*}{R_0\nu },1,\dfrac{\alpha U_{02}^*}{R_0\nu },1 \Big ). \end{aligned}$$

From above we have that

$$\begin{aligned} Q(x)=w^T T^{-1} x=\dfrac{\alpha U_{01}^*I_1}{R_0 \nu (\gamma _1+\mu )}+\dfrac{V_1}{\nu } +\dfrac{\alpha U_{02}^*I_2}{R_0 \nu (\gamma _2+\mu )}+\dfrac{V_2}{\nu }=Q_1(x)+Q_2(x), \end{aligned}$$

is a Lyapunov function. Moreover $\dot{Q}<0$ since $(x,y) \in \Gamma .$

Therefore $P_0$ is globally asymptotically stable if $R_0<1.$

Appendix D: Stability at $P_1$ or $P_2$

The characteristic polynomial of Jacobian matrix evaluated at the equilibrium point $P_{1}$ is

$$\begin{aligned}&\frac{1}{\nu }(L+\mu ) (L+\nu ) (L+\gamma _1+\mu ) (L+\gamma _2+\mu ) (L+\mu +m_{12}) (L+\mu +m_{21}) (L+\mu + \beta _{12} \rho _2 V_{12}^{*}) \Big (L ^2 \nu + L\nu (\gamma _1+\mu +\nu )\\&\quad +\nu ^2 (\gamma _1+\mu )- \alpha \Omega _1 (\beta _1 S_{11}^{*}+\beta _{21} \rho _{1} Z_{121}^{*}) \Big )\\&\quad \Big (L^4+q_1 L^3 +q_2 L^2 +q_3 L +q_4\Big )=0. \end{aligned}$$

Where

$$\begin{aligned} q_1= & {} \gamma _2+\alpha I_{22}^{*}+3 \mu +\nu +m_{12}+m_{21}+\beta _2 V_{12}^{*},\\ q_2= & {} 2 \gamma _2 \mu +\alpha I_{22}^{*} (\gamma _2+3 \mu +m_{12}+m_{21}\\&+ \, \beta _2 V_{12}^{*})+3 \mu ^2+2 \mu \nu +m_{12} (\gamma _2+2 \mu +\nu +\beta _2 V_{12}^{*})\\&+\, \gamma _2 m_{21}+2 \mu m_{21}+\nu m_{21}+\beta _2 \gamma _2 V_{12}^{*}+2 \beta _2 \mu V_{12}^{*}+\beta _2 \nu V_{12}^{*},\\ q_3= & {} \alpha I_{22}^{*} \Big (3 \mu ^2+\gamma _2 m_{12}+2 \mu (\gamma _2+m_{12}+m_{21}\\&+\, \beta _2 V_{12}^{*})+\beta _2 m_{12} V_{12}^{*}+\gamma _2 m_{21}+\beta _2 \gamma _2 V_{12}^{*}\Big )\\&+\, m_{12} (\gamma _2+\mu +\nu ) (\mu +\beta _2 V_{12}^{*})+\nu (\mu (\mu +m_{21})\\&+ \, \beta _2 V_{12}^{*} (\gamma _2+2 \mu ))+\mu (\gamma _2+\mu ) (\mu +m_{21}+\beta _2 V_{12}^{*}),\\ q_4= & {} (\gamma _2+\mu ) (\alpha I_{22}^{*} (m_{12} (\mu +\beta _2 V_{12}^{*})+\mu (\mu +m_{21}\\&+\beta _2 V_{12}^{*}))+\beta _2 \nu V_{12}^{*} (\mu +m_{12})). \end{aligned}$$

Note that $q_1, q_2, q_3, q_4 \in \mathbb {R}^{+}$ and

$$\begin{aligned} D_2= & {} q_1 q_2-q_3=\alpha ^2 I_{22}^{*2} (\gamma _2+3 \mu +m_{12}+m_{21}+\beta _2 V_{12}^{*})+\alpha I_{22}^{*} \left( \nu (\gamma _2+5 \mu +2 m_{12}+2 m_{21}+ 2 \beta _2 V_{12}^{*})\right. \\&\left. +\, (\gamma _2+3 \mu +m_{12}+m_{21}+\beta _2 V_{12}^{*})^2\right) +m_{12}^2(\gamma _2+2 \mu +\nu +\beta _2 V_{12}^{*})+m_{12}\left( m_{21} (2 (\gamma _2+2 \mu +\nu )\right. \\&\left. +\, \beta _2 V_{12}^{*})+(\gamma _2+2 \mu +\nu +\beta _2 V_{12}^{*}) (\gamma _2+4 \mu +\nu +\beta _2 V_{12}^{*})\right) +\nu \left( 8 \mu ^2+m_{21}^2+2 m_{21} (\gamma _2+3 \mu +\beta _2 V_{12}^{*})\right. \\&\left. +\, \mu (4 \gamma _2+5 \beta _2 V_{12}^{*})+\beta _2 V_{12}^{*} (\gamma _2+\beta _2 V_{12}^{*})\right) +(\gamma _2+2 \mu ) (2 \mu +m_{21}+\beta _2 V_{12}^{*}) (\gamma _2+2 \mu +m_{21}+\beta _2 V_{12}^{*})+\nu ^2 (2 \mu +m_{21}+\beta _2 V_{12}^{*})>0. \end{aligned}$$

Using Mathematica we obtain

$$\begin{aligned} D_3= & {} \left( V_{12}^{*2}(\gamma _2+\mu +\nu ) \beta _2^2+V_{12}^{*} \left( \gamma _2^2+(4 \mu +\nu ) \gamma _2+3 \mu ^2+\nu ^2+3\mu \nu \right) \beta _2\right. \\&\left. +\,\mu (\gamma _2+\mu +\nu ) (\gamma _2+2\mu +\nu )\right) m_{12}^3+\left( (V_{12}^{*} \beta _2+\gamma _2+5 \mu +\nu ) \left( V_{12}^{*2} (\gamma _2+\mu +\nu ) \beta _2^2\right. \right. \\&\left. \left. +\,V_{12}^{*} \left( \gamma _2^2+4 \mu \gamma _2+\nu \gamma _2+3 \mu ^2+\nu ^2+3 \mu \nu \right) \beta _2+\mu (\gamma _2+\mu +\nu ) (\gamma _2+2 \mu +\nu )\right) \right. \\&\left. +\,m_{21} \left( V_{12}^{*2} (\gamma _2+\mu +\nu ) \beta _2^2+2 V_{12}^{*} \left( \gamma _2^2+4 \mu \gamma _2+\nu \gamma _2+3 \mu ^2+\nu ^2+3 \mu \nu \right) \beta _2\right. \right. \\&\left. \left. +\,3 \mu (\gamma _2+\mu +\nu ) (\gamma _2+2 \mu +\nu )\right) \right) m_{12}^2\\&+\left( \left( 3 \mu (\gamma _2+\mu +\nu ) (\gamma _2+2 \mu +\nu )+V_{12}^{*} \beta _2 \left( \gamma _2^2+4 \mu \gamma _2+\nu \gamma _2+3 \mu ^2+\nu ^2+3 \mu \nu \right) \right) m_{21}^2\right. \\&\left. +\, \left( (V_{12}^{*} \beta _2+2 \mu ) \nu ^3+\left( 16 \mu ^2+(13 V_{12}^{*} \beta _2+6 \gamma _2) \mu +V_{12}^{*} \beta _2 (2 V_{12}^{*} \beta _2+3 \gamma _2)\right) \nu ^2\right. \right. \\&\left. \left. +\,(V_{12}^{*} \beta _2+2 \mu ) \left( 17 \mu ^2+(7 V_{12}^{*} \beta _2+16 \gamma _2) \mu +3 \gamma _2 (V_{12}^{*} \beta _2+\gamma _2)\right) \nu \right. \right. \\&\left. +\,(\gamma _2+\mu ) (2 V_{12}^{*} \beta _2+\gamma _2+5 \mu ) (2 \mu (\gamma _2+2 \mu )+V_{12}^{*} \beta _2 (\gamma _2+3 \mu ))\right) m_{21}\\&+\,(V_{12}^{*} \beta _2 (\gamma _2+3 \mu +\nu )+\mu (3 \gamma _2+8 \mu +3 \nu )) \left( V_{12}^{*2} (\gamma _2+\mu +\nu ) \beta _2^2\right. \\&\left. \left. +\,V_{12}^{*} \left( \gamma _2^2+4 \mu \gamma _2+\nu \gamma _2+3 \mu ^2+\nu ^2+3 \mu \nu \right) \beta _2+\mu (\gamma _2+\mu +\nu ) (\gamma _2+2 \mu +\nu )\right) \right) m_{12}\\&+\,I_{22}^{*3} \alpha ^3 (m_{12}+m_{21}+V_{12}^{*} \beta _2+2 \mu ) (m_{12} (V_{12}^{*} \beta _2+\gamma _2+2 \mu )+(\gamma _2+2 \mu ) (m_{21}\\&+\,V_{12}^{*} \beta _2+\gamma _2+2 \mu ))+\left( (m_{21}+V_{12}^{*} \beta _2+\mu ) \nu ^2\right. \\&\left. +\,\left( m_{21}^2+2 (V_{12}^{*} \beta _2+\gamma _2+2 \mu ) m_{21}+3 \mu ^2+V_{12}^{*} \beta _2 (V_{12}^{*} \beta _2+\gamma _2)+(3 V_{12}^{*} \beta _2+2 \gamma _2) \mu \right) \nu \right. \\&\left. +\,(m_{21}+V_{12}^{*} \beta _2+\mu ) (\gamma _2+\mu ) (m_{21}+V_{12}^{*} \beta _2+\gamma _2+2 \mu )\right) \left( 2 (\gamma _2+2 \mu +\nu ) \mu ^2+m_{21} (\gamma _2+2 \mu +\nu ) \mu \right. \\&\left. +\,V_{12}^{*} \beta _2 (\gamma _2+2 \mu ) (\mu +\nu )\right) +I_{22}^{*2} \alpha ^2 \left( (V_{12}^{*} \beta _2+\gamma _2+2 \mu ) m_{12}^3\right. \\&+\,\left( 2 V_{12}^{*2} \beta _2^2+V_{12}^{*} (4 \gamma _2+11 \mu +3 \nu ) \beta _2+2 \gamma _2^2+14 \mu ^2+11 \gamma _2 \mu +m_{21} (2 V_{12}^{*} \beta _2+3 \gamma _2+6 \mu )\right. \\&\left. +\,2 \gamma _2 \nu +5 \mu \nu \right) m_{12}^2+\left( V_{12}^{*3} \beta _2^3+V_{12}^{*2} (4 \gamma _2+11 \mu +3 \nu ) \beta _2^2\right. \\&\left. +\,2 V_{12}^{*} \left( 2 \gamma _2^2+2 (6 \mu +\nu ) \gamma _2+\mu (17 \mu +8 \nu )\right) \beta _2+\gamma _2^3+32 \mu ^3+34 \gamma _2 \mu ^2+11 \gamma _2^2 \mu \right. \\&\left. +\,m_{21}^2 (V_{12}^{*} \beta _2+3 \gamma _2+6 \mu )+\left( \gamma _2^2+10 \mu \gamma _2+18 \mu ^2\right) \nu +m_{21} \left( 2 V_{12}^{*2} \beta _2^2+V_{12}^{*} (7 \gamma _2+17 \mu +3 \nu ) \beta _2\right. \right. \\&\left. \left. +\,4 \gamma _2^2+28 \mu ^2+22 \gamma _2 \mu +4 \gamma _2 \nu +10 \mu \nu \right) \right) m_{12}\\&+\,m_{21}^3 (\gamma _2+2 \mu )+(V_{12}^{*} \beta _2+2 \mu ) (\gamma _2+2 \mu ) (V_{12}^{*} \beta _2+\gamma _2+2 \mu ) (V_{12}^{*} \beta _2+\gamma _2+3\mu )\\&+\,m_{21} (\gamma _2+2 \mu ) \left( 3 V_{12}^{*2} \beta _2^2+2 V_{12}^{*} (2 \gamma _2+7 \mu ) \beta _2+\gamma _2^2+16 \mu ^2+9 \gamma _2 \mu \right) \\&+\,\left( 3 V_{12}^{*2} (\gamma _2+2 \mu ) \beta _2^2+V_{12}^{*} (\gamma _2+4 \mu ) (2 \gamma _2+5 \mu ) \beta _2+2 \mu (\gamma _2+2 \mu ) (\gamma _2+4 \mu )\right) \nu +m_{21} \left( \gamma _2^2+10 \mu \gamma _2+18 \mu ^2+V_{12}^{*} \beta _2 (5 \gamma _2+11 \mu )\right) \nu \\&\left. +\,m_{21}^2 ((\gamma _2+2 \mu ) (3 V_{12}^{*} \beta _2+2 \gamma _2+7 \mu )+(2 \gamma _2+5 \mu ) \nu )\right) +I_{22}^{*} \alpha \left( \left( (V_{12}^{*} \beta _2+\gamma _2+2 \mu )^2+(2 V_{12}^{*} \beta _2+\gamma _2+3 \mu ) \nu \right) m_{12}^3+\left( (3 V_{12}^{*} \beta _2+\gamma _2+4 \mu ) \nu ^2+\left( m_{21} (4 V_{12}^{*} \beta _2+3 \gamma _2+9 \mu )+2 \left( 2 V_{12}^{*2} \beta _2^2\right. \right. \right. \right. \\&\left. \left. +\,V_{12}^{*} (3 \gamma _2+10 \mu ) \beta _2+\gamma _2^2+11 \mu ^2+7 \gamma _2 \mu \right) \right) \nu \\&\left. +\,(V_{12}^{*} \beta _2+\gamma _2+2 \mu ) \left( V_{12}^{*2} \beta _2^2+3 V_{12}^{*} \gamma _2 \beta _2+\gamma _2^2+11 \mu ^2+8 (V_{12}^{*} \beta _2+\gamma _2) \mu +m_{21} (V_{12}^{*} \beta _2+3 \gamma _2+6 \mu )\right) \right) m_{12}^2 \end{aligned}$$

$$\begin{aligned}&+\,\left( 2 V_{12}^{*3} (\gamma _2+2 \mu +\nu ) \beta _2^3+V_{12}^{*2} \left( 4 \gamma _2^2+22 \mu \gamma _2+6 \nu \gamma _2+27 \mu ^2+3 \nu ^2+20 \mu \nu \right) \beta _2^2\right. \\&+\,V_{12}^{*} \left( 2 (\gamma _2+7 \mu ) \nu ^2+(3 \gamma _2+7 \mu ) (\gamma _2+8 \mu ) \nu +2 \left( \gamma _2^3+11 \mu \gamma _2^2+33 \mu ^2 \gamma _2+29 \mu ^3\right) \right) \beta _2\\&+\,\mu \left( 4 \gamma _2^3+27 \mu \gamma _2^2+58 \mu ^2 \gamma _2+40 \mu ^3+(4 \gamma _2+13 \mu ) \nu ^2+8 (\gamma _2+2 \mu ) (\gamma _2+3 \mu ) \nu \right) \\&+\,m_{21}^2 \left( 2 V_{12}^{*} \beta _2 (\gamma _2+2 \mu +\nu )+3 \left( (\gamma _2+2 \mu )^2+(\gamma _2+3 \mu ) \nu \right) \right) \\&+\,m_{21} \left( 4 V_{12}^{*2} (\gamma _2+2 \mu +\nu ) \beta _2^2+V_{12}^{*} \left( 7 \gamma _2^2+34 \mu \gamma _2+39 \mu ^2+3 \nu ^2+10 (\gamma _2+3 \mu ) \nu \right) \beta _2\right. \\&+\,2 \left( \gamma _2^3+10 \mu \gamma _2^2+27 \mu ^2 \gamma _2+22 \mu ^3+(\gamma _2+4 \mu ) \nu ^2\right. \\&\left. \left. \left. +\,2 \left( \gamma _2^2+7 \mu \gamma _2+11 \mu ^2\right) \nu \right) \right) \right) m_{12}\\&+\,\left( 3 V_{12}^{*2} (\gamma _2+2 \mu ) \beta _2^2+V_{12}^{*} (\gamma _2+4 \mu )^2 \beta _2+2 \mu ^2 (2 \gamma _2+5 \mu )\right) \nu ^2\\&+\,(V_{12}^{*} \beta _2+2 \mu ) (\gamma _2+2 \mu ) (V_{12}^{*} \beta _2+\gamma _2+2 \mu ) (V_{12}^{*} \beta _2 (\gamma _2+2 \mu )+\mu (2 \gamma _2+3 \mu )) \end{aligned}$$

$$\begin{aligned}&+\,(V_{12}^{*} \beta _2+\gamma _2+2 \mu ) \left( 16 \mu ^3+8 (2 V_{12}^{*} \beta _2+\gamma _2) \mu ^2\right. \\&\left. +\,V_{12}^{*} \beta _2 (4 V_{12}^{*} \beta _2+9 \gamma _2) \mu +V_{12}^{*} \beta _2 \gamma _2 (2 V_{12}^{*} \beta _2+\gamma _2)\right) \nu +m_{21}^3 \left( (\gamma _2+2 \mu )^2+(\gamma _2+3 \mu ) \nu \right) \\&+\,m_{21}^2 \left( (\gamma _2+4 \mu ) \nu ^2+2 \left( \gamma _2^2+7 \mu \gamma _2+11 \mu ^2+V_{12}^{*} \beta _2 (2 \gamma _2+5 \mu )\right) \nu +(\gamma _2+2 \mu ) \left( \gamma _2^2+8 \mu \gamma _2+11 \mu ^2\right. \right. \\&\left. \left. +\,3 V_{12}^{*} \beta _2 (\gamma _2+2 \mu )\right) \right) +m_{21} \left( (2 V_{12}^{*} \beta _2 (2 \gamma _2+5 \mu )+\,\mu (4 \gamma _2+13 \mu )) \nu ^2\right. \\&+\,\left( V_{12}^{*2} (5 \gamma _2+11 \mu ) \beta _2^2+V_{12}^{*} \left( 5 \gamma _2^2+31 \mu \gamma _2+46 \mu ^2\right) \beta _2+8 \mu (\gamma _2+2 \mu ) (\gamma _2+3 \mu )\right) \nu \\&+\,(\gamma _2+2 \mu ) \left( 3 V_{12}^{*2} (\gamma _2+2 \mu ) \beta _2^2\right. \\&\left. \left. \left. +\,2 V_{12}^{*} \left( \gamma _2^2+8 \mu \gamma _2+11 \mu ^2\right) \beta _2+\mu \left( 4 \gamma _2^2+19 \mu \gamma _2+20 \mu ^2\right) \right) \right) \right) , \end{aligned}$$

which is always positive.

$D_4=q_4D_3>0.$

By the Routh-Hurwitz criterion [30], we obtain that all roots of $L^4+q_1 L^3 +q_2 L^2 +q_3 L +q_4$ have negative real part. On the other hand

$$\begin{aligned} \nu ^2 (\gamma _1+\mu )-\alpha \Omega _1 (\beta _1 S_{11}^{*}+\beta _{21} \rho _{1} Z_{121}^{*})>0, \end{aligned}$$

if

$$\begin{aligned}&\frac{\alpha \Omega _1 (\beta _1 S_{11}^{*}+\beta _{21} \rho _{1} Z_{121}^{*})}{\nu ^2 (\gamma _1+\mu )}\\&\quad =R_1\left( \frac{S_{11}^*}{S_{01}^*}+\frac{\rho _1\beta _{21}Z_{121}^*}{\beta _1S_{01}^*}\right)&<1. \end{aligned}$$

By the Routh-Hurwitz criterion, we obtain that all roots of quadratic polynomial have negative real part.

Therefore, if $R_1\left( \frac{S_{11}^*}{S_{01}^*}+\frac{\rho _1\beta _{21}Z_{121}^*}{\beta _1S_{01}^*}\right) <1$ then $P_1$ is locally asymptotically stable.

In the same way, we have that if $R_2\left( \frac{S_{22}^*}{S_{02}^*}+\frac{\rho _2\beta _{12}Z_{212}^*}{\beta _2 S_{02}^*} \right) <1$ then $P_2$ is locally asymptotically stable at $\Gamma .$

Appendix E: Expressions for $F_1$ and $F_2$

$$\begin{aligned} F_1(m_{21})= & {} \Big (m_{21} (m_{21} (m_{21} (3.04787\times 10^{204} m_{21}+6.0108\times 10^{204})+2.7477\times 10^{204})\\&-\,6.2832\times 10^{202})+3.6616\times 10^{200}\Big ) ^{\frac{1}{2}}\Big ( (8.5094\times 10^{-50} m_{21}+3.4102\times 10^{-52}) m_{21}\\&+\,2.5976\times 10^{-57}\Big ) +4.9705\times 10^{43}-1.4856\times 10^{53} m_{21}^4-1.4122\times 10^{53} m_{21}^3\\&+\,1.0647\times 10^{51} m_{21}^2+6.5213\times 10^{48} m_{21},\\ F_2(m_{21})= & {} m_{21} \Big (m_{21}(2.2879\times 10^{53} m_{21}+9.1691\times 10^{50})+6.9841\times 10^{45}\Big ). \end{aligned}$$