Introduction

In the case of BVPs for quasilinear systems of fractional differential equations (FDEs) we use an original technique of the numerical–analytic approximation, that was initially suggested for the periodic BVPs for ordinary differential equations (see [17]) and later on modified for the fractional differential systems (FDSs) (see discussions in [2,3,4, 9, 10]).

The main idea of the mentioned method is to construct a sequence of functions \(\{x_m\}_{m\in {\mathbb {N}}}\), that under additional assumptions converges to the limit function \(x_{\infty }\), depending on unknown parameters. The question to be answered is: how to define the sequence \(\{x_m\}_{m\in {\mathbb {N}}}\) that in case of the two-point BVPs already anticipates invertible matrixes. Even though there are new developments in the theory of FDEs (see discussions in [1, 5, 6, 8, 11, 12]), it is restrictive enough not to cover a wide class of problems that are of high interest. To cope with this we suggest an approach of parametrization that has essential differences in application to different types of boundary conditions.

In the current paper it is shown, how the aforementioned technique can be applied to the Cauchy–Nicoletti type boundary conditions and enables to substitute the degenerate matrixes in the given boundary restrictions by the non-degenerate ones via the introduction of some scalar parameters.

Note, that since the approximate solutions of the studied BVP are constructed analytically, one can also study behavior of the exact solution using the special mathematical software, e.g. Matlab, Maple etc.

Main Definitions

Let \(J=[a, b]\) \((-\infty<a<b<\infty )\) be a final interval of \({\mathbb {R}}\). Throughout this paper under \(\Gamma (z)\) we understand the Gamma function, defined by the integral

$$\begin{aligned} \Gamma (z)=\int _{0}^{\infty }e^{-t}t^{z-1}dt, \end{aligned}$$

which converges in the right half of the complex plane \(Re(z)>0\) [20].

Definition 1

[13] The left and right Riemann–Liouville fractional integrals of order \(\alpha \in {\mathbb {R}}^+\) are defined by

$$\begin{aligned} _{a}D_{t}^{-\alpha }f(t)=\frac{1}{\Gamma (\alpha )}\int _{a}^{t}(t-s)^{\alpha -1}f(s)ds,\ t>a,\ \alpha >0 \end{aligned}$$

and

$$\begin{aligned} _{t}D_{b}^{-\alpha }f(t)=\frac{1}{\Gamma (\alpha )}\int _{t}^{b}(s-t)^{\alpha -1}f(s)ds,\ t<b,\ \alpha >0 \end{aligned}$$

respectively, provided the right-hand sides are pointwise defined on [a, b].

Definition 2

[13] The left and right Riemann–Liouville fractional derivatives of order \(\alpha \in {\mathbb {R}}_+\) are defined by

$$\begin{aligned} _{a}D_{t}^{\alpha }f(t)= & {} \frac{d^n}{dt^n}{_{a}D_{t}^{-(n-\alpha )}}f(t)\\= & {} \frac{1}{\Gamma (n-\alpha )}\frac{d^n}{dt^n}\int _{a}^{t}(t-s)^{n-\alpha -1}f(s)ds, t>a \end{aligned}$$

and

$$\begin{aligned} _{t}D_{b}^{\alpha }f(t)= & {} (-1)^n\frac{d^n}{dt^n}{_{t}D_{b}^{-(n-\alpha )}}f(t)\\= & {} \frac{1}{\Gamma (n-\alpha )}(-1)^n\frac{d^n}{dt^n}\int _{t}^{b}(s-t)^{n-\alpha -1}f(s)ds, t<b \end{aligned}$$

respectively, where \(n=[\alpha ]+1\), \([\alpha ]\) means the integer part of \(\alpha \).

Definition 3

[20] The left and right Caputo fractional derivatives of order \(\alpha \in {\mathbb {R}}_+\) are defined by

$$\begin{aligned} ^C_{a}D_{t}^{\alpha }f(t)= {_{a}D_{t}^{\alpha }}\left[ f(t)-\mathop {\sum }\limits _{k=0}^{n-1} \frac{f^{(k)}(a)}{k!}(t-a)^k\right] \end{aligned}$$
(1)

and

$$\begin{aligned} ^C_{t}D_{b}^{\alpha }f(t)={_{t}D_{b}^{\alpha }\left[ f(t)-\mathop {\sum }\limits _{k=0}^{n-1} \frac{f^{(k)}(b)}{k!}(b-t)^k\right] } \end{aligned}$$

respectively, where \(n=[\alpha ]+1\), for \(\alpha \notin {\mathbb {N}}_0\); \(n=\alpha \) for \(\alpha \in {\mathbb {N}}_0\).

In particular, when \(0<\alpha <1\), then

$$\begin{aligned} ^C_{a}D_{t}^{\alpha }f(t)={_{a}D_{t}^{\alpha }}(f(t)-f(a)) \end{aligned}$$

and

$$\begin{aligned} ^C_{t}D_{b}^{\alpha }f(t)={_{t}D_{b}^{\alpha }}(f(t)-f(b)). \end{aligned}$$

Under assumption, that operations \(|\cdot |\), \(=\), \(\le \), \(\ge \), \(\max \), etc. between matrixes and vectors are understood componentwise, let us introduce the following notations.

Definition 4

For any non-negative vector \(\rho \in {\mathbb {R}}^{3}\) of the form

$$\begin{aligned} \rho :=\frac{(b-a)^pM}{2^{2p-1}\Gamma (p+1)} \end{aligned}$$
(2)

under the componentwise \(\rho -\)neighbourhood of a point \(z_0\in {\mathbb {R}}^{3}\) we understand

$$\begin{aligned} B(z,\rho ):=\left\{ z_0\in {\mathbb {R}}^{n}:\left| z_0-z\right| \le \rho \right\} , \end{aligned}$$
(3)

where \(M\in {\mathbb {R}}^3\) is a given constant vector.

Definition 5

For a given bounded connected set \(\ D_{a}\subset \mathbb {R }^{3}\) introduce its componentwise \(\rho -\)neighbourhood as follows

$$\begin{aligned} D:=B(D_{a},\rho ). \end{aligned}$$
(4)

Definition 6

For a set \(D\subset {\mathbb {R}}^{3}\), closed interval \(\left[ a,b\right] \subset {\mathbb {R}}\), Caratheodory function \({f:\left[ a,b\right] \times D\rightarrow {\mathbb {R}}^{3}}\), three-dimensional square matrix K with non-negative entires, we write

$$\begin{aligned} f\in Lip(K,D) \end{aligned}$$
(5)

if the inequality

$$\begin{aligned} \left| f(t,u)-f(t,v)\right| \le K\left| u-v\right| \end{aligned}$$
(6)

holds for all \(\left\{ u,v\right\} \subset D\) and a.e. \( t \in \left[ a,b\right] .\)

Problem Setting

We study a two-point boundary value problem for a system of FDEs of the form:

$$\begin{aligned} \begin{aligned} ^C_{a}D_{t}^{p}x=f(t,x(t)), \ t\in [a, b], x, f \in {\mathbb {R}}^3, \end{aligned} \end{aligned}$$
(7)

for some \(p \in (0, 1]\), and subjected to the Cauchy–Nicoletti type two-point boundary conditions

$$\begin{aligned} Ax(a)+Cx(b)=d, \end{aligned}$$
(8)

where \(^C_{a}D_{t}^{p}\) is the left Caputo fractional derivative with lower limit at a (see (1), Definition 3), \(f:G_f \rightarrow {\mathbb {R}}^{3}\) is a continuous vector-function, \({G_f:=\left[ a,b\right] \times D}\), \(D\subset {\mathbb {R}}^{3}\) is a closed and bounded domain, matrixes A, C and vector d have the form

$$\begin{aligned} A=\left( \begin{array}{ccc} 1&{}0&{}0\\ 0&{}1&{}0\\ 0&{}0&{}0 \end{array}\right) , C=\left( \begin{array}{ccc} 0&{}0&{}0\\ 0&{}0&{}0\\ 0&{}0&{}1 \end{array}\right) , d=\left( \begin{array}{c} x_{a1}\\ x_{a2}\\ x_{b3} \end{array}\right) . \end{aligned}$$

The problem is to find an explicit solution of the FDS (7), satisfying the two-point Cauchy–Nicoletti type boundary constraints (8), in the space of continuous vector-functions \({x:[a, b] \rightarrow D}\).

Remark 1

The practical interest to the problem (7), (8) is explained by its application. Let function \(x_1(t)\) interprets the gross domestic product (GDP), \(x_2(t)\)—inflation and \(x_3(t)\)—unemployment rate (UE) at time t. Then the system (7) describes the history of development of the modeled economy in time, which is represented by triples of the values of GDP, inflation, and UE (see also discussion in [18]). On the other hand, boundary conditions (8) give us values of the observable quantities at certain time \(t=t^{*}\). This also applies to the perturbed Cauchy problem, investigated on the later stage.

Auxiliary Lemmas

To prove the main result of the paper we need to generalize some auxiliary lemmas, initially formulated by Fečkan, Marynets in [2], in terms of the interval [a, b].

Lemma 1

Let f(t) be a continuous function for \(t \in [a, b]\). Then for all \(t \in [a, b]\) the following estimate is true:

$$\begin{aligned} \begin{aligned}&\biggl |\frac{1}{\Gamma (p)}\int _{a}^{t}(t-\tau )^{p-1}f(\tau )d\tau -\left( \frac{t-a}{b-a}\right) ^p\frac{1}{\Gamma (p)}\int _{a}^{b}(b-\tau )^{p-1}f(\tau )d\tau \biggr |\\&\quad \le \alpha _1(t)\max \limits _{t \in [a, b]}|f(t)|, \end{aligned} \end{aligned}$$
(9)

where

$$\begin{aligned} \alpha _1(t)=\frac{2(b-t)^p}{\Gamma (p+1)}\left( 1-\frac{b-t}{b-a}\right) ^p. \end{aligned}$$
(10)

Proof

It is obvious that

$$\begin{aligned} \begin{aligned}&\biggl |\frac{1}{\Gamma (p)}\int _{a}^{t}(t-\tau )^{p-1}f(\tau )d\tau -\left( \frac{t-a}{b-a}\right) ^p\frac{1}{\Gamma (p)}\int _{a}^{b}(b-\tau )^{p-1}f(\tau )d\tau \biggr |\\&\quad \le \frac{1}{\Gamma (p)}\biggl |\int _{a}^{t}(t-\tau )^{p-1}f(\tau )d\tau -\left( \frac{t-a}{b-a}\right) ^p\int _{a}^{t}(b-\tau )^{p-1}f(\tau )d\tau \\&\qquad -\left( \frac{t-a}{b-a}\right) ^p\int _{t}^{b}(b-\tau )^{p-1}f(\tau )d\tau \biggr |\\&\quad \le \frac{1}{\Gamma (p)}\biggl [\biggl |\int _{a}^{t}\left[ (t-\tau )^{p-1} -\left( \frac{t-a}{b-a}\right) ^p(b-\tau )^{p-1}\right] f(\tau )d\tau \biggr |\\&\qquad +\biggl |\left( \frac{t-a}{b-a}\right) ^p\int _{t}^{b}(b-\tau )^{p-1}f(\tau )d\tau \biggr |\biggr ]\\&\quad \le \frac{1}{\Gamma (p)}\biggl [\int _{a}^{t}\left[ (t-\tau )^{p-1} -\left( \frac{t-a}{b-a}\right) ^p(b-\tau )^{p-1}\right] |f(\tau )|d\tau \\&\qquad +\left( \frac{t-a}{b-a}\right) ^p\int _{t}^{b}(b-\tau )^{p-1}|f(\tau )|d\tau \biggr ]\\&\quad \le \frac{1}{\Gamma (p)}\biggl [\int _{a}^{t}\left[ (t-\tau )^{p-1} -\left( \frac{t-a}{b-a}\right) ^p(b-\tau )^{p-1}\right] d\tau \\&\qquad +\left( \frac{t-a}{b-a}\right) ^p\int _{t}^{b}(b-\tau )^{p-1}d\tau \biggr ]\mathop {\max }\limits _{t \in [a, b]}|f(t)|\\&\quad =\frac{2(b-t)^p}{\Gamma (p+1)}\left( 1-\frac{b-t}{b-a}\right) ^p\mathop {\max }\limits _{t \in [a, b]}|f(t)|=\alpha _1(t)\mathop {\max }\limits _{t \in [a, b]}|f(t)|. \end{aligned} \end{aligned}$$

since

$$\begin{aligned} \begin{aligned}&(t-\tau )^{{p-1}}-\left( \frac{t-a}{b-a}\right) ^{p}(b-\tau )^{{p-1}}\\&\quad =(t-\tau )^{{p-1}} \left( 1-\left( \frac{t-a}{b-a}\right) ^{p}\left( \frac{b-\tau }{t-\tau }\right) ^{p-1}\right) \\&\quad \ge (t-\tau )^{{p-1}}\left( 1-\left( \frac{t-a}{b-a}\right) ^{p}\left( \frac{b-a}{t-a}\right) ^{p-1}\right) \\&\quad =(t-\tau )^{{p-1}}\left( 1-\frac{t-a}{b-a}\right) =(t-\tau )^{{p-1}}\frac{b-t}{b-a}\ge 0, \end{aligned} \end{aligned}$$

for any \(\tau \in [0,t)\) and

$$\begin{aligned} \begin{aligned}&\frac{1}{\Gamma (p)}\int _{a}^{t}\left[ (t-\tau )^{p-1} -\left( \frac{t-a}{b-a}\right) ^p(b-\tau )^{p-1}\right] d\tau \\&\quad +\left( \frac{t-a}{b-a}\right) ^p\frac{1}{\Gamma (p)}\int _{t}^{b}(b-\tau )^{p-1}d\tau =\frac{2(b-t)^p}{\Gamma (p+1)}\left( 1-\frac{b-t}{b-a}\right) ^p=\alpha _1(t). \end{aligned} \end{aligned}$$

This completes the proof. \(\square \)

Lemma 2

Let \(\{\alpha _m(t)\}_{m\in {\mathbb {N}}}\) be a sequence of continuous functions at the interval [a, b] given by

$$\begin{aligned} \begin{aligned} \alpha _{m}(t):=\frac{1}{\Gamma (p)}\biggl [\int _{a}^{t}\left[ (t-\tau )^{p-1} -\left( \frac{t-a}{b-a}\right) ^p(b-\tau )^{p-1}\right] \alpha _{m-1}(\tau )d\tau \\ +\left( \frac{t-a}{b-a}\right) ^p\int _{t}^{b}(b-\tau )^{p-1}\alpha _{m-1}(\tau )d\tau \biggr ],\ m \in {\mathbb {N}}, \end{aligned} \end{aligned}$$
(11)

where \(\alpha _0(t)=1\) and \(\alpha _1(t)\)—defined by formula (10). Then the following estimate holds:

$$\begin{aligned} \alpha _{m+1}(t)\le \frac{(b-a)^{mp}}{2^{m(2p-1)}\Gamma ^{m}(p+1)}\alpha _1(t)\le \frac{(b-a)^{(m+1)p}}{2^{(m+1)(2p-1)} \Gamma ^{m+1}(p+1)}, \end{aligned}$$
(12)

for \(m\in {\mathbb {N}}_0\).

Proof

We will use the method of mathematical induction. First we prove (12) for \(m=0\) as follows:

$$\begin{aligned} \begin{aligned} \alpha _1(t)&=\frac{2(b-t)^p}{\Gamma (p+1)}\left( 1-\frac{b-t}{b-a}\right) ^p= \frac{2(b-a)^p}{\Gamma (p+1)} \left( \frac{b-t}{b-a}\left( 1-\frac{b-t}{b-a}\right) \right) ^p\\&\le \frac{(b-a)^p}{2^{2p-1}\Gamma (p+1)} \end{aligned} \end{aligned}$$

since the inequality \(\eta \nu \le \frac{(\eta +\nu )^2}{4}\) for any \(\eta \ge 0\) and \(\nu \ge 0\) holds. It means that function \(\alpha _1(t)\) satisfies an inequality (12) for \(m=0\). Suppose that the relation (12) holds for some \(m\in {\mathbb {N}}_0\), i.e. the estimate

$$\begin{aligned} \alpha _{m}(t)\le \frac{(b-a)^{(m-1)p}}{2^{(m-1)(2p-1)}\Gamma ^{m-1}(p+1)}\alpha _1(t)\le \frac{(b-a)^{mp}}{2^{m(2p-1)} \Gamma ^{m}(p+1)} \end{aligned}$$

holds.

Let us prove it for \((m+1)\). In virtue of (12), from the recurrent formula (11) for \((m+1)\) we obtain:

$$\begin{aligned} \begin{aligned} \alpha _{m+1}(t)&=\frac{1}{\Gamma (p)}\biggl [\int _{a}^{t}\left[ (t-\tau )^{p-1} -\left( \frac{t-a}{b-a}\right) ^p(b-\tau )^{p-1}\right] \alpha _{m}(\tau )d\tau \\&\quad +\left( \frac{t-a}{b-a}\right) ^p\int _{t}^{b}(b-\tau )^{p-1}\alpha _{m}(\tau )d\tau \biggr ]\\&\le \frac{1}{\Gamma (p)}\biggl [\int _{a}^{t}\left[ (t-\tau )^{p-1} -\left( \frac{t-a}{b-a}\right) ^p(b-\tau )^{p-1}\right] (\tau )d\tau \\&\quad +\left( \frac{t-a}{b-a}\right) ^p\int _{t}^{b}(b-\tau )^{p-1}(\tau )d\tau \biggr ]\frac{(b-a)^{mp}}{2^{m(2p-1)} \Gamma ^{m}(p+1)}\\&=\frac{(b-a)^{mp}}{2^{m(2p-1)} \Gamma ^{m}(p+1)}\alpha _1(t)\le \frac{(b-a)^{(m+1)p}}{2^{(m+1)(2p-1)} \Gamma ^{m+1}(p+1)}, \end{aligned} \end{aligned}$$

that proves lemma.\(\square \)

Approximation of Solutions Via the Numerical–Analytic Technique

Since matrix C in the boundary restrictions (8) is degenerate, the approach of the numerical–analytic method in its classical form [14,15,16,17], is impossible to apply.

Hence, a proper parametrization

$$\begin{aligned} x_1(b)=\lambda _1, x_2(b)=\lambda _2 \end{aligned}$$
(13)

transforms conditions (8) with degenerate matrix C to the parametrized ones

$$\begin{aligned} Ax(a)+C_1x(b)=d(\lambda ), \end{aligned}$$
(14)

where \(C_1\equiv I_3\), \(I_3\)—is the unit three-dimensional matrix, \(d(\lambda ):=\left( \begin{array}{c} x_{a1}+\lambda _1\\ x_{a2}+\lambda _2\\ x_{b3} \end{array}\right) \) and \(\lambda :=(\lambda _1, \lambda _2) \in \Lambda \)—are the artificially introduced vector-parameter, such that the triplex \((\lambda _1, \lambda _2, x_{b3}) \in D\).

Let us connect with the two-point FBVP (7) and (8) the following sequence of functions:

$$\begin{aligned} \begin{aligned} x_{m}(t, \xi _{a3}, \lambda )&:=\xi _0+\frac{1}{\Gamma (p)}\int _a^t(t-s)^{p-1}f(s, x_{m-1}(s, \xi _{a3}, \lambda ))ds\\&\quad -\left( \frac{t-a}{b-a}\right) ^p\frac{1}{\Gamma (p)}\int _a^b(b-s)^{p-1}f(s, x_{m-1}(s, \xi _{a3}, \lambda ))ds\\&\quad + \left( \frac{t-a}{b-a}\right) ^pC_1^{-1}[d(\lambda )-(A+C_1)\xi _0], m\in {\mathbb {N}}, \end{aligned} \end{aligned}$$
(15)

where \(t\in [a, b]\), \(\xi _{a3} \in \Xi \) is such that \(\xi _0=col(x_{01}, x_{02}, \xi _{a3}) \in D_{a}\) and

$$\begin{aligned} x_0(t, \xi _{a3}, \lambda )=\xi _{0}+\left( \frac{t-a}{b-a}\right) ^pC_1^{-1}[d(\lambda )-(A+C_1)\xi _0] \end{aligned}$$

is considered as a zero-approximation.

Remark 2

Note that the functions \(x_m\) in (15) are constructed in such a way, that they satisfy the two-point parametrized boundary restrictions (14) a priory, for all \(m \in {\mathbb {N}}\).

We can prove the following convergence theorem.

Theorem 1

Assume that

(i) there exists a non-negative vector \(\rho \), satisfying the inequality (3);

(ii) \(f:G_f\rightarrow {\mathbb {R}}^{3}\) be a function satisfying the Caratheodory and the Lipschitz condition \(f\in Lip(K,D)\) in the domain D of the form (4) with matrix K;

(iii) for the spectral radius of the matrix

$$\begin{aligned} Q=\frac{(b-a)^pK}{2^{2p-1}\Gamma (p+1)} \end{aligned}$$
(16)

estimate

$$\begin{aligned} r(Q) <1 \end{aligned}$$
(17)

holds.

Then, for all fixed \(\xi _{a3} \in \Xi \) and \(\lambda \in \Lambda \):

1. The functions of the sequence (15) are absolutely continuous functions on the interval \(t\in \left[ a,b\right] ,\) have values in the domain D andsatisfy the two-point boundary conditions

$$\begin{aligned} Ax_m(a, \xi _{a3}, \lambda )+C_1x_m(b, \xi _{a3}, \lambda )=d(\lambda ). \end{aligned}$$

2. The sequence of functions (15) converges uniformly for \(t\in \left[ a,b\right] \) as \(m\rightarrow \infty \) to the limit function

$$\begin{aligned} x_{\infty }\left( t, \xi _{a3}, \lambda \right) =\underset{m\rightarrow \infty }{\lim } x_{m}(t, \xi _{a3}, \lambda ). \end{aligned}$$
(18)

3. The limit function satisfies the initial condition

$$\begin{aligned} x_{\infty }\left( a, \xi _{a3}, \lambda \right) =\xi _0 \end{aligned}$$
(19)

and the two-point boundary conditions

$$\begin{aligned} Ax_{\infty }(a, \xi _{a3}, \lambda )+C_1x_{\infty }(b, \xi _{a3}, \lambda )=d(\lambda ). \end{aligned}$$

4. The function \(~x_{\infty }\left( \cdot , \xi _{a3}, \lambda \right) \) is a unique absolutely continuous solution of the integral equation

$$\begin{aligned} \begin{aligned} x(t)&:=\xi _0+\frac{1}{\Gamma (p)}\int _a^t(t-s)^{p-1}f(s, x(s))ds\\&\quad -\left( \frac{t-a}{b-a}\right) ^p\frac{1}{\Gamma (p)}\int _a^b(b-s)^{p-1}f(s, x(s))ds\\&\quad + \left( \frac{t-a}{b-a}\right) ^pC_1^{-1}[d(\lambda )-(A+C_1)\xi _0]. \end{aligned} \end{aligned}$$
(20)

In other words, \(x_{\infty }\left( \cdot , \xi _{a3}, \lambda \right) \) satisfies the Cauchy problem for the modified system of FDEs:

$$\begin{aligned} ^C_{a}D_{t}^{p}x=f(t,x(t))+\frac{p}{(b-a)^p}\Delta (\xi _{a3}, \lambda ),~ \end{aligned}$$
(21)
$$\begin{aligned} x\left( a\right) =\xi _0, \end{aligned}$$
(22)

where \(\Delta : \Xi \times \Lambda \rightarrow {\mathbb {R}}^{3}\) is a mapping given by formula

$$\begin{aligned} \Delta (\xi _{a3}, \lambda ):=-\int _{a}^{b}(b-s)^{p-1}f(s, x(s))ds+\Gamma (p)C_1^{-1}[d(\lambda )-(A+C_1)\xi _0]. \end{aligned}$$
(23)

5. The following error estimate holds:

$$\begin{aligned} \left| x_{\infty }\left( t, \xi _{a3}, \lambda \right) -x_{m}\left( t, \xi _{a3}, \lambda \right) \right| \le \frac{(b-a)^{p}}{2^{2p-1} \Gamma (p+1)}Q^{m}(I_3-Q)^{-1}M. \end{aligned}$$
(24)

Proof

As already mentioned in the Sect. 4, the sequence (15) is constructed in accordance to the boundary conditions (14). This means that the statement 1 of the theorem holds.

Now we show, that independently from the number of iterations, all functions \(x_m\) of the sequence (15) will remain in the domain D of their definition. For \(m=1\) we get

$$\begin{aligned} \begin{aligned}&|x_{1}(t, \xi _{a3}, \lambda )-x_{0}(t, \xi _{a3}, \lambda )|\\&\quad =\biggl |\frac{1}{\Gamma (p)}\int _{a}^{t}(t-s)^{p-1}f(s,x_{0}(s, \xi _{a3}, \lambda ))ds\\&\qquad -\left( \frac{t-a}{b-a}\right) ^p\frac{1}{\Gamma (p)}\int _{a}^{b}(b-s)^{p-1}f(s, x_{0}(s, \xi _{a3}, \lambda ))ds\biggr |\\&\quad \le \alpha _1(t)M\le \frac{(b-a)^pM}{2^{2p-1}\Gamma (p+1)}:=\rho , \end{aligned} \end{aligned}$$
(25)

where \(M:=\mathop {\max }\limits _{t\in [a, b]}|f(t,\cdot )|\).

For \(m=2\) we obtain the estimate

$$\begin{aligned} \begin{aligned}&|x_{2}(t, \xi _{a3}, \lambda )-x_{0}(t, \xi _{a3}, \lambda )|\\&\quad =\biggl |\frac{1}{\Gamma (p)}\int _{a}^{t}(t-s)^{p-1}f(s,x_{1}(s, \xi _{a3}, \lambda ))ds\\&\qquad -\left( \frac{t-a}{b-a}\right) ^p\frac{1}{\Gamma (p)}\int _{a}^{b}(b-s)^{p-1}f(s, x_{1}(s, \xi _{a3}, \lambda ))ds\biggr |\\&\quad \le \alpha _1(t)M\le \frac{(b-a)^pM}{2^{2p-1}\Gamma (p+1)}=\rho . \end{aligned} \end{aligned}$$

Suppose, that for \(m-1\) the inequality holds

$$\begin{aligned} |x_{m-1}(t, \xi _{a3}, \lambda )-x_{0}(t, \xi _{a3}, \lambda )|\le \alpha _1(t)M\le \frac{(b-a)^pM}{2^{2p-1}\Gamma (p+1)}=\rho , \end{aligned}$$

and let us prove it for m:

$$\begin{aligned} \begin{aligned} |x_{m}(t, \xi _{a3}, \lambda )-x_{0}(t, \xi _{a3}, \lambda )|&=\biggl |\frac{1}{\Gamma (p)}\int _{a}^{t}(t-s)^{p-1}f(s,x_{m-1}(s, x_{0}(t, \xi _{a3}, \lambda )))ds\\&\quad -\left( \frac{t-a}{b-a}\right) ^p\frac{1}{\Gamma (p)}\int _{a}^{b}(b-s)^{p-1}f(s, x_{m-1}(s, x_{0}(t, \xi _{a3}, \lambda )))ds\biggr |\\&\le \alpha _1(t)M\le \frac{(b-a)^pM}{2^{2p-1}\Gamma (p+1)}=\rho . \end{aligned} \end{aligned}$$

Let us now estimate the differences of the form \(|x_{m+1}(\cdot , \xi _{a3}, \lambda )-x_{m}(\cdot , \xi _{a3}, \lambda )|\).

For \(m=1\) we already obtained an inequality

$$\begin{aligned} |x_{1}(t, \xi _{a3}, \lambda )-x_{0}(t, \xi _{a3}, \lambda )|\le \alpha _1(t)M\le \frac{(b-a)^pM}{2^{2p-1}\Gamma (p+1)}. \end{aligned}$$

Then for \(m=2\) it is easy to derive

$$\begin{aligned} \begin{aligned} |x_{2}(t,\xi _{a3}, \lambda )-x_{1}(t, \xi _{a3}, \lambda )|&= \frac{1}{\Gamma (p)}\biggl |\int _{a}^{t}(t-s)^{p-1}f(s,x_{1}(s, \xi _{a3}, \lambda ))ds\\&\quad -\left( \frac{t-a}{b-a}\right) ^p\int _{a}^{b}(b-s)^{p-1}f(s, x_{1}(s, \xi _{a3}, \lambda ))ds\\&\quad -\int _{a}^{t}(t-s)^{p-1}f(s, x_{0}(s, \xi _{a3}, \lambda ))ds+\left( \frac{t-a}{b-a}\right) ^p\int _{a}^{b}(b-s)^{p-1}f(s, x_{0}(s, \xi _{a3}, \lambda ))ds\biggr |\\&\le \frac{KM}{\Gamma (p)}\biggl [\int _{a}^{t}\left[ (t-s)^{p-1} -\left( \frac{t-a}{b-a}\right) ^p(b-s)^{p-1}\right] \alpha _{1}(s)ds\\&\quad +\left( \frac{t-a}{b-a}\right) ^p\int _{t}^{b}(b-s)^{p-1}\alpha _{1}(s)ds\biggr ]=KM\alpha _2(t)\\&\le \frac{(b-a)^pKM}{2^{2p-1}\Gamma (p+1)}\alpha _1(t)\le \frac{(b-a)^{2p}KM}{2^{2(2p-1)}\Gamma ^2(p+1)} \end{aligned} \end{aligned}$$

Under assumption that for m the estimate

$$\begin{aligned} |x_{m}(t,\xi _{a3}, \lambda )-x_{m-1}(t,\xi _{a3}, \lambda )|\le \frac{(b-a)^{(m-1)p}K^{m-1}M}{2^{(m-1)(2p-1)}\Gamma ^{m-1}(p+1)}\alpha _1(t) \end{aligned}$$

holds we prove it for \(m+1\). So we obtain

$$\begin{aligned} \begin{aligned} |x_{m+1}(t, \xi _{a3}, \lambda )-x_{m}(t, \xi _{a3}, \lambda )|&= \frac{1}{\Gamma (p)}\biggl |\int _{a}^{t}(t-s)^{p-1}f(s,x_{m}(s, \xi _{a3}, \lambda ))ds\\&\quad -\left( \frac{t-a}{b-a}\right) ^p\int _{a}^{b}(b-s)^{p-1}f(s, x_{m}(s, \xi _{a3}, \lambda ))ds\\&\quad -\int _{a}^{t}(t-s)^{p-1}f(s, x_{m-1}(s, \xi _{a3}, \lambda ))ds\\&\quad +\left( \frac{t-a}{b-a}\right) ^p\int _{a}^{b}(b-s)^{p-1}f(s, x_{m-1}(s, \xi _{a3}, \lambda ))ds\biggr |\\&\le \frac{KM}{\Gamma (p)}\biggl [\int _{a}^{t}\left[ (t-s)^{p-1} -\left( \frac{t-a}{b-a}\right) ^p(b-s)^{p-1}\right] \alpha _{m}(s)ds\\&\quad +\left( \frac{t-a}{b-a}\right) ^p\int _{t}^{b}(b-s)^{p-1}\alpha _{m}(s)ds\biggr ]=K^mM\alpha _{m+1}(t)\\&\le \frac{(b-a)^{mp}K^mM}{2^{m(2p-1)} \Gamma ^{m}(p+1)}\alpha _1(t)\le \frac{(b-a)^{(m+1)p}K^mM}{2^{(m+1)(2p-1)} \Gamma ^{m+1}(p+1)}. \end{aligned} \end{aligned}$$

Summarizing, in view of (12), we get the following estimates

$$\begin{aligned} \begin{aligned}&|x_{m+j}(t, \xi _{a3}, \lambda )-x_{m}(t, \xi _{a3}, \lambda )|\\&\quad \le \sum \limits _{k=1}^{j} |x_{m+k}(t, \xi _{a3}, \lambda )-x_{m+k-1}(t, \xi _{a3}, \lambda )|\\&\quad \le \sum \limits _{k=1}^{j} K^{m+k-1}M\alpha _{m+k}(t)\le \sum \limits _{k=1}^{j}\frac{K^{m+k-1}(b-a)^{(m+k-1)p}}{2^{(m+k-1)(2p-1)}\Gamma ^{m+k-1}(p+1)}M\alpha _1(t)\\&\quad =\sum \limits _{k=0}^{j-1}Q^{m+k}M\alpha _1(t)= Q^{m}\sum \limits _{k=0}^{j-1}Q^kM\alpha _1(t). \end{aligned} \end{aligned}$$
(26)

As the maximum eigenvalue of matrix Q of the form (16) is less than 1, we get the following relations:

$$\begin{aligned} \mathop {\sum }\limits _{k=0}^{j-1}Q^{k}\le (I_3-Q)^{-1}, \quad \lim \limits _{m \rightarrow \infty } Q^{m}=O_3, \end{aligned}$$

where \(O_3\) is the zero three-dimension matrix. Letting \(j \rightarrow \infty \) in (26), we get the estimate (24). According to the Cauchy criteria, the sequence of functions \(\{x_m\}\), defined by (15), uniformly converges in the domain \([a, b] \times D_{a}\) to the limit function \(x_{\infty }(\cdot , \xi _{a3}, \lambda )\).

Since all functions of the sequence (15) satisfy the two-point parametrized boundary conditions (14), the limit function (18) satisfies them as well. Passing in (15) to the limit as \(m \rightarrow \infty \), we get that function \(x_{\infty }(\cdot ,\xi _{a3}, \lambda )\) satisfies the integral equation (20).

In order to show that (20) has a unique continuous solution, suppose that \(x_1(t)\) and \(x_2(t)\) be two solutions of (20). Then like above, we get

$$\begin{aligned} \begin{aligned} |x_{1}(t)-x_{2}(t)|&\le \frac{K}{\Gamma (p)}\biggl [\int _{a}^{t}\left[ (t-s)^{p-1} -\left( \frac{t-a}{b-a}\right) ^p(b-s)^{p-1}\right] ds\\&\quad +\left( \frac{t-a}{b-a}\right) ^p\int _{t}^{b}(b-s)^{p-1}ds\biggr ]\max _{t\in [a,b]}\left| x_{1}(t)- x_{2}(t)\right| \\&= K\alpha _1(t)\max _{t\in [a,b]}\left| x_{1}(t)- x_{2}(t)\right| \le \frac{K(b-a)^{p}}{2^{2p-1}\Gamma (p+1)}\max _{t\in [a,b]}\left| x_{1}(t)- x_{2}(t)\right| \\&=Q\max _{t\in [a,b]}\left| x_{1}(t)- x_{2}(t)\right| , \end{aligned} \end{aligned}$$

for all \(t\in [a, b]\). Hence

$$\begin{aligned} \max _{t\in [a,b]}\left| x_{1}(t)- x_{2}(t)\right| \le Q\max _{t\in [a,b]}\left| x_{1}(t)- x_{2}(t)\right| , \end{aligned}$$

which by (17) gives \(\mathop {\max }\limits _{t\in [a,b]}\left| x_{1}(t)- x_{2}(t)\right| =0\), so \(x_1(t)=x_2(t)\) for all \(t\in [a,b]\). Furthermore, the initial-value problem (21), (22) is equivalent to the integral equation [19],

$$\begin{aligned} \begin{aligned} x(t)&=\xi _0+\frac{1}{\Gamma (p)}\int _{a}^{t}(t-s)^{p-1}f(s, x(s))ds+\frac{\Delta (t-a)^p}{\Gamma (p+1)}\\&=\xi _0+\frac{1}{\Gamma (p)}\int _a^t(t-s)^{p-1}f(s, x(s))ds\\&\quad -\left( \frac{t-a}{b-a}\right) ^p\frac{1}{\Gamma (p)}\int _a^b(b-s)^{p-1}f(s, x(s))ds\\&\quad + \left( \frac{t-a}{b-a}\right) ^pC_1^{-1}[d(\lambda )-(A+C_1)\xi _0], \end{aligned} \end{aligned}$$
(27)

where the perturbation \(\Delta (\xi _{a3}, \lambda )\) is given by (23). By comparing (20) with (27), and recalling that \(x_\infty (t,\xi _{a3}, \lambda )\) is the unique continuous solution of (20), we see that \(x(t)=x_\infty (t,\xi _{a3}, \lambda )\) in (27), i.e., \(x_\infty (t,\xi _{a3}, \lambda )\) is the unique solution of (21), (22). This completes the proof. \(\square \)

Relation of the Limit Function to the Solution of the FBVP

Let us consider the Cauchy problem for a perturbed differential equation

$$\begin{aligned} \begin{aligned} ^C_{a}D_t^px =f(t,x(t))+\frac{p}{(b-a)^p}\zeta , \end{aligned} \end{aligned}$$
(28)

with the initial data (22), where \(t \in [a, b]\) and \(\zeta \in {\mathbb {R}}^{3}\) is a control parameter.

The following theorem holds.

Theorem 2

Let \(\xi _{a3} \in \Xi \), \(\lambda \in \Lambda \) and \(\zeta _0 \in {\mathbb {R}}^{3}\) be some given vectors. Suppose that all conditions of Theorem 1hold for the system of FDEs (7).

Then the solution \(x=x(\cdot ,\xi _{a3}, \lambda , \zeta )\) of the initial-value problem (28), (22) satisfy also boundary conditions (14) if and only if

$$\begin{aligned} \zeta :=\Delta (\xi _{a3}, \lambda ), \end{aligned}$$
(29)

where \(\Delta \) is given by (23). In that case

$$\begin{aligned} x(t,\xi _{a3}, \lambda ,\zeta )=x_{\infty }\left( t,\xi _{a3}, \lambda \right) . \end{aligned}$$
(30)

Proof

First we note that the existence and uniqueness of \(x(t,\xi _{a3}, \lambda ,\zeta )\) on [a, b] and its smooth dependence on \(\xi _{a3}, \lambda \) and \(\zeta \) follow from the classical theory in [7, 20].

Sufficiency Suppose that vector parameter \(\zeta \) in the right hand-side of the perturbed FDS (28) is given by (29). According to Theorem 1, the limit function (18) of the sequence (15) is the unique solution of the BVP problem (28), (14). Moreover, function \(x_{\infty }(t,\xi _{a3}, \lambda )\) satisfies the initial conditions (22), i.e., it is the unique solution of the Cauchy problem (28), (22) for \(\zeta \) defined by the relation (29). It means also that the equality (30) takes place.

Necessity Let us show that the parameter value (29) is unique. Let there exists \({\overline{\zeta }}\) and the solution \({\overline{x}}(t, \xi _{a3}, \lambda , {\overline{\zeta }})\) of the initial-value problem

$$\begin{aligned} ^C_{a}D_t^px(t) =f(t,x(t))+\frac{p}{(b-a)^p}{\overline{\zeta }},\, t\in [a,b],\quad x(a)=\xi _0 \end{aligned}$$

that satisfies also the boundary restrictions (14). It means by [7, Corollary 3.24], [20, Lemma 3.3] that function \({\overline{x}}(t, \xi _{a3}, \lambda , {\overline{\zeta }})\) is a continuous solution of the integral equation:

$$\begin{aligned} \begin{aligned} {\overline{x}}(t, \xi _{a3}, \lambda , {\overline{\zeta }})&= \xi +\frac{1}{\Gamma (p)}\int _{a}^{t}(t-s)^{p-1}f(s, {\overline{x}}(s, \xi _{a3}, \lambda , {\overline{\zeta }}))ds\\&\quad +\frac{{\overline{\zeta }}(t-a)^p}{\Gamma (p)(b-a)^p}. \end{aligned} \end{aligned}$$
(31)

By assumption, function \({\overline{x}}(t, \xi _{a3}, \lambda , {\overline{\zeta }})\) satisfies two-point parametrized boundary constraints (14) and the initial condition (22), that is,

$$\begin{aligned} \begin{aligned} A{\overline{x}}(a, \xi _{a3}, \lambda , {\overline{\zeta }})+C_1{\overline{x}}(b, \xi _{a3}, \lambda , {\overline{\zeta }})&=d(\lambda ), \\ {\overline{x}}(a, \xi _{a3}, \lambda , {\overline{\zeta }})&=\xi _0. \end{aligned} \end{aligned}$$
(32)

Then \({\overline{x}}(b, \xi _{a3}, \lambda , {\overline{\zeta }})=C_1^{-1}[d(\lambda )-A\xi _{0}]\) and substituting this into the relation (31) for \(t=b\) we get

$$\begin{aligned} {\overline{\zeta }}=-\int _{a}^{b}(b-s)^{p-1}f(s, {\overline{x}}(s, \xi _{a3}, \lambda ), {\overline{\zeta }})ds+\Gamma (p)C_1^{-1}[d(\lambda )-(A+C_1)\xi _0]. \end{aligned}$$
(33)

Putting (33) into (31), we come to the relation:

$$\begin{aligned} \begin{aligned} {\overline{x}}(t, \xi _{a3}, \lambda , {\overline{\zeta }})&= \xi _0+\frac{1}{\Gamma (p)}\int _{a}^{t}(t-s)^{p-1}f(s, {\overline{x}}(s, \xi _{a3}, \lambda , {\overline{\zeta }}))ds\\&\quad - \left( \frac{t-a}{b-a}\right) ^p\frac{1}{\Gamma (p)}\int _{a}^{b}(b-s)^{p-1}f(s, {\overline{x}}(s, \xi _{a3}, \lambda ), {\overline{\zeta }})ds\\&\quad +\left( \frac{t-a}{b-a}\right) ^pC_1^{-1}[d(\lambda )-(A+C_1)\xi _0]. \end{aligned} \end{aligned}$$
(34)

As \(\xi _0 \in D_{a}\) and \(\lambda \in \Lambda \), according to the integral equation (34) and the definition of the set D, it can be proved that all values of function \({\overline{x}}(t,\xi _{a3}, \lambda , {\overline{\zeta }})\) are contained into the domain D. By comparing (20) with (34), we know from the statement 4 of Theorem 1 that \({\overline{x}}(t, \xi _{a3}, \lambda , {\overline{\zeta }})=x_\infty (t, \xi _{a3}, \lambda )\) and then \({\overline{\zeta }}\) equals to \(\zeta \) given by (29). This finishes the proof. \(\square \)

Theorem 3

Let conditions of Theorem 1hold. Then \(x_{\infty } (\cdot , \xi _{a3}^*, \lambda ^*)\) is the solution of (7) and (8) if and only if the point \((\xi _{a3}^*, \lambda ^*)\) is the solution of the determining system:

$$\begin{aligned} \Delta (\xi _{a3}, \lambda )=0. \end{aligned}$$
(35)

Proof

The result follows directly from Theorem 2 by observing that the perturbed FDS (21) coincides with (7) if and only if the point \((\xi _{a3}^*, \lambda ^*)\) satisfies the system of determining Eq. (35). \(\square \)

The next statement claims that the system of determining Eqs. (35), in fact, determines all possible solutions of the original FBVP (7), (8).

Theorem 4

Assume that conditions of Theorem 1are satisfied. If there exist the values \(\xi _{a3} \in \Xi \) and\(\lambda \in \Lambda \) that satisfy the system of determining Eq. (35), then the FBVP (7), (8) has a solution \( x^{0}(\cdot )\) such that

$$\begin{aligned} x_3^{0}(a)=\xi _3^0,\ x_1^{0}(b)=\lambda _1^0,\ x_2^{0}(b)=\lambda _2^0 \end{aligned}$$

and

$$\begin{aligned} A x^{0}(a)+C x^{0}(b)=d, \end{aligned}$$
(36)

Moreover, this solution is given by the limit function of the sequence (15):

$$\begin{aligned} x^{0}(t)=x_{\infty }\left( t,\xi _3^0, \lambda ^0\right) =\underset{m\rightarrow \infty }{\lim }x_{m}(t, \xi _3^0, \lambda ^0),~t\in \left[ a,b\right] . \end{aligned}$$
(37)

Conversely, if the FBVP (7), (8) has a solution \(x^{0}(\cdot ),\) then \(x^{0}(\cdot )\) necessarily has form (37) and the system of determining Eq. (35) is satisfied with

$$\begin{aligned} \xi _3^0=x_3^{0}(a),\ \lambda _1^0=x_1^{0}(b),\ \lambda _2^0=x_2^{0}(b). \end{aligned}$$
(38)

Proof

If there exist the values \(\xi _3^0, \lambda _1^0, \lambda _2^0\) that satisfy the system of determining Eq. (35), then according to Theorem 1 the function (37) is a solution of the given FBVP (7), (8).

On the other hand , if \(x^{0}(\cdot )\) is the solution of the original problem (7), (8), then this function is a solution of the Cauchy problem (28), (22) with

$$\begin{aligned} \zeta =0\text { and }\xi =x^{0}(a). \end{aligned}$$
(39)

As \(x^{0}(\cdot )\) satisfies the linear two-point boundary restrictions (8), by virtue of equality (30) of Theorem 2 the equality ( 37) holds.

Moreover,

$$\begin{aligned} \begin{aligned} \zeta :=-\int _{a}^{b}(b-s)^{p-1}f(s, x_{\infty }(s, \xi _{a3}, \lambda ))ds\\+\Gamma (p)C_1^{-1}[d(\lambda )-(A+C_1)\xi _0]=0, \end{aligned} \end{aligned}$$
(40)

where \(\xi _{a3}\), \(\lambda \) are defined by (38 ).

From (40) we have that the determining system (35) is satisfied, if \(\xi _{a3}\), \(\lambda \) are given by (38).

We have thus specified in (38) the values of \(\xi _{a3}\), \(\lambda \) that satisfy the system of determining Eq. (35), which proves the theorem. \(\square \)

Remark 3

For the practical application of the aforementioned method it is reasonable to use an approximate determining equation

$$\begin{aligned} \Delta _m (\xi _{a3}, \lambda )=0, \end{aligned}$$
(41)

instead of the exact one (35) where \(\Delta _m: \Xi \times \Lambda \rightarrow {\mathbb {R}}^3\) is the m-th determining function defined by formulae

$$\begin{aligned} \Delta _m(\xi _{a3}, \lambda ):=-\int _{a}^{b}(b-s)^{p-1}f(s, x_m(s, \xi _{a3}, \xi _{a3}, \lambda ))ds+\Gamma (p)C_1^{-1}[d-(A+C_1)\xi ] \end{aligned}$$

and \(x_m\left( \cdot ,\xi _{a3}, \lambda \right) \) is given by (15).

Example

Let us study a fractional boundary value problem for a FDS

$$\begin{aligned} \left\{ \begin{array}{l} ^C_{0}D_{t}^{\frac{1}{2}}x_1(t)=\frac{4}{3}\sqrt{\frac{t}{\pi }}x_2(t) (:=f_1(t, x_1, x_2, x_3)),\\ ^C_{0}D_{t}^{\frac{1}{2}}x_2(t)=2\sqrt{\frac{t}{\pi }}x_3(t) (:=f_2(t, x_1, x_2, x_3)),\\ ^C_{0}D_{t}^{\frac{1}{2}}x_3(t)= \frac{x_1(t)-x_3(t)^2}{3\sqrt{\pi }}-\frac{t^2}{24\sqrt{\pi }} (:=f_3(t, x_1, x_2, x_3)), \end{array} \right. \end{aligned}$$
(42)

for \(t\in [0, 1]\), subjected to the Cauchy–Nicoletti boundary constraints

$$\begin{aligned} Ax(0)+Cx(1)=d, \end{aligned}$$
(43)

where \(x(\cdot )=col(x_1(\cdot ), x_2(\cdot ), x_3(\cdot ))\) and

$$\begin{aligned} A=\left( \begin{array}{ccc} 1&{}0&{}0\\ 0&{}1&{}0\\ 0&{}0&{}0 \end{array}\right) , C=\left( \begin{array}{ccc} 0&{}0&{}0\\ 0&{}0&{}0\\ 0&{}0&{}1 \end{array}\right) , d=\left( \begin{array}{c} -\frac{1}{16}\\ \ \ 0\\ \ \ \frac{1}{4} \end{array}\right) . \end{aligned}$$

Let the solution of the BVP (42), (43) be defined in the domain \(D\subset {\mathbb {R}}^3\), defined as

$$\begin{aligned} D: \left\{ (x_1, x_2, x_3): |x_1|\le \frac{1}{2}, |x_2|\le \frac{1}{2}, |x_3|\le \frac{1}{3}\right\} . \end{aligned}$$

Note, that in the domain \(G_f=[0, 1]\times D\) the vector-function

$$\begin{aligned} f(t, x_1, x_2, x_3)=col(f_1(t, x_1, x_2, x_3), \ f_2(t, x_1, x_2, x_3), \ f_3(t, x_1, x_2, x_3)) \end{aligned}$$

is bounded by a constant vector

$$\begin{aligned} M=col\left( \frac{2}{3\sqrt{\pi }}, \frac{2}{3\sqrt{\pi }}, \frac{1}{6\sqrt{\pi }}\right) \end{aligned}$$

and satisfies the Lipschitz condition with a matrix

$$\begin{aligned} K=\left( \begin{array}{ccc} 0&{}\frac{4}{3\sqrt{\pi }}&{}0\\ 0&{}0&{}\frac{2}{\sqrt{\pi }}\\ \frac{1}{3\sqrt{\pi }}&{}0&{}\frac{2}{9\sqrt{\pi }} \end{array}\right) . \end{aligned}$$

Moreover, the spectral radius r(Q) of the matrix Q, defined by formula (16) satisfies an inequality

$$\begin{aligned} r(Q)<0.67. \end{aligned}$$

In addition, there exists a non-negative vector

$$\begin{aligned} \rho =col\left( \frac{4}{3\sqrt{\pi }}, \frac{4}{3\sqrt{\pi }}, \frac{1}{3\sqrt{\pi }}\right) , \end{aligned}$$

of the form (2) and for which condition (3) holds.

Let us now introduce a parametrization:

$$\begin{aligned} x_1(1)=\lambda _1, \ x_2(1)=\lambda _2,\ x_3(0)=\xi _{03}. \end{aligned}$$
(44)

Using (44), we pass from the original boundary conditions (43) with homogeneous matrix C to the parametrized ones of the form:

$$\begin{aligned} Ax(0)+C_1x(1)=d(\lambda ), \end{aligned}$$
(45)

where \(C_1\equiv I_3\), \(d(\lambda )=\left( \begin{array}{c} \lambda _1-\frac{1}{16}\\ \ \ \lambda _2\\ \ \ \frac{1}{4} \end{array}\right) \) and \(\lambda =(\lambda _1, \lambda _2)\) is such that \({\left( \lambda _1, \lambda _2, \frac{1}{4}\right) \in D}.\)

Since all conditions of Theorem 1 are fulfilled, we can construct an iterative scheme (15) that is a successive approximation to the exact solution of the original BVP (42), (43).

Hence, for the parametrized problem (42), (45) the approximate solution has the form

$$\begin{aligned} \begin{aligned} x_{1,m}(t, \xi _{03}, \lambda )&:=-\frac{1}{16}+\frac{1}{\Gamma \left( \frac{1}{2}\right) }\int _0^t(t-s)^{-\frac{1}{2}}f_1(s, x_{m-1}(s, \xi _{a3}, \lambda ))ds\\&\quad -\frac{\sqrt{t}}{\Gamma \left( \frac{1}{2}\right) }\int _0^1(1-s)^{-\frac{1}{2}}f_1(s, x_{m-1}(s, \xi _{a3}, \lambda ))ds+\sqrt{t}\lambda _1, \end{aligned} \end{aligned}$$
(46)
$$\begin{aligned} \begin{aligned} x_{2,m}(t, \xi _{03}, \lambda )&:=\frac{1}{\Gamma \left( \frac{1}{2}\right) }\int _0^t(t-s)^{-\frac{1}{2}}f_2(s, x_{m-1}(s, \xi _{a3}, \lambda ))ds\\&\quad -\frac{\sqrt{t}}{\Gamma \left( \frac{1}{2}\right) }\int _0^1(1-s)^{-\frac{1}{2}}f_2(s, x_{m-1}(s, \xi _{a3}, \lambda ))ds+\sqrt{t}\left( \lambda _2-\frac{4\xi _{03}}{\pi }\right) , \end{aligned} \end{aligned}$$
(47)
$$\begin{aligned} \begin{aligned} x_{3,m}(t, \xi _{03}, \lambda )&:=\frac{1}{\Gamma \left( \frac{1}{2}\right) }\int _0^t(t-s)^{-\frac{1}{2}}f_3(s, x_{m-1}(s, \xi _{a3}, \lambda ))ds\\&\quad -\frac{\sqrt{t}}{\Gamma \left( \frac{1}{2}\right) }\int _0^1(1-s)^{-\frac{1}{2}}f_3(s, x_{m-1}(s, \xi _{a3}, \lambda ))ds\\&\quad +\sqrt{t}\left( \frac{1}{4}+\frac{1}{24\pi }-\left( \frac{4}{9\pi }+1\right) \xi _{03}\right) ,\ m=1, 2, 3, \ldots , \end{aligned} \end{aligned}$$
(48)

where \(t\in [0, 1]\), \(\xi _{03} \in \Xi \), such that \(\xi _0=col(-\frac{1}{16}, 0, \xi _{03}) \in D_{0}\) and \(\lambda \) are considered as parameters, and

$$\begin{aligned} x_{m-1}(\cdot , \xi _{a3}, \lambda )=(x_{1,m-1}(\cdot , \xi _{a3}, \lambda ), x_{2, m-1}(\cdot , \xi _{a3}, \lambda ), x_{3, m-1}(\cdot , \xi _{a3}, \lambda )). \end{aligned}$$

At the same time a zero approximation is given by expressions:

$$\begin{aligned} \begin{aligned} x_{1,0}(t, \xi _{03}, \lambda )&=-\frac{1}{16}+\sqrt{t}\lambda _1,\\ x_{2,0}(t, \xi _{03}, \lambda )&=\sqrt{t}\left( \lambda _2-\frac{4\xi _{03}}{\pi }\right) ,\\ x_{3,0}(t, \xi _{03}, \lambda )&=\xi _{03}+\sqrt{t}\left( \frac{1}{4}+\frac{1}{24\pi }-\left( \frac{4}{9\pi }+1\right) \xi _{03}\right) . \end{aligned} \end{aligned}$$

Using the mathematical software Maple, we calculated three approximations to the exact solution of the fractional BVP (42), (43).

On the first iteration step we obtained:

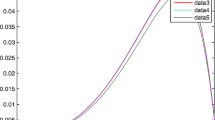
$$\begin{aligned} \begin{aligned} X_{1,1}(t)&=0.131956t^{\frac{3}{2}}-0.0625-0.015906\sqrt{t},\\ X_{2,1}(t)&=-0.021059t^{\frac{3}{2}}+0.001864-2\sqrt{t} +0.24906t,\\ X_{3,1}(t)&=-0.0000932t^{\frac{3}{2}}-0.0138398t^{\frac{5}{2}} -0.032191\sqrt{t}\\&\quad +0.0211481t+0.25277. \end{aligned} \end{aligned}$$
(49)

Moreover, the graphs of the components of the error function, obtained after the substitution of (49) into the differential system (42), are given at Fig. 1.

Fig. 1
figure 1

The first, second and third components of the error function in the first approximation

Full size image

The second approximation to the exact solution of the original BVP (42), (43) is given by:

$$\begin{aligned} \begin{aligned} X_{1,2}(t)&=0.000176t^{\frac{3}{2}}-0.0096127t^{\frac{5}{2}}+ 0.000069\sqrt{t}-0.0625+0.122429t^2,\\ X_{2,2}(t)&=-0.02747t^{\frac{3}{2}}-0.0000656t^{\frac{5}{2}}-0.00785168t^{\frac{7}{2}}-0.001576\sqrt{t}\\&\quad +0.0155104t^2+0.249751t,\\ \\ X_{3,2}(t)&=-0.00163856t^{\frac{3}{2}}-0.0138883t^{\frac{5}{2}}-0.000086088t^{\frac{7}{2}}\\&\quad -0.0000145431t^{\frac{11}{2}}-0.0274086\sqrt{t}+0.000714048t^3\\&\quad +0.0162403t^2 +0.0001485t+0.0000517757t^4+0.253476. \end{aligned} \end{aligned}$$

The graphs of the components of the error function in the second approximation are given at Fig. 2.

Fig. 2
figure 2

The first, second and third components of the error function in the second approximation

Full size image

Calculations show, that the third approximation to the exact solution of the problem (42), (43) is:

$$\begin{aligned} \begin{aligned} X_{1,3}(t)&=-0.000869t^{\frac{3}{2}}-0.012186t^{\frac{5}{2}}-0.00002528t^{\frac{7}{2}}\\&\quad -0.00263084t^{\frac{9}{2}}-0.000116\sqrt{t}+0.00630618t^3+0.122447t^2-0.0625,\\ X_{2,3}(t)&=-0.0228866t^{\frac{3}{2}}+0.0099121t^3+0.00037998t^4\\&\quad -0.0000433263t^{\frac{9}{2}}+0.0000273411\sqrt{t}+0.249788t\\&\quad +0.000097t^2+0.0000247048t^5-0.0000060999t^{\frac{13}{2}}\\&\quad -0.00108818t^{\frac{5}{2}}-0.00787925t^{\frac{7}{2}},\\ X_{3,3}(t)&=-0.0001161t^{\frac{3}{2}}-0.00017223t^3+0.000012389t^4\\&\quad -0.0000285152t^{\frac{9}{2}}-0.0000164325t^{\frac{11}{2}}-0.026747\sqrt{t}\\&\quad +0.0022767t+0.0001277t^2+0.0000363159t^5-0.0012022t^{\frac{5}{2}}\\&\quad -0.000106874t^{\frac{7}{2}}+0.00000219497t^6+0.253512. \end{aligned} \end{aligned}$$

The components of the error function in the third iteration are presented at Fig. 3.

Fig. 3
figure 3

Components of the error function in the third approximation

Full size image

It is easy to see, that by increasing the number of iterations the approximate solutions get closer to the exact solution of the original BVP (42), (43).

This confirms the applicability of the suggested numerical–analytic technique in study of the nonlinear fractional boundary value problems and it can be used for more complex systems.