A Note on Some Qualitative Properties of a Tuberculosis Differential Equation Model with a Time Delay

Abstract

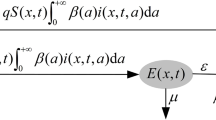
Tuberculosis is a global disease with much significant impact. Well over two million deaths are recorded each year due to Mycobacterium tuberculosis. The work by Colijn et al. (J Theor Biol 247, 765–774, 2007) examined two mathematical models (delay differential equation and network models) that explored the role of the contact structure of the population and found that in declining epidemics, localized outbreaks may occur as a result of contact heterogeneities even in the absence of host or strain variability. In this work, we carry out several qualitative studies (including the use of Sturm sequences for obtaining conditions on bifurcations) on the differential equation model with a time delay in Ref. Colijn et al., J Theor Biol 247, 765–774 (2007), and explicitly obtain threshold conditions for disease eradication as well as existence of bifurcations depending on a critical delay value which characterize the duration of fast latency. Further analysis showed the existence of a transcritical bifurcation when the reproduction number was less than one with the disease-free equilibrium co-existing with just one endemic state that was shown to be stable; the period of fast latency and the reinfection progression rate were shown to be very significant in the dynamics of the disease viz a viz the individuals who progressed to active TB within 5 years of their infection.

Appendices

Appendix A

Sturm sequences are obtained by the division algorithm thus: Let $f$ be a polynomial assumed not having repeated roots. Let $f=f_0$, $f'=f_1$. The sequences then becomes $f_0=q_0f_1 - f_2$, $f_1=q_1f_2 - f_3$,..., $f_{s-2}=q_{s-2}f_{s-1} - k$, where k is a constant. To determine the number of real roots of the polynomial in a given interval, plug in each end point of the interval, and obtain a sequence of signs. The number of real roots in the interval is the difference between the number of sign changes in the sequence at each end point. A complete proof of the method of Sturm sequences can be seen in [20].

Appendix B

The coefficient of the polynomial for the endemic state for I, given in (5), and reproduced below

$$\begin{aligned} Y_1{I^*}^3 + Y_2{I^*}^2 + Y_3I^* + Y_4 = 0 \end{aligned}$$

is given below:

$$\begin{aligned} Y_1&= \beta (z(r\beta +x_3)-k_2(r\beta +r_{TR}x_1+x_3)-k_1(z\beta -\beta k_2-x_1)(\mu -\mu _{TB})\nonumber \\&+\,x_1(-z\mu -x_5+z(r_{TR}+\mu _{TB}))),\nonumber \\ Y_2&= \beta (rz\beta \mu -z\beta \mu x_2+z\beta r_{TR}x_2+z\mu x_3+p_2(r\beta +x_3)+rz\beta x_4\nonumber \\&-\,k_2(r_{TR}(\mu x_1+\beta x_2)+\mu x_3+r\beta (\mu +x_4))-\beta x_2x_5+x_1(z\beta \mu +(z\mu +r_{rel})r_{TR}\nonumber \\&-\,\mu x_5\!-\!x_4(x_5\!+\!z(\mu \!-\!\mu _{TB})))\!+\!z\beta x_2\mu _{TB}+k_1(\beta (z\beta \mu +(x_2-zx_4)(\mu -\mu _{TB}))\nonumber \\&+\,\beta p_2(\mu _{TB}-\mu )-\beta k_2(\beta \mu +x_4(\mu _{TB}-\mu ))-x_1(\beta \mu +x_4(\mu _{TB}-\mu )))),\nonumber \\ Y_3&= r_{rel}r_{TR}(\mu x_1+\beta x_2)+\mu x_4(-r\beta k_2+\beta k_1(z\beta - \beta k_2 - x_1)+z\beta (r+x_1)\nonumber \\&-\,x_1x_5)+\beta x_2(z\beta \mu +\mu (z-k_2)r_{TR}-\mu x_5 -x_4(x_5+z(\mu -\mu _{TB}))\nonumber \\&-\,k_1(\beta \mu \!+\! x_4(\!-\!\mu \!+\!\mu _{TB})))\!+\! p_2(\mu x_3+r\beta (\mu \!+\!x_4)+\beta k_1(\beta \mu +x_4(\mu _{TB}-\mu ))),\nonumber \\ Y_4&= \mu (r_{rel}r_{TR}x_2+x_4((r+\beta k_1)p_2+x_2(z\beta - \beta k_1-x_5))) \end{aligned}$$

(23)

where $z=\mathrm{e}^{-\mu \tau }\hbox { and }x_5=r+\mu _{TB}+r_{TR}$.