Time series forecasting: problem of heavy-tailed distributed noise

Abstract

Time series forecasting has been the area of intensive research for years. Statistical, machine learning or mixed approaches have been proposed to handle this one of the most challenging tasks. However, little research has been devoted to tackle the frequently appearing assumption of normality of given data. In our research, we aim to extend the time series forecasting models for heavy-tailed distribution of noise. In this paper, we focused on normal and Student’s t distributed time series. The SARIMAX model (with maximum likelihood approach) is compared with the regression tree-based method—random forest. The research covers not only forecasts but also prediction intervals, which often have hugely informative value as far as practical applications are concerned. Although our study is focused on the selected models, the presented problem is universal and the proposed approach can be discussed in the context of other systems.

1 Introduction

Time series forecasting for many years was a great challenge in various applications. Words by Niels Bohr ‘Prediction is difficult, especially if it’s about the future’ capture the essence of the long-lasting challenge—the applied models may fit nicely for the past, they may be even quite good, but we literally never know what the future will bring us.

For years, the researchers and practitioners have tried to get better and better on prediction. The basic approaches include naive and seasonal naive, drift [1] or distribution-based methods. Naive methods repeat last period(s) of data; drift leverages past average change to estimate forecasts. Distribution methods do not assume any change in time; they are based on distribution-related metrics like mean, median or quantiles that are calculated either for the whole series or for its observations within a user defined window. For the purposes of the accurate prediction intervals, distribution-based forecasting may be also parametric. In such a case, firstly statistical tests are performed to fit the most appropriate distribution. Finally, the theoretical quantiles of the fitted distribution are calculated [2]. Distribution can be also leveraged in a nonparametric way. When thinking about the future in a scenario planning way, Monte Carlo approach can be used, especially for prediction intervals creation [3, 4]. Those basic approaches are sometimes referred to as ’benchmark methods’ as their simplicity can be seen as a perfect referral point to more sophisticated methods.

In the 40s and 50s of the twentieth century, the exponential smoothing family of methods has appeared. The concept is based on balancing the newer and older observations of time series. Such ‘smoothing’ can be applied to level trends as well as seasonality [1, 5]. This approach was extended from point forecasts to statistical models, known as ETS, which stands for error, trend seasonality [1]. Given ETS can handle only single seasonality, the model was further enhanced to include complex seasonal patterns, as well as Box–Cox transformation and the TBATS (exponential smoothing state space model with Box–Cox transformation, ARMA errors, trend and seasonal components) [6].

This brings us to the not yet defined ARMA—autoregressive moving average, which emerged in the middle of twentieth century [7, 8]. Similarly to the exponential smoothing, the concept of ARMA also evolved over the years and finally formed SARIMAX, which stands for seasonal autoregressive integrated moving average with exogenous variables [8]. SARIMAX is a generalization of ETS, as far as additive errors are concerned. It is possible to calculate appropriate parameters in SARIMAX that correspond to parameters in ETS [1]. SARIMAX was extended in a few directions. VARMAX is its vector variant, which handles multivariate time series. GARCH (generalized autoregressive conditional heteroskedasticity) is designed for heteroskedastic settings [9]. Multi-seasonal SARIMAX addresses the issue of complex seasonalities [10]. X-13ARIMA-SEATS chooses appropriate orders, handles outliers and special events (like holidays), see, for instance, [11].

The oldest in the origin is linear regression, which eldest form reaches back to the beginning of XIX. Beautifully easily to interpret, yet quite effective if profiting from creative independent variables. Quite recently Facebook has proposed the Prophet [12] algorithm, which does leverage quite a few effective exogenous variables, while estimating parameters with MAP (maximum a posteriori) estimation. When regression is not enough, one may resolve to its generalized form—generalized additive models (GAM) [13]. It not only uses link function, but also predictor variables are modelled with functions that can be either predefined or approximated by splines [14].

The era of machine learning brought on light tree-based models, SVR [15] or neural networks. Decision trees-based methods have been widely appreciated, for example, in the summary [16] of M5 competition (a famous competition for forecasting Walmart sales data [17]). Decision trees themselves were introduced later than exponential smoothing, ARMA, and CART, being one of the most popular algorithms [18]. Random forest (a set of decision trees) followed, first with random subspace method [19] and then also with bagging [20]. Idea of leveraging many weak learners has been also used by gradient boosted trees (GBT) [14], which trains trees iteratively instead of in parallel. However, GBT has not gained the proper fame until quite recent performance enhancements introduced by XGBoost [21] or LightGBM [22].

Deep learning also influenced time series forecasting. Modelling started with artificial neural networks (ANN) [14], but they do not explicitly take into account time dependence in their architecture. First time-dependence was introduced by recurrent neural network (RNN) [23]. In 1997 long short-term memory networks (LSTM) were invented [24]. They are based on RNN and aim at addressing some of the issues like exploding/disappearing weights. Next breakthrough came almost 20 years later, when the temporal convolutional network (TCN) was proposed [25]. This time architecture mixes temporal dependence with convolutions similar to those used frequently to solve image related challenges (convolutional neural network, CNN [26]). It is also worth mentioning that there have been attempts to create hybrid solutions of statistical and machine learning approaches, for example, M4 ES-RNN winner  [27, 28].

Although the evolution in the development of methods is happening very quickly, the search for a perfect forecast is not over yet and the list of models is still growing [29]. No model is universal enough to be perfect for all the cases and at the same time the models still usually assume normality, which is not necessarily a case for real datasets. In our research we improve SARIMAX parameters estimation and prediction intervals for heavy-tailed distribution case. The exemplary heavy-tailed distribution is the Student’s t [30]. However, the considered approach can be extended to any other distribution from the heavy-tailed class.

Simultaneously, we aim to compare the SARIMAX model (with maximum likelihood method) performance with machine learning-based approaches. The main focus is paid to the tree-based methods, which are considered very good performers. We aim to leverage SARIMAX’s idea of self-lags to create features for machine learning models. We aim to compare both the prediction errors itself and prediction intervals. Given that there is no underlying distribution assumption for tree-based models, we propose to leverage the out-of-bag samples to generate residuals and create such artificial prediction intervals.

This article is structured as follows. In Sect. 2 we start with recalling two models of particular interest. Next, in Sect. 3 we explain the methodology and purpose of our research. In Sect. 4 we present the simulation results. The last section summarizes the presented results.

2 Two models for time series forecasting

2.1 SARIMAX

Before defining SARIMAX model, let first establish the basic notation. We will denote time series of interest by $\{Y_t\}$, $t\in \mathbb {Z}$. Further, we assume $t\in \mathcal {T}=\{1, 2, \ldots , T\}$ where T is the length of a series. We denote the period by m and forecasting horizon by h. $X_t$ stands for exogenous variables associated with $Y_t$, $X_t = (X_{t,1}, \ldots , X_{t,k})$, where k is the number of features. Please note that even though the typical notation encountered in the literature denotes the number of features by p and period by P, we have chosen other letters in order not to mix up the number of features with orders from SARIMAX definition (which we present below).

Definition 1

[8] A time series $\{Y_t\}$, $t\in \mathbb {Z}$ is called the SARIMAX(p, d, q)(P, D, Q)m model if it assumes seasonality, trend and regressors and satisfies the following equation:

$$\begin{aligned}&\phi _p(B) \Phi _P(B^m) (1-B)^d (1-B^m)^D (Y_t-c-\beta _t X_t) \nonumber \\&\quad = \theta _q(B)\Theta _Q(B^m) Z_t, \end{aligned}$$

(1)

where $\{Z_t\}$ is the series of uncorrelated random variables with zero mean and variance equal to sigma$^2$. Moreover, the nonseasonal autoregressive (AR) and moving average (MA) operators are as follows:

$$\begin{aligned} \phi _p(B) = 1 - \phi _1 B - \cdots - \phi _p B^p \\ \theta _q(B) = 1 + \theta _1 B + \cdots + \theta _q B^q. \end{aligned}$$

The seasonal AR and MA operators are given by:

$$\begin{aligned} \Phi _P(B) = 1 - \Phi _1 B - \cdots - \Phi _P B^P \\ \Theta _Q(B) = 1 + \Theta _1 B + \cdots + \Theta _Q B^Q \end{aligned}$$

and B is the backward shift operator.

In general, the SARIMAX model does not assume normality. However, the most common estimation algorithm used for parameters estimation is the maximum likelihood estimation (MLE) and in the classical version it assumes the normality of the series $\{Z_t\}$ in Eq. (1), i.e. it assumes $Z_t \sim \mathcal {N}(0, \sigma ^2)$. The likelihood function $L(\cdot )$, that is part of MLE algorithm, is the joint density function of the data, but treated as a function of the unknown parameters, given the observed data $y_1, \ldots , y_T$ being the realization of the time series $\{Y_t\}$ given in Definition 1. The maximum likelihood estimates (MLEs) are the values of the parameters that maximize this likelihood function, that are the “most likely” parameter values given the data we actually observed. It should be noted, even if the assumption of the normality of the data is not satisfied, the classical MLE algorithm is often used. If the deviation from normality is not significant, the obtained estimators performance can be acceptable. However, when the distribution of the data under consideration is far from the normal distribution, the classical MLE algorithm needs to be modified, see, for instance, [31]. This problem is discussed also in this paper in the simulation studies.

2.2 Random forest

Random forest (RF) comprises a set of trees. Assuming we grow B trees, each of trees $T_b, b = 1, 2, \ldots , B$ is constructed as follows:

• 1. The process starts off with so-called bagging, namely drawing observations randomly with replacement. In case of time series, it comes down to repeating some $Y_t$ and associated p covariates while putting aside other observations. Removed samples are called out-of-bag (OOB) samples.

• 2. Tree on the modified data is grown by recursively repeating (till stopping criterion) the steps:

  • Random subspace of $j, j\le k$ is chosen. In case of one feature, it does not affect the artificially created dataset at all, but it matters for higher number of features. Usually $j={\lfloor }\sqrt{k}{\rfloor }$ or $j={\lfloor }\frac{k}{3}{\rfloor }$.

  • Best variable and split point are picked up among j features. For regression trees the best split is chosen based on variance reduction. The variance reduction of a node N is defined as the total reduction of the variance of the target variable Y due to the split into left $N_l$ and right $N_r$ nodes:

    $$\begin{aligned} {\mathrm{Var}}(N)&= \frac{1}{|N|} \sum _{y \in N} (y - \bar{y})^2\\ {\mathrm{reduction}}&= {\mathrm{Var}}(N) - (\frac{|N_l|}{|N|} {\mathrm{Var}}(N_l) \\&\quad + \frac{|N_r|}{|N|} {\mathrm{Var}}(N_r)). \end{aligned}$$

  • Node is split into two child notes.

Final RF prediction aggregates results returned by B trees, that is:

$$\begin{aligned} \hat{y}_t = \frac{1}{B} \sum _b T_b(x_t) \end{aligned}$$

(2)

The algorithm is presented visually in Fig. 1. Note that constructed trees differ slightly between each other. Moreover, OOB samples have the great side effect of being an inner-algorithm test set.

Fig. 1

Random forest algorithm

Random forest does not deliver clearly interpretable parameters like SARIMAX method. However, it produces the so-called variable/feature importance. For a given feature, it accumulates improvements in split-criterion in all B trees, when the split was performed using that feature.

3 Methodology

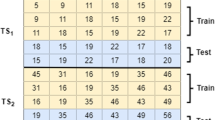
We followed one of the classical time series evaluation methodologies—temporal splits with an expanding window. In machine learning applications, such an approach is frequently used both for model evaluation and hyper parameters tuning. Even though in this particular research we have not performed hyperparameters tuning yet, we still follow the methodology with the purpose of future extensions (for example, SARIMAX orders space search vs classical partial autocorrelation PACF or Akaike information criterion AIC usage). Please note that as a side effect of such an approach, we are able to examine metrics dependence on the series length.

Formally, for a split at cvth point in time, the train set can be defined as $\{Y_t: t \le \text {cv}\}$, while test set as: $\{Y_t: t > \text {cv}, \, t <= \text {cv} + h\}$. The procedure repeats such a split CV times, extending the window (enlarging cv) each time. Exemplary results for 7 days-ahead forecasts, with one test–train split and 12 train splits are presented in Fig. 2.

The evaluation methodology together with its visualization was implemented in python package sklearn-ts. It was necessary to implement a new package, as existing ones either have not provided all models (kats), prediction intervals (scikit-learn) or flexible regressors usage (sktime). The sklearn-ts is based on the scikit-learn framework.

Fig. 2

Temporal splits 7 days-ahead forecasts, with one train–test split (bottom left chart) and 12 train splits (top left chart). Residuals distribution (top tight) as well as series together with the forest (bottom right) are presented

Metrics of our focus are mean absolute percentage error (MAPE) and prediction interval coverage (PIC). Denoting the forecasting horizon by h, the $t_i$-th observation by $y_{t_i}, \, i=1, 2, \ldots , h$, the $t_i$-th forecast by $\hat{y}_{t_i|t_1-1}, \, i=1, 2, \ldots , h$ and $\hat{\mathbf {y}} = (\hat{y}_{t_1|t_1-1}, \ldots , \hat{y}_{t_h|t_1-1})$, $\mathbf {y} = (y_{t_1}, \ldots , y_{t_h})$, MAPE is defined as follows:

$$\begin{aligned} \text {MAPE}(\mathbf {y}, \hat{\mathbf {y}}) = \frac{100\%}{h} \sum _{i=1}^h \left| \frac{\hat{y}_{t_i|t_1-1} - y_{t_i}}{y_{t_i}} \right| . \end{aligned}$$

(3)

Denoting lower and upper prediction interval estimates by $\hat{y}^{(\mathrm{lower})}_{t_i|t_1-1}$ and $\hat{y}^{(\mathrm{upper})}_{t_i|t_1-1}$ respectively, PIC is defined as:

$$\begin{aligned}&\text {PIC}(\mathbf {y}, \hat{\mathbf {y}}^\mathrm{lower}, \hat{\mathbf {y}}^\mathrm{upper}) \nonumber \\&\quad = \frac{100\%}{h} \sum _{i=1}^{h} \mathbf {I}\left( \hat{y}^\mathrm{lower}_{t_i|t_1-1} \le y_{t_i} \le \hat{y}^\mathrm{upper}_{t_i|t_1-1}\right) . \end{aligned}$$

(4)

4 Initial results

To make the analysis simpler, in this paper we focus on the special cases of SARIMAX model, namely on AR and seasonal AR models only.

4.1 Daily time series

First, we assume a daily frequency and forecasting horizon equal to the period (length of week), i.e. $h=m=7$. We have generated $\text {MC} = 100$ time series of length $T=7 * 52 * 2$ (about 2 years of data) type SARIMAX(0, 0, 0)(1, 0, 0)7 given by:

$$\begin{aligned} Y_t - \Phi Y_7 - c = Z_t. \end{aligned}$$

(5)

We check both $\Phi =0.7$ and $\Phi =0.2$, in both cases setting $c=100$. Given that the results were almost the same, we decided to present the first variant, namely:

$$\begin{aligned} Y_t - 0.7 * Y_7 - 100 = Z_t \end{aligned}$$

(6)

We deliberately made $h=m=7$, $P=1$ and $p=0$, so that it’s easy for trees to work with correctly lagged regressor, without the problem of regressor values being absent for future forecasts. However, it is worth pointing out that in real applications it is not possible to have the comfort of such an assumption. This is one of the advantages of SARIMAX—it is possible to look back freely, without it being dependent on the forecast horizon. Computationally, it is possible to create one-step-ahead forecasts and use them as ‘history’ to create the next one-step-ahead forecast, but such an approach is risky as it may accumulate errors in case of inaccurate predictions.

To check the effect of the heavy-tailed noise, we focused on two distributions of the noise $\{Z_t\}$: normal $\mathcal {N}(0, \sigma ^2)$, $\sigma ^2=21$ and Student’s t. In case of Student’s t distribution we consider two cases: with finite (2.1 degrees of freedom, $t_{2.1}$) and infinite (1.1 degrees of freedom, $t_{1.1}$) variance. Please note that variance for $\mathcal {N}(0, 21)$ and $t_{2.1}$ takes the same value.

The evaluation procedure created the $h=7$ step-ahead forecasts every $\text {gap} = 60$ days, repeating $\text {CV} = 13$ times in total (counted together with train–test split). As mentioned, we simulated series with length $T=7 * 52 * 2$, but since we evaluated models leveraging the above-mentioned evaluation procedure (see Sect. 3 for details), we actually received results for 13 various series lengths $T_i, i=1, 2, \ldots , 13$:

$$\begin{aligned} T_i = T-h-(i-1)*{\mathrm{gap}}. \end{aligned}$$

(7)

We called one run of one simulation for one train-validation set and experiment. We ran a total of $\text {CV} * \text {MC} = 1300$ experiments.

In each experiment, we fitted both SARIMAX(0,0,0)(1,0,0)7 and RF (with a lagged 7 steps feature being a regressor). For SARIMAX implementation from python statsmodels package, the convergence problem appeared in 15% cases for normal distribution and in 10% cases for Student’s t, finite variance. The default maximal iteration parameter was not tampered with.

4.1.1 Parameters estimation

We started off with examining the convergence of the parameter estimate $\hat{\Phi }$ to parameter assumed value ($\Phi =0.7$). In Fig. 3 we present 10 and 90 percentile of $\text {MC} = 100$ simulations along the length of the sample. Naturally, the estimates improve together with increasing series length. What is interesting although is that parameter estimation is very promising, regardless of the considered distribution. Given that for large enough samples, Student’s t may be approximated with normal distribution (when the number of degrees of freedom tends to infinity), we check also smaller sample sizes (see the next section).

Fig. 3

Parameter estimates convergence (not distribution dependent)

4.1.2 Distribution of residuals

For each experiment we examined the normality of error using the Shapiro–Wilk test [32]. Then we counted positive and negative test results and calculated their proportion to all experiments. Results are presented in Table 1.

Table 1 Percentage of experiments with positive normality test for residuals

Naturally, SARIMAX preserves normality/lack of normality of its residuals. However, interestingly enough, RF seems to have the same property, even though the model itself does not assume any distribution for the errors. This result lets us believe it may be a direction worth further exploration. It would be a very interesting property of RF, especially by its application to more complicated models.

For a simple model and one-dimensional regressors matrix $\mathbf {x}=(x_1, \ldots , x_T)$, the one RF tree model comes down to:

$$\begin{aligned} \hat{y}_{t+h|t} = \frac{1}{|L|} \sum _{i: x_i \in L} y_i, \end{aligned}$$

(8)

where $x_{t+h} \in L$, L being the leaf. It means the model is an average of subset of the series variables, so it also follows SARIMAX model:

$$\begin{aligned} \frac{1}{|L|} \sum _i Y_i - 0.7 * \frac{1}{|L|} \sum _i Y_{i-7} - 100 = \tilde{Z}, \end{aligned}$$

(9)

where $\tilde{Z}=\frac{1}{|L|} \sum _i Z_i \sim \mathcal {N}(0, \frac{\sigma ^2}{|L|})$ (in case of normal distribution of $Z_i$).

Focusing on RF residuals only:

$$\begin{aligned} \tilde{Z}_{t+h|t}= & {} \hat{Y}_{t+h|t} - Y_{t+h} = 0.7 \frac{1}{|L-1|} \sum _{i: x_i \in L, i \ne t+h} Y_{i-7} \nonumber \\&+ \frac{1}{|L-1|} \sum _{i: x_i \in L, i \ne t+h} Z_{i} \end{aligned}$$

(10)

assuming $t+h-7 \in \{i: x_i \in L\}$. If $t+h-7 \not \in \{i: x_i \in L\}$, we would proceed using Eq. (6) in an iterative way. When considering RF, the set of trees, $\tilde{Z}$ will have a slightly more complicated formula, as each $Y_i$ may be repeated a few times. Let us, for simplicity, take $B=2$:

$$\begin{aligned} \hat{y}_{t+h|t} = \frac{1}{B} \sum _{b=1}^B \frac{1}{|L^{(b)}|} \sum _{i: x_i \in L^{(b)}} y_i, \end{aligned}$$

(11)

where $\forall b \, x_{t+h} \in L^{(b)}$, which means that:

$$\begin{aligned} \tilde{Z} = \frac{1}{|L^{(1)} \cap L^{(2)}|} \sum _{i: x_i \in L^{(1)} \cap L^{(2)}} 2 Z_i + \frac{1}{|L^*|} \sum _{i: x_i \in L^*} Z_i, \end{aligned}$$

(12)

where $L^*=L^{(1)} \cup L^{(2)} - L^{(1)} \cap L^{(2)}$ and assuming both $L^{(1)} \cap L^{(2)}$ and $L^*$ are not empty. Then we have the following:

$$\begin{aligned} \tilde{Z} \sim \mathcal {N}\left( 0, \sigma ^2\left( \frac{4}{|L^{(1)} \cap L^{(2)}|} + \frac{1}{|L^*|} \right) \right) . \end{aligned}$$

(13)

Using the same reasoning as for a single tree seen above in Eq. (10), we also stay within AR behaviour. This explains the preservation of the distribution for RF model for data following SARIMAX(0, 0, 0)(1, 0, 0)7.

4.1.3 Prediction intervals

Lastly, we examined the prediction interval coverage. To achieve it we used all experiments and empirically evaluated such coverage using PIC calculated for each experiment.

The average estimated (over all experiments) prediction interval coverage presented in Table 2 lets us believe that using incorrect assumptions for the SARIMAX model substantially interferes with their quality. It seems to be a promising area for further research, especially given that SARIMAX performs better (at least for this simple model) as far as MAPE is concerned, see Table 3 for details.

Table 2 Average empirical prediction interval coverage, for theoretical coverage at 0.8

Table 3 Average empirical MAPE

In Fig. 4 we compared the distributions of empirical prediction intervals coverage for the three considered distributions and two examined models. They confirm the consistency of RF prediction intervals regardless of the error distribution and the lack of such for SARIMAX. This leads us to the initial conclusion that predictions intervals are the main pain points of SARIMAX with non-normal distribution of noise.

Fig. 4

Prediction intervals quality for three examined distributions

4.2 Monthly time series

In real live cases, daily time series appear similarly frequently to monthly ones. Monthly time series are harder to predict, as they are naturally usually much shorter.

We simulated $\text {MC} = 100$ times 12 years of monthly data coming from SARIMAX(5, 0,0)(0,0,0)12:

$$\begin{aligned} Y_t - \phi _3 Y_{t-3} - \phi _4 Y_{t-4} - \phi _5 Y_{t-5} -c = Z_t \end{aligned}$$

(14)

where $\phi _3=0.5, \,\phi _4=-0.4, \,\phi _2=-0.2, \,c=100$.

The evaluation procedure involves three-step-ahead forecasts, every 9 months, performed 16 times. The shortest series has 12 observations.

4.2.1 Parameters estimation

Similarly to daily simulations, monthly parameters’ estimates converge to correct values regardless of the noise distribution, see Fig. 5. Chart presents all three estimated parameters $\phi _3, \phi _4, \phi _5$ and their convergence with increasing sample size to the correct parameters values: $\phi _3=0.5$, $\phi _4=-0.4$, $\phi _5=-0.2$ for examined distributions: $\mathcal {N}(0, 21)$, $t_{2.1}$, $t_{1.1}$. Regardless of the noise distribution, errors of parameter estimates $\hat{\phi }_i - \phi _i, i=3, 4, 5$ are slightly skewed, which means they are more frequently underestimated than overestimated (see bottom right chart). Shockingly, even though the difference is small, normal distribution median (bottom right chart) is the one the furthest from 0, which is counter-intuitive given MLE assumed normal distribution.

Fig. 5

Parameters estimation for SARIMAX(5,0,0)(0,0,0)12

4.2.2 Prediction intervals

Fig. 6

Prediction intervals quality for three examined distributions for SARIMAX(5,0,0)(0,0,0)12

This time the prediction intervals for RF, shown in Fig. 6, are of worse quality than for the daily case presented previously. The distribution for PIC estimates is skewed and bimodal—instead of hitting mostly 0.8 it’s either close to 0.65 or 1. The plus side is RF prediction intervals still preserve the quality of being consistent across all 3 distributions and still being slightly better than too wide SARIMAX intervals.

5 Summary and initial conclusions

Initial research has led us to a few interesting findings. First of all, MLE parameter estimation for AR models has similar quality regardless of underlying distribution being normal or Student’s t. They improve with sample size as expected and are rather poor for series shorter than about 30 observations. One may be tempted towards further research of the same properties having place for other heavy-tailed distributions. It would be similarly interesting to explore the behaviour of estimates for more complex SARIMAX models than pure AR. Furthermore, it is clear that prediction intervals for SARIMAX with Student’s t distributed noise need to be improved, as they are too wide and do not narrow down the probable values in a correct way. The hypothesis that the same property accompanies other heavy-tailed distributions is yet to be confirmed. Thirdly, RF Out-Of-Bag samples for underlying AR model could be used to create reasonable, consistent prediction intervals, regardless of errors being normal or Student’s t. That could be a very valuable insight for practical applications as well as a promising area for further research regarding more complex models. Finally, random forest preserves normality of residuals for data that follow AR models.

Apart from parameters’ estimation and prediction intervals, another challenge of SARIMAX that was not addressed in this paper is the correct choice of order. In practice, it seems to be even bigger challenge than parameters estimation itself. In the future, we aim to research and propose a machine learning-based approach. The idea is to mix and match the beauty of SARIMAX theory with the power of machine learning techniques, already proven to be worth exploring in so many practical applications.