1 Introduction

High-frequency (HF) combustion instability has always posed a significant threat to the reliable operation of liquid rocket engines (LREs). It is the product of a complex coupling between acoustics, hydrodynamics, and heat release that sustains severe pressure oscillations. Combustion instability occurs when the peak-to-peak amplitude of these pressure oscillations is equal to or exceeds 10% of the mean chamber pressure [1]. Following a classification based on the frequency of fluctuations, the most harmful instability is the high-frequency one (usually > 1 kHz), also called “screaming”, characterized by the interaction between unsteady heat release and chamber acoustic modes. When this phenomenon occurs, the engine is subjected to cyclic excitation, experiencing strong vibrations, mechanical loads, and thermal loads significantly higher than those expected under nominal conditions. These elevated stresses can potentially lead to damage or even complete destruction of the propulsion system [2,3,4]. Despite several decades of research since the late 1950s [5], the intricate multi-physics mechanism underlying the instability is not yet fully comprehended. Consequently, there is a pressing need to enhance our understanding and devise reliable predictive tools to mitigate risks and minimize costs associated with the development of new engines.

HF combustion instability is currently investigated through a synergistic approach that combines lab-scale experiments and a hierarchy of numerical models. Experimental studies have demonstrated the significant impact of injector design on the stability of liquid rocket engines [1]. Shear coaxial injectors, commonly used in LOX/\(\hbox {H}_2\) and LOX/\(\hbox {CH}_4\) systems, have received extensive attention in this regard [3, 6,7,8,9,10]. The acoustics of the injector has been identified as a key element for thermo-acoustic coupling, with several experimental campaigns revealing a strict relationship between the heat release rate spectrum and the longitudinal acoustic spectrum in the oxidizer post [3, 7, 8, 11,12,13].

In parallel with experiments, high-fidelity numerical simulations, such as Large Eddy Simulations (LESs) and Detached Eddy Simulations (DESs), have been employed to gain valuable insights into HF combustion instability [14,15,16,17]. In particular, DES simulations have shown that the instability in coaxial injectors can be driven by cyclic fuel accumulation and release, which is attributed to the intrinsic characteristics of these injectors, designed with a radial density gradient in the recess zone where oxidizer and fuel mix [15].

The interaction between the intrinsic radial density gradient and the axial pressure gradients, resulting from the propagation of acoustic disturbances inside the injectors, gives rise to a baroclinic torque (\(\nabla \rho \times \nabla p\)), which acts as a vorticity source (see also Fig. 1) [15]. Strong upstream pressure waves can intensify vortices and slow down the flow, hindering the passage of fuel which is instead trapped inside the vortices. Similarly, downstream pressure waves can push vortices and the related trapped fuel toward the flame. The local modification of the mixture ratio causes fluctuations in the heat release and subsequent pressure oscillations, potentially closing the thermo-acoustic feedback loop and ultimately leading to an injection-coupled HF combustion instability.

Fig. 1
figure 1

Close-up of a typical shear coaxial injector showing the interaction between longitudinal pressure gradient and radial density gradient

Full size image

Although unique to reveal details of the combustion instability dynamics, both sub-scale experiments and high-fidelity computations can hardly be considered suitable for the design of new engines. As far as lab-scale experiments are concerned, despite being a cost-effective alternative to full-scale tests, they are indeed not representative of full-scale LREs stability, since instability is a scale-dependent phenomenon.

Regarding high-fidelity simulations, despite being able to capture several crucial aspects of the flowfield thanks to the highly detailed physics employed, they rely on case-specific modeling assumptions, which introduce approximation errors that can negatively impact the predictive capabilities or the ability to even detect the presence of a thermo-acoustic feedback loop [16]. Furthermore, the computational requirements of this approach are substantial, making it unsuitable as a standalone tool for the design of new engines, but rather as a supplementary tool especially useful in scientific research.

For these reasons, the research community has increasingly focused on low-order models [18,19,20], which employ simplified physics to improve computational efficiency. However, the reduction in the physical model complexity can hinder the detection of thermo-acoustic coupling which has to be enforced through the use of a so-called response function (RF).

The primary objective of a low-order model is to provide a fast and reasonably accurate assessment of chamber stability by effectively capturing the fundamental driving mechanisms of thermo-acoustic combustion instability. The determination of the response function plays a critical role in this modeling approach. Response functions are typically derived by analyzing experimental data or high-fidelity simulations. A widely used approach is the \(n-\tau\) model, based on Crocco’s time-lag theory [21], which establishes a direct relationship between acoustic and heat release fluctuations through the proportionality index n and a time-lag \(\tau\). Several studies have successfully applied this approach, demonstrating its capability to reproduce high-fidelity data and experimental results, given appropriate tuning of the parameters [22, 23].

A more physically informed response function has been proposed by D’Alessandro et al. [24], which mimics the fuel modulation mechanism in shear coaxial injectors by linking the injected fuel mass flow rate to pressure fluctuations in the recess, indirectly closing the feedback loop. Despite its simplicity, this approach has effectively captured both longitudinal and transverse instabilities in ideal and real fluid Eulerian frameworks [24, 25]. Although the calibration of several parameters is crucial for predicting even longitudinal instabilities in a one-dimensional framework [24], it is noteworthy that this response function formulation does not rely on high-fidelity or experimental data. Hence, a low-order model based on such a response function holds the potential to be used as a standalone tool for the design of liquid rocket engines.

Despite extensive efforts in the literature, achieving predictive capability for high-frequency combustion instability remains a challenge for numerical tools. The a priori prediction of these instabilities using low-order models would significantly reduce the reliance on expensive experimental tests and high-fidelity simulations, thereby positively impacting the development costs of new liquid rocket engines.

In this paper, we tackle the prediction of spontaneous self-sustained transverse combustion instabilities in multi-injector engines using a multi-dimensional non-linear low-order Eulerian model. Our approach employs a response function that directly links pressure oscillations to fuel mass flow rate, independently of external data, as in [24, 25]. This physically aware approach accurately captures the characteristics of shear coaxial injectors and the presence of the accumulation and release dynamics of fuel pockets in response to acoustic waves.

To validate our methodology, we employ a test case performed by NASA as a reference [8]. A comprehensive analysis of the test case is conducted, encompassing various aspects such as the system thermo-fluid dynamics, the influence of the model free parameters, and the impact of damping devices.

This paper is structured as follows: Sect. 2 describes in detail the low-order model, focusing on governing equations, response function description, boundary conditions, and equation of state. The experimental setup of the NASA test case is described in Sect. 3. Lastly, results are presented in Sect. 4.

2 Mathematical model

This section presents the mathematical model which constitutes the low-order solver for the analysis of combustion instabilities. The governing equations are first described, followed by a detailed description of the response function used. Then, the multi-dimensional approach is presented, followed by the description of the available Equations of State (EoS) to compute the fluid properties.

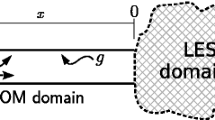
In order to study transverse combustion instability, a three-dimensional (3D) description of the whole system is required. However, the flow dynamics taking place in the injectors can be approximated to be basically one-dimensional. For this reason, we adopt the original approach of splitting the computational domain into a three-dimensional part, the chamber, and a certain number of quasi one-dimensional domains (Q1D, i.e. one-dimensional with variable cross-sectional area), one for each injector, with the former handled by an existing, already validated, in-house software for three-dimensional multi-species reactive flows [25, 26]. A detailed description of both solvers will be given in the following Section. These Q1D and 3D domains are merged to form a so called “hybrid-D” solver. This approach highly increases the computational efficiency of the numerical tool, as it is in line with the principles of low-order modeling.

2.1 Governing equations

The governing equations for the injector domains are the Q1D multi-species Euler equations. Three chemical species are taken into account, i.e. fuel, oxidizer, and combustion products (subscript “ox” for oxidizer, “f” for fuel, and “p” for combustion products). Although combustion instability is characterized by significant variations in mixture ratio, leading to differences in the composition of combustion products, a simplification is made where the combustion products are treated as a single species with the properties of the mixture composed of the resulting species from the oxidizer and fuel combustion under stoichiometric conditions. These properties are computed using the CEA software [27]. This modeling choice significantly reduces computational costs.

During the unstable regime, the cyclic accumulation and release of fuel pockets from the injectors generate regions in the combustor where the mixture reaches stoichiometric conditions, leading to peaks in thermal release. Given the importance of capturing correctly these heat peaks for predicting thermo-acoustic coupling, the stoichiometric ratio is chosen as a reference for computing the properties of the combustion products single species.

The governing equations read as:

$$\begin{aligned} \left\{ \begin{array}{lll} {}\left( \rho A \right) _t + \left( \rho u A \right) _x = \dot{\omega }_\textrm{f1} {}\quad (2.1)\\ {}\left( \rho u A\right) _t + \left[ \left( \rho u^2 + p \right) A\right] _x - p A_x = u_\textrm{f} \dot{\omega }_\textrm{f1}{}\quad (2.2)\\ {}\left( \rho A Y_\textrm{ox}\right) _t + \left( \rho u A Y_\textrm{ox}\right) _x = -\dot{\omega }_\textrm{ox} {}\quad (2.3)\\ {}\left( \rho A Y_\textrm{f}\right) _t + \left( \rho u A Y_\textrm{f}\right) _x = \dot{\omega }_\textrm{f1} - \dot{\omega }_\textrm{f2} {}\quad (2.4)\\ {}\left( \rho e_0 A\right) _t + \left( \rho u h_0 A\right) _x = \dot{\omega }_\textrm{f1} h_\textrm{0,f} + \dot{Q} {}\quad (2.5) \end{array}\right. \end{aligned}$$

where A is the cell cross-sectional area on the yz-plane; \(\rho\), u, p, \(Y_\textrm{ox}\), and \(Y_\textrm{f}\) are, respectively, density, velocity, pressure, and mass fractions of oxidizer and fuel; \(e_0\) and \(h_0\) are the specific total internal energy and total enthalpy; and subscripts \(\textrm{f1}\) and \(\textrm{f2}\) represent, respectively, fuel addition in the recess and fuel consumption due to the combustion reaction.

The right-hand side of Equations (2.1)–(2.5) incorporates several source terms. Specifically, Equation (2.5) accounts for the heat released from the combustion of propellants:

$$\begin{aligned} \dot{Q} = \dot{\omega }_\textrm{ox} \Delta h_\textrm{f,ox}^0 + \dot{\omega }_\textrm{f2} \Delta h_\textrm{f,f}^0 - \dot{\omega }_\textrm{p} \Delta h_\textrm{f,p}^0 \end{aligned}$$
(2.6)

where \(\Delta h^0_{\textrm{f},i}\) is the the standard formation enthalpy and \(\dot{\omega }_i\) is the rate of production per unit length of the i-th species. To properly take into account phenomena such as mixing, atomizazion, and vaporization, combustion is inhibited in the domain up to an abscissa \(x_\textrm{c}\), measured from the beginning of the combustion chamber. The combustion reaction is modeled as an Arrhenius-like single-step global reaction between the fuel and the oxidizer, and reads as follows:

$$\begin{aligned} \dot{\omega }_\textrm{f2}= G A \dfrac{Y_\textrm{ox} Y_\textrm{f}}{\delta } e^{- T_\textrm{r} / T} \qquad \textrm{if} \qquad x>x_\textrm{c} \end{aligned}$$
(2.7)
$$\begin{aligned} \dot{\omega }_\textrm{ox}&= \left( \mathrm {O/F}\right) _\textrm{st} \dot{\omega }_\textrm{f2} \end{aligned}$$
(2.8)
$$\begin{aligned} \dot{\omega }_\textrm{p}&= \dot{\omega }_\textrm{f2} + \dot{\omega }_\textrm{ox} \end{aligned}$$
(2.9)

where G is the local mass flux, T is the mixture temperature, \(\delta\) and \(T_\textrm{r}\) are tuning parameters through which the heat release curve can be modified, and \(\mathrm {O/F}\) is the mixture ratio. It is assumed that the oxidizer reacts with the fuel at the stoichiometric proportion (subscript “st”).

It must be underlined that the parameter \(x_\textrm{c}\), representing mixing and breakup delays, is the starting point of the combustion reaction. On the other hand, the parameters \(\delta\) and \(T_\textrm{r}\), affect the flame length by modifying the slope of the heat release curve. These parameters are introduced as surrogates of complex physical phenomena which are not modeled in the solver, in line with low-order modeling assumptions. They can be easily inferred through preliminary tuning, or by using data from steady-state high-fidelity simulations or experimental data.

Regarding mass addition, fuel is introduced in the recess in a length \(l_\textrm{f}\), usually equal to the recess length itself, assuming a constant mass flow rate per unit length \(\dot{\omega }_\textrm{f1}\):

$$\begin{aligned} \dot{\omega }_\textrm{f1} = \dfrac{\dot{m}_\textrm{f}}{l_\textrm{f}} \end{aligned}$$
(2.10)

where \(\dot{m}_\textrm{f}\) is the overall injected fuel mass flow rate. Oxidizer is instead introduced at the left boundary, where oxidizer mass flow rate \(\dot{m}_\textrm{ox}\) and total temperature \(T_0\) are enforced as boundary conditions for the subsonic inflow (see Fig. 3b), resulting in a reflective boundary condition. It must be underlined that, as a consequence of the non-linear nature of the Eulerian model, no acoustic boundary condition is enforced.

The governing equations for the 3D flow are analogous, adding the second and third components of the velocity vector, and the second and third equations for the momentum conservation. Their compact form reads as:

$$\begin{aligned} \varvec{U}_t + \varvec{F}_x + \varvec{G}_y + \varvec{H}_z = S \end{aligned}$$
(2.11)

where \(\varvec{U}\) is the state vector, while \(\varvec{F}\), \(\varvec{G}\), and \(\varvec{H}\) are the convection flux vectors, respectively along the x, y, and z directions, which are written as:

$$\begin{aligned} \varvec{U}&= \left\{ \rho , \rho u , \rho v , \rho w , \rho e_0 , \rho Y_\textrm{ox} , \rho Y_\textrm{f} \right\} \end{aligned}$$
(2.12)
$$\begin{aligned} \varvec{F}&= \left\{ \rho u, \rho u^2 + p , \rho u v , \rho u w , \rho u h_0 , \rho u Y_\textrm{ox} , \rho u Y_\textrm{f} \right\} \end{aligned}$$
(2.13)
$$\begin{aligned} \varvec{G}&= \left\{ \rho v, \rho u v , \rho v^2 + p , \rho v w , \rho v h_0 , \rho v Y_\textrm{ox} , \rho v Y_\textrm{f} \right\} \end{aligned}$$
(2.14)
$$\begin{aligned} \varvec{H}&= \left\{ \rho w, \rho u w , \rho v w , \rho w^2 + p , \rho w h_0 , \rho w Y_\textrm{ox} , \rho w Y_\textrm{f} \right\} \end{aligned}$$
(2.15)
$$\begin{aligned} \varvec{S}= \left\{ 0 , 0 , 0 , 0 , \dot{Q}/A , \dot{\omega }_\textrm{ox}/A , \dot{\omega }_\textrm{f2}/A \right\} \end{aligned}$$
(2.16)

The mass addition terms are not present in the source vector \(\varvec{S}\) since the recess is solely part of the Q1D domains. Supersonic outflow conditions are enforced at the right boundary of the 3D domain, while Eulerian wall conditions are applied at the chamber solid surfaces.

The described equations are discretized using a finite volume method. The numerical fluxes at the interfaces are computed utilizing the Roe approximated Riemann solver [28]. To achieve second-order accuracy in space, a Godunov-like integration approach with MinMod reconstruction is employed, while second-order accuracy in time is achieved through a second-order Runge–Kutta integration scheme.

2.2 Response function

As previously mentioned, the presence of a thermo-acoustic feedback loop, which drives the combustion instabilities, can be detected in low-order models thanks to the action of a response function. A physically aware calibration-free approach is adopted, which relies on the methodology proposed in [24]. With this method, in order to mimic the dynamics of fuel accumulation and release specific to shear coaxial injectors, a direct correlation between the oscillations in fuel mass flow rate and pressure oscillations is established:

$$\begin{aligned} \dot{m}_\textrm{f}&= \dot{m}_\textrm{f,n} + \dot{m}_\textrm{f}' \end{aligned}$$
(2.17)
$$\begin{aligned} \hat{\dot{m}}_\textrm{f}'&=\dot{m}_\textrm{f,n} \left[ \exp \left( -\sigma \dfrac{p(t,x_\textrm{s})-p_\textrm{s}(t,x_\textrm{s})}{p_\textrm{s}(t,x_\textrm{s})}\right) -1\right] \end{aligned}$$
(2.18)
$$\begin{aligned} \dot{m}_\textrm{f}'&= \min \left[ \hat{\dot{m}}_\textrm{f}' , \dfrac{m_\textrm{f,acc}}{\delta t} \right] \end{aligned}$$
(2.19)

where \(\dot{m}_\textrm{f}'\) represents the fuel mass flow rate fluctuation induced by acoustic propagation in the injectors, \(\dot{m}_\textrm{f,n}\) is the nominal fuel mass flow rate, \(\sigma\) is an amplification parameter, \(x_\textrm{s}\) is the abscissa where pressure is sampled (measured from the recess starting abscissa, also called “backstep”, see also Fig. 3b), \(p_\textrm{s}\) is the runtime averaged pressure at the sampling point (\(x_\textrm{s}\)), and \(m_\textrm{f,acc}\) is the instantaneous fuel mass trapped into the vortex at the recess, introduced to ensure mass conservation and computed at runtime as:

$$\begin{aligned} m_\textrm{f,acc} = - \int _0^t \dot{m}_\textrm{f}' \textrm{d}t \end{aligned}$$
(2.20)

The parameter \(\sigma\) represents mathematically the normalized slope of the mass flow rate variation induced by pressure waves (i.e. the absolute relative variation of fuel mass flow rate per unit variation of pressure), as can be seen computing \(\dfrac{|\partial \hat{\dot{m}}'_\textrm{f} / \partial p |}{\hat{\dot{m}}'_\textrm{f}} = \sigma\). Physically, the higher is the value of \(\sigma\), the stronger will be the baroclinic torque induced by the passage of pressure waves in the recess (resulting in a stronger mass flow rate variation \(\hat{\dot{m}}'_\textrm{f}\)).

A typical behavior of the response function with respect to pressure is shown in Fig. 2.

Fig. 2
figure 2

Typical behavior of the fuel mass flow rate with respect to pressure fluctuations

Full size image

2.3 Hybrid-D approach

A distinguishing feature of the current low-order model is its ability to handle multi-injector geometries by treating each injector as a Q1D domain, while preserving the 3D nature of the combustion chamber to capture transverse gasdynamics phenomena. This modeling approach significantly reduces computational demands while necessitating an accurate treatment of the connection between the sub-domains.

Specifically, the interface between the Q1D and 3D regions is handled as follows (refer to Fig. 3): a designated surface \(\mathcal {B}_j\) is associated with the j-th injector. Numerical fluxes are computed between each cell of the 3D domain that comprises the \(\mathcal {B}_j\) surface and the rightmost cell of the j-th Q1D domain. Null momentum fluxes are assumed in the y and z directions (i.e., axial flow in the injectors). The mass, x-momentum, and energy fluxes are then integrated over \(\mathcal {B}_j\) and added to the corresponding Q1D cell.

Fig. 3
figure 3

Domain splitting

Full size image

2.4 Equation of state

To complete the system of equations presented in Sect.  2.1, an equation of state is necessary to calculate the essential thermodynamic properties of the mixture. Given that many liquid rocket engines utilize cryogenic propellants, there may be specific scenarios where real fluid modeling is required.

The thermodynamic states within a liquid rocket engine can vary significantly across different locations, typically exceeding their critical pressures, but not always surpassing their critical temperatures. Specifically, the fuel from the cooling jacket is generally hot and above its critical temperature, while downstream from the ignition location, the temperature of the combustion products rises significantly above the critical temperature of the mixture. The oxidizer instead, whether from tanks or pumps, tends to be cold and below its critical temperature. This condition results in a thermodynamic behavior that strongly deviates from the one described by the ideal gas law, especially in terms of speed of sound, a key quantity in thermo-acoustic dynamics. Therefore, to accurately simulate acoustic propagation, which is crucial for predicting combustion instability, a proper thermodynamic modeling through a real fluid equation of state is essential.

In this paper, we propose the original approach of treating only the oxidizer as a real fluid species, while the fuel and combustion products are assumed to behave as ideal gas species. This hybrid real-ideal approach allows for a substantial simplification of the equations of state for the real fluid. Thus, based on the original formulation by Kim et al. [29], the specialized cubic equation of state for the described mixture has been reformulated into:

$$\begin{aligned} p(\rho ,T,\chi _\textrm{ox}) &= \dfrac{\rho R_u T}{{\mathfrak {w}} - \chi _\textrm{ox} b_\textrm{ox} \rho } + \nonumber \\ & \quad - \dfrac{\chi _\textrm{ox}^2 a_\textrm{ox}\alpha _\textrm{ox} \left( T\right) \rho ^2}{ \left( {\mathfrak {w}} + \rho \chi _\textrm{ox} b_\textrm{ox} \right) {\mathfrak {w}} } \end{aligned}$$
(2.21)

where \({\mathfrak {w}}\) represents the molar weight of the mixture, \(R_u\) is the universal gas constant, \(\chi _\textrm{ox}\) the oxidizer molar fraction, while \(a_\textrm{ox}\alpha _\textrm{ox}(T)\) and \(b_\textrm{ox}\) are model parameters for real fluid effects which are listed in [29]. This equation of state formulation is reminiscent of the Soave-Redlich-Kwong (SRK) EoS, as introduced in the pioneering work [30].

In the hybrid real-ideal EoS configuration, the computation of numerical fluxes at cell interfaces necessitates the utilization of a generic fluid Riemann solver. In this regard, a modified version of the Glaister formulation of the Roe approximated Riemann solver [31] is employed. A comprehensive determination of the thermodynamic quantities from Eq. (2.21) can be found in [32]. Details regarding the validation of the discussed EoS and Riemann solver can be found in [33].

It is important to emphasize that the adoption of the hybrid real-ideal EoS, although already significantly simplified compared to its original formulation, leads to a notable increase in computational demands. Consequently, it is not suitable to be used in a low-order framework involving complex multi-injector systems. However, it can be highly valuable in the analysis of such systems within a fully Q1D reduced framework, as demonstrated in the subsequent Sections.

3 Experimental setup

The experimental data used in this study come from a test campaign performed within the LOX/Hydrocarbon Combustion Instability Investigation Program at NASA in the late 80 s (NAS3-24612 [8]). The primary objective of this experimental campaign was to evaluate the stability characteristics of the LOX/\(\hbox {CH}_4\) propellant combination in comparison to LOX/\(\hbox {H}_2\).

The thrust chamber employed in the program at NASA Lewis Research Center (now known as Glenn Research Center) belongs to the class of 178 kN thrust chambers frequently utilized in U.S. combustion instability studies [1]. Referred to in this paper as “NASA-LeRC”, the engine consists of a combustion chamber with a diameter of 14.38 cm, where propellants are introduced through a system of 82 recessed shear coaxial injectors, with each LOX post supplied by a cavitating venturi. The length of the oxidizer post is 9.16 cm, and the recess measures 5.13 mm. The cylindrical portion of the chamber extends for 24.23 cm and is followed by a 14.32 cm long convergent–divergent nozzle, featuring a contraction ratio of 2.92. Details of the thrust chamber assembly are depicted in Fig. 4.

Fig. 4
figure 4

Details of the NASA-LeRC thrust chamber assembly. Image credits: [8]

Full size image

A total of 17 tests were conducted in this campaign, with variations in the engine load point for each case. Specifically, the mixture ratio ranged from 2.5 to 3.7, employing a fuel-rich mixture in all instances, while the nominal chamber pressure was approximately 13.8 MPa. Out of the 17 tests, 6 investigated the onset of spontaneous instability, with two resulting in unstable operations. The pressure signal spectra recorded during these two experiments revealed that the majority of the power spectral density was centered around the first tangential mode (1T) of the chamber (5.2 kHz). For the purpose of studying tangential instability phenomena, the load point labeled as “Test 014-004” represents an ideal candidate and is therefore chosen as reference. Complete information regarding the engine geometry and details of the selected load point operational conditions are reported in Table 1.

Table 1 Geometrical data of the NASA-LeRC combustor and details of the Test 014-004 load point
Full size table

4 Results and discussion

The low-order solver discussed in this study has been tested using the NASA-LeRC experimental test case. An important peculiarity of the selected test case is that the oxygen in the post is at supercritical pressure and subcritical temperature, in a so-called dense fluid state (liquid-like state), which requires a proper thermodynamic modeling through a real fluid equation of state [25], as mentioned in Sect. 2.4. Initially, a preliminary analysis is conducted on the complex multi-injector system within a reduced single-injector Q1D framework. This simplified geometry enables the use of the hybrid real-ideal equation of state described in Sect. 2.4. A comprehensive parametric analysis is performed to evaluate the significance of the various free parameters of the model.

Subsequently, the full-scale geometry is considered and analyzed using the hybrid-D solver. A parametric analysis is also conducted for this configuration. Finally, the behavior of the low-order numerical tool when dealing with damping devices is assessed. The implementation of baffles is, therefore, discussed and the corresponding results are presented.

4.1 Reduced single-injector configuration

4.1.1 Numerical setup

The unstable dynamics of the NASA-LeRC engine is approached at first in a Q1D fashion, as a preliminary step towards the analysis of the entire engine. The hybrid real-ideal equation of state is used in this case because of the simplified computational setup. The Q1D solver is employed to analyze the entire domain.

This modeling choice implies some geometrical modifications in order to reproduce the self-excited nature of the actual 3D multi-injector engine. Injector cross-sectional areas are preserved, while the engine throat area has been downscaled by a factor of 82 to preserve the nominal chamber pressure, since only a single-injector element out of the total 82 is considered. Consequently, the chamber diameter is also downscaled to maintain the original convergent nozzle contraction ratio.

Given the significant influence of injector acoustics on the unstable dynamics of an engine and considering that the employed equation of state commits approximately an 18% error when predicting the speed of sound in the oxidizer post [33], the length of the injector oxidizer post has been adjusted to ensure that the first longitudinal numerical frequency (1 L) of the injector aligns with the experimental frequency, according to:

$$\begin{aligned} \left( \frac{l_\textrm{inj}}{a+u} + \frac{l_\textrm{inj}}{a-u}\right) _\textrm{num} = \left( \frac{l_\textrm{inj}}{a+u} + \frac{l_\textrm{inj}}{a-u}\right) _\textrm{exp} \end{aligned}$$
(4.1)

where \(l_\textrm{inj} = l_\textrm{po} + l_\textrm{rec}\) is the length of the injector (subscript “inj” for injector, “po” for post, and “rec” for recess). It must be underlined that only the post length has to be modified, while the recess length is kept fixed.

Furthermore, to capture transverse instabilities within a one-dimensional framework, the chamber length is scaled to align the first longitudinal mode (1 L - numerical) frequency with the experimental 1T frequency. The scaling of the chamber length is performed based on the assumption of linear acoustics regime and a closed-closed cylinder geometry for the chamber:

$$\begin{aligned} f_{1T,\textrm{exp}} = \dfrac{a_\textrm{c}}{2 l_\textrm{c}} \left( 1-M_\textrm{c}^2 \right) \end{aligned}$$
(4.2)

where the subscript “c” means that the quantities are evaluated in the combustion chamber, a is the speed of sound, and M is the Mach number. Details of the analyzed single-injector configuration are shown in Table 2.

Table 2 Geometrical data and operating conditions of the single-injector NASA-LeRC configuration
Full size table

The domain is discretized into 2713 cells, which are not uniformly spaced due to the specific characteristics of the flow in the recess. This careful arrangement of the mesh is necessary to prevent resolution issues of convected fuel pockets. In this region, the flow velocity is relatively low, and coupled with the high frequencies associated with thermo-acoustic phenomena, it results in a small spatial wavelength of the convected fuel pockets. To accurately capture the convection of these high-wavenumber entropy waves, a sufficient number of cells must be employed in the region of interest (between the fuel injection zone and the flame front). Details of the domain discretization are shown in Fig. 5.

Fig. 5
figure 5

Details of the NASA-LeRC test case Q1D numerical domain

Full size image

It is worth to remind that an appropriate choice of the model free parameters, as described in Sect. 2, is crucial for its application. For the analyzed case, the combustion starting abscissa \(x_\textrm{c}\) (Eq. (2.9)) has been chosen to be placed at the beginning of the combustion chamber (\(x_\textrm{c}=0\) mm, flame anchored to the faceplate), the amplification parameter of the response function \(\sigma\) (Eq. (2.17)) has been set to 40, and the sampling abscissa \(x_\textrm{s}\) (Eq. (2.17)) to 2 mm from the backstep. The heat release calibration parameters, \(\delta\) and \(T_\textrm{r}\) (Eq. 2.9), are carefully selected to achieve the steady-state temperature (\(T_\textrm{c}\), i.e. with the response function “switched off”) after complete combustion at 5% of the chamber length. The values of these tuning parameters have been chosen according to previous works [24, 25] and are labeled in the following as “Configuration A”.

4.1.2 Reference configuration results

Results for Configuration A are presented in Figs. 6 and 7. Clearly, the low-order numerical tool accurately predicts the occurrence of combustion instabilities, capturing the typical evolution of a thermo-acoustic instability. Figure 6a displays the pressure signal over time, specifically sampled at the end of the chamber. The signal exhibits an exponential growth in the amplitude of the oscillations (Fig. 6b), followed by a limit cycle (Fig. 6c). The power spectral density (PSD) of the pressure signal is depicted in Fig. 6d.

Fig. 6
figure 6

Computed chamber pressure sampled at the end of the chamber cylindrical section for Configuration A

Full size image

The dynamics of the fuel pockets, represented by the fuel mass fraction, and its impact on the chamber temperature are illustrated in Fig. 7. The Figure clearly shows the cyclic accumulation and release of fuel pockets, resulting in alternating zones with complete fuel depletion and fuel-rich regions, which is a product of the response function action. As the engine nominal mixture ratio is fuel-rich, areas with stronger fuel dilution exhibit a decrease in temperature. This behavior leads to unsteady heat release, thereby closing the feedback loop responsible for the instability.

Fig. 7
figure 7

Dynamics of fuel mass fraction and chamber temperature during an instability for Configuration A

Full size image

The predicted instability corresponds to the modal shape of the first longitudinal mode of the chamber (1 L), with a peak-to-peak amplitude of 4.8 MPa and a dominant frequency of 5483 Hz (see Fig. 6d). Table 3 provides a comparison between the experimental and computed characteristics of the instability limit cycle. A 5.44% accuracy is achieved in terms of frequency of the limit cycle, while a larger discrepancy is observed for the peak-to-peak amplitude. This difference can be attributed to the simplification of the complex multi-injector 3D dynamics to a single-element representation, which lacks interaction among the different injector elements. However, the injector model functionality in terms of response function dynamics is confirmed.

Table 3 Comparison between the limit cycle obtained with the one-dimensional solver and the experimental data (Test 014-004 [8])
Full size table

It must be underlined that the prediction of a 1 L behavior does not disagree with the experimental data. In fact, the numerical result stems from the reduction of the original 3D multi-injector system to a Q1D single-injector system. Consequently, the combustor length is scaled to align the 1T mode of the multi-injector system with the 1 L mode of the single-injector system. The presence of the 1 L mode in the numerical simulations mirrors the occurrence of the 1T mode in the multi-injector system, in line with the experimental data.

4.1.3 Sensitivity analysis

A parametric analysis is conducted to evaluate the impact of the free parameters \(x_\textrm{c}\) and \(x_\textrm{s}\) in the low-order model. Previous studies in an ideal gas framework [25, 34] have already demonstrated a significant influence of these parameters on both the peak-to-peak amplitude and frequency of the limit cycles. In fact, the distance between \(x_\textrm{c}\) and \(x_\textrm{s}\) introduces a space-time lag between pressure oscillations and unsteady heat release, thereby affecting the overall instability behavior. Moreover, a parametric analysis with respect to \(x_\textrm{c}\), provides insights into how delays in mixing, breakup, evaporation, and ultimately in the chemical reaction onset might impact the results.

In the current test case, various configurations are examined, with \(x_\textrm{c}\) ranging from 0 to 2 mm (from the faceplate), and \(x_\textrm{s}\) ranging from 1 to 5 mm (from the backstep). The results, depicted in Fig. 8, illustrate the frequencies and peak-to-peak amplitudes of the limit cycles for each configuration.

The frequency analysis reveals the presence of two dominant modes: the first longitudinal mode of the chamber (1 L) at approximately 5500 Hz, and the first longitudinal mode of the entire system at around 2000 Hz. This non-linear behavior highlights that changes in the distance \(x_\textrm{c}-x_\textrm{s}\) can lead to bifurcations in the solution. The cycle amplitude also displays a strong dependence on the analyzed parameters, with values ranging from 3 to 9 MPa. Unsurprisingly, high amplitude values are associated to the lower dominant frequency (2000 Hz), due to its lower numerical diffusion and due to the lower energy required to excite this resonance mode (with respect to a higher frequency one, such as 5500 Hz).

Through the reconfiguration of the model parameters, the predicted amplitude has nearly doubled compared to the reference configuration. However, these values still deviate significantly from the experimental data of 20 MPa, and a direct comparison between the amplitudes of the tested configurations is challenging due to the different characteristics of the fluctuation spectra.

Fig. 8
figure 8

Limit cycle features for different configurations of \(x_\textrm{c}\) and \(x_\textrm{s}\) (larger symbols for Configuration A)

Full size image

Despite this dependency of limit cycles features on (\(x_\textrm{c}\), \(x_\textrm{s}\)), the spontaneous instability is always captured.

4.2 Complete multi-injector configuration

4.2.1 Numerical setup

The NASA-LeRC test case is then examined in its full-scale configuration with multiple injectors employing the hybrid-D solver. Considering the computational demands associated with the analysis of the full-scale system, the ideal equation of state is employed. This choice is made to maintain the primary advantage of a low-order model, which is its computational efficiency, as the inclusion of a real fluid treatment would significantly increase the computational time. Previous applications of the presented low-order model with the ideal gas equation of state can be found in [24, 34] for a reduced single-injector system and in [25, 26] for a 3D multi-injector system. In particular, in [25, 34], the ideal gas equation of state is used for test cases employing a cryogenic oxidizer.

In an ideal gas framework, the supercritical propellant is replaced with thermally perfect gas, retaining the LOX injection temperature (115.4 K). In order to preserve the acoustic features of the injector within an ideal gas framework, the length of the oxidizer post needs to be rescaled such that the fundamental injector frequency in the ideal case matches the experimental injector frequency (as performed in Sect. 4.1.1, using Eq. (4.1)). This “acoustically equivalent” version of the injector yields an oxidizer post length of 19.39 mm (Fig. 9), as expected shorter with respect to the real one.

Fig. 9
figure 9

Acoustic rescaling of the oxidizer post length

Full size image

In the hybrid-D model, the injectors are represented by 82 identical Q1D domains, each consisting of 500 equispaced cells. Conversely, the combustion chamber is described by a three-dimensional 5-blocks domain with approximately \(\sim\)400k cells. The geometry and discretization details of the domain can be found in Fig. 10. Notably, Fig. 10a illustrates the significant axial mesh refinement near the injection plate that, as explained in Sect. 4.1.1, is necessary to prevent numerical diffusion in slow moving regions. Specifically, to manage efficiently the computational resources, the axial cell size has been selected to ensure that each fuel pocket is adequately captured by a suitable number of cells. This approach strikes a balance between capturing the details of the convected fuel pockets and controlling the computational demands associated with a 3D analysis.

Fig. 10
figure 10

Details of the NASA-LeRC domain in the hybrid-D framework

Full size image

As demonstrated in the sensitivity analyses presented in Sect. 4.1.3, the unstable dynamics exhibits a clear dependence on the space-time lag represented by the parameters (\(x_\textrm{c}\),\(x_\textrm{s}\)). Since \(x_\textrm{s}\) is a purely numerical parameter which lacks physical significance, its value cannot be deduced a priori from experimental data or high-fidelity steady-state simulations, unlike \(\delta\), \(T_\textrm{r}\), and \(x_\textrm{c}\), which all have physical bases. Moreover, sampling the pressure for the injector response at a single point in the recess can activate the response function on numerically generated spurious oscillations, compromising the quality of the result to some extent. Therefore, to ensure that the solution is not influenced by this parameter in a manner that is neither physical nor controllable, the dependence on \(x_\textrm{s}\) is eliminated.

This modification is obtained by redefining the sampled pressure value \(p\left( t,x_\textrm{s}\right)\) and the reference pressure value \(p_\textrm{s}(t,x_\textrm{s})\), which are no longer sampled at a specific abscissa \(x_\textrm{s}\), but rather averaged over the entire recess:

$$\begin{aligned} \hat{\dot{m}}_\textrm{f}'&=\dot{m}_\textrm{f,n} \left[ \exp \left( -\sigma \;\dfrac{\overline{p}(t)-\overline{p}_\textrm{s}(t)}{\overline{p}_\textrm{s}(t)}\right) -1\right] \end{aligned}$$
(4.3)
$$\begin{aligned} \overline{f}(t)&{:=}\int _{x_\textrm{rec,m}}^{x_\textrm{rec,M}}f(x,t) dx \end{aligned}$$
(4.4)

The value of \(\overline{p}_\textrm{s}(t)\) is determined by calculating the time-averaged \(\overline{p}{(t)}\) over a 2 ms window, which corresponds to approximately 10 periods of the experimentally measured instability. Using the pressure averaged in the recess not only disentangles the solver from a physically meaningless parameter (\(x_\textrm{s}\)), but also enables the filtering of numerically generated waves, thus preserving the quality of the result.

For the analyzed case, \(x_\textrm{c}\) is set to 0 mm (flame anchored to the faceplate) and \(\sigma\) is assigned a value of 300. The heat release calibration parameters, \(\delta\) and \(T_\textrm{r}\), are selected to achieve the steady-state temperature after complete combustion at 15% of the chamber length. Again, the values of these tuning parameters have been chosen according to previous works [25, 35]. In the following, this specific parameters configuration is referred to as “Configuration B”.

4.2.2 Reference configuration results

Fig. 11
figure 11

Chamber pressure field at 4 consecutive time instants \(t_i\) within a limit cycle period for Configuration B, showing a 1T1L mixed mode (\(f_\textrm{lim}\) is the computed dominant limit cycle frequency)

Full size image

The results obtained with Configuration B are presented in Figs. 11 through 14. Figure 11 shows the chamber pressure at four equispaced consecutive time instants within a limit cycle period. It is clear that the hybrid-D model successfully captures the instability associated with the first tangential mode (1T) of the chamber. In fact, within each time frame \(t_i\), a distinct nodal line becomes apparent, dividing the faceplate into two nearly equal regions, one characterized by high pressure (with respect to the average pressure) and the other one by low pressure. It is worth noting the rotational displacement of the pressure nodal line, indicating the spinning nature of the instability. This behavior is consistent with the experimental observations [8]. Additionally, the computed instability exhibits a combination of longitudinal and transverse dynamics. The axial topology of the pressure field reveals an excitation of the first longitudinal chamber mode (1 L), resulting in a mixed 1T1L mode.

Fig. 12
figure 12

Lateral view of pressure field at 2 time instants for Configuration B

Full size image

The lateral views of the pressure field in Fig. 12 provide valuable insights into the complex coupling dynamics between the combustion chamber and the injectors. As the high-pressure wave intersects an injector, a shock wave propagates upstream, leading to fuel accumulation within the recessed region due to the action of the response function. Subsequently, the lack of convected fuel into the chamber results in off-stoichiometric conditions and a sudden decrease in heat release rate. This thermal event generates an intense isotropic rarefaction. The rarefaction travels upstream into the injector along the \(u-a\) characteristic line, causing the release of the accumulated fuel and initiating a new thermo-acoustic cycle. Hence, the model effectively captures the complex thermo-acoustic feedback mechanism.

The complex dynamics of fuel accumulation and release is illustrated in Fig. 13, which depicts the spatial distribution of temperature and fuel mass fraction within the chamber at a specific time instant (\(t_3\)). The snapshots in Fig. 13 reveal an intricate pattern characterized by alternating regions with fuel-rich conditions and oxidizer-rich conditions. These regions exhibit mixture ratios deviating from stoichiometry. The reduced heat release associated with these non-stoichiometric conditions leads to low temperature zones within the chamber, as shown in Fig. 13a. It is worth noting that each Q1D domain of the injectors has its own response characteristics due to their distinct response functions. This results in a pronounced phase difference among the convected fuel pockets, leading to significant heterogeneity in the temperature and fuel mass fraction fields, as observed in Fig. 13b. However, the azimuthal phase shift of these pockets is a reflection of the spinning tangential nature of the instability interacting with the injectors.

Fig. 13
figure 13

Temperature and fuel mass fraction fields at \(t_3\) for Configuration B

Full size image

Figure 14 presents the pressure signal sampled at the outer edge of the injection plate, along with its corresponding PSD. The temporal evolution of a spontaneous thermo-acoustic instability is clearly observed, initially exhibiting an exponential growth of oscillation amplitude (Fig. 14b), followed by the emergence of a limit cycle regime characterized by non-linearities (Fig. 14c).

Fig. 14
figure 14

Pressure signal sampled at the outer edge of the injection plate for Configuration B

Full size image

The maximum peak-to-peak amplitude of the pressure field is measured at 8 MPa, with a relative error of 60% compared to experimental data. Although still considerably distant from the experimental data, this value marks a substantial improvement compared to the results obtained using Configuration A with the Q1D model, with the predicted peak-to-peak amplitude going from 4.8 to 8 MPa. Moreover, the dominant frequency of 5350 Hz is captured with a small error margin of 2.88%.

In Fig. 14d, distinct secondary harmonic peaks emerge at approximately 7763 Hz and 10652 Hz. These peaks are likely associated with the second tangential mode (2T) and the first radial mode (1R) of the chamber. Indeed, by computing the theoretical eigenfrequencies of the combustor within the framework of linear acoustics using Bessel functions [36], frequencies of 8942 Hz and 11223 Hz are derived for the 2T and 1R modes, respectively. These values can be considered comparable to the numerically obtained ones, particularly when considering the differences between linear acoustics and the observed unstable regime, characterized by high amplitude oscillations.

Table 4 provides a comparison between the experimental and computed characteristics of the instability limit cycle. It is important to note that the discrepancy in amplitude can be attributed in this case to the use of the ideal gas model. In fact, the ideal gas model deviates significantly from more refined thermodynamic formulations in the cryogenic regime found in the oxidizer post of the analyzed test case, particularly in terms of acoustic impedance (\(\rho a=824\) kg/(\(\textrm{m}^2\)s) in the experimental case and 91 kg/(\(\textrm{m}^2\)s) using ideal EoS), which can affect the amplitude of acoustic waves.

Table 4 Comparison between the limit cycle obtained with the hybrid-D solver and the experimental data (Test 014-004 [8])
Full size table

In conclusion, the results obtained with both the Q1D and hybrid-D solvers demonstrate the model capability to capture the essential characteristics of a thermo-acoustic instability, including its temporal evolution and dominant frequency. This showcases the effectiveness of using the presented calibration-free response function as the main driving factor for self-sustained instabilities. Although there are some discrepancies in accurately predicting the amplitude of the observed limit cycles, the excellent agreement in terms of frequency with experimental measurements highlights the model potential for guiding the design and optimization of liquid rocket engines.

4.2.3 Sensitivity analysis

As for the one-dimensional solver, conducting a comprehensive sensitivity analysis of the hybrid-D model parameters is crucial to understand its key dependencies. Specifically, in this section, we investigate the impact of the proportionality factor \(\sigma\), the combustion starting abscissa \(x_\textrm{c}\), the pressure sampling abscissa \(x_\textrm{s}\), and the calibration parameters of the thermal release curve, \(\delta\) and \(T_\textrm{r}\). The reference configuration used throughout the analysis is Configuration B. All pressure signals considered are sampled at the outer edge of the faceplate.

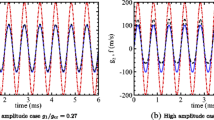
The dependence on the proportionality factor \(\sigma\) is illustrated in Fig. 15, displaying the characteristics of the limit cycle. Remarkably, very low values of \(\sigma\) result in a stable system. As \(\sigma\) increases, a plateau-like behavior emerges, indicating that the thermo-acoustic characteristics become insensitive to further variations of the pressure proportionality factor beyond a certain threshold. This behavior stems from the structure of the response function, since surpassing the threshold value of \(\sigma\) disrupts entirely the fuel flow during the accumulation phase, causing the response function to reach a state of “saturation”.

Fig. 15
figure 15

Limit cycle characteristics with respect to \(\sigma\) (larger symbols for Configuration B)

Full size image

The sensitivity analysis for the combustion starting abscissa \(x_\textrm{c}\) and the pressure sampling abscissa \(x_\textrm{s}\) is presented in Fig. 16, focusing on the peak-to-peak amplitude and frequency of the limit cycle. It is noteworthy that, given Configuration B as the reference setup, the sensitivity analysis for \(x_\textrm{c}\) has been performed employing the redefined response function (Eq. (4.4)), where the sampling pressure is averaged across the recess. Conversely, the sensitivity analysis for \(x_\textrm{s}\) has been conducted using the response function defined in Equation (2.17), where pressure is sampled at a specific location within the recess. The purpose of the parametric analysis on \(x_\textrm{s}\) is to evaluate the extent to which numerical effects can impact the results and to assess the distinctions between these two response functions. Both peak-to-peak amplitude and frequency of the limit cycle exhibit similar trends with respect to \(x_\textrm{c}\). Specifically, as \(x_\textrm{c}\) increases, the peak-to-peak amplitude and frequency decrease. Stability is achieved for \(x_\textrm{c} \ge 7.5\) mm (Fig. 16a). The decrease in frequency can be attributed to the reduced temperature near the faceplate, which leads to a lower average speed of sound and subsequently lower acoustic eigenfrequencies of the chamber. The decrease in amplitude with increasing \(x_\textrm{c}\) is not solely due to the variation in the spatial-temporal lag between pressure oscillations and heat release, but can also be influenced by numerical diffusion of slow fuel pockets, as they travel for a larger distance before combustion, and as they move along increasingly larger cells in the x-axis direction (Fig. 10a).

Fig. 16
figure 16

Limit cycle characteristics as functions of \(x_\textrm{c}\) and \(x_\textrm{s}\) (larger symbols for Configuration B)

Full size image

The pressure sampling abscissa \(x_\textrm{s}\), as expected, has an impact on the thermo-acoustic characteristics. Figure 16b demonstrates the diverse behavior of limit cycles as \(x_\textrm{s}\) varies, with fluctuations in peak-to-peak amplitude of about 2 MPa and in frequency of about 1500 Hz. This phenomenon arises from the complex interplay between the sampling location, convective transport, and heat release dynamics within the combustion chamber. The observed chaotic nature, both for the Q1D and hybrid-D solvers (Figs. 8 and 16b) with respect to \(x_\textrm{s}\) reinforces the decision to decouple the behavior of the response function from this unphysical parameter with the redefined response function (Eq. (4.4)).

Fig. 17
figure 17

Sensitivity analysis with respect to the heat release curve calibration parameters

Full size image

An analysis has been conducted on the calibration parameters of the heat release curve, namely \(\delta\) and \(T_\textrm{r}\). The aim of this analysis is to understand how changes in flame length might affect the results. A simulation was performed to achieve the steady-state temperature after complete combustion at 5% of the combustion chamber. A comparison between the resulting pressure fields and Configuration B, where the steady-state temperature after complete combustion is reached at 15% of the combustion chamber, is shown in Fig. 17. While the amplitude of the pressure oscillations is comparable, the fields differ in their longitudinal dynamics. Configuration B exhibits a 1 L longitudinal mode superimposed on the dominant 1T mode, whereas the new setup shows 2 L longitudinal activity. This difference results in an increase in the dominant frequency, which is 6182 Hz for the new setup (see Fig. 17c).

Given the significance demonstrated by the spatial-temporal lag between the recess and \(x_\textrm{c}\), a modified geometrical configuration was considered. Specifically, the length of the recess \(l_\textrm{f}\) (Eq. (2.10)) was doubled while maintaining the overall length of the injectors. This change had two thermo-fluid dynamic consequences. Firstly, the distance traveled by each fuel pocket before combustion was doubled. Secondly, the evolution of flow variables inside the recess exhibited a quantitatively different behavior, resulting in a slight change in the injector longitudinal frequency. Both of these effects led to variations in the spatial-temporal lag between pressure and heat release oscillations, which are crucial for the self-sustaining nature of thermo-acoustic instability.

Fig. 18
figure 18

Sensitivity analysis with respect to the recess length

Full size image

Figure 18 shows the results obtained with the modified configuration, which remains unstable but exhibits pronounced variations in the characteristics of the associated limit cycle. The instability primarily affects the first longitudinal mode of the combustion chamber (1 L), with a dominant frequency of 2240 Hz and a peak-to-peak amplitude of the pressure signal equal to 5 MPa, as shown in Fig. 18c and d. This finding further emphasizes the important roles played by injector design and by the lag between pressure and heat release oscillations in determining the onset and the thermo-acoustic characteristics of the instability.

In conclusion, the sensitivity analyses performed for both the Q1D and hybrid-D solvers provide valuable insights into the intricate relationships between the free parameters and the thermo-acoustic behavior of the model. These analyses contribute to the refinement of the model and enhance its predictive capabilities for practical applications.

4.2.4 Damping devices

To assess the predictive capability of the hybrid-D model and its ability to distinguish between stable and unstable setups, the effect of damping devices within the combustion chamber is examined. Damping devices, such as baffles and acoustic cavities, have been widely used in liquid rocket engines to control and dampen high-frequency combustion instabilities [1, 37]. In this study, baffles are implemented and analyzed within the hybrid-D formulation, as they have a historical usage and have proven effective in stabilizing tangential modes [5].

Fig. 19
figure 19

Details on the disposition and geometry of the baffles used for the NASA-LeRC engine

Full size image

From a modeling perspective, baffles are represented as infinitesimally thin solid walls placed within the flow field. Once the number and arrangement of baffles in the chamber are determined, they are treated as wall boundary conditions on the transverse plane relative to the x-axis. Figure 19 illustrates the geometric characteristics of the 3-baffle configuration chosen as a test case in this work. Following the guidelines outlined in [38], the length of the baffles is set to 20% of the chamber diameter. The free parameters of the low-order model are kept constant, adhering to the specifications defined in Configuration B.

Fig. 20
figure 20

NASA-LeRC unstable mode using baffles

Full size image

The results obtained in terms of the chamber pressure field with the presence of baffles are depicted in Fig. 20a and b, clearly demonstrating the impact of the three baffles on the pressure field topology. The presence of the baffles introduces noticeable distortions compared to the characteristic symmetry of the first tangential chamber mode. The interaction between the azimuthal high-pressure wave associated with the instability and the baffles leads to partial reflection and bypassing of these solid obstacles. The gas dynamic phenomena resulting from this interaction significantly influence the thermo-acoustic characteristics of the engine, as shown in Fig. 20c and d, which presents the pressure signal acquired at the outer edge of the injection plate. A comparison of this signal with the one shown in Fig. 14 reveals a reduction in the peak-to-peak amplitude of around 3 MPa (from 8 MPa to 5 MPa). Furthermore, the altered structure of the pressure field leads to a change in the dominant frequency, with the case featuring baffles exhibiting a frequency of 5800 Hz, compared to the 5350 Hz observed in the configuration without baffles. The increase in the limit cycle frequency and decrease in amplitude are consistent with the partial obstruction of pressure wave propagation caused by the interaction with the solid walls. This interaction disrupts the spinning mode of the waves, resulting in a decrease in the energy of the oscillation.

In conclusion, while the introduction of baffles did not stabilize the engine, a significant reduction in the intensity of pressure oscillations was observed, along with a variation in the dominant frequency due to the breaking of symmetry. It should be noted that a comprehensive analysis of engine stabilization through baffles would require an extensive parametric study considering the number, geometry, and arrangement of the baffles within the chamber, which is beyond the scope of this analysis. Moreover, a thorough evaluation of the solver behavior with baffles would necessitate access to a substantial amount of experimental data, particularly on the reference test case, which is currently unavailable. Lastly, it’s crucial to emphasize that the incorporation of baffles does not automatically guarantee engine stabilization, as demonstrated by the F-1 engine campaign, which demanded approximately 3200 full-scale tests before declaring the engine ready for flight [39].

5 Conclusions

In this study, we have presented a comprehensive investigation of spontaneous self-sustained transverse combustion instabilities in multi-injector engines using a low-order modeling framework. Our approach utilized a multi-dimensional non-linear low-order Eulerian model, incorporating a physically aware response function that directly links pressure oscillations to fuel mass flow rate. The model mimics the characteristics of shear coaxial injectors, characterized by a peculiar dynamics of cyclic fuel accumulation and release in response to acoustic waves.

The NASA-LeRC test case has been taken as reference for the validation of our approach. At first, the test case has been analyzed in a simplified one-dimensional framework by reducing the complex multi-injector configuration to a single-injector configuration. The lower computational demands associated to this setup allowed the use of a hybrid real-ideal equation of state, more appropriate when dealing with cryogenic propellants. Results obtained prove the viability of the low-order approach and of the employed response function. Predictions are in fact perfectly in line with the experimental data in terms of frequency, while the lack of predictability in the peak-to-peak amplitude is attributable to the adoption of a simplified single-injector configuration.

The low-order model is then assessed in its multi-D configuration with respect to the test case full-scale geometry. The model has also in this case proven its capabilities to capture the essential features of the thermo-acoustic instability, including its temporal evolution, dominant frequency, and pressure field topology. The model successfully reproduced the experimentally observed spinning nature of the first tangential mode, as well as the coexistence of longitudinal and transverse dynamics. The agreement in terms of frequency with experimental measurements was excellent. The lack of predictability with respect to the peak-to-peak amplitude, despite being improved with respect to the one-dimensional solver, can be in this case attributed to the ideal fluid assumption, a necessary choice to reduce the computational demands.

Additionally, a sensitivity analysis has been performed in both the one and multi-dimensional setups to assess the impact of the model free parameters on the predicted thermo-acoustic behavior. The results highlighted the significant influence of most of these parameters, especially the combustion starting abscissa, pressure sampling abscissa, and recess length. These findings provided valuable insights for refining the model and improving its accuracy in predicting the amplitude and frequency of the instability.

Lastly, we investigated the effect of introducing damping devices in the form of baffles within the combustion chamber. Although the dampers did not stabilize the engine, they led to a reduction in pressure oscillation intensity and a variation in the dominant frequency. The altered pressure field topology demonstrated the model ability to capture the gas dynamic interactions between the acoustic waves and solid obstacles.

In conclusion, the presented low-order modeling framework offers a viable approach for predicting transverse combustion instabilities in multi-injector engines and assess the characteristics of unstable modes. The model accuracy, computational efficiency, and capability to capture the essential thermo-acoustic characteristics make it a potentially interesting option for the design and optimization of new liquid rocket engines.