Abstract
This paper presents a streamlined design procedure for water-based noise suppression systems that are applicable to multiple classes of rocket engines. A newly adapted steady quasi-one-dimensional two-phase model is employed to predict the evolution of the exhaust gases interacting with water droplets. Such a model is embedded into a two-step optimization procedure with the objective of finding the most efficient combination of the suppressor operative parameters. This information is then used to design the hardware of the system, which consists in a set of injectors, with the task of producing atomized water jets directed towards the exhaust gases, and a toroidal manifold, with the task of delivering water to the injectors at uniform conditions of pressure and velocity. Finally, the proposed design procedure is applied to a 15 kN thrust class oxygen/methane liquid rocket engine. Technical specifications of the resulting water-based noise suppression system are provided along with a detailed three-dimensional CAD model.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
In the vicinity of a rocket, acoustic levels can reach up to 200 dB [1, 2]. Such extremely high fluctuating acoustic loads can critically affect the correct operation of the rocket, its components, and supporting structures. Even a small reduction in the acoustic load can result in substantial cost savings, since it reduces the effort needed to design and test each single component of the launch system. It should be noted that the maximum admissible overall sound power level (OASPL) for payload integrity is approximately 145 dB [3], while for residential areas around the launch or ground test pad the maximum allowed noise is around 65 dB.
Water injection is a particularly common application for both static testing and the launch of large-scale rocket engines, as it not only mitigates all jet noise sources [4], but also cools the exhaust plume and the facilities structures. Concerning acoustic suppression, two main mechanisms leading to noise reduction are present: reduction of jet velocity and jet temperature [5]. The decrease of jet velocity is achieved through momentum transfer between liquid and gas phase, which leads to significant variations of the turbulent structures, associated to low frequency noise [6, 7]. On the other hand, there is a reduction in jet temperature due to partial vaporization of the injected water [8]. As a result, the jet density increases, affecting the typical shock structures that characterize any supersonic jet. Specifically, the shocks contribution to the overall noise power level (associated to high frequency noise) is reduced.
The water injection systems implemented by NASA and ESA in their launch pads can attenuate the sound levels of an amount up to 12 dB, according to their reports [9,10,11]. Such noise reduction has been also confirmed by many experimental studies performed with subscale cold and hot supersonic jets [5, 12,13,14,15]. These studies have shown that even a small amount of water (water-to-jet mass flow ratio MFR < 1) significantly reduces the acoustic level associated with broadband shock noise and screech tones, whereas a high MFR (> 3) is needed to significantly attenuate low-frequency turbulent mixing noise.
Another outcome evolving out of the aforementioned experiments has been the definition of the optimal injection parameters and water jet features needed to achieve the highest noise reduction. Firstly, the water jet should be atomized, since atomization induces faster mixing with less impact and drag noise. Injection angles \(\alpha _\text {inj}\) are preferable in the range of 45–60 deg due to a compromise between significant penetration and low impact noise. As a matter of fact, the higher the injection angles (close to 90 deg, perpendicular to the jet), the higher the penetration of water in the exhaust jet, yielding faster mixing, however, the produced low-frequency impact, drag, and obstacle noise increase as well. The injection position must be close to the nozzle to maximize momentum transfer between exhaust gases and water, and to act directly on the peak noise-producing region (tip of the potential core, see also Sect. 2.1, Fig. 2) [16], affecting all the shock cells involved in the noise generation process. Lastly, the optimum water-to-jet MFR is in the range of \(\sim 3\)–5. Even if the noise reduction increases with the amount of injected water, beyond a certain value there is no effective momentum transfer and hence noise reduction. For hot jets, due to the evaporation of injected water, higher MFRs are required for maximum noise reduction, as compared to cold jets.
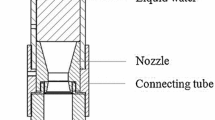
Although water-based systems appear to be efficient tools for containing acoustic emissions and reducing the overall cost of firing tests and launches, the literature lacks a comprehensive hardware design procedure. Thus, in this paper, a general sizing method for static firing water-based noise suppressors is presented in detail. The typical layout of a suppressor for static firing applications is composed of two main subsystems. The first one is the set of injectors, which have the task of producing atomized water jets directed towards the exhaust gases. The second one is the toroidal manifold, with the task to collect water and distribute it to the injectors with uniform conditions of pressure and velocity. A simplified scheme of such a system is shown in Fig. 1. For simplicity and conciseness, accessory subsystems such as water pressurization, guidance tube (if present), piping required to deliver water to the manifold, and power supply are not considered in this paper.
To be able to appropriately design the hardware of a water-based noise suppression system, it is important to highlight how the characteristic features of the suppressor affect the emitted noise. Thus, a theoretical understanding of the mechanisms that lead to noise reduction is mandatory. Two methods are commonly used to address this problem. The first one consists in performing high-fidelity computations involving coupled CFD-CAA (computational fluid dynamics-computational aero-acoustics) simulations [17,18,19]. However, this approach needs significant computational efforts, since high-order low-dissipation numerical schemes are required together with high resolution computational grids in both space and time to properly resolve the spectrum of interest. On the other hand, the second approach consists in the development of simplified theoretical models capable of capturing the main features of the phenomena, thus resulting of great interest especially for industrial purposes [9, 20]. Following this method, multiple simplifying assumptions are made and the model needs therefore to be calibrated on a reference experimental test case.
In this paper, the second strategy is followed. A newly adapted steady quasi-one dimensional (Q1D) two-phase model is developed and used to compute the properties of the nozzle exhaust gases (necessary to estimate the noise emissions) as nonlinear functions of the suppressor design parameters. After a thorough parametric analysis, carried out to assess the effect of the suppressor design on noise reduction, the Q1D model is embedded into a two-step optimization procedure with the objective of finding the most efficient combination of the aforementioned system control parameters for a target engine. Finally, the obtained optimal configuration can be used for the hardware design, consisting of injectors and a toroidal manifold. This general design procedure is applied here to size a suppressor for a 15 kN thrust class LOX/CH4 liquid rocket engine, assuming a total mass flow rate of 5.1 kg/s.
The paper is structured as follows. In Sect. 2 the Q1D model is presented alongside its governing equations (Sect. 2.1), and its submodels for water atomization (Sect. 2.1.1) and noise propagation (Sect. 2.1.2). Validation of the model against CFD data is also provided. The main features of the optimization procedure are presented in Sect. 2.2, with the hardware sizing methodology described shortly after in Sect. 2.3 for injectors (Sect. 2.3.1) and manifold (Sect. 2.3.2). Finally, in Sect. 3, results are discussed. First, the outcome of the parametric analysis performed with the Q1D code is presented and the effect on noise suppression of each system parameter is analyzed (Sect. 3.1). Then, results of the optimization and hardware sizing are presented in detail along with a 3D CAD model of the system and its technical specifications (Sect. 3.2).
2 Methodology and models
The first part of this section introduces the steady quasi-one-dimensional model used to calculate the noise emitted by the engine as a function of the exhaust gas properties and the suppressor control parameters. The second part is dedicated to the description of the optimization procedure used to obtain the optimal combination of the water-based system features. Finally, the third part presents a general methodology for hardware sizing.
2.1 Description and validation of the Q1D model
A steady quasi-one-dimensional two-phase model has been developed to obtain the mean velocity, temperature, and jet diameter evolution as functions of the axial distance from the nozzle exit section. Equations for mass, momentum and energy conservation for both liquid phase (subscript “\(\text {p}\)” for water particle) and gaseous phase (subscript “\(\text {g}\)”), have been adapted from [21, 22]. Specifically, mass, momentum, and energy conservation for gaseous phase, and momentum and energy conservation for liquid phase have been taken from [16], while mass conservation for liquid phase from [22]. In [16], in fact, the rate of mass transfer between a water droplet and the surrounding gas is assumed to be determined by the difference between concentrations of water vapor at the droplet surface and away from it. The assumption is valid for cold jets but not for hot jets (which characterize liquid rocket engines). For this reason, mass conservation for the liquid phase has been taken from [22], where water droplet evaporation rate is assumed to be driven by heat transfer rather than diffusion (more accurate for hot jets). The equations are listed in the following ODE system:
where n is defined as the ratio between water mass flow rate and droplet mass, \(T_\text {sat}\) is the saturation temperature of the liquid phase, \(\kappa\) is the thermal conductivity, \(\text {Nu}\) the Nusselt number, and B is the Spalding transport parameter for heat transfer defined as:
where \(L_\text {v}\) is the latent heat of vaporization for the liquid phase.
In the system of equations shown above, Eq. (2.1) is the continuity equation for liquid phase, Eq. (2.2) the liquid momentum conservation, and Eq. (2.6) its energy conservation. On the other hand, Eqs. (2.3), (2.4), and (2.5) are, respectively, mass, momentum, and energy conservation for the gaseous phase.
This Q1D model is well suited to assess the weight that each control parameter of the system (ie, water-to-jet MFR, water injection angle \(\alpha _\text {inj}\), injection pressure \(p_\text {w}\), and number of injectors \(N_\text {inj}\)) has on the evolution of the flow, which is directly related to the generation of sound waves.
The evaporation rate of a water droplet is driven by the difference between the heat transfer that occurs between the inside and the surface of the droplet and the heat transfer between the surface of the droplet and the surrounding gas [22]. Therefore, there is a link between the amount of evaporated water and the amount of injected water (related to MFR), and also a dependence on the degree of atomization (related to MFR, \(p_\text {w}\), and \(N_\text {inj}\)). Droplet dynamics has been modeled using a suitable drag function to assess the droplet acceleration process within the computational domain. Therefore, a dependence on the initial water velocity can be observed, which results directly from the injection pressure \(p_\text {w}\) and angle \(\alpha _\text {inj}\). The droplet drag coefficient \(C_D\) is defined according to [9].
where \(\text {Re}_\text {p}\) is the droplet Reynolds number defined on the basis of the particle diameter and slip velocity:
where \(\mu _\text {g}\) is the dynamic viscosity of the gaseous phase. The dependence on B shows how the drag coefficient decreases in the presence of evaporation with an increase in the evaporation rate.
The mass entrainment of ambient air has been modeled to monitor the spread rate of the shear layer in the potential core region (a schematic view of the flow structure can be seen in Fig. 2). Specifically, the definition of mass entrainment rate is given by [23] as:
where \(\dot{m}_\text {ex}\) is the mass flow rate at the nozzle exit, \(d_\text {ex}\) is the nozzle exit diameter, and \(\rho _*\) is the ratio between the entrained and initial fluid densities. \(K_\text {e}\) is a dimensionless entrainment rate coefficient, which is defined according to [24] as follows:
being \(\theta _\text {jet}\) the half angle of the jet cone. In [24], Medrano et al. observed a reasonable agreement between the presented entrainment model and experimental data in the intermediate and far-field regions. The air entrainment modeling allows to observe the dependence of the emitted noise with the injection axial position, since the effect of water injection decreases as the amount of entrained air increases.
It must be underlined that, since the interaction between the two jets is analyzed in a one dimensional framework, complete penetration of the water jet in the exhaust gases is intrinsically assumed. For this reason, the results obtained with the Q1D model can only be considered as the maximum theoretical performance achievable with the analyzed suppressor configuration. Nevertheless, the assumption of complete penetration can be considered valid when sufficiently high values of the injection angle \(\alpha _\mathrm {inj}\) (at least \(>30\) deg), water pressure \(p_\mathrm {w}\) (\(>3\) bar), and mass flow ratio \(\mathrm {MFR}\) (\(>2\)) are used [5].
The correct implementation of the Q1D model has been assessed by reproducing the results in the reference NASA report [21], as shown in Fig. 3.
Comparison between present results and results obtained by NASA in [21]
An exhaust jet of a 10-tons class, oxygen-methane, liquid rocket engine has been adopted as a reference for validation. A CFD RANS simulation of the jet plume in quiescent air at sea level has been carried out resorting to a well-established numerical framework [25,26,27,28,29]. The velocity and temperature fields obtained are shown in Fig. 4.
Concurrently, a simulation with the Q1D model without water injection has been carried out to compare the ensuing results with suitably cross-section averaged values extracted from the CFD simulation, as shown in Fig. 5. More specifically, the average temperature and velocity are obtained by weighted averages with the total mass flow rate, and the average pressure by weighted average with the area. Regarding the average velocity (Fig.5a) and temperature (Fig. 5b), although they show roughly the same variation between the end and the beginning of the simulated region, the results obtained in the CFD simulation are characterized by less regular trends compared to those obtained in the Q1D simulation, as expected from a multidimensional computation. Concerning the contour of the plume instead, the reduced model seems to perfectly match the CFD simulation (Fig. 5c). In general, the CFD and Q1D results can be considered sufficiently in agreement with each other to establish a reasonable validity of the adopted model.
The Q1D model makes the stringent assumption of constant pressure along the flow axis. Such hypothesis holds only if one considers a perfectly expanded jet. The reference jet, as can be seen in Fig. 4, is clearly overexpanded, hence, such an assumption is not valid. However, the CFD simulation shows that the average pressure is quite constant and close to the ambient pressure value downstream of the Mach disk (see Fig. 6a). As a result, the Q1D model can be applied to simulate this region.
Although the validation of the Q1D model has been carried out on the plume portion after the Mach disk to be consistent with the constant pressure assumption, all the analyses shown hereafter assume as initial conditions those corresponding to the exhaust of a perfectly expanded nozzle. This choice has been made because a large amount of air entrainment is present downstream of the Mach disk, which strongly reduces the sensitivity of the flow properties to variations in the control parameters of the sound suppression system.
2.1.1 Simplified atomization model
Water jet misting has a remarkable effect on noise reduction, as it affects both the droplet dynamics and the evaporation rate. As a matter of fact, the performance of the noise suppressor greatly improves as the diameter of the droplets decreases due to faster mixing, reduced drag and impact noise, and a larger surface available for heat exchange [5, 14]. For this reason, the Q1D model has to take into account the physics underneath water droplets formation.
Misting is the direct consequence of the breakdown of liquid ligaments, which in turn arise from the destabilization of a water jet through its interaction with the surroundings [30, 31]. Specifically, surface tension and dynamic viscosity tend to stabilize the structure, while shear forces associated to relative velocity between water and air represent a source of disruption leading to breakup. The resulting droplets diameter must also be related to the initial water jet diameter. A smaller jet will indeed produce smaller droplets if compared to a larger one under the same conditions.
Due to the complex physics behind water droplets formation, it is difficult to find an analytical model generalizing the aforementioned dependencies, therefore, a semi-empirical model has been implemented in the Q1D numerical tool [32, 33]:
where \(b_\text {inj}\) is the characteristic dimension of the injector exit, \(u_\text {w}\) the water exit velocity, \(\sigma _\text {w}\) the surface tension, and \(\rho _\text {w}\) and \(\rho _\text {a}\) the densities of water and air, respectively. Note that Eq. (2.12) is valid only for hydraulic injectors, where water flows through pressure and liquid breakup is the result of the jet interaction with surrounding quiescent air (see Fig. 8). As shown in Fig. 7, a higher exit velocity leads to smaller droplets due to an increase in the water-air shear forces, while a larger initial jet leads to larger droplets due to the increased amount of water to atomize.
Misting behavior with respect to water exit velocity and injector dimension according to Eq. (2.12)
In the Q1D model, the water droplets dimension is fixed once the water injection pressure \(p_\text {w}\), mass flow rate \(\dot{m}_\text {w}=\mathrm {MFR} \times \dot{m}_\text {jet}\), and number of injectors \(N_\text {inj}\) are known. In fact, the water exit velocity is determined by the pressure difference at either end of the injector using Bernoulli’s equation, while the characteristic dimension of the injector can be known once the total mass flow rate flowing through the element is given:
where \(b_\text {inj}\) is considered to be the minor semi-axis of an injector elliptical exit with area equal to \(A_\text {inj}\) and aspect ratio 3/2, and \(C_d\) is the nozzle discharge coefficient. The injectors orifice is here assumed to be elliptical because the injector class chosen for the problem at hand is the flat-fan injector (see Sect. 2.3.1), which requires that specific shape of the exit section.
2.1.2 Sound propagation model
To assess the noise level at a certain distance from the engine exhaust, the correlation presented by Kandula and Vu in [34] has been adopted. This correlation is based on a point source model for sound propagation which has been validated with test data for the overall sound power level over a wide range of jet temperatures and Mach numbers.
Once the mean velocity, temperature and exhaust jet diameter have been calculated through the Q1D model downstream of the water injection station, they are exploited to get the sound pressure level (SPL) at a generic distance from the noise source:
where \(G_1\) is a directivity factor which depends on the convective Mach number \(M_c\) and directivity angle \(\theta\). The \(G_2\) term accounts for the spectral distribution of the sound power, while \(K_1\) is a proportionality constant that needs to be calibrated. In the present case, a calibration procedure for \(K_1\) has been carried out with respect to the NASA SP-8072 model [16]. In particular, \(K_1\) has been chosen to ensure that the OASPL predicted by the Q1D model matches as best as possible the one predicted by the SP-8072 empirical model, for any engine in the range of validity of the latter. Lastly, the term SPL\(_{\text {abs}}\) includes dissipation effects due to atmospheric absorption [35]:
where \(f_\text {r,O}\) and \(f_\text {r,N}\) are the relaxation frequencies of oxygen and nitrogen, respectively, whose equations are reported in [35]. As a result, the OASPL at a generic distance r from the source is calculated by integrating the sound pressure level over all frequencies and propagation directions:
2.2 Optimization procedure
The Q1D numerical tool can be used within a constrained optimization procedure to find the best combination of injection parameters (namely, MFR, \(\alpha _\text {inj}\), \(p_\text {w}\), and \(N_\text {inj}\)) which guarantees the highest noise reduction in the most efficient way possible. A vector \(\varvec{X}\) with constrained lower \(\varvec{b}_\text {L}\) and upper bounds \(\varvec{b}_\text {U}\), composed of the variables to be optimised, is constantly changed according to specific algorithms in order to find the minimum of a cost function J:
where, in this case:
A two-step hybrid optimization has been chosen to handle the problem at hand. The first part of the procedure consists of a particle swarm optimization (PSO) [36]. This algorithm is inspired by the behavior of flocks, very useful to test wide sections of the domain and to find the location of the global minimum in a strongly nonlinear function with multiple local minimums. In this case, a suitable initial condition is not required. Then, an interior point algorithm is applied, which is a gradient-based procedure to find the local minimum of large-scale problems [37]. A suitable initial condition is required. Therefore, the output of the PSO is used for this purpose. The use of the PSO output as the first guess in the second part of the procedure allows to start around the global minimum, overcoming the intrinsic drawback of gradient-based algorithms which can only find local minimums, strongly dependent on the initial condition.
The cost function used for the procedure has been structured as follows:
where \(c_1\) and \(c_2\) are constant values, \(\delta\) is the target noise reduction, and \(r_*\) is a target location. The cost function works on three levels; the first term \(|\delta -\mathrm {OASPL}(r_*) |\) ensures that the noise suppressor will reach a chosen performance, avoiding the waste of resources that could occur by designing an over-performing system. The term \(c_1 \mathrm {MFR}\) ensures that the target \(\mathrm {OASPL}\) is reached using the least water possible, allowing the design of an efficient system. Lastly, \(c_2 N_\text {inj}\) is related to the dimensions of the suppressor, dependent on the number of injectors. Its aim is to force the optimizer to find an optimal design with an acceptable footprint. Since the three terms of the cost function have intrinsically different units of measure, the constants \(c_1\) and \(c_2\) must be chosen to make the three terms of the same order of magnitude (ideally also with the same unit of measure). This way they will have the same impact on the solution and the optimizer will not prioritize the minimization of any of them. These coefficients are purely artificial and have no physical meaning, but are essential to guide the operations of the optimizer. Lower \(\varvec{b}_\text {L}\) and upper \(\varvec{b}_\text {U}\) bounds have been chosen according to the best practices identified in literature [5, 12,13,14,15] as:
2.3 Design strategy
The optimal combination of the noise suppressor parameters \(\varvec{X}_\text {inj}\), which is the result of the optimization procedure, can finally be used to design the hardware, in particular the injectors and the toroidal manifold.
2.3.1 Injectors
For this particular application, only hydraulic injectors have been considered, where the fluid acceleration is driven by pressure, and atomization is produced thanks to the relative velocity between the outgoing jet and ambient air. Despite only granting coarse atomization (500 \(\upmu\)m–2 mm) and requiring four times the pressure to double the mass flow rate, simplicity and compactness of the hardware outweigh the drawbacks.
Regarding the flow shape, a flat-fan has been chosen to focus the fluid ejected on a section as narrow as possible, which guarantees better performance. In fact, it should be recalled that the efficiency of the suppressor is higher as the water jets are closer to the exit section of the nozzle. An example of hydraulic injectors and flat-fan flows can be seen in Fig. 8.
The exit section of a flat-fan injector must be elliptical, and must be obtained cutting the surface of an ellipsoid with symmetrical V-shaped planes. The properties of the injector, specifically its effective exit area and jet angle \(\theta _0\), are defined by its characteristic geometric parameters, also shown in Fig. 9. These are: (i) the injector diameter \(d_{\mathrm {inj}}\), (ii) the inclination of the planes used to cut the ellipsoid, also called half-V cut angle \(\alpha _{\text {V}}\), (iii) the distance between the intersection of the planes and the center of the ellipsoid, or cut offset \(b_\text {V}\), and (iv) the major axis of the ellipsoid \(a_2\).
The required exit area \(A_\text {inj}\) for each injector has been computed assuming a discharge coefficient \(C_d = 0.9\) [38], while its diameter \(d_\text {inj}\) is assumed to be equal to the major axis of an ellipsis with an aspect ratio of 3/2.
According to [39], the cut angle \(\alpha _\text {V}\) is related to the exit jet angle through the following empirical model:
therefore, the value of \(\alpha _\text {V}\) can be set once the required jet exit angle is known using Eq. 2.23. In this case, \(\theta _0\) has been chosen to guarantee that the coverage of the water jet once reached the hot flow is about 0.75 times the diameter of the nozzle exit section \(d_\text {ex}\). Finally, assuming a semi-spherical design (\(a_2=0.5d_{\mathrm {inj}}\)) of the surface to be cut to simplify the manufacture of the element, the cut offset \(b_\text {V}\) has been computed forcing the injector effective exit area (which is the area of the injector orifice projected on an horizontal plane) to be equal to the required area \(A_{\mathrm {inj}}\).
Once the properties of the injector exit section and its diameter are chosen, the length and shape of its inner channel must be defined. According to [40, 41], to ensure reproducible operating conditions, to obtain a sufficiently high discharge coefficient, and to avoid flow separation, it is suggested to keep \(L_\text {inj}/d_{\mathrm {inj}}\) at least equal to 4, where \(L_\text {inj}\) is the length of the injector inner channel. Furthermore, the use of a rounded inlet with \(R_\text {inj}/d_{\mathrm {inj}}\) at least equal to 0.3, where \(R_\text {inj}\) is the inflow bend radius, greatly increases the reliability of the hardware with respect to injectors with a sharp inlet, while using a value greater than 1 also ensures a sufficiently high discharge coefficient. These characteristic quantities are schematically shown in Fig. 10. Hence, the system injectors have been designed with \(L_\text {inj}/d_{\mathrm {inj}} \simeq 6\) and \(R_\text {inj}/d_{\mathrm {inj}} \simeq 1.5\).
2.3.2 Toroidal manifold
The toroidal manifold must deliver water to the injectors under uniform pressure and velocity conditions, and its geometry is uniquely defined by its internal and external diameters. The first one has to be designed according to the target flow velocity. In fact, due to mass conservation, the smaller the diameter, the higher the velocity:
where \(A_\text {m}\) is the inner channel area of the manifold, \(\dot{m}_\text {w}\) the total water mass flow rate, and \(N_\text {m}\) the number of inlets of the manifold. Inspired by the DLR (Germany) experimental suppressor [42], the inner diameter of the toroidal manifold assuming four inlets (Fig. 1) has been chosen to obtain a flow velocity lower than 1 m/s using Eq. (2.24). Having a slow-moving flow inside the manifold is crucial in containing pressure losses. Moreover, to reduce uneven distributions of the water flow, the manifold inlets must be designed as symmetrically as possible.
On the other hand, the external diameter must be chosen to ensure that all budgeted injectors fit in the manifold. For this purpose, an artificial parameter has been conceived:
where \(d_\mathrm {max}\) is the maximum diameter of the injectors and H is the vertical distance between the tip of the injectors and the tip of the nozzle exit. The parameter \(\Phi\) in Eq. (2.25) represents the total length occupied by the injectors over the perimeter of a circle with radius equal to approximately the external diameter of the manifold \(d_\mathrm {max,m} \simeq H+0.5d_\mathrm {ex}\). Therefore, the geometrical feasibility of the system is ensured if \(\Phi\) is less than 1. For the specific application described in this paper, \(\Phi\) has been constrained to values lower than 0.8, due to a safety factor. Heating of the injectors due to the hot gases from the nozzle has not been taken into account, since the entrainment of ambient air and the water flowing inside the elements should provide sufficient cooling. A schematic flowchart of the entire design methodology presented in this section is shown in Fig. 11.
3 Results and applications
In the first part of this section the outcome of the parametric analysis performed with the Q1D model is reported, along with a detailed discussion on the effect of the water-based suppressor parameters on its performance. The second part presents the results of the optimization procedure, obtained by embedding the Q1D model into an iterative process, and the results of the sizing of the hardware. Detailed technical specifics and a 3D CAD model are also provided.
All analyses shown in this section assume as reference engine a 15 kN thrust class LOX/CH4 liquid rocket engine characterized by a nominal mixture ratio equal to 3.4, which is the optimal value for the selected propellant combination. The engine chamber pressure and mass flow rate are, respectively, 52.8 bar and 5.1 kg/s. A truncated ideal contour (TIC) nozzle geometry is assumed to ensure adaptation of the nozzle to the assigned ambient pressure, resulting in an expansion ratio of \(\sim 7\).
3.1 Parametric analysis
The Q1D code is used to perform a parametric analysis to highlight the influence of the main parameters of the water-based noise suppressor on its performance. The results are shown in Fig. 12, where the OASPL is shown with respect to the distance from the nozzle exit plane for different configurations of the suppressor. Figure 12a reports the effect of the water over exhaust gases mass flow rate, MFR, showing how an increase in the water used generally translates into a decrease in the acoustic emission.
From a numerical point of view, the angle of the injector axis with respect to the axis of the engine \(\alpha _\text {inj}\) does not seem to affect the overall performance, as shown in Fig. 12b (only a small performance improvement with the angle is noticeable). This is due to the fact that the Q1D model intrinsically assumes complete penetration of the water jet in the exhaust gases, neglecting the major contribution of \(\alpha _\text {inj}\) as observed in Sect. 2.1. It must also be underlined that the model does not take into account the impact noise produced when the water jet interacts with the exhaust gases. This so called parasitic noise increases with the inclination of the jet and its pressure. The injection angle must therefore be contained in order to avoid excessive parasitic noise but, at the same time, should not be too small to guarantee water injection as close as possible to the nozzle exit section and a sufficient penetration of the water inside the exhaust jet.
The water injection pressure \(p_\text {w}\) positively affects both the exit velocity of the water jet and the overall atomization, improving the performance of the system, as shown in Fig. 12c. However, the benefits of using a larger injection pressure decrease with the pressure itself. As previously said, the parameter must be contained to avoid the presence of non negligible parasitic noise and also to avoid overloading the pressurization system.
Lastly, in Fig. 12d, it is shown how the number of injectors \(N_\text {inj}\) has a remarkable effect on the suppressor performance. This is due to an improvement in the water jet atomization. In fact, increasing the number of injectors allows to manufacture smaller elements, which are associated to smaller water droplets. However, a large number of injectors cannot be used due to the geometrical constraints of the system.
For the analysis, each suppressor parameter has been individually varied, while the others are kept fixed at a reference value of, respectively, \(\mathrm {MFR}=5\), \(\alpha _\text {inj} = 50 \ \text{deg}\), \(p_\text {w} = 6 \ \mathrm {bar}\), and \(N_\text {inj} = 32\).
3.2 Results of the optimization procedure and preliminary design
Assuming a target noise reduction of 10 dB at 100 m from the acoustic source, following the procedure mentioned in Sect. 2.2, the following results are obtained:
The coefficients of the cost function, introduced in Eq. (2.20), are \(\delta =10\) dB, \(r_*=100 \ \text {m}\), \(c_1=0.1 \ \text {dB}\), and \(c_2=0.01 \ \text {dB}\). It is important to underline that the coefficients \(c_1\) and \(c_2\) are purely artificial, but needed to make the three terms of the cost function of the same order of magnitude.
The optimal combination of system parameters is used for the design of the hardware following the procedure described in Sect. 2.3, with the resulting dimensions shown in Table 1.
The designed water-based noise suppressor is able to reduce the emitted noise of a 15 kN thrust class LOX/CH4 liquid rocket engine by 10 dB using 32 injectors, inclined by 60 degrees with respect to the engine axis, and fed by a nominal water mass flow rate of 13 kg/s at the pressure of 8 bar. It should be underlined that the problem of cavitation in the designed injectors can be neglected due to the strongly rounded inlet employed. In fact, according to [43, 44], injectors with rounded inlets are less prone to cavitation with respect to sharp inlets. Indeed, the absence of cavitation in the designed injectors has been checked using the experimental relationships found in [43]. At this stage the system has still one degree of freedom; in fact, once the geometry of the injectors is fixed, performance can be tuned by changing the pressure level, which affects both mass flow rate and misting, allowing to work off-design as shown in Fig. 13. Moreover, regarding the position of the suppressor with respect to the engine, as previously said, the efficiency of the system increases the closer the water jet is to the nozzle exit section. Therefore, the suppressor must be positioned accordingly, depending on the constraints of the test bench facility.
Lastly, to simplify hardware visualization, a detailed 3D CAD model of the injector is provided in Fig. 14.
4 Conclusions
A general design procedure of water-based noise suppression systems for static firing tests is proposed in this paper. To understand the complex relationship between the system main parameters and noise emissions, a newly adapted steady quasi-one dimensional two-phase model is employed, whose features are presented alongside its validation against CFD data. The results of the model are sufficiently in agreement with CFD data in the simulated region, with the main issue being the assumption of constant jet pressure equal to ambient pressure along the engine axis, valid only for adapted jets or for regions of the flow downstream the core acoustic waves. The model is then used to perform a comprehensive parametric analysis to highlight the effect of water-to-jet mass flow ratio, water injection angle, injection pressure, and the number of injectors on the performance of the noise suppression system. With the exception of the injection angle, each one of these quantities seem to have a remarkable influence on the acoustic emissions damping according to the employed numerical tool.
Embedding the Q1D model into an iterative procedure, a two-step optimization of the system parameters which combines particle swarm and internal-point methods is performed, and the most efficient combination of MFR, \(\alpha _\text {inj}\), \(p_\text {w}\), and \(N_\text {inj}\) for a general target engine is achieved. Optimized parameters are finally used for hardware sizing, which is composed by two main subsystems: injectors and manifold. Hydraulic flat-fan injectors are chosen for the problem at hand, to guarantee that the water jet is focused on a section as narrow as possible, ideally as close as possible to the nozzle exit section. Characteristic dimensions of the injector elliptical orifice can be obtained once the required coverage of the water jet and the required effective area of the injector are known. The inner channel shape is designed according to best practices available in literature. In particular, reproducibility of the operative conditions, stability of the flow, and a high discharge coefficient can be granted using a ratio length-to-diameter of the channel \(L_\text {inj}/d_\text {inj}\) greater than 4, and a rounded inlet with bend-radius-to-diameter of the channel \(R_\text {inj}/d_\text {inj}\) greater than 1. The toroidal manifold is, instead, uniquely defined by its internal and external diameters. Using the principle of conservation of mass, the inner diameter can be sized by fixing the maximum velocity allowed. This constraint is useful to avoid high pressure losses and flow inhomogeneities. Lastly, the external diameter is related to the dimensions of the manifold, which must be sufficiently large to host all the budgeted injectors.
Finally, the proposed procedure is applied to a 15 kN thrust class LOX/CH4 liquid rocket engine with a mass flow rate of 5.1 kg/s, resulting in the design of a suppression system able to reduce the emitted noise by 10 dB, using 32 injectors fed by 13 kg/s of water at a nominal pressure of 8 bar. Water pressure can still be used as a degree of freedom to adjust the overall performance of the designed noise suppression system.
Abbreviations
- A :
-
Area \(\text {m}^2\)
- \(C_\mathrm{D}\) :
-
Droplets drag coefficient
- \(C_\mathrm{d}\) :
-
Injectors discharge coefficient
- c :
-
Speed of sound \(\text {m/s}\)
- \(c_\mathrm{p}\) :
-
Constant pressure specific heat \(\text {J/(kg} ~\text {K)}\)
- d :
-
Diameter \(\text {m}\)
- f :
-
Frequency \(\text {Hz}\)
- H :
-
Height \(\text {m}\)
- h :
-
Specific enthalpy \(\text {J/kg}\)
- L :
-
Length \(\text {m}\)
- m :
-
Mass \(\text {kg}\)
- \(\dot{m}\) :
-
Mass flow rate \(\text {kg/s}\)
- Nu:
-
Nusselt number
- n :
-
Water flow over droplet mass \(\text {1/s}\)
- p :
-
Pressure \(\text {Pa}\)
- R :
-
Bend radius \(\text {m}\)
- r :
-
Distance from noise source \(\text {m}\)
- T :
-
Temperature \(\text {K}\)
- u :
-
Velocity \(\text {m/s}\)
- x :
-
Distance from nozzle \(\text {m}\)
- \(\alpha\), \(\theta\) :
-
Angle \(\text {rad}\)
- \(\kappa\) :
-
Thermal conductivity \(\text {W/(m}~\text {K)}\)
- \(\mu\) :
-
Dynamic viscosity \(\text {Pa} ~\text {s}\)
- \(\rho\) :
-
Density \(\text {kg}/\text {m}^3\)
- \(\sigma\) :
-
Surface tension \(\text {N/m}\)
- \(\text {a}\) :
-
Ambient
- \(\text {e}\) :
-
Entrainment
- \(\text {ex}\) :
-
Exit
- \(\text {g}\) :
-
Gas phase
- \(\text {sat}\) :
-
Saturation conditions
- \(\text {i}\) :
-
Injectors i-th element
- \(\text {inj}\) :
-
Injector
- \(\text {jet}\) :
-
Nozzle jet
- \(\text {m}\) :
-
Toroidal manifold
- \(\text {p}\) :
-
Liquid phase
- \(\text {V}\) :
-
V-cut
- \(\text {v}\) :
-
Vapor
- \(\text {w}\) :
-
Water
- \(\text {0}\) :
-
Total quantities
- CAA:
-
Computational aero-acoustics
- CFD:
-
Computational fluid dynamics
- MFR:
-
Water-to-jet mass flow ratio
- OASPL:
-
Overall sound power level
- PSO:
-
Particle swarm optimization
- Q1D:
-
Quasi-one dimensional
- SPL:
-
Sound pressure level
References
Lubert, C.P.: Sixty years of launch vehicle acoustics. In: Proceedings of Meetings on Acoustics, New Orleans, LA, vol. 31, p. 040004 (2017). https://doi.org/10.1121/2.0000704
Stephan, S., Radespiel, R.: Propulsive jet simulation with air and helium in launcher wake flows. CEAS Space J. 9(2), 195–209 (2017). https://doi.org/10.1007/s12567-016-0142-4
Dougherty, N., Guest, S.: A correlation of scale model and flight aeroacoustic data for the space shuttle vehicle. In: 9th Aeroacoustics Conference, Williamsburg, AIAA 84-2351 (1984). https://doi.org/10.2514/6.1984-2351
Tam, C.K.: Supersonic jet noise. Annu. Rev. Fluid Mech. 27(1), 17–43 (1995). https://doi.org/10.1146/annurev.fl.27.010195.000313
Zoppellari, E., Juve, D.: Reduction of hot supersonic jet noise by water injection. In: 4th AIAA/CEAS Aeroacoustics Conference, Toulouse, AIAA 98-2204 (1998). https://doi.org/10.2514/6.1998-2204
Krothapalli, A., Venkatakrishnan, L., Lourenco, L., Elavarasan, R.: Supersonic jet noise suppression by water injection. In: 6th Aeroacoustics Conference and Exhibit, Lahaina, AIAA 2000-2025 (2000). https://doi.org/10.2514/6.2000-2025
Krothapalli, A., Venkatakrishnan, L., Lourenco, L., Greska, B., Elavarasan, R.: Turbulence and noise suppression of a high-speed jet by water injection. J. Fluid Mech. 491, 131–159 (2003). https://doi.org/10.1017/S0022112003005226
Li, J., Jiang, Y., Yu, S., Zhou, F.: Cooling effect of water injection on a high-temperature supersonic jet. Energies 8(11), 13194–13210 (2015). https://doi.org/10.3390/en81112363
Kandula, M.: Prediction of turbulent jet mixing noise reduction by water injection. AIAA J. 46(11), 2714–2722 (2008). https://doi.org/10.2514/1.33599
Himelblau, H., Manning, J.E., Piersol, A.G., Rubin, S.: Nasa handbook 7005: dynamic environmental criteria. Technical report, NASA HDBK-7005 (2001). https://ntrs.nasa.gov/citations/20190026820
Gely, D., Elias, G., Bresson, C., Foulon, H., Radulovic, S., Roux, P.: Reduction of supersonic jet noise-application to the ariane 5 launch vehicle. In: 6th Aeroacoustics Conference and Exhibit, Lahaina, AIAA 2000-2026 (2000). https://doi.org/10.2514/6.2000-2026
Ignatius, J.K., Sankaran, S., Kumar, R.A., Satyanarayana, T., Chakravarthy, S.R.: Suppression of jet noise by staged water injection during launch vehicle lift-off. Int. J. Aeroacoust. 7(3–4), 223–241 (2008). https://doi.org/10.1260/1475-472X.7.3.223
Ignatius, J.K., Sathiyavageeswaran, S., Chakravarthy, S.R.: Hot-flow simulation of aeroacoustics and suppression by water injection during rocket liftoff. AIAA J. 53(1), 235–245 (2015). https://doi.org/10.2514/1.J053078
Sankaran, S., Ignatius, J.K., Ramkumar, R., Satyanarayana, T., Chakravarthy, S.R., Panchapakesan, N.: Suppression of high Mach number rocket jet noise by water injection. J. Spacecr. Rockets 46(6), 1164–1170 (2009). https://doi.org/10.2514/1.43421
Norum, T.: Reductions in multi-component jet noise by water injection. In: 10th AIAA/CEAS Aeroacoustics Conference, Manchester, AIAA 2004-2976 (2004). https://doi.org/10.2514/6.2004-2976
Langley Research Center, Eldred, K.: Acoustic loads generated by the propulsion system. Technical report, NASA-SP-8072 (1971). https://ntrs.nasa.gov/citations/19710023719
Lyrintzis, A.S.: Surface integral methods in computational aeroacoustics-from the (cfd) near-field to the (acoustic) far-field. Int. J. Aeroacoust. 2(2), 95–128 (2003). https://doi.org/10.1260/147547203322775498
Lyrintzis, A.S., Coderoni, M.: The use of large eddy simulations in jet aeroacoustics. In: AIAA Scitech 2019 Forum, San Diego, AIAA 2019-0633 (2019). https://doi.org/10.2514/6.2019-0633
Salehian, S., Kourbatski, K., Golubev, V.V., Mankbadi, R.R.: Numerical aspects of rocket lift-off noise with launch-pad aqueous injection. In: AIAA Aerospace Sciences Meeting, Kissimmee, AIAA 2018-0519 (2018). https://doi.org/10.2514/6.2018-0519
Kandula, M.: Broadband shock noise reduction in turbulent jets by water injection. Appl. Acoust. 70(7), 1009–1014 (2009). https://doi.org/10.1016/j.apacoust.2008.12.001
National Aeronautics and Space Administration.: Quasi 1-d analysis of a circular, compressible, turbulent jet laden with water droplets. appendix c. Technical report, NASA (2001). https://ntrs.nasa.gov/citations/20020051137
Balasubramanyam, M.S., Trinh, H.P.: Evaporating spray in supersonic streams including turbulence effects. In: 44th AIAA Aerospace Sciences Meeting and Exhibit, Reno, AIAA 2006-1338 (2006). https://doi.org/10.2514/6.2006-1338
Post, S., Iyer, V., Abraham, J.: A study of near-field entrainment in gas jets and sprays under diesel conditions. J. Fluids Eng. 122(2), 385–395 (2000). https://doi.org/10.1115/1.483268
Franco Medrano, F., Fukumoto, Y., Velte, C.M., Hodžić, A.: Mass entrainment rate of an ideal momentum turbulent round jet. J. Phys. Soc. Jpn. 86(3), 034401 (2017). https://doi.org/10.7566/JPSJ.86.034401
Pizzarelli, M., Nasuti, F., Paciorri, R., Onofri, M.: Numerical analysis of three-dimensional flow of supercritical fluid in cooling channels. AIAA J. 47(11), 2534–2543 (2009). https://doi.org/10.2514/1.38542
Betti, B., Martelli, E., Nasuti, F., Onofri, M.: Numerical study of heat transfer in film cooled thrust chambers. In: 48th AIAA/ASME/SAE/ASEE Joint Propulsion Conference & Exhibit, AIAA 2012-3907 (2012). https://doi.org/10.2514/6.2012-3907
Betti, B., Nasuti, F., Martelli, E.: Numerical evaluation of heat transfer enhancement in rocket thrust chambers by wall ribs. Numer. Heat Transf. Part A Appl. 66(5), 488–508 (2014). https://doi.org/10.1080/10407782.2014.885233
Betti, B., Pizzarelli, M., Nasuti, F.: Coupled heat transfer analysis in regeneratively cooled thrust chambers. J. Propul. Power 30(2), 360–367 (2014). https://doi.org/10.2514/1.B34855
Betti, B., Bianchi, D., Nasuti, F., Martelli, E.: Chemical reaction effects on heat loads of CH4/O2 and H2/O2 rockets. AIAA J. 54(5), 1693–1703 (2016). https://doi.org/10.2514/1.J054606
Kooij, S., Sijs, R., Denn, M.M., Villermaux, E., Bonn, D.: What determines the drop size in sprays? Phys. Rev. X 8(3), 031019 (2018). https://doi.org/10.1103/PhysRevX.8.031019
Elkotb, M.: Fuel atomization for spray modelling. Prog. Energy Combust. Sci. 8(1), 61–91 (1982). https://doi.org/10.1016/0360-1285(82)90009-0
Semião, V., Andrade, P., da Graça Carvalho, M.: Spray characterization: numerical prediction of Sauter mean diameter and droplet size distribution. Fuel 75(15), 1707–1714 (1996). https://doi.org/10.1016/S0016-2361(96)00163-9
Post, S.L., Hewitt, A.J.: Flat-fan spray atomization model. Trans. Am. Soc. Agric. Biol. Eng. 61(4), 1249–1256 (2018). https://doi.org/10.13031/trans.12572
Kandula, M., Vu, B.: On the scaling laws for jet noise in subsonic and supersonic flow. In: 9th AIAA/CEAS Aeroacoustics Conference and Exhibit, Hilton Head, AIAA 2003-3288 (2003). https://doi.org/10.2514/6.2003-3288
Sutherland, L.C., Piercy, J.E., Bass, H.E., Evans, L.B.: Method for calculating the absorption of sound by the atmosphere. J. Acoust. Soc. Am. 56(S1) (1974). https://doi.org/10.1121/1.1914056
Poli, R., Kennedy, J., Blackwell, T.: Particle swarm optimization. Swarm Intell. 1(1), 33–57 (2007). https://doi.org/10.1007/s11721-007-0002-0
Byrd, R.H., Hribar, M.E., Nocedal, J.: An interior point algorithm for large-scale nonlinear programming. SIAM J. Optim. 9(4), 877–900 (1999). https://doi.org/10.1137/S1052623497325107
Post, S.L., Roten, R.L., Connell, R.J.: Discharge coefficients of flat-fan nozzles. Trans. Am. Soc. Agric. Biol. Eng. 60(2), 347–351 (2017). https://doi.org/10.13031/trans.12064
Zhou, Q., Miller, P., Walklate, P., Thomas, N.: Prediction of spray angle from flat fan nozzles. J. Agric. Eng. Res. 64(2), 139–148 (1996). https://doi.org/10.1006/jaer.1996.0055
Bazarov, V., Yang, V., Puri, P.: Design and dynamics of jet and swirl injectors, pp. 19–103 (2004). https://doi.org/10.2514/5.9781600866760.0019.0103
Gill, G., Nurick, W.H.: Liquid rocket engine injectors. Technical report, NASA-SP-8089 (1976). https://ntrs.nasa.gov/citations/19760023196
Kallina, P., Böhm, C., Kruhsel, G.: Rocket engine noise reductions by water injection at dlr test bench p8. In: 49th AIAA/ASME/SAE/ASEE Joint Propulsion Conference, San Jose, AIAA 2013-4020 (2013). https://doi.org/10.2514/6.2013-4020
Chaves, H., Bauz, F., Lopez, E.: Scaling of cavitation in nozzles depending on rounding of the inlet and on fuel properties using transparent nozzles. In: ILASS—27th Annual Conference on Liquid Atomization and Spray Systems, Brighton (2016)
Mohamed, M.A.E.-A., Abdel Hameed, H.E.-S., Shaltout, R.E., El-Salmawy, H.A.A.: Prediction of the impact of nozzle geometry on spray characteristics. ACS Omega 6(9), 6218–6230 (2021). https://doi.org/10.1021/acsomega.0c05767
Funding
Open access funding provided by Università degli Studi di Roma La Sapienza within the CRUI-CARE Agreement. The present work has been carried out within the contribution of CRAS (Centro Ricerca Aerospaziale Sapienza) to the industrial research program GENERAZIONE E–Ricerca e sperimentazione di materiali, sistemi diagnostici e di controllo ambientale per i veicoli funded by the Italian Ministry of University and Research in the area of aerospace with reference no. ARS01_01318.
Author information
Authors and Affiliations
Contributions
The contributions of M. Bernardini, F. Creta, B. Favini, R. Paciorri, S. Pirozzoli, and M. Valorani to the study and realization of the noise suppression device foreseen in the above research program and that allowed carrying out the present study are greatly acknowledged.
Corresponding author
Ethics declarations
Conflict of interest
On behalf of all authors, the corresponding author states that there are no competing interests to declare that are relevant to the content of this article.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Zolla, P.M., Fiore, M., Lapenna, P.E. et al. A design strategy for water-based noise suppression systems in liquid rocket engines firing tests. CEAS Space J 15, 597–611 (2023). https://doi.org/10.1007/s12567-022-00467-8
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s12567-022-00467-8