Hypersonic retro propulsion for reusable launch vehicles tested in the H2K wind tunnel

Abstract

In the frame of the RETALT (RETro propulsion Assisted Landing Technologies) project, the aerodynamics of reusable launch vehicles reentering the atmosphere and descending and landing with the aid of retro propulsion are studied. In particular, series of wind tunnel tests are performed to assess the aerodynamic properties of such a vehicle in the various flight phases from hypersonic and supersonic re-entry down to subsonic conditions at touch down. This paper discusses the results of wind tunnel tests in the Hypersonic Wind Tunnel Cologne (H2K) at the Supersonic and Hypersonic Flow Technologies Department of the German Aerospace Center (DLR) in Cologne for the hypersonic retro propulsion maneuver during the re-entry burn. Mach numbers of 5.3 and 7.0 were tested with a variation of thrust coefficient, Reynolds number, angle of attack, cold and heated air. A single-engine configuration and a configuration with three active engines were tested. In all tests, the engine exhaust was simulated using ambient temperature or heated air. Dependencies of the flow features of the square root of the thrust coefficient known from literature for the single-engine case can be confirmed and extended to the three-engine configuration. For the single-engine case, the formation of vortex rings was observed, which eventually leads to strong individual vortices and extensive flow field disturbances. The heating of the supply air up to 600 K mitigates condensation in the retro plume, while the overall flow structures remained unchanged. High thrust coefficients generally lead to vanishing pressure coefficients on the engine bay. The single and the three-engine cases are comparable in this sense. The Mach number and Reynolds number are of subordinate importance for the pressures on the vehicle, while the thrust coefficient is the dominating similarity parameter. Pressure coefficients far downstream of the retro plume are affected less and, therefore, are not negligible at non-zero angles of attack. In this paper, the methodology of the wind tunnel tests and the results obtained are described in detail.

1 Introduction

Since the first successful recovery of a SpaceX Falcon 9 booster stage by powered vertical landing in 2015, the interest in this technology for reusable launch vehicles has increased significantly in Europe. Projects range from system studies, e.g. Ariane NEXT [1] and ENTRAIN [2], over small-scale demonstrators for the demonstration of control laws (EAGLE [3], FROG [4], DTV [5]), to the development of larger scale flight demonstrators (CALLISTO [6], Themis [7]). In the ESA project RETPRO, the validation of Wind Tunnel Tests and CFD is performed for vertically landing configurations based on the Falcon 9 [8].

In this environment of European research in this field, the RETALT (RETro propulsion Assisted Landing Technologies) project is funded in the frame of the Horizon 2020 framework program (grant agreement No 821890) and is investigating key technologies for the descend and vertical landing of launcher configurations with the aid of retro propulsion, where the engines are firing against the flight velocity vector. The project was summarized in [9]. Marwege et al. „Retro Propulsion Assisted Landing Technologies (RETALT): Current Status and Outlook of the EU Funded Project on Reusable Launch Vehicles“

Two reference configurations are being studied in the project which are:

• RETALT1: A heavy lift launcher configuration with a payload of up to 14 t into the Geostationary Transfer Orbit (GTO)

• RETALT2: A smaller Single Stage To Orbit (SSTO) configuration able to transfer 500 kg into Low Earth Orbits (LEO)

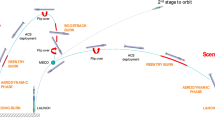
This paper focuses on the RETALT1 configuration, shown in Fig. 1a in its ascent configuration and in Fig. 1b in its descent configuration. The mission return concept is summarized in Fig. 2. After the Main Engine Cut Off (MECO), the first stage returns either to the launch site (RTLS) or lands downrange on a seagoing platform (DRL). Further details on the RETALT1 configuration can be found in [10].

Fig. 1

RETALT1 configuration

Fig. 2

RETALT1 return mission concept [13]

During atmospheric entry of the first stage, it performs a re-entry burn using three active engines. This hypersonic retro propulsion maneuver was investigated in the Hypersonic Wind Tunnel Cologne (H2K) in the present study, where the engine exhaust jets were simulated with ambient temperature (namely cold) and heated air. A preparatory test series with the objective to investigate the driving similarity parameters, presented in [12], was conducted in the H2K using a simplified model with a single center engine. This paper focuses on the full RETALT1 model using one or three active engines. A first comparison of the experimental test results with CFD computations performed with the NSMB solver by CFSE and the DLR flow solver TAU was presented in [11]. Commonly in the literature, the term Supersonic Retro Propulsion (SRP) has been established for such retro-jet environments as discussed in this paper. As the re-entry burn of RETALT1, however, is mainly performed at hypersonic Mach numbers, Mach numbers of 5.3 and 7.0 were tested in the test series presented here. Therefore, this test series covers cold Hypersonic Retro Propulsion (HRP) flow fields. The main aim of the test series was the understanding of the complex unsteady flow fields for retro propulsion maneuvers with a single active engine and with three active engines, the assessment of condensation mitigation through heating of the supply air, and the analysis of the influence of the retro-jet on the pressure distribution on the vehicle.

Results of the wind tunnel experiments on the aerodynamic phase of the RETALT1 configuration in the Trisonic Wind Tunnel Cologne (TMK) are presented in [14], aerodynamic CFD results with a focus on different types of aerodynamic control surfaces are discussed in [15]. Aerothermodynamic CFD results on the RETALT1 configuration are presented in [16].

A similar study as presented here, focusing on aerodynamic and aerothermal measurements in the wind tunnels at the Supersonic and Hypersonic Technologies Department of DLR in Cologne based on the Flacon 9 descent trajectory, is being performed in the frame of the RETPRO project [8].

The structure of the paper is as follows: Sects. 2 and 3 provide a description of the H2K facility and the wind tunnel model setup, while Sect. 4 handles the test results and discussion in detail. A final conclusion and an outlook on potential and envisaged future activities is provided in Sect. 5.

2 Hypersonic wind tunnel cologne (H2K)

The hypersonic wind tunnel cologne is a blow down facility from 60 bar pressurized air down to vacuum. A scheme of the wind tunnel is shown in Fig. 3. The wind tunnel nozzle with a diameter of 600 mm ends inside a free-jet test chamber. With the maximum total electrical power of 5 MW, stagnation temperatures of up to 1000 K can be reached. The typical test duration is around 30 s, depending on the test conditions. Mach numbers of 4.8, 5.3, 6.0, 7.0, 8.7 and 11.2 can be obtained by exchanging the wind tunnel nozzle. The operating range of unit Reynolds number is between $\text{2.0}\times{10}^{6}$ and $\text{20.0}\times{10}^{6} \, {\text{m}}^{-1}$ depending on the total pressure and total 7temperature. Quartz glass windows provide visual access to the test chamber. The facility is described in more detail in [17]. Owing to the use of compatible model adapters, the same wind tunnel models can be used in the Hypersonic Wind Tunnel Cologne and in the Trisonic Wind Tunnel Cologne.

Fig. 3

Scheme of the Hypersonic Wind Tunnel Cologne (H2K)

3 Test setup

3.1 Wind tunnel model and instrumentation

A schematic of the RETALT1 model is shown in Fig. 4 and the wind tunnel model mounted in the H2K facility is shown in Fig. 5. The model was designed in a manner that a short and a long version could be tested by adding or removing the cylindrical segment shown in Fig. 4. While the long model version is used for force measurements, the short model version is intended for detailed analyses of the base flow using high frequency pressure measurements. In this paper, results obtained with the short model are discussed. The model is scaled by 1/130 with respect to the RETALT1 flight configuration. The reference length for the nondimensionalization is the diameter of 6 m in the flight configuration (hence 46.154 mm in the experiment). The reference area is the base area, ${A}_{B}$, of 28.27 m² for the flight configuration. For the simulation of the exhaust plume, air was blown out through a hollow model support sting and a model Laval nozzle (see Fig. 4). Various nozzle segments were manufactured for tests on different engine combinations, i.e. one active engine or three active engines, and different engine deflection angles. The model can be equipped with a tubular four-component balance. However, for the runs presented in the paper at hand, the model was solely equipped with pressure sensors. The locations of the high-frequency pressure sensors are shown in Fig. 6. The pressure sensors were distributed in three measurement planes. One close to the interstage (plane 1), one close to the folded landing legs (plane 2) and one at the model base (plane 3). Furthermore, the sensors were numbered in the clockwise direction, when looking at it on the model base. This is represented by the second index. The third index for the sensors on the base plane defines the radial positioning from a position close to the center with index 1 to the outermost sensor with index 3. The pressure in the wake was measured with a pressure tube (pSTAGE).

Fig. 4

RETALT1 wind tunnel model design

Fig. 5

RETALT1 wind tunnel model mounted in H2K

Fig. 6

RETALT1 distribution of pressure sensors

3.2 Design of the wind tunnel model nozzles

A detailed view of the inner flow contour inside the wind tunnel model for one and three active engines is shown in Fig. 7. The expansion ratio of the wind tunnel model nozzles was chosen to be 2.5, which is shortly motivated in the following.

Fig. 7

Detail of the inner flow contour

The main similarity parameters to be matched for supersonic (and hypersonic) retro propulsion flows are the thrust coefficient and the ambient pressure ratio (APR), ${p}_{e}/{p}_{\infty }$ (the ratio between the nozzle exit pressure ${p}_{e}$ and the freestream pressure ${p}_{\infty }$) [18]. The thrust coefficient, ${C}_{T}$, is defined as:

$$C_{T} = \frac{{F_{T} }}{{q_{\infty } A_{B} }},$$

(1)

where ${F}_{T}$ is the thrust, ${q}_{\infty }$ is the dynamic pressure in the free stream and ${A}_{B}$ is the reference area, which is the base area in the case of RETALT1. Neglecting the pressure loss of the engine, the thrust coefficient can be written as a function of the engine scaling parameter $\mathrm{\rm K}$ [18]:

$${C}_{T}=\frac{1}{{M}_{\infty }^{2}}\cdot \frac{{ p}_{e}}{{p}_{\infty }}\cdot \frac{2{A}_{e}}{{\gamma }_{\infty }{A}_{B}}\left(1+{\gamma }_{e}{M}_{e}^{2}\right)=\frac{1}{{M}_{\infty }^{2}}\cdot \frac{{ p}_{e}}{{p}_{\infty }}\cdot \frac{1}{\mathrm{\rm K}}.$$

(2)

Here, ${C}_{T}$ is the thrust coefficient, ${M}_{\infty }$ and ${M}_{e}$ are the freestream and nozzle exit Mach numbers, ${A}_{e}$ is the nozzle exit area, and ${\gamma }_{e}$ and ${\gamma }_{\infty }$ are the heat capacity ratios at the nozzle exit and in the freestream.

The engine scaling parameter only depends on the nozzle exit parameters and ${\gamma }_{\infty }$ [18]:

$$\mathrm{\rm K}=\frac{{\gamma }_{\infty }}{2}\frac{{A}_{B}}{{A}_{e}}\frac{1}{1+{\gamma }_{e}{M}_{e}^{2}}.$$

(3)

The thrust coefficient similarity and the APR similarity between the experiment (subscript $exp$) and the flight (subscript $Fl$) are proportional to the ratio of the engine scaling parameters which can be shown as follows:

$$\frac{{C}_{T,exp}}{{C}_{T,Fl}}=\frac{\frac{1}{{M}_{\infty ,exp}^{2}}}{\frac{1}{{M}_{\infty ,Fl}^{2}}}\cdot \frac{{\left(\frac{{ p}_{e}}{{p}_{\infty }}\right)}_{exp}}{{\left(\frac{{ p}_{e}}{{p}_{\infty }}\right)}_{Fl} }\cdot \frac{\frac{1}{\mathrm{\rm K}{}_{exp}} }{\frac{1}{{\mathrm{\rm K}}_{Fl}} }=\frac{{\left(\frac{{ p}_{e}}{{p}_{\infty }}\right)}_{exp}}{{\left(\frac{{ p}_{e}}{{p}_{\infty }}\right)}_{Fl}}$$

(4)

$$\underbrace {{\frac{{C_{{T,exp}} }}{{C_{{T,Fl}} }}}}_{{\begin{array}{*{20}c} {Thrust{\kern 1pt} coefficient} \\ {similarity} \\ \end{array} }} = \underbrace {{\frac{{M_{{\infty ,Fl}}^{2} }}{{M_{{\infty ,exp}}^{2} }}}}_{{\begin{array}{*{20}c} {Mach{\kern 1pt} number} \\ {similarity} \\ \end{array} }} \cdot \underbrace {{\frac{{\left( {\frac{{p_{e} }}{{p_{\infty } }}} \right)_{{exp}} }}{{\left( {\frac{{p_{e} }}{{p_{\infty } }}} \right)_{{Fl}} }}}}_{{\begin{array}{*{20}c} {Ambient{\kern 1pt} pressure} \\ {ratio{\kern 1pt} similarity} \\ \end{array} }} \cdot \underbrace {{\frac{{{\text{K}}_{{Fl}} }}{{{\text{K}}_{{exp}} }}}}_{{\begin{array}{*{20}c} {Engine{\kern 1pt} scaling} \\ {parameter{\kern 1pt} ratio} \\ \end{array} }}$$

(5)

If the ratio of the engine scaling parameters equals one, and if the Mach number similarity is fulfilled, the thrust coefficient similarity and the APR similarity are matched at the same time.

Assuming that ${A}_{B}$, ${A}_{e}$, ${\gamma }_{\infty }$ and ${\gamma }_{e}$ are constants, the engine scaling parameter solely depends on ${M}_{e}$ which depends on the nozzle expansion ratio of the model nozzle, $\epsilon$. $\mathrm{\rm K}$ versus the expansion ratio is plotted in Fig. 8; for reference also ${M}_{e}$ is shown. The engine scaling parameter for the flight condition is 1.31. Hence, matching this engine scaling parameter in the experiment would require an expansion ratio of 5.5 (see Fig. 8).

Fig. 8

Engine scaling parameter and nozzle exit Mach number in dependence of the expansion ratio

Defining the subscript $exp/Fl$ for the ratios of the various similarity parameters, equation (5) can be rewritten as:

$${C}_{T, exp/Fl}={M}_{\infty ,Fl/exp}^{2}\cdot {\left(\frac{{p}_{e}}{{p}_{\infty }}\right)}_{exp/Fl}\cdot \frac{1}{{\mathrm{\rm K}}_{exp/Fl}}.$$

(6)

If ${M}_{\infty ,Fl/exp}^{2}=1$ and ${\left(\frac{{p}_{e}}{{p}_{\infty }}\right)}_{exp/Fl}=1$ it follows:

$${C}_{T, exp/Fl}=\frac{1}{{\mathrm{\rm K}}_{exp/Fl}}.$$

(7)

If ${M}_{\infty ,Fl/exp}^{2}=1$ and ${C}_{T, exp/Fl}=1$ it follows:

$${\left(\frac{{p}_{e}}{{p}_{\infty }}\right)}_{exp/Fl}={\mathrm{\rm K}}_{exp/Fl}$$

(8)

In Fig. 9, the relation of equation (7) and (8) are plotted. This visualizes that at expansion ratios unequal to 5.5 if either the thrust coefficient similarity or the APR similarity is met, the other one is compromised. At an expansion ratio of 5.5 both similarities equal 1.

Fig. 9

Exit pressure ratio similarity and thrust coefficient similarity as function of the nozzle expansion ratio as in Eq. (7) and (8) (for${M}_{\infty ,Fl/exp}^{2}=1$)

With the required exit pressure ratio similarity ${({p}_{e}/{p}_{\infty } )}_{exp/Fl}$, and ${p}_{e}$ and ${p}_{\infty }$ known for the flight condition (${p}_{e}$=0.874 bar, ${p}_{\infty }$=0.002125 bar for Mach 5.3), the total pressure in the wind tunnel model ${p}_{CC}$ can be derived with the isentropic relations. The baseline freestream total pressure for the experiments was chosen to be 4 bar. The total pressures in the wind tunnel model, necessary to reach the thrust coefficient similarity and the APR similarity for these test conditions are shown in Fig. 10. At an expansion ratio of 5.5, both similarities are reached at a total pressure of 120 bar. This pressure is unfeasibly high for the design of the model. In addition, it could not be guaranteed that these pressures could be provided by the high-pressure air supply of the wind tunnel facility. For this reason, ${p}_{CC}$ was limited to 60 bar. As the thrust coefficient is the main similarity parameter, it was prioritized over the ambient pressure ratio and the nozzle expansion ratio was chosen to provide thrust coefficient similarity at 60 bar, which results in an expansion ratio of 2.5.

Fig. 10

Total pressure in the wind tunnel model for thrust coefficient and APR similarity as function of the nozzle expansion ratio

It shall be noted that the discussion in this chapter applies equally for the single- and for the three-engine case. For the case of three active engines, the thrust multiplies by three, which translates to a multiplication of ${A}_{e}$ by three in equation (2). As this applies equally for flight and experiment, the similarity ratios are not affected.

3.3 Test conditions

Figure 11 shows the Mach numbers selected for the wind tunnel tests at DLR in Cologne, mapped onto the reference trajectory presented in [9]. As mentioned in the introduction, the tests performed in the H2K rebuild the hypersonic part of the retro propulsion maneuver during the re-entry burn.

Fig. 11

Mapping of Mach numbers tested in the wind tunnel facilities over the reference trajectory presented in [9]

Table 1 summarizes the freestream conditions tested in the H2K. For comparison, also the Reynolds numbers of the reference trajectory for the respective Mach numbers are given. The characteristic length for the Reynolds number is the model diameter. The baseline test condition is at Mach 5.3 with a total pressure of 4 bar and a total temperature of 450 K. A Reynolds number variation was performed with the second condition at Mach 5.3 with a total pressure of 12 bar. In addition, tests were performed at Mach 7.0, with the Reynolds number matched to the baseline tests at Mach 5.3. At Mach 7.0 the Reynolds number is in the same order of magnitude as for the flight point in the reference trajectory.

Table 1 Freestream conditions tested in H2K

As described in Sect. 3.1 a single-engine configuration and a three-engine configuration were tested. The total thrust for the three engines case is defined as:

$${C}_{T, Total}=3\cdot {C}_{T} .$$

(9)

The total thrust coefficient will be used in the remainder of this paper.

To generate a better understanding of the three-engine case, it was tested in the two configurations visualized in Fig. 12. One with the engines active in the angle of attack plane ($\alpha$-plane) and one perpendicular to it. The angle between the $\alpha$-plane and the engine plane is denoted $\phi$. Especially for an angle of attack of 0°, the two cases represent the same configuration but it can be inspected via schlieren imaging in two planes. The schlieren view path is sketched in Fig. 12.

Fig. 12

Three-engine configurations with three active engines in the $\alpha$-plane (left) and three active engines perpendicular to the $\alpha$-plane (right)

The thrust coefficients which could be tested were limited by two factors. As was presented in [12] for large thrust coefficients, partly blockage of the wind tunnel freestream appears, which is first observable in the rear of the configuration. In the experiments presented here it was, however, observed that even before a noticeable disturbance of the pressures on the wind tunnel model appears, a rise in the wind tunnel nozzle exit pressure can be measured. Hence, the thrust coefficients were limited such that no influence of the retro plume on the wind tunnel nozzle exit pressure is observed. This leads to maximum total thrust coefficients of 3.8 for the single-engine case and 7.2 for the three-engine case. The total thrust coefficients for the flight points at Mach 5.3 and Mach 7.0 are 33.7 and 211.2, respectively. Hence the flight thrust coefficients cannot be matched in the experiments, which is why in this paper the general trend of the data in dependence on the thrust coefficient is presented for an extrapolation to the flight configuration in the future.

For the baseline experiments, pressurized ambient temperature air (${T}_{CC}\approx 300 \space \mathrm{K}$) was used for the generation of the exhaust jet. However, due to the high Mach numbers and, therefore, low pressures and temperatures, condensation was observed in the highly underexpanded retro plume in the experiments presented in [12]. To study the influence of the condensation on the flow field, the air was heated to a temperature of ${T}_{CC}\approx 600 \space \mathrm{K}$ in some tests. As the pressure sensors could not withstand these high temperatures, they were not installed in these tests.

The condensation was visualized with five laser beams with an optical power of 0.7 mW (class 2 laser) stretched out with a plano-concave cylindrical lens in the area were the plume was expected. The resulting laser lines in a plane parallel to the $\alpha$-plane are shown in Fig. 13.

Fig. 13

Laser lines for the visualization of condensation in the plume

The tests conditions for all results presented in the paper at hand are summarized in Tab. 2.

Table 2 Summary of test conditions of results presented

4 Results and discussion

4.1 Discussion of flow features

First the single-engine case shall be analyzed. Figure 14 shows a schlieren image for a thrust coefficient of 3.69 at a Mach number of 5.3 where the most important flow features are highlighted. Figure 15 shows a more detailed scheme of the dominating flow features of retro propulsion flow fields for a single-engine case taken from [12].

Fig. 14

Schlieren image with highlighted flow features for ${M}_{\infty }=5.29$ and ${C}_{T}=3.69\pm 0.21$

Fig. 15

Flow features of a hypersonic retro propulsion flow field for the single-engine case [12]

The flow field is balanced between the freestream coming from the left and the jet stream from the right. The two streams are separated by the contact surface. The freestream is decelerated by a bow shock and a subsequent subsonic deceleration. The jet stream is expanded in a highly underexpanded plume and is then decelerated over a Mach disc and a subsequent subsonic deceleration. At the free stagnation point the total pressure of the freestream and the jet stream are equal.

In literature, the described mode of the flow field is named blunt mode [18]. For very low thrust coefficients, a second mode exists, the so-called long penetration mode, where the bow shock is positioned far upstream of the nozzle exit due to the jet penetrating upstream into the incoming freestream [18]. This mode is known to be very unsteady [18][19]. For the hypersonic and supersonic re-entry burn of a launcher first stage as described in this paper, the single-engine long penetration mode does not occur as the thrust coefficients are sufficiently high, such that only the blunt mode appears.

In the experiments, an interesting dynamic phenomenon was observed: frequently vortex rings emerged from the Mach disc, moved away from it and interacted with the subsonic area in the contact surface. This is shown in Fig. 16. The majority of the vortex rings are small and do not generate large flow field disturbances, especially if the vortex is formed on the symmetry line of the model nozzle. This can be observed in the time series depicted in Fig. 17. However, as can be observed in Fig. 18, if the vortex rings do not appear symmetrically the vortex is subjected to different flow fields around its perimeter. This can result in an unsymmetrical energy absorption of the vortex, which leads to a growing single vortex, rolling off to one side of the Mach disc and consequently leading to large flow field disturbances.

Fig. 16

Vortex ring formation moving away from the Mach disc (schlieren image at ${{M}_{\infty }=5.29, C}_{T}=3.69\pm 0.21,$ ${T}_{CC}=300 \space \mathrm{K}, {p}_{0}=4 \space \mathrm{bar}, {T}_{0}=450 \space \mathrm{K}$)

Fig. 17

Symmetric dynamic vortex rings at ${M}_{\infty }=5.29, {C}_{T}=3.69\pm 0.21,$ ${T}_{CC}=300 \mathrm{K}, {p}_{0}=4 \mathrm{bar}, {T}_{0}=450 \mathrm{K}$ with a time step of $50 \space \mu \mathrm{s}$ (frame rate of 20 kHz) (vortex rings highlighted with dashed circle)

Fig. 18

Asymmetric dynamic vortex rings at ${{M}_{\infty }=5.29, C}_{T}=3.69\pm 0.21,$ ${T}_{CC}=300\space \mathrm{K}, {p}_{0}=4 \space \mathrm{bar}, {T}_{0}=450 \space \mathrm{K}$ with a time step of $50 \space \mu \mathrm{s}$ (frame rate of 20 kHz) (vortex rings and resulting larger vortices highlighted with dashed circle)

To verify that this effect is not specific for this particular wind tunnel model, the data of the preparatory experiments presented in [12] were examined for this effect. In [12], the nozzle shape was designed as ideal contour with the method of characteristics. The emerging of vortex rings followed by a larger single vortex was also observed in the data of [12] (see Figure 19).

Fig. 19

Vortex emerging from the Mach disc observed in the preparatory experiments for ${C}_{T}=4.16\pm 0.23,{M}_{\infty }=5.287, \epsilon =2.5$; from left to right and from top to bottom with a time step of $80 \space \mu \mathrm{s}$ (frame rate of 12.5 kHz)

Even though not mentioned explicitly in their paper, such vortex rings were also observed in a DNS (Direct Numerical Simulation) performed by Montgomery et al. [24] in a video which was provided as complementary data to the paper [25] (see Fig. 20). As the simulation was performed as an axisymmetric computation, the vortex naturally appears in the symmetrical configuration and hence, as stated above, leads to only little disturbing effects on the flow field.

Fig. 20

Vortex ring observable in a snapshot of the video provided in [25] complementing [24] (${M}_{\infty }=2.0$)

In Fig. 21, the flow field is shown for a test run for the three-engine case where the engines are active in the $\alpha$-plane. In general, the flow field is dominated by the coalescence of the three nozzle plumes and the balancing of the exhaust jets with the freestream. It can be observed that similar to the single-engine case, there are two modes, a blunt mode shown in Fig. 21a and Fig. 21b and a long penetration mode shown in Fig. 21c. The blunt mode does not occur in a symmetrical configuration but tends to stabilize in a configuration where the bow shock stand-off distance is either larger above the symmetry plane of the nozzle exits (Fig. 21a) or below it (Fig. 21b). The long penetration mode (Fig. 21c) shows a stronger symmetry, however, also this configuration showed strong unsteady behavior. In general the flow field is very unstable and constantly changes between the blunt modes and the long penetration mode with other flow field structures appearing between these; as can be seen in Fig. 21e and f where a symmetrical blunt mode and a snapshot of the transition of the long penetration mode to the blunt mode are shown. Hence, the modes do not appear to be stable points but rather labile. As for the single-engine case, the condition needs to be satisfied that the total pressure of the free stream and the jet stream equal in the contact surface. Hence, the reason for the longer persistence of the penetration modes and the asymmetric blunt modes in the flow field is presumably due to their better match of this condition. In Fig. 21d, the schlieren image of the experiment was compared to RANS (Reynolds Averaged Navier Stokes) computations which was presented in [11]. The CFD results converged at the long penetration mode and matched the overall flow structure well.

Fig. 21

Three-engine configuration in the $\alpha$-plane for ${M}_{\infty }=5.29, {C}_{T}=2.29\pm 0.13,$ ${T}_{CC}=300\,\mathrm{K}, {p}_{0}=4 \,\mathrm{bar}, {T}_{0}=450 \,\mathrm{K}$

When considering the plane perpendicular to the $\alpha$-plane for the three-engine case, one can observe a good similarity with the single-engine case (compare Fig. 22 with Fig. 14). Figures 22a, b show the blunt and the long penetration mode for the same thrust coefficient as in Fig. 21 (where the engines are active in the $\alpha$-plane). Figure 22c, d shows them for smaller thrust coefficients.

Fig. 22

Three-engine configuration observed perpendicular to the $\alpha$-plane for ${M}_{\infty }=5.29,$ ${T}_{CC}=300\mathrm{K}, {p}_{0}=4 \mathrm{bar}, {T}_{0}=450 \mathrm{K}$

To quantify these observations, the axial and radial distance of the triple point and the axial distance of the Mach disc location and bow shock location were measured from the nozzle exit and were tracked throughout two tests where the thrust coefficient was successively increased for the single-engine and the three-engine cases. The bow shock location for the three-engine case was extracted from the configuration of active engines perpendicular to the $\alpha$-plane. For this configuration, the flow structure appears symmetrically for the blunt modes, and hence, the bow shock location is more clearly defined (see Fig. 22a and c). For the long penetration mode, the distance at the symmetry axis was used. The flow features plotted versus the square root of the thrust coefficient are depicted in Fig. 23 were the single-engine case is represented by the orange lines and the pink line, and the blue lines represent the three-engine case.

Fig. 23

Measured distances of single-engine and three-engine cases for varying thrust coefficients (orange/pink: single-engine case, blue: three-engine case, dashed: linear fit, dotted: ${C}_{T}^{(1-\gamma )/4\gamma }$ fit); (${M}_{\infty }=5.29,\, {T}_{CC}=300\,\mathrm{K},\, {p}_{0}=4 \, \mathrm{bar}, \,{T}_{0}=450\,\mathrm{K}$)

For the single-engine case, the plotted results show the blunt mode, which established for ${C}_{T}\gtrsim 0.25$. In [17], it was found that the transition of the long penetration mode to the blunt mode appears near ${C}_{T}=1.0$ and that it depends on the ratio of the nozzle exit pressure (${p}_{e}$) and the freestream pressure (${p}_{\infty }$). Korzun and Cassel [26] linked the transition to the ratio of the nozzle exit pressure to the total pressure in the stagnation point. Daso et al. [19] postulated that the transition occurs due to a change of the exhaust jet transitioning from being overexpanded to fully expanded, to underexpanded. Gutsche et al. [12] stated that there might not be a universal value for the determination of the transition. However, what can be stated generally is that the transition commonly occurs at low thrust coefficients. This correlation seems to be valid throughout the literature, even though it cannot be fixed to one specific value. In [18], the transition was observed at lower thrust coefficients for higher freestream Mach numbers. As the Mach numbers tested in this test series were relatively high, this might explain the comparably small thrust coefficient at which the transition occurred (for comparison, Jarvinen and Adams [18] observed a transition at ${C}_{T}=1$ for ${M}_{\infty }=2.0$ and at ${C}_{T}=2$ at ${M}_{\infty }=1.5$). This underpins the statement made above in this section, that the long penetration mode is not decisive for the single-engine case, considering the flow conditions and thrust coefficients of interest for the re-entry burn of a returning first stage, as they are much larger than unity. In case of RETALT1 they are 11.1 and 76.8 for Mach 5.3 and Mach 7.0, respectively.

It was observed and stated by Jarvinen and Adams [18] that the flow features of the supersonic retro propulsion flow in the blunt mode vary with the square root of the thrust coefficient. For the detailed reasoning for this statement Jarvinen and Adams referred to reference [20]. To the knowledge of the authors, this report is not accessible anymore. However, the analytical procedure applied by Jarvinen and Adams is closely linked to the analysis performed earlier by Finley [21]. Finley based his analysis on a correlation by Love et al. [22] which states a linear dependency of the flow features of a jet exhausting into still air with the square root of the exit pressure ratio at the nozzle exit with the ambient air. In the case of the blunt mode retro propulsion flow field, this ratio is ${p}_{e}/{p}_{d}$ were ${p}_{d}$ is the dead air pressure in the recirculation zone (see Fig. 15). Jarvinen and Adams, however, use the correlation by Charwat [23] to model the jet boundary which suggests a dependency of the radial extent of the jet on the pressure ratio of ${{p}_{e}/{p}_{d}}^{(1-\gamma )/4\gamma }$. In Fig. 23, a linear fit of the different measured distances with the square root of the thrust coefficients was added (dashed lines) as well as a fit with ${C}_{T}^{(1-\gamma )/4\gamma }$(dotted lines). It can be observed that for the single-engine case, all flow features follow the linear trend of the thrust coefficient well. A scaling of the features with ${C}_{T}^{(1-\gamma )/4\gamma }$ seems to fit better for $\sqrt{{C}_{T}}<0.7$. However, the general trend is better captured by the linear correlation. For the thrust coefficients studied here, the differences between both correlations are small.

For the three-engine case, the bow shock distance is plotted in blue in Fig. 23. Two dashed lines indicate the linear fit for the blunt mode and the long penetration mode for this configuration. The linear trend with the square root of the thrust coefficient can be observed for both modes. In contrast to the single-engine case the bow shock distance is constantly switching between the blunt mode and the long penetration mode along the complete range of thrust coefficients tested. The trend of the blunt mode follows the bow shock distance of the blunt mode of the single-engine case closely, while the slope for the increase of the bow shock distance for the long penetration mode is steeper.

4.2 Comparison of cold and heated jets

Measurements in [12] showed that condensation occurs in the highly underexpanded plume of the retro propulsion jet. This was locally visualized using a laser beam, crossing the jet flow region. It was therefore of interest to investigate if the condensation is a local phenomenon or if it occurs in the complete jet. The visualization of the condensation with laser lines in the plume revealed that the condensation is not locally but appears in the complete plume area. This is shown in Fig. 24 for the single-engine case (Fig. 24a) and the three-engine case (Fig. 24b) for the baseline flow condition no. 1 (${M}_{\infty }=5.3, \,{p}_{0}=4\, \mathrm{bar}, \,{T}_{0}=450 \,\mathrm{K}$) and a total temperature of the jet of ${T}_{CC}\approx 300 \,\mathrm{K}$. Due to the condensation the laser lines in the $\alpha$-plane are clearly visible, they are highlighted with the dashed circle in Fig. 24. The effect is the largest for the higher thrust coefficients shown here, but it was also observed for lower values of the thrust coefficient. To mitigate the condensation, the stagnation temperature in the model was raised to 600 K. For these temperatures, no condensation was observed. This is shown exemplarily for a single-engine case with a thrust coefficient of 6 in Fig. 24c.

Fig. 24

Visualization of condensation in the retro plume, highlighted with dashed circle (${M}_{\infty }=5.29,\, {p}_{0}=4\, \mathrm{bar},\, {T}_{0}=450 \,\mathrm{K}$)

In Fig. 25, the schlieren images of the single-engine case are compared for the cold gas case (303 K) and the heated air case (589 K). Due to the heating of the supply air, the density in the heated case is lower, and therefore, the schlieren images have a slightly different appearance. However, it is apparent that the flow features are very similar. In Fig. 26, the comparison between the cold and the heated case is shown for the three-engine case for the long penetration mode. Also for this case, the heating seems to have a minor influence on the flow field structure. For the heated case, the blunt mode can be observed for the three-engine case too (see Fig. 27), however, in the high-speed schlieren videos, the blunt mode was observed less for the heated case and the flow structure tended to stabilize in the long penetration mode.

Fig. 25

Comparison of cold air (upper part) vs. heated air (lower part) in retro plume — single-engine case

Fig. 26

Comparison of cold air (upper part) vs. heated air (lower part) in retro plume — three-engine case

Fig. 27

Blunt mode for the three-engine case with heated air (${T}_{CC}={632} \, {\text{K}}$, ${C}_{T}=2.43 \pm 0.14, {M}_{\infty }=5.29,$ ${p}_{0}=4\,\mathrm{ bar}, \,{T}_{0}=450\, \mathrm{K}$)

For the single-engine case, the phenomenon of the building up of vortex rings was observed too. It seems that these vortices are larger than the ones that occurred for the cold case. An example is shown in Fig. 28.

Fig. 28

Vortex ring formation in heated single-engine case (${T}_{CC}=589 \,\mathrm{K},$ ${C}_{T}=3.85 \pm 0.22,$ ${M}_{\infty }=5.29$ ${p}_{0}=4 \,\mathrm{bar},\, {T}_{0}=450 \, \mathrm{K}$), with a timestep of $50 \,\mu \mathrm{s}$ (frame rate of 20 kHz)

4.3 Discussion of pressure measurements

In this section the pressure measurements performed in the wind tunnel tests are discussed. The pressure sensors were sampled at 50 kHz. For the static evaluation performed in the following they were resampled to 1000 Hz and then filtered using a low-pass filter with a cut-off frequency of 4 Hz. The pressure coefficients are defined based on the free stream conditions:

$${c}_{p}=\frac{p-{p}_{\infty }}{{q}_{\infty }}$$

(10)

where $p$ is the measured pressure, ${p}_{\infty }$ is the free stream static pressure and ${q}_{\infty }$ is the dynamic pressure in the free stream.

4.3.1 Single-engine case

In Fig. 29 the pressure coefficients are shown for the single-engine case and the baseline flow condition (${M}_{\infty }=5.29,$ ${p}_{0}=4 \, \mathrm{bar},\, {T}_{0}=450\, \mathrm{K}$). The coefficients are plotted over the square root of the thrust coefficient. For the sake of a less overloaded plot, the error bars are only shown in the top for the larger pressure coefficients and at the bottom for the lower pressure coefficients. It can be observed, as expected from literature [12][18] that the pressure coefficients do not follow a linear trend with the square root of the thrust coefficient. Hence, the pressure coefficients are plotted over the thrust coefficient in the following. The pressure coefficients for the same conditions as in Fig. 29, but plotted against the thrust coefficient, are shown in Fig. 30.

Fig. 29

Pressure coefficients ${C}_{p}$ over square root of the thrust coefficient for the single-engine case (${M}_{\infty }=5.29,$ ${p}_{0}=4\, \mathrm{bar},\, {T}_{0}=450\, \mathrm{K}$)

Fig. 30

Pressure coefficients ${C}_{p}$ over thrust coefficient for the single-engine case (${M}_{\infty }=5.29,$ ${p}_{0}=4\, \mathrm{bar}, \,{T}_{0}=450 \,\mathrm{K}$)

As expected, the pressure coefficients generally tend towards zero for larger thrust coefficients [20][21]. The pressures in plane 1, which are the sensors that are positioned the farthest downstream along the cylindrical body, are close to ambient pressure. In [14], it was shown, that pressure coefficients in this location of the configuration are expected to be close to zero in the aerodynamic phase where the engines are not active. Here, it seems that this assumption also holds for the retro propulsion phase. The pressures in plane 2 (sensors 21, 22, 23 and 24) are located directly behind the folded landing legs. These pressures slightly rise with increasing thrust coefficient. The pressure coefficients at the base area of the configuration in plane 3 also generally tend to very small values with increasing thrust coefficients. The pressure sensors located closer to the center of the base (sensors 311 and 331), see higher pressures if the engine is not active, however, the pressures for these decreases more rapidly with increasing thrust coefficient. The pressure in the wake of the configuration (CpSTAGE) is relatively independent of the thrust coefficient. The conditions described in Fig. 30 are used in the following as baseline condition for the discussion of parameter variations.

Figure 31 shows the influence of a variation of the freestream Mach number on the pressure coefficients. The Mach number was increased to 7 but the Reynolds number was kept at the baseline value of 2.36E + 05. The thin lines represent the baseline configuration while the variation is shown by the thick lines. It can be observed that the trends of the values are the same. Especially in plane 1 and 2, the pressure coefficients are nearly equal. The pressure in the base is offset from the baseline case for higher thrust coefficients. In [12], it was proposed to use the total pressure behind the bow-shock for the scaling of the pressures. It was reasoned that this would lead to better similarity close to the engine, which would relate well with the work by Korzun and Cassel [26] suggesting the ratio of exit pressure to total pressure as scaling parameter for the expansion conditions. However, with increasing distance from the engine, the conventional pressure coefficient leads to very good similarity as observed in Fig. 31. This is reasonable as these parts are less influenced by the wake of the plume. Hence, no effort was taken in this work to investigate further similarity parameters. Furthermore, in Fig. 31, it can be observed that the pressure coefficient in the wake of the configuration (CpSTAGE) is offset by the same amount as the pressure coefficients near the engine. This indicates a Mach number independence of the drag coefficient of the configuration which is reasonable as also the flow features are relatively independent of the Mach number as already found in [12].

Fig. 31

Mach number variation for the single-engine case for ${M}_{\infty }=5.29$ (thin lines) and ${M}_{\infty }=7.04$ (tick lines) (${M}_{\infty }=5.29,$ ${p}_{0}=4 \,\mathrm{bar}, \,{T}_{0}=450\, \mathrm{K}$ and ${M}_{\infty }=7.04,$ ${p}_{0}=12.73 \,\mathrm{bar},\, {T}_{0}=610 \,\mathrm{K}$)

In Fig. 32, the results of a variation in Reynolds number are shown. It can be observed that the measured pressure coefficients are independent of the two Reynolds numbers tested. The Reynolds number, hence, seems not to be the main driver for the retro propulsion flows. However, it should be remarked that for the higher Reynolds number, the fluctuations in the pressure coefficients are lower. Due to the higher measured overall pressures, the uncertainties in the pressure coefficients decrease.

Fig. 32

Reynolds number variation for the single-engine case with $R{e}_{\infty }=2.36\mathrm{E}+05$ (thin lines) and $R{e}_{\infty }=7.07\mathrm{E}+05$ (thick lines) (${M}_{\infty }=5.29,$ ${p}_{0}=4 \,\mathrm{bar}, \,{T}_{0}=450 \,\mathrm{K}$ and ${M}_{\infty }=5.32,$ ${p}_{0}=12 \,\mathrm{bar},\, {T}_{0}=450 \,\mathrm{K}$)

The influence of a variation of the angle of attack is shown in Fig. 33. As expected, the pressure on the base on the windward side (sensor 342, see Fig. 6) is increased as it is moved further in the wind and as the shielding of the plume is less efficient. The pressure on the leeward side (sensor 322), in turn, is decreased. The pressures close to the engine (sensors 331 and 311) are not affected by the angle of attack, the pressures of sensors 313 and 332 which are on the outer rings of the sensor positions but perpendicular to the alpha plane are only affected by the angle of attack when the thrust coefficient is very low (${C}_{T}<0.6$); for larger thrust coefficients, they equal the pressures at 0° angle of attack. In plane 2, were the pressure sensors are positioned behind the landing legs, the pressure on the windward side increases (sensor 22), the pressures perpendicular to the $\alpha$-plane (sensors 21 and 23) decrease, but the pressure on the leeward side remains close to zero as for the case with 0° angle of attack. In plane 1 far downstream, the pressure on the windward side are increased by the angle of attack, the ones on the leeward side are decreased, the pressures on the plane perpendicular to the $\alpha$-plane (21 and 23) follow the trend of the pressure on the leeward side. This can be reasoned as these sensors are less influenced by the plume and hence follow a pressure trend similar to the trend in the aerodynamic phase with no active engines. For this case, the pressure on the windward side was found to follow the modified Newtonian law, and the pressures on the leeward side and the perpendicular locations approximately follow a negative modified Newtonian law [14]. However, it can be observed that for the sensors on the windward side, the pressure decreases notably with increasing thrust coefficient, while the pressures on leeward side and the perpendicular pressures are relatively independent of the thrust coefficient.

Fig. 33

Angle of attack variation for the single-engine case $\alpha =0^\circ$ (thin lines) and $\alpha =10^\circ$ (thick lines) (${M}_{\infty }=5.29,$ ${p}_{0}=4 \,\mathrm{bar}, \,{T}_{0}=450 \,\mathrm{K}$)

4.3.2 Three-engine case

In the following the results of the pressure measurements for the three-engine configuration are discussed. Figure 34 shows a comparison of the pressure coefficients of the single-engine and three-engine configurations for the baseline freestream condition. They are compared as function of the total thrust coefficient, which corresponds to three times the single-engine thrust coefficient for the three-engine case. The pressure coefficients in plane 1 and 2 for the three-engine case are very similar to the single-engine case, showing that the total thrust coefficient is an adequate scaling parameter to assess the influence of retro prolusion flows even between different engine configurations. Especially for the pressures farther downstream of the plume. For the three-engine case, the engines are active in the $\alpha$-plane. In plane 3, the pressures close to the center engine are the lowest (sensors 311 and 331), followed by the pressures on the outer ring but in the plane of the active engines (322 and 342) and finally the pressures with the largest distance to the plume (sensors 313 and 332). While the sensors close to the plumes experience similar pressures as in the single-engine case, the ones with the largest distance to the plumes (sensors 313 and 332) experience higher pressures as in the single-engine case. However, if the single-engine thrust coefficient is taken for the scaling, it is apparent that also for these locations the pressures are significantly smaller than of the single-engine case.

Fig. 34

Comparison of the single-engine case (thin lines) and three-engine case (thick lines) active in the $\alpha$-plane (${M}_{\infty }=5.29,$ ${p}_{0}=4 \,\mathrm{bar},\, {T}_{0}=450 \,\mathrm{K}$)

As for the single-engine case, a Mach number variation (Fig. 35), a Reynolds number variation (Fig. 36), and a variation of the angle of attack (Fig. 37, Fig. 38) was performed. Note that the scale for the thrust coefficient was extended to larger thrust coefficients as larger total thrust coefficients were measured for the three-engine cases. The Mach number variation shows that mainly the pressure coefficients close to the central engine (sensors 311 and 331) are offset from the baseline case. For all other pressure locations, the Mach number variation has little influence. For higher thrust coefficients, however, the offset becomes small. The Reynolds number variation (Fig. 36) shows that as for the single-engine case, the Reynolds number is not a driving similarity parameter. The influence on the static pressures seems to be negligible. The angle of attack variation (Fig. 37) shows that due to the larger plume building up for the three-engine case, the influence of the angle of attack on the surface pressures is smaller than for the single-engine case. In general, the pressures on the windward side are higher (sensors 331, 21, 11), while the pressures on the leeward side are lower (sensors 322, 24, 14). For higher thrust coefficients, however, the pressure coefficients at all pressure locations vanish. Higher pressures only persist at sensors directly in the wind and far enough downstream of the plume (sensors 24, 14). It should be noted, that these pressures seem to be independent of the thrust coefficient meaning that also at high thrust coefficients the influence of the angle of attack on the normal force on the configuration and on the moment coefficient is not negligible. In Fig. 38, the configuration was rotated by 90° such that the active engines were positioned in the plane perpendicular to the $\alpha$-plane (note that also the sensor locations are rotated by 90°), it is compared to the case shown in Fig. 37. Generally, the measured pressures still follow the same trend as the baseline configuration. However, it is noticeable that the pressure at 332, which is in this case the most windward position, is considerably higher which only vanish for thrust coefficients larger than 4. This is comparable to the single-engine case (see Fig. 33). Hence, if the engines are active in the $\alpha$-plane, they provide a stronger shielding effect for the pressures on the base plane than if they are active in the plane perpendicular to the $\alpha$-plane. However, the pressures in plane 1 and 2 are smaller for this configuration. Finally, a variation of the location of the exit plane of the central engine was performed (Fig. 40). In the reference configuration, the nozzle exit plane of the central engine is offset by 150 mm (in flight scale) out of the plane of the nozzle exit planes of the outer engines, for this variation, it was moved back into the same plane (see Fig. 39). This change in configuration only seems to have an influence on the pressures very close to the center engine (sensors 311 and 331). They are higher for lower thrust coefficients. However, for thrust coefficients larger than 1.5 the pressures are nearly equal.

Fig. 35

Mach number variation for the three-engine case for ${M}_{\infty }=5.29$ (thin lines) and ${M}_{\infty }=7.04$ (tick lines) (${M}_{\infty }=5.29,$ ${p}_{0}=4\, \mathrm{bar},\, {T}_{0}=450 \,\mathrm{K}$ and ${M}_{\infty }=7.04,$ ${p}_{0}=12.73\, \mathrm{bar}, \,{T}_{0}=610 \,\mathrm{K}$, engine plane: $\alpha$-plane)

Fig. 36

Reynolds number variation for the three-engine case $R{e}_{\infty }=2.36\mathrm{E}+05$ (thin lines) and $R{e}_{\infty }=7.07\mathrm{E}+05$ (thick lines) (${M}_{\infty }=5.29,$ ${p}_{0}=4 \,\mathrm{bar}, \,{T}_{0}=450 \,\mathrm{K}$ and ${M}_{\infty }=5.32,$ ${p}_{0}=12 \,\mathrm{bar},\, {T}_{0}=450 \,\mathrm{K}$, engine plane: $\alpha$-plane)

Fig. 37

Angle of attack variation for pressure coefficients ${C}_{p}$ vs. thrust coefficient for the single-engine case $\alpha =0^\circ$ (thin lines) and $\alpha =10^\circ$ (thick lines) (${M}_{\infty }=5.29,$ ${p}_{0}=4 \mathrm{bar}, {T}_{0}=450 \mathrm{K}$, engine plane: $\alpha$-plane)

Fig. 38

Angle of attack variation with engines active in the plane perpendicular to the $\alpha$-plane for the three-engine case $\alpha =10^\circ$, $\phi =0^\circ$ (thin lines) and $\alpha =10^\circ$, $\phi =90^\circ$ (thick lines) (${M}_{\infty }=5.29,$ ${p}_{0}=4 \mathrm{bar}, {T}_{0}=450 \mathrm{K}$)

Fig. 39

Center nozzle exit plane moved into the exit plane of the outer engines

Fig. 40

Variation of the engine exit plane: offset by 150 mm in flight scale (thin lines) and 0 mm (thick lines) (${M}_{\infty }=5.29,$ ${p}_{0}=4 \,\mathrm{bar},\, {T}_{0}=450 \,\mathrm{K}$, engine plane: $\alpha$-plane)

To conclude this section, the following observations and statements can be made. For high thrust coefficients, the pressure coefficients along the configuration with retro propulsion generally tend to very small values. The total thrust coefficient is suitable as a similarity parameter for the comparison of configurations with different engine configurations. The Mach number is of subordinate importance, the Reynolds number effect, as far as static pressure evaluations are considered, probably can be neglected. Due to the shielding effect of the plume the angle of attack is of less importance, however, at locations far enough downstream of the plume its influence seems not to be fully negligible. The relative position of the exit plane of the center engine in relation to the outer engines has only minor effects on the pressures on the base of the vehicle.

5 Conclusions and outlook

The paper describes the experimental results of the hypersonic part of the re-entry burn maneuver of the RETALT1 launcher configuration. Detailed measurements are presented for the RETALT1 configuration with one and three active engines, for several freestream and jet conditions.

An analysis of the flow features confirmed results from literature that the flow features for the single-engine case scale with the square root of the thrust coefficient. This could also be shown for the three-engine case. For the three-engine case, a constantly repeating switch from the blunt mode to the long penetration mode and vice versa was observed for all thrust coefficients tested. For the single-engine case, the building up of vortex rings was observed. These vortex rings move upstream from the Mach disc and lead to significant flow disturbances when interacting with the contact surface. For the three-engine cases, in general, an unsteady flow behavior was identified.

Condensation in the ambient temperature air plume was visualized and found not to be a local phenomenon in the underexpanded plume of retro propulsion flow fields. It was shown that this could be mitigated by heating the supply air to approximately 600 K. The heating did not influence the static flow features, though it might have an influence on the dynamic features. The analysis of the pressures along the model surface shows that the Mach number plays a subordinate role, and the Reynolds number seems to have negligible influence on the pressure distribution. The dominating similarity parameter is the thrust coefficient. For high thrust coefficients, the pressure coefficients generally tend to very small values, however, the pressure in the wake of the launcher configuration is independent of the thrust coefficient. Also the pressures far downstream are less dependent on the thrust coefficient. At an angle of attack, these pressures do not tend to zero, indicating that the normal forces and moment coefficients on the configuration are not negligible even for high thrust coefficients. A variation of the offset of the center engine nozzle exit plane with respect to the nozzle exit planes of the outer engines showed that the influence is small and is mainly present for small thrust coefficients.

This paper focused mainly but not only on static flow features, also some dynamic effects were observed. In future work, the frequencies of the measured pressures and the dynamic behavior observed in the flow fields shall be quantified and studied in detail. Furthermore, tests on the RETALT1 configuration during the final landing burn at subsonic velocities are ongoing in the Vertical Free-Jet Facility Cologne (VMK). They will complement the tests presented in this paper, as then, the complete RETALT1 descent trajectory will have been analyzed and understood by means of wind tunnel tests and complementary CFD computations.