1 Scientific motivation

Observational astronomy is a science and technology driver since the lifetime of Galileo Galilei. Roughly 100 years ago, observational astronomy discovered the amazing world of galaxies and opened the window into the remote universe, a research field that in our days is called cosmology. According to our present understanding, all observational data support the picture that the universe started with a Big Bang about 13.6 Gyr ago. Since then, it is expanding. It now contains billions of galaxies and sextillions of stars. All stars, like our sun, have finite lifetimes since they are powered by nuclear fusion reactions. These lifetimes range from many billions of years for the less massive stars down to just some million years for the most massive stars.

The expansion of the universe has the interesting consequence that the more distant an object is, the more its emitted light is shifted into the red. In combination with the cosmological redshift, this finally leads to the situation that the most distant objects cannot be detected anymore at visible wavelengths. This holds also for the exploding stars: on the way toward the observer their optical photons are absorbed by hydrogen atoms that are located in their host galaxies or in between the galaxies. However, observations in the near-infrared (NIR) can still detect these exploding stars.

In astronomy, first NIR observations were performed in the 1970s. Meanwhile, NIR detectors belong to the standard instrumentation of all modern telescopes. Compared to observations in the optical bands, observations in the NIR bands are much more affected by the emission and absorption properties of the atmosphere. Consequently, all observations are performed in certain wavelength regions using appropriate filters. In astronomy, the classical NIR bands are called J (centred around 1250 nm), H (centred at ~ 1650 nm), and K (centred at ~ 2200 nm). Modern detectors for NIR light are even sensitive down to 800 nm, so that they can even cover the astronomical z and Y bands (centred at ~ 900 and ~ 1000 nm, respectively).

This opened the possibility to cover the astronomically very interesting optical-NIR transition region (800–1700 nm) with a single detector type, as opposed to the GROND concept with a separate detector for each channel [1]. Consequently, the question arose how to focus split beams on the same detector plane. Based on the Koesters-principle [2], a novel four-channel beam splitter was conceived [3], which enables observations in four photometric bands, simultaneously. This led to the SkyHopper space mission concept [4], where the small mass, size and power requirements of our 4-channel camera concept made a CubeSat mission feasible. With observations in the bands z, Y, J, and H, Skyhopper will hunt for the most distant exploding stars.

The novel four-channel beam splitter [5] is based on a Kösters-type prism. For the sake of simplicity, we will refer to the all-glass four-channel beam splitter as “Kösters prism”. Here, we describe its first technological realization as a proof of concept. This includes studies of the optical design, the dichroic coatings, the bonding technique, and the mechanical mounting of the entire optical element. The theoretical and experimental studies result in the manufacturing of a demonstrator. The demonstrator is the basis for future environmental, optical and mechanical testing to validate the design results.

2 Technical layout

2.1 Optical design

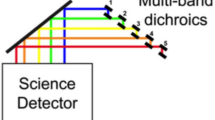
Figure 1 shows the ray paths in the novel Kösters prism [3]. After exiting the telescope optics and after passing through an anti-reflection coated surface, the light enters the prism that is arranged in front of the detector. Inside the Kösters prism three beam splitters chromatically separate the light into four bands and, together with additional internal total reflection, direct the resulting four beams (four wavelength bands) to separate regions on the detector. While the principle of this beam splitter works for several telescope designs, we used a three mirror anastigmat (TMA) with 1.76° x 0.44° field of view (FOV), originally developed for the SkyHopper mission. It has an entrance pupil diameter of 224 mm and a f-number of 4.14. The lens is designed for the application with a Hawaii-2RG detector array (pixel size 18 µm). As described in [3], the image of each channel has an aspect ratio of 1:4 and the images of all four channels together fit in the quadratic detector array. The performance of the beam splitter coatings determines the quality of the wavelength separation. Since the first beam splitter needs to work over the full wavelength range from 800 to 1700 nm, a long-pass filter and a short-pass filter enhance the accuracy of the wavelength separation.

Fig. 1
figure 1

Ray path of white light coming from a telescope (bottom left). The chromatic separation of the ray paths is shown on the three beam splitter coatings (thick red lines) in the Kösters prism

Full size image

For the numerical tolerance analysis, we used the raytracing software Zemax OpticsStudio. The model included the complete optical system consisting of telescope and Kösters prism. In addition, we analyzed the stray light behavior with respect to the coating design and added measurement data using the software FRED.

The long optical path (about 24 mm) through the six fused silica prisms causes chromatic aberrations due to the dispersion. However, fused silica has a low dispersion indicated by an Abbe number of 67.8. This decreases the influence of the long optical path in comparison to other glass types. Besides, the chromatic separation of the setup allows the correction of the optical path difference for each wavelength band. This correction can be realized at the exit surface of the prisms, using small glass plates or varying the prism lengths accordingly. The impact of these modifications on the image contrast is investigated amongst others in the following section.

2.1.1 Tolerance analysis

To specify the manufacturing tolerances of the demonstrator prisms, we set up a model in Zemax OpticsStudio (Sequential Mode), which contains the physical dependencies of the prism group. Vice versa, from the manufactured prisms, we also analyzed the influence of the measured surface deformations and geometry deviations. The market research showed that current manufacturing tolerances of the prism lengths make it critical to stay diffraction limited. Table 1 shows in the first column the prism tolerance values provided by the manufacturer and used in the numerical analysis. Manufacturing tolerances of ± 10 µm on the prism length would be necessary, in result of the tolerance analysis. However, with ± 50 µm length tolerance, the impact on the image quality is as large as from the mentioned chromatic optical path differences (Fig. 2). The used prisms were manufactured according to the requested tolerance, except the prism length, as visible in the second column in Table 1.

Table 1 Prism tolerances used for the tolerance analysis and measured from the manufactured prisms
Full size table
Fig. 2
figure 2

Results of the tolerance analysis. The graphs show the overlaid results of the ensquared energy of the optical system for several tolerance combinations, within the calculated tolerance limits (Monte Carlo analysis). The ensquared energy shows, which portion of the light of a point source (e.g., a star) would fall on a certain number of of pixels on the sensor. The black curve indicates the theoretical diffraction limit (marked by the red arrow). The graph on the top left shows the results obtained using the tolerance values given in of Table 1. The graph on the right shows the results obtained when only the correction of the optical path length difference (OPD) is eliminated. The graph on the bottom shows the results with the OPD correction but allowing for a less accurate prism length. The influence on the image quality of both steps is comparable

Full size image

The graphs shown in Fig. 2 result from a Monte Carlo analysis using 100 trials with a parabolic distribution of the tolerance values within the limits given in Table 1. In the analysis, we used the distance between the telescope and the Kösters prism as compensator for focusing. Hence, the optical path differences (OPD) between the prisms affect the aberrations but not the optical path length. To solve this problem, the tolerances of the fabricated prisms were measured with high precision (Table 1, right column). Identical prism lengths avoid further optical path differences. Different prism lengths could also be paired to compensate for the chromatic optical path differences.

We calculated the surface deformations, which occur due to cryogenic temperatures, with the finite element (FEA) analysis. The tolerance analysis showed that these deviations (1.6 nm peak-to-valley, 0.2 nm rms) are within the determined tolerance specifications (Table 1).

2.1.2 Stray light analysis

To support the development of the coating design, we investigated their impact onto the stray light behavior with the focus on the ghost analysis. Thereto, the design of the developed coatings (Sect. 3.1) were included in the analysis. The stray light analysis considered reflections on prism faces, residual reflections, and residual transmissions of the coatings and stray light on the telescope mirrors. The investigated model contained both the telescope as well as the Kösters prism together with the bonded base plate. The stray light behavior of the dichroic mirrors was included in the simulations with the Harvey-Shack model, based on representative measurements of manufactured dichroic mirrors. Real measurement data of the angular resolved scattering on the manufactured bond surfaces was added to the simulation in the last part of the presented results (Fig. 5).

For astronomical applications, it is favorable to suppress the intensity of the stray light on the detector to at least seven magnitudes (corresponding to a factor of about 600). Therefore, we performed a stray light analysis for two representative cases. In case 1, the dielectric coatings were included as they could be technologically realized in the demonstrator (Sect. 0). Case 2 included optimized coatings, which can only be manufactured with further technical and financial effort. The analysis of case 1 showed ghost images, resulting from residual reflections and residual transmission in the coating layers. These ghost images still showed a good resolution on the detector, but they represent false light because of their wavelengths. Therefore, the suppression of false light was prioritized in the coating design (Sect. 3.1). The results of this analysis showed that three of four channels can match the criteria of damping the false light by seven magnitudes (Fig. 3). In the worst case, the intensity of the ghost image lies five magnitudes (a factor of 100) below the signal intensity (Fig. 3, bottom right).

Fig. 3
figure 3

Relative intensity of the illumination on the detector (in logarithmic scale) for the coating design of the demonstrator. The diagrams show the results for a point source (e.g., a star)—in the first row from the Y band and in the second row from the z band. The graphs on the right show sectional data from the false color images (on the left) at 858 nm (Y band, upper diagram) and 1042 nm (z band, lower diagram). The numbers ± 20 are the dimensions of the detector expressed in units of mm

Full size image

Our numerical studies showed that the intensity of the ghost images can be reduced further when coatings of higher complexity are used (case 2). The implementation of these coating designs to the stray light analysis showed the successful suppression of ghost images in all four channels to seven magnitudes below the signal (Fig. 4).

Fig. 4
figure 4

Results of the stray light analysis. Shown here is the relative intensity of the illumination on the detector (in logarithmic scale) for a point source. With optimized coatings, the ghost images for all four bands (H, J, Y, z) are successfully suppressed by seven magnitudes below the signal

Full size image

In addition, the straylight analysis investigated the effect of secondary reflexes on the surfaces between glass and air, together with an exemplary detector reflectivity of 10%. The resulting stray light on the detector shows a suppression of 6.7 magnitudes, which is slightly above our 7 magnitudes limit. This stray light scales linearly with the reflectivity on the exit surfaces and the reflectivity of the sensor. Hence, an anti-reflection coating on the exit surfaces will sufficiently reduce this effect.

Finally, measurements of the real stray light behavior on the manufactured bond surfaces after coating and bonding were included in the analysis. These results showed that the stray light of the whole system on the detector is seven magnitudes below the image intensity of the light source and therefore not critical (Fig. 5).

Fig. 5
figure 5

Relative intensity of the illumination on the detector (in logarithmic scale). The diagrams show the results obtained using with measured data of real stray light behavior on the bonding surfaces for a point source. The stray light intensity meets the criteria of a damping by seven magnitudes below the signal strength. Other details follow Fig. 3

Full size image

2.2 Mechanical design

We performed finite element method (FEM) simulations with the software package ANSYS to ensure that the mount together with the beam splitter withstands the challenging requirements of a rocket launch and a space-based application. Therefore, a quasi-static load of 100 g (standard gravity) in all three spatial directions was applied in the simulation, i.e., on the mount and on the beam splitter. We optimized the geometry of the mount to ensure that the first eigenfrequency is in the range of 1000 Hz to minimize excitations due to sine/random vibrations during a rocket launch [6]. To account for the operating temperature of the beam splitter in the NIR (near infrared) spectral range, a thermal load of 140 K was simulated [3].

To realize the necessary vacuum gap in the design of the beam splitter (Fig. 1), we decided to bond the prism pairs to a base plate made of fused silica. In the following the term optical element refers to the combined Kösters prism and base plate.

2.2.1 Design of the mount

To develop a mount for the optical element we considered several approaches: (i) a model that uses adhesive contacts between the mount and the base plate (Fig. 6, left), (ii) a model that uses solder contacts between the mount and the base plate (Fig. 6, middle), (iii) a mount that clamps the optical element. Main criteria for the evaluation and comparison of these models were the stress in the contact area, the eigenfrequency, and the mass. In all models a quasi-static load of 100 g in all three spatial directions and a thermal load of 293 ± 40 K was applied.

Fig. 6
figure 6

Different options for the mechanical mount of the optical element. Left: Tripod construction that uses adhesive contacts between the pin and the base plate made of fused silica. Middle: Tripod construction that uses solder contacts between the pin and base plate. Right: Mechanical mount with spacers and springs that hold the optical element

Full size image

Connecting metal mounts with fused silica using adhesives is an established technique in terrestrial and space applications [7, 8]. Therefore, we chose a model (Fig. 6, left), where the optical component is hold by three bipods consisting of Ti-6Al-4 V. Each bipod head contains a pin, made of Invar 36, which is attached to base plate via a 0.1 mm thick adhesive bond. The frame is isostatically mounted to the optical bench by three contact points (Ti-6Al-4 V). For the adhesive we selected Scotch Weld EC 2216 B/A as it was already used for space applications [9, 10]. Masterbond EP21TCHT-1 was chosen as an alternative glue for cryogenic applications [7]. Applying quasi-static loads of 100 g in all three spatial directions resulted in a maximum von Mises stress of 7.5 MPa in the standard adhesive joint with an initial radius of 3.5 mm. This stays well below the targeted value of 10 MPa (Ultimate tensile strength, UTS, of ~ 20 MPa [9] divided by a factor of safety, FoS, of 2). Simulating thermal terrestrial loads (293 ± 40 K) resulted in a maximum von Mises stress of 9 MPa in the joint, which is within the margin of safety. The optimal radius r of the adhesive amounts to 5 mm, resulting in minimal von Mises stress (3 MPa) in the joint and a maximum principal stress of 5 MPa in the base plate (fused silica). The maximum von Mises stress in the titanium bipod flexures is < 90 MPa and within the safety margin of 448 MPa (UTS of 895 for Ti-6Al-4 V divided by an FoS of 2). The average mass of the mount is ~ 130 g. With an optimized diameter of 0.9 mm for the bipod flexures, the first eigenfrequencies was simulated to amount to ~ 1040 Hz. Using the parameters for cryogenic temperatures of the Scotch Weld adhesive yields a maximum principal stress of > 100 MPa in the adhesive joint. Using the Masterbond adhesive in the cryogenic environment, with a CTE of ~ 20 × 10–6 K−1 at room temperature, the simulations showed a maximum principal stress in the adhesive of ~ 26 MPa, which complies with the targeted value of ~ 28 MPa (UTS of 55 MPa divided by a FoS of 2; see Fig. 7). The singularity in Fig. 7 (right) is caused by the geometry of the adhesive joint. Due to limitations of the edge length of the elements it is not possible to eliminate the area of steep stress increase at the edge. Therefore, the outermost elements with a suitable small size of 0.05 mm were excluded from our numerical analysis. Based on this, it is of utmost importance to verify these numerical results, experimentally.

Fig. 7
figure 7

Mechanical stress in an adhesive joint (Masterbond EP21TCHT-1) with a radius of 5 mm; Left: at a mechanical load of 100 g; Middle: no mechanical load and ΔT = 40 K; Right: no mechanical load and ΔT = 153 K. The sharply increasing stress at a distance of ~ 0.02 mm from the edge of the adhesive joint in the right image is due to a numerical singularity

Full size image

An alternative method of attaching the optical assembly to the metallic mount is soldering. Solderjet bumping allows precise soldering of metallized glass surfaces with minimal heat input [11]. For our application solder balls with a diameter of 760 μm consisting of Sn96.5Ag3Cu0.5 (SAC305), which is the largest size available, were selected for the joint. For this model a structure of three bipods with different arrays of punctual and/or extended solder joints connecting to the fused silica were investigated. The model with the minimized stress is a set of circular extended joints surrounded by punctual solder dots (see Fig. 6, middle). The maximum von Mises stress in the solder joints during quasi-static loads of 100 g is ~ 20 MPa, which exceeds the targeted level of 15 MPa (UTS of ~ 31 MPa [11], FoS = 2). The highest maximum principal stress in the base plate for a mechanical load of 100 g is 27 MPa. Due to the large cage structure, which is necessary for the model, the first eigenfrequency lies at around 800 Hz. The mass of the mount is about 190 g.

We finally studied the concept of clamping based on the presented design in [3]. In our case the optical element is held by brackets which are pulled toward the center by springs. Securing the beam splitter in the vertical direction is realized by a metal plate and additional springs in vertical orientation in the upper part of the cage structure. Such a model has the advantage that there is no adhesive or solder that can break. Furthermore, the springs are designed to compensate for thermal expansion when cooling the entire opto-mechanical element down to 140 K. Compared to the aforementioned models, the usage of a plate (for example copper, with excellent thermal conduction properties) at the top leads to a more uniform temperature distribution in the presence of a temperature gradient. Adding the base plate separates the mechanical parts from the prisms, which minimizes the risk of damaging the prisms when metal is pressed onto the fused silica. Simulations show that the stress in the base plate at the contact points is in the range of 10–15 MPa, or higher. The other models yield lower stress in the base plate, as mentioned earlier. In comparison, for the adhesive-based model the maximum principal stress in the fused silica is smaller than 6 MPa. The mass of the entire structure, which includes three bipods to create isostatic mounting, is ~ 280 g, which is significantly heavier than other models. A modal analysis shows that the first eigenfrequency lies at about 700 Hz. This is lower than the other models, due to the larger mass. One way to increase the eigenfrequency could be accomplished using three solid joints instead of the bipods.

The most important results of these three models are summarized in Table 2. Based on this summary, we have finally chosen the model with the adhesive joints. Among all three considered models, this model offers the lowest mass. In addition, it has the highest first eigenfrequency and is therefore less likely to react to sine or random vibrations during a rocket launch. For all tested loads (mechanical and thermal) the stress in the joints and the base plate stays within the margin of safety. Finally, also the maximum principal stress in the base plate is lowest.

Table 2 Overview of the results of the optimization of the three different mounting models
Full size table

2.2.2 Mechanical design adjustment of the optical element

In addition to the mount of the beam splitter, the design of the optical element itself was optimized to reduce internal stress. In doing so, particular attention was drawn on the thickness of the base plate (Fig. 8). We applied a quasi-static load of 100 g and varied the thickness d of the plate between 5 and 40 mm. For d < 10 mm, the stress in the contact area between the Kösters prism and the base plate increased substantially and reached 20 MPa. We finally found that a thickness of d = 12 mm is best with respect to stiffness, mass, and stress.

Fig. 8
figure 8

Left: The optical element consisting of three prism pairs AB, CD, and EF (representing the Kösters prism) and the base plate with thickness d. The prisms are silicate bonded onto the base plate. Right: The base plate with channels to drain excess silicate solution during the bonding process. Between prisms B and C as well as D and F is a vacuum gap (see Fig. 1)

Full size image

We further investigated if there is a limiting size for the vacuum gap between prisms B and C as well as D and F in terms of the stress in the contact area between the Kösters prism and the base plate. In doing so, the size of the gap s (Fig. 9, right) was varied between 0.05 and 0.6 mm, while keeping the thickness of the base plate at d = 12 mm. Figure 9 shows the normal stress in the contact area between the individual prisms and the base plate. The normal stress at the surface of the plate turned out to be roughly the same for all studied gap sizes (Fig. 9, left). This is due to the 0.2 mm chamfer of the prisms, which separate the contact areas of all prism pairs by 0.2 mm, in addition to the gap size. Furthermore, channels with a width of 1.5 mm and a depth of 0.5 mm were introduced (see Fig. 8 right), to drain excess silicate solution during the bonding process, which creates an additional separation of the contact areas. Excess silicate solution in the air gaps would lead to closing of the air gap, due to capillary forces. Finally, for the parameter range studied here, no preferred gap size has been found; its chosen size depends on the optical design.

Fig. 9
figure 9

Left: normal stress perpendicular to the surface of the base plate along the marked path in the contact area, starting at the tip of the prism (black solid line in the right figure) for different widths of the vacuum gap (parameter "s”) as a function of the distance to the corner (tip). Right: Normal stress at the surface of the base plate in the area where the prisms B, C, D, and E meet, adopting a width of the vacuum gap of s = 0.6 mm (top) and s = 0.05 mm (bottom). The dashed lines show the contact area of the prisms and the dotted lines are at the position of the actual vacuum gap. Note that very high stress values at the corner of the triangular prisms are the result of a numerical singularity (red- and yellow-colored regions). Consequently, the mechanical stability needs to be verified experimentally

Full size image

For fabricating the Kösters prism, we determined how much area of each prism pair (AB, CD) needs to be bonded to the base plate to provide a stable connection when applying a mechanical load of 100 g. We considered two scenarios: (i) both prisms are bonded to the base plate. (ii) Only a single prism of each prism pair is bonded to the base plate. For the sake of simplicity, in the simulation of scenario (ii), the non-bonded prisms (A, C, E) rest without contact or friction on the base plate. Figure 10 shows that in the second scenario for both pairs, the stress at the bonded areas increases, especially at the edges and the corners. However, for both cases, the stress is below the required limit of 20 MPa. Even in case (ii) the entire mechanical structure withstands high mechanical loads. Rounding the corners at the contact area to a radius of ~ 1 mm reduces the stress even more. A modal analysis showed that in case (ii) the eigenfrequency of the optical element amounts to more than 2000 Hz. Due to the simplification of scenario (ii) a potential damage of the base plate by the non-bonded prism cannot be evaluated. Therefore, we adjusted the geometry in the FEA by moving the non-bonded prisms 100 µm away from the base plate. In this configuration, the non-bonded prisms do not touch the base plate. The occurring stresses in this case are below 20 MPa.

Fig. 10
figure 10

Normal stress perpendicular to the contact area within the bonded area of the base plate with two different prism pairs (AB and CD) for two scenarios: (i) two prisms connected with the base plate, and (ii) a single prism is connected with the base plate. Left: prism pair C/D. Right: prism pair A/B

Full size image

3 Fabrication

3.1 Coating design and realization

To achieve the desired optical functionality, each prism pair is equipped with a different dichroic coating. The design of these coatings meets the requirements on the optical performance over the spectral range from 800 to 1700 nm (Sect. 2.1.2). At the same time, the three beam splitting coatings must provide an interface for the joining of the prism pairs and must be stable under harsh conditions in space. Therefore, two approaches were considered here, either two or three different coating materials were used. To meet the high requirements on the optical performance of the entire Kösters prism assembly, an anti-reflection (AR) coating on the entrance surface of the beam as well as a short-pass and long-pass filter at the exit faces of the first prism pair are used. The filter coatings improve the splitting properties of the first beam splitter, since unwanted spectral bands are blocked from entering the second and third beam splitters. Table 3 lists the spectral properties of the various coatings.

Table 3 Spectral properties of the coatings used in the Kösters prism
Full size table

3.1.1 Evaluation and optimization of relevant materials

Sputtered SiO2, Si, Si3N4, Ta2O5 and Nb2O5 were evaluated and optimized for the use in the Kösters prism. SiO2 was used as low-index material and silicon as high-index material. Si3N4, Ta2O5 and Nb2O5 were evaluated as medium-index materials in the ternary design or as high-index materials in the binary design. Firstly, optical constants from previous experiments of the materials were used to evaluate the feasibility of the different approaches with various combinations of the materials. For all three material combinations SiO2-Si3N4, SiO2-Ta2O5 and SiO2-Nb2O5 an overall thickness around 10 µm would be needed to achieve an acceptable optical performance. The combination SiO2-Si enabled a lower thickness. The extinction coefficient of the deposited Si was too high in lower wavelength regions. Therefore, and to keep the thickness of the different coating designs below 4 µm, we decided to evaluate a ternary design. Subsequently, single layers of all coating materials were deposited and spectrally measured by a Perkin Elmer Lambda spectrophotometer. The extinction coefficient and index of refraction were determined using LCalc software.

The resulting optical constants for Si are presented in the left diagram in Fig. 11. The deposited silicon layers exhibit an undesirable high extinction coefficient for shorter wavelength, which is attributed to dangling bonds in the amorphous silicon structure [14]. During heating, the dangling silicon bonds can recombine [15]. Hence, the extinction coefficient could be decreased by annealing (Fig. 11, left). Annealing at 350 °C reduces the extinction coefficient over the whole considered spectral region. In addition, the compressive film stress was decreased from ~ 1 GPa after deposition to 240 MPa. Annealing up to 550 °C has no influence on the extinction coefficient but decreases the film stress to 28 MPa (tensile stress). To keep the thermal load on the components low, we chose an annealing temperature of 350 °C. Since, Si is used in a multilayer coating, the other coating materials are also affected by annealing. Therefore, all other materials were examined after annealing to 350 °C. We observed an unchanged or decreased extinction coefficient for SiO2, Si3N4 and Ta2O5. Only, the extinction coefficient of Nb2O5 increased. Thus, we dismissed Nb2O5 as coating material. Ta2O5 has a higher index of refraction (nTa2O5 = 2.10 – 2.07; λ = 800 – 1800 nm) compared to Si3N4 (nSi3N4 = 2.00 – 1.97; λ = 800 – 1800 nm). Therefore, a further reduction of the layer thickness is possible with Ta2O5. We use a ternary coating, consisting of SiO2-Ta2O5-Si, for the final designs. Also, the coating of the beam splitters must provide a bonding interface to the fused silica prism. Therefor a thick SiO2 layer was included in the coating design as top layer. This SiO2 layer was smoothed by polishing (see Sect. 3.2).

Fig. 11
figure 11

Left: extinction coefficient k of silicon, compared to values from the literature [13]. Right: index of refraction n and k for the medium index materials Si3N4 and Ta2O5

Full size image

Coated and bonded test samples were cooled to 140 K to simulate the application temperature of the Kösters prism. Reflection R and transmission T of test samples were measured before and after cooling with a Perkin Elmer Lambda spectrophotometer. In Fig. 12 left no difference in transmission and reflection is visible before and after treatment at 140 K. In conclusion, our coating is resistant against a temperature change of 480 K.

Fig. 12
figure 12

Left: reflection and transmission of coated test sample before and after exposition to 140 K measured at 6° AOI; middle: reflection and transmission of the deposited beam splitter 1 at 6°AOI (angle of incidence) with air as incident medium before and after annealing; right: measurement of bonded dichroic beam splitter 1 at 6° and 30° AOI, no correction of front and backside reflection

Full size image

To evaluate the optical performance in terms of reflection and transmission, round fused silica test samples (diameter = 25 mm; thickness = 1 mm) were coated and spectrally measured. The coatings were then annealed and measured again. Figure 12 middle shows the positive effect of the annealing. Subsequently, the beam splitter coatings were bonded and measured at different angles of incidence (AOI), as visible in Fig. 12 right. Note that no correction of the front and backside reflection of the glass samples was performed.

After designing and optimizing of the different coatings, the dichroic beam splitters were deposited on the corresponding prisms. Afterward, the prisms were polished, cleaned, and bonded. Then the AR, short-pass and long-pass coatings were deposited on the first prism pair in three different coating runs. Special support structures were designed to protect the already coated surfaces of the prism pair.

Due to the limitation of the coating thickness by our goal to keep the overall thickness below 4 µm, the optical performance of the deposited coatings is limited as well. In a design study, we developed coatings with the same composition but higher overall thickness and therefore could achieve a better optical performance.

3.2 Bonding

Joining of optical components is mainly realized using adhesives. Adhesives are easy to use but have the drawback of outgassing and limited chemical resistance. This is even more critical when adhesives are used in space, with its harsh environment (extreme temperatures, vacuum, ionizing radiation). Therefore, care must be taken on the choice of the right joining technology. In the past, hydrophilic direct bonding was successfully used to join silicon wafers in semiconductor industry [16]. This process was also successfully used to join fused silica optical components [17]. For the Kösters prism, dielectric coatings on fused silica prisms (Suprasil 3301) had to be bonded, where fundamental functionality has been presented earlier [18]. Three different coatings were applied on the beam splitting prisms that had to be bonded. The assembly of the three single beam splitters to form the Kösters prism was another challenge. As elucidated in Sect. 2.2, different mechanical design approaches of the assembly were studied, regarding the requisites of the bonding technology. For the Kösters prism vacuum gaps are necessary to provide the optical functionality. The necessary tolerances are summarized in Table 2. To provide the necessary precision of the vacuum gaps regarding gap length and parallelism we used silicate bonding with special high-precision fixtures.

3.2.1 Direct bonding of coated samples

For the joining of the coated prisms hydrophilic direct bonding was adapted to bond the coated beam splitter prisms. Hydrophilic direct bonding is possible on surfaces with low roughness and high flatness. The root mean square (rms) roughness σrms, measured in a 10 × 10 µm2 measurement area of an atomic force microscope (AFM), shall amount to σrms = 0.5 nm [19]. The flatness in surface figure deviation from a plane surface measured by Fizeau interferometry is limited to λ/10 (measuring wavelength λ = 633 nm) for stiff bodies. With increasing layer thickness of the optical coatings, the surface roughness increases [20]. Hence a ~ 200 nm thick SiO2 layer was applied on top of the coating. This coating was smoothed by chemical mechanical polishing (CMP) prior to bonding. This approach was tested using round fused silica substrates (diameter: 25 mm; thickness: 6.35 mm). Therefore, the surfaces were checked with AFM before coating, after coating, and after CMP. The CMP process was optimized in terms of pressure and duration to achieve low roughness with only small removal of the SiO2 layer thickness. The roughness before CMP amounts to σrms > 1 nm. CMP reduced the roughness to σrms = 0.3 nm, which is sufficient for bonding (Fig. 13).

Fig. 13
figure 13

Images from AFM measurements (measurement size: 10 × 10 µm2) with their corresponding roughness value after coating and before CMP (left) and after CMP (right)

Full size image

Bonding was performed in a clean room environment (class ISO 4, defined by ISO 14644-1). Samples were prepared for bonding by cleaning with ultrasonic assisted bath cleaning steps. Subsequent spin cleaning with mega sonic assistance in a clean room environment provided clean surfaces. Prior to contacting, samples were activated in low-pressure plasma with oxygen and nitrogen. A subsequent water cleaning step provided hydrophilic surfaces. It is assumed that such surfaces are saturated with OH groups [16]. The surfaces are brought into contact at moderate pressure. A bond via weak atomic interactions is established. A further annealing step at 250 °C enhances the formation of strong covalent bonds between the surfaces. The OH groups react with each other to form strong X-Si–O-Si-X connections under the formation of water. This procedure was applied successfully to bond coated with uncoated fused silica substrates (Fig. 14).

Fig. 14
figure 14

Exemplary photo of a successfully directly bonded fused silica round substrate, where one substrate is uncoated and the other is coated with a beam splitter coating and CM polished

Full size image

A rocket launch of such optical components requires high mechanical strength of the connection (see Sect. 2.2.2). Therefore, bonded coated samples were tested in a three point bending test. From round substrates cuboid samples with a square cross section (~ 5 × 5 mm2) were manufactured by sawing. A plunger applied a compressive force onto the sample within a materials testing machine (Zwick Roell Allround Line 20 kN). Samples with different layer thickness (1 µm or 3 µm) as well as different composition (SiO2-Si3N4-Si or SiO2-Ta2O5-Si) were examined and compared to uncoated fused silica substrates (Fig. 15). A breaking strength of 50 MPa was achieved independent of the underlying coating composition and thickness. This amounts to 50% of the breaking strength of uncoated fused silica substrates and is comparable to the breaking strength of adhesive bonded glass samples (50 MPa). It is five times the breaking stress of optically contacted substrates.

Fig. 15
figure 15

Comparison of breaking strength of different coatings with different thickness and of bare fused silica

Full size image

3.2.2 Mounting of the Kösters prism

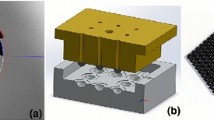
After characterizing the direct bonding performance of test substrates, we bonded the prism pairs. Therefore, the prisms were coated with dichroic beam splitters, CM polished and bonded directly as described earlier. As discussed in Sect. 2.1.1, care must be taken on the angular orientation of the prism pairs to each other. Special mechanical fixtures which allowed for precision bonding, were designed and manufactured at Fraunhofer IOF. To reduce stray light from scratches on the optical surfaces of the prisms, the fixtures were designed to protect the clear aperture. The positioning of the prism pairs after bonding was verified by means of three coordinate measurements.

For mounting the Kösters prism three different approaches were evaluated in Sect. 2.2. As mentioned earlier, we decided to use adhesive bonding to connect bipods with a glass base plate. The three prism pairs are separated by small vacuum gaps (Fig. 1) to provide the necessary reflection within prisms B and E (Fig. 8 left). To realize an all-glass Kösters prism we decided to use silicate bonding [21] to join the prism pairs with the base plate, which was already used successful in other space related projects, like LISA pathfinder [22]. Compared to adhesive bonding, silicate bonding leads to better thermal properties of the Kösters prism with an appropriate bonding strength of 50 MPa. For silicate bonding a sodium silicate solution is applied on one of the surfaces to be bonded. The other surface is brought into contact. At the interface a chemical reaction takes place, where a silicate network is formed [23]. Curing at elevated temperature accelerates this chemical reaction. Since a liquid solution is used, the requirements on the surface topography are less tight than for direct bonding. Surface flatness of 3 µm and roughness of 1 nm rms are sufficient for silicate bonding [24]. At first the three prism pair surfaces which had to be silicate bonded (Fig. 8 left) were prepared to form a uniform surface. Therefore, the surfaces were grinded and polished altogether. Silicate bonding was executed in special high-precision fixtures to provide accurate positioning of each prism pair, showing an air gap parallelism of better than ± 0.05°, which is below the required value of ± 0.1° from tolerance analysis (see Table 2). In this way, we successfully fabricated an all-glass Kösters prism for future use in space (Fig. 16).

Fig. 16
figure 16

Successfully fabricated all-glass Kösters prism by direct bonding coated prisms and afterwards silicate bonding the prism pairs to the fused silica base plate

Full size image

4 Conclusions and outlook

We reported on the results of a design and realization of an all-glass Kösters prism for use in space, with emphasize on observational astronomy. We performed optical design studies to evaluate the influence of the coating performance, the mechanical and the joining tolerance on the imaging system. This design studies provided guidelines for the optimization of the coating and the mounting of the Kösters prism. We showed that a coating design can be developed to meet the high scientific requirements.

The mechanical design included the evaluation of different mounting approaches of the Kösters prism. Mechanical and thermal loads were included in numerical simulations to evaluate the influence of the harsh conditions in space on the mounting of the Kösters prism. Further simulations of the mounting of the detector are planned.

A main feature of the Kösters prism are dichroic beam splitter coatings to provide splitting of the incident light into the four different channels. We evaluated and tested different coating designs, materials, and thicknesses. As a result, we deposited a ternary coating (SiO2-Ta2O5-Si) on the beam splitter prisms. With the realized coating composition, we did not meet the full requirements on the optical performance. For fabrication of a flight model, optimization of the coatings design will be performed. This includes thicker coatings, fabricated with alternative coating equipment have to be tested.

Direct bonding of coated prisms was successful. We developed a new approach to join coated glass samples by polishing a final SiO2 layer. We used silicate bonding to mount the Kösters prism on a fused silica base plate. Further testing of such Kösters prism is planned in the near future. The optical performance of the Kösters prism at 140 K is of central interest. A future shaker test will validate the overall strength of the joining connections.