Abstract
The European project RETALT (Retro Propulsion Assisted Landing Technologies), funded by the Horizon 2020 framework program (Grant agreement No 821890), has as main objective to investigate critical technologies for the assisted descent and landing of re-usable first stages. Among these technologies, one can find aerodynamics, aerothermodynamics, flight dynamics, guidance navigation and control (GNC), Structures, mechanisms, thrust vector control (TVC) and thermal protection systems (TPS). The present paper focuses in particularly on the aerodynamics technology applied to a vertical landing launcher configuration, called RETALT1, including retro-propulsion. During the landing phase of the first stage of the launcher, the main devices for control and trim of the vehicle (besides the retro-propulsion) are the aerodynamic control surfaces (ACS). Three types of aerodynamic control surfaces are investigated by means of numerical computations, using the NSMB (Navier Stokes Multi Block) CFD code. The control surfaces considered are the deployable interstage segments (also named petals), grid fins and planar fins. Aerodynamic coefficients as well as forces acting on the control surfaces are extracted from the CFD computations to assess the efficiency of each type of devices and to populate the Aerodynamic Database (AEDB) for flight dynamic analysis.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The European project RETALT (Retro Propulsion Assisted Landing Technologies), funded by the EU Horizon 2020 framework program (Grant agreement No 821890), has as main objective to investigate critical technologies for the assisted descent and landing of re-usable launchers. Among these technologies, one can find aerodynamics, aerothermodynamics, flight dynamics, guidance navigation and control (GNC), structures, mechanisms, thrust vector control (TVC) and thermal protection systems (TPS). Two reference configurations are studied in the project: RETALT1, a Two Stage To Orbit (TSTO) Vertical Take-off Vertical Landing (VTVL) Launcher and RETALT2, a Single Stage To Orbit (SSTO) VTVL. An overview of the project as well as the current progress is summarized in [1, 2].
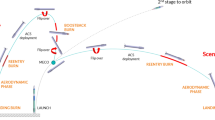
This paper focuses in particularly on the Aerodynamics technology applied to the vertical landing launcher configuration, called RETALT1. RETALT1 is a Two Stage to Orbit Vertical Take-off Vertical Landing Launch Vehicle. It is similar to the Falcon 9 by SpaceX, or the New Glenn by Blue Origin, but using only European technologies. RETALT1 is able to transport 20 tons to a Low Earth Orbit (LEO), or 14 tons in the Geostationary Transfer Orbit (GTO). For a faster market readiness, as well as for reducing risks and costs, the reference configuration employs available propulsion technologies using liquid oxygen and hydrogen (LOX/LH2). Both the first and second stages use the same type of engine that is similar to the Vulcain 2 engine, but with expansion ratios adjusted for optimum thrust at sea level. The first stage of RETALT1 is powered by nine engines [1]. This stage is recovered using retro-propulsion. For LEO launch missions, it is possible that this stage can perform a Return to Launch Site, for GTO missions, a landing on a seagoing platform can be performed. When returning to the Launch site, it is necessary to make a flip over after stage separation and to perform a boost back burn. A second flip over is then needed to permit the use of the engines to reduce the landing speed. When a landing on a seagoing platform is foreseen, only one flip-over maneuver is required [3]. When entering the earth atmosphere, the aerodynamic control surfaces are deployed, and at an altitude of around 70 km, a first braking maneuver is made using three active engines (re-entry burn). This is followed by an aerodynamic phase, followed by the landing burn using the central engine to decelerate the vehicle until touchdown.
During the aerodynamic phase of the first stage of the launcher until touchdown, the main devices for control and trim of the vehicle (besides the retro-propulsion) are the aerodynamic control surfaces (ACS). Three types of control surfaces are investigated using numerical computations performed by CFS Engineering, and wind tunnel experiments by DLR. The control surfaces considered are the deployable interstage segments (also named petals), the grid fins and the planar fins as shown in Fig. 1.
The sizing of the control surfaces is discussed in detail in [4]. The underlying assumption is that ACS should be able to trim the vehicle flying at a maximum angle of attack of 10° [3].
The use of petals has the advantage to reduce the mass and complexity of the ACS as no additional aerodynamic control surfaces are needed. The interstage segments are 6.5 m long, but to trim the vehicle at a maximum angle of attack of 10° a petal height of 3.8 m is sufficient [4]. This means that the interstage segment is split into a fixed part, and a moving part (the petal). Grid fins offer more possibilities for aerodynamic control, the grid fins used here were selected for the comparison of the novel ACS concept with the technology currently operated in flight. Hence, they are inspired by the Grid Fin design of the Flacon 9 which in turn uses a DLR patent to reduce the wave drag [5]. The size of the grid fin was taken as the size of the grid fins used on SpaceX, scaled to the size of the RETALT1 launcher. For the planar fins, the chord of the fin was set equal to the radius of the cylindrical body (3 m) to permit a tight folding of the fins during the ascent phase, and the requirement to trim the vehicle at a maximum angle of attack of 10° resulted in a span of 5 m for each fin.
CFD simulations were made at flight conditions, for Mach numbers ranging from 0.4 to 7.0 and altitudes up to 60 km. Aerodynamic coefficients as well as forces acting on the control surfaces are extracted from the Computational Fluid Dynamics (CFD) simulations to assess the efficiency of each type of device, and to populate an aerodynamic database (AEDB) used for flight dynamic analysis. The reference frame for the extraction of the aerodynamic coefficients as well as the numbering of the ACS for the configurations with grid fins (left) and planar fins (right) are shown in Fig. 2. The length of the vehicle (without the nozzles) is about 71.2 m, and the CoG is located at x = − 41.6 m using the axis definition shown in the figure.
2 Computational setup
2.1 NSMB CFD solver
The CFD simulations were carried out using the Navier Stokes Multi Block solver (NSMB) which is developed in a consortium composed of different universities and industries [6]. NSMB is a cell-centered finite volume solver using multi-block structured grids. The code has a parallel and a vectorial structure and it can run on high-performance computers to solve a wide range of industrial aerodynamics design problems, and is mainly used for aeronautics and aerospace applications since more than 30 years.
Both the patch grid and chimera method are available to simplify the mesh generation for complex geometries. NSMB includes remeshing algorithms that are employed for bow shock capturing for hypersonic flow problems. A large variety of turbulence models that are standard in the aeronautical and aerospace industry are available in the solver. For all the configurations investigated, the one-equation Spalart–Allmaras [7] has been selected. For Mach numbers of 0.8 and 3.5, calculations were also made using the k–w Menter Shear Stress model [8] for the configuration with grid fins. At Mach = 3.5, differences in computed drag coefficients of the vehicle were between 0.7 and 1.8%. At Mach = 0.8, differences in computed drag were around 1% at an angle of attack of 10°, and around 5% at an angle of attack of 0°. Comparing the solutions showed small differences, in particular in the wake region.
NSMB includes a large variety of chemistry models for hypersonic applications. The chemistry modeling for the simulations including retro-propulsion is based on the thermally perfect gas assumption combined with the conserved scalar approach. The conserved scalar is used describe the mixing of the main flow (N2, O2) and the flow downstream of the nozzle exhaust (H2O, OH, H2, O2, etc.), and is only used when one or three of the engines are active. The thermodynamic properties of the different gases are computed using polynomials provided by NASA. The engine conditions are applied at the throat of the nozzle. The thermodynamic conditions used in the computations with engines as well as the species mass fractions are summarized in Tables 1 and 2, and were obtained using the Rocket Propulsion Analysis software [9].
2.2 Mesh generation
The ANSYS® ICEM CFD™ pre-processer tool was used to generate the multi-block structured grids needed by the NSMB flow solver.
The patched mesh approach as well as the Chimera overlapping technique have been applied to simplify the mesh generation. Indeed, these techniques allow to create a structured grid for a baseline configuration, and to obtain the other configurations applying only rotations and displacements of partial grid elements (structured blocks) like for the aerodynamic control surfaces. For the RETALT1 configuration, the baseline grid is composed of the main cylindrical body, the base plate with the engine nozzles and the folded landing legs. The control surfaces, such as the grid fins or the planar fins are patched on this baseline grid, allowing to have a similar grid with the same mesh cells density for all unchanged components of the RETALT1 configuration.
To resolve the viscous boundary layer, O-grid topologies with a geometric cell distribution were used close to the solid walls (body and control surfaces). The first cell height in the wall normal direction was set to obtain a y + (non-dimensional distance to the wall based on the local friction velocity at the wall) value close to/below 1 to ensure the proper use of low-Reynolds turbulence modeling, and the growth ratio of the cells normal to the wall was typically close to 1.2. Particular attention was paid also to the refinement of the mesh in the bow shock region for the computations in supersonic and hypersonic regimes.
For each configuration, a fine grid was generated using 2 levels of multigrid, which permitted to generate a coarse grid by taking every 2nd grid point in each direction. Most calculations were made on the coarse grid.
Figure 3 shows the typical structured grid used for the computations presented in this paper with a global overview of the mesh, and the refinement in the region of the bow shock (for super/hypersonic cases) is clearly visible. Some details of the grid are highlighted in Fig. 4, where one can see the surface mesh in the base region with the nozzles of the engines, and the Chimera grid around the petals. Only the centerline nozzle exit is left open since initially it was foreseen to perform simulations using a single engine. All other nozzle exits have been closed for simplicity and little influence is expected when keeping them open. For the configurations with the grid fins or the planar fins, the control surfaces are patched into the base grid using the Chimera overlapping technique, as shown in Fig. 5. One can note that the control surfaces around the Y axis are deflected for these two configurations, which is obtained quickly and automatically from the baseline grid with only a rotation of local grid around each component. Figure 5 gives the impression that upstream of the fins a coarse grid (on the left) is connected to a very fine grid. This is caused by the fact that the block boundaries are also shown in the figures. In reality, the grid densities are comparable across the patched interface.
Table 3 summarizes the mesh characteristics of the coarse grids for the three configurations that were investigated. The number of cells includes the number of overlapped cells. For the configuration with grid fins, more cells are needed to better capture the flow physics around the control surfaces. The large number of blocks for this configuration is explained by the geometrical characteristics of the grid fin itself (Fig. 6). Each cell in the grid fin has a constant thickness in x-direction, and on the windward side, the edges have a smooth valley shape to reduce the wave drag [5]. The structured mesh generation for the grid fins components was a challenging task with a huge number of structured blocks (around 3000 per fin), and a grid sensitivity analysis was performed to ensure the accuracy of the results obtained with the baseline mesh. This analysis is presented in Sect. 3.2.3 of this paper. At several Mach numbers, calculations were made for the configuration with petals and with grid fins on both the fine and coarse grid, showing that the difference in computed overall drag coefficient was less than 1.5%. Due to the very high computational costs of the fine grid calculations, it was decided to perform all calculations using the coarse grid.
3 Computational results
3.1 RETALT1 configuration with petals
Two configurations of the RETALT1 first stage with petals were investigated: the configuration at roll angle φ = 0° with only one petal deployed at δ = 45° and the configuration at roll angle φ = 45° where two petals are deployed by δ = 45°. These two configurations are shown in Fig. 7, and the pressure coefficient is depicted on the surface. A total of 16 RANS simulations were performed on this configuration, without retro-propulsion, in the supersonic regime from Mach number 2 to Mach number 4.5, and for angles of attack of, respectively, 0° and 10°. In addition, four calculations were made on the fine grid for the configuration at roll angle φ = 0°.
Table 4 summarizes the forces acting on the petals only. For the configuration at roll angle φ = 45°, this is the sum of the forces on each petal, which explains the higher forces for this configuration. The forces are reported with the magnitude of the force as sum the norm of the axial and normal forces, and are given in kN. For the configuration with φ = 0° flying at an angle of attack 0°, the forces on the petals contribute between 8.3% (Mach = 4.5) and 16.8% (Mach = 2.0) to the total drag force of the vehicle. As can be seen from Table 4, the aerodynamic loads on the aerodynamic control surfaces are very high, from around 150 kN up to 540 kN in the low supersonic regime. Assuming that the center of pressure is at 50% of the petal height, and that the hinge line is at the base of the petal, this leads to very high hinge moments [10]. This puts severe constraints on the structure and actuators, and for this reason, it was decided to investigate other types of control surfaces. They will be presented in the following sections. It should be mentioned that due to the positioning of the petals, see Fig. 7, they will generate a lift force and pitching moment at zero angle of attack. Comparing the forces on the petals for the cases at AoA = 0° for the two configurations show that they differ less than a factor 2. Further analysis showed that the axial forces differ around a factor 2 (± 5%), while the normal forces differ much less due to the influence of flow separations in the base region. Table 4 also includes the forces computed on the fine grid, and a maximum difference in the order of 10% was found. But as mentioned before, the difference in computed drag for the complete configuration using the coarse and fine grid is less than 1.5%. Finally comparing the drag forces for the complete configuration (including petals) show that they are between 7 and 20% lower for the configuration φ = 0° compared to the configuration φ = 45°.
3.2 RETALT1 configuration with grid fins
The computational matrix on the configuration with grid fins was mainly defined to compare the CFD results with results from experimental measurements that will be performed at DLR. This represents a total amount of 66 RANS simulations, without retro-propulsion, from the subsonic (M = 0.6) to the supersonic regime (M = 4.5), for two angles of attack 0° and 10°, and with fins deflection of 0°, 10° and 20° for the two fins located on the sides of the body (with respect to the angle of attack plane). Figure 8 shows the Cp distribution on the configuration without fins deflection at Mach = 2.0.
3.2.1 Comparison with the petal’s configuration
A first set of computations was performed to compare the results with the configuration with petals. In particular, the configuration with φ = 45° was used in the comparison since the deflected surface area is the closest to the deflected surface area of the grid fins. The cases considered were in the Mach number range from 2 to 4.5, for two angles of attack and with all grid fins deployed but without deflection. The computed drag, lift and pitching moment coefficients are shown in Fig. 9. They indicate a lower drag for the cases with the grid fins for all the cases considered except at a Mach number of 4.5 with an angle of attack of 10°. In terms of lift, the configuration with grid fins produces no lift at the angle of attack of 0°, as expected, but the lift is drastically increased at an angle of attack of 10° compared to the results for the configuration with petals. This is due to the fact that in the configuration with petals, these control surfaces are completely or partially “hidden” by the main body (configuration φ = 0° or φ = 45°, see Fig. 7) whereas in the configuration with grid fins, the two lateral fins (#1 and #3) as well as the fin on the lower side (#4) face the flow (see also Figure 8) and produce a non-negligible contribution to the lift. As mentioned in the previous section, the configuration with petals will generate a (negative) lift force at zero angle of attack. The pitching moment coefficients for the two configurations are comparable at an angle of attack of 10°. At an angle of attack of 0° the configuration with petals has a small pitching moment, while the configuration with grid fins has a zero pitching moment coefficient.
Finally, the total forces acting on a single grid fin are summarized in Table 5 for the cases at angle of attack 0°, and includes the results of the two fine grid calculations. If one compares these forces with the forces acting on the single petal for the configuration φ = 0°, see in Table 4, one can note that they are a factor 4.5–6 lower. The grid fins have a height of 2.9 m (compared to 3.8 m for the petals), and hinge moments for the grid fins are about a factor 6–7 lower compared to the hinge moments for the petals. Compared to using petals as control surfaces, one can conclude that there is a significant reduction of the aerodynamic forces and moments applied to the control surfaces, which inherently reduces the structural loads on them. Moreover, the overall drag of the vehicle is of the same order of magnitude for both configurations, in the range of the studied Mach number, but the overall lift presents a wider variation between angle of attack 0° and angle of attack 10° for the configuration with grid fins. This allows for a better control of the vehicle through the adjustment of the angle of attack to obtain the desired lift.
3.2.2 Analysis of the grid fins mesh density
The default mesh for the grid fins configuration, presented in paragraph 2.2, comprises around 2 million cells for each grid fin. To evaluate the accuracy of the results obtained with the default mesh, a simplified configuration with only one fin and the main cylindrical part of the RETALT1 configuration has been generated. Based on this default mesh, three finer meshes were generated increasing each time the number of the cells by a factor 1.3 in each direction. The number of cells for the four meshes generated are reported in Table 6.
Two cases were computed on these four meshes, with flow conditions at Mach number M = 2, and for two grid fin deflections δ = 0° and δ = 20°. The Mach number distribution is depicted in Fig. 10, for the deflection δ = 0° on the upper row and for the deflection δ = 20° on the lower row. One can observe that the flow pattern is similar for all the four levels of grid refinement. Obviously, the accuracy of the shock waves that occur downstream of the grid fin is better on the finest grid with sharper contours; however, the shock in the front of the fin is located at approximately the same position for the four meshes. For the case with a deflection of δ = 20°, the shock–shock interactions that occur just downstream of the grid fin are clearly visible on all four meshes used.
The magnitude of the force acting on the isolated grid fin was extracted from the eight computed cases and are summarized in Table 7. As expected, the cases with a deflection angle of 20° present a higher force on the grid fin (approximately 1.5 times) since the internal surfaces of the grid facing the flow increases. Without deflection, the force is mainly resulting from the drag (including viscous effects), which is overpredicted by around 10–15% depending on the mesh refinement. However, increasing the number of cells from 15 to 84 million does neither change the drag drastically nor the total force. With deflection, side forces become important, and the influence of the viscous forces on the total force is small. As a result, the effect of the mesh refinement on the total force is negligible (less than 0.3%).
For the purpose of the present study, it is concluded that the default mesh with 2 million cells for each grid fin provides an acceptable accuracy with respect to the huge increase of computational resources that would be required by the finer meshes. Regarding the computations on the whole RETALT1 configuration, for the cases without fin deflection and without angle of attack, we can assume that we will obtain a slight overestimated contribution of the fin’s forces on the global coefficients, but for all other cases, with fins deflection and/or angle of attack, the accuracy of the fin’s contribution will be very good.
3.2.3 Complete computational matrix with grid fins
Finally, 66 computations were performed on the configuration with grid fins following the computational matrix (11 Mach numbers, 2 Angles of Attack and 3 fin deflections). For each computation, the aerodynamic coefficients CD, CL, Cm have been extracted, as well as the forces (in kN) acting on each grid fin. Only the forces acting on the grid fins are presented in this paper.
The forces acting on the grid fins as function of the Mach number are shown in Fig. 11. As expected, the lateral fins (#1 and #3) show the same force evolution for all configurations with a maximum force of around 160 kN that occurs between Mach number 2.5 and 3.5 for the computations with an angle of attack of 10°. The increase of the fin deflection reduces the force for the case at angle of attack 10° since the relative angle of attack of the flow facing the fin is reduced, while the opposite trend is observed for the cases with an angle of attack of 0°. The grid fin #2 is located on the leeward side of the cylindrical part, and for this reason, the forces acting on the fin for the different cases remain relatively low, below 80 kN. The only visible effect is due to the variation of the angle of attack, otherwise the deflection of the lateral fins (#1 and #3) does not modify the flow in the region surrounding the fin #2. The same trend is observed for the grid fin #4 on the windward side, where the flow in not affected by the deflection of the lateral fins; however, the increase of the angle of attack leads to an increase of the force acting on the fin, over 160 kN. Comparing the sum of the drag forces on the four grid fins with the total drag force of the vehicle shows that the four grid fins contribute to about 25% of the total drag force in the subsonic and low supersonic regimes, which decreases to about 5–8% for the highest Mach numbers.
Figure 12 shows the Mach number distribution in the symmetry plane for the configuration at angle of attack AoA = 10° and the grid fins deflection Eta = − 20° for various Mach number in range of 0.6–4.5. The pattern of the wake behind the cylindrical part of the vehicle indicates an unsteadiness of the flow in this region for the subsonic cases, while in the supersonic regime, the flow pattern is steadier due to the sharp shocks that occur at different locations (bow shock facing the vehicle, shocks attached to the folded landing legs, shocks attached to the fins , etc.).
Figure 13 shows the Mach number distribution in two planes through the grid fins for Mach numbers ranging from 0.8 to 2.0. One can clearly observe that from Mach = 1.0 onwards sonic conditions are reached inside the grid fins (right images). The left images show the creation of the shock wave in front of the grid fins with increasing Mach number, behind the shock wave a subsonic region is visible, and the flow reaches sonic conditions inside the fins.
3.3 RETALT1 configuration with planar fins
Figure 14 shows a picture of the RETALT1 configuration with planar fins. The computations performed on this configuration are summarized in the computational matrix detailed in Table 8. This computational matrix has been defined mainly to populate the aerodynamic database (AEDB), and to compare the results with wind tunnel test measurements (not reported in this paper). This represented a total of 233 RANS simulations, with and without retro-propulsion depending on the conditions, from the subsonic to the hypersonic regime. In this table, S1_UFN means engines off, S1_UF1 means that the central engine is activated, and S1_UF3 means that three engines are activated. One can observe that the cases at angle of attack 15° were computed only for the UF1 configuration (one engine active).
3.3.1 Comparison with petals and grid fins configurations
Several results of the computations with planar fins can be compared with the results of configurations with petals and with grid fins. Due to the few numbers of cases computed on the configuration with petals, only the supersonic cases between M = 2 and M = 4.5 are compared, and only the results obtained with φ = 45° are shown. For the configurations with grid fins and planar fins, the deflection angle was set to 0°. The aerodynamic coefficients for the three different configurations are extracted and the drag and lift coefficients curves for the entire configuration are plotted in Fig. 15.
The drag is the lowest on the configuration with planar fins (without deflection) in comparison to the other two configurations, for both angles of attack 0° or 10°. Regarding the lift, as expected, for the configuration with grid fins and planar fins there is no lift for the configuration with an angle of attack 0°. As already mentioned before, the configuration with petals generates a negative lift, which is due to the fact that the petals are deflected only at one side of the vehicle, see Fig. 7. At an angle of attack of 10°, the configuration with planar fins produces more lift than the other two configurations because the wetted area of the aerodynamic control surface facing the flow is larger compared to the other two devices.
At an angle of attack of 0°, and when not deflected, the planar fins are aligned with the flow, and as a result, the loads on them are small compared to loads on the petals or grid fins. This also explains the difference in drag coefficient for the entire vehicle. At higher angle of attack, the planar fins will produce lift, and this can be clearly seen in the lift coefficient for the whole configuration.
3.3.2 Complete computational matrix with planar fins
For all the 233 RANS simulations, the main aerodynamic coefficients CD, CL, Cm, CA, CN, and CmCoG, as well as the force coefficients (x, y, z components) and the total force (in kN) acting on each planar fin are extracted for the computations without retro-propulsion (UFN) and for the computations with one or three engines active (UF1/UF3). These coefficients are extracted on all the solid surfaces of the vehicle, and the contributions of the internal parts of the nozzles are subtracted from these coefficients for the cases with one or three engines active.
Two criteria have been applied to evaluate the convergence of the aerodynamic coefficients for all the computations:
-
the first criterion is the convergence of the mean solution. It represents the ratio between the mean value taken from iterations 3000–4000 and the mean value taken from iterations 4000–5000 (assuming the total number of iterations per computation is 5000).
-
the second criterion corresponds to the ratio between the standard deviation and the mean value over the last 1000 iterations. This criterion is an indication of the fluctuation of the solution with respect to its mean value.
The convergence of the aerodynamic coefficients (CD, CL and Cm) based on these criteria is for the different cases shown in the charts in Fig. 16. On the left-hand side, the first criterion is reported while the second criterion is shown on the right-hand side of Fig. 16. It can be noted that the scale of the convergence criterion is not the same for all cases. For the UFN cases, the scale is between 0 and 10%, for the UF1 cases, it is between 0 and 100%, while for the UF3, the scale is up to 20%.
Globally, both criteria show that the more critical cases in terms of convergence are the subsonic cases with one engine active (UF1). For two UF1 cases (Mach = 0.4 and Mach = 0.8), unsteady RANS calculations were made to see if the same mean value and standard deviation is obtained. For both calculations, the standard deviation of the computed drag coefficient was lower than for the corresponding steady calculations. For the lift and pitching moment coefficients, the standard deviations for the unsteady calculations were higher for the Mach = 0.4 calculation, and lower for the Mach = 0.8 calculation. Computed mean values of lift and drag coefficients differed between 4 and 9.5%; for the pitching moment coefficient, they differed 12.9% at Mach = 0.4, and 47.5% at Mach = 0.8 due to the unsteady flow behavior for this case.
For the subsonic cases without retro-propulsion, the mean convergence of the aerodynamic coefficients is good for all cases (below 1%). One can note some higher differences on CL and Cm, but that is for conditions where these coefficients are equal or close to zero. The second criterion indicates mainly a fluctuation of the solution between 1 and 5%.
For the supersonic and hypersonic cases without retro-propulsion, a very good convergence is observed using both criteria, except for the two hypersonic cases at M = 6.0 an M = 7.0 where it has been observed that the mean convergence is around 1% for the drag coefficient, and higher for the lift and pitching moment coefficients. The convergence at the higher Mach number is more difficult to achieve because of the bow shock located closer to the base of RETALT1 body. In this region, the surfaces are not a blunt body due to the presence of the engine nozzles, and it has been observed that the bow shock position oscillates during the computations at high Mach numbers, while this effect tends to disappear as the shock moves away from the body for the lower Mach numbers.
The trend observed in the convergence of the coefficients can be confirmed by looking at the flow distribution around the RETALT1 vehicle. The Mach number distribution in the symmetry plane is shown in Fig. 17 for one subsonic case at M = 0.6 (left) and one supersonic case at M = 3.5 (right). One can observe that the wake at the base of the body and behind the landing legs region has a wavy pattern, which indicates oscillations of the flow in this region, that affect the convergence of the coefficients in terms of fluctuations around a mean value. In the contrary, for the supersonic case, with the presence of sharp shocks in the flow field, the solution is more stable as observed with both criteria on the aerodynamic coefficients.
The computations with one engine active (UF1) have been mainly performed in the subsonic regime, except for one case at Mach number 1.1. The convergence observed for these computations is not optimal, with strong fluctuations as indicated by the second criterion (> 10%). This can be explained by the strong oscillation of the exhaust plume of the active engine facing the flow in the subsonic regime. The top/left picture in Fig. 18 shows clearly this oscillatory behavior at M = 0.5, while in the transonic regime M = 0.9, the plume looks more stable (top/right picture) even if the flow field around still has some wavy patterns. Once the supersonic regime is reached at M = 1.1 the convergence becomes good with the convergence criteria percentages dropping below 5%, and the Mach number distribution shows a much smoother distribution, bottom/left picture in Fig. 18, that confirms the better convergence of this computation. When looking at the forces on the fins a similar behavior is observed, in the subsonic region the ratio of the standard deviation and the mean value of the forces on the fin is between 11 and 86%, which drops to zero at M = 1.1.
Finally, the computations on the configuration with three engines actives (UF3) at supersonic and hypersonic have a quite good convergence. Only the hypersonic cases at M = 6.0 and M = 7.0 show some fluctuations of the drag coefficient, but this remains below 5%. One case at M = 3.5 is depicted in Fig. 18 (bottom/right) and shows nicely the bow shock in front of the plume and a quite smooth distribution downstream all along the vehicle.
4 Conclusions
More than 300 RANS CFD simulations were carried out on the RETALT1 configuration with 3 different types of aerodynamic control surfaces. The first objective of these simulations was to assess the efficiency of different aerodynamic control surfaces, and, in a later stage of the project, to compare these CFD calculations with Wind Tunnel results (not discussed in this paper). The second objective of these simulations was to populate the aerodynamic database for the flight dynamic analysis to be performed by DEIMOS [3] (another partner in the RETALT project).
The first investigations were performed on the configuration using petals as aerodynamic control surfaces. These simulations were made in the supersonic flight regime, and it was found that using petals as aerodynamic control surfaces resulted in high aerodynamic loads on the deployable interstage segments, which would lead to a substantial increase in required mass for the structure and actuators. This led to the decision to investigate additionally planar fins as aerodynamic control surfaces.
The configuration using grid fins as aerodynamic control surfaces was investigated first. Comparison with the results obtained using petals as control surfaces showed that the aerodynamic loads on the control surfaces were significantly reduced, while at the same time, the vehicle could be trimmed. A preliminary aerodynamic database was successfully generated by performing simulations from the low subsonic to hypersonic conditions.
The configuration using planar fins as aerodynamic control surfaces was investigated as second. This configuration produced the lowest drag and the highest lift in the supersonic regime compared to the configurations with petals and grid fins as aerodynamic control surfaces. The ability to produce easily lift while keeping structural loads small was the main motivation to select the planar fins as aerodynamic control surfaces for the RETALT1. For this configuration, a total number of 233 RANS simulations were carried out, and aerodynamic characteristics were extracted to populate the AEDB in combination with Euler simulations performed by DLR (not discussed in this paper). A very good convergence was obtained for all these computations except for the ones in the subsonic regime with one engine active due oscillations generated by the exhaust plume facing the flow. These calculations would require expensive unsteady computations to better capture and analyze the flow properties, which is outside the scope of the project. The AEDB was successfully used by DEIMOS, see [3] for more details.
Abbreviations
- CFD:
-
Computational fluid dynamics
- WTT:
-
Wind tunnel tests
- NSMB:
-
Navier Stokes Multi Block
- RANS:
-
Reynolds-averaged Navier stokes
- AEDB:
-
Aerodynamic database
- ACS:
-
Aerodynamic control surfaces
- CD:
-
Drag coefficient
- CL:
-
Lift coefficient
- Cm:
-
Pitching moment coefficient
- CoG:
-
Center of gravity
References
Marwege, A., Gülhan, A., Klevanski, J., Riehmer, J., Kirchheck, D., Karl, S., Bonetti, D., Vos, J., Jevons, M., Krammer, A., Carvalho, J.: Retro Propulsion Assisted Landing Technologies (RETALT): current status and outlook of the EU funded project on reusable launch vehicles. In: 70th International Astronautical Congress (IAC), Washington D.C., United States, 21–25 October 2019
Guelhan, A.; Marwege, A.; Klevanski, J.; Karl, S.; Bonetti, D.; Vos, J.; Jevons, M.; Krammer, A.: Carvalho, J.: RETALT—RETro propulsion Assisted Landing Technologies. IN: International Planetary Probe Workshop, Oxford, UK, 8–12 July 2019
De Zaiacomo G., Gonzalo Blanco A., Bunt R., Bonetti D.: Mission engineering for the RETALT VTVL launcher. CEAS Space J. Spec. Issue (2022)
Marwege, A., Gülhan, A., Klevanski, J., Karl, S., Bonetti, D., De Zaiacomo G., Vos, J.B., Jevons, M., Krammer, A., Carvalho, J.: RETALT: review of technologies and overview of design changes. CEAS Space J. Spec. Issue (2022)
Schülein, E., Guyot, D.: Novel high-performance grid fins for missile control at high speeds: preliminary numerical and experimental investigations. RTO-MP-AVT-135 (2006)
Hoarau, Y., Pena,, D., Vos J.B., Charbonnier, D., Gehri, A., Braza, M., Deloze, T., Laurendeau, E.: Recent developments of the Navier Stokes Multi Block (NSMB) CFD solver. AIAA Paper 2016-2056 (2016)
Spalart, P.R., Allmaras, S.R.: A one-equation turbulence model for aerodynamic flows. AIAA Paper 92-0439 (1992)
Menter, F.R.: Influence of freestream values on the k–ω turbulence model predictions. AIAA J. 30 (1992). https://doi.org/10.2514/3.11115
Marwege, A., Klevanski, J., Riehmer, J.: System definition report. Deliverable D2.1, RETALT project, RETALT_DLR_D2.2_System Definition Report_2019-08–30.docx
Krammer, A., Blecha, L., Lichtenberger, M.: Fin actuation, thrust vector control and landing leg mechanisms design for the RETALT VTVL launcher. CEAS Space J. Spec. Issue (2022)
Acknowledgements
The RETALT project has received funding from the European Union’s Horizon 2020 research and innovation framework program under Grant agreement No 821890.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Charbonnier, D., Vos, J., Marwege, A. et al. Computational fluid dynamics investigations of aerodynamic control surfaces of a vertical landing configuration. CEAS Space J 14, 517–532 (2022). https://doi.org/10.1007/s12567-022-00431-6
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s12567-022-00431-6