Abstract
In the RETALT (RETro propulsion Assisted Landing Technologies) project vertical landing launcher configurations are investigated. In the aerodynamic phase of retro propulsion assisted descent and landing, the main devices for control and trim of the vehicle are the aerodynamic control surfaces. In this paper, experimental data of a novel concept where the interstage is divided in four segments which are used as aerodynamic control surface during the aerodynamic descent of the first stage is presented. The results are compared to theoretical results obtained using a simplified modelling of supersonic and hypersonic flow fields. The interstage segments show to be very effective in creating drag for aerodynamic deceleration in the atmosphere. A large deflection of the interstage segments can lead to largely unsteady flows. The deflection of only one interstage segment does not yield statically stable configurations.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
RETALT (RETro propulsion Assisted Landing Technologies) is a European Project funded in the frame of the Horizon 2020 framework program (grant agreement No 821890). An overview of the project and the current status is given in Ref. [1]. The project aims at investigating key technologies for the descent and landing of reusable launcher configurations with the aid of retro propulsion. For this purpose, two reference configurations are investigated, namely (for details refer to Ref. [1]):
-
RETALT1: A heavy lift launcher configuration with a payload of up to 14 t into the Geo Transfer Orbit (GTO)
-
RETALT2: A smaller Single Stage To Orbit (SSTO) configuration with 500 kg into Low Earth Orbits (LEO)
This paper concentrates on the aerodynamic design of the Aerodynamic Control Surfaces (ACS) for the aerodynamic descent phase of the RETALT1 configuration (see Fig. 1). The aerodynamic phase is the flight phase after the reentry burn and before the landing burn, where no engines are active (see Fig. 2). A more detailed descriptions of the flight phases of the RETALT1 configuration can be found in [1] and [2].
RETALT1 return mission concept [2]
A main objective of the project was to investigate the use of interstage segments as ACS for the RETALT1 configuration [1]. This concept is shown in Fig. 1a where the interstage was divided in four segments. The interstage segments will also be called “petals” in the following. This concept has the potential of reducing the vehicle mass and complexity as no additional ACS are needed. Besides the petals, planar fins and grid fins were also investigated as ACS in the project Fig. 1b and c.
This work will focus on the aerodynamic properties of the petal concept. Wind Tunnel Test (WTT) results of the RETALT1 configuration in the Trisonic Wind Tunnel Cologne (TMK) at the Supersonic and Hypersonic Technologies Department of the German Aerospace Center (DLR e.V.) will be presented and discussed. They will be compared to simplified analytical approaches which were used in the early project phase to estimate the free stream conditions at the ACS for their design. An aerothermal analysis of the planar fins can be found in [3]. A numerical study and comparison of the petals with planar fins and with grid fins is presented in [4].
This paper is organized as follows. First the TMK facility and the tests setup will be introduced shortly, followed by a description of the analytical concepts applied. Then, the wind tunnel test results will be presented and discussed. Finally, a conclusion and outlook will be given.
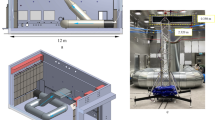
2 Trisonic Wind Tunnel Cologne (TMK)
The results presented in this paper were obtained in the Trisonic Wind Tunnel Cologne (TMK). Figure 3 shows the test section of the TMK. The operation range is shown in Fig. 4, and a schematic of the facility can be seen in Fig. 5. The wind tunnel is a blow down facility using pressurized air (up to 60 bar) down to atmospheric conditions with a rectangular test section of 60 cm × 60 cm and an operational range of Mach numbers between 0.5 up to 4.5 without the use of the additional ejector and up to 5.7 with the use of the ejector. The air is supplied from a high-pressure reservoir and passes the storage heater, settling chamber, the Laval nozzle, the test chamber and the diffuser to ultimately flow out into the atmosphere. Due to a hydraulic adaptable nozzle, several Mach numbers can be tested in one run in the supersonic regime. In the subsonic regime the Mach numbers are set by the variation of the stagnation pressure (up to \({p}_{0}=25 bar\)) and the total temperature (\({T}_{0}=550 K\)). In the subsonic regime only one Mach number can be tested per run. A motion control device on which the 3s are mounted allows for continuous polars of the angle of attack.
In the subsonic and transonic regime (\(M<1\).2), the facility is commonly operated at a dynamic pressure of \({q}_{\infty }\approx 1 bar\). In the supersonic regime (\(M>1.2\)), it is operated at a static pressure of \({p}_{\infty }\approx 1 bar\). The Reynolds number ranges from \(Re=1.2\times {10}^{7} {m}^{-1}\) (\(M=0.5\)) to \(Re=3.7\times {10}^{7} {m}^{-1}\) (\(M=1.2\)) in the subsonic and transonic regime. In the supersonic regime it can be varied between \(Re=2.6\times {10}^{7} {m}^{-1}\) and \(Re=7.6\times {10}^{7}{ m}^{-1}\). This range can be enhanced by the use of the ejector.
High speed schlieren videos can be recorded in the supersonic regime through the quartz windows giving visual access to the test chamber. In the transonic and subsonic regime, a test section with perforated walls is installed downstream of the supersonic test section for boundary layer suction. For this reason, schlieren imaging is not possible in these regimes.
A more detailed description of the wind tunnel facility TMK can be found in [5].
3 Wind tunnel model
3.1 Model configurations
Three types of aerodynamic control surfaces have been tested for RETALT1, namely interstage segments (or petals), planar fins and grid fins. The model configuration with petals mounted in the wind tunnel is shown in Fig. 6. The scaling of the wind tunnel models is 1/130 from the original RETALT1 configuration having a diameter of the first stage of 6 m and a length of 64.7 m excluding the interstage [1].
RETALT1 3 with petals mounted in the TMK
The aim of the test series was to assess three main aspects: the stability and trimmability of the RETALT1 vehicle with the different types of control surfaces, the efficiency of the control surfaces to generate aerodynamic forces and moments and the evaluation of pressure data on selected sensor positions.
The reference frame used for the data acquisition is shown in Fig. 7, where CA is the axial force coefficient, CN the normal force coefficient and CY the side force coefficient. CMx, CMy and CMz define the moment coefficients in the reference point around the respective axes. The reference point is defined to be the foremost point of the cylindrical body of the RETALT1 configuration in the x-direction excluding the interstage.
For the identification of the configurations the following definition was used:
-
PF: Planar Fin
-
GF: Grid Fin
-
B: Petal (“Blume” is the German word for flower and is less confusing than a “P” for petal)
The deflection angles of the ACS are denoted separately behind the identifier for the ACS type. The aerodynamic control surfaces are numbered from 1 to 4 in the clockwise direction looking at the base plane of the configuration (see Fig. 8a).
Example:
B0,10,0,0: Petals: Petal 1: 0°, Petal 2: 10°, Petal 3: 0°, Petal 4: 0° (resulting in a pitch moment).
For the Petals, the deflection \(\delta\) is defined from its folded state 0° which resembles a conventional interstage (see Fig. 8e). Some examples of different configurations are given in Fig. 8.
The X-configuration is rotated by 45° around the x-axis in the clockwise direction with view on the base of the configuration (see Fig. 8d).
3.2 Model Instrumentation
For the measurement of the aerodynamic forces and moments, a DLR inhouse 6 components strain gauge balance was utilized. In Fig. 9 the model mounted on the balance is sketched. Pressures were measured in three measurement planes as shown in Fig. 10. Plane 1 is close to the fins, plane 2 at roughly two thirds of the length of the model and plane 3 at the base plane. The sensor numbering follows the numbering of the aerodynamic control surfaces. Starting from the left (1) in the clockwise direction with view on the base plane to the top (2) to the right (3) to the bottom (4). The sensors at the base plane have an additional number defining their radial position. While (1) is close to the x-axis, (2) is the position close to the outer diameter of the configuration. Due to their small form factor and their capabilities of measuring high frequencies, Kulite sensors were used for the pressure measurements. Due to space requirements LQ 062 sensors were used on the sensor locations on the cylindrical part of the configuration and XCQ 080 sensors were employed for the sensor location on the base plane. Additionally, two pressure tubes were implemented on the model support sting below the interstage segments (pSTAGE) (Fig. 10) and in the balance (pBALANCE) for static pressure measurements.
The measurement uncertainties were determined with Gaussian error propagation of the measurement uncertainties for the measured quantities.
3.3 Test conditions
In Fig. 11, the Mach numbers tested in the three DLR wind tunnels are mapped on the reference trajectory presented in [1]. It can be seen that the reference trajectory can be represented well within the wind tunnels at DLR Cologne. The aerodynamic descent phase where the engines are off is simulated in the TMK. The tested Mach numbers were 4.0, 3.5, 2.5 and 2.0 in the supersonic regime and 0.9, 0.8, 0.6 and 0.5 in the subsonic regime. However, not all configurations were tested at all Mach numbers. Alpha polars of \(\pm 10^\circ\) were tested in all test runs, which was defined according to the mission design needs described in [2]. Figure 12 shows a comparison of the Reynolds numbers of the flight configuration with the Reynolds numbers tested in TMK. The Reynolds numbers at flight conditions are about one order of magnitude larger than the Reynolds numbers simulated in the wind tunnel. Boundary layer tripping experiments were performed in the CALLISTO project in the TMK for configurations similar to RETALT1 [6, 7]. The results showed that the influence of the tripping on the measured forces and moments is minor indicating that the Reynolds number has only a minor effect for these configurations. It shall, however, be noted that different aerodynamic control surfaces (planar fins) were tested in these tests.
Mapping of Mach numbers tested in the wind tunnel facilities over the reference trajectory presented in [1]
4 Analytical description of the descending first stage in supersonic flow
In the design phase of the aerodynamic control surfaces for the RETALT1 configuration, an analytical approach was used for the estimation of the free stream conditions at the location of the fins in the supersonic regime, as this enabled a preliminary sizing of the ACS for the RETALT1 configuration without the use of CFD. This approach will be laid out in the following as a comparison with the theoretical results adds value to the interpretation of the measured data and vice versa the analytical approach can be verified with the measured data. The analytical approach is built on classic methodologies for the modelling of hypersonic flows namely: the blast wave analogy, the modified Newtonian law and the shock relations.
Figure 13 shows the RETALT1 fist stage with petals as ACS, deflected by \(\delta =20^\circ\), at a Mach number of 3.5. The free stream is coming from the left. A bow shock is forming in front of the engines, i.e., the expansion nozzles without a plume. Downstream of the engines the flow is expanded around the base area. A shock system emerges from the folded landing legs and oblique shocks from the petals, which bend with further distance from the axis.
The static pressure at the ACS location can be derived indirectly by the application of the blast wave analogy. The blast wave analogy transfers principles of an unsteady moving shock wave from an instantaneous energy release in a single point (of a blast at an origin) to a blunt body moving at hypersonic speeds [8], the analogy is sketched in Fig. 14 for a blunt-nosed cylinder. Referring to Fig. 13 it seems reasonable as a first approach to assume that the backwards oriented first stage of RETATL1 is similar to a blunt-nosed cylinder. For a blunt-nosed cylinder Sakuri [10] obtained with the blast wave analogy, the second approximation of the pressure distribution along the cylinder surface as follows:
Blast-wave analogy for a blunt-nosed cylinder [8]
where \({x}_{S}/D\) is the distance downstream of the bow shock normalized with the diameter of the cylindrical body \(D\), \({C}_{D}\) is the drag coefficient, \({M}_{\infty }\) the free stream Mach number, \(p\) the static pressure at the surface of the cylinder at the distance \({x}_{S}/D\) from the bow shock and \({p}_{\infty }\) the free stream pressure. Note that \({x}_{S}\) defines the distance downstream of the bow shock which is different from the overall \(x\) coordinate of the body fixed reference frame with its origin at the interstage as defined in Fig. 10. The second approximation only differs from the first approximation in the constant 0.44 which is missing in the first approximation, see [8] and [9]. Lukasiewicz [11] suggests that \(p\) shall be set equal to \({p}_{\infty }\) if the blast wave solution results in pressure values lower than \(p/{p}_{\infty } =1\). This can be seen in Fig. 15, where the results of the blast wave analogy were compared to results obtained with the method of characteristics by Van Hise [12].
Rearranging Eq. (1) and isolating \({x}_{S}/D\) on the left-hand side of the equation yields:
Setting \(p/{p}_{\infty }=1\) in Eq. (2) results in the simple relation:
Hence if \({x}_{S}/D\) exceeds a certain value depending on the free stream Mach number \({M}_{\infty }\) and the drag coefficient\({C}_{D}\), then \(p\) can be set equal to \({p}_{\infty }\). In Fig. 16, Eq. (3) is evaluated for several Mach numbers and drag coefficients. Referring back to Fig. 10 one can see that the pressure measurements close to the ACS are more than \({x}_{S}/\mathrm{D}=11\) downstream of the base plane of the configuration. The pressure measurement in the plane 2 are roughly at \({x}_{S}/\mathrm{D}=7\). Figure 16 shows that for both sensor positions the value of \({x}_{S}/D (p/{p}_{\infty } =1)\) lies below 4 for Mach numbers smaller than 4. Only for values of \({C}_{D}>4\) it can get higher. However, as can be seen in the results discussed in section 6 the drag coefficient of the cylindrical body lies in the range of 1.2 (in the concept phase this was known from preliminary computations). Hence the pressure at the location of the ACS can be assumed to be equal to the static free stream pressure.
Eq. ( 3 ) for several Mach numbers and drag coefficients
Further assumptions made are that the shock system coming from the folded landing legs is weak (see Fig. 13) and that the flow expansion downstream of the stagnation point behind the bow shock is isentropic. With these assumptions, it can be assumed that the total pressure downstream of the bow shock is conserved along the cylindrical body of the RETALT1 configuration.
With the normal shock relations, the total pressure behind the normal shock portion of the bow shock can be calculated. With the assumption that the static pressure at the ACS location equals the static free stream pressure upstream of the bow shock and the total pressure equals the total pressure downstream of a normal shock, the Mach number at the ACS location can be calculated directly with the isentropic relations. The Mach number at the location of the Aerodynamic Control Surfaces \({M}_{ACS}\) can be expressed depending solely on the free stream Mach number \({M}_{\infty }\) and the heat capacity ratio \(\gamma\).
Equation (4) is plotted in Fig. 17. As visualized in Fig. 13 the shock angle at the petal was measured and the corresponding Mach number was computed from the 20° deflection of the petal for the free stream Mach numbers of 4.0, 3.5, 2.5 and 2.0. The experimental points fit the analytical model well and show that it is valid as a first approach of estimating the free stream conditions at the location of the ACS.
Free Stream Mach number at the location of the aerodynamic control surfaces versus the free stream Mach number, Eq. ( 4 )
The static pressure at the location of the ACS for an angle of attack of \(\alpha \ne 0^\circ\) on the windward side can be computed as the sum of the pressure from the blast wave solution and the pressure resulting from the modified Newtonian law. This approach was applied by Anderson [13] to describe the pressure distribution on the windward side of the Space Shuttle and shows a good fit with fight data. Seltner [14] showed a good agreement for the force and moment coefficients estimated with the Newtonian law, compared to measured force and moment coefficients during free flight experiments in the H2K wind tunnel facility.
The pressure coefficient \({C}_{p}\) is defined as:
where \(p\) is the pressure, \({p}_{\infty }\) the free stream pressure and \({q}_{\infty }\) the dynamic pressure. As discussed above the pressure at the ACS location for an angle of attack of 0° can be assumed to be equal to the free stream pressure. Hence, the \({C}_{p}\) value following from the blast wave solution equals approximately zero. Therefore the pressure on the windward side of RETALT1 at the ACS location is just defined by the \({C}_{p}\) of the modified Newtonian law. It is defined as [8]:
where \({C}_{{p}_{max}}\) is the pressure coefficient of the stagnation pressure downstream of the normal shock \({p}_{\mathrm{0,2}}\):
With the estimation of the varying pressure as function of the angle of attack, the variation of the Mach number at the ACS can be estimated with the same methodology as described above.
5 Results and discussion
5.1 Discussion of pressure coefficients
Figure 18 shows the pressure coefficients in plane 1, which are the pressure sensors close to the interstage of RETALT1 (see Fig. 10), for the configuration with all petals fully folded (B0,0,0,0). The data resampled to 500 Hz is shown by the light solid lines. It was filtered with 3 Hz with a low pass filter (dark solid lines). The uncertainties for the filtered data are shown by the dashed lines. The uncertainties for the angle of attack which are \(\pm\) 0.25° [5] are not shown. Additionally, the pressure coefficients of the sensor below the interstage (pSTAGE) and the sensor in the balance (pBALANCE) are plotted.
For an angle of attack of 0°, the pressure coefficients in plane 1 are very close to zero. This confirms the assumptions drawn from the blast wave analogy in section 5, that the pressures at the ACS locations are close to the free stream pressures.
The pressure coefficients are furthermore compared to the pressure coefficient obtained using the modified Newtonian law. It can be observed, that the trend of the pressures is reflected well by the modified Newtonian law. The sensor 14 at the bottom side (windward side at positive angles of attack) follows the modified Newtonian law for positive angles of attack. For Mach 2.5 (Fig. 18c) also the upper side pressure was measured with sensor 12. As expected, it follows the modified Newtonian law for negative angles of attack.
The shape of the pressure polars suggests plotting also the modified Newtonian law with a negative sign:
This line is denoted by “Cp Newton min” in the plots. It can be observed, that the pressure at the bottom of the model (sensor 14) follows the general trend of the negative modified Newtonian law down to angles of attack of \(-7^\circ\). For larger negative angles of attack it tends to deviate.
The pressures at the sides of the model, sensors 11 and 13, are important when using planar fins or grid fins as ACS, as these define the local free stream condition experienced by the fins providing the pitch moment. If petals are applied, these sensors provide information on the flow conditions for the petals providing the yaw moment. It can be observed that these pressures closely follow the pressure at the leeward side of the model. They follow the trend of the negative modified Newtonian Law up to an angle of attack of \(\pm 7^\circ\). At \(\pm 8^\circ\) a pressure plateau can be observed at Mach 4.0 and 3.5. This plateau might have several reasons. Schlieren images of this configuration are shown in Fig. 19. Probably the assumption of a static pressure at the ACS equal to the free stream pressure is not valid anymore. Furthermore, due to the higher angle of attack, the shock system of the landing legs gets stronger. A flow separation at the leeward side seems not to be the reason, as this cannot be observed in the schlieren images. Additionally, for angles of attack larger than \(\pm 9^\circ\) the pressure decreases further, which supports the reasoning that a flow separation should not be the reason for the pressure decrease.
The pressures below the interstage and in the balance nearly coincide, which is reasonable, as the pressure in the wake region downstream of the interstage is present at both measurement locations. The absolute value of the pressure coefficients increases with decreasing Mach numbers.
Figure 20 shows the pressure coefficients of the sensors in the second plane, again for the Mach numbers 4.0, 3.5, 2.5 and 2.0. While the sensor at the bottom side (24) follows the modified Newtonian law well, the pressures of the sensor on the upper side (22) is shifted to negative values. The reason might be a slight side slip angle or due to the influence of the landing legs. The general trend of the modified Newtonian law can, however, also be observed in this plane. For lower Mach numbers (Mach 2.0 and 2.5), a pressure plateau around the angle of attack of 0° can be observed. It seems that for the lower Mach numbers the shielding effect of the landing legs is stronger, such that higher angles of attack need to be reached before the pressure increases.
Figure 21 shows the pressure coefficients in plane 3, which is the base plane of the RETALT1 configuration. For the positioning of the sensors refer back to Fig. 10. While the sensors 312 and 332 are in the plane perpendicular to the alpha-plane, 341 lies in the alpha-plane. Furthermore, the sensor 341 lies in between the central nozzle and the circle of outer nozzles, while the sensors 312 and 332 lie outside of the outer engine circle.
As the sensors are positioned on the base plane, which is offset downstream of the plane of the nozzle exits, the pressures are smaller than the pitot pressure. Due to their position on the plane perpendicular to the alpha-plane, the pressure polars of sensors 312 and 332 are symmetric for negative and positive angles of attack. Due to its position in the alpha-plane, the pressure of sensor 341 is slightly depending on the angle of attack. As it is positioned more central on the base plane the pressure is higher than for sensors 312 and 332.
Additionally, it can be observed, that the pressure fluctuations at the base plane are high compared to the fluctuation in the other planes, especially at an angle of attack of 0°.
Figure 22 shows the pressure coefficients in plane 1 for a configuration with all petals deflected by 20° (B20,20,20,20). The decrease of the static pressure over the oblique shock forming upstream of the petal, leads to a decrease in the wake pressure downstream of the petals and hence results in more negative pressure coefficient of pSTAGE and pBALANCE. The pressure coefficients near the petals are not influenced by their deflection up to a deflection of 20°. This can be verified by comparing the pressure coefficients in plane 1 in Fig. 22 to Fig. 18 where the pressure coefficients in plane 1 are plotted for a deflection of 0° of all petals.
However, this behavior changes for a deflection by 45° which can be observed in Fig. 23 where all petals are deflected by 45°. The pressures reach a plateau at an angle of attack of 0°. This plateau is smaller for larger Mach numbers and occurs at higher angles of attack for smaller Mach numbers. In Fig. 24 the Mach numbers at the location of the ACS are plotted as calculated with the methodology described in section 5. Furthermore, Fig. 24 shows the maximum deflection angle at which a solution with the oblique shock relations exists for the Mach number at the ACS location; it is denoted \({\beta }_{max}\). Here the static pressures from the modified Newtonian law and the negative counterpart were used to estimate the dependency of the Mach number and \({\beta }_{max}\) on the angle of attack. For all Mach numbers \({\beta }_{max}\) lies far below 45°. However, except for the case of Mach 2.0, it lies above 20°.
In Fig. 25, the flow fields for \(\delta =20^\circ\) and \(\delta =45^\circ\) are shown at Mach 4.0. For \(\delta =20^\circ\) an oblique shock is forming upstream of the petal transforming to a bow shock which passes the outer part of the petal. Exceeding \({\beta }_{max}\) for the case of \(\delta =45^\circ\) leads to a large unsteady region upstream of the petal, presumably due to a recirculation region. A separation shock is forming far upstream of the petal. In Fig. 25 also the sensor plane 1 is depicted. For the deflection of 45°, the detached separation shock moves over the sensor position, which is why large pressure fluctuation are measured. Such large pressure fluctuation upstream of a wedge are a known phenomenon and should be avoided as they can lead to high structural loads on the ACS. As can be seen in the schlieren images in Fig. 26, the separation region gets smaller with increasing angle of attack. On the leeward side, this is due to the reduced effective angle of attack of the petal. On the windward side, the reason is the increasing static pressure with increasing angel of attack, which leads to an increase of the local Mach number and hence the local \({\beta }_{max}\). Fig. 27 shows the same schlieren images for the deflection of \(\delta =20^\circ\). A close inspection of Fig. 27c for Mach 2.0 reveals that as \({\beta }_{max}\) is slightly lower than the deflection angle, the separation region is somewhat larger than for Mach 4.0 (Fig. 27a) where \({\beta }_{max}\) is larger than the deflection angle. It should be mentioned that these unsteady phenomena could depend on the Reynolds number, which is why a Reynolds number variation or experiments with boundary layer tripping should be performed in the future to assess this dependency.
Concluding this analysis four main key facts can be pointed out. First, the pressure on the windward side near the ACS follows approximately the modified Newtonian law. Second, the pressure on the leeward side near the ACS follows approximately a negative modified Newtonian law up to a certain angle of attack (in this case approximately \(\pm 7^\circ\)). Third, the pressure on the sides near the ACS follows the pressure of the leeward side, meaning approximately the negative modified Newtonian law. Fourth, deflecting the petals more than \({\beta }_{max}\) leads to largely unsteady flow phenomena which can be critical for the structural loads on the ACS.
5.2 Discussion on forces and moments
In this section, the force and moment coefficients of the RETALT1 configuration with petals will be discussed. Throughout the section the solid lines in the graphs show the data resampled to 1000 Hz and filtered with 3 Hz with a low pass filter (except for the case B0,0,0,0 which was resampled to 500 Hz). The dashed lines show again the measurement uncertainties. The uncertainty in the angle of attack of \(\pm\) 0.25° [5] is not plotted. The Moment coefficient \(CMy(CoG)\) was computed around the center of gravity at \(x=-40.6\,m\) (scaled down with the model) which is the location of the center of gravity estimated for the aerodynamic phase.
Figure 28 shows the aerodynamic coefficients for an equal deflection of all petals for Mach numbers of Mach 4.0 down to 0.6. Without any deflection of the petals (B0,0,0,0 – black line) the configuration is unstable at an angle of attack of 0° for all Mach numbers. For Mach 4.0 two stable trim points can be observed at approximately –9° and + 9° angle of attack. With increasing deflection angles the trim points move closer to \(\alpha =0^\circ\) and merge at 0° for a deflection of 20°. Hence the configuration is stable at \(\alpha =0^\circ\) for all supersonic Mach numbers for a deflection of 20° of all petals. With decreasing Mach numbers, the outer trim points move to larger angles of attack. Due to the change in the flow field for a deflection of 45° of the petals, the shape of the polar for this deflection angle is significantly different from the other deflections in the supersonic regime. Especially at 0° angle of attack a very steep slope can be observed. In the subsonic regime, already smaller deflection angles of 10° yield a stable configuration.
For the discussion of the axial force coefficient in the following, “larger” shall be used for “more negative” as it is defined positive from the interstage pointing toward the base of the launcher (see Fig. 7) and hence the measured force coefficients are all negative.
As expected, the axial force coefficient increases with decreasing Mach numbers in the supersonic regime and increases with increasing Mach numbers for the subsonic regime. Here the same effect as for the moment coefficient can be observed; the petals need to be deflected by more than 20° for an effective increase in the force coefficient for Mach 4.0 and Mach 3.5. For the Mach numbers smaller than 2.0 smaller deflection angles already have a larger effect. The change in the dominating flow phenomena from a deflection of 20° to 45° is clearly visible as the shape of the polar is changed from a plateau to a doghouse shape. From the point of view of drag generation, which is favorable for a lower dynamic pressure during the aerodynamic phase and less fuel consumption during the reentry and landing burns, the deflection of the petals by 45° is favorable as it drastically increases the generated axial force, and therefore, the generated drag. However, the large pressure fluctuations described in section 5 need to be considered too.
Figure 29 shows the aerodynamic coefficients for the deflection of one single petal at the top of the configuration (petal 2). For deflections larger than 20°, the shape of the curves indicates trim points at an angle of attack larger than 10° for the Mach numbers 4.0, 3.5 and 2.5. To trim the vehicle at angles of attack between 0° and 9° the petal on the bottom of the configuration (petal 4) needs to be deflected. As example this is plotted for Mach 3.5 in Fig. 29b, where the black dots indicate a deflection of petal 4. However, at \(\alpha =0^\circ\) the configuration is generally unstable. For Mach 2.0 and lower Mach numbers, the configuration seems to be generally unstable for all deflection angles. The deflection of only one petal only slightly increases the axial force coefficient. As expected, the generated axial force is larger if the petal is deflected on the windward side.
Naturally the question arises to whether a rotation of the configuration by 45° and a deflection of two petals (see Fig. 8d) increases the efficiency and enhances the aerodynamic properties of the configuration. In Fig. 30, the moment and axial force coefficients are plotted for the RETALT1 vehicle in the X-configuration with the two upper petals deflected (petal 1 and 2). It can be observed, that the general shape of the curves is similar to those for the “ + ” configuration with only the upper petal deflected. The efficiency of the two petals is slightly larger than the single petal in the “ + ” configuration. However, for this configuration stable trim points are only obtained for angles of attack larger than 10° for Mach numbers of 2.5 and higher; for Mach numbers of 2.0 and lower unstable behavior is observed.
Lastly, the deflection of only one petal on the side of the configuration for the generation of a yaw moment around the z-axis is analyzed. For this analysis, the petal 3 was deflected by 20° (B0,0,20,0). The results for this configuration are shown for several Mach numbers in Fig. 31. \(CMz(CoG)\) is the yaw moment coefficient in the center of gravity around the z-axis. Fig.31 shows that the sideward deflection of the petal creates a yaw moment which is relatively independent of the angle of attack, especially in the subsonic regime. In the supersonic regime the generated yaw moment decreases with increasing Mach number, in the subsonic regime the yaw moment seems to be independent of the Mach number. The deflection of the petal slightly increases the axial force coefficient with respect to a fully folded configuration. This can be verified by a comparison of the axial force coefficient \(CA\) of the configuration B0,0,20,0 with the configuration B0,0,0,0 in Fig. 28. Due to the increase of the axial force, the deflection of the sideward petal leads to a slight increase of the stability of the configuration around the y-axis as it was observed for the equal deflection of all petals. This can be verified by a comparison of the pitch moment coefficient \(CMy(CoG)\) of B0,0,20,0 and B0,0,0,0.
6 Conclusions and outlook
This paper focused on the use of interstage segments as Aerodynamic Control Surfaces (ACS) for a reusable launcher configuration. The free stream conditions at the location of the ACS in the supersonic regime can be estimated with classic methodologies for hypersonic flow. An analysis of pressure measurements close to the ACS showed that the deflection angle of the ACS should not exceed the maximum deflection at which a solution with the oblique shock relations exists, as larger deflection angles can lead to largely unsteady flow fields that generate high structural loads on the ACS and has a potential negative impact on the flying qualities of the spacecraft. If high deflection angles are required for future configurations, this phenomenon should be analyzed further performing an analysis of the power spectral density of the pressure measurements to extract dominant frequencies of the occurring pressure fluctuations.
The analysis of the force and moment coefficients showed that the control of the vehicle solely with the aid of the interstage segments is challenging. The configurations are only statically stable around an angle of attack of zero degrees for large deflection angles of all interstage segments, which leads to high structural loads on the segments. The additional structural mass needed for such heavy structures needs to be traded off with the possible fuel savings due to the higher drag coefficients in the aerodynamic phase. A possible application could be the use of the interstage segments solely as breaking devices for lighter smaller launchers rather than heavy lift launchers. The vehicle can only be trimmed at certain angles of attack by the deflection of only one segment. However, a large deflection of all segments, but each at different angles, could possibly lead to a trimmable configuration for more angles of attack, which should be investigated further in the future.
In conclusion: using the interstage segments as aerodynamic control surfaces is not easy and should be studied in detail before a possible use on a next generation launcher.
Abbreviations
- ACS:
-
Aerodynamic control surfaces
- CoG:
-
Center of gravity
- CA:
-
Axial force coefficient
- CM:
-
Moment coefficient
- CM (CoG):
-
Moment coefficient in the center of gravity
- CN:
-
Normal force coefficient
- CY:
-
Side force coefficient
- CD :
-
Drag coefficient
- CP :
-
Pressure coefficient
- D:
-
Diameter
- DRL:
-
Down range landing
- GTO:
-
Geo transfer orbit
- H2K:
-
Hypersonic wind tunnel Cologne
- LEO:
-
Low earth orbit
- M:
-
Mach number
- \({\mathrm{M}}_{\infty }\) :
-
Free stream mach number
- DRL:
-
Down range landing
- Re:
-
Reynolds number
- \(\mathrm{p}\) :
-
Static pressure
- \({\mathrm{p}}_{\infty }\) :
-
Free stream static pressure
- RTLS:
-
Return to launch site
- SSTO:
-
Single stage to orbit
- TMK:
-
Trisonic wind tunnel Cologne
- T:
-
Temperature
- WTT:
-
Wind tunnel tests
- \(\mathrm{x}\) :
-
Down stream distance from bow shock
- \(\mathrm{\alpha }\) :
-
Angle of attack
- \({\upbeta }_{\mathrm{max}}\) :
-
Maximum deflection angle at which a solution with the oblique shock relations exists
- \(\updelta\) :
-
Deflection angle
- 0:
-
Index for total conditions
References
Marwege, A., Gülhan, A., Klevanski, J., Riehmer, J., Kirchheck, D., Karl, S., Bonetti, D., Vos, J., Jevons, M., Krammer, A., Carvalho, J.: “Retro propulsion assisted landing technologies (RETALT): Current status and outlook of the EU funded project on reusable launch vehicles”, 70th International Astronautical Congress (IAC), pp. 21–25. Washington D.C, United States (2019)
De Zaiacomo, G., Blanco Arnao, G., Bunt, R., Bonetti, D.: “Mission Engineering for the RETALT VTVL Launcher”, CEAS Space J (2022). https://doi.org/10.1007/s12567-021-00415-y
Laureti, M., Karl, S.: “Aerothermal databases and load predictions for Retro Propulsion Assisted Launch Vehicles(RETALT)”, CEAS Space J (2022). https://doi.org/10.1007/s12567-021-00413-0
Charbonnier, D., Vos, J., Marwege, A., Hantz, C.: “Computational fluid dynamics investigations of Aerodynamic Control surfaces of a vertical landing configurations”, CEAS Space J (2022)
Esch, H.:“Die 0.6-m x 0.6-m – Trisonische Meßstrecke (TMK) der DFVLR in Köln-Porz (Stand 1986)“ DFVLR-Mitt. 86–21, Cologne (1986)
Marwege, A., Riehmer, J., Klevanski, J., Gülhan, A., Dumont, E.: “Wind Tunnel investigations in CALLISTO - Reusable VTVL Launcher First Stage Demonstrator”, 70th International Astronautical Congress (IAC), pp. 21–25. Washington D.C, United States (2019)
Riehmer, J., Marwege, A., Klevanski, J., Gülhan, A., Dumont, E.: “Subsonic and Supersonic Ground Experiments for the CALLISTO VTVL Launcher Demonstrator”, International Conference on Flight Vehicles, Aerothermodynamics and Re-entry Missions & Engineering (FAR), Monopoli, Italy, September (2019)
Anderson, J. D.: “Hypersonic and high temperature gas dynamics” AIAA, 2 edition (2006)
Sakurai, A.: “On the Propagation and Structure of the Blast Wave I,” J. Phys. Soc. Japan. 8, 662 (1953)
Sakurai, A., “On the Propagation and Structure of the Blast Wave II,” J. Phys. Soc. Japan, 9, 256, (1954)
Lukasiewicz, J.: Blast-Hypersonic flow analogy—theory and application. Am Rocket Soc J 32(9), 1341–1346 (1962)
Van Hise, V.: “Analytic study of induced pressure on long bodies of revolution with varying nose bluntness at hypersonic speeds,” NASA TR-R-78, (1960)
Anderson, John D., Jr., “A Survey of Modern Research in Hypersonic Aerodynamics,” AIAA Paper 84–1578, June 1984
Seltner, P., Willems, S., Gülhan, A.: “Experimental determination of aerodynamic coefficients of simple-shaped bodies free-flying in hypersonic flow”, HiSST, Moscow, Russia, 26–29, (2018)
Acknowledgements
The authors want to thank the TMK team for their support and expertise. Without them acquiring the results presented in this paper would not have been possible. The RETALT project has received funding from the European Union’s Horizon 2020 research and innovation framework program under grant agreement No 821890.
Funding
Open Access funding enabled and organized by Projekt DEAL.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Marwege, A., Hantz, C., Kirchheck, D. et al. Wind tunnel experiments of interstage segments used for aerodynamic control of retro-propulsion assisted landing vehicles. CEAS Space J 14, 447–471 (2022). https://doi.org/10.1007/s12567-022-00425-4
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s12567-022-00425-4