Abstract
Launcher reusability is the most effective way of reducing access to space costs, but remains a great technical challenge for the European aerospace industry. One of the challenges lies in the recovery GNC strategy and algorithms, in particular those of the powered-landing phase, which must enable a precise landing with low fuel margins and significant dispersions. While state-of-the-art solutions for Navigation and control problems can be applied, namely, hybrid Navigation techniques and robust control, for the powered descent guidance problem novel techniques are required to enable on-board optimization, that is necessary to achieve the landing accuracy required to recover the first stage of a launcher. This paper presents the GNC solution currently in development by DEIMOS Space for RETALT (Retro Propulsion Assisted Landing Technologies), an EU Horizon 2020 funded project for studying launch system re-usability technologies for different classes of vertical take-off vertical-landing vehicles. At first, the architecture of the GNC solution identified for the return mission of the launcher is presented. Then, the paper focuses on the landing phase guidance solution, whose performance is critical to enable the recovery and, therefore, the reusability of the launcher making use of retro-propulsion. The guidance strategy is based on direct optimal control methods via on-board optimization, which is necessary to satisfy the pinpoint landing requirement in a high uncertain dynamic system, such as a booster recovery mission. Online convex optimization and successive convexification are explored for the design of the guidance function. The proposed guidance solution was integrated and tested in a high-fidelity simulator and the performance was preliminary assessed. The guidance assessment allowed selecting the best algorithms to be further consolidated and integrated in an end-to-end GNC solution for the return mission.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Launch vehicle reusability is currently the most effective way of reducing the cost of access to space, which is a key endeavour to the commercialization of space [1]. Despite this, it remains a great technical challenge, with only two US companies (SpaceX and Blue Origin) having developed the necessary technology to carry out routinely successful launcher recovery missions, both using retro-propulsive vertical landing as the recovery strategy, and both reporting significant cost savings due to the reusability effort. On the other hand, the European aerospace industry remains largely behind in this effort, risking being far outcompeted if it does not catch up with its US counterparts.
In this context, the EU and ESA have made increasing efforts to achieve the goal of making launcher reusability the state-of-the-art in Europe. One such effort is RETALT (Retro Propulsion Assisted Landing Technologies) [2], a Horizon 2020 project with six partners in four European countries, with the goal of investigating launch system re-usability technology for two classes of launch vehicles with retro-propulsive recovery (Fig. 1): RETALT1, a 103 m tall two-stage to orbit (TSTO) launcher, similar to SpaceX’s Falcon 9; RETALT2, a 17.6 m tall single stage to orbit (SSTO), similar to the DC-X. For the former, only a first stage recovery is performed. The project aims to increase the Technology Readiness Level (TRL) of the recovery technologies up to 5 for structures and mechanisms (to demonstrate the critical functionalities in a relevant laboratory environment), and up to TRL 3 for GNC (to demonstrate the validity of the proposed GNC solutions in a high-fidelity simulation environment), to pave the way for future ground and flight tests for the RETALT technologies.
2 Mission scenario
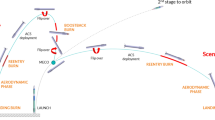
The baseline configuration and the main focus of the project and this paper is RETALT1. Originally, the use of the interstage petals was proposed as main aerodynamic control surfaces (ACS), but in the end planar fins were adopted for the baseline configuration (see Fig. 2 and [3]). The vehicle operates similarly to a typical launcher until separation, after which two scenarios for the first stage recovery are considered: Downrange Landing (DRL) and Return to Launch Site (RTLS), illustrated in Fig. 3. The latter differs in the use of a post-separation flip manoeuvre and boostback burn that modifies the ballistic arc to allow a landing at or near the launch site, while the former foresees a landing at sea on a floating barge. Both scenarios employ a re-entry burn to reduce velocity and dispersions, and an active aerodynamic descent phase enabled by the use of control surfaces. Finally, the first stage recovery mission ends with an engine-powered descent, which slows the vehicle down to a pinpoint and soft vertical landing [3].
RETALT1 ACS configurations: interstage petals (left), and planar fins (right) [4]
RETALT1 return mission concept [3]
One of the great technical challenges in this endeavour lies in the recovery guidance, navigation and control (GNC) system, of which DEIMOS Space is in charge for RETALT. In particular, the design of the powered landing phase GNC offers a difficult challenge, since it must allow the system to perform a precision landing in a fast-dynamic environment, with limited fuel margins, and with significant unknown dispersions accumulated during prior phases.
After the definition of the functional architecture and the modes for the end-2-end GNC solution (from MECO to landing), the preliminary design of the GNC solutions is presented focusing on the novel online optimized guidance for the powered landing phase. Section 3 presents the overall GNC architecture considered for RETALT, while Sect. 4 presents in detail the powered landing guidance solutions identified. Sections 5 reports the preliminary results obtained, and, finally, Sect. 6 shows the main conclusions and the way forward.
3 GNC architecture
The GNC is split into the following sub-functions:
-
Navigation: this consists of a navigation position, velocity and attitude estimate solution, served primarily by Inertial Navigation System (INS), or IMU, products, and hybridized with a GNSS. The use of (D)GNSS, altimeter and (F)ADS is also under evaluation.
-
Guidance: this consists of a guidance algorithm whose aim is to define the re-entry, descent, and landing trajectories during the return phases. This serves to ensure the vehicle is able to perform a pinpoint landing, respecting the mission and flight path constraints.
-
Control: the control tracks the guidance trajectory and ensures a stable attitude, using the effective actuators for the phase. This includes the actuator management.
This architecture is illustrated in Fig. 4, which includes the interactions between each sub-function, the Flight Manager, the sensors and actuators. The GNC operational modes are defined by the mission phase in Table 1, together with the sensors and actuators applicable for each mode.
The guidance commands the attitude maneuvers required in each phase of the flight, the modulation of the attitude during the re-entry burn and the aerodynamic phase to target the correct location at the start of the landing burn. The Control takes care of executing these maneuvers while rejecting perturbations, making use of Thrust Vectoring Control (TVC), Reaction Control System (RCS), and Aerodynamic Control Surfaces (ACS) based on their availability during the flight. The Navigation could also use (F)ADS, altimeter and (D)GNSS, if needed, to further improve the estimation accuracy close to the landing site.
Although autonomous powered-landing GNC strategies and algorithms have been available from past Moon and Mars robotic landing missions, their direct application to the landing burn of a booster recovery mission is not possible due to the additional difficulties of the present mission. These include a higher Earth gravity and hence faster dynamics, a non-negligible atmosphere and, therefore, non-negligible aerodynamic forces and winds, and minimal fuel available due to the recovery not being the primary mission.
In particular, the guidance sub-function for the present design requires sophisticated state-of-the-art algorithms based on online optimization [5]. The strategy is to formulate an optimal control problem (OCP), and solve it directly in real time with a numerical optimization solver. The output of the optimization is a landing trajectory and thrust profile that are dynamically feasible, fuel optimal, and which take into account certain operational and system constrains. This methodology is further described in Sect. 4.
4 Landing guidance
The purpose of the landing guidance during the landing phase is to steer the booster to the desired landing site, either the launch site or a barge depending on the return scenario, and guarantee a pinpoint landing. The guidance shall cope with the fast dynamics of the return phase, especially during the powered landing phase, and shall be robust to the vehicle and environmental uncertainties, including winds. The guidance has to generate a reference trajectory and attitude commands that will be tracked by the control. It typically runs in closed loop but at a low frequency to decouple it from the closed-loop behaviour of the control. Furthermore, the guidance strategy varies for each specific phase of the return mission, due to the different objectives and dynamics encountered for each of the phases. In this paper the focus will be the guidance solution for the powered landing phase.
As mentioned in Sect. 3, the solution selected for the RETALT landing burn relies on the definition of an Optimal Control Problem (OCP) that is optimized on-board. The OCP is defined with a dynamic model, an objective function, and a set of constraints, discretized, and then solved at a low frequency in real time using available optimization solvers, as illustrated in Fig. 5. Extensive research has been successfully conducted in the last years to study how this methodology can be applied to the powered descent guidance problem for Mars landing missions [6, 7] aiming at fuel optimal solutions in presence of non-negligible aerodynamic forces [8]. The adaptation of these techniques to the booster recovery problem has been studied [9, 10] and has been proposed for the CALLISTO experiment [11]. More notably, the guidance employed by SpaceX for the Falcon 9 landing also utilizes this type of strategy [5].
This type of online strategy is necessary for the landing phase due to its challenging nature, since a feasible trajectory must be computed from an initial condition which has accumulated considerable dispersions from previous phases, to a precise final position with an accuracy of a few meters. Moreover, several operational constraints exist that condition the feasibility of the generated reference trajectory, such as the available propellant, the thrust capabilities of the vehicle, namely, throttling, and attitude constraints, including the maximum angle of attack and a near-vertical final orientation, which more traditional trajectory planning methods do not allow to implicitly satisfy. The resulting trajectory is then tracked by a low-level and high-frequency attitude controller in the control sub-function, utilizing the available actuators, i.e., TVC, RCS and ACS. Furthermore, the guidance is also complemented with an outer control loop that closes the loop between optimizations.
The largest limitation of the selected strategy is the relatively high computational load necessary for solving the optimization problem, which must be sufficiently complex to capture the fast dynamics and constraints of the guidance problem. The dynamic modelling is the most critical step in the design of this algorithm: the model may be arbitrarily realistic and complex, which improves the fidelity of the guidance output, but also increases the computational effort required to obtain it. The most important modelling decisions are identified in Table 2. Therefore, the formulation of the optimal control problem is a trade-off between the fidelity and complexity of the problem, and the computational effort required to solve it.
4.1 Optimal control formulation
While a simple 3-DoF model can be linear, introducing attitude dynamics makes the problem highly nonlinear and non-convex. Furthermore, the modelling of drag forces introduces a quadratic non-linearity, which may be possible to linearize with sufficient accuracy, and modelling lift forces introduces even more significant non-linearities. Finally, while modelling the change of vehicle mass introduces a non-convexity in the dynamic model and thrust constraints, a lossless convexification technique is available [6], which makes the problem linear without loss of generality or optimality. Another important design decision in the formulation of the optimal control problem is the online optimization of the landing burn duration. The engine ignition and shutdown time instants may be variables of the optimization, in which case the guidance selects the optimal values that minimize the propellant mass, or these values may be fixed a priori. As can be expected, free final-time and free initial-time optimal control problems make the problem non-convex and, therefore, harder to optimize than fixed-time problems.
This guidance strategy also allows for the implicit satisfaction of operational constraints: the optimal control approach generates a trajectory and attitude that, apart from perturbations, lead the vehicle to the landing site while simultaneously satisfying those constraints. Examples of relevant constraints are reported in Table 3. Similarly to the dynamic modelling, these constraints have different complexities and may possibly render the problem non-convex. For example, while the terminal state constraint is a simple linear and convex constraint, the angle of attack constraint is highly non-convex. The thrust magnitude constraint is also non-convex in the case that the variable mass model is utilized, along with the previously mentioned change of variable, although a lossless convexification of this constraint is possible [6].
The final step in the design of the optimal control problem is the choice of objective function, for which the suitable option is a linear cost function proportional to the propellant expended, which results in the generated trajectory being fuel optimal. Two possibilities include the maximization of the final mass, or the minimization of the integral of the thrust magnitude.
4.2 Landing guidance trade off
The selection of the guidance optimization formulation is, therefore, a trade-off between the computational complexity and robustness of solving the OCP in real time, and the fidelity of the resulting trajectory and control profile. Two main approaches within this framework are identified and discussed next, differing mainly on the dynamic modelling, and consequently also on the method of optimization.
4.2.1 Single convex optimization
The first and simplest approach relies on employing a simple linear model of the vehicle dynamics (e.g., 3-DoF, no/linearized aerodynamics, fixed final time, etc.) and linear or second-order state and control constraints. This approach yields a convex OCP, therefore, allowing it to be solved with convex programming techniques, namely, second-order cone programming (SOCP) [6]. This is desirable for a real-time application, since there are robust convex programming algorithms with convergence guarantees in polynomial time readily available [12].
To compensate for the low-fidelity dynamic model utilized in the guidance, which results in a trajectory that is increasingly infeasible to track with time, the problem is re-solved periodically with an updated state estimate, thus closing the guidance loop, similar to a model predictive control (MPC) approach. On the other hand, as previously mentioned, there is a limitation on the guidance re-solve rate, which must be significantly lower than the control frequency to decouple the frequency response of the two sub-functions, which otherwise may interfere in the control closed-loop performance and stability (about 1–2 orders of magnitude, see Sect. 5).
4.2.2 Successive convexification
The second and more complex approach includes nonlinear dynamic models (e.g., 6-DoF dynamics, aerodynamics, free final time, etc.), which result in a solution with a higher fidelity reference trajectory and control profile, but also in a non-convex optimization problem. Solving this requires non-linear programming (NLP) algorithms, which are undesirable to use in real-time applications, since they are highly dependent on the initial guess and offer few bounds on the computational effort required to convergence, if any. On the other hand, convexification techniques represent significant advancements in guidance optimization problems. Sequential Convex Programming (SCP) and successive convexification techniques offer a framework for solving more general non-convex optimal control problems, and do not make use of second-order information as in Sequential Quadratic Programming (SQP) methodologies.
The work presented here aims at exploiting the benefits of successive convexification techniques: good convergence properties and low computation effort [8]. The basic idea is to successively linearize the dynamic model and constraints around the previous solution, and solve a sequence of SOCP optimizations that iteratively converge to a solution of the original non-linear OCP. The linearization method exploits the benefits of convexity, but it also introduces two undesired effects, namely, artificial infeasibility and artificial unboundedness [13].
Even if the original non-convex problem is feasible, the convexification through linearization approach could engender infeasibilities in any iteration that will obstruct the algorithm and prevent convergence. This phenomenon is known as artificial infeasibility. To prevent this artificial infeasibility, additional control input, typically called virtual control, is introduced to the linear dynamic equations. The virtual control is unconstrained and makes any state to be reachable in finite time. Since their magnitude should be as small as possible, it is heavily penalized via an additional term in the objective function. Another possible strategy to avoid artificial infeasibility consists in relaxing terminal constraints and adding largely penalized optimization variables to the cost function.
Artificial unboundedness comes into sight due to the fact that the iterative linearization approach is a valid approximation of the non-linear function only in the neighborhood of the previous solution. Therefore, to ensure the validity of linearization, the search space must be bounded via a so-called trust region. Thus, the states and/or controls are limited to a fixed (hard trust region constraint) or a variable (soft trust region constraint) radius. In the case of a soft trust region, a penalized weight is added to the objective function and its value is a trade-off between time duration and linearization validity.
Due to the nature of the non-convex problem, the time complexity of this algorithm is naturally higher than performing a single convex optimization, and depends on the degree of nonlinearity of the dynamic model and constraints. However, given the potential higher fidelity of the trajectory and control profile generated with this approach, there will be less demand for re-solving the guidance at a high rate, and it may even enable the guidance to run in open loop, i.e., optimizing only once at the beginning of the landing burn.
4.2.3 Optimization formulations and results
Different optimization formulations have been considered, and the results are compared. The parameters and initial conditions considered are those for the RETALT1 DRL nominal scenario [3]. Table 4 contains OCP options and the computational performance for the optimizations. The 6-DoF dynamic modelling option is discarded at this time in favor of 3-DoF modelling, due to its significant non-linearity and non-convexity resulting in a computationally intractable optimization problem for a real-time application, even with the use of successive convexification. The main advantage in using such a model would be the ability to separately model the vehicle attitude and the commanded thrust vector, and, therefore, modelling the moment generated from engine gimballing. Furthermore, 6-DoF modelling would allow for formulating attitude and TVC deflection constraints separately. On the other hand, with the selected 3-DoF modelling the commanded thrust vector is assumed to correspond to the vehicle attitude, which is used as a reference for control to track with the available actuators, namely, RCS, TVC and ACS. The computational times are not representative of a final real flight implementation, because the coding has not been optimized in this sense, but they are still useful for giving intuition on the real-time feasibility of each of the formulations.
When no aerodynamic model is considered, and the vehicle mass and landing burn duration are fixed, the guidance may be solved with convex programming (single SOCP). An almost constant thrust profile is commanded (Fig. 6). The result is expected to be highly inaccurate due to the lack of aerodynamic modeling, since drag forces are non-negligible at ignition, where the Mach number is approximately 0.7. Furthermore, since the change of vehicle mass due to propellant consumption is also not modeled, the real acceleration due to thrusting will be higher than expected, and increasingly so during the descent, since the vehicle mass may decrease by up to approximately 15%. Finally, the generated profile may not be optimal with respect to the landing burn duration, given that this value is set a priori. If varying mass dynamics is included, the predicted thrust acceleration now takes into account the change of vehicle mass due to propellant expended from the optimized thrust profile (Fig. 7), which leads to a significantly more accurate result.
When a linearized aerodynamic drag model is included (assuming a constant 180 deg AoA, and the interstage petals configuration originally proposed [2]), the computation time increases. The aerodynamics is linearized with respect to the velocity around an initial guess. For subsequent re-optimizations, the velocity profile from previous solutions may be used for the linearization. On the other hand, the guidance now takes into account the drag acceleration, which yields a significantly more accurate result despite the fact that it is an approximation (Fig. 8). Furthermore, given that the guidance now predicts the deceleration due to drag, it generates a commanded thrust profile that allows for a significant propellant reduction (Fig. 9). If the real non-linear drag dynamics is included, given the non-linearity, the problem may no longer be solved with a single SOCP, and therefore, successive convexification is employed. This method uses a similar linearization as the previous option, but the problem is re-solved again with the solution of that optimization, until the solution converges. The solution only converges after 10 SOCP optimizations, increasing the execution time. Furthermore, the final converged solution is very similar to that obtained for the previous test. Then, the touchdown time instant is added as an optimization variable to determine the fuel-optimal landing burn duration. The resulting optimal touchdown instant is now 20.9 s after ignition, for which the maneuver expends 0.11 tons of propellant less than for the previous case. On the other hand, the computational time required to solve the problem increases by nearly 50%. To evaluate the sensitivity of the required propellant with respect to the landing burn duration, Fig. 10 is presented, containing the optimal propellant consumption computed by the guidance as a function of that time. Although the propellant is quite sensitive to the final time, this variation is well within the propellant margins for RETALT1. Therefore, the final-time formulation is deemed to not be necessary for the RETALT1 guidance formulation.
For its application to the interstage petals configuration, given the relatively low increase in fidelity gained by employing a nonlinear drag model versus linearized drag when compared to the significant increase in computational complexity, and given that the free final-time formulation is not necessary, the guidance solution based on convex programming was initially selected, namely, the formulation with fixed final time, variable mass, and linearized drag model (line 3 in Table 4).
Preliminary tests carried out showed some weaknesses of this choice due to the lack in modeling of the lift contribution (see Sect. 6), that becomes even more relevant when the new baseline configuration with planar fins is considered, due to higher aerodynamic performance [3]. Therefore, lift and side forces should also be included in the dynamic model, leading to highly non-linear dynamic equations. An AoA constraint is also introduced in the formulation of the optimal control problem, to explicitly take into account in the guidance the available entry corridor [3]. This is a nonconvex–nonconcave inequality constraint, and it is difficult to handle by successive convexification algorithm. In the present work, a linearization using its first-order Taylor approximation has been considered. However, future work could include linearization of the constraint using second-order Taylor approximation, and a convex feasible set (CFS) method [14]. In addition to virtual control and trust region, and to avoid infeasibilities and to enhance convergence, AoA and terminal state constraints have been relaxed. In the case of AoA relaxation, additional optimization variables have been added and penalized in the cost function. In the case of terminal state constraints, a range of values, according to accuracy, has been used.
This configuration produces more accurate results at the cost of slightly increasing the computational time. For the final development of the landing guidance solution for the planar fins configuration of RETALT1, among the different configurations, the one including drag, lift and side forces and AoA different from 180 deg is selected to be implemented in real time due to the higher fidelity of the resulting trajectory. The major drawback of this configuration for real-time applications is the high computational time needed to find the optimal solution.
The formulation of the OCP for the selected configuration is described in a target-centered Earth-North-Up (ENU) reference frame. The equations of motion are defined by
where \({\varvec{r}}\), \({\varvec{v}}\) and \(z\) are the states and correspond to the position, velocity vector and logarithm of the mass of the vehicle, and \({u}_{mag}\) is the thrust acceleration magnitude.Then, \({{\varvec{a}}}_{{\varvec{T}}}\), \({{\varvec{a}}}_{{\varvec{R}}}\), \({{\varvec{a}}}_{{\varvec{A}}}\) and \({\varvec{g}}\) are the accelerations to which the vehicle is subjected and represent the thrust, centrifugal and centripetal, aerodynamic and gravity accelerations, respectively. It is noted that this formulation considers the thrust acceleration and logarithm of mass, rather than simply using thrust and mass, since it is necessary for the lossless convexification of the min/max thrust constraint [6]. Note also that non-inertial terms due to the rotation of the Earth are also considered. Although the contribution of these terms is minimal, due to the initial position and velocity of the spacecraft, they are still included in order maximize the fidelity of the trajectory, given that their impact on the problem complexity is also very low. The state and control variables of the system are, therefore
where vector \({\varvec{u}}\) consists of the thrust acceleration at each axis (\(x, y, z\)) and the thrust acceleration magnitude, which is the Euclidean norm of the three components. Note that \({u}_{mag}\) is a separate control variable, for which consistency is ensured with the lossless convexification constraint
The problem is then discretized into \(N\) gridpoints, where a first order hold discretization has been used for both states and control discretization. The total number of unknowns depends on the number of gridpoints, and it is computed by
where \({n}_{states}\) and \({n}_{control}\) are the number of states and controls, and \({n}_{vc}\), \({n}_{tr}\) and \({n}_{AoA}\) are the number of virtual controls, trust regions, and angle-of-attack variables per gridpoint. For an optimization with \(N=30\) gridpoints, the total number of unknowns is 949. The additional constraints used in the presented configuration are: glide slope constraint, tilt angle constraint near touchdown, angle of attack constraint and other soft constraints to relax the landing point. Finally, a simplified version of the successive convexification algorithm is presented in Table 5, which is computed in real time at time \({t}_{k}\):
4.3 Trajectory tracker
A technique commonly used with this guidance strategy that improves its performance is the inclusion of a trajectory tracker, which minimizes the dispersions accumulated between optimizations. The trajectory tracker is a controller that precedes the attitude controller and thus minimizes the dispersions accumulated between optimizations by running at a higher frequency than the main guidance algorithm. The reference thrust profile from the optimization is used as a feed-forward control, around which the tracker computes a small thrust deviation such that the real position and/or velocity is controlled to the reference ones from the optimization. This sub-function does not substitute the main attitude control feed-back loop, and is interpreted as being part of the guidance, since it does not directly compute actuator commands.
This architecture is similar to that used in the CALLISTO GNC [11], which after the guidance has an outer and inner control loop. For the results discussed in Sect. 6, a simple trajectory tracker implemented with an LQR controller has been implemented, based on the same state and control variables as the main guidance algorithm.
5 Preliminary guidance performance
To support the GNC testing and evaluate the preliminary performance of the landing guidance solution defined for RETALT, a Functional Engineering Simulator (FES) was developed (Fig. 11). The RETALT-FES is a high-fidelity simulation environment based on SIMPLAT [15], that includes detailed vehicle configurations and mission scenario models [2, 3].
The guidance solution preliminary selected as a result of the trade-off is tested assuming perfect Navigation to be able to evaluate the isolated guidance functioning. The simulations were run in the RETALT-FES in 3-DoF, with the thrust attitude commanded by the guidance directly translated to the attitude of the vehicle. Initially, the RETALT1 DRL scenario for the interstage petals configuration is considered [2]. The guidance solves the optimization problem at a frequency of 0.25 Hz, and the trajectory tracker runs at 10 Hz. Although the final landing time is fixed a priori, upon each guidance re-computation it is updated based on the expected and real change in the state. In nominal conditions, the guidance is able to land the vehicle with the desired performance (Table 6). The effect of the trajectory tracker can be seen in Fig. 12, as it commands a value around the reference thrust profile to follow the reference state defined by the optimization solution. The critical thresholds for the pitch angle and the vertical velocity at touchdown are 5 deg and 3 m/s, respectively.
However, in the real mission the arrival conditions at the beginning of the landing phase are not perfect. When dispersions in position are considered, in line with the trajectory control capability of the vehicle [3], the guidance is proven able to correctly steer the vehicle to the desired landing site. Once again, all landing performance requirements were satisfied for all shots of the Monte Carlo campaign (see Fig. 13 and Table 7). However, a significant horizontal diversion manoeuvre is required in some cases, and the AoA deviates considerably from the AoA = 180 deg reference attitude. In this case, a lift force is generated. Therefore, the guidance would also benefit from modelling the lift forces, although, once again, that requires a successive convexification approach. Similarly, the guidance is shown to be able to correctly compensate relevant atmospheric (derived from the NRLMSISE00 model [16] for the Kourou-Atlantic region) and aerodynamic drag dispersions (as specified within the AEDB model). The results are presented in Table 8. The guidance is fully able to compensate the uncertainty and satisfy all performance requirements. The guidance is able to satisfy in general all requirements also in case winds and wind dispersions are considered (derived from the NOAA model [17] for the Kourou-Atlantic region), except for the pitch requirement in some extreme cases (Fig. 14 and Table 9). The winds have a great effect on the trajectory, since they are completely unpredicted in the guidance planner. The performance may be improved by modelling the winds in the guidance dynamic model, which will allow it to take their effect into account. This requires measuring or estimating the winds, which will be subject to a knowledge error, although it may be sufficient to guarantee a successful landing in the worst-case scenarios. When dispersions on the lift model are included, the guidance performance is highly depreciated and does not satisfy the touchdown requirements in some extreme cases (Table 10). This is due to the lift dispersions veering the vehicle to off-nominal conditions, where the lift forces increasingly act on the vehicle. Therefore, since the guidance does not model these lift forces, the real trajectory deviates significantly from the reference one.
Finally, a simulation campaign is carried out with the new planar fins baseline [3]. The guidance generates a landing solution with significant AoA manoeuvring, and with poor results even in nominal conditions (Fig. 15 and Table 11), which again exposes the limitations of the current guidance model. Therefore, this campaign further underlined the need for a more realistic aerodynamic model including lift, and for constraining the AoA, both of which result in an optimal control problem that requires successive convexification to solve. Given the higher altitude at which the landing burn starts, it is also advantageous to improve the guidance atmospheric model to consider altitude-varying parameters, such as atmospheric density, maximum thrust, and specific impulse, at the cost of slightly more complex optimization. Preliminary results of this updated formulation of the guidance problem showed that in nominal conditions the guidance is able to correctly find a solution with the right precision and satisfying all constraints also for the planar fins configuration (Fig. 16).
6 Conclusions and way forward
This paper has presented the current status in the development of the RETALT recovery GNC, including the general high-level GNC architecture.
The landing guidance was addressed, which is based on state-of-the-art optimization algorithms. Two main approaches were identified and addressed, namely, single convex optimization, and successive convexification. Given the computational limitations identified for the latter versus the low benefit expected with respect to the former, the design principle for RETALT was based on the simplest option, single convex optimization, until the need for greater fidelity was encountered. When the interstage petal configuration is considered, characterized by a low L/D performance, the guidance performed adequately in nominal conditions, satisfying all performance requirements when tested in a high-fidelity simulation environment. In some off-nominal cases, however, the limitation of the aerodynamic guidance model, namely, the lack of lift modelling, resulted in the violation of the performance requirements. When the guidance solution was applied to the more performant planar fins configuration, that also requires to start the landing burn at a higher velocity, the simplest option is no longer able to produce a valid solution, and a more complex solution is necessary. A lift model was thus included, and successive convexification implemented, with promising preliminary results. Future work will further consolidate this work by testing the new solution in the RETALT-FES, and extending the guidance to the previous phases of the return mission (aerodynamic phase, re-entry burn, and boostback burn).
Also, while the control sub-function has not been addressed in this work, an optimum control solution based on H-infinity is under development. The simulations presented will then be extended to include 6-DoF dynamics with the attitude controller in the loop, which may prompt another development iteration of the present guidance solution, given that it was only tested on the 3-DoF simulator. Finally, the navigation solution under development is based on a Considered Kalman Filter and a sensor suite that includes an INS/GNSS coupled system.
Abbreviations
- ACS:
-
Aerodynamic Control Surface
- CFS:
-
Convex Feasible Set
- DoF:
-
Degree(s) of Freedom
- DRL:
-
Down Range Landing
- EKF:
-
Extended Kalman Filter
- FES:
-
Functional Engineering Simulator
- (F)ADS:
-
Flush Air Data System
- FM/MVM:
-
Flight Management/Mode Vehicle Manager
- GNC:
-
Guidance Navigation and Control
- GNSS/GPS:
-
Global Navigation Satellite System/Global Positioning System
- LQR:
-
Linear Quadratic Regulator
- IMU/INS:
-
Inertial Measurement Unit/Inertial Navigation System
- MECO:
-
Main Engine Cutoff
- MPC:
-
Model Predictive Control
- NLP:
-
Non-linear Programming
- NOAA:
-
National Oceanic and Atmospheric Administration
- OCP:
-
Optimal Control Problem
- RCS:
-
Reaction Control System
- RETALT:
-
Retro Propulsion-Assisted Landing Technologies
- RTLS:
-
Return to launch site
- SIMPLAT:
-
SIMulation PLATform
- SOC:
-
Second-Order Cone
- SOCP:
-
Second-Order Cone Programming
- SSTO:
-
Single stage to orbit
- TRL:
-
Technology Readiness Level
- TSTO:
-
Two stage to orbit
- TVC:
-
Thrust Vector Control
References
Patureau de Mirand, A., et al.: Ariane next, a vision for a reusable cost-efficient European rocket. In: 8th European Conference for Aeronautics and Space Sciences (EUCASS), Madrid, Spain (2019)
Marwege, A., et al.: Retro propulsion assisted landing technologies (RETALT): current status and outlook of the EU funded project on reusable launch vehicles. In: 70th International Astronautical Congress (IAC), Washington D.C., United States (2019)
De Zaiacomo G., et al.: Mission engineering for the RETALT VTVL launcher. Special CEAS J. TBC (2022)
Marwege A., et al.: Wind Tunnel experiments of interstage segments used for aerodynamic control of retro-propulsion assisted landing vehicles (RETALT). Special CEAS J. TBC (2022)
Blackmore, L.: Autonomous precision landing of space rockets. In: Frontiers of Engineering: Reports on Leading-Edge Engineering from the 2016 Symposium., vol. 46 (2016)
Acikmese, B., Scott, R.P.: Convex programming approach to powered descent guidance for mars landing. J. Guid. Control Dyn. 305, 1353–1366 (2007)
Acikmese, B., et al.: G-fold: A real-time implementable fuel optimal large divert guidance algorithm for planetary pinpoint landing. Concepts Approach. Mars Explor. 1679, 4193 (2012)
Szmuk, M., et al.: Successive convexification for fuel-optimal powered landing with aerodynamic drag and non-convex constraints. In: AIAA Guidance, Navigation, and Control Conference (2016)
Lee, U., Mesbahi, M.: Constrained autonomous precision landing via dual quaternions and model predictive control. J. Guid. Control. Dyn. 40(2), 292–308 (2017)
Simplício, P., Marcos, A., Bennani, S.: Guidance of reusable launchers: improving descent and landing performance. J. Guid. Control. Dyn. 42(10), 2206–2219 (2019)
Sagliano, M., et al.: Guidance and control strategy for the CALLISTO flight experiment. In: 8th European Conference for Aeronautics and Aerospace Sciences (EUCASS), Madrid, Spain (2019)
Domahidi, A., Chu, E, Boyd, S.: ECOS: an SOCP solver for embedded systems. In: 2013 European Control Conference (ECC), IEEE (2013)
Benedikter, B., et al.: A convex approach to rocket ascent trajectory optimization. In: 8th European Conference for Aeronautics and Aerospace Sciences (EUCASS), Madrid, Spain (2019)
Xie, L., Zhang, H., Zhou, X., Tang, G.: A convex programming method for rocket powered landing with angle of attack constraint. IEEE Access 8, 100485–100496 (2020)
Fernandez, V., De Zaiacomo, G., et al.: The IXV GNC functional engineering simulator. In: 11th International Workshop on Simulation and EGSE facilities for Space Programmes—SESP, Noordwijk, The Netherlands (2010)
https://ccmc.gsfc.nasa.gov/modelweb/atmos/nrlmsise00.html. Accessed 30 Mar 2020
https://www.nesdis.noaa.gov. Accessed 30 Mar 2020
Acknowledgements
The RETALT project has received funding from the European Union’s Horizon 2020 research and innovation framework program under grant agreement No 821890.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Botelho, A., Martinez, M., Recupero, C. et al. Design of the landing guidance for the retro-propulsive vertical landing of a reusable rocket stage. CEAS Space J 14, 551–564 (2022). https://doi.org/10.1007/s12567-022-00423-6
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s12567-022-00423-6