1 Introduction

The impact of non-uniform Earth scenes on the spectral response of slit-based imaging spectrometers was identified by several operational Earth observation missions such as the Ozone Monitoring Instrument (OMI) [33] and TROPOMI [16, 20] as well as upcoming missions as for example the Sentinel-4/UVN [23] and Sentinel-5/UVNS [6, 21] instruments. Therefore, a set of stringent spectral requirements of current missions are parametrized in the stability of the Instrument Spectral Response Function (ISRF), which is the radiometric response of a single spectral channel as a function of the wavelength of light incident on the instrument. The ISRF is a function of the slit illumination in along track direction of the satellite, the spectrometer point spread function, and the detector pixel response on the focal plane array (FPA). The ISRF fully describes the spectral response of the instrument, and establishes a direct link between the forward radiative transfer model of the retrieval algorithm and the spectra measured by the instrument. Hence, any uncertainty of the ISRF knowledge has an immediate impact on the measured \(\hbox {CO}_{2}\) concentration in terms of column-averaged dry mixing ratio (\(\hbox {XCO}_2\)). Even after extensive on-ground calibration of the ISRF for homogeneous scenes, there remains a pseudo-random in-orbit uncertainty of the ISRF knowledge due to non-uniform Earth scenes arising from albedo variations or clouds. To stabilize the ISRF in-orbit, the upcoming Sentinel-5/UVNS mission is the first space-borne instrument to employ an onboard hardware solution called Slit-Homogenizer (SH). Sentinel-5/UVNS is a push-broom imaging spectrometer. In such instruments, a telescope images the ground scene onto the entrance slit of the spectrometer. The projection of the slit on-ground in across-track (ACT) defines the swath width, which corresponds to the spatial coverage of the instrument. In the subsequent spectrometer, the light collected during the platform motion in along-track (ALT) direction gets spectrally dispersed using a diffraction grating. In this project, the Earth scene contrast is mitigated by replacing the classical spectrometer slit by two parallel mirrors. By multiple reflections between these mirrors the light is scrambled in along-track (spectral) direction, whereas the light in across-track (spatial) direction passes the slit without any scrambling effect. As the light is only scrambled in one direction, this slit homogenizer concept is also called 1D-Slit Homogenizer (1DSH). With this concept, the in-orbit knowledge of the ISRF can meet the requirements of the Sentinel-5/UVNS instrument over a representative heterogeneous scene [18].

The \(\hbox {CO}_{2}\) Monitoring Mission (CO2M) aims to quantify sources and sinks of carbon dioxide (\(\hbox {CO}_{2}\)) and methane (\(\hbox {CH}_4\)) by measuring their concentration in the atmosphere. In order to differentiate anthropogenic \(\hbox {CO}_{2}\) emission from biogenic \(\hbox {CO}_{2}\) fluxes, an instrument was proposed, which is capable of observing \(\hbox {CO}_{2}\) at a precision of \(<0.7 \text { ppm}\), with a systematic accuracy of \(0.4\text { ppm}\) and with a spatial sampling resolution of \(2 \ \text {km} \times 2 \ \text {km}\) [9]. The mission consists of a total of four instruments: the \(\hbox {NO}_2\) imager (NO2I), operating in the visible spectral range (405–490 \(\text {nm}\)), the multi-angle polarimeter (MAP), measuring and characterizing the aerosol contribution in the atmosphere, a high-resolution cloud imager (CLIM), detecting cloud contamination within a spatial sample and the \(\hbox {CO}_2\) imager (CO2I), measuring the spectral radiances and solar irradiance in the NIR (747–773\(\text { nm}\)), SWIR-1 (1595–1675\(\text { nm}\)) and SWIR-2 (1990–2095\(\text { nm}\)). Similar to Sentinel-5/UVNS, CO2I is also operating in a push-broom configuration. Identifying plumes of elevated \(\hbox {CO}_{2}\) requires high single-sounding precision without regional and temporal averaging [19]. The stringent precision and accuracy requirements correspond to only \(0.1{\%}\) of today’s typical \(\hbox {CO}_{2}\) background values around \(400 \text { ppm}\). Along with the small ground sampling distance (\(2\text { km}\)), corresponding to a significant fraction of the instantaneous field of view in ALT direction, this leads to a higher sensitivity of the CO2I instrument to ISRF distortion than atmospheric chemistry missions like Sentinel-5/UVNS. The CO2M requirement for ISRF stability over scenes with sharp contrast, i.e. a sudden transition from bright to dark irradiance in the centre of a spatial sample, requires the ISRF in-flight shape knowledge to be better than \(1.5\%\) and the position of the spectral channel centre shall be known with accuracy better than \(0.002 \ \text {nm}\) (NIR) [9]. Simulations indicate, that these ISRF stability requirements under sharp contrast scenes cannot be met with the 1DSH model implemented in the Sentinel-5/UVNS instrument [18]. Furthermore, the sensitivity of \(\hbox {XCO}_2\) retrieval to topography imposes extremely strong requirements on the spatial co-registration between spectral channels of \(5\%\) of the spatial sampling distance (SSD) [29]. This accuracy is necessary, as several data products of the three simultaneously measured channels (NIR, SWIR-1, SWIR-2) are required to determine the \(\hbox {XCO}_{2}\) retrieval. Therefore, any spatial mismatch between the channels would lead to further \(\hbox {XCO}_{2}\) error contributions.

To address both critical requirements, ISRF stability and spatial co-registration, we investigated a new slit concept called 2D-Slit Homogenizer (2DSH). In this concept, the classical slit is replaced with a bundle of multimode fibres. The dimension of each rectangular fibre core in along-track direction (ALT) defines the spectral extent of the slit and the dimension in across-track direction (ACT) represent the spatial sampling. The full swath width is given by the total size of the adjoined fibres in ACT direction. Compared to the 1D slit homogenizer from Sentinel-5/UVNS, in addition to the spectral direction, piece-wise homogenization is now also performed in the ACT direction. The heritage of efficient scrambling capabilities of multimode fibres and the application as spectrograph entrance slits originates from on-ground radial velocity (RV) spectrographs such as for example CARMENES [31], HARPS [24] or ESPRESSO [25]. Initial concepts of using a 2DSH for space-based imaging spectrometers were proposed by Guldimann and Minoglou [13] and the performance characterized by Amann et al. [2]. In this paper we extend the above studies and discuss further implications on the optical system when using a 2DSH. Besides the unprecedented stabilization of the slit illumination, several drawbacks and efficiency parameters have been identified, namely the phenomena of Focal Ratio Degradation (FRD), the dependency of the scrambling efficiency on the fibre length or the modification of the spectrograph pupil intensity distribution due to heterogeneous scenes. Here, we present a fibre-based slit concept for space-based imaging spectrometers and investigate key parameters for an efficient fibre scrambling performance in the near- (NF) and far field (FF). For that purpose, we developed an experimental setup and measurement procedure to quantify the ISRF stability for several applied Earth scene contrasts in ALT and ACT direction. Further, we discuss and assess the impact of FRD effects based on the Telescope F-number proposed in the framework of the Airbus CO2M A/B1 study.

This paper continues the work started by Hummel et al. [17] and presented at the International Conference on Space Optics (ICSO) 2021. It contains several graphs and results that have been already published by Hummel et al. [17]. This paper is structured as follows: Sect. 2 describes the experimental optical setup we deployed for the 2DSH performance assessment. In Sect. 3 we investigate the scrambling performance in the NF for different fibre lengths and quantify the impact on ISRF stability merit functions in the NIR. Furthermore, we discuss the impact of spectrograph pupil illumination variations induced by a 2DSH and quantify the resulting ISRF errors in for a short and long fibre. A measurement procedure to investigate radiometric losses due to FRD effects is proposed in Sect. 4. Finally, we summarize and discuss our results in Sect. 5.

2 Experimental setup

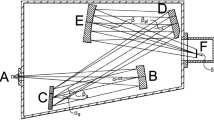
To probe the fibre characteristics for non-uniform illumination, we designed and constructed an experimental setup, which allows to detect either the near-field (NF) or far-field (FF) pattern of light transmitted through the fibre, while precisely controlling the illumination pattern inserted into the fibre. A schematic overview of the setup is given in Fig. 1. Depending on the spectral band of interest, different coherent and incoherent light sources were used to probe the fibre. As light sources, we used tunable monochromatic lasers (NIR: Laser Sacher TEC-500-0770-030; SWIR: Toptica CTL 1550). The light source of choice for the corresponding test is connected to an input port of an integrating sphere (Thorlabs IS236A-4) via an optical fibre. The integrating sphere ensures a homogeneous intensity distribution of the beam across the telescope pupil plane. However, when using monochromatic laser light, the surface roughness of the sphere’s internal material leads to a speckle pattern in the emitted beam. To get rid of this effect, a speckle reducer is mounted at the output opposing the regular beam output. The speckle reducer itself consists of diffusing material (Spectralon) placed just outside the integrating sphere and mounted on a rotor which is continuously spun by a motor. The rotating diffuser material eliminates the spatial coherence by averaging over the detector integration time and thus significantly reduces the amplitude of the averaged speckle patterns. A field stop, that is adjustable in two-dimensions and placed on the regular beam output secures full control over the shape and size of the emitted beam. In turn, this controls the illumination pattern at the image plane, which is later coupled onto the fibre. A lens (lens 1—Edmund Optics #49-366) with a \(250\text { mm}\) focal length collimates the beam from the light source assembly. The collimated beam is divided by a 50–50-beam-splitter. The transmitted part is sent through an adjustable aperture and imaged telecentric onto the fibre facet by a lens (lens 2—Thorlabs AL 1225H-B/J-C) with a \(25\text { mm}\) focal length. The telecentricity ensures that each point at the fibre entrance receives the same cone of light. Tuning the diameter of the aperture allows us to change the F-number (F#) of the beam-cone sent onto the fibre tip. NF images are obtained by projecting the exit facet of the fibre on a sensor (NIR: Basler Aca-1600; SWIR: Photonic Science InGaAs detector). The projection is performed with a microscope objective (0.1 NA, Olympus RMSx4) and an achromatic lens (Edmund optics #49-332) both mounted in a tube system (lens 3 in Fig. 1). FF images are obtained with a bar camera sensor located at a known distance from the fibre exit. The distance is much larger than the typical fibre core size and features no optics between the fibre exit and the sensor (free space propagation). Light reflected by the fibre tip (front facet), as well as light coupled into the fibre and reflected by the facet on the back site is again collimated by lens 2. This reflected beam is sent onto the beam-splitter and the reflex is imaged via another 4-fold magnification microscope objective (identical to lens 1). The NF image of the fibre front facet allows to monitor the illumination pattern on the facet when tuning the stop on the light source assembly. The light reflected at the backside of the fibre appears as a homogeneous illumination of the fibre core due to the scrambling. The brighter reflection of the illumination pattern on the front facet overlays the faint core illumination from the fibre output side and can be precisely tuned with the adjustable stop on the light source assembly over the entire facet (including cladding).

Fig. 1
figure 1

Sketch of the fibre-test setup. Next to each camera, associated false colour images are displayed. The dashed blue line indicate optional fibre-connection for near-field (NF) or far-field (FF) measurements

Full size image

2.1 2D-slit homogenizer

In this study, we tested two different lengths of rectangular core COTS fibres provided by Optec. They share the same core dimension of \(300 \times 100\ \upmu \mathrm{m}\pm 2\%\) (ACT/ALT) and a cladding of \(350 \times 180\ \upmu \mathrm{m}\pm 2\%\) (ACT/ALT). One set of fibres is \(5\ \mathrm{cm}\pm \text 0.3\,{cm}\) long and the other set is \(100\,{\text{cm}} \pm 5\,{\text{mm}}\) long. All the tests in this study have been repeated and confirmed with a representative pre-development model of a 2DSH sample, consisting of 25 adjoined multimode fibres of 100 cm as shown in Fig. 2. The depicted 2DSH sample is made of two optical heads. One is mounted at the telescope image plane, and another one on the spectrometer object focal plane. They are connected by the bundle of fibres. Within each optical head, the ribbon of fibres shaping the slit is bonded on a silica plate with NOA-88 UV adhesive. On the spectrometer side, the silica plate is polished with a small radius of curvature for smile correction. Depending on the instrument design and the mission requirements, the 2DSH entrance and exit plane can be slightly curved to compensate smile effects on both, the spectrometer and telescope side. This is achieved by assembling the fiber core positions of the bundle in a parabolic shape instead of a straight line. A potting epoxy sealant is used to guarantee global stability of the fibres. Moreover, a second silica plate is glued on top to form the silica-plate/ fibre-ribbon/ silica-plate sandwich. Two additional silica plates are glued on the edges of the slit to form a complete casing. An AR-coated window is bonded at 2DSH entrance and output facets to avoid stray light and maximize transmission.

Fig. 2
figure 2

2DSH pre-development model provided by Optec consist of 25 adjoined rectangular multimode fibres with a length of \(100\ \mathrm{cm}\). The fibres within each optical head are bonded on a silica plate. The spectrometer facing output optical head is curved for smile correction (image courtesy of Optec)

Full size image

The separation between the fibre cores due to the cladding results in a stripe pattern at the 2DSH output plane (Fig. 2). Between the illuminated cores there are dark areas where there is no light. The reason for this is that the light entering the cladding at the 2DSH entrance plane is not propagated through the fibres. Thus, the binning of the spatial samples is already defined in the slit by design. As the NO2I and CO2I share a common 2DSH, this allows for a binning-strategy with almost perfect co-registration between the wavelength channels. However, the cladding gaps also lead to gaps in the imaged swath on-ground and reduced SNR. Note that the gaps are not completely unsampled, as the telescope PSF and scrambler pattern blur the slit projection on-ground.

3 Scrambling performance

For the ISRF stability with regard to non-uniform scenes, two scrambling parameters of the fibre have to be considered. First, the ISRF is directly dependent on the slit illumination which, besides some spectrometer magnification, corresponds to the NF after the fibre. Second, the ISRF is a function of the spectrograph PSF. A scene-dependent variation in the FF of the fibre will change the spectrograph pupil illumination and therefore create a scene-sensitive weight of the aberrations present in the spectrograph. This alters the PSF of the spectrometer on the FPA and consequently also the ISRF. The following scrambling gain measurements were performed in the NIR at \(780 \text { nm}\) and with a circular F/3.28 telescope pupil.

3.1 Near field measurements

The light scrambling inside a multimode fibre is achieved by mode to mode coupling between the fibre propagation modes. Yet, the illumination pattern entering the fibre may be partially maintained in the output due to insufficient scrambling. One parameter that determines the scrambling efficiency is the fibre length. Figure 3 shows the NF scrambling performance for a short fibre with a length of \(5\text { cm}\). The input scenes correspond to a high contrast scene with sharp transitions from dark to bright (Type-A scene) and bright to dark (Type-B scene) of the ALT slit illumination. Note that this kind of ALT transitions are impossible to be observed by a push-broom spectrometer with finite field of view and integration. Instead, the scene would be smeared out by the satellite motion. However, static scenes are conveniently used in experimental measurements and represent the worst case. To the contrary, heterogeneous scenes in ACT are not smeared by the platform motion and may also create distortions in the ISRF stability, particularly in the presence of spectrometer smile [5].

Even though the fibre NF output for the short fibre seems visually uniform, the ALT cross section highlights the imperfect homogenization of the scene. The residual position information of the input scene remains as a prominent gradient in the fibre intensity output. This residual gradient impacts both, the ISRF shape and the centroid position. Note that the ripples on top of the gradients are due to measuring with a coherent light source combined with modal noise as a result of the limited excitation of fibre modes guided in the fibre.

Fig. 3
figure 3

Short fibre (\(5\text { cm}\)) NF output intensity distribution for scene heterogeneity in ALT direction in the NIR (\(770\text { nm}\)). The residual symmetry of the input illumination pattern is partly preserved through the fibre and is still visible as a gradient in the ALT output cross section

Full size image

The same experiment was repeated for the 100 cm long fibre. Here, the power exchange among the guided modes in the fibre is more efficient and clearly improves the homogeneity of the fibre NF output. In fact, there is no visually noticeable difference for the intensity distribution at the fibre output between the case of homogeneous and \(50{\%}\) fibre entrance illumination (see Fig. 4). Here, we illuminate with a \(50\ \%\) type-B scene and measure the cross section in the NF output. From the comparison of the results for the 5 cm and 100 cm long fibres we conclude that the fibre length is a crucial parameter for the scrambling performance and hence a driver for the ISRF stability in the context of non-uniform scenes.

Fig. 4
figure 4

Long fibre (\(100\text { cm}\)) NF output intensity distribution for scene heterogeneity in ALT direction in the NIR (\(770\text { nm}\)). The \(100{\text { cm}}\) long fibre yields very high scrambling performance and greatly desensitizes the fibre output from any given input illumination heterogeneity

Full size image

3.2 Near field impact on ISRF

To quantify the fibre scrambling performance in more detail, we investigate the impact of the fibre NF on the ISRF stability merit functions for the long \(100\text { cm}\) in the NIR. More precisely, to obtain the ISRF on the FPA, we propagate the measured fibre NF output through the subsequent spectrograph model.

To this end, we calculate the ISRF as the convolution of the NF intensity after the fibre, a representative spectrograph PSF, and the pixel response of the detector. In spectral coordinates, the ISRF is then given as:

$$\begin{aligned}&\widetilde{\mathrm {ISRF}}(\lambda ) = \mathrm {Slit}(\lambda ) \otimes \mathrm {PSF} (\lambda ) \otimes \mathrm {Pixel} (\lambda ) \end{aligned}$$
(1)
$$\begin{aligned}&\mathrm {ISRF}(\lambda ) = \frac{\widetilde{\mathrm {ISRF}}(\lambda )}{\int \widetilde{\mathrm {ISRF}} (\lambda ) \ \mathrm{d}\lambda }, \end{aligned}$$
(2)

where \(\otimes\) is the convolution symbol, \(\lambda\) is the wavelength and representing the spectral dimension on the FPA, Slit the NF fibre output scaled to the FPA as a function of \(\lambda\), PSF is the optical point spread function (PSF) of the spectrograph and Pixel is the detector response (boxcar). The ISRF and the constituting functions are given in binary units. The PSF was generated by raytracing through a representative optical instrument model of the CO2M A/B1 study. To assess the stability of the ISRF, we define two merit functions:

  • Shape error defined as the absolute difference between the ISRF for a homogeneous fibre entrance illumination and the ISRF for a heterogeneous illumination

    $$\begin{aligned} \text {Shape error}:=\max _{\lambda } \left|\frac{\mathrm{ISRF}_\mathrm{hom}(\lambda )-\mathrm{ISRF}_\mathrm{het}(\lambda )}{\displaystyle \max _{\tilde{\lambda }}\mathrm{ISRF}_\mathrm{hom}\left( \tilde{\lambda }\right) }, \right|\end{aligned}$$
    (3)

  • Centroid error defined as the absolute difference between the centroid for a homogeneous fibre entrance illumination and the centroid for a heterogeneous illumination. The centroid is defined as:

$$\begin{aligned} \text {Centroid}:=\frac{\int \limits _\mathrm{FPA} \mathrm{ISRF}(\lambda ) \ \lambda \ \mathrm{d}\lambda }{\int \limits _\mathrm{FPA} \mathrm{ISRF}(\lambda )\ \mathrm{d}\lambda }. \end{aligned}$$
(4)

These merit functions are calculated for several type-A and type-B scenes, where we decrease the fraction of the fibre illumination area, ranging from 100 to \(20\%\). Figure 5a shows the evolution of the ISRF shape and centroid error for partial fibre illuminations relative to a full illumination which corresponds to a homogeneous scene. The centroid shift on the FPA is given in spectral dimension, i.e. representing the spectral drift of the ISRF centroid. Even for the extreme case of only \(20\%\) fibre illumination with a sharp contrast, the fibre homogenizes the contrast with high efficiency, leading to a maximum absolute ISRF shape error of \(0.461\%\). This is well below the CO2M requirement of \(1.5\%\) shape error. We also observed very low sensitivity with regard to the input scene for the stability of the centroid error. The maximum spectral centroid drift on the FPA for a \(20\%\) partial fibre illumination is \(<0.25\text { pm}\), which easily satisfies the requirement of \(2\text { pm}\). The residual centroid drift is dependent on the symmetry of the applied input illumination. The centroid drifts in the opposite direction when the partial fibre illumination is at the bottom (type-A scene) or top (type-B scene) of the fibre. This is confirmed when we compare the shape difference between an ISRF for a homogeneous scene and a heterogeneous scene of \(20\%\) fibre illumination as depicted in Fig. 5b. The shape difference inversion of the ISRF follows the inversion of the ALT illumination symmetry of either bottom (left plot) or top (right plot) illumination of the fibre entrance.

Fig. 5
figure 5

a ISRF shape and centroid error in the NIR for several high-contrast scenes for the \(100\text { cm}\) fibre. Red and blue data points correspond to fibre partial illumination fraction, moving from bottom-top and top-bottom, respectively. The reference for the relative error is the homogeneous illumination of the fibre entrance. b Shape difference between an ISRF of \(20\%\) fibre illumination starting at bottom (type-A scene) and top (type-B scene) respectively, and a homogeneous fibre illumination. The symmetry of the input illumination is still visible as asymmetric shape behaviours in the ISRF

Full size image

3.3 Far field measurements

The heritage of RV-measurements of ground-based telescopes indicate that the FF after the fibre depends on the input illumination of the fibre. Contrary to classical slits, this means that the telescope pupil intensity distribution is not preserved in the spectrograph pupil when using a fibre based slit under the condition of non-uniform fibre illumination [10, 14]. Figure 6 depicts the FF intensity distribution obtained with a \(5\text { cm}\) and \(100\text { cm}\) fibre. All measurements in this section were done with a circular F/3.28 telescope pupil and the FF was imaged at a distance of \(6 \text { cm}\) from the fibre exit. We apply different input illumination symmetries, in which we move a small rectangle through the fibre input core in ACT direction. We observe, that for both fibre lengths, the FF intensity patterns have symmetric shapes with either a dip or a peak in the centre. The intensity profiles become flat when placing the illumination rectangle in the fibre centre. These findings have also been reported by other studies in the context of RV ground-based spectrographs [3, 10, 14]. In our study, this effect has been observed in both, the NIR (\(780\text { nm}\)) and SWIR (\(1550\text { nm}\)) wavelength. The amplitude of the peak/dip asymmetry is significantly stronger for the short fibres. This confirms the assumption that the mode-to-mode coupling increases with fibre length. The limited mode excitation due to the small excitation area at the fibre input core is compensated by small random variations of the optical and geometrical properties of the fibre. The root cause for these perturbations could be microscopic random bends or refraction fluctuations which are generated during the fibre manufacturing process. Due to the longer interaction length, the mode coupling mechanisms are stronger for longer fibres and therefore support the homogeneity of both, the NF- and, more prominently, the FF intensity distribution [30].

Fig. 6
figure 6

Fibre FF intensity distribution obtained in the NIR (\(770\text { nm}\)) for a short- (\(5\text { cm}\)) and long (\(100\text { cm}\)) fibre for different input illumination symmetries. The FF intensity patterns have symmetric shapes with either a peak or a dip in the centre, depending on the location of the fibre input. Partial but symmetric fiber input illumination results in a flat but noisy FF due to limited modes (modal noise). The amount of mode-to-mode coupling with fibre length is clearly visible in the FF patterns of the two fibre lengths

Full size image

3.4 Far field impact on ISRF

The impact of a non-uniform spectrograph pupil illumination on the ISRF stability is mainly driven by the scene-dependent weighting of the aberrations present in the spectrograph optics. Consequently, this results in a scene-dependent optical PSF, which serves as a kernel for the ISRF, and, therefore, adds another error contribution to the ISRF. Note that this effect is independent of the NF error contribution and puts additional uncertainty to the ISRF knowledge. To quantify the FF impact on the ISRF for the CO2M model of Phase A/B1 we follow a slightly different approach than for the NF. We propagated the dip and peak FF intensity maps of long and short fibre results from Fig. 6 (first and third row of the long and short fibres respectively) through the Airbus CodeV model and compared the ISRF shape and centroid changes with respect to a homogeneous spectrograph pupil intensity distribution. The FF intensity maps, i.e. the spectrograph pupil illumination, were used as a CodeV spectrograph pupil input for three spatial field points and three spectral points on the FPA grid in each wavelength channel (NIR, SWIR-1, SWIR-2). By doing so, we wanted to account for the fact that different areas of the detectors have different aberrations. This 3 \(\times\) 3 grid covers the center and edge parts of each respective spectral band detector. For the analysis, we only quantify the FF effects and assume a homogeneous NF output of the fibre. Therefore, the outcome of the analysis corresponds only to ISRF errors due to PSF variation accounting for optical aberration and the spectrograph pupil intensity distribution. The results for the figures of merit are shown in Fig. 7. The more distorted FF with respect to the intensity peak-to-valley amplitude variation of the short fiber directly leads to larger errors in the ISRF compared to the long fibre. The maximum ISRF shape error for the short fibre is \(2.8\%\) (see Fig. 7a) compared to \(0.78\%\) (Fig. 7b) for the long fibre. The result for the short fibre exceeds the ISRF shape requirement by almost a factor of 2. Relative to the requirements, the centroid shift for the short fibre is mainly affected in the SWIR-1 channel. It has a spectral shift of \(2.95\text { pm}\) which corresponds to \(59\%\) of the global centroid stability budget. The long fibre has the largest error contributor in the NIR with \(28\%\) of the overall budget corresponding to a centroid shift of \(0.56\text { pm}\). Note that the associated shape and centroid errors are only caused by the FF variations and neglect heterogeneity in the NF. The NF errors, as characterized (for the long fibre) in chapter 3.2, would contribute to the total error in addition to the FF errors.

In general, the impact of the spectrograph pupil intensity is directly linked to the aberrations in the specific instrument. Therefore, it is not possible to generally quantify the impact on the ISRF. However, our results suggest that shorter fibres cause larger FF variations than longer fibres, resulting in a significant increase in ISRF errors. Since the FF errors of the long fibre also account for \(50\%\) of the total ISRF shape error budget, we explored a way to homogenize the FF.

Fig. 7
figure 7

Impact of the modified spectrograph illumination on the ISRF merit functions. The presented errors compare the difference of the ISRF shape and centroid for the measured long and short fibre FFs, with either a dip (squares) or a peak (circles) in the centre, to a homogeneous FF. The FF intensity maps serve as an input of the Airbus CodeV model for three spatial field points (ACT) and three spectral samples in each spectral channel (NIR, SWIR-1, SWIR-2). The three ACT and ALT field points are positioned at the edges and center of the respective FPA. FP1 corresponds to a left edge-, FP2 to a center- and FP3 to a right-edge field point of the FPA. a Depicts the ISRF shape error for the long fibre, b the ISRF shape error for the short fibre, c the ISRF centroid shift for the long fibre and d the ISRF centroid shift for the short fibre

Full size image

To do so, we investigated a technique to induce appropriate mechanical stress on the fibre. This is done by applying small bending radii of the fibre in a sinusoidal shape and thereby stimulate the mode-to-mode coupling of the light propagating in the fibre. The initially finite number of traversing modes within the multi-mode fibre get rearranged into a more evenly distributed population of the possible propagation modes (see Fig. 8a). The result is a stronger decorrelation of the fibre output, in particular of the FF, from fibre input illuminations. Figure 8b shows the fibre input illumination and Fig. 8c the resulting FF intensity distribution for the \(100\text { cm}\) fibre. Compared to the previously observed strong variations, the FF is homogeneous and therefore independent of the fibre input. Hence, the spectrograph pupil illumination is stable also for heterogeneous scenes and does not affect the ISRF stability. The remaining ISRF errors after propagation by the aberration model are found to be negligible.

Fig. 8
figure 8

a Fibre bending scheme. The fibre is arranged in a sinusoidal shape with bending applied in the vertical and horizontal plane. b Fibre input illumination and c the corresponding fibre output FF intensity distribution after applying fibre bending. Measurements are shown as examples in the NIR, but were verified by measurements in the SWIR

Full size image

In conclusion, a sufficiently long fibre for a 2DSH is a necessary condition for efficiently homogenizing the fibre NF output. Further, it is essential to stimulate the mode-to-mode coupling inside the fibre to retrieve a homogeneous FF output. We investigated and tested a method to recover the FF homogeneity of the long fibre by applying appropriate stress on the fibre by means of small bending radii. For practical reasons this is only possible for sufficiently long fibres.

4 Focal ratio degradation (FRD)

Another important property of a fibre is the conservation of system F# as it is, depending on the sizing of the collimator optics, a significant contributor to the optical transmission through the instrument and hence to the system’s signal to noise ratio. The so-called focal ratio degradation (FRD) is an unavoidable effect in optical multimode fibres and describes the change between the input and output F# of the light cone entering the fibres. The schematic principle is depicted in Fig. 9. The causes for this effect have not yet been fully understood. Candidates are imperfections of the fibre material, quality of the fibre end facet, microscopic deformations of the core shape, stress inside the fibre and micro- and macro bending of the fibre [3, 8, 11]. All these effects eventually trigger physical processes such as scattering, diffraction and modal diffusion of the light, which alter the output cone of the light exiting the fibre [15]. FRD has been extensively studied in on-ground spectrograph fibre links. The amplitude of the F# degradation depends on the working F# of the light input cone into the fibre. In general, faster F# are reported to show better FRD performance [3, 32].

Fig. 9
figure 9

Focal ratio degradation (FRD) effect in optical multimode fibres. The input F# gets degraded by scattering effects inside the fibre

Full size image

We tested the FRD losses for a circular F/3.28 telescope pupil. In the Airbus CO2M A/B1 instrument design, the telescope pupil is oversized and the radiometric stop of the system is located on the spectrograph pupil plane. Therefore, to assess the impact of the FRD on the radiometry, we have to compare the flux collected by the spectrograph pupil without and with FRD. The ratio between these two fluxes is defined as the FRD loss in this paper. Figure 10 shows a typical FF illumination after the fibre for a homogeneous input scene with a F/3.28 telescope. The blue circle depicts the telescope pupil projected on the FF image without FRD. The red circle corresponds to F/2.28 and is used for an overall flux summation exiting the fibre (\(F_\mathrm{sum} \#\)); it accounts for all possible FRD effects. The black rectangular shape with cut corners is the baseline for the spectrometer pupil aperture in our model. The FRD is computed as follows: we sum the intensities of all pixels inside the red circle which gives the total signal collected in the FF (see Fig. 10). Without any FRD effects, the total intensity would be uniformly spread within the telescope pupil (blue circle). This homogeneous illumination would then be cut out by the spectrograph pupil (black shape) and represents the case of a classical slit. We quantify the FRD losses as the ratio between the pixel intensities in the black area assuming a homogeneous intensity distribution in the FF and the measured distribution.

We determined the FRD losses for the above-described approach in the NIR and SWIR-1 wavelength band. Mechanical stress also is known to increase the magnitude of FRD losses. Therefore, we tested different stress cases on the \(100\ cm\) fibre. We observed major FRD contribution by the used mount of the fibre front and end facet. Our test scenarios are fibres attached with mechanical clamping mounts, a bended configuration for the FF homogeneity stability and fibres glued on a glass substrate (2DSH-bundle, two separate fibre-cores tested).

We measured FRD losses in the range of 2.1–\(8.8\%\). The glued fibres of the 2DSH-bundle had the best FRD performance. Besides the gentle mounting, another reason for the superior performance could be the separate polishing and termination processes, which might have been more thorough in the 2DSH bundle pre-development. Both possibilities are in line with the findings by Allington-Smith et al. [1], where the authors associate the primary generation of FRD to the fibre-ends configuration. They conclude, that minimized physical perturbations of the fibre-end improve the FRD performance. According to our measurements, applied stress by bending in the middle parts of the fibre link seems to have limited impact on the FRD and therefore seems feasible in terms of radiometric losses. Despite several efforts to characterize FRD dependency on wavelength in theoretical models as well as in experiments, the issues remains open as several findings are inconsistent. A theoretical modal diffusion model by Gloge [12] predicts FRD increasing with longer wavelength, which was confirmed by experimental studies from Carrasco and Parry [7] and Poppett and Allington-Smith [26]. Other studies conducted by Murphy et al. [22], Schmoll et al. [28] and Crause et al. [8] found no measurable wavelength dependency. Note that all of those studies were performed at UV-Vis and NIR wavelength regimes. In our measurements, we found no convincing evidence for wavelength dependency between FRD in the NIR (\(780\text { nm}\)) and SWIR (\(1550\text { nm}\)) wavelength channel. Table (1) summarizes our FRD results. We stress, that they are linked to the spectrograph pupil stop shape of our model and the F# of the system.

In this study, we did not investigate the effect of the fibre length on FRD losses. While theoretical prediction models again suggest an increase of FRD losses with fibre lengths [12], several experimental studies have disproved this. Avila et al. [4] and Poppett and Allington-Smith [27] found no evidence for increasing FRD of longer fibres and conclude that within the experimental uncertainty, no length dependence is observed. If there is a dependency, it is a small one, which is especially the case for relatively short fibres as proposed for the 2DSH in space-borne imaging spectrometers.

Fig. 10
figure 10

Typical fibre output in the FF for a homogeneous input in the NIR with a circular F/3.28 telescope pupil. The black rectangle with rounded corners indicates the spectrograph pupil baseline of our model. The blue circle is the telescope pupil corresponding to F/3.28 (\(F_\mathrm{tel}\#\)). The larger red circle (\(F_\mathrm{sum}\#\)) is the summation area to take possible FRD broadening into account (F/2.28)

Full size image
Table 1 Radiometric losses due to FRD for a 100 cm long fibre in several mount and stress conditions
Full size table

5 Conclusion

The presented study continues the development of next-generation slit homogenizer designs for spatially and spectrally high-resolution space-based imaging spectrometers. While previous concepts consist of a 1D mirror-based solution, as employed on-board the Sentinel-5/UVNS spectrometer, we investigated a 2D-slit homogenizer design which is based on rectangular core multimode-fibres. Entrance slits based on wave-guides were shown to be an effective design solution for the prospective European CO2M mission, and to meet its demanding co-registration requirements as well as ISRF stability under extreme spatial variations in the Earth scene radiances. We investigated the NF and FF scrambling performance of the 2DSH for \(5\text { cm}\) and \(100\text { cm}\) long fibres under the condition of high contrast Earth scenes in the ALT and ACT direction. Further, we translated the resulting slit homogenization and spectrograph pupil modification into ISRF shape and centroid error, which translate into errors in terms of retrieved greenhouse gas concentration. Furthermore, we tested the radiometric transmission losses due to FRD effects in multimode-fibres for a specific CO2M phase A/B1 instrument design.

Our work suggests that the fibre length is a crucial parameter for the power exchange among guided modes and therefore for the fibre homogenization efficiency. The short fibre of \(5\text { cm}\) length preserves the contrast of the input illumination pattern injected into the fibre-entrance as a prominent gradient in the output intensity distribution. The slope of the gradient is directly correlated to the position of the input illumination of the fibre. In contrast, the long fibre shows strongly enhanced scrambling performance. The mode coupling mechanisms evolve stronger for longer fibres and therefore increase the homogeneity after the fibre. Under the extreme case of \(20\%\) partial fibre illumination, the maximum uncertainty for the long fibre in the ISRF shape is \(<0.5\%\). For the centroid position, we measured a maximum spectral drift of \(<0.25\text { pm}\) (NIR).

Contrary to classical slits, a fibre-fed slit induces scene-dependent spectrograph pupil illuminations. Together with geometrical optical aberrations present in the spectrograph, this leads to another source of ISRF instability, besides the slit illumination. Depending on the strength and type of aberrations, the error can significantly contribute to the global ISRF stability budget. For the aberrations present in our spectrometer design, we quantify the ISRF shape error induced by the modified spectrograph pupil intensity distribution as \(2.8\%\) for the short fibre and \(0.77\%\) for the long fibre (requirement: \(1.5\%\)). The centroid error for the short fibre corresponds to \(59\%\) of the overall error budget (\(2.95\text { pm}\) shift in SWIR-1, requirement: \(5\text { pm}\)) and \(28\%\) for the long fibre (\(0.56\text { pm}\) shift in NIR, requirement: \(2\text { pm}\)). These results again highlight the poorer scrambling performance of the short fibre. In our specific instrument design, the short fibre does not provide the required performance to meet the system requirements. Since also the long fibre FF distortions create significant ISRF errors, accounting for almost half of the global error budget, we propose a solution to recover the FF uniformity by inducing appropriate stress through bending of the fibre. By doing so, the traversing modes within the fibre get rearranged into a more evenly distributed population of the propagation modes, resulting in a homogenized NF and FF.

Even though the 2DSH has unprecedented homogenizing capabilities, a drawback is that the \(F\#\) exiting the fibre is decreased compared to the initially injected telescope \(F\#\). The transmission loss caused by this effect affects the radiometric performance in terms of SNR, but may also be compensated by appropriate sizing of the spectrometer optics. We quantify the transmission loss for our model of the CO2M phase A/B1 study ranging from 2 to 9\(\%\). We observed a strong dependency of the fibre end-facet mounting scheme on the FRD losses. Gently gluing the fibre onto a glass-substrate using special adhesives and thorough fibre polishing minimizes the stress on the fibre and yields the best performance. The bending of the fibre in order to homogenize the FF seems to have a limited impact on the FRD losses and therefore seems appropriate.

Our results indicate, that under extreme heterogeneity in the Earth scene radiances the 2DSH scrambling performance is superior compared to previous slit designs. In light of its other advantages, such as nearly perfect co-registration due to the cladding induced blind gaps between adjacent spatial samples, we conclude that the presented slit design offers an adequate solution for future space-based imaging spectrometers to solve the issues caused by heterogeneous Earth scenes on the instrument spectral accuracy.