1 Introduction

Many satellites operate in low-Earth orbit, providing communication services and Earth observation data to support a wide range of applications related to the atmosphere, weather, oceans, climate change, cryosphere and land surfaces. With the advance of small, low-cost satellites, space applications have become commercially interesting to companies such as SpaceX and Amazon, who are planning to launch large constellations of nanosatellites. As a consequence, the number of objects in low-Earth orbit will increase drastically in the coming years, increasing the risk of collisions. Accurate orbit predictions are necessary to detect the risk of collisions and plan evasive maneuvers with sufficient advance warning time. A significant source of uncertainty for orbit predictions is drag caused by the residual atmospheric gases in the thermosphere, which is the layer of Earth’s atmosphere that stretches from an altitude of 100 km to approximately 600 km. The thermosphere is a highly variable system, which is driven to a large extend by solar extreme ultraviolet emissions and the interaction of the solar wind with Earth’s magnetosphere [12]. Accurate observations of thermospheric mass density are needed to improve models of the thermosphere and our ability to predict orbits, with applications in mission planning, lifetime prediction, collision risk assessment, and planning of collision avoidance maneuvers.

The objective of the Cold Atom Space PAyload Atmospheric Drag Mission (CASPA-ADM) study is to develop a mission concept for observing thermospheric mass density with an accelerometer based on Cold Atom Interferometry (CAI) as a technology demonstrator. CAI technology has undergone rapid development in recent years and experimental systems have been flown on the International Space Station [1] and in sounding rockets [4] for CAI research purposes. Despite this, CAI has not yet been used as the fundamental sensor technology in a science mission, so CASPA-ADM would be a significant advancement. CAI relies on cooling a vapor of atoms in a vacuum chamber close to absolute zero temperature using lasers [51] and using the properties of the atoms to form a matter-wave interferometer that is extremely sensitive to accelerations. The CAI accelerometer is an evolution of the concept described by Devani et al. [9]. This demonstrated cold atom cooling of Rubidium atoms in a 6U CubeSat form factor in a miniaturized and ruggedized package. Using this as a basis, the instrument will be upgraded to add the additional functionality required to cool the atoms further and perform the accelerometer interferometry sequence.

CAI accelerometers rely on the physical properties of atomic transitions, which has the advantage that the acceleration measurements are not affected by biases or scale factors as opposed to classical accelerometers. This is a key difference to previous space accelerometers that all rely on the electrostatic principle and require calibration, which is typically performed using GPS receiver data [40, 45, 48]. Since 2000, a number of satellites were launched with electrostatic accelerometers and GPS receivers as part of the scientific payload, namely, the CHAllenging Minisatellite Payload (CHAMP) satellite [38], the Gravity Recovery And Climate Experiment (GRACE) satellites [41], the Gravity field and steady-state Ocean Circulation Explorer (GOCE) satellite [14], the Swarm satellites [33], and the GRACE Follow-on (GRACE-FO) satellites [19]. However, all of these were designed primarily for a different purpose. In fact, except for the Swarm mission, observing mass density was not foreseen as a mission objective. It is therefore not surprising that neither the scientific payload nor the orbits were optimized for observing thermosphere density.

In this paper, we provide an overview of the CASPA-ADM mission concept in Sect. 2, followed by the orbit selection in Sect. 3. The CAI accelerometer measurements and the method to derive thermosphere density observations are described in Sects. 4 and 5, respectively. The operational concept and the needed on-ground characterization of the satellite are outlined in Sects. 6 and 7, respectively. Finally, we summarize the paper in Sect. 8.

2 Mission concept and objectives

The technology demonstration of a CAI accelerometer was the most important aspect in the study, which therefore aimed at developing a mission concept, in which the CAI acceleration measurements play a central role. It was important to avoid being overly demanding in terms of instrument performance, so that the instrument design would remain as simple as possible and the mission concept feasible. Observing thermosphere density was quickly identified as the science case that would best fit into this framework.

CASPA-ADM would not be the first satellite to collect acceleration measurements that can be converted to density observations. In the 1970s, a number of satellites were flying that had accelerometers on board [12]. These were the Atmospheric Explorer missions during 1974–1977 [7] and the Castor satellite during 1975–1979 [5]. Since 2000, the CHAMP, GRACE, GOCE, Swarm and GRACE-FO satellites collect accelerometer measurements that are used to derive density observations. Only the Swarm mission listed observing thermosphere mass density as one of the mission objectives. The others are missions of opportunity since the accelerometers served a different purpose, namely, removing the effect of the non-gravitational acceleration from the other measurements (CHAMP, GRACE, GRACE-FO) or measuring gravity gradients (GOCE). Yet, all of these missions provide valuable density observations of the very sparsely sampled thermosphere.

The objective that can be addressed by CASPA-ADM is first and foremost collecting thermosphere density observations in regions that are not yet well observed by the current and past missions [6]. This drives the selection of the orbit, which will be elaborated in Sect. 3. Further, the CASPA-ADM measurements will allow aerodynamic studies to verify and improve models of gas–surface interactions based on in-situ observations. A significant step forward requires acceleration measurements with an accuracy of about 1% [24]. This can only be achieved when the acceleration measurements are supplemented with measurements of the atmospheric composition, temperature, and in-track wind. For this purpose, a mass spectrometer and a ram wind sensor are part of the scientific payload. Improved gas–surface interaction models could then be retroactively applied to the data of all missions of opportunity, which would improve all thermosphere mass density observations collected since 2000, which represent 50 + years’ worth of data taking time overlaps between missions into account. Such an accuracy boost for the existing multi-mission database will in turn be a great asset for improving empirical and physics-based thermosphere models.

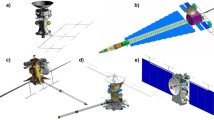
Considering the dimensions of the CAI accelerometer and that some additional space is needed for the other instruments, including the mass spectrometer and ram wind sensor, a 16U CubeSat was identified as the smallest possible satellite bus. Solar arrays with an area of 100 cm × 40 cm are needed to satisfy the CAI accelerometer’s high power demand, which necessitates a design with deployable solar arrays as illustrated in Fig. 1. To keep the satellite system as small and simple as possible, it is not equipped with a propulsion system.

Fig. 1
figure 1

Satellite shape and dimension of the CASPA-ADM satellite

Full size image

A multi-frequency GNSS receiver is added to the scientific payload, which will allow derivation of thermosphere density observations independently from the CAI accelerometer measurements [46]. This redundancy will allow validation of the CAI accelerometer measurements, albeit at low resolution along the orbit. Finally, a star sensor will enable accurate attitude measurements, from which the satellite angular velocity and angular acceleration will be derived. These are needed to correct for accelerations that arise from measuring in a rotating reference frame.

Observing atmospheric waves was added to the scientific objectives since this would require the same level of accuracy as verifying gas–surface interactions. In the following, we will discuss atmospheric waves that are expected be observable by CASPA-ADM, structuring them as in Emmert [12].

2.1 Local time migrating solar tide

The extreme and far ultraviolet irradiance of the Sun is the main heat source for the thermosphere. It produces a bulge of high density near 14–15 local time on the dayside and a trough of low density near 5 local time on the nightside. The latitude of the maximum density will migrate north- and southwards following seasonal changes of the subsolar point. In addition to the latitudinal variations of the subsolar point, the changes in the distance between the Sun and the Earth cause variations in received solar irradiance and, consequently, variations in the thermosphere density. During the mission lifetime of 8–15 months, the CASPA-ADM satellite will cover all local times at least twice, so that we obtain two samples of the largest variation in thermosphere density, potentially at similar solar activity levels, but during different seasons.

2.2 Nonmigrating tides

Nonmigrating tides are global oscillations in the atmospheric density that do not migrate with the apparent motion of the Sun. Instead, they can be described as a function of time and longitude [15]:

$$\psi_{n,s} \left( {t,\lambda } \right) = A_{n,s} \cos \left( {n\omega t + s\lambda + \phi_{n,s} } \right),$$
(1)

where \(t\) is universal time, \(\omega\) is Earth’s rotation rate, \(\lambda\) is the longitude, \({A}_{n,s}\) is the amplitude, \({\phi }_{n,s}\) is the phase, \(n\) is the subharmonic index (\(n= 0, 1, 2,\dots\)), and \(s\) is the zonal wave number (\(s= 0, \pm 1, \pm 2,\dots\)). The diurnal tide is obtained for \(n= 1\) and denoted by “D”, and the semidiurnal tide \(n= 2\) and denoted by “S”. A subharmonic index \(s<0\) represents eastward propagating tides denoted by “E”, and \(s<0\) represents westward propagating tides denoted by “W”. The final element in the notation is the zonal wave number. For example, “DE3” denotes the eastward propagating diurnal tide of zonal wavenumber \(s=3\).

The sources for nonmigrating tides are tropospheric heating, momentum and energy exchange with the magnetically constrained ionosphere, and nonlinear tide-tide interactions. The longitudinal variations in thermosphere density can reach 10% at an altitude of 400 km, which is observable by CASPA-ADM. Inclined orbits give a fast local time sampling, which is advantageous for observing tides [18]. We expect that CASPA-ADM will sample all local times at least twice within the mission lifetime. This will allow a comprehensive analysis of thermosphere density variations due nonmigrating tides, which in combination with measurements of the atmospheric composition will advance our understanding of atmospheric tides and their sources.

2.3 Equatorial density anomaly

A well-known feature of the ionosphere is equatorial ionization anomaly (EIA). It is located in the F region of the ionosphere and characterized by enhanced electron density at 15°–20° on either side of the magnetic equator on the dayside and at post-sunset local times [2]. Between the crests of enhanced electron density lies a trough of ~ 30% lower electron density. A similar feature called the equatorial mass density anomaly (EMA) is found in the thermosphere, which was noted already in CHAMP data [20]. The crests of the EMA appear at magnetic latitudes of ± 25°. Ion-neutral coupling is likely to play a role in the formation of the EMA, though their relation is not clear from an observational as well as theoretical point-of-view. The mechanisms that were proposed for the formation of the EMA include chemical heating, field-aligned ion drag, and ion drag-modified tides. Simultaneous in-situ observations of thermosphere density, ion and neutral number densities, winds, and TEC will improve the observation base and facilitate more advanced analyses of the mechanisms that are driving the formation of the EMA.

2.4 Atmospheric waves in response to geomagnetic activity

The solar wind is composed of charged particles and a frozen-in magnetic field ejected from the Sun. When the solar wind reaches the Earth, it interacts with the magnetosphere to create an electric dynamo, which generates large electric fields in the polar regions of the ionosphere. Charged particles from the solar wind and magnetotail enter the Earth's atmosphere guided along magnetic field lines to the polar regions. These enhance the conductivity of the ionosphere. Consequently, large electrical currents flow through the ionosphere resulting in Joule heating. The heated atmosphere expands and pushes denser air upwards into higher regions of the thermosphere, before breaking and creating horizontal waves that are often referred to as travelling atmospheric disturbances. This causes significant density variations within the thermosphere, in particular within the auroral region. Even though the CASPA-ADM orbit’s inclination will exclude observations at high latitudes, the travelling atmospheric disturbances will be observable as they propagate equatorward.

Strong events such as solar coronal mass ejections result in geomagnetic storms, during which the thermosphere density can enhance by several hundreds of percent for periods up to a few days, which has a significant effect on satellite orbits. Since geomagnetic storms are highly variable events, it is very challenging to estimate the total amount of energy disposition and, thus, predict their effect on the thermosphere. Observations of thermosphere density and composition will improve our understanding of geomagnetic storms and help to develop better proxies and methods for modelling and predicting the response of the thermosphere during and after such events.

2.5 Lower atmospheric waves

Atmospheric waves originating from the lower layers of the atmosphere represent the third important driver of thermosphere density variations after solar and geomagnetic activity. Such waves include travelling planetary waves, gravity waves [35, 42], and acoustic waves, which travel upward, dissipate, and generate secondary and tertiary waves until they interact with the thermosphere. Travelling planetary waves are global-scale oscillations with periods longer than one day. Depending on their wavelength and the interaction with other waves, they can penetrate into the thermosphere, where they cause density variations that range from a few percent up to ten percent. Gravity waves are generated by convection and wind-topography interaction in the troposphere [43, 44]. In addition, acoustic waves can propagate into the thermosphere. Like gravity waves, they can be caused by wind-topography interaction, but also for example by seismic activity [17]. Both gravity and acoustic waves can cause variations in thermosphere density of several percent, and therefore be observable by CASPA-ADM.

3 Orbit selection

The selection of the orbit is closely related to the objectives of collecting thermosphere density observations in regions that are not well observed and achieving a fast local time sampling. To illustrate the sampling of the thermosphere with accelerometer-derived density observations, Fig. 2 shows the distribution of the density observations from accelerometer carrying satellites since 2000 with respect to altitude and solar activity as indicated by the 81-day moving-average of the F10.7 index. All satellites were launched into an orbit with an approximate altitude of 500 km and then allowed to drift. The exception is the GOCE satellite, which is a special case since it was equipped with an ion thruster to compensate the effect of drag, allowing the satellite to fly much lower than the other satellites, though with limited local time coverage due to the sun-synchronous orbit. The figure clearly shows that most density observations were collected in the altitude range of 400–500 km. In the altitude range of 300–400 km, the observations are collected primarily during times of low solar activity. Below an altitude of 300 km are hardly any density observations except the ones of the GOCE mission, which is simply due to the fact that the large atmospheric drag at such low altitudes causes the satellites to decay extremely fast. Therefore, we identify the altitude range of 300–400 km and medium–high solar activity as an observational gap that can be addressed by CASPA-ADM.

Fig. 2
figure 2

Distribution of accelerometer-derived density observations with respect to altitude and solar activity as indicated by the 81-day moving-average of the F10.7 index. The region that is presently not well-observed is marked in blue as the region of interest for CASPA-ADM. It is compatible with a launch from the ISS

Full size image

To fill the present gap in thermosphere density observations, the local time needs to be fully sampled at least twice and preferably several times at different altitudes within the range of 300–400 km. Since the satellite will not be equipped with thrusters for orbit control, the time in which it will fly within this range of altitudes is limited. A preliminary assessment of the mission lifetime is presented in Fig. 3. We assume a circular orbit with an initial altitude of 400 km and an inclination of 51° (compatible with a launch from the ISS), the satellite shape presented in Fig. 1, average solar activity, and satellite masses of 15 kg and 25 kg to cover a wide range of configurations, noting that the design of the satellite is still likely to change during the further development of the mission concept. With these assumptions, we predict that the mission lifetime will be 8–15 months, which poses an upper limit on the inclination as explained in the following.

Fig. 3
figure 3

Orbit evolution assuming the satellite shape presented in Fig. 1 and masses of 15 kg (blue curve) and 25 kg (red curve), a circular orbit with an initial altitude of 400 km and an inclination of 51°, and average solar activity. The solid and dashed purple lines show the LTAN evolution for a satellite mass of 15 kg and 25 kg, respectively. The altitude is defined as the height above the WGS84 reference ellipsoid

Full size image

Other important features of the orbit are the inclination and the eccentricity since they relate to the time needed to sample all local times. The rate of the ascending node of the orbit is

$${\dot{\Omega }} = \frac{3}{2}\frac{{J_{2} \sqrt \mu R^{2} }}{{a^{7/2} \left( {1 - e^{2} } \right)^{2} }}\cos i,$$
(2)

where \({J}_{2}\) = 0.0010826, \(R\) = 6378 km, and \(\mu\) = 398,600.4415 km3/kg/s2 are Earth’s dynamical form factor, radius and gravitational constant, respectively, and \(a\), \(e\), and \(i\) are the semi-major axis, eccentricity and inclination of the orbit [30]. Taking into account Earth’s rotation rate of 360° per 365.25 days (0.9856°/d), the local time of the orbit’s ascending node (LTAN) progresses by \(\dot{\Omega }\) – 0.9856°/d.

The progression is illustrated in Fig. 4 for circular orbits at an altitude of 400 km. Since the CHAMP, GRACE, and GRACE-FO satellites fly in circular orbits with very high inclinations (CHAMP: 87.2°, GRACE/GRACE-FO: 89°, Swarm A/C: 87.4°, Swarm B: 88.0°), they need 4.5–6 months to cover all local times, taking into account ascending and descending tracks. Due to its sun-synchronous orbit, the GOCE satellite is in fact limited to dusk/dawn local times and therefore not shown in the figure. For applications such as observing atmospheric waves, a faster sampling of the local time would be an advantage [18], which can only be achieved with low inclinations. Choosing the inclination very low would result in very fast local time sampling, however, at the cost of limited global coverage since the inclination limits the latitudinal coverage. This trade-off between spatial and local time sampling could be overcome by launching more satellites. However, the CASPA-ADM concept is intended to be a technology demonstrator, for which a single satellite is sufficient.

Fig. 4
figure 4

LTAN progression as a function of inclination for a circular orbit at an altitude of 400 km (left). The right panel zooms in on near-polar orbits and highlights the LTAN progression of accelerometer carrying satellites

Full size image

There is no definitive preference for a specific inclination, which means that a launch opportunity is expected to decide the inclination as long as the LTAN progression is fast enough to sample all local times at least twice within the mission lifetime. Since the expected mission lifetime is at least 8 months, the LTAN progression needs to be − 360° in 4 months, i.e. − 3°/d, which sets the upper bound for the acceptable inclination range to 76°. We select 40° the lower bound for the inclination, so that the large mountain ranges such as the Andes and the Himalayans, which could generate detectable secondary and higher order gravity waves [35, 42], are covered. In the same way as for inclination, there is no definitive preference for the eccentricity, noting that the orbit will circularize over time due to the absence of a propulsion system. For simplicity, we assume an initial eccentricity of zero. It is worthwhile to note that the orbit is compatible with a launch from the ISS, which orbits a few kilometers above 400 km altitude at an inclination of 51.6°, which results in a LTAN progression of 24 h (360°) in 61 days. This orbit would provide a full local time coverage at least four times during the expected lifetime of CASPA-ADM.

An advantage of the selected inclination range, as opposed to polar inclinations, is the increased frequency of crossovers at low latitudes with the orbits of the Swarm and GRACE-FO satellites, which are flying in polar orbits and might still be in orbit at the time that CASPA-ADM is launched. In this context, we highlight that thermosphere density is much more dynamic in the polar regions compared to low latitudes [35, 42]. For a meaningful comparison of density observations from two satellites, the time difference between those satellites crossing over the same location needs to be much shorter when the crossover occurs at polar latitudes. Thus, crossovers at low latitudes would facilitate the direct inter-mission comparisons. Should there be the possibility to launch more than one CASPA-ADM satellite, then the second satellite could be launched into a polar orbit to complete the global coverage.

4 CAI accelerometer

A cold atom sensor works by allowing a cloud of cold atoms to interact with its environment over an interaction time, T. The state of the atoms is measured at the beginning and the end of the interaction time using lasers to give a measure of the environmental parameter being assessed, in this case acceleration. This is known as Cold Atom Interferometry (CAI).

Before a CAI sequence can be completed the atoms need to be cooled and constrained so that the atoms exhibit a wave like behavior, which is required for interferometry. This is done using lasers tuned close to the frequency of the atoms’ energy levels applied orthogonally in all 3 axes within a magnetic field to trap and slow the atoms until they are almost stationary. This stage of trapping and cooling is known as a magneto-optical trap (MOT). After loading the trap, the magnetic field is switched off and a short (∼10 ms) optical cooling phase, known as “molasses” or “optical molasses”, is applied to cool the atoms from ∼200 to ∼2 μK [29]. Once cooling is complete the cloud of atoms is released from the trap, and the phase of the atomic wave function, imprinted by three laser pulses, changes as it accelerates. This is a Mach–Zehnder type interferometer configuration as described for example by Wu et al. [51] and Barrett et al. [3]. The phase determines the population of atoms in two internal states at the end of the interferometer. The acceleration of the atoms relative to the laser, \({a}_{||}\), is measured by reading out these internal state populations by detecting laser-induced fluorescence. The final populations of these two states are proportional to the square of the sine and cosine of the interferometer phase \(\phi ={a}_{||}{ k}_{\mathrm{eff}} {T}^{2}\). Here, \(T\) is the duration between interferometer pulses, \({k}_{\mathrm{eff}}\approx 4\pi /\lambda\) and \(\lambda\) is the wavelength of the laser. In our model we take \(\lambda =780\) nm to match the D2 transition in rubidium.

The fundamental limit on the noise in our measurement of \({a}_{||}\) using this type of sensor has an inverse square relationship with T. In general, it is therefore desirable to maximize the available T. In low-altitude or ground applications, T is limited by the length of the free-fall (i.e. size of the instrument along the gravitational force axis) but in microgravity it is the thermal expansion of the cloud that is the limiting factor due to the size of the cloud exceeding the detection area. The thermal expansion rate of the cloud is defined by the initial temperature of the atoms; so there is therefore a drive to achieve lower initial atom temperatures.

In the case of CASPA-ADM, as the satellite must be nadir-pointing for the accelerometer to constantly point along track, it has to constantly rotate at a rate of approximately 1 mrad/s. This rotation causes a reduction in interferometer contrast that constrains the interferometer duration.

Figure 5 shows this tradeoff and the achievable sensitivity when the signal is averaged over 10 s for various atom temperatures. For this calculation an additional dead-time has been introduced at the end of the sequence to keep the average power consumption within the constraints of the platform. From these curves it can be seen that the sensitivity improves as the optimum interferometer duration is increased from zero. As T is increased further, the thermal motion of the atoms, combined with the rotation of the satellite result in a loss of sensitivity. Additionally, as described previously, colder atoms allow reduced noise and longer interferometer durations. For a 2 μK atom cloud the optimum interferometer duration is shown to be 56 ms and the mission targets can be achieved.

Fig. 5
figure 5

Quantum Projection Noise when averaged over 10 s with different temperature atoms with respect to interferometer duration (colored lines). The black dashed line marks the targeted accuracy. The blue-shaded area indicates the size of accelerations signals encountered within the altitude range of 300–400 km as listed in Table 2

Full size image

The CAI payload is a further development of the 6U CASPA CubeSat previously built by Teledyne e2v and partners and described in Devani et al. [9]. Several different concepts have been considered for the implementation of the physics package including prism MOT and atom chip concepts. Whilst not necessarily required for molasses cooling, the atom chip concept has been selected as it offers a potential route to further cooling in future programs. Basing the space suitable physics package design on an atom chip solution at this stage will retire technology risks early in the development and will reduce additional rework and requalification activity in future if lower atom temperatures are required (i.e. for enhanced sensitivity or gravity missions).

Figure 6 depicts the CAI Accelerometer Vacuum Chamber Concept which is currently under development.

Fig. 6
figure 6

CAI Accelerometer Vacuum Chamber Concept

Full size image

5 Deriving density from the CAI acceleration measurements

The aerodynamic coefficient vector \({{\varvec{C}}}_{aero}\), which combines the effects from drag and lift, relates mass density \(\rho\) to the aerodynamic acceleration vector \({{\varvec{a}}}_{aero}\) through

$${\varvec{a}}_{aero} = \frac{1}{2}\rho \frac{{A_{ref} }}{m}v_{rel}^{2} { }{\varvec{C}}_{aero} ,$$
(3)

where \({A}_{ref}\) is the reference area, \(m\) is the satellite mass, \({v}_{rel}\) is the velocity of the satellite relative to the surrounding atmosphere, i.e. the length of the velocity vector \({{\varvec{v}}}_{rel}\) [10]. Equation (3) demonstrates that all mass density observations derived from acceleration measurements depend directly on the aerodynamic coefficient. Any error in the aerodynamic coefficient will result in a wrong scale of the mass density observations and, consequently, thermosphere models that are derived from those observations. Since this has implications for applications such as orbit prediction, it is important that the aerodynamic coefficient is modelled accurately. This is a challenging task because the aerodynamic coefficient is a function of the satellite shape and size, the atmospheric composition and temperature, and the gas–surface interaction (GSI) model. The latter describes the exchange of energy and momentum of incident gas particles with the satellite surface. Several GSI models are discussed in the literature and the subject is still debated despite of extensive research. We summarize in the following key elements and assumptions of GSI models, based on the excellent reviews presented by [31] and [49], and the references therein. Since the altitude range of interest is 300–400 km, a good approximation of physical reality is fully diffuse reflections of the incident atoms and molecules with an incomplete accommodation of their temperature to the wall temperature of the satellite.

The aerodynamic acceleration \({{\varvec{a}}}_{aero}\) is part of the non-gravitational acceleration \({{\varvec{a}}}_{ng}\) experienced by the satellite:

$${\varvec{a}}_{ng} = {\varvec{a}}_{aero} + {\varvec{a}}_{rp} ,$$
(4)

where \({{\varvec{a}}}_{rp}\) represents the sum of all accelerations due to radiation pressure, i.e. solar radiation pressure, Earth albedo radiation pressure, Earth infrared radiation pressure, and the satellite’s infrared emission radiation pressure. The drag acceleration \({a}_{drag}\) is defined to be the aerodynamic acceleration projected onto the direction of the relative velocity:

$$a_{drag} \mathop = \limits^{{{\text{def}}}} {\varvec{a}}_{aero} \cdot \frac{{{\varvec{v}}_{rel} }}{{v_{rel} }} = \frac{1}{2}\rho \frac{{A_{ref} }}{m}v_{rel}^{2} {\varvec{C}}_{aero} \cdot \frac{{{\varvec{v}}_{rel} }}{{v_{rel} }}.$$
(5)

Note that the dot (\(\bullet\)) denotes the dot product. The drag coefficient \({C}_{D}\) is related to the aerodynamic coefficient by

$$C_{D} = {\varvec{C}}_{aero} \cdot \frac{{{\varvec{v}}_{rel} }}{{v_{rel} }}.$$
(6)

The CAI accelerometer will measure the acceleration \({a}_{CAI}\) along the axis defined by the laser that interferes with the atom cloud, which generally does not agree with the direction of the relative velocity vector. Thus, the density cannot be inferred from Eq. (5). Instead, we infer the density from

$$a_{CAI} = {\varvec{a}}_{aero} \cdot {\varvec{u}}_{CAI} = \frac{1}{2}\rho \frac{{A_{ref} }}{m}v_{rel}^{2} {\varvec{C}}_{aero} \cdot {\varvec{u}}_{CAI} ,$$
(7)

where \({{\varvec{u}}}_{CAI}\) is a unit vector parallel to the laser beam of the CAI. Thus, the direction of the laser beam with respect to the satellite needs to be known. Assuming that \({{\varvec{a}}}_{aero}\) is independent of the measurement direction, a pointing error of 2.5° in \({{\varvec{u}}}_{CAI}\) changes \({a}_{CAI}\) by 0.1%. In reality \({{\varvec{a}}}_{aero}\) will depend on the measurement direction. Nevertheless, since we strive for a measurement accuracy of 1% of the signal, we may conclude from this simple consideration that the direction of the laser beam needs to be known with an accuracy of a few degrees.

5.1 Signal range of CAI accelerometer

The satellite size and shape illustrated in Fig. 1 was translated into a panel model of the satellite for the purpose of assessing first the aerodynamic coefficient and then the dynamic range of the acceleration signal. The cross section exposed to the incoming flow of atmospheric particles has an area of 0.04 m2, plus a small contribution from the deployable solar arrays, for which we assume a thickness of 1 cm. Obviously, the cross-sectional area increases when the sideslip and attack angles are not zero, i.e. when the flight direction is not perfectly aligned with direction of the relative velocity with respect to the surrounding atmosphere. This will give larger drag coefficients, which is taken into account in the calculations using Sentman’s equations [39] and the panel model specified in Table 1.

Table 1 Panel model used for the calculation of the drag coefficient
Full size table

The drag coefficient for a reference area of 1 m2 is reported as a function of the sideslip and attack angles in Fig. 7. It is approximately 0.18 for small attack and sideslip angles. Larger drag coefficients are not necessarily bad because they will increase the signal for the CAI accelerometer. The signal ranges for the CAI accelerometer, are inferred from the density calculated from the NRLMSISE-00 model [36] along two circular orbits with an altitude of 300 km and 409 km, both with an inclination of 51°. These two altitudes are the boundaries of the altitude range of interest identified in Sect. 3. We consider the solar activity in January 2002, 2004, and 2009 as representative cases for solar maximum, mean, and minimum conditions. We use the value of 0.18 for the satellite’s drag coefficient and assume a satellite mass of 25 kg. It should be emphasized that the satellite mass is not well-known at this stage of the development and that any change of the satellite mass will result in corresponding change of the signal ranges for the CAI accelerometer. The resulting signal ranges are presented in Table 2. First of all, we notice that the signal at 300 km altitude is a few μm/s2, which always gives an interferometer phase \(\phi <\pi\), for the considered interrogation times. This means there is no ambiguity in interpreting the interferometer signal.Footnote 1 Thus, a tracking of cycles is considered to be not necessary for deriving the acceleration from the phase measurement. At the altitude of 409 km, the acceleration signal reduces to 0.03–0.23 μm/s2, which is just above the CAI accelerometer noise level of 0.02 μm/s2. In solar minimum, it will therefore not be possible to achieve the desired accuracy of 1% from the beginning of the mission, but only once the satellite has descended to lower altitudes. However, the acceleration signal is much stronger during solar maximum. There, the acceleration signal is in the range of 0.61–2.38 μm/s2, which enables to reach the accuracy of 1% almost from the beginning of the mission. For solar medium activity, the acceleration signal is 0.12–0.71 μm/s2, which enables an accuracy of at least 10% from the beginning of the mission. This is an additional motivation to launch during medium to high solar activity and we conclude that the minimum acceptable F10.7 index at the time of launch is 110 sfu (solar flux units).

Fig. 7
figure 7

Drag coefficients multiplied with cross section area (CD × A) for the satellite shape and size presented in Fig. 1 as function of sideslip and attack angles

Full size image
Table 2 Ranges of the acceleration signal within one orbital revolution.
Full size table

5.2 Corrections for rotational and gravity gradient effects

An accelerometer on board of a satellite takes measurement in a reference frame that is typically rotating. In such a case, the acceleration measured in the rotating reference frame \({{\varvec{a}}}_{r}\) is related to the inertial acceleration \({{\varvec{a}}}_{i}\) by

$${\varvec{a}}_{r} = - {\varvec{Vr}} +{\varvec{\Omega}}^{2} {\varvec{r}} + \varvec{\dot{\Omega }r} + \varvec{\Omega \dot{r}} + {\varvec{a}}_{i} ,$$
(8)

where \({\varvec{r}}\) is the vector from the satellite centre of mass to the centre of the proof mass of the accelerometer, \({\varvec{V}}\) is the gravity gradient tensor, \(\varvec{\Omega }\) is the angular velocity tensor. The vector \(\dot{{\varvec{r}}}\) and the tensor \(\dot{\varvec{\Omega }}\) are the first time derivative of vector \({\varvec{r}}\) and tensor \(\varvec{\Omega }\), respectively. It should be emphasized that \(\dot{\Omega }\) in Eq. (2) has a completely different meaning than \(\dot{\varvec{\Omega }}\) in Eq. (8). The terms \({\varvec{\Omega }}^{2}{\varvec{r}}\), \(\dot{\varvec{\Omega }}{\varvec{r}}\), and \(\varvec{\Omega }\dot{{\varvec{r}}}\) represent the centrifugal, Euler, and Coriolis acceleration, respectively. The first three terms on the right-hand side of Eq. (8) scale with vector \({\varvec{r}}\), which can have a length of a few centimetres since it is expected that it will not be possible to accommodate the CAI accelerometer such that the atom cloud is in the satellite center of mass. On the other hand, the length of vector \({\varvec{r}}\) is limited by the dimension of the 16U CubeSat. A simulation with realistic attitude dynamics indicated that a star sensor with an accuracy of 50 arc seconds would be sufficient to correct for the centrifugal, Euler, and gravity gradient accelerations. The Coriolis acceleration cannot be corrected for because it is linked to the velocity \(\dot{{\varvec{r}}}\), which is partly caused by the random thermal motion of the atoms. Thus, this term simply contributes to the noise in the CAI accelerometer measurements and can only be counteracted by either reducing the satellite angular velocity or cooling the atoms to a lower temperature to reduce their thermal motion.

5.3 Required accuracy for atmospheric composition and temperature observations

The aerodynamic coefficient vector in Eq. (3) depends in a non-linear way on the atmospheric composition and temperature. For all missions of opportunity we rely on thermosphere models to provide this information, which presents a significant error source for the thermosphere density observations. CASPA-ADM will therefore be equipped with a mass spectrometer to replace the model by observations. In this section, we identify acceptable error levels for the observations of atmospheric composition and temperature.

Since thermosphere density observations derived from acceleration measurements depend in a non-linear way on atmospheric composition and temperature, we use a Monte Carlo simulation to investigate how composition and temperature errors affect thermosphere density observations. Let \({\rho }_{j}\) denote the mass density of the atmospheric species indicated by subscript \(j\), e.g., diatomic Nitrogen (N2). We assume that the mass density observations:

$$\rho_{j,n}^{obs} = \rho_{j}^{true} + \rho_{j,n}^{err}$$
(9)

compose of the true values \({\rho }_{j}^{true}\) and the errors \({\rho }_{j,n}^{err}\), where subscript \(n\) indicates the sample in the Monte Carlo simulation. Further, we assume that the errors are proportional to the signal, which we achieve by selecting

$$\rho_{j,n}^{err} = f_{j,n} \rho_{n}^{true} ,$$
(10)

where the factors

$$f_{j,n} \sim N\left( {\mu_{j} , \sigma_{j}^{2} } \right)$$
(11)

are Gaussian (normal) distributed random numbers with mean \({\mu }_{j}\) and variance \({\sigma }_{j}^{2}.\) In the same way, we assume that the temperature observations

$$T_{n}^{obs} = T^{true} + T_{n}^{err}$$
(12)

compose of the true value \({T}^{true}\) and the errors \({T}_{n}^{err}\), and that the latter is proportional to the signal, that is

$$T_{n}^{err} = f_{T,n} T^{true} ,$$
(13)

where the factors \({f}_{T,n}\) follow the Gaussian distribution:

$$f_{T,n} \sim N\left( {\mu_{T} , \sigma_{T}^{2} } \right).$$
(14)

Information on the accuracy of present-day space mass spectrometers is sparse, possibly due to the fact that the last of these instruments was successfully flown nearly four decades ago [34]. The situation might change in the near future, as miniaturized mass spectrometers will be launched on the Satellite for Orbital Aerodynamics Research (SOAR) satellite [8] and the two Coordinated Ionospheric.

Reconstruction CubeSat Experiment (CIRCE) satellites [32]. For CASPA-ADM we preliminary selected the same mass spectrometer as for the SOAR and CIRCE satellites.

In our simulation, we assume that the mass spectrometer observations are free of any bias, i.e. \({\mu }_{j}=0\) and \({\mu }_{T}=0\). Further, we select the accuracy of the mass density and temperature observations as 10% and 3% of the signal, respectively, i.e. \({\sigma }_{j}^{2}={0.1}^{2}\) and \({\sigma }_{T}^{2}={0.03}^{2}.\) These values were found by trial and error and represent acceptable error levels, which we will learn in the following. We generate 1000 samples for solar minimum and maximum conditions at altitudes of 300 km and 400 km to cover all extremes within the target altitude range. For each sample, the thermosphere density observations are calculated using the equations presented in Sect. 5 and Doornbos [10], where all quantities are assumed to be free of errors except atmospheric composition and temperature. For the satellite geometry, we use the panel model in Table 1. The true thermosphere is represented by the NRLMSISE-00 model and the true observations are generated along an orbit with an inclination of 51°. Further, we select a constant value of 0.9 for the energy accommodation coefficient and a satellite wall temperature of 400 K, noting that these values are well within the plausible range [10, 23, 25, 37]. To better understand the effect of the errors in the atmospheric composition of the individual species and the temperature, we also consider each error \({\rho }_{j,n}^{err}\) and \({T}_{n}^{err}\) separately, e.g. \({\rho }_{1,n}^{err}\ne 0\) and \({\rho }_{2,n}^{err}={\rho }_{3,n}^{err}=\dots ={T}_{n}^{err}=0\). The results are presented in Fig. 8, which shows the RMS of the thermosphere density observations as a percentage of the signal as defined by

$$RMS_{\rho ,rel} = \frac{1}{{\rho^{true} }}\sqrt {\frac{1}{N}\mathop \sum \limits_{n = 1}^{N} \left( {\rho^{true} - \rho^{obs} } \right)^{2} .}$$
(15)
Fig. 8
figure 8

Impact of the accuracy of number density and temperature measurements on the mass density observations

Full size image

The percentage in the legend in the brackets behind the symbol of the atmospheric species shows the species’ mean mass concentration and the mean temperature, respectively. In solar maximum conditions at an altitude of 400 km for instance (top left panel), Helium contributes only 0.4% to the thermospheric mass, whereas Oxygen and diatomic Nitrogen contribute 83.9% and 13.7%, respectively. Generally, Oxygen has with 68.6–89.9% by far the largest concentration in the altitude range of 300–400 km, followed by diatomic Nitrogen. In solar minimum conditions at 400 km altitude, the concentration of Helium becomes appreciable with a concentration of 4.7%. This is due to the low temperature, which causes the thermosphere to contract and thereby brings the more light-weight atoms to somewhat lower altitudes. We can also see that the thermosphere temperature in solar maximum conditions is about 500 K hotter than in solar minimum conditions, whereas the difference in altitude of 100 km does not cause a significant difference in temperature.

When inspecting Fig. 8, we first notice that the RMS of the total density errors (black curves) stays well below 1% for all cases, except for solar minimum at 400 km altitude. For the latter, the total density error reaches a maximum of 1.2%. Considering that CASPA-ADM targets medium to high solar activity, we may conclude that 10% errors in composition and 3% errors in temperature are acceptable. For the individual error contributions (colored curves), we see that the temperature errors have the largest influence on the RMS of the density errors (dark red curves), which are about 0.6%. The next largest error source is the composition error of Oxygen, which ranges from 0.2 to 0.8% depending on the solar activity and altitude. The influence of the composition errors of diatomic Nitrogen is at the same level than that of Oxygen, except for solar minimum conditions at 400 km. For the latter, the influence of the composition errors of Helium is almost at the same level than that of Oxygen. Thus, the composition measurement of Helium is important at an altitude of 400 km in solar minimum conditions. The influence of composition errors of the other atoms and molecules appears to be negligible compared to that of Oxygen, diatomic Nitrogen and Helium. This conclusion may change, however, for the re-entry of CASPA-ADM, where we expect that the influence of atoms and molecules with a larger molar mass increases in importance.

5.4 Required accuracy for in-track wind observations and attitude control of the satellite

Another point of attention is the influence of wind on the density observation. Wind could change the magnitude of the relative velocity vector in the Eq. (7) and therefore contributes to the total error of the density observations. The relative velocity vector:

$${\varvec{v}}_{rel} = {\varvec{v}}_{sat} + {\varvec{v}}_{co - rot} + {\varvec{v}}_{wind} ,$$
(16)

composes of the inertial satellite velocity \({{\varvec{v}}}_{sat}\), the velocity \({{\varvec{v}}}_{co-rot}\) of the atmosphere that is co-rotating with Earth, and the velocity \({{\varvec{v}}}_{wind}\) of the thermospheric wind. The satellite velocity is well-determined by the GNSS measurements and the velocity of the co-rotating atmosphere is also accurately known. Therefore, the velocity of the wind represents the largest source of uncertainty. In the following, we will derive the requirements for the accuracy of in-track wind measurements and the attitude control of the satellite. The latter defines the pointing of the wind sensor and, hence, the direction in which the wind is measured.

To study the influence of wind on the magnitude of the relative velocity vector, and hence the density observations, we introduce the error vector \({{\varvec{v}}}_{err}\) in Eq. (16) to obtain the erroneous relative wind vector:

$${\varvec{v}}_{rel,err} = {\varvec{v}}_{rel} + {\varvec{v}}_{err} .$$
(17)

For the squared magnitude, we find

$$v_{rel,err}^{2} = v_{rel}^{2} + 2\user2{ v}_{rel} \cdot {\varvec{v}}_{err} + v_{err}^{2} = v_{rel}^{2} \left( {1 + 2\cos \gamma \frac{{v_{err} }}{{\user2{ }v_{rel} }} + \frac{{v_{err}^{2} }}{{v_{rel}^{2} }}} \right),$$
(18)

where \(\gamma\) is the angle between the vectors \({{\varvec{v}}}_{rel}\) and \({{\varvec{v}}}_{err}\). Considering that winds have a velocity of a few hundreds of m/s and that the relative velocity is on the order of 7.7 km/s due to the satellite velocity, it is reasonable to assume that the error vector is more than ten times smaller than the relative velocity vector. Thus, the term \({v}_{err}^{2}/{v}_{rel}^{2}\) will change \({v}_{rel}^{2}\) by less than 1% and may therefore be neglected, which leaves

$$2\cos \gamma \frac{{v_{err} }}{{\user2{ }v_{rel} }}$$
(19)

as the main error term. Since the term is proportional to \(\mathrm{cos}\gamma\), only the part of the error vector projected onto the direction of the relative velocity vector \({{\varvec{v}}}_{rel}\) contributes to a change in the squared magnitude \({v}_{rel,err}^{2}\) of the relative velocity vector. Consequently, this part has to be accounted for by either using a wind model or measuring the wind velocity into that direction.

Should a wind sensor be used for measuring wind, it needs to point into the direction of the relative velocity vector as discussed in Sect. 5. In case of perfect pointing, Eq. (19) reduces to \(2{v}_{err}/{\boldsymbol{ }v}_{rel}\) since \(\mathrm{cos}\gamma =1\). Assuming a typically value of 7.7 km/s for the relative velocity \({v}_{rel}\), we find that the acceptable error \({v}_{err}\) in the wind measurement is about 40 m because this limits the term \(2{v}_{err}/{\boldsymbol{ }v}_{rel}\) to 0.01, which is equivalent to errors of 1% in the density observations.

In case the wind sensor deviates from that direction by a small angle \(\Delta \alpha\), the wind measurement will change by \(\Delta \alpha {v}_{wind}\mathrm{sin}\alpha\) as illustrated in Fig. 9, where \({v}_{wind}\) is the magnitude of the wind vector and \(\alpha\) is the angle between the relative velocity vector and the wind vector. This can be interpreted as changing the wind measurement by the fraction \(\Delta \alpha\) of the part of the wind vector that is perpendicular to the direction of the relative velocity.

Fig. 9
figure 9

Change of the wind measurement due to mispointing the wind sensor by a small angle \(\Delta \boldsymbol{\alpha }\)

Full size image

In the worst case, the wind direction is perpendicular to the relative velocity vector, i.e.\(\alpha =90^\circ\), which results in \(\mathrm{sin}\alpha =1\). Then, a small angle \(\Delta \alpha =12^\circ =0.2 rad\) would result in an error of 20% of the magnitude of the wind vector. When assuming that the magnitude of the wind vector is 350 m/s, which is within the expected range of wind speeds [11], a 20% error in the wind measurement would be \({v}_{err}=70 m/s\). Entering this into Eq. (3) results in errors of less than 1% in the squared magnitude of the relative velocity vector. Thus, a pointing error of 12° seems acceptable for the wind measurement, which represents the most stringent requirement for the attitude control of CASPA-ADM.

5.5 Verification of aerodynamic modelling and gas–surface interactions

Excellent and extensive reviews of aerodynamic modelling and gas–surface interaction models are presented by Mehta et al. [27], Mostaza Prieto et al. [31], and Livadiotti et al. [21]. While the verification of aerodynamic modelling and gas–surface interactions using CASPA-ADM data needs to be studied in more detail and supported by simulations once the satellite design is in a more mature state, we outline here how this could in principle be achieved.

Gas–surface interactions are expected to depend on the atmospheric composition and temperature. Choices include the type of the reflection for incident molecules and atoms, which can be fully diffuse, specular, or quasi-specular [49], the energy accommodation of the incident molecules and atoms to the satellite surface, and the fraction of clean and adsorbate (atomic oxygen) covered surfaces [28]. For instance, the semiempirical model for satellite energy accommodation coefficients (SESAM; [37] describes the momentum exchange between incident gas molecules and atoms with the satellite surface as a function of the atmospheric temperature and the number density of atomic oxygen. Since atmospheric temperature and composition are variable with respect to local time, altitude, solar activity, etc., we expect that the energy accommodation coefficient will change significantly along the CASPA-ADM orbit and during its lifetime. Figure 10 shows how much the energy accommodation coefficient varies according to SESAM in the altitude range of 300–400 km for January 2002 and 2004, which we use as representative cases for solar maximum and medium activity conditions. To demonstrate the impact of the energy accommodation coefficient on the aerodynamic coefficient, we calculate the latter using Sentman’s equations [39] and the satellite geometry shown in Fig. 1, assuming zero attack and sideslip angles. The result obtained when using the SESAM model for the energy accommodation coefficient is shown Fig. 10 in the mid panel and the differences to the case of using a constant energy accommodation coefficient of 0.9 are displayed in the right panel. We can clearly see that the size of the difference in the aerodynamic coefficient is 0.3–1.0%, which will result in a corresponding density error according to Eq. (7).

Fig. 10
figure 10

Energy accommodation coefficient according to the SESAM model for January 2002 (solar maximum conditions) and 2004 (solar medium conditions) in the altitude range of 300–400 km (left), x-component of the aerodynamic coefficient vector calculated using Sentman’s equations and the SESAM energy accommodation coefficient for the satellite shown in Fig. 1 (mid), and the difference to the same, when replacing the variable energy accommodation coefficient by a constant αE = 0.9 (right). The dark colored lines are the minimum, mean, and maximum values, and the areas shaded in lighter colors indicate the range of values encountered from − 75° to + 75° latitude, in agreement with the inclination range for CASPA-ADM

Full size image

From the above discussion it is clear that thermosphere density observations derived from the CAI accelerometer measurements depend on the aerodynamic modelling and gas–surface interaction models. The neutral mass spectrometer provides measurements that allow the derivation of thermosphere density observations in a completely independent way. Thus, we consider a direct comparison of the CAI-derived density observations with the ones derived from the neutral mass spectrometer measurements as an excellent means to verify aerodynamic modelling and gas–surface interaction models, including the choices for the parameters that drive the models. Unfortunately, the accuracy of present-day neutral mass spectrometers is not well-known. However, we can conclude that an accuracy of 1% or better for thermosphere density observations from the neutral mass spectrometers should be sufficient to detect systematic differences with respect to the CAI-derived thermosphere density observations already after several orbits. For this reason, we specify 1% as the requirement for the accuracy of the thermosphere density observations from the neutral mass spectrometer as a goal. Assuming that a statistical analysis of the data from the entire 8–15 months of mission lifetime will average out random errors, we expect that also a lower accuracy will allow the verification of aerodynamic modelling and gas–surface interaction models. Therefore, we specify 5% as a threshold requirement for the accuracy of the thermosphere density observation from the neutral mass spectrometer, noting that these requirements need to be confirmed by simulations.

Another possibility to verify aerodynamic modelling and gas–surface interaction models is the comparison of thermosphere density observation from different missions. March et al. [25] present such an analysis for the CHAMP, GOCE, GRACE, and Swarm missions, demonstrating that a well-chosen constant energy accommodation coefficient gives the highest consistency between the missions, which leads to the conclusion that models for variable energy accommodation coefficients can still be improved. Depending on the launch date, we expect that either the GRACE-FO and Swarm satellites are still in orbit or future gravity satellites have been launched [26] and provide thermosphere density observations.

5.6 Summary of instrument requirements

In the previous sections we derived the signal range for the acceleration measurements and the required accuracy for the CAI accelerometer, star sensor, neutral mass spectrometer, and ram wind sensor. The GNSS receiver is assumed to be sufficiently accurate as long as it collects multi-frequency carrier phase measurements, so that ionospheric effects can be accounted for. An overview of the instrument requirements is presented in Table 3.

Table 3 Overview of instrument requirements
Full size table

6 Operational concept

Due to the power demand of the CAI accelerometer, it will not be possible to continuously operate the instrument. Depending on the available power and time needed to charge the batteries, we expect that it will be possible to collect acceleration measurements 1–4 times per day. Each time, the acceleration measurements will be collected uninterruptedly within 1.5 orbital revolutions, where half an orbital revolution is intended to avoid transients in the CAI measurements that may occur after powering the instrument, and one full orbital revolution is required to detect variations in thermosphere density, e.g. due to differences between the nightside and dayside of Earth. After operating the CAI accelerometer continuously for 1.5 orbital revolutions, the batteries will be depleted and need 3–14 orbital revolutions to recharge fully, depending on available power from the solar arrays, which in turn depends on the orbital configuration. Since the LTAN progression is on the order of a few degrees per day (confer Sect. 3), such an intermittent operation will have no impact on the coverage of local times. The CAI accelerometer could be operated continuously and also at a higher measurement rate if substantially more power was available, noting that the CAI accelerometer alone has then a power demand of about 100 W. Raising that much power can only be achieved by moving from a CubeSat to a larger platform, which would allow for much larger solar arrays and more capable batteries. Welcome side effects would be a longer mission lifetime due to the potentially larger ballistic coefficient and the possibility to implement a propulsion system. However, it is obvious that the costs for the mission would increase accordingly, which was the reason for not considering larger platforms in this study.

The other instruments have a much lower power demand and we expect that it will be possible to continuously operate them. This includes in particular the GNSS receiver and the neutral mass spectrometer, which both provide thermosphere density observations. Considering that the CAI accelerometer will operate a few times each day, it will be possible to intercalibrate and verify the measurements of these instruments frequently. We may therefore conclude that the intermittent operation of the CAI accelerometer will have only a very small impact on the scientific return of the mission.

In addition to the scientific objectives, the measurements of CASPA-ADM are expected to be useful for near real-time assimilation in thermosphere models. Some authors claim improvements of 20% in the accuracy of the thermosphere density [16], which is expected to significantly enhance the accuracy for operational orbit prediction and collision warning. This would require to transmit and process the data 1–2 times per day in an automated and robust way. The main limitation is the limited lifetime of CASPA-ADM, which is expected to be about 8–15 months.

7 Supplementary satellite characterization

Before the launch of the satellite, it is important to characterize the satellite as outlined in this section. Only then it will be possible to fully exploit the accuracy of the CAI accelerometer and obtain accurate density observations. This mean that we need to determine the exact size, shape and mass of the satellite and characterize the thermo-optical properties of materials that cover the outer surfaces. This will enable accurate modelling of the aerodynamic coefficient of the satellite in Eq. (7) and the radiation pressure acceleration in Eq. (4), which gives a more accurate aerodynamic acceleration and, consequently, more accurate observations of thermosphere density.

The data that is needed encompasses a CAD model of the satellite that specifies the exact geometry of the outer surfaces [22] and the materials that are used on each surface element. For each material, the coefficients of absorption, specular and diffuse reflection for visible (optical) wavelength and coefficients of absorption/emission in the infrared (thermal) wavelength need to be determined. Should aging effects change these coefficients, then this needs to be determined as well. In addition, temperature measurements need to be performed in flight, so that the radiation pressure acceleration due to re-emission of thermal energy can be accurately modelled [47, 50]. These temperature measurements can also be used to enhance the GSI modelling, where the energy exchange between incident molecules and the satellite depends to a small extent on the temperature of the satellite surfaces.

Other quantities that need to be known are the positions of the satellite center of mass, the GNSS antenna phase center, and the atom cloud. In addition, the orientation of the star cameras with respect to the satellite needs to be known. Which elements need to be characterized for the mass spectrometer and wind sensor is not clear at this stage of the study. It is nevertheless expected that also these instruments need a characterization on-ground.

8 Summary

The CASPA-ADM mission concept aims at filling the present gap in thermosphere density observations in the altitude range of 300–400 km, while providing a much faster local time sampling as opposed to the missions of opportunity. The lifetime of the CASPA-ADM mission is expected to be about 8–15 months, which is long enough for technology demonstration. The first science objective is the verification of gas–surface interaction models, which requires in-situ measurements of the acceleration together with measurements of atmospheric composition, temperature, and in-track wind. Any improvement of our aerodynamic modelling capabilities can then be retroactively applied to the CHAMP, GRACE, GRACE-FO, GOCE, and Swarm missions, which together collected more than 50 years’ worth of data.

Since it requires the same level of accuracy, we also added the observation of atmospheric waves to the scientific objectives of the CASPA-ADM mission. Combining the density observations with those of atmospheric composition and wind will enable more comprehensive analyses of the observable atmospheric waves. In particular the analysis of tidal atmospheric waves is expected to benefit from a fast local time sampling, which necessitates an inclined orbit. As a downside, this restricts the analysis to non-polar latitudes. Yet, there are many types of atmospheric waves that could be sensed by CASPA-ADM, namely: local time depending, migrating solar tide, nonmigrating tides, the equatorial density anomaly, atmospheric waves in response to geomagnetic activity, and secondary/tertiary atmospheric waves originating from the lower layers of the atmosphere. In view of the sampling defined by the orbit, the measurement rate, and the operational concept for the CAI accelerometer, we emphasize that observing all types of atmospheric waves is a very ambitious objective that needs further investigation. We propose to perform mission simulations to study which atmospheric waves will be observable by CASPA-ADM and how to discern them. Such simulations are complex (e.g., confer Annex A in [13] and, thence, beyond the scope of this paper.

The goal for the accuracy of the thermosphere density observations is one percent. The implications for the measurement concept and the satellite operations are discussed in Sect. 5. We address in particular the consequences of the one-axis acceleration and wind measurements for the density observations, and describe how to operate the satellite and process the measurements to reach the required accuracy. In addition, we investigated the required accuracy of atmospheric composition and temperature observations. For the target altitude range of 300–400 km, we find that composition errors of 10% and temperature errors of 3% result in density errors of less than 1%, which is acceptable.

Finally, we note that we expect that the CASPA-ADM mission could be launched in mid-2020s to late 2020s should the required funding be available. Though several studies are running in parallel to advance and develop the relevant technology, the implementation of the mission is presently not funded.